Sesto foglio di esercizi di Algebra

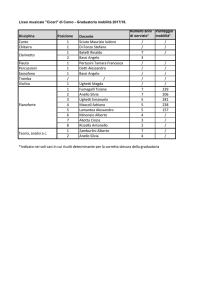
Sesto foglio di esercizi di Algebra
Esercizio 1. Sia G un gruppo abeliano in notazione additiva e sia End(G) l’insieme degli
endomorfismi di G (i.e. End(G) è l’insieme degli omomorfismi da G in G). Provare che End(G)
è un anello dove per ogni f, g ∈ End(G) definiamo f + g e f g ponendo
(f + g)(x) = f (x) + g(x)
e
(f g)(x) = f (g(x))
per ogni x ∈ G. Mostrare in particolare che, per f, g ∈ End(G), f + g e f g sono ancora in
End(G), notando che l’ipotesi che G sia abeliano è cruciale.
Esercizio 2. Mostrare che l’insieme
Z[i] = {m + ni : m, n ∈ Z, i2 = −1}
è un sottoanello di C. (L’anello Z[i] si dice anello degli interi di Gauss). Mostrare che
Q[i] = {a + bi : a, b ∈ Q, i2 = −1}
è un sottocampo di C.
Esercizio 3. Mostrare che l’insieme
√
√
Z[ 2] = {m + n 2 : m, n ∈ Z}
è un sottoanello di R. Mostrare che
√
√
Q[ 2] = {a + b 2 : a, b ∈ Q}
è un sottocampo di R.
Esercizio 4. Sia X un insieme non vuoto e P (X) l’insieme delle parti di X. Provare che P (X)
è un anello con operazione somma la differenza simmetrica ∆ e operazione prodotto l’intersezione
∩ tra insiemi (ricordiamo che, dati A, B insiemi, la differenza simmetrica tra A e B è definita
da A∆B = (A ∪ B) \ (A ∩ B). In particolare risulta 0P (X) = ∅ e 1P (X) = X.
Esercizio 5. Sia A l’anello
a 0
A=
: a, b, c ∈ Z
b c
rispetto a somma e prodotto di matrici. Si determinino gli elementi unitari e i divisori dello zero
di A.
Esercizio 6. Un elemento e di un anello A si dice idempotente se e2 = e. In ogni anello 0 e 1
sono idempotenti. Se A è un dominio di integrità allora 0 e 1 sono gli unici elementi idempotenti
(perchè?). Mostrare che se A è un anello in cui ogni elemento è idempotente, allora 1A = −1A
e A è commutativo.
Esercizio 7. Un elemento a di un anello A si dice nilpotente se esiste n ≥ 1 (che, in generale
dipende da a) tale che an = 0. Mostrare che se a è un elemento nilpotente, allora 1 − a è
unitario.
1
2
Esercizio 8. Sia RR l’insieme delle funzioni da R in R. Mostrare che RR è un anello dove per
ogni f, g ∈ RR definiamo f + g e f g ponendo
(f + g)(x) = f (x) + g(x)
e
(f g)(x) = f (x)g(x)
per ogni x ∈ R. Per a ∈ R sia I l’insieme
I = {f ∈ RR : f (a) = 0}
Provare che I è un ideale principale e massimale di RR .
Esercizio 9. Sia RR l’anello delle funzioni da R in R definito nell’esercizio precedente. Sia I
l’insieme
I = {f ∈ RR | ∃ af ∈ R : f (x) = 0, ∀x ≥ af }
Provare che I è un ideale non principale di RR .
Esercizio 10. Provare che il coniugio σ : C → C, che ad ogni a+ib ∈ C associa σ(a+ib) = a−ib
è un automorfismo del campo C.
Esercizio 11. Siano ϕ, ψ : R → M at(2, R), le applicazioni definite da
a 0
a 0
ϕ(a) =
, e ψ(a) =
,
0 a
0 0
per ogni a ∈ R. Provare che ϕ è un omomorfismo di anelli mentre ψ non lo è.
Esercizio 12. Sia a ∈ R. Provare che l’applicazione sostituzione σa : RR → R definita da
σa (f ) = f (a) è un omomorfismo di anelli. Determinarne il nucleo.
Esercizio 13. Sia A un anello commutativo e sia I A. Sia a ∈ A, si provi che l’insieme
NI (a) = {x ∈ A | xa ∈ I}
è un ideale di A. Come caso particolare, quando I = {0} si ha che
N (a) = {x ∈ A | xa = 0}
è un ideale di A.
Esercizio 14. Sia A un anello commutativo e sia I = {x ∈ A | x non è unitario}. Si provi che
sono equivalenti
(1) I è un ideale di A;
(2) esiste un ideale proprio di A che contiene tutti gli ideali propri di A.
(Sugg.: l’ideale proprio di A che contiene tutti gli ideali propri di A è I stesso)
Esercizio 15. Siano I, L e K ideali di un anello A tali che I + L = A e L ∩ K ⊆ I. Provare
che K ⊆ I.
(Sugg.: poichè I + L = A esistono x ∈ I e y ∈ L tali che 1 = x + y. Per a ∈ K osservare che
a − xa = ya ∈ K ∩ L)
3
Esercizio 16. Sia A l’insieme
A=
a
−b
b
: a, b ∈ R .
a
(1) Provare che A è un sottoanello di M at(2, R).
(2) Provare che l’applicazione ϕ : A → C definita da
a b
ϕ
= a + ib
−b a
è un isomorfismo di anelli.
Esercizio 17. Sia A un anello commutativo. Provare, per induzione su n, che per ogni a, b ∈ A
e per ogni n ∈ N vale la formula del binomio di Newton
n X
n k n−k
n
(a + b) =
a b
.
k
k=0
Esercizio 18. Sia A un anello commutativo e sia I = {x ∈ A | x non è unitario}. Si provi che
sono equivalenti
(1) I è un ideale di A;
(2) per ogni a ∈ A o a è unitario oppure 1 − a è unitario.