PROBLEMA 11
SIA DATO UN SOLENOIDE RETTILINEO DI LUNGHEZZA d, RAGGIO R e COSTITUITO
DA N SPIRE.
A) DETERMINARE IL CAMPO MAGNETICO PRODOTTO LUNGO L’ASSE DEL
SOLENOIDE.
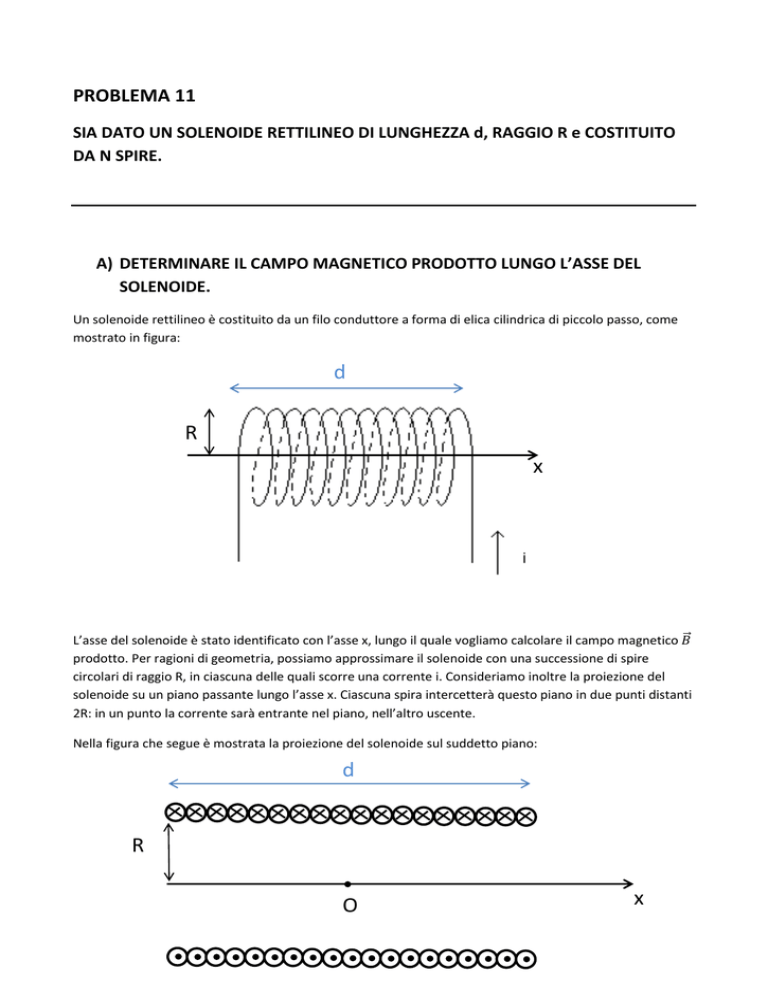
Un solenoide rettilineo è costituito da un filo conduttore a forma di elica cilindrica di piccolo passo, come
mostrato in figura:
d
R
x
L’asse del solenoide è stato identificato con l’asse x, lungo il quale vogliamo calcolare il campo magnetico ⃗
prodotto. Per ragioni di geometria, possiamo approssimare il solenoide con una successione di spire
circolari di raggio R, in ciascuna delle quali scorre una corrente i. Consideriamo inoltre la proiezione del
solenoide su un piano passante lungo l’asse x. Ciascuna spira intercetterà questo piano in due punti distanti
2R: in un punto la corrente sarà entrante nel piano, nell’altro uscente.
Nella figura che segue è mostrata la proiezione del solenoide sul suddetto piano:
d
R
O
x
Il punto O in figura è il centro del solenoide sull’asse.
Introduciamo la densità lineare n di spire, definita come il numero di spire per unità lunghezza. Poiché
lungo tutto il solenoide ci sono N spire, allora la densità di spire n sarà:
Vogliamo determinare il campo magnetico ⃗ in un punto generico dell’asse.
Dalla teoria è noto che data una spira circolare attraversata da una corrente i e di raggio R, il campo
magnetico ⃗ prodotto in un punto P sull’asse della spira, distante r dalla spira stessa, è pari a:
⃗
̂
(1)
r
𝑖
R
O
𝑢
̂𝑛
P
Il campo magnetico nei punti dell’asse è diretto sempre parallelamente all’asse. Poiché non cambia mai
direzione, possiamo passare ad una trattazione scalare del problema.
Nel caso del solenoide, consideriamo un elemento infinitesimo di lunghezza dx del solenoide e un generico
punto P sull’asse. Vogliamo determinare inizialmente il campo magnetico infinitesimo dB prodotto da dx
nel punto P dell’asse. All’interno dell’elemento di lunghezza dx ci sono ndx spire (in quanto n è la densità
lineare di spire) e in ciascuna delle quali scorre una corrente i: quindi il campo magnetico dB sarà pari a,
utilizzando la (1):
(2)
In figura è mostrata la situazione creata:
d
dx
r
R
P
φ
x
x
x0
O
Il campo magnetico nel punto P sarà la somma di tutti i contributi di tipo (2) dati da tutti gli elementi dx che
compongono il solenoide, ovvero un’integrazione. D’altronde al variare di dx, varia anche r. Dobbiamo
cercare di ricondurre la (2) ad un’unica variabile, in modo da poter integrare più facilmente.
Consideriamo il triangolo rettangolo di lati R, r e
.
Dalla trigonometria è noto che:
(3)
e
Differenziando ambo i membri di quest’ultima, si ottiene (ricordando che
)
(4)
Inserendo la (3) e la (4) nella (2), si ottiene:
Siamo riusciti ad ottenere un’espressione per dB che dipenda da una sola variabile, l’angolo φ. Per
determinare il campo magnetico B nel punto P, possiamo integrare l’espressione appena trovata per dB, tra
l’angolo φ1e l’angolo φ2. Qquesti ultimi, assieme all’angolo φ’2 sono mostrati in figura:
d
φ2
R
P
φ1
x
φ'2
x
x0
O
(
∫
)
Dalla figura si evince che:
e quindi:
(
)
Sostituendo nell’espressione appena trovata per B si ha:
(
)
(5)
Cerchiamo ora di esprimere questo risultato in termini della distanza di P da O. Detta x la distanza di P da O,
e considerando le notazioni introdotte nella figura che segue:
d
r1
R
P
φ1
d/2
O
h1
x
x0
φ'2
x
(6)
Dalla figura si evince che:
e usando il teorema di Pitagora:
( )
√
√
(
)
Inserendo questi ultimi due risultati nella (6) si ha:
√
Stesso discorso per l’angolo
(
)
(
√
(7)
)
. Utilizzando la notazione introdotta nella figura che segue:
d
r2
P
φ1
x
O
x0
R
φ'2
x
d/2
h2
(8)
Dalla figura si evince che:
e usando il teorema di Pitagora:
√
(
Inserendo questi ultimi due risultati nella (8) si ha:
)
√
(
)
√
(
)
(
√
(9)
)
Inseriamo ora la (7) e la (9) nella (5). Si ottiene:
(
)
(
(
√
)
(
√
)
)
Al centro del solenoide, ovvero quando x = 0, il campo magnetico sarà:
(
√
)
(
√
)
Se supponiamo che il solenoide siamo molto lungo e molto stretto, ovvero ci mettiamo
nell’approssimazione di d >> R, nell’ultima espressione trovata possiamo trascurare al denominatore
rispetto a
(in quanto quest’ultimo molto più grande) e si ottiene:
(
√
)
In definitiva, per un solenoide molto lungo e raggio molto piccolo, il campo magnetico al centro di esso è
costante e dipende esclusivamente dalla densità n di spire e dalla corrente i che l’attraversa.












