alimentatori switching

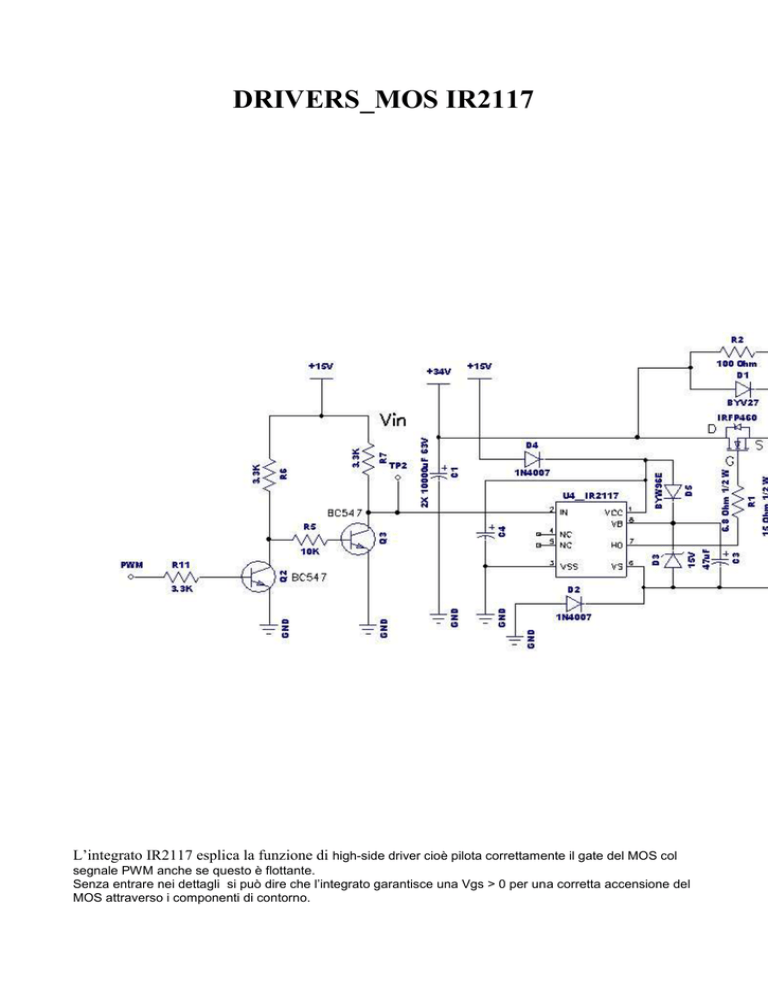
DRIVERS_MOS IR2117
L’integrato IR2117 esplica la funzione di high-side driver cioè pilota correttamente il gate del MOS col
segnale PWM anche se questo è flottante.
Senza entrare nei dettagli si può dire che l’integrato garantisce una Vgs > 0 per una corretta accensione del
MOS attraverso i componenti di contorno.
Il diodo D5 impedisce agli spike negativi di influenzare il normale funzionamento dell’integrato; il
condensatore C3 inizialmente scarico ,si carica attraverso R3,L1,C5,C6.
Il diodo zener D3 da 15V in parallelo al condensatore di bootstrap garantisce che la tensione non superi il
limite di 15V.Il segnale PWM proveniente dal microcontrollore viene
applicato ai 2 transistor BC547 che aumentano l’ampiezza, portandola da 5V a 15V.La rete snubber formata
da R2,D1,C2 protegge il MOS nelle fasi di accensione e spegnimento
dello stesso. Bisogna fare in modo che la dVDS/dt durante lo spegnimento del mos non superi quella fornita
dal costruttore per non distruggere il dispositivo;mentre in accensione bisogna limitare la corrente di drain
dovuta alla scarica del condensatore per salvaguardare la giunzione .
Perciò durante lo spegnimento per avere un dVDS/dt piccolo il condensatore deve caricarsi subito; mentre
durante l’accensione deve scaricarsi lentamente attraverso la resistenza
snubber.Le formule per il calcolo di C2 ed R2 sono funzione della frequenza di switching ( 40KHZ ), della
corrente max Iout, e del tempo Tfall del MOS che si può ricercare nelle caratteristiche
del dispositivo.In questo caso per il MOS IRFP460 Tfall =58 nS.
Csnubber = Ion * tfall / 2Voff = 10 A * 58 *10^-9 S / 2* 34V ~ 8.5 nF .Sperimentalmente i risultati migliori gli
ho ottenuti con 22nF.
Rsnubber = D* Tsw/2 * Csnubber= 0.353 * 2.5 ^ -5 / 2 * 10 nF ~ 441Ohm . il valore 0.353 ( D = 35.5 % ) è il
Duty Cicle che permette di avere circa 12V partendo da 34V.
Sperimentalmente il valore migliore però è risultato pari a circa 100 Ohm.
Ricordo infatti che negli alimentatori Buck si ha: Vout = Vi * D con D = Ton / T
Per il diodo ho scelto uno veloce tipo BYV 27
Per dimensionare L bisogna conoscere i seguenti parametri:
• Massima tensione in ingresso
• Tensione d’uscita
• Frequenza di Switching
• Massimo ripple di corrente
• Duty cycle .
Scegliendo un ripple di corrente pari a 1A e ipotizzando che
Vi = Vi ± 20%
Frequenza switching = 40 KHZ
δmin = Vo/ Vimax=12V/40,8V=0.294
δmax = Vo/ Vimin=12V/27,2=0,442
L= ( Vimax –Vo) * δmin / Fsw * ΔI = (40,8 – 12) * 0,294 / 40 *10 ^3 *1= ~ 212 uH.
Scelgo L=250uH.Per il calcolo della C si sceglie una frequenza di risonanza pari ad almeno 1/10 di quella
di commutazione;
si sceglie 4Khz . Dalla formula della frequenza di risonanza
f = 1/ 2π √(LC) da cui C=1/( 2π f)^2 *L = 1/4 * 9,86 *16*10^ 6* 250 * 10^ - 6 = ~ 6.3uF.
Per migliore il ripple di tensione ho aggiunto poi aumentato la capacità complessiva portandola a 320uF.
Le 2 resistenze di 220 Ohm sono di “zavorra”. La scelta del MOS e del diodo Schottky deve essere
ragionevole; la corrente del mos deve essere almeno di 20 A e la tensione di lavoro almeno 200V.
Per il diodo la corrente diretta superiore a 25A mentre la tensione inversa almeno di 100V. i componenti
scelti
da me rispettano queste caratteristiche anche se sono componenti che possedevo già.
Il mos e il diodo Schottky sono montati su un dissipatore generoso ma è possibile ridurre le dimensioni (
durante le prove a 5 A
era completamente gelato! ).
Per una maggiore comprensione potete leggere anche il seguente articolo teorico “spulciato” su internet.
ALIMENTATORI SWITCHING
Costituiscono l’altra categoria dei convertitori CC/CC impiegati per le applicazioni di piccola po_
tenza ( 10  100 Watt ) e, più in particolare, per l’alimentazione di carichi passivi prevalentemente
resistivi, quali quelli appartenenti all’elettronica di consumo ( computer, stereo, TV, e così via ).
Sono degli ottimi stabilizzatori di tensione, cioè presentano una tensione v0 in uscita abbastanza
costante, e a seconda che questa tensione sia minore o maggiore di quella in ingresso si dividono in
due categorie :
-
alimentatori switching abbassatori o tipo BUCK
alimentatori switching elevatori o tipo BOOST
ALIMENTATORI SWITCHING ABBASSATORI
Uno schema di alimentatore switching abbassatore è il seguente :
vCE
is
C
iL
E
Q
L
vL
K
B
i0
iC
IB
V
vAK
D
C
vC
v0
zR
A
in cui l’induttanza va a spianare la forma d’onda della corrente che altrimenti risulterebbe molto
ondulata ( carico resistivo ), mentre la capacità funge da stabilizzatore della tensione in uscita v0 .
Le frequenze di commutazione di questo circuito sono elevate, dell’ordine dei 10  100 kHz ; ciò
ci consentirà di linearizzare la forma d’onda della corrente i0 .
Facciamo cominciare la nostra analisi da una condizione circuitale in cui il circuito è spento ; in
questa situazione non circola corrente nel circuito, la capacità e l’induttanza sono scariche, il
diodo interdetto ed il transistor polarizzato direttamente :
vCE = V
tuttavia spento ( non c’è segnale di pilotaggio alla sua base ).
Supponiamo che all’istante t = 0 venga applicato il segnale di pilotaggio alla base di Q : il
componente passa a condurre in quanto polarizzato direttamente.
A partire da tale istante, il diodo risulta contropolarizzato ( vAK = - V ) e la corrente assorbita dalla
rete va a caricare l’induttanza e a dividersi in parte nel carico, in parte nella capacità.
La carica dell’induttanza dura per un intervallo di tempo molto breve ( elevate frequenze di commutazione ) arrestandosi al termine del tratto lineare della curva di carica ; per questo motivo possiamo
supporre lineare l’andamento della corrente di carica.
Al termine di un piccolo ton quindi, viene annullato il segnale alla base di Q , causando lo spegni_
mento del componente.
A partire dall’istante di spegnimento di Q , la scarica dell’induttanza mantiene la circolazione di
corrente nel carico grazie alla via di richiusura offerta dal diodo che, nel contempo, si è acceso,
mentre la capacità tende a mantenere costante la tensione sul carico al valore che aveva nell’istante
in cui è avvenuta la commutazione del transistor.
Per le stesse ragioni viste per la corrente di carica, anche l’andamento di quella di scarica si può
approssimare a lineare.
Il ciclo riprende nell’istante in cui il transistor commuta nuovamente su ON , e si ripete identico a
quello descritto.
Le grandezze elettriche descritte hanno quindi i seguenti andamenti a regime :
iB
toff
ton
t
T
iL
Imax
Imin
t
0
v0
KV
t
vAK
t
-V
vCE
V
t
Per renderci conto dell’andamento di v0 , valutiamone l’espressione analitica ; a tale scopo ingigan
tiamo l’andamento della iL in un periodo :
iL
Imax
iL/( t )
iL( t )
Imin
t
t
0
t
ton
toff
T
0  t  ton
:
Q On
 vCE  0
;
 D Off
vAK = - V
V = vCE + vL + vC  vL + vC = vL + v0
da cui :
v0 = V – vL = V - L d iL
dt
Osserviamo che é :
iL( t ) = Imin + iL( t )
e che :
Imax – Imin : iL( t ) = ton : t

iL( t ) = ( Imax – Imin ) t = I t
ton
ton
da cui si ricava :
iL( t ) = Imin + I t
ton

d iL = I = cost
dt
ton
Si ha dunque :
v0 = V - L I = V01
ton
ton  t  T

Q Off , D On

vAK  0
0  t  ton
vCE = V
V = vCE + vL + vC = V + vL + vC = V + vL + v0
da cui :
v0 = - vL = - L d iL
dt
Osserviamo che è :
iL( t ) = Imax - iL/ ( t )
e che :
Imax – Imin : iL/ ( t ) = T - ton : t - ton
da cui :
iL/ ( t ) = ( Imax – Imin )( t - ton ) = I t - ton
T - ton
T - ton
e quindi :
iL( t ) = Imax - iL/ ( t )

iL( t ) = Imax - I t - ton
T - ton
La derivata di iL( t ) è pertanto data da :
d iL = - I = cost
dt
T - ton
e in definitiva si ha :
v0 = - vL = - L d iL =
dt
L I = V02
T - ton
ton  t  T
Poichè ai capi di una capacità la tensione non può variare con discontinuità, deve essere :

v0( ton- ) = v0( ton+ )
V01 = V02
e quindi :
V - L I = L I
ton
T - ton
da cui possiamo ricavare I :
V = L I
T - ton
+ L I
ton

V = I [ ton + T - ton ] = I
T
.
L
( T - ton ) ton
( T - ton ) ton
I = V ton ( T - ton )
L T
e di qui la tensione v0 :
v0 = V01 = V02 = L I = L . V ton ( T - ton )
T - ton
T - ton L T
v0 = ton V
T
che è costante.
Posto K = ton / T = duty cycle si ha :
v0 = KV
dove K è un numero positivo minore di uno, per cui in uscita al circuito abbiamo una tensione
costante di valore minore rispetto all’ingresso ( circuito abbassatore ).
Vedremo fra poco come questa conclusione circa la tensione v0 non è vera, cioè la tensione ai capi
della capacità non è costante ma possiede una certa ondulazione ; ciò emerge dal calcolo con cui si
va a dimensionare il flitro L - C presente nel circuito.
Il calcolo dell’induttanza L è presto fatto, infatti dall’equazione di I :
I = V ton ( T - ton ) = V K T ( 1 – K ) = V K ( 1 – K )
L T
L
L f
si ottiene subito :
L = V K(1–K)
I f
relazione che lega l’induttanza L al ripple di corrente I ed alla frequenza f .
Emerge allora che, più piccolo è il ripple di corrente richiesto, maggiore deve essere l’induttanza .
Non è comunque possibile scegliere una induttanza grande a piacere ; la sua scelta nasce da due
esigenze contrastanti : quella di ridurre il più possibile il ripple e quella, non meno importante, di
ridurre l’ingombro creato dalla bobina.
Per il resto, il ripple di corrente può essere ridotto anche aumentando la frequenza di commutazione.
Per quanto riguarda il dimensionamento della capacità, osserviamo che si ha :
iL = iC + i0 = iC + I0
in cui abbiamo supposto costante la corrente nel carico ; ciò è lecito in quanto il carico è prevalentemente resistivo e sottoposto ad una tensione v0 costante.
Calcolando il valore medio di ambo i membri della relazione sulle correnti :
ILm = 1  iC dt + I0 = 1  C d vC dt + I0 = C  dvC + I0 = C  dv0 + I0
T( T )
T ( T ) dt
T ( T )
T ( T )
si ricava ILm = I0 , in quanto dv0 = 0 ( v0 = KV = costante ).
Con buona approssimazione inoltre, possiamo porre :
ILm = Imax + Imin = I0
2
In questo modo possiamo subito disegnare l’andamento di iC = iL – I0 = iL – ILm :
iB
toff
ton
t
T
iL
Imax
Imin
iC
ILm
t
I
2
- I
2
t
Noto l’andamento della iC , possiamo risalire a quello della vC = v0 tramite la relazione :
vC = 1  iC dt
C
da cui si deduce che la tensione vC = v0 ai capi della capacità e del carico non può essere costante;
infatti se iC ha andamento ondulatorio con i tratti lineari ( iC  t ) , anche vC ha andamento
ondulatorio con tratti proporzionali a t 2 :
iB
toff
ton
t
T
iC
I
2
C
A
- I
2
t
B
vC = v0
v0
KV
t
Scopo della capacità è quello di agire da stabilizzatore della tensione sul carico, e quindi di ridurre il
ripple di tensione v0 ; quest’ultimo si può esprimere in funzione di C :
v0 = Q
C
dove è :
Q =  iC dt = area del triangolo ABC
ABC
e quindi :
Q = 1 ( ton + toff ) I = 1 I ( ton + toff ) = 1 I T = I
2 2
2 2
8
8
8f
Essendo :
I = V K ( 1 – K )
L f
la carica Q può essere così espressa :
Q = V 1 K( 1 – K )
8f 2 L
e quindi il ripple di tensione è dato da :
v0 = Q = V 1 K( 1 – K )
C
8f 2 LC
da cui si ricava l’equazione di progetto della capacità :
C = V 1 1 K( 1 – K )
8f 2 L v0
e da cui si evinde che per ridurre il ripple di tensione v0 , e quindi per stabilizzare il più possibile la
tensione v0 , occorre aumentare la capacità .
Anche in questo caso non è possibile scegliere una capacità grande a piacere ; la sua scelta nasce da
due esigenze contrastanti : quella di stabilizzare il più possibile la tensione v0 e quella, non meno
importante, di ridurre l’ingombro creato dal condensatore.
Per il resto, il ripple di tensione può essere ridotto anche aumentando la frequenza di commutazione,
e a maggior ragione in questo caso, visto che v0 è proporzionale a 1 / f 2 .
Alla luce di quanto detto allora, ci rendiamo conto che l’espressione precedentemente ricavata per la
tensione :
v0 = ton V = KV
T
è in realtà un valore medio Vm , intorno al quale oscilla la tensione v0 .
Il valore medio Vm viene regolato agendo su ton ; tuttavia nel funzionamento del circuito da
stabilizzatore è necessario che Vm si mantenga costante nel tempo, e poichè la tensione V in
ingresso è soggetta a variazioni, occorre che ton venga regolato di volta in volta, in modo che il
prodotto ton V resti costantemente uguale al valore impostato, fermo restando il valore di T.
Ciò si realizza con un controllo in retroazione avente il seguente schema :
vCE
is
C
iL
E
Q
L
vL
K
B
vAK
D
V
i0
iC
IB
C
vC
v0
zR
A
DRIVER
ton
REGOLATORE
V0
KvV0
+
-
KvV0*
in cui il valore di riferimento KvV0* viene confrontato con quello prelevato all’uscita tramite un
partitore, e dando luogo, nel caso in cui il confronto produce un segnale di errore V0 , all’azione
del regolatore ( PI ) che va a regolare opportunamente ton in modo che l’uscita torni al valore di
riferimento.
ALIMENTATORI SWITCHING ELEVATORI
Uno schema di alimentatore switching elevatore è il seguente :
D
L
iL
K
A
vL
vAK
i0
iC
C
Q
vCE
V
B
IB
C
vC
zR
v0
E
Partiamo da una condizione di circuito inerte, in cui non c’è alimentazione ( la tensione in ingresso
è nulla ) e gli elementi conservativi sono scarichi.
Supponiamo che all’istante t = 0 venga applicata la tensione V in ingresso e contemporaneamente
inviato il segnale di pilotaggio alla base del transistor, che si accende in quanto polarizzato diretta_
mente ; il diodo è polarizzato inversamente in t = 0 ( l’anodo si trova a - V ) e la corrente passa
tutta in Q.
Per tutto il tempo ton durante il quale Q è acceso quindi, l’alimentazione è cortocircuitata e la
corrente circolante iL carica l’induttanza ; anche in questo caso, date le elevate frequenze di com_
mutazione, l’andamento della corrente di carica può approssimarsi lineare, in quanto abbiamo
ragione di credere che la carica si arresti al tratto lineare della curva di carica.
Terminato ton , il segnale alla base di Q viene annullato e l’induttanza si scarica attraverso D
nella maglia più esterna, dove la corrente di scarica si divide in due parti, una che alimenta il carico,
l’altra che carica la capacita C ; tutto ciò per tutto il tempo toff in cui Q è spento.
Rinnovato il segnale alla base di Q, segue una nuova fase di carica di L, mentre il diodo si è nuova
mente interdetto ed il carico viene alimentato dalla scarica della capacità ; scopo del diodo è quello
di impedire che la corrente di scarica del condensatore vada ad interessare la maglia a monte di esso.
Il funzionamento del circuito si ripete poi ciclicamente, alternando fasi di carica e scarica di L e di
C , complementari tra loro.
Possiamo allora disegnare l’andamento della corrente iL :
iB
toff
ton
t
0
T
iL
Imax
Imin
0
I
t
supposto appunto lineare sia nella fase di carica che in quella di scarica :
iL( t ) = Imin + I t
ton
0  t  ton
iL( t ) = Imax - I t - ton
T - ton
ton  t  T
dove il ripple di corrente I lo possiamo calcolare facendo riferimento alla maglia attiva per
0  t  ton :
V = vL = L d iL = L I 
I = V ton
dt
ton
L
Il fatto di aver supposto lineare l’andamento della iL ha come conseguenza che la tensione vL sia
costante :
vL = Ld iL = I
0  t  ton
dt
ton
vL = Ld iL = - L I
dt
T - ton
ton  t  T
e che quindi lo sia anche la tensione v0 sul carico ; difatti per ton  t  T possiamo scrivere :
V = vL + vAK + v0  vL + v0
ton  t  T
da cui :
V = - LI + v0 = - V Lton + v0 = - Vton + v0
T - ton
L T - ton
T - ton
e quindi :
v0 =
Vton + V = V ( ton + T - ton ) = V T
T - ton
T - ton
T - ton
che possiamo scrivere :
ton  t  T
v0 = V 1
1–K
introducendo ancora una volta il duty cycle K = ton / T .
Osserviamo comunque che questa espressione della tensione v0 = vC è valida anche per 0  t  ton ;
infatti poichè la tensione vC non può variare con discontinuità, deve essere :
vC( ton- ) = vC( ton+ ) = V 1
1–K
e
vC( T + ) = vC( T - ) = V
1
1–K
cioè all’inizio ed alla fine dell’intervallo di tempo in cui Q è acceso la tensione vC ai capi della
capacità assume lo stesso valore, pari a V / ( 1 – K ) ; l’unico modo che ciò sia possibile è che sia
vC = V / ( 1 – K ) per ogni 0  t  ton .
In altre parole la tensione v0 ai capi del carico è costante durante tutto il periodo T ed è pari a :
v0 = V 1
1–K
In realtà sappiamo bene che la tensione vC non può essere costante, in quanto il condensatore si
carica e si scarica, per cui essa ha andamento ondulatorio, così come ondulatorio è in realtà l’anda_
mento di v0 , sicchè il valore trovato per la tensione sul carico è in realtà un valore medio Vm.
Esiste quindi anche un ripple di tensione v0 e si possono fare le stesse considerazioni fatte per
il circuito abbassatore, circa il dimensionamento del filtro L C .
Essendo 0  K  1 si ha v0 > V, cioè la tensione in uscita al circuito è sempre maggiore di quella
in ingresso ; possiamo diagrammare la v0 in funzione di K :
v0 / V
1
1
K
da cui si nota che il guadagno in tensione v0 / V cresce all’aumentare di K è diventa infinito per
K = 1 ; in realtà il guadagno v0 / V non cresce oltre un certo massimo, raggiunto il quale comincia
a decrescere a causa delle perdite interne.
Il valore medio Vm viene regolato agendo su ton ; tuttavia nel funzionamento del circuito da
stabilizzatore è necessario che Vm si mantenga costante nel tempo, e poichè la tensione V in
ingresso è soggetta a variazioni, occorre che ton venga regolato di volta in volta, fermo restando il
valore di T.
Ciò si realizza con un controllo in retroazione avente lo stesso schema visto per il circuito abbassa_
tore.