Le orbite: applicazioni
M.C Falvella, Agenzia Spaziale Italiana -
Corso di Metodi per l'Astrofisica Spaziale A.A. 2005-2006
In base all'energia posseduta dal corpo le orbite possono
essere chiuse e periodiche oppure aperte e non
periodiche, in quest’ultimo caso si parla più propriamente
di traiettorie:
•Orbita ellittica: l'orbita è chiusa ed è un ellisse se
l'energia totale E del corpo è minore di zero (ovvero se
l'energia cinetica è minore dell'energia potenziale). Sono
ellittiche le orbite dei pianeti del sistema solare e di
tutti i loro satelliti.
M.C Falvella, Agenzia Spaziale Italiana -
Corso di Metodi per l'Astrofisica Spaziale A.A. 2005-2006
In astronomia, un'orbita è la traiettoria di un corpo celeste,
di un satellite artificiale o di un veicolo spaziale, nello
spazio, dove in genere è presente il campo gravitazionale
generato da un altro corpo celeste.
In principio, imprimendo ad un satellite un’opportuna
velocità, è possibile ottenere qualunque orbita e raggiungere
qualunque punto nello spazio. In pratica ogni satellite viene
portato nell’orbita migliore per portare a termine la sua
missione ottimizzando il consumo di carburante e i tempi di
percorrenza.
M.C Falvella, Agenzia Spaziale Italiana -
Corso di Metodi per l'Astrofisica Spaziale A.A. 2005-2006
•Traiettoria iperbolica: l'orbita è aperta ed è un iperbole
se l'energia totale E del corpo è maggiore di zero (ovvero
se l'energia cinetica è maggiore dell'energia potenziale).
Sono iperboliche le orbite delle sonde spaziali inviate al
di fuori del sistema solare.
•Traiettoria parabolica: da un punto di vista teorico
occorre inoltre aggiungere che se E=0, l'orbita risulterà
una parabola; tale orbita rappresenta l'elemento di
separazione tra la famiglia di orbite chiuse e di orbite
aperte.
M.C Falvella, Agenzia Spaziale Italiana -
Corso di Metodi per l'Astrofisica Spaziale A.A. 2005-2006
In base all'inclinazione, un’ orbita può essere:
• equatoriale: se l'inclinazione è circa zero (ad
esempio tutte le orbite geostazionarie)
• polare: se l'inclinazione è quasi uguale a 90°
•eclittica: se l'inclinazione dell'orbita coincide
con l'eclittica del pianeta
In base all'altitudine si parla di:
•Low Earth Orbit, nel caso di orbite comprese tra
400 e 600 Km
•Medium Earth Orbit: nel caso di orbite
comprese tra 600 e 30000 Km
•High Earth Orbit, nel caso di orbite sopra i
30.000 Km
M.C Falvella, Agenzia Spaziale Italiana -
Corso di Metodi per l'Astrofisica Spaziale A.A. 2005-2006
M.C Falvella, Agenzia Spaziale Italiana -
Corso di Metodi per l'Astrofisica Spaziale A.A. 2005-2006
1
Orbita ellittica intorno alla terra con perigeo a 630 km e apogeo a 11650 km dalla superficie terrestre
M.C Falvella, Agenzia Spaziale Italiana -
Corso di Metodi per l'Astrofisica Spaziale A.A. 2005-2006
Orbita iperbolica intorno alla terra con perigeo a 5275 km dalla superficie terrestre.
M.C Falvella, Agenzia Spaziale Italiana -
Corso di Metodi per l'Astrofisica Spaziale A.A. 2005-2006
I satelliti di osservazione della Terra, ad esempio,
vengono di solito messi in orbite circolari basse (4001.000 km). Questo permette loro di compiere un giro
intorno alla Terra in poche ore e di ricavare immagini
dettagliate della superficie del pianeta.
Il percorso migliore per questi satelliti è un'orbita
'polare', che li porta sopra il polo nord ed il polo sud.
Poiché la Terra ruota sotto di loro, i satelliti possono
osservarla direttamente e studiare l'intero pianeta – una
striscia dopo l'altra - in pochi giorni.
M.C Falvella, Agenzia Spaziale Italiana -
Corso di Metodi per l'Astrofisica Spaziale A.A. 2005-2006
I satelliti metereologici e per le comunicazioni spesso
sorvolano la stessa parte della Terra per 24 ore al
giorno con orbite geosincrone.
Le orbite geosincrone sono caratterizzate dall’avere
lo stesso periodo di rotazione della Terra ( circa 24h,
86400sec).
Un satellite in orbita geosincrona passa sopra lo
stesso punto della superficie terrestre ogni 24 ore.
Se l’orbita è anche equatoriale, il satellite resta
sempre sullo stesso punto della superficie terrestre
(orbita geostazionaria).
M.C Falvella, Agenzia Spaziale Italiana -
Corso di Metodi per l'Astrofisica Spaziale A.A. 2005-2006
M.C Falvella, Agenzia Spaziale Italiana -
Corso di Metodi per l'Astrofisica Spaziale A.A. 2005-2006
Velocità orbitale in un'orbita circolare terrestre
Consideriamo un corpo di massa m che si muove su un'orbita
circolare ad una distanza r dal centro della terra (ovvero ad
una quota h = r - RT, dove RT è il raggio della terra).
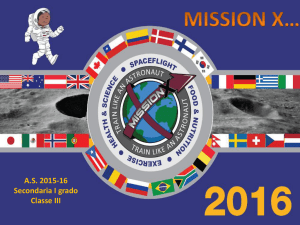
Tale corpo è soggetto alla forza di gravità
essendo G = 6.672 × 10 N (m/kg)² è la costante di
24
gravitazione universale e M = 5,9736 10 kg la massa
della terra.
11
M.C Falvella, Agenzia Spaziale Italiana -
Corso di Metodi per l'Astrofisica Spaziale A.A. 2005-2006
2
Per poter rimanere su una traiettoria circolare di raggio r, il
corpo deve peraltro essere soggetto ad una forza centripeta
Tenendo conto che la velocità tangenziale è
legata al periodo orbitale dalla relazione
essendo v la velocità tangenziale.
Perché il corpo continui a percorrere l'orbita circolare,
la forza di gravità deve quindi uguagliare la forza centripeta,
Fg = Fc:
è possibile esprimere T in funzione di r,
ottenendo
Semplificando m ed r e risolvendo rispetto a v si ottiene:
M.C Falvella, Agenzia Spaziale Italiana -
Corso di Metodi per l'Astrofisica Spaziale A.A. 2005-2006
La terza legge di Keplero permette di determinare l'altezza
di un'orbita geostazionaria il cui periodo è pari al giorno
siderale della Terra, Trot = 23 h 56 min 4,09 sec = 86.164,09
sec:
Questa non è altro che la terza legge di
Keplero. La costante K che compare nella
terza legge è quindi definita da
M.C Falvella, Agenzia Spaziale Italiana -
Corso di Metodi per l'Astrofisica Spaziale A.A. 2005-2006
Un satellite posto in tale orbita può osservare quasi un
intero emisfero terrestre, poiché l'ampiezza del suo
orizzonte equivale ad un cerchio con un diametro di circa
18.000 chilometri, che è sempre centrato sull'equatore.
Questa dimensione corrisponde a 81,4 gradi di latitudine
o longitudine in ogni direzione.
L'orbita geostazionaria ha quindi un raggio di 42.168 Km,
pari a circa 6,6 raggi terrestri. Poiché il raggio dell'orbita si
misura a partire dal centro del pianeta, l'orbita
geostazionaria si trova a circa 35.790 chilometri sopra la
superficie terrestre. La velocita' del satellite e' ora
ricavabile e cioe': v = 2*3.14*r/T = 3.1 km/sec
M.C Falvella, Agenzia Spaziale Italiana -
Corso di Metodi per l'Astrofisica Spaziale A.A. 2005-2006
M.C Falvella, Agenzia Spaziale Italiana -
Corso di Metodi per l'Astrofisica Spaziale A.A. 2005-2006
Per rimanere in orbita quindi un satellite deve spostarsi
una velocità molto elevata che dipende dall'altezza per
compensare l'attrazione della gravità della Terra .
Esempio: Per un'orbita circolare a un'altezza di 300 km
sopra la superficie terrestre, è necessaria una velocità di
7,8 chilometri al secondo, cioè 28.000 chilometri all'ora.
A questa velocità, il satellite completerà un'orbita
attorno alla Terra in 90 minuti.
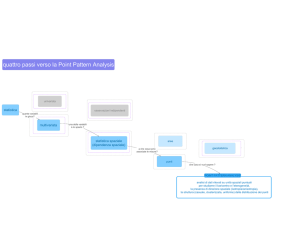
La figura rappresenta il grafico della velocità tangenziale in funzione
del raggio dell'orbita per orbite intorno alla Terra.
M.C Falvella, Agenzia Spaziale Italiana -
Corso di Metodi per l'Astrofisica Spaziale A.A. 2005-2006
M.C Falvella, Agenzia Spaziale Italiana -
Corso di Metodi per l'Astrofisica Spaziale A.A. 2005-2006
3
La maggior parte dei veicoli spaziali viene messa in orbita
attorno alla Terra. Ma questo non è sempre il luogo
ottimale per i satelliti scientifici che esplorano l'Universo.
Esempio
Il telescopio spaziale Hubble segue ad esempio un'orbita
circolare a 600 km al di sopra del suolo, inclinato di 28,5
gradi rispetto all'equatore. Questa orbita terrestre
semplifica le operazioni di riparazione e assistenza
dell'osservatorio. Tuttavia, la Terra e la Luna ostruiscono
gran parte del cielo.
Il telescopio spaziale James Webb, che sostituirà Hubble,
funzionerà da una distanza ancora maggiore. Sarà infatti
portato in un'orbita stabile al cosiddetto punto L2 di
Lagrange, a 1,5 milioni di chilometri, sul lato notturno della
Terra.
M.C Falvella, Agenzia Spaziale Italiana Corso di Metodi per l'Astrofisica Spaziale A.A. 2005-2006
Il sistema solare
Il nostro sistema solare comprende il Sole, nove pianeti (con
relativi satelliti), asteroidi, comete, meteore, polvere e
particelle gassose:
8
• il suo diametro è circa 60x10 km, dimensioni pari a circa
1/30.000 della distanza dalla stella più vicina>>> le forze
esercitate da corpi esterni al sistema solare trascurabili
• i pianeti sono suddivisi in interni (Mercurio, Venere, Terra,
Marte) ed esterni (Giove,Saturno, Urano, Nettuno e Plutone).
8
La loro massa totale è circa lo 0.2% della massa totale
del
sistema solare >>> la massa è praticamente tutta concentrata
nel Sole
• le orbite sono tutte ellittiche con eccentricità inferiore a
0.1 (ad eccezione di Mercurio e Plutone) ed inclinazione
sull’eclittica minore di 3.5°>>> orbite circolari e complanari
M.C Falvella, Agenzia Spaziale Italiana -
Corso di Metodi per l'Astrofisica Spaziale A.A. 2005-2006
L’ orbita di trasferimento di Hohman, rappresenta l'orbita
più efficiente, dal punto di vista del consumo energetico,
per trasferire un'astronave da un'orbita circolare ad
un'altra sullo stesso piano. Una tale orbita è un'ellisse
kepleriana tangente sia all'orbita più grande nel punto di
massima distanza che all'orbita più piccola nel punto di
minima distanza.
LE MISSIONI INTERPLANETARIE
Le missioni interplanetarie sono caratterizzate dallo
studio di una serie di problematiche orbitali specifiche
che dipendono, oltre che dalle enormi distanze percorse,
dalla conformazione del nostro sistema solare e dal ruolo
gravitazionale che al suo interno giocano il Sole e le
masse degli altri pianeti incontrati nel corso di ciascun
trasferimento.
M.C Falvella, Agenzia Spaziale Italiana -
Corso di Metodi per l'Astrofisica Spaziale A.A. 2005-2006
LE ORBITE DI TRASFERIMENTO
Se si vuole lanciare da terra un veicolo spaziale per
fargli raggiungere un altro pianeta o un punto preciso
dello spazio, fra le diverse soluzioni si deve cercare
quella più favorevole rispetto a varie esigenze,
soprattutto la brevità del percorso e il bilancio
energetico.
Una pratica soluzione è quella di sfruttare il campo
gravitazionale del sistema del Sole e l’ellissi di Keplero.
La prima tappa è lanciare il veicolo spaziale in un'orbita
temporanea intorno alla terra e di qui in un'orbita di
trasferimento: fra tutte le possibili orbite di
trasferimento, il caso più semplice è quello delle orbite
bicotangenziali, dette anche orbite di Hohman.
M.C Falvella, Agenzia Spaziale Italiana -
Corso di Metodi per l'Astrofisica Spaziale A.A. 2005-2006
Seguendo l’orbita di Hohman:
• il veicolo lascia la terra all’afelio e raggiunge il pianeta
bersaglio al perielio.
•non è necessario accendere i motori finché non si
raggiunge l’orbita del pianeta bersaglio: nel tragitto
energia e momento della quantità di moto rimangono
costanti.
•tutto il lavoro è compiuto dalla forza gravitazionale del
Sole e quindi questa parte del viaggio è gratuita.
Quando il veicolo raggiunge l’orbita del pianeta bersaglio
si devono accendere i razzi per toglierlo dall’orbita di
trasferimento e collocarlo nell’orbita bersaglio.
M.C Falvella, Agenzia Spaziale Italiana -
Corso di Metodi per l'Astrofisica Spaziale A.A. 2005-2006
M.C Falvella, Agenzia Spaziale Italiana -
Corso di Metodi per l'Astrofisica Spaziale A.A. 2005-2006
4
Le orbite di trasferimento impongono limitazioni ai
viaggi perché il lancio deve essere effettuato quando la
terra e il bersaglio si trovano nelle posizioni relative
corrette, agli estremi dell’asse maggiore dell’orbita.
Quest’evento è noto come opportunità di lancio.
Quando si presenta un’opportunità di lancio il veicolo, si
deve trovare in un orbita temporanea intorno alla Terra
detta orbita di parcheggio; durante un’opportunità di
lancio il veicolo deve trovarsi in un punto particolare per
essere lanciato:la finestra di lancio.
M.C Falvella, Agenzia Spaziale Italiana -
Corso di Metodi per l'Astrofisica Spaziale A.A. 2005-2006
Poiché infatti è importante che al lancio la velocità
impressa al satellite abbia una direzione ben precisa, il
lancio risulta limitato a quegli istanti di tempo in cui il sito
di lancio, che segue il moto di rotazione del pianeta,
coincida con un accettabile punto di immissione nell’orbita
definitiva.
>>> L’utilizzo di un’orbita di parcheggio, cioè di un’orbita
circolare intermedia da raggiungere prima dell’immissione
nell’orbita iperbolica di fuga, garantisce una maggiore
flessibilità in relazione alla finestra di lancio.
M.C Falvella, Agenzia Spaziale Italiana -
Corso di Metodi per l'Astrofisica Spaziale A.A. 2005-2006
Esempio
Un’orbita di parcheggio posta a 322km di quota ha un
periodo di rotazione pari a 90,96 min.
>>>effettua 16 rivoluzioni intorno alla Terra al giorno
>>>si avrebbero 16 opportunità di immissione nell’orbita
finale contro 1 sola possibilità se si fosse lanciato
direttamente dalla superficie terrestre
In generale minore è il periodo dell’orbita maggiori sono
le opportunità di lancio.
Le orbite di trasferimento di Hohman (orbite
semiellittiche circum-solari tangenti sia all’orbita della
Terra che a quella del pianeta bersaglio) sono sì le più
economiche ma il tempo di trasferimento può essere
eccessivamente lungo.
Si può allora sfruttare la cosiddetta “fionda
gravitazionale” per acquistare più spinta ed abbreviare
la durata del viaggio.
La presenza dell’atmosfera è il limite fisico alle quote
delle orbite di parcheggio (circa 250 km)
M.C Falvella, Agenzia Spaziale Italiana -
Corso di Metodi per l'Astrofisica Spaziale A.A. 2005-2006
LA FIONDA GRAVITAZIONALE
Un veicolo spaziale può ottenere uno o più “passaggi
gravitazionali” (fly-by) nel corso del suo viaggio nel
sistema solare risparmiando prezioso carburante.
Questo aiuto gravitazionale, o effetto fionda, si fa
sentire quando un veicolo spaziale vola oltre un pianeta
o una luna di grandi dimensioni. Ciò permette alla
gravità del pianeta di attrarre il veicolo spaziale e
modificarne l'orbita. A volte il veicolo accelera, a volta
rallenta, a seconda che passi dietro o davanti al pianeta.
M.C Falvella, Agenzia Spaziale Italiana -
Corso di Metodi per l'Astrofisica Spaziale A.A. 2005-2006
M.C Falvella, Agenzia Spaziale Italiana -
Corso di Metodi per l'Astrofisica Spaziale A.A. 2005-2006
L'incremento di velocità dipende dalla geometria
dell'incontro, dalla massa del pianeta e naturalmente dalla
velocità iniziale della sonda.
Il veicolo aumenta la propria velocità a spese di quella del
pianeta, ma questo scambio avviene in ragione inversa delle
masse, per cui, dato che la massa del veicolo è
enormemente inferiore a quella del pianeta, quest'ultimo
rallenta in modo impercettibile.
La fionda gravitazionale cambia anche la direzione del
percorso del veicolo spaziale.
M.C Falvella, Agenzia Spaziale Italiana -
Corso di Metodi per l'Astrofisica Spaziale A.A. 2005-2006
5
Nel sistema di riferimento del
Sole, invece, il pianeta è in moto
e dunque alla velocità di
avvicinamento della sonda va
sommata vettorialmente la
velocità del pianeta (in blu), sia
prima che dopo l'incontro.
Notiamo che in avvicinamento le
due velocità sono discordi, in
allontanamento invece la
velocità del pianeta si somma a
quella della sonda e dunque
l'effetto netto è una
accelerazione, a volte
imponente, del veicolo spaziale.
Per capire meglio il fenomeno, analizziamolo in due
sistemi di riferimento distinti.
Nel sistema di riferimento
del pianeta, la sonda si
avvicina con una velocità v,
percorre una traiettoria
curva intorno ad esso per
effetto della gravità, e si
allontana con la stessa
velocità v ma la direzione è
variata di un angolo a.
Dunque in questo sistema di
riferimento la sonda non
acquista maggiore velocità.
M.C Falvella, Agenzia Spaziale Italiana -
Corso di Metodi per l'Astrofisica Spaziale A.A. 2005-2006
Dalla figura appare ugualmente chiaro che se il satellite ,
invece di passare dietro, passasse davanti al pianeta le due
velocità nella traiettoria di allontanamento si sottrarrebbero
perché di direzione opposta e quindi si otterrebbe un
rallentamento.
M.C Falvella, Agenzia Spaziale Italiana -
Corso di Metodi per l'Astrofisica Spaziale A.A. 2005-2006
Uno degli esempi più strabilianti di applicazione di questo
effetto è quello della missione Ulysses dell'ESA. Passando
sopra al polo nord di Giove, Ulysses è stata scagliata in
un'orbita che la ha trasportata sui poli del Sole.
Utilizzando il fly-by è possibile:
• effettuare una singola osservazione di un pianeta o di un
satellite
•cambiare il modulo e/o la direzione del vettore velocità di una
traiettoria eliocentrica senza l’utilizzo di propulsori
• cambiare il piano orbitale di una traiettoria
• mantenere invariato e in alcuni casi addirittura diminuire il
tempo di volo complessivo di una missione
• ridurre sostanzialmente il carico di propellente a bordo
M.C Falvella, Agenzia Spaziale Italiana -
Corso di Metodi per l'Astrofisica Spaziale A.A. 2005-2006
Gli sforzi per progettare e portare a termine con successo
una missione che preveda uno o più fly-by sono enormi come
pure i vantaggi che derivano dall’uso di questo tipo di
manovra.
Un fly-by presuppone:
• precisione nel calcolo dei parametri orbitali e della
traiettoria
Ulysses' unique orbit
M.C Falvella, Agenzia Spaziale Italiana -
Corso di Metodi per l'Astrofisica Spaziale A.A. 2005-2006
LA MISSIONE CASSINI
La missione Cassini-Huygens,dedicata allo studio del
sistema planetario di Saturno, ha utilizzato quattro
fionde gravitazionali (una con la Terra, due con Venere e
una con Giove) lungo il suo percorso verso Saturno e
prevede numerosi fly-by ravvicinati per osservare tutti i
satelliti .
• affidabilità del sistema di guida e di controllo di assetto
• ottimo controllo da terra del veicolo
M.C Falvella, Agenzia Spaziale Italiana -
Corso di Metodi per l'Astrofisica Spaziale A.A. 2005-2006
M.C Falvella, Agenzia Spaziale Italiana -
Corso di Metodi per l'Astrofisica Spaziale A.A. 2005-2006
6
CASSINI (dal sito ASI.it)
•La Missione Cassini-Huygens,
realizzata in collaborazione tra NASA,
ESA ed ASI, ha come scopo lo studio
di Saturno e del suo sistema di
satelliti ed anelli con particolare
riguardo al satellite Titano. La
missione è partita nell'Ottobre
1997, le osservazioni del Sistema
di Saturno sono iniziate dal 11
giugno con il fly-by di Phoebe. Il
1 luglio è avvenuto l’inserimento
in orbita attorno a Saturno
(Saturn Orbit Insertion , SOI) e
l’inizio del Tour orbitale. La
sonda Huygens è arrivata su
Titano il 14 gennaio 2005.
•Lo studio di Saturno e del suo sistema di satelliti ed anelli è un elemento
cardine per la decodifica di alcuni dei processi primari dell’evoluzione del Sistema
Solare.
M.C Falvella, Agenzia Spaziale Italiana -
Corso di Metodi per l'Astrofisica Spaziale A.A. 2005-2006
M.C Falvella, Agenzia Spaziale Italiana -
Corso di Metodi per l'Astrofisica Spaziale A.A. 2005-2006
La determinazione orbitale nel primo tratto della
missione Cassini ha permesso di superare con estremo
successo il fly-by intorno a Venere (a soli 284 km dalla
superficie del pianeta)>>>>è importante determinare con
grande precisione la traiettoria a priori e poi seguirne
passo dopo passo l’evoluzione (propagazione dell’orbita).
Nel corso del trasferimento l’orbita può essere
perturbata da:
• deviazioni o errori dovuti alla messa in orbita
• fasi di congiunzione con il Sole
• drag atmosferico
• Reset h/w e attività di manutenzione a bordo
• errori o imprecisioni di puntamento a bordo
M.C Falvella, Agenzia Spaziale Italiana -
Corso di Metodi per l'Astrofisica Spaziale A.A. 2005-2006
M.C Falvella, Agenzia Spaziale Italiana -
Corso di Metodi per l'Astrofisica Spaziale A.A. 2005-2006
Conclusioni
La traiettoria di una sonda, pur considerata sempre come un
problema di due corpi, è influenzata da centinaia di variabili.
Anche le manovre più semplici, come la lubrificazione degli
ingranaggi o il dispiegamento di uno strumento, necessitano
approfondite analisi e devono essere opportunamente
controbilanciate per evitare deviazioni nella traiettoria.
Le fonti di indeterminazione più importanti sono:
• gli effetti della pressione solare
•L’incertezza legata alle efemeridi dei pianeti che la sonda
incontra sul suo cammino
•Le interferenze ed il rumore nelle comunicazioni con le
stazioni di terra che possono inficiare i dati di tracking
• le variazioni nella posizione delle stazioni di terra dovute a
parametri come rotazione, precessione luna-sole, maree.
M.C Falvella, Agenzia Spaziale Italiana -
Corso di Metodi per l'Astrofisica Spaziale A.A. 2005-2006
7