1
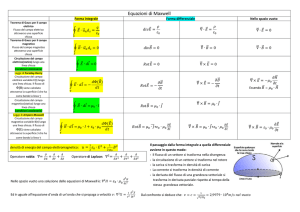
Campi elettrici e magnetici statici
Flusso di un campo vettoriale. Consideriamo una zona di spazio in
Si
v
cui sia presente un certo campo vettoriale v e, in questo spazio, una
certa superficie S (aperta o chiusa). Dividiamo l'intera superficie in
tanti elementi così piccoli che la superficie di ognuno di essi si possa
considerare praticamente piana e che il campo v non cambi in Fig. 1
maniera apprezzabile, né in direzione, né in modulo, da un punto all'altro. Ogni elemento di
superficie definisce un modulo (il valore della sua area), una direzione e un verso (quelli della
normale alla sua superficie rivolta verso l'esterno; se poi la superficie è chiusa, si può parlare di
interno ed esterno senza ambiguità). Possiamo quindi rappresentare l'elemento di superficie con un
vettore, che indica l'area e la sua orientazione. Se vi è il vettore relativo all'elemento di superficie
Si, chiamiamo flusso del campo v attraverso quell'elemento di superficie la quantità i = vi⋅Si .
Il nome ha origine dal fatto che, se v rappresenta la velocità di un fluido in movimento, per
esempio dell'acqua in un fiume, allora i è la portata (ovvero il volume nell'unità di tempo)
dell'acqua che attraversa l'elemento di superficie Si. Per ottenere il flusso complessivo attraverso la
superficie S, sommiamo il flusso attraverso tutti gli elementi: v =∑ i =∑ vi⋅S i .
i
i
Supponendo poi di far diventare ogni elemento sempre più piccolo ed il loro numero sempre più grande, passiamo dalla
S .
somma all'integrale di superficie: v =∫S v⋅d
.
Teorema di Gauss. Prendiamo in considerazione il campo elettrico E
La situazione più semplice è quella del campo generato da una singola carica puntiforme isolata q e
di una superficie sferica di raggio r e centro nella posizione della carica. In questo caso, il campo è
E
costante in ogni punto della superficie, e la sua direzione e verso coincidono
dS
con quelli della normale esterna alla superficie in quel punto. Quindi:
=E⋅Atot =
E
1 q
q
2
⋅4 r =
.
2
4 0 r
0
Osserviamo che il flusso non dipende dalle dimensioni della sfera.
q
Fig. 2
Consideriamo ora una seconda superficie chiusa di forma qualsiasi che racchiuda la prima.
Affermiamo che il flusso totale attraverso questa superficie è lo stesso di quello attraverso la sfera.
Intuitivamente, tutte le linee di forza che attraversano la sfera tagliano anche la superficie esterna.
In termini più rigorosi, consideriamo un cono con vertice in q che tagli una piccola porzione di superficie s sulla
2
sfera ed una
S sulla superficie esterna, a distanza R dalla carica. L'area di
S è
E
maggiore di quella di s per due motivi: il fattore di similitudine R/ r 2 dovuto alla
θ
S
diversa distanza dalla carica ed il fattore 1/ cos dovuto all'inclinazione. Quindi il
contributo di tale area al flusso è:
R
r
2
q R 1
q
S = E
S ⋅
s .
E
S =E S ⋅S cos =k 2⋅s 2
⋅cos =k 2⋅s=E s⋅s= E
R
r cos
r
s
q
Poiché ogni porzione della superficie esterna può essere messa in corrispondenza in
questo modo con una parte della superficie sferica, il flusso totale attraverso le due
superfici è lo stesso.
Come corollario, possiamo osservare che il flusso totale attraverso una
superficie chiusa è zero se la carica si trova al di fuori della superficie.
Fig. 3
La figura seguente può suggerire il modo di dimostrare questa
affermazione.
S'
S
I risultati ottenuti possono sembrare ovvi se immaginiamo che in q vi
sia una sorgente che emetta particelle in tutte le direzioni con frequenza
costante. Il flusso di particelle in un elemento di superficie decrescerà
q
q
con l'inverso del quadrato della distanza da q, proprio come il campo
elettrico. E' chiaro che il flusso di particelle attraverso una superficie
chiusa che contiene q non dipenderà dalle dimensioni e dalla forma
Fig. 4
della superficie, e sarà uguale al numero di particelle emesse nell'unità di tempo.
Infine, se sono presenti diverse cariche, ricordiamo che, per il principio di sovrapposizione, il
campo elettrico complessivo è la somma vettoriale dei campi dovuti alle singole sorgenti.
Osserviamo che anche il flusso è una quantità additiva, pertanto il flusso del campo elettrico dovuto
a più cariche è la somma dei flussi dati dalle singole cariche, ognuno dei quali è dato da q /0 .
Possiamo quindi enunciare il teorema di Gauss: il flusso del campo elettrico attraverso una
qualunque superficie chiusa è direttamente proporzionale alla carica contenuta all'interno della
superficie.
S chiusa =
In formula: E
∑ qint
0
.
Osserviamo che la dimostrazione precedente è imperniata sulla dipendenza del campo dall'inverso del quadrato della
distanza, oltre che sul principio di sovrapposizione.
Ne segue che, ad esempio, il teorema di Gauss non sarebbe valido se il campo dipendesse dall'inverso del cubo della
distanza. In questo caso, il flusso del campo attraverso una sfera centrata sulla carica sarebbe:
=∫ E
⋅d
E
S=
1 q
q
⋅4 r 2=
4 0 r 3
0 r
e quindi dipenderebbe dal raggio.
Vediamo, inoltre, che il teorema di Gauss non è valido esclusivamente per il campo elettrico, ma per qualsiasi campo
variabile secondo la legge dell'inverso del quadrato della distanza, come, ad esempio, quello gravitazionale. Il nostro
3
teorema è equivalente alla legge di Coulomb o a quella di Newton, con l'ipotesi aggiuntiva che il campo abbia simmetria
sferica, e potrebbe quindi essere assunto come legge fondamentale delle interazioni elettrostatiche o gravitazionali.
Conseguenze del teorema di Gauss. In particolari condizioni di simmetria, il teorema di Gauss ci
permette di determinare il campo elettrico prodotto da una determinata distribuzione di cariche
senza dover ricorrere ad un integrale.
a. Consideriamo una carica Q distribuita in maniera uniforme all'interno di
una sfera di raggio R. Per simmetria, il campo elettrico deve essere
E2
R
P1
P2
diretto radialmente e la sua intensità deve essere costante su tutti i punti
di una sfera concentrica con quella in cui è distribuita la carica.
r2
Considerando come superficie chiusa la sfera di raggio r1, maggiore di
R, ed applicando su di essa il teorema di Gauss, ricaviamo:
=
E
qint
0
⇒ E 1 4 r 12 =
E1
r1
Fig. 5
Q
1 Q
⇒ E 1=
.
0
4 0 R12
Vediamo quindi che il campo elettrico all'esterno della sfera è uguale a quello che si avrebbe se
la carica fosse concentrata nel centro della sfera.
Lo stesso ragionamento, applicato al campo gravitazionale, ci dice che la Terra, considerata come una sfera
omogenea, attrae gli altri corpi con la stessa forza con cui li attirerebbe se la sua massa fosse concentrata nel centro.
Questa non è una proprietà ovvia del centro di massa: ad esempio, un cubo di densità uniforme non attrae i corpi
esterni come se la sua massa fosse concentrata nel centro. Anche per Newton questo risultato non era affatto
scontato, ed egli lo dimostrò in maniera assai più laboriosa.
Se ora consideriamo come superficie chiusa la sfera di raggio r2, minore di R, ed applichiamo su
di essa il teorema di Gauss, ricaviamo:
=
E
qint
0
3
Q r2
1 Q
⇒ E 2 4 r = ⋅ 3 ⇒ E 2=
⋅r 2 .
0 R
4 0 R 3
2
2
Quindi, il campo elettrico all'interno della sfera cresce linearmente con la distanza dal centro.
b. Nel caso in cui la carica Q sia distribuita in maniera uniforme sulla superficie di una
sfera, è evidente che il campo all'esterno non cambia rispetto al caso precedente,
E=0
mentre il campo all'interno della sfera è uguale a zero.
c. Consideriamo una distribuzione lineare di carica, ovvero un “filo” composto da
Fig. 6
cariche, di lunghezza infinita (ovvero, molto maggiore delle dimensioni che stiamo
considerando). Esso può essere caratterizzato dalla sua densità lineare di carica l (carica per
unità di lunghezza). Per simmetria, il campo elettrico deve essere radiale ed il suo modulo deve
dipendere unicamente dalla distanza r dal “filo”.
4
Prendiamo come superficie chiusa un cilindro avente come asse la
E
distribuzione di cariche. Applicando il teorema di Gauss, vediamo l
r
che il flusso del campo elettrico attraverso le due basi è zero, per cui:
=
E
qint
0
⇒ E⋅2 r l=
l
1
⇒ E=
.
0
2 0 r
l
Fig. 7
Quindi, il campo elettrico di una distribuzione lineare di carica varia con l'inverso della distanza
dalla distribuzione stessa.
d. Consideriamo una distribuzione di cariche piana e infinitamente estesa (ovvero, le cui
dimensioni sono molto maggiori di quelle che stiamo considerando). Essa può essere
caratterizzata dalla sua densità superficiale di carica s (carica per unità di superficie). Per
simmetria, il campo elettrico deve essere perpendicolare allo strato su cui
sono distribuite le cariche ed il suo modulo deve dipendere unicamente
s
dalla distanza r dallo strato stesso.
E
Prendiamo come superficie chiusa un cilindro avente asse perpendicolare
al piano su cui sono distribuite le cariche. Applicando il teorema di Gauss,
S
vediamo che il flusso del campo elettrico attraverso la superficie laterale è
E
zero, per cui:
=
E
qint
0
⇒ 2 E⋅S =
S
⇒ E=
.
0
2 0
Fig. 8
Quindi, il campo elettrico di una distribuzione piana di carica non dipende dalla distanza dalla
distribuzione stessa.
e. Consideriamo due distribuzioni di carica piane, parallele, infinitamente
estese ed aventi densità superficiale di carica opposta ± (è il nostro
modello per schematizzare un condensatore a facce piane e parallele).
Applicando il risultato precedente e tenendo conto del segno delle
cariche, è immediato ricavare che il campo elettrico all'esterno delle
E+
+s
EEtot=0
E+
EEtot
-s
E+
EEtot=0
Fig. 9
armature è nullo, mentre quello all'interno ha modulo:
E int =
ed è uniforme e perpendicolare alle armature.
0
Flusso del campo magnetico. Come sappiamo, non esistono in natura delle cariche magnetiche. Ne
segue che le linee di forza del campo magnetico sono linee chiuse e, di conseguenza, ogni superficie
chiusa viene attraversata da un uguale numero di linee di forza entranti ed uscenti.
5
Quindi il flusso del campo magnetico attraverso una qualunque superficie chiusa è
S
uguale a zero:
i
S chiusa =0 .
B
B
Fig. 10
Circuitazione di un campo vettoriale. Consideriamo una zona di spazio in cui sia presente un
certo campo vettoriale v e, in questo spazio, una certa curva chiusa (non necessariamente piana)
C. Dividiamo la curva in tanti elementi così piccoli che ognuno di essi si possa considerare un
segmento e che il campo v non cambi in maniera apprezzabile, né in direzione, né in modulo, da
un punto all'altro. Se vi è il vettore relativo all'elemento di curva l i , chiamiamo circuitazione
del campo v lungo la curva la quantità C v =∑ vi⋅l i .
i
Supponendo poi di far diventare ogni elemento sempre più piccolo ed il loro numero sempre più grande, passiamo dalla
somma all'integrale di linea:
C v =∮ v⋅d l .
E
Circuitazione del campo elettrico. Consideriamo il campo generato da una
D
carica puntiforme q e la curva chiusa ABCD in figura. Nei tratti AB e CD il C
contributo alla circuitazione è uguale a zero perché il campo elettrico è radiale,e
quindi perpendicolare allo spostamento. I tratti BC e DA forniscono dei contributi
E
B
diversi da zero, ma tra di loro opposti, in quanto in un caso lo spostamento ha la
A
stessa direzione del campo elettrico, e nell'altro caso ha direzione opposta.
Concludiamo che la circuitazione del campo elettrico su questa curva chiusa è
E
E
q
Fig. 11
uguale a zero.
Accenniamo a come questo risultato possa essere generalizzato. Supponiamo di voler calcolare la E
F
circuitazione del campo elettrico lungo il percorso chiuso ABCDEFG. Essa sarà uguale alla somma
della circuitazione lungo il cammino ABCG e di quella lungo il cammino DEFG, in quanto entrambiC
D
G
i percorsi contengono il tratto DG, che, però, viene percorso in sensi opposti, e quindi fornisce un
contributo nullo. Per entrambi i percorsi considerati vale il risultato precedente, e, quindi, la
B
A
circuitazione complessiva è nulla. Qualunque curva chiusa può essere considerata come il limite di
un percorso di questo genere. Inoltre, il principio di sovrapposizione del campo elettrico ci permette
Fig. 12
di passare da una carica puntiforme ad una generica distribuzione di cariche elettriche.
q
=0 .
In conclusione, la circuitazione del campo elettrico è uguale a zero: C E
.
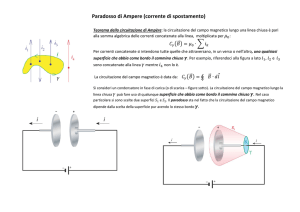
Teorema di Ampère. Consideriamo come campo vettoriale il campo magnetico B
La situazione più semplice è quella di un filo conduttore rettilineo e infinito (ovvero, di lunghezza
6
molto maggiore rispetto alle distanze prese in considerazione) percorso da una corrente i.
In questo caso, le linee di forza del campo magnetico sono circonferenze
B
giacenti sui piani perpendicolari al filo. Vogliamo calcolare la
circuitazione del campo magnetico lungo una di tali circonferenze. Poiché
B
campo e spostamento sono sempre paralleli, abbiamo:
=B⋅l=
CB
i
B
0 i
⋅2 r=0 i .
2 r
Osserviamo che la circuitazione non dipende dal raggio della
circonferenza. Il risultato ottenuto è valido anche per qualsiasi altra curva
B
Fig. 13
chiusa che racchiuda al suo interno il filo conduttore.
Per dimostrarlo, possiamo prendere in considerazione un piccolo arco
θ
l sulla circonferenza ed il corrispondente arco L sulla curva esterna.
B
L
La lunghezza di L è maggiore di quella di l per due motivi: il fattore
l
r
R
di similitudine R/ r dovuto alla diversa distanza dal filo conduttore ed il
i
fattore 1/ cos dovuto all'inclinazione. Quindi:
L = B
L⋅L =B L⋅L cos =k i ⋅l R 1 ⋅cos =
C B
R r cos
i
l
=k ⋅l =B l ⋅l=C B
r
Fig. 14
.
Poiché ogni arco della curva esterna può essere messo in corrispondenza in questo modo con un arco di circonferenza,
la circuitazione del campo magnetico lungo le due curve è la stessa.
C'
C
Come corollario, possiamo osservare che la circuitazione
totale lungo una linea chiusa è zero se la curva non i
racchiude alcuna corrente al suo interno.
i
La figura a fianco può suggerire il modo di dimostrare questa
affermazione.
Fig. 15
Infine, se sono presenti diverse correnti, ricordiamo che, per il principio di sovrapposizione, il
campo magnetico complessivo è la somma vettoriale dei campi dovuti alle singole sorgenti.
Osserviamo che anche la circuitazione è una quantità additiva, pertanto la circuitazione del campo
magnetico dovuto a più correnti è la somma delle circuitazioni dovute alle singole correnti, ognuna
delle quali è data da 0 i .
Possiamo quindi enunciare il teorema di Ampère: la circuitazione del campo magnetico lungo una
qualunque curva chiusa è direttamente proporzionale alla corrente concatenata con la curva.
In formula: C B=
0 ∑ i conc .
7
Anche il teorema di Ampère permette, in particolari condizioni di simmetria, di determinare il
campo magnetico generato da una data distribuzione di correnti senza dover svolgere un integrale.
L'esempio più semplice è quello del campo magnetico all'interno di un solenoide rettilineo (pag. 185
del libro di testo).