Prof. A.Guarrera Liceo Scientifico
Galilei - Catania
Applicazioni del teorema di Gauss
Campo elettrostatico di una distribuzione di carica uniforme e filiforme (filo carico) di densità
lineare di carica .
Osserviamo che in un punto esterno al “filo infinito” (distante da questi) il vettore campo elettrico
ha direzione perpendicolare alla distribuzione.
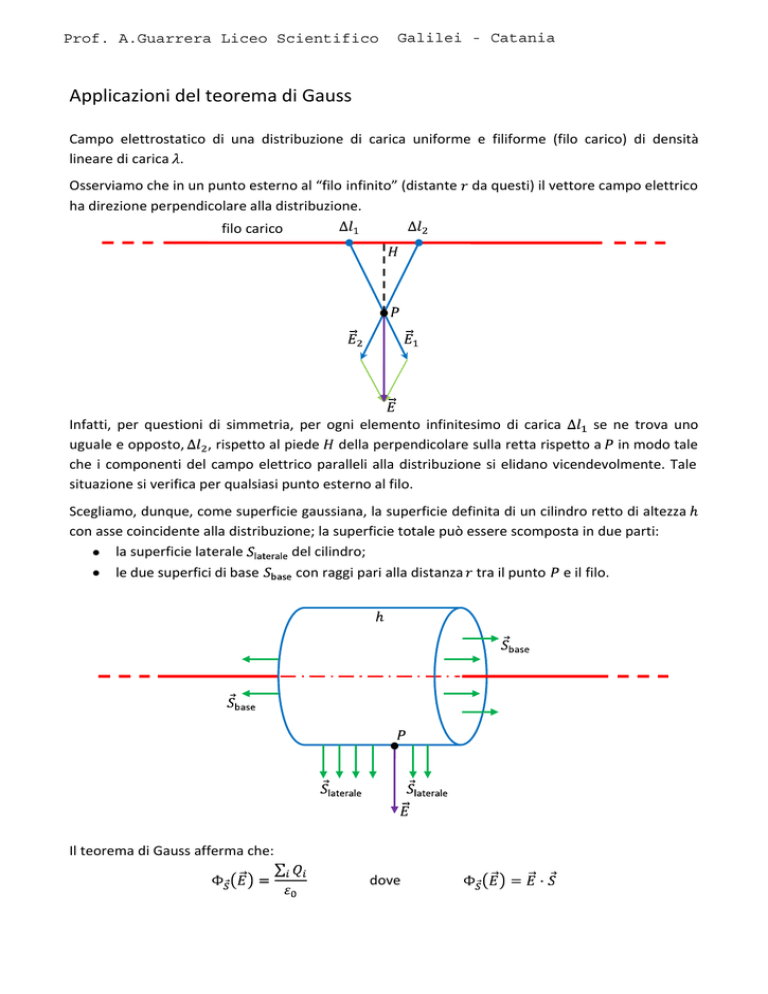
filo carico
se ne trova uno
Infatti, per questioni di simmetria, per ogni elemento infinitesimo di carica
, rispetto al piede della perpendicolare sulla retta rispetto a in modo tale
uguale e opposto,
che i componenti del campo elettrico paralleli alla distribuzione si elidano vicendevolmente. Tale
situazione si verifica per qualsiasi punto esterno al filo.
Scegliamo, dunque, come superficie gaussiana, la superficie definita di un cilindro retto di altezza
con asse coincidente alla distribuzione; la superficie totale può essere scomposta in due parti:
la superficie laterale
del cilindro;
le due superfici di base
con raggi pari alla distanza tra il punto e il filo.
Il teorema di Gauss afferma che:
dove
Sulla superficie laterale si può osservare il parallelismo tra il vettore campo elettrico
superficie (esterno)
, cioè tali vettori formano un angolo di ampiezza
e il vettore
; per definizione di
prodotto scalare
Sulle superfici di base si può osservare la perpendicolarità tra il vettore campo elettrico
vettore superficie (esterno)
, cioè tali vettori formano un angolo di ampiezza
e il
; per
definizione di prodotto scalare
In altri termini, riguardando tutta la superficie cilindrica, si ha
Ricordando che il cilindro ha raggio
laterale misura
(pari alla distanza tra il filo e il punto) e altezza , la superficie
; se la densità di carica lineare è costante ed è
carica situata sul tratto del filo, si può ottenere, tramite la formula inversa (
carica presente all’interno della superficie gaussiana scelta:
.
Dall’uguaglianza
, nel caso in questione, si ottiene
esplicitando il campo elettrico (intensità) si giunge a
, dove
è la
), il valore della
, cioè
;
Applicazioni del teorema di Gauss
Campo elettrostatico di una distribuzione di carica uniforme e superficiale (piano carico) di densità
superficiale di carica .
Osserviamo che in un punto esterno al “piano” (distante
direzione perpendicolare alla distribuzione.
da questi) il vettore campo elettrico ha
Infatti, per questioni di simmetria, per ogni elemento
se ne trova uno uguale e opposto,
infinitesimo di carica
, rispetto al piede
della perpendicolare sulla retta
in modo tale che i componenti del campo
rispetto a
elettrico paralleli alla distribuzione si elidono
vicendevolmente. Tale situazione si verifica per qualsiasi
punto esterno al piano.
piano carico
Scegliamo, dunque, come superficie gaussiana, la superficie di un cilindro retto di altezza
asse perpendicolare al piano; la superficie totale può essere scomposta in due parti:
la superficie laterale del cilindro;
le due superfici di base di raggio , una
e l’altra simmetrica
contenente
rispetto al piano.
Il teorema di Gauss afferma che:
dove
con
Sulle superfici di ciascuna base si può osservare il parallelismo tra il vettore campo elettrico
vettore superficie (esterno)
, cioè tali vettori formano un angolo di ampiezza
e il
; per definizione
di prodotto scalare
Sulla superficie laterale si può osservare la perpendicolarità tra il vettore campo elettrico
vettore superficie (esterno)
e il
, cioè tali vettori formano un angolo di ampiezza
; per
definizione di prodotto scalare
In altri termini, riguardando tutta la superficie cilindrica e, in particolare, le superfici delle due basi,
si ha
Ricordando che il cilindro ha raggio
, la superficie di ciascuna base misura
densità di carica superficiale è costante ed è
, dove
è la carica situata nella regione
piano, si può ottenere, attraverso la formula inversa (
all’interno della superficie gaussiana scelta:
.
Dall’uguaglianza
del
), il valore della carica presente
, nel caso in questione, si ottiene
esplicitando il campo elettrico (intensità) si giunge a:
; se la
, cioè
;
; si osserva l’indipendenza del modulo
del vettore campo elettrico dalla distanza del punto dal piano.
Applicazioni del teorema di Gauss
Campo elettrostatico di una distribuzione di carica uniforme e sferica di carica complessiva
raggio .
CASO 1: il punto
e
è interno alla sfera.
Osserviamo che in un punto interno alla “sfera” il vettore
campo elettrico ha direzione radiale. Infatti, per questioni di
simmetria, per ogni elemento infinitesimo di carica
se ne
sfera carica
, tale che la distanza tra
e sia la
trova uno uguale,
medesima presente tra
e ; in tal modo i componenti del
campo elettrico perpendicolari alla distanza tra il centro
della sfera e il punto si elidono vicendevolmente.
Tale situazione si verifica per qualsiasi punto interno alla sfera.
Scegliamo, dunque, come superficie gaussiana, la superficie di una sfera con centro in
(pari alla distanza tra il centro della sfera e il punto ).
e raggio
Il teorema di Gauss afferma che:
dove
Sulle superficie gaussiana si può osservare il parallelismo tra il vettore campo elettrico
superficie (esterno)
, cioè tali vettori formano un angolo di ampiezza
e il vettore
; per definizione di
prodotto scalare
Ricordiamo che la superficie gaussiana è data da
carica
, dove
Dall’uguaglianza
; tale superficie gaussiana racchiude la
.
, nel caso in questione, si ottiene
esplicitando il campo elettrico (intensità) si giunge a:
campo elettrico aumenta proporzionalmente con la , con
, cioè
;
; si osserva che il modulo del vettore
.
CASO 2: il punto
è sulla superficie della sfera.
Osserviamo che in un punto sulla superficie della “sfera” il
vettore campo elettrico ha direzione radiale. Infatti, per
sfera carica
questioni di simmetria, per ogni elemento infinitesimo di
carica
se ne trova uno uguale,
, tale che la
distanza tra
e sia la medesima presente tra
e
; in tal modo i componenti del campo elettrico perpendicolari alla distanza tra il centro della
sfera e il punto si elidono vicendevolmente. Tale situazione si verifica per qualsiasi punto sulla
superficie della sfera.
Scegliamo, dunque, come superficie gaussiana, la superficie di una sfera con centro in
(pari al quello dell’intera sfera carica).
e raggio
Il teorema di Gauss afferma che:
dove
Sulle superficie gaussiana si può osservare il parallelismo tra il vettore campo elettrico
superficie (esterno)
, cioè tali vettori formano un angolo di ampiezza
e il vettore
; per definizione di
prodotto scalare
Ricordiamo che la superficie gaussiana è data da
Dall’uguaglianza
.
, nel caso in questione, si ottiene
esplicitando il campo elettrico (intensità) si giunge a:
, cioè
;
; si osserva che il modulo del
vettore campo elettrico è uguale a quello di una carica puntiforme: è come se tutta la carica della
sfera fosse concentrata nel suo centro.
CASO 3: il punto
è esterno alla sfera
Osserviamo che in un punto esterno alla “sfera” il vettore campo elettrico ha direzione radiale.
Infatti, per questioni di simmetria, per ogni
elemento elementare di carica
se ne
sfera carica
trova uno uguale
tale che la distanza tra
e sia la medesima presente tra
e ;
in tal modo le componenti del campo elettrico
perpendicolari alla distanza tra il centro della sfera e il punto si elidono vicendevolmente. Tale
situazione si verifica per qualsiasi punto esterno alla sfera.
Scegliamo, dunque, come superficie gaussiana, la superficie di una sfera con centro in
(pari alla distanza tra il centro della sfera e il punto ).
e raggio
Il teorema di Gauss afferma che:
dove
Sulle superficie sferica si può osservare il parallelismo tra il vettore campo elettrico
superficie (esterno)
, cioè tali vettori formano un angolo di ampiezza
e il vettore
; per definizione di
prodotto scalare
Ricordiamo che la superficie sferica ha raggio , cioè
l’intera carica della sfera.
Dall’uguaglianza
; la superficie gaussiano racchiude
, nel caso in questione, si ottiene
esplicitando il campo elettrico (intensità) si giunge a:
, cioè
;
; si osserva che il modulo del
vettore campo elettrico è uguale a quello di una carica puntiforme: è come se tutta la carica della
sfera fosse concentrata nel suo centro.
Riassumendo i tre casi:
per un punto interno
alla sfera
per un punto sulla
superficie della sfera
per un punto esterno
alla sfera
Analizziamo il campo nel caso limite in cui da il punto interno sia il centro della sfera:
Analizziamo il campo nel caso limite in cui da un punto interno si passa a un punto sulla superficie:
Analizziamo il campo nel caso limite in cui da un punto esterno si passa a un punto sulla superficie:
Rappresentazione del modulo del campo elettrico ( ) in funzione della distanza ( )
N.B. Analizziamo la situazione in cui vi siano due lastre di carica opposta, l’una di fronte all’altra
come in figura. (Si suppone che le due lastre abbiano la stessa densità di carica)
Dato che vale il principio di sovrapposizione, è facile notare come nell’area compresa tra le due
lastre i vettori campo si sommino, mentre all’esterno si annullino. (Ricordiamo che i vettori
rappresentanti un campo si disegnano entranti se le cariche sono negative, uscenti se sono positive).
Il campo totale è dato dalla somma algebrica dei due campi. Etot =
σ
σ
σ
+
=
2⋅ε0 2⋅ε0 ε0












