Lezione2011.05.12_000

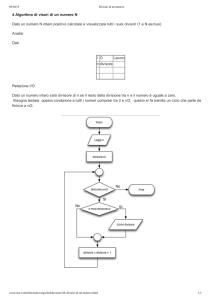
Teoria dei numeri e Crittografia: lezione del 12 maggio 2011
Il teorema di Pepin permette di costruire un algoritmo deterministico di primalità per i numeri di
r
Fermat Fr = 2( 2 ) +1 (con r>0):
Fr -1
1) si calcola la riduzione 3 2 modFr
2) se tale riduzione è = (n -1) si esce con output “Fr è primo”; in caso contrario si esce con
output “Fr è composto”.
Poiché si può utilizzare l’esponenziazione modulare, la complessità di tale test è  O(x3), dove
r
r
x=L(Fr)=2r+1 (perché 2( 2 ) < Fr< 2( 2 +1) ).
I numeri di Fermat Fr hanno alcune interessanti applicazioni geometriche relative al cosiddetto
problema della “ciclotomia”: fissato un naturale n>2, suddividere una circonferenza in n parti
uguali (equivalentemente disegnare un poligono regolare di n lati iscritto nella circonferenza)
usando solo riga e compasso.
Per quali valori di n>2 il problema ha soluzione ?
Per esempio per n=6 il problema ha soluzione: il lato dell’esagono regolare si può costruire con riga
e compasso perché la sua ampiezza è uguale a quella del raggio della circonferenza circoscritta.
Esiste un importante Teorema (di cui diamo solo l’enunciato):
Teorema.
Il problema della ciclotomia ha soluzione per tutti e soli i valori n>2 tali che n sia della forma:
n = 2t Fr1 Fr2 .....Frm
dove t 0, e Fr1 , Fr2 ,....., Frm sono numeri primi di Fermat distinti (al limite può essere anche m=0,
quando n è una potenza di 2)
Per esempio per n=7 il problema della ciclotomia non ha soluzione (perché 7 è primo ma non è un
primo di Fermat): non è possibile costruire con riga e compasso il lato dell’ettagono regolare.
Anche per n=9=32 il problema della ciclotomia non ha soluzione (perché 9 è il quadrato di un
primo di Fermat): non è possibile costruire con riga e compasso il lato dell’ennagono regolare.
Dimostriamo che i fattori primi dei numeri di Fermat Fr hanno una struttura particolare, per r>1.
Teorema.
Se r>1, per ogni divisore primo p di Fr= 2( 2 ) +1 si ha p  1 (mod 2r+2), quindi p=1+k2r+2 con k
numero naturale.
Dimostrazione:
r
r
Per ipotesi p è divisore del numero dispari Fr, quindi p è primo >2. Si ha 2( 2 )  -1 (mod p).
r +1
Essendo 2, p coprimi si ha [2] Zp* , [2]( 2 ) =[-1] 2 = [1], e se s=ord([2]) in Zp* , s è divisore di
2r+1, quindi s=2d con d r+1. Dimostriamo che d=r+1. Se per assurdo fosse d<r+1, sarebbe:
r
d
r -d
r -d
[2]( 2 ) = ([2]( 2 ) )2 = ([2]s ) 2 =[1]
r
ed essendo 2( 2 )  -1 (mod p) si avrebbe 1  -1 (mod p), contraddizione perché p>2.
Dunque d=r+1, s=2r+1. Ma il s=ord([2]) è divisore della cardinalità p-1 di Zp* , p-1=2r+1z con z
naturale, e dunque p-1 è multiplo di 8 (perché r+1>2), ossia p  1 (mod 8).
Per le proprietà del simbolo di Legendre si ha (2/p)=1, e per il criterio di Eulero 2(p-1)/2  1 (mod p),
[2] (p-1)/2=[1], dunque s=ord([2]) è divisore di (p-1)/2, cioè (p-1)/2=hs=h2r+1 con h naturale da cui
p-1=h2r+2 cioè la tesi.
Per trovare un divisore primo di Fr (con r>1), si può allora implementare il seguente algoritmo: si
fanno assumere in successione al parametro k i valori interi positivi k=1,2,…., verificando con
l’algoritmo della divisione se il numero p=1+k2r+2 è divisore di Fr. Il minimo valore di k per cui
p=1+k2r+2 è divisore di Fr fornisce con certezza un divisore primo p di Fr (se p per assurdo non
fosse primo, p avrebbe un divisore primo p1<p, ma p1 sarebbe a maggior ragione divisore di Fr,
quindi sarebbe della forma p1=1+k12r+2 con k1<k, contro la minimalità di k).
Dopo avere trovato un divisore primo p di Fr, si può ripetere il ragionamento sul numero Fr /p per
trovare altri divisori primi di Fr /p (e quindi di Fr) e pervenire infine alla completa fattorizzazione di
Fr in prodotto di primi.
Numeri di Mersenne.
Dopo avere studiato i numeri di Fermat (successivi di una potenza di 2), studieremo i numeri che
precedono una potenza di 2.
Poniamo Mk=2k-1, con k>1: un tale numero naturale (dispari) è detto numero di Mersenne.
Come per i numeri di Fermat, studiamo quando un numero di Mersenne Mk è primo: vedremo in
tale caso che k non può essere un esponente qualunque.
Teorema.
Se Mk=2k-1 (con k>1) è un numero primo, l’esponente k è necessariamente primo.
Dimostrazione:
Per assurdo sia k non primo, e sia k=ts, con 1<t,s<k.
Sfruttando la proprietà (già considerata in altre dimostrazioni) che per ogni s>1 si ha:
(x-y)(xs-ys)
con y=1, x=2t, si ottiene che x-y=2t-1 è divisore di xs-ys=2ts-1=2k-1=Mk , con 2t-1>1 (perché t>1) e
2t-1<Mk (perché t<k), contraddizione perché Mk è primo.
Dunque, per cercare valori primi di Mk=2k-1 si deve restringere la ricerca al caso in cui l’esponente
k sia primo.
Esistono tuttavia esponenti k primi per cui Mk non è primo: per esempio per k=11 si ha
Mk=211=2047=2389, non primo.
Notizie sulla situazione attuale della ricerca sui numeri di Mersenne primi si possono trovare sul
sito: www.mersenne.org (progetto GIMPS: Great Internet Mersenne Primes Search).
A tutt’oggi sono stati trovati 46 numeri di Mersenne primi: il più grande è stato scoperto
nell’Agosto del 2008: è il numero 243.112.609-1, ed ha 12.978.189 cifre in base 10.
Le tecniche per verificare se un numero di Mersenne è primo fanno uso del cosiddetto criterio di
Lucas-Lehmer, che ora esporremo.
Definiamo la successione S1, S2, …., Sn,….. di numeri naturali nel modo seguente:
S1 = 4; per ogni i>1: Si = Si-12-2
(quindi per esempio S2=42-2=14, S3=142-2=194 etc.)
Il criterio di Lucas-Lehmer è enunciato nel seguente Teorema (di cui omettiamo la dimostrazione):
Teorema di Lucas-Lehmer.
Dato un numero di Mersenne Mp=2p-1, con p primo >2, si ha:
Mp è primo  Sp-1  0 (mod Mp)
Si può allora costruire un algoritmo deterministico di primalità per i numeri di Mersenne Mp=2p-1,
con p primo >2, nel modo seguente:
1) Si calcolano i numeri interi T1, T2, …., Tp-1 ponendo:
T1 = 4; per ogni i>1: Ti = (Ti-12-2)modMp
(notare che per ogni i si ha 0 Ti<Mp ; inoltre per ogni i si ha anche SiTi (mod Mp) come si
dimostra facilmente per induzione)
2) Se Tp-1=0 (ciò equivale ad Sp-1  0 (mod Mp)) si esce con output “Mp è primo”; in caso
contrario si esce con output “Mp è composto”.
Il numero Mp ha lunghezza binaria p (in base 2 ha p cifre tutte =1). Esaminando la complessità
dell’algoritmo, si nota che il calcolo di ognuno dei Ti comporta:
il calcolo del prodotto Ti-12 di 2 fattori <Mp quindi di lunghezza  p (complessità  O(p2)); il calcolo
della differenza Ti-12-2, dove Ti-12 ha lunghezza  2p (complessità  O(p))); il calcolo della
riduzione (Ti-12-2)modMp, dove (Ti-12-2) ha lunghezza  2p (complessità  O(4p2)=O(p2)).
In totale il calcolo di ognuno dei Ti ha complessità  O(p2); poiché il numero dei Ti è (p-1), la
complessità totale del test è  O(p3).
Anche nel caso in cui il numero di Mersenne Mp non sia primo, i suoi divisori primi (almeno nel
caso p primo >2) hanno una struttura particolare:
Teorema.
Se p è un primo >2, per ogni divisore primo q di Mp=2p-1 si ha q  1 (mod p), quindi q=1+kp con k
naturale, e inoltre si ha q  1,7 (mod 8).
Dimostrazione:
Essendo Mp dispari, si ha q dispari. Poiché 2p  1 (mod q), si ha [2] p=[1] in Zq* e se s=ord([2]) è
il periodo di [2] in Zq*, si ha sp, da cui, essendo p primo, s=p (perché s1 in quanto [2] [1]).
Il periodo s=p è divisore della cardinalità q-1 di Zq* , dunque q  1 (mod p), q=1+kp con k naturale
e in particolare k pari perché q, p sono dispari).
Infine, posto k=2t, [2] (q-1)/2=([2] p)t=[1] in Zq* , 2(q-1)/2  1 (mod q), e per il criterio di Eulero 2 è
resto quadratico modulo q, dunque (2/q)=1, e ciò sappiamo che avviene solo per q  1,7 (mod 8).
Per trovare un divisore primo di Mp (con p primo >2 fissato), si può procedere allora facendo
assumere in successione al parametro t i valori interi positivi t=1,2,…., e verificando con
l’algoritmo della divisione se il numero q=1+2tp è  1,7 (mod 8) ed è divisore di Mp. Il minimo
valore di t per cui ciò avviene fornisce con certezza un divisore primo q di Mp (se q non fosse primo
avrebbe un divisore primo q1<q, ma q1 sarebbe a maggior ragione divisore di Mp, quindi sarebbe
 1,7 (mod 8) e della forma q1=1+2t1p con t1<t, contro la minimalità di t).
Dopo avere trovato un divisore primo q di Mp, si può ripetere il ragionamento sul numero Mp/q per
trovare altri divisori primi di Mp e pervenire infine alla completa fattorizzazione di Mp in prodotto di
primi.
Numeri perfetti.
Un numero naturale n>1 è detto perfetto se n coincide con la somma dei suoi divisori <n.
Per esempio n=6 è perfetto in quanto 6=1+2+3; n=8 non è perfetto in quanto 81+2+4.
Se per ogni naturale n>1 definiamo la funzione (n) uguale alla somma di tutti i divisori di n
(incluso n), si ha che un naturale n>1 è perfetto se e solo se (n)=2n.
Se n è un naturale >1, e se la fattorizzazione di n in prodotto di potenze di primi distinti è:
n= p1k1 p2 k2 .... pr kr (pi primi distinti, ki >0)
allora (per la fattorizzazione unica) ogni divisore d di n ha la forma:
d= p1h1 p2h2 .... pr hr con 0  hi  ki per ogni i=1,….,r
dunque si ha la seguente formula per il calcolo di (n):
(n) =
r

i 1
0 hi  ki
p1h1 p2 h2 .... pr hr
Teorema.
Se n,m sono naturali >1 coprimi, si ha (nm)=(n)(m).
Dimostrazione:
Se le fattorizzazioni di n,m in prodotto di potenze di primi distinti sono rispettivamente:
n= p1k1 p2 k2 .... pr kr
m= pr 1kr 1 pr  2 kr 2 .... ps ks
(i fattori primi di n sono distinti da quelli di m perché n, m sono coprimi) la fattorizzazione di nm in
prodotto di potenze di primi distinti è:
nm= p1k1 p2 k2 .... pr kr pr 1kr 1 pr  2 kr 2 .... ps ks
e per la proprietà distributiva si ottiene:
(n)(m)= (
r

i 1
0 hi  ki
s
p1h1 .... pr hr )(

i  r 1
0 hi  ki
s
pr 1hr 1 .... ps hs ) =

i 1
0 hi  ki
p1h1 p2 h2 .... pr hs =(nm).
Vedremo che vi è uno stretto legame fra la teoria di numeri perfetti e quella dei numeri di
Mersenne.
Cominceremo con la dimostrazione del seguente risultato di Euclide:
Teorema (Euclide).
Se il numero di Mersenne Mk=2k-1 è primo, il numero n=2k-1(2k-1)=2kM è perfetto (e ovviamente
pari).
Dimostrazione.
Essendo Mk dispari, i numeri 2k-1, Mk sono coprimi, e per un risultato precedente si ha:
(n)=(2k-1)(Mk).
Essendo Mk primo si ha (Mk)=1+Mk=1+(2k-1)= 2k.
I divisori di 2k-1 sono le potenze 20, 21, …., 2k-1, dunque (2k-1)= 20+21+22+….+2k-1=2k-1 (dove si è
sfruttata l’identità (xk-yk)=(x-y)(xk-1+xk-2y+….+xyk-2+ yk-1) per x=2, y=1).
In totale si ottiene (n)=2k(2k-1)=2[2k-1(2k-1)]=2n ed n è perfetto.
Eulero dimostrò il viceversa:
Teorema (Eulero).
Se n è un numero naturale pari perfetto, allora n è della forma n=2k-1Mk dove Mk=2k-1 è un numero
di Mersenne primo.
Dimostrazione:
Poiché n è pari, se 2t (con t>0) è la massima potenza di 2 che divide n, si può scrivere n=2tm con m
dispari.
Poniamo k=t+1>1, in modo che n=2k-1m.
Essendo m dispari, i numeri 2k-1, m sono coprimi, e dunque (n)=(2k-1)(m).
Come nella dimostrazione del Teorema precedente si ha (2k-1)=2k-1.
Poiché n è perfetto per ipotesi, si ottiene 2km=2n=(n)=(2k-1)(m)=(2k-1)(m).
Dunque 2k-1 è divisore del prodotto 2km; ma 2k, 2k-1 sono coprimi (perché consecutivi), quindi 2k-1
è divisore del fattore m, e si ha m=(2k-1)M, con M naturale divisore di m.
Sostituendo si ha: 2km=2k(2k-1)M=(2k-1)(m), da cui (m)=2kM.
Si ha allora m+M=(2k-1)M+M=2kM=(m).
Essendo m,M entrambi divisori di m, ed essendo (m) la somma di tutti i divisori di m, concludiamo
che m,M sono gli unici divisori di m (e dunque necessariamente M=1), ossia m è primo ed inoltre:
m=(2k-1)M=(2k-1)=Mk, ed n=2k-1m=2k-1Mk, come voleva la tesi.