LA VARIABILE CASUALE “CHI QUADRO” 2
Si chiama chi quadro con k gradi di libertà la somma dei quadrati di k variabili gaussiane
indipendenti, centrate e ridotte (sono anche dette gaussiane standardizzate).
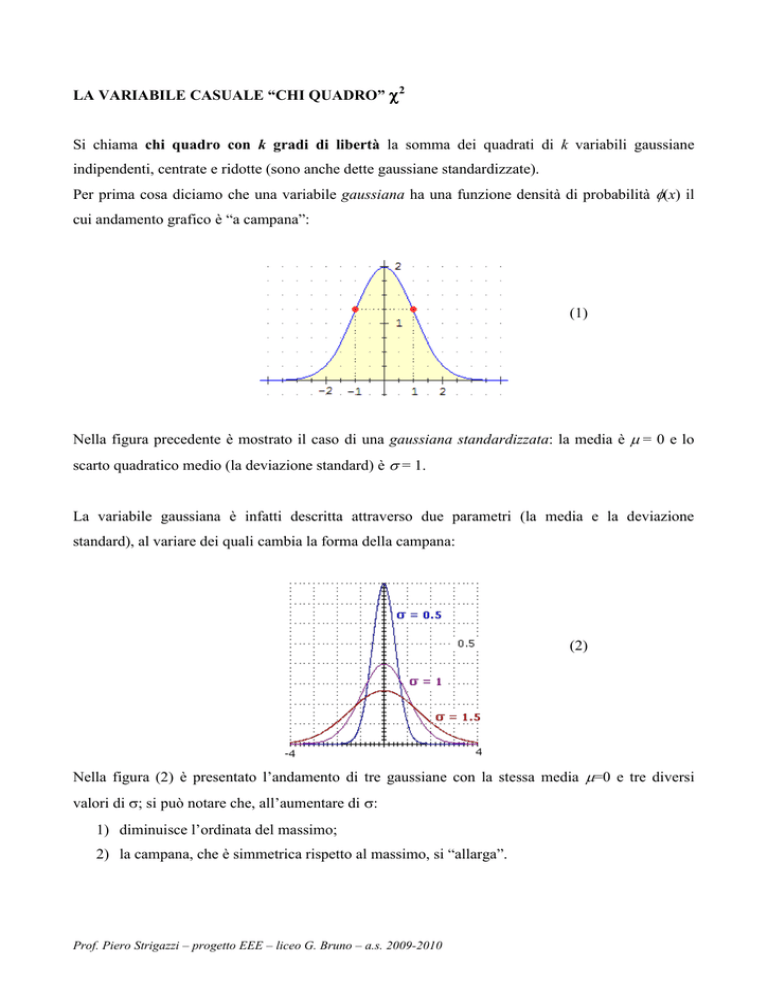
Per prima cosa diciamo che una variabile gaussiana ha una funzione densità di probabilità (x) il
cui andamento grafico è “a campana”:
(1)
Nella figura precedente è mostrato il caso di una gaussiana standardizzata: la media è = 0 e lo
scarto quadratico medio (la deviazione standard) è = 1.
La variabile gaussiana è infatti descritta attraverso due parametri (la media e la deviazione
standard), al variare dei quali cambia la forma della campana:
(2)
Nella figura (2) è presentato l’andamento di tre gaussiane con la stessa media =0 e tre diversi
valori di ; si può notare che, all’aumentare di :
1) diminuisce l’ordinata del massimo;
2) la campana, che è simmetrica rispetto al massimo, si “allarga”.
Prof. Piero Strigazzi – progetto EEE – liceo G. Bruno – a.s. 2009-2010
Il parametro , invece, rappresenta la posizione (in ascissa) del massimo: nella figura successiva si
vede che cosa capita se variano sia che .
Premesso questo, la definizione di una variabile 2 è:
2 z12 z 2 2 ...... z k 2
Per rendere standardizzata una variabile gaussiana x che ha media e deviazione standard , è
sufficiente definire la trasformazione:
z
x
Quindi una variabile 2 con k gradi di libertà si presenta nella forma:
2
x1 1 2 x2 2 2
12
22
.......
xk k 2
k2
La funzione densità di probabilità di una variabile 2 ha l’andamento presentato nel grafico
successivo: (in ascissa c’è la variabile 2 , in ordinata il valore della densità di probabilità
corrispondente; la probabilità che 2 sia compreso fra due valori a e b è l’area sottesa dal grafico fra
quei due valori):
Prof. Piero Strigazzi – progetto EEE – liceo G. Bruno – a.s. 2009-2010
Funzione densità di probabilità di 2 con k gradi di libertà
A parte il caso “degenere” k=1, in cui la somma che definisce il 2 ha un solo addendo, in tutti gli
altri casi la funzione densità di probabilità assume il valore massimo in corrispondenza dell’ascissa:
2 max k 2
Come tutte le funzioni densità di probabilità, le ordinate assumono soltanto valori positivi o nulli;
essendo la variabile 2 definita come una somma di quadrati, anche le ascisse assumono solo valori
positivi o nulli (quindi è corretto che il grafico precedente sia tutto contenuto nel I quadrante).
Si può notare una asimmetria del grafico rispetto al massimo, così come una asimmetria rispetto a
qualunque altra retta verticale: si osserva, però, che all’aumentare di k la simmetria sembra
presentarsi. Infatti si può dimostrare che, se k diventa “molto grande”, il 2 diventa una variabile
gaussiana (è una delle tesi del “teorema del limite centrale”).
Si può dimostrare che la media della variabile 2 con k gradi di libertà è:
= k
e che la deviazione standard è:
=
2k
Prof. Piero Strigazzi – progetto EEE – liceo G. Bruno – a.s. 2009-2010
In conclusione, il grafico della funzione densità di probabilità per una variabile 2 con k gradi di
libertà (da k=2 in poi) è:
(2)
2
1) Osserviamo che, in generale, il punto di massimo di una densità di probabilità non
necessariamente coincide con il valore più probabile (chiamato valore atteso o media): è proprio il
caso della variabile 2 . Per essa, infatti, il valore più probabile è = <2> = k mentre il massimo
ha ascissa 2max = k-2.
2) Lo scarto quadratico medio è un indice (chiamato di dispersione) che informa su come la
variabile indipendente è distribuita intorno al valore medio: dire che =
2k significa che i valori
della variabile chi quadro sono massimamente concentrati, rispetto al valore <2> = k, in un intorno
di ampiezza
2k .
Un esempio finale:
Se k = 9, allora il massimo della distribuzione si trova per il valore della variabile 2 = 7; il valore
più probabile della variabile è <2> = 9; i valori del 2 sono massimamente distribuiti attorno al
valore 9 in un intervallo che è:
9- 18 ≤ 2 ≤ 9 + 18 ,
cioè circa
4.8 ≤ 2 ≤ 13.8
Prof. Piero Strigazzi – progetto EEE – liceo G. Bruno – a.s. 2009-2010
IL FORMULARIO:
Per chi fosse interessato al calcolo, la funzione densità di probabilità del 2 con k gradi di libertà è:
x N x
k
1
2
e
x
2
dove:
x = 2 è la variabile casuale,
N è un coefficiente “di normalizzazione”, definito in modo che l’area sottesa dal grafico di (x) tra
0 e +∞ sia 1 (cioè in modo che sia un evento certo il fatto che 2 assuma uno dei suoi possibili
valori…!); N = 2 k/2 (2k-1)(2k-3)…..1∙ /2k
Il valore medio si calcola:
x x dx
0
la varianza 2 (da cui =
2 ) si calcola:
x x 2 dx
2
0
Prof. Piero Strigazzi – progetto EEE – liceo G. Bruno – a.s. 2009-2010