Problema Faro - Europa Digital School

Calcolare l’altezza di una torre (o di un albero, o di un’antenna, ecc..) AB il cui
piede A non appoggia sul piano orizzontale ove opera l’osservatore
Le condizioni di questo problema si possono schematizzare supponendo, ad esempio,
che la torre da misurare si trovi su una strada in salita o in discesa.
Come nel problema precedente dobbiamo distinguere due casi.
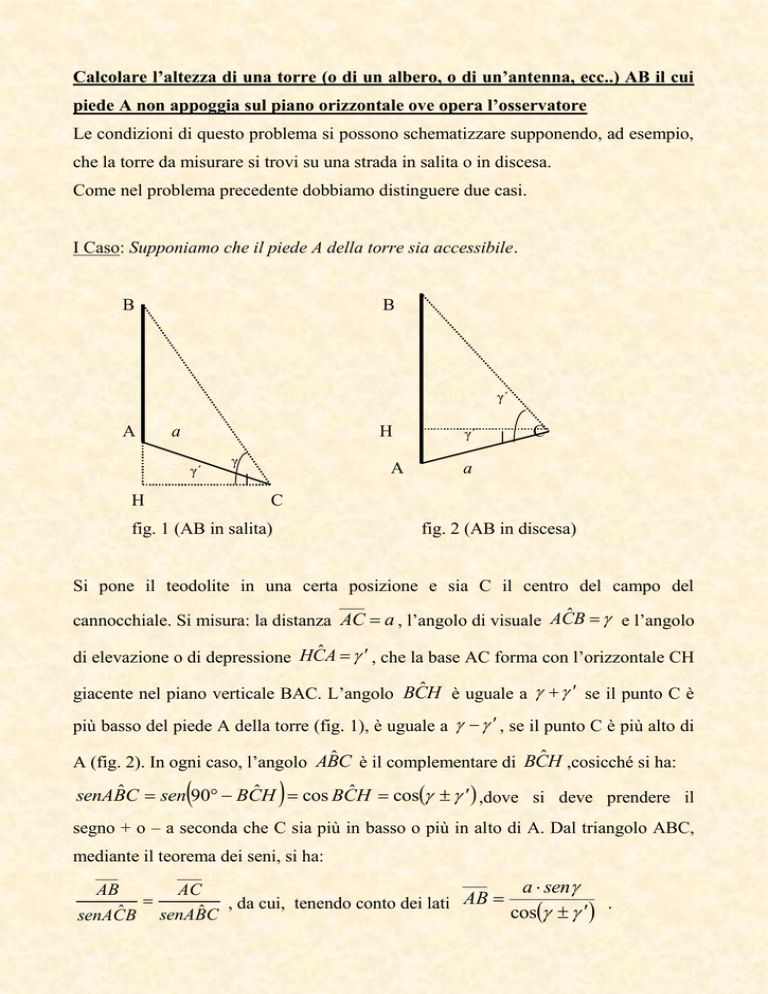
I Caso: Supponiamo che il piede A della torre sia accessibile.
B
B
γ΄
A
a
H
γ΄
H
γ
A
γ΄
C
a
C
fig. 1 (AB in salita)
fig. 2 (AB in discesa)
Si pone il teodolite in una certa posizione e sia C il centro del campo del
cannocchiale. Si misura: la distanza AC  a , l’angolo di visuale ACˆ B   e l’angolo
di elevazione o di depressione HCˆ A    , che la base AC forma con l’orizzontale CH
giacente nel piano verticale BAC. L’angolo BCˆ H è uguale a     se il punto C è
più basso del piede A della torre (fig. 1), è uguale a     , se il punto C è più alto di
A (fig. 2). In ogni caso, l’angolo ABˆ C è il complementare di BCˆ H ,cosicché si ha:


senABˆ C  sen 90  BCˆ H  cos BCˆ H  cos    ,dove si deve prendere il
segno + o – a seconda che C sia più in basso o più in alto di A. Dal triangolo ABC,
mediante il teorema dei seni, si ha:
a  sen
AB
AC
AB 

,
da
cui,
tenendo
conto
dei
lati
.
cos   
senACˆ B senABˆ C
II Caso: Supponiamo che il piede A della torre sia inaccessibile.
B
A
H
B
K
γ
α
C δ
α
K
γ
H
D
fig. 3 (AB in salita)
α
α
δ
D
C a
A
fig. 4 (AB in discesa)
Supponiamo, che sia possibile prendere una base CD  a , allineata con A, e si
misurino gli angoli
ACˆ B   ,
ADˆ B   , sotto cui è vista la torre AB,
rispettivamente, da C e D. Si misura, poi, l’angolo α, di elevazione o di depressione,
che la base CD forma con le orizzontali CH e DK, passanti rispettivamente per C e , e
giacenti nel piano verticale ABC. Osserviamo, inoltre, che CBˆ D     , e quindi,
per il teorema dei seni, dal triangolo BCD si ricava che BC 
a  sen
. Inoltre, se la
sen   
ˆ C  90   , mentre, se è più alta di A
base CD è più bassa di A (fig. 3) risulta BA
ˆ C  90   . Di conseguenza, applicando il teorema dei seni al
(fig. 4) risulta BA
triangolo ABC si ottiene che AB 
BC  sen
. Tenendo conto delle quantità trovate
senBAˆ C
in precedenza e sapendo che sen90     cos , si deduce che l’altezza della torre
è data da AB 
a  sen  sen
.
cos   sen   