CAPITOLO 5
Il campo magnetico (4° parte)
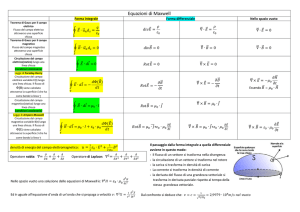
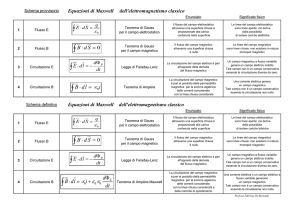
Il flusso del campo magnetico B attraverso una superficie S è uguale al prodotto scalare tra il vettore B e il versore n
perpendicolare alla superficie, moltiplicato per il valore della superficie S. Φ = B ∙ n S = B S cosα
In generale dove la superficie non è piana o il campo non è uniforme in tutti i punti della superficie è necessario
suddividere la superficie in parti molto piccole da considerarle piane e sommare i flussi.
Il flusso generato da un filo percorso da corrente su una superficie cilindrica è nullo; infatti la direzione del
campo è parallela alle basi e il campo non le attraversa, ma non attraversa neanche la superficie laterale perché è
diretto lungo la tangente. Se consideriamo uno spicchio di cilindro dove non passa il filo conduttore possiamo dire
che il flusso è nullo sulle superfici superiore, inferiore, frontale, posteriore. Sulla superficie destra e sinistra
avremo Φ = BS e Φ = -BS. Perché esse sono disposte lungo i raggi del cilindro e sono perpendicolari alla direzione
del campo, però il verso delle superfici è opposto quindi i due flussi sono uguali, ma di segno opposto; sommando
tutte le componenti torniamo sempre a 0 quindi possiamo concludere che il flusso del campo magnetico
attraverso una qualsiasi superficie chiusa è 0. Questo è il teorema di Gauss. Questo ci fa capire che a differenza
del campo elettrico le linee del campo sono aperte, mentre le linee del campo magnetico sono chiuse, perché nel
campo magnetico non è possibile separare i poli, mentre nel campo elettrico possiamo separare le cariche.
La circuitazione del campo B lungo una linea chiusa è Cb = ∑ B ∙ ∆s dove si intende che la linea generica chiusa sia
stata suddivisa in intervalli piccolissimi ∆s in cui il campo B possa esse considerato costante. La circuitazione è
quindi la somma dei prodotti scalari tra B e ∆s.
Consideriamo il campo generato da un filo percorso da corrente. Le linee di forza del campo sono circonferenze
concentriche con il filo; il modulo del campo è B = ki/r e come ∆s possiamo indicare la circonferenza 2πr quindi
Cb = ∑ B ∙ ∆s = ki2πr/r = μ0 i2πr/2πr = μ0 i. Da qui è evidente che la circuitazione non dipende dal raggio della
circonferenza.
Consideriamo ora la circuitazione lungo una linea ABCDA che non circonda il filo. La circuitazione risulta nulla nei
tratti AB e CD perché in questi tratti il campo è perpendicolare allo spostamento. Nei tratti BC e DA siccome la
circuitazione non dipenda dal raggio è uguale nei due tratti, ma il segno è opposto perché i due tratti vengono percorsi
in senso opposto: i loro contribuiti alla circuitazione si annullano e la circuitazione totale lungo i due tratti è uguale a
0. Possiamo concludere dicendo che la circuitazione lungo una linea chiusa che non circonda il filo è uguale a 0.
Se prendiamo diversi fili percorsi da corrente la circuitazione lungo una linea chiusa che li circonda è la somma
delle circuitazioni dei campi generati dalle singole correnti, ma occorre associare un segno algebrico ad ogni
circuitazione: positivo se il campo generato ha lo stesso verso di percorrenza della linea chiusa, negativo nel caso
opposto. La circuitazione risulta Cb = μ0 (i1 + i2 + i3).
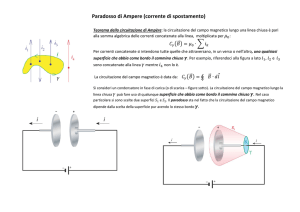
Per determinare quanto detto si introduce in concetto di corrente concatenata. Una corrente si dice concatenata a una
linea chiusa se attraversa la superficie delimitata dalla linea chiusa. Arriviamo cosi ad enunciare il teorema di
Ampere: la circuitazione di un campo magnetico B lungo una linea chiusa è uguale alla somma algebrica delle
correnti concatenate alla linea stessa Cb = μ0 ∑ i. Il teorema di Ampere mette in relazione cosi come il teorema di
Gauss per il campo elettrico, il campo con le sue sorgenti: il campo elettrico e le cariche, il campo magnetico e le
correnti: poiché il campo magnetico ha una circuitazione lungo una linea chiusa diversa da 0 esso non è conservativo
e non è possibile parlare di energia potenziale magnetica. Una forza si dice conservativa quando la sua
circuitazione lungo una linea chiusa è 0.
© Federico Ferranti S.T.A.
www.quintof.com