Correnti alternate con i numeri complessi

ELETTROTECNICA CON I NUMERI COMPLESSI
Premessa
Abbiamo visto (TESTO DI FISICA WALKER pag 63) che in regime di corrente
alternata C.A. in presenza di elementi come condensatori ed induttori viene introdotta
una grandezza detta impedenza che ricopre lo stesso ruolo della resistenza nei circuiti
in corrente continua C.C. in modo da poter continuare ad utilizzare la legge di Ohm
V=RI anche in regime di C.A.
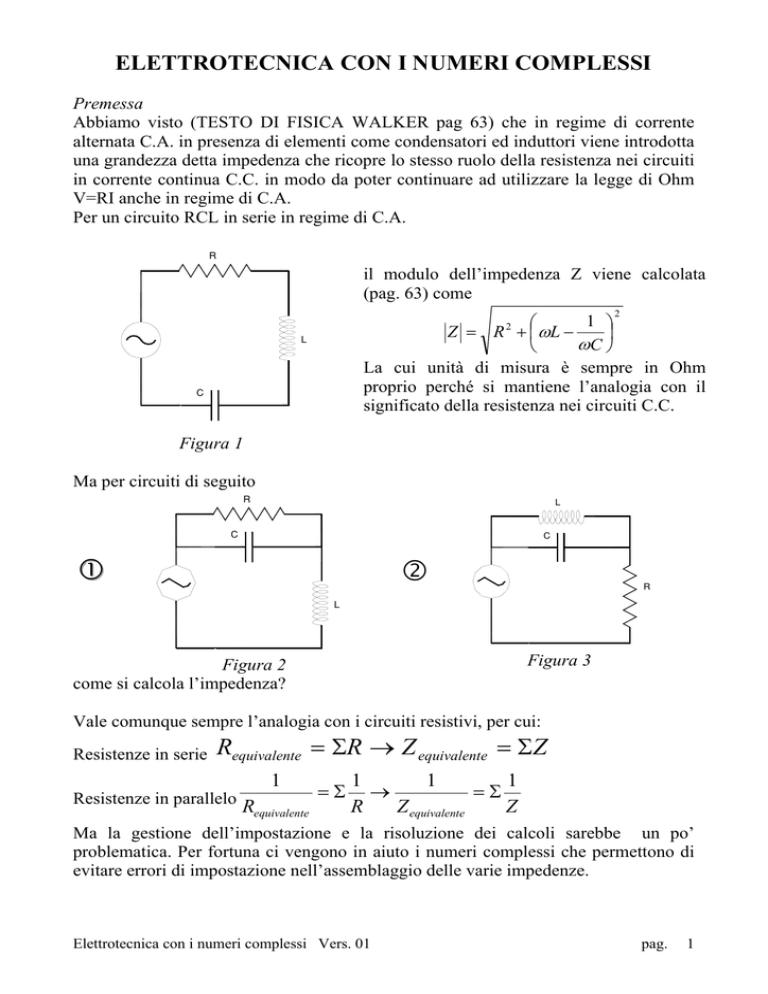
Per un circuito RCL in serie in regime di C.A.
R
il modulo dell’impedenza Z viene calcolata
(pag. 63) come
2
1 

Z  R   L 

C 

La cui unità di misura è sempre in Ohm
proprio perché si mantiene l’analogia con il
significato della resistenza nei circuiti C.C.
2
L
C
Figura 1
Ma per circuiti di seguito
R
L
C
C


R
L
Figura 3
Figura 2
come si calcola l’impedenza?
Vale comunque sempre l’analogia con i circuiti resistivi, per cui:
Resistenze in serie
Requivalente  R  Z equivalente  Z
1
Resistenze in parallelo
Requivalente

1
1
1


R
Z equivalente
Z
Ma la gestione dell’impostazione e la risoluzione dei calcoli sarebbe un po’
problematica. Per fortuna ci vengono in aiuto i numeri complessi che permettono di
evitare errori di impostazione nell’assemblaggio delle varie impedenze.
Elettrotecnica con i numeri complessi Vers. 01
pag.
1
Numeri immaginari e numeri complessi.
La quantità indicata con la lettera i viene assunta unità immaginaria.
Moltiplicando l’unità per sé stessa si ha
i  i  i 2  1
e
di
i 3  i  i 4  i  i  i 2   1  1
i 2  i  i 3  1  i  i
seguito
e così via. Si vede così che alcune potenze
non contengono l’unità immaginaria e quindi risultano numeri reali
Introducendo la rappresentazione del piano di Gauss o Argand l’asse orizzontale
rappresenta i numeri reali, l’asse verticale i numeri immaginari.
Le potenze elencate in precedenza hanno pertanto rappresentazione
i
2
4
i =−1
i=1
3
i=−i
Figura 4
Si può notare che moltiplicando una quantità per l’unità immaginaria i il risultato è
ruotato di /2 in senso antiorario rispetto la quantità iniziale
i
ixi
1xi


4
2
i=1
i =−1

−1 x i
3
i=−i

−i x i
Figura 5
Il numero complesso si scrive (in forma cartesiana)
z  a  ib
Elettrotecnica con i numeri complessi Vers. 01
pag.
2
Dove a è la parte reale e b il coefficiente della parte immaginaria.
La rappresentazione sul piano di Argand allora è
z=a+bi
b
a
O
Figura 6
Il modulo di z indicato anche con si ottiene applicando la regola di Pitagora così
come il modulo di un vettore espresso mediante le componenti cartesiane:
z    a 2  b2
(1)
Nello stesso modo è possibile calcolare l’angolo  che il modulo  del numero
complesso forma con il semiasse positivo orizzontale (numeri reali)
  arctan
b
a
(2)
Z



b
O
a
Figura 7
Moltiplicando un numero complesso per i se ne ottiene un altro ruotato di /2 rispetto
a quello iniziale
Esempio z  4  3i
z  i  4  3i   i  4i  3i 2  3  4i
Dalla rappresentazione cartesiana è evidente che il prodotto z  i è ruotato di /2
Elettrotecnica con i numeri complessi Vers. 01
pag.
3
antiorario rispetto ad z
5
z=−3+4i
4
z=4+3i
3
2


1
1
0
2
3
4
5
Figura 8
Utilizzando la notazione trigonometrica dei numeri complessi questo è maggiormente
evidente.
Il numero complesso z  a  ib espresso in forma trigonometrica è
z   cos   i sin  
dove e sono ottenuti mediante le precedenti formule (1) e (2)
Il prodotto tra due numeri complessi
z1  1 cos 1  i sin 1  e z2   2 cos  2  i sin  2 
si ottiene con la formula z1  z 2  1  2 cos1   2   i sin 1   2  (3)


La quantità immaginaria i si esprime come i  1 cos
Moltiplicando un numero complesso

2
 i sin

.
2
z   cos   i sin  



per i  1 cos  i sin 
2
2

si ottiene
 

 

z  i   cos    i sin    ,
2
2 

 
si vede chiaramente che il risultato del prodotto non è altro che il numero complesso
iniziale ruotato di /2 in senso antiorario
La formula (3) è suscettibile di una ulteriore importante spiegazione fondamentale
nel proseguo. Infatti è possibile interpretare il prodotto di due numeri complessi
considerando z1 come un vettore con l’estremo iniziale nell’origine degli assi e quello
finale in corrispondenza del numero complesso che venendo moltiplicando da z2
modifica il suo modulo 1 del fattore 2 ed è ruotato di un angolo 2
Elettrotecnica con i numeri complessi Vers. 01
pag.
4
Z1 Z

2
2
Z1
2

1

1
1
Dalla figura si vede che il vettore z1
quando è moltiplicato dal vettore z2
modifica il valore del modulo e ruota
dell’angolo 2
(Nota: il ragionamento vale anche
quando ad essere ruotato è z2)

Z2
2
2
O
Figura 9
Con queste premesse allora è possibile esprimere le impedenze in presenza di
condensatori ed induttori: in elettrotecnica per evitare confusioni con il simbolo
della corrente l’unità immaginaria viene indicata con la lettera j
Nello studio delle correnti alternate per poter comprendere meglio il fenomeno si
utilizza il diagramma a fasori (pag. 49) in cui Vmax ed Imax sono rappresentati come
vettori rotanti con velocità di rotazione pari ad  (la pulsazione della tensione
alternata che alimenta il circuito).
I valori istantanei di V ed I sono le proiezioni sull’asse verticale del riferimento di
Vmax ed Imax
Circuito Induttivo
Nel circuito che presenta una in’induttanza L sappiamo dalla legge di Ohm che
V  X L  I  L   I
con la tensione V che anticipa la corrente I di /2. (pag 59).
Il diagramma dei fasori è:


max
V(t)


t
I(t)
max
Figura 10
Elettrotecnica con i numeri complessi Vers. 01
pag.
5
Considerando il piano di riferimento xy come se fosse il piano di Gauss cioè trattando
sia V che I come numeri complessi possiamo esprimere il fatto che la tensione V
anticipa la corrente I di /2, moltiplicando la corrente I oltre che per il modulo di XL
anche per l’unità immaginaria j ovvero
V  L  I  j
V  Lj   I
X L  Lj
Inglobando l’unita immaginaria nella reattanza
si ha in definitiva:
Circuito Capacitivo
Nel circuito che presenta un condensatore C sappiamo dalla legge di Ohm che
 1 
V  XC  I  
I
 C 
con la tensione V che ritarda sulla corrente I di /2. (pag 55).
Il diagramma dei fasori è:


max
I(t)


t
V(t)
max
Figura 11
Come nel caso precedente trattando sia V che I come numeri complessi esprimiamo il
fatto che la tensione V ritarda sulla corrente I la corrente I di /2, moltiplicando la
corrente I oltre che per il modulo di XC anche per -j (con segno negativo perché si
deve ottenere una rotazione oraria) si ha:
V 
1
 I   j 
C
Inglobando l’unita immaginaria nella reattanza si ha
 j
V 
 I
C



per cui si ottiene
XC  
j
C
Tuttavia si preferisce esprimere la reattanza capacitiva nel seguente modo
j j  j 2   1
1
XC  


 XC 
C j Cj
Cj
Cj
Elettrotecnica con i numeri complessi Vers. 01
pag.
6
In conclusione le reattanze per condensatori ed induttanze si esprimono mediante i
numeri complessi:
X L  Lj
XC 
1
Cj
Questa notazione delle Reattanze rende il calcolo delle impedenze più facile.
Riprendiamo in esame il circuito RLC in serie di cui già conosciamo il valore
dell’impedenza.
Con l’utilizzo dei numeri complessi tutto ilo calcolo è più rapido.
I tre elementi sono disposti in serie perciò
Z equivalente  Z  R  X L  X C  R  Lj 
1
Cj
Applicando le regole di calcolo dei numeri complessi
Z eq  R  Lj 
1 j
1 
j

  R  Lj 




R
L

j
2
Cj j
Cj
C 

Cioè Z è espresso mediante un numero complesso
aR
z  a  jb
b  L 
e
con
1
C
Il modulo si calcola mediante la formula (1) e vale:
Z  a b 
2
2
1 

R   L 

C 

2
2
come già calcolato con altro metodo (pag. 63)
CALCOLO DELLO SFASAMENTO TRA LA TENSIONE e LA CORRENTE
I e V sono sfasati ma non di /2 come nei circuiti elementari con solo condensatore e


solo induttanza ma di un angolo     
2
2
Riprendiamo la legge in Ohm riscritta in forma generale V  Z  I
Considerando Z ed I come numeri complessi e tenendo presente la formula di
moltiplicazione tra due numeri complessi e con quanto detto in precedenza (figura 9)
la tensione V risulta ruotata rispetto alla corrente I dall’impedenza Z.
Quanto vale questa rotazione?
Elettrotecnica con i numeri complessi Vers. 01
pag.
7
Z è espresso nella forma Z  R  Xj dove R indica la parte reale dell’impedenza
(e non la resistenza) ed X (detta Reattanza) il coefficiente della parte immaginaria
quindi mediante la formula (2) possiamo esprimere l’angolo che V ed I formano
  arctan
X
R
(4)
X
 0 allora la tensione V precede I
R
X
 0 allora la corrente I precede V
Se   0 
R
Se   0 
Risultato generale: Espressa l’impedenza come numero complesso lo sfasamento
non
è altro che l’arcotangente del rapporto tra le componenti immaginaria
(reattanza X) e la componente reale dell’impedenza.
ATTENZIONE questi valori forniscono il valore dell’impedenza equivalente e dello
sfasamento tra la tensione e la corrente che passa al generatore. Sui singoli rami
bisogna ragionare localmente
Consideriamo ora il circuito ccoom
mppoossttoo ddaa uunnaa rreessiisstteennzzaa R
R eedd uunn ccoonnddeennssaattoorree ddii
ccaappaacciittàà C
C ddiissppoossttii iinn ppaarraalllleelloo.. SSii hhaa
R
Si ha allora
z1  R
C
z2  X C 
1
Cj
Figura 12
1
1 1
1  RCj
R
    Cj 
 Z eq 
1  RCj
Z eq
Z R
R
M
Maa llaa ZZeeeqqq vvaa eesspprreessssaa ppeerr eesssseerree uuttiilliizzzzaattaa pprrooffiiccuuaam
meennttee nneellllaa ffoorrm
maa z  a  jb
quindi vanno applicato le tecniche di calcolo per i numeri complessi. Moltiplicando
numeratore e denominatore per il coniugato del denominatore si ha
Elettrotecnica con i numeri complessi Vers. 01
pag.
8
Z eq ,TOTALE  Z eq1 / 2
R
R  R 2 Cj
R
R 2 C
1  RCj
 Z3 


j


1  RCj 1  RCj 1   2 R 2 C 2 j 2 1   2 R 2 C 2 1   2 R 2 C 2
Il modulo di z vale
Z eq 
1  
R2
2
2
RC

 2 R 4C 2
 1  
2 2
2
2
RC

2 2

1  
R2
2
2
RC

2 2
1  
2
R 2C 2
cioè
Z eq 
R2
1   2 R 2C 2


Applicando la legge di Ohm è possibile ricavare la corrente I al generatore
I
1
V
1

 I V 
 Z eq  V    Cj 
Z eq
Z eq
R

Lo sfasamento vale
R 2 C
X 1   2 R 2C 2
  arctan 
 arctan RC 
R
R
1   2 R 2C 2
  arctan RC 

Consideriamo ora il circuito
ccoom
mppoossttoo ddaa R
R ee C
C iinn ppaarraalllleelloo ddiissppoossttoo
iinn sseerriiee ccoonn LL
Z 1= R
Z 2= 1
 Cj
Z 3= Lj
Figura 13
Per il parallelo tra Z1 e Z2 si può utilizzare il precedente risultato ottenuto per cui
aggiungendo Z3 in serie
Elettrotecnica con i numeri complessi Vers. 01
pag.
9

Z eq ,TOTALE  Z eq1/ 2
da cui

R
R 2 C
 Z 3  

2 2 2
1
1   2 R 2C 2
  R C
Z eq ,TOTALE

j   Lj



R
R 2C
j


L



2 2 2 

1   2 R 2C 2
1

R
C



Ovviamente il calcolo del modulo di Z si fa con la medesima formula precedente
anche se il risultato diventa estremamente ingombrante.
Ed è possibile calcolare lo sfasamento sfruttando la relazione sulle componenti
dell’impedenza


R 2C

  L 
2 2 2 
R
C

1

b
 L   2 LR 2C 2  R 2C


  arctan  arctan 
 arctan
R
a
R
2 2 2
1  R C


Era più rapido ragionare partendo dalle singole impedenze
1
Z Z
j C
 1 2  Z3 
 Lj
svolgendo i calcoli
1
Z1  Z 2
R
j C
R
1  RjC
R
R
j C

 Lj 
 Lj 

 Lj 
RjC  1
RjC  1
RjC  1 1  RjC
j C
R
Z eq ,TOTALE
Z eq ,TOTALE


R 2C
R
R  R 2 j C

j







L
Lj
2 2 2 

1  R 2 2C 2
1   2 R 2C 2
1


R
C


Elettrotecnica con i numeri complessi Vers. 01
pag. 10
Z1=Lj

Consideriamo ora il circuito
ccoom
mppoossttoo ddaa LL ee C
C iinn ppaarraalllleelloo ddiissppoossttoo
iinn sseerriiee ccoonn R
R
Z2= 1
 Cj
Z3= R
R
Figura 14
Possiamo ragionare velocemente
1
L
Z Z
Lj
j C
 1 2  Z3 
 R  2 2C
R
R
2
1

j
LC
1

Z1  Z 2
1


LC
j L 
jC
j C
j L
Z eq ,TOTALE
Z eq ,TOTALE  R 
Modulo Z eq
L
j
1   2 LC
 2 L2
 R 
1   2 LC 2
2
L
b
1   2 LC  arctan


arctan

arctan
Sfasamento
a
R
con
L
R 1   2 LC 
  0 se 1 -  2 LC  0
Elettrotecnica con i numeri complessi Vers. 01
pag. 11
A questo punto possiamo ampliare i
casi, ad esempio
Z 1= R 1
Z 2= 1
 Cj
Z 3=  L1 j
Z 4= L2 j
Figura 15
Z 5= R 2
Applichiamo le regole di composizione delle impedenze:
Z eq ,TOTALE 
Z1  Z 2
Z Z
 Z3  4 5
Z1  Z 2
Z 4  Z5
1
jL2  R2
R1
jL2  R2
j C

 jL1 

 jL1 
1
jL2  R2 jR1C  1
jL2  R2
R1 
j C
R1
Z eq ,TOTALE
Applicando alle frazioni il coniugato del denominatore
Z eq ,TOTALE 
R1
1  jR1C
jL2  R2 1  jR2C



 jL1 
jR1C  1 1  jR1C
jR2C  1 1  jR2C
R1  R12Cj
 2 L2  R22C  L2 R2 j

 jL1 
1   2 R12C 2
1   2 R22C 2
Ed infine
Z eq ,TOTALE

R1
R12C
 2 L2  R22C  
L2 R2 j 

j

L

 




1
2 2 2
2 2 2 
2 2 2
2 2 2 

1   R2 C  
1   R1 C 1 1   R2 C 
 1   R1 C
Buon divertimento per il calcolo del modulo e dello sfasamento tra corrente e
tensione al generatore sempre applicando le formule precedenti.
Elettrotecnica con i numeri complessi Vers. 01
pag. 12
Z 1= R 1
E ci possiamo sbizzarire
Z 2= 1
 C1 j
Z 3= L1 j
Z 4= L2 j
Z 5= R 2
Figura 16
Z 6= 1
 C2 j
Per le impedenze in parallelo Z4 , Z5 e Z6 vale:
1
Z equivalente4 / 5 / 6

 Z equivalente4 / 5 / 6 
1
1
1
1
Z5  Z6  Z4  Z6  Z4  Z6





Z Z 4 Z 5 Z 6 Z 4  Z 5  Z 6 Z 4  Z 5  Z 4  Z 6  Z 5  Z 4
Z 4  Z 5  Z 6
Z 4  Z5  Z4  Z6  Z5  Z4
Per cui la formula generale dell’impedenza equivalente per il circuito di figura 16
risulta:
Z eq ,TOTALE 
Z1  Z 2
Z 4  Z 5  Z 6
 Z3 
Z1  Z 2
Z 4  Z5  Z 4  Z6  Z5  Z 4
Tuttavia il calcolo delle tre impedenze in parallelo conviene farlo direttamente
1
Z equivalente4 / 5 / 6
1
1
R2  L2 j   2 L2 R2C2


 C 2 j 

L2 j R2
L2 R2 j
Z equivalente4 / 5 / 6 
L2 R2 j
R2  L2 j   2 L2 R2C2
moltiplicando per il coniugato del denominatore
Z equivalente 4 / 5 / 6
L2 R2 j
R2   2 L2 R2 C 2  L2 j


R2  L2 j   2 L2 R2 C 2 R2   2 L2 R2 C 2  L2 j
Elettrotecnica con i numeri complessi Vers. 01
pag. 13
Si ha infine per le tre impedenze in parallelo:
Z equivalente  4 / 5 / 6
 2 L22 R2  L2 R22 1   2 L2C2  j

2
R22 1   2 L2C2    2 L22
Ovviamente questa soluzione parziale
del circuito di figura 16 è direttamente
applicabile anche
nel caso siano
presente SOLO le tre impedenze R, C ed
L parallelo
Z 1= Lj
Z 2= R
Z 3= 1
 Cj
Figura 17
Z equivalente RCL in parallelo 
 2 L2 R  LR 2 1   2 LC  j


R 2 1   2 LC   2 L2
2
Riprendiamo in esame l’impedenza del circuito di figura 16
1
 2 L22 R2  L2 R22 1   2 L2C2 j
j C

 jL1 

2
2
2
2 2
1
R2 1   L2C2   L2
R1 
j C

R1
Z eq ,TOTALE





R1
 2 L22 R2  L2 R22 1   2 L2C2 j

 jL1 

2
2
2
2 2
jR1C  1
R2 1   L2C2   L2

R1  R12Cj
2

 jL1 
1   2 R12C 2

L R  L R 1   L C  j
..............continua
R 1   L C    L
2
2
2
2
2
Elettrotecnica con i numeri complessi Vers. 01
2
2
2
2
2
2
2
2
2
2
2
2
2
pag. 14