Il triangolo

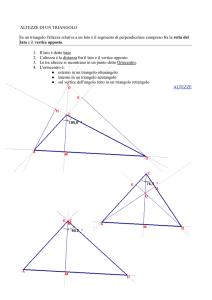
Il triangolo
Il triangolo ha sempre esercitato un fascino particolare sui matematici di tutti i tempi,
infatti è la figura geometrica sulla quale si sono maggiormente concentrati gli studi e della
quale sono stata scoperte più proprietà. Già Euclide gli aveva riservato molto spazio, a
partire dalla prima proposizione del suo primo libro degli ”Elementi”, dove viene
dimostrata la costruibilità le triangolo equilatero a partire da un lato. Euclide dedica allo
studio del triangolo gran parte del primo libro che si conclude con la dimostrazione del
Teorema di Pitagora. Anche nel Libro II ci sono due proposizioni che trattano del triangolo
(note oggi come Teorema di Carnot). Nei Libri IV e VI Euclide torna a parlare di triangolo,
fino alla proposizione 8 e al suo corollario dove si dimostrano i teoremi noti oggi come I e
II Teorema di Euclide.
Ma la geometria non si esaurisce con il lavoro del suo fondatore, infatti moltissimi
matematici dopo di lui hanno scoperto importanti proprietà delle figure, in particolar modo
dei triangoli; per esempio Euclide non ne trattò mai i punti notevoli, probabilmente perché
questi argomenti non erano finalizzati ai suoi scopi.
Nella pratica scolastica i triangoli andrebbero introdotti nel primo biennio delle scuole
superiori in modo rigoroso, in modo da inserirli nel sistema formale che si sta costruendo.
Dopo la trattazione degli enti primitivi e degli assiomi, si passa alla
Definizione: Dati tre punti non allineati A,B,C, si dice triangolo ABC il sottoinsieme del
piano dato dall’intersezione dei tre angoli convessi CAB, ABC e BCA
A questo punto si tratta la relazione di congruenza e la congruenza dei segmenti nei
triangoli per stabilire la classificazione dei triangoli e la loro costruzione con riga e
compasso. Si descrivono poi i concetti di bisettrice, punto medio, perpendicolare, asse e le
relative costruzioni, con la funzione di tracciare i segmenti notevoli di un triangolo.
Si introduce poi la congruenza dei triangoli con il primo criterio di congruenza dei triangoli
(introdotto come assioma) grazie al quale si possono dimostrare il secondo e il terzo
criterio. E’ giunto il momento di passare alla dimostrazione dei primi risultati sul triangolo,
già presenti in Euclide; sono teoremi la cui verità sembra molto intuitiva ma la loro
dimostrazione permette di addentrarci nel sistema di regole che si sta costruendo:
- Angoli opposti al vertice sono congruenti, Teorema dell’angolo esterno
- In un triangolo a lato maggiore è opposto angolo maggiore
- In un triangolo, ad angoli congruenti sono opposti lati congruenti
- In un triangolo ad angolo maggiore è opposto lato maggiore
- Teorema della disuguaglianza triangolare
- Assioma della parallela e sue conseguenze, Teorema di Talete
- La somma degli angoli interni di un triangolo è un angolo piatto
Una volta verificati questi prerequisiti passiamo ora a descrivere un percorso didattico sul
triangolo, partendo proprio dai suoi punti notevoli. Di ognuno di essi mostriamo prima
l’esistenza, tramite la costruzione effettiva il laboratorio di informatica. A tal proposito
verrà data la seguente scheda ai ragazzi:
Passo 1) Circocentro
∙ Costruire un triangolo ABC
∙ Costruire
- l’asse a di BC
- l’asse b di CA
- l’asse c di AB
I tre assi a,b,c si incontrano in un punto?
Se sì, chiamare il punto K (è il CIRCOCENTRO), se no, provare a rifare la costruzione.
∙ Muovere i punti A,B,C e rispondere alle seguenti domane:
- Se il triangolo è rettangolo in A, dove si trova K?
- Se il triangolo è ottusangolo?
- Se il triangolo è rettangolo?
∙ Costruire la circonferenza con centro in K e passante per uno dei vertici del triangolo
- Cosa puoi notare?
- Come è il punto K rispetto ai vertici del triangolo?
Passo 2) Incentro
∙ Cancellare la costruzione sul triangolo e mantenere solo il punto K (etichettato)
∙ Costruire
- la bisettrice in A
- la bisettrice in B
- la bisettrice in C
Le tre bisettrici si incontrano in un punto?
Se sì, chiamare il punto I (è l’INCENTRO), altrimenti rifare la costruzione.
∙ Muovere i punti A,B,C
- Come si posiziona I?
- E’ possibile farlo uscire dal triangolo?
∙ Costruire la circonferenza con centro in I e tangente ad uno dei lati del triangolo
- Cosa noti?
- Come è il punto I rispetto ai lati del triangolo
Passo 3) Ortocentro
∙ Cancellare la costruzione sul triangolo e mantenere solo i punto K ed I (etichettati)
∙ Costruire la perpendicolare ad AB passante per C (altezza relativa ad AB)
∙ Costruire la perpendicolare a BC passante per A (altezza relativa a BC)
∙ Costruire la perpendicolare ad AC passante per B (altezza relativa ad AC)
Le tre altezze si incontrano in un punto?
Se sì, chiamare il punto O (è l’ORTOCENTRO), altrimenti, rifare la costruzione.
Muovere i punti A,B,C
- Come si posiziona O?
- E’ possibile farlo uscire dal triangolo?
Passo 4) Baricentro
∙ Cancellare la costruzione sul triangolo e mantenere solo i punto O, K ed I (etichettati)
∙ Costruire :
- il segmento passante per il punto medio del lato AB e il punto C
- il segmento passante per il punto medio del lato AC e il punto B
- il segmento passante per il punto medio del lato CB e il punto A
Sono le tre mediane del triangolo
Le tre mediane si incontrano in un punto?
Se sì, chiamare il punto G (è il BARICENTRO), se no, rifare la costruzione.
∙ Muovere i punti A,B,C
- Come si posiziona G?
- E’ possibile farlo uscire dal triangolo?
Passo 5) LA
RETTA DI EULERO
Muovendo i vertici del triangolo noti che tre punti sono sempre allineati?
Costruisci la retta che passa per due di essi e verificalo!
Quali sono questi tre punti?
Misura le distanze che intercorrono tra questi punti: cosa puoi notare?
La retta che hai costruito è la Retta di Eulero e non sono in molti a conoscerla tu sei uno di
essi!!
Motivazioni al percorso didattico
Completata la scheda, potrebbe succedere che qualche alunno si mostri perplesso sul
risultato ottenuto, infatti secondo la geometria che stiamo costruendo prevede, per dirla alla
Euclide, una retta senza larghezza, ma questo nel laboratorio non può accadere perché
stiamo lavorando con oggetti reali: sullo schermo del computer le rette assumono una
larghezza, data dalle dimensioni dei pixel. Quindi è lecito il dubbio che la concorrenza di
tre rette in un punto sia soltanto apparente, dovuta agli spessori delle rette. Se la
discussione non nasce spontanea, è compito dell’insegnante stimolare una riflessione sui
limiti del laboatorio e sulla sua insufficienza per validare una proprietà nel sistema formale.
E’ necessario sottolineare il fatto che la congettura fatta in laboratorio debba essere
confermata, facendo sviluppare i concetti intuiti in un sistema teorico con un linguaggio
preciso e rigoroso. Se non ci si riesce, si deve provare a cercare un controesempio,
esibendo una figura particolare, ove questo non accade. Per esempio, se la congettura fosse
”il circocentro è sempre all’interno di un triangolo” e questa non trovasse riscontro nella
teoria, si può provare a cercare una figura dove questo non accade, come nel caso del
triangolo ottusangolo. Per fugare i nostri dubbi sull’esattezza delle congetture, allora
cerchiamone una dimostrazione formale. Un modo per comprendere meglio le
dimostrazioni eseguite in classe è quello di rifarle a casa, ricostruendo i vari passaggi
matematici sul software Cabri, così da seguirne meglio lo sviluppo, esaminando i vari casi
particolari.
Per questo è stato scelto un percorso didattico di questo tipo: le dimostrazioni di questo
segmento partono da congetture elaborate in laboratorio con l’ausilio del software Cabri
che permette il passaggio tra l’immagine e la teoria, grazie a disegni molto precisi. Oltre ad
aiutare a scoprire relazione nelle figure, il Cabri collabora attivamente anche nella
comprensione delle dimostrazioni seguenti, infatti esse sono tutte costruttive, nelle quali il
risultato viene costruito con passaggi successivi che possono essere seguiti facilmente e
analizzati nei casi particolari, una volta riportati sullo schermo.
Queste due fasi diverse ma complementari sono caratteristiche della geometria euclidea,
cui spetta il ruolo, nella scuola superiore, di stimolare ad operare congetture, sviluppare
intuizione spaziale e infine cercare di ricavare dimostrazioni. Il segmento didattico
seguente si muove in tal senso, in quanto viene stimolato l’approccio deduttivo, dopo una
fase di congettura. Ad esempio l’esistenza e l’unicità del circocentro, congetturate in
laboratorio, dimostrate in classe, portano a pensare che esso è il centro del cerchio
circoscritto e siamo così stimolati a cercarne le dimensioni.
Una volta ottenuti i punti notevoli gli studenti possono essere incuriositi dall’esistenza di
relazioni tra di essi: nascono così le problematiche relative alla retta di Eulero e alla
circonferenza dei nove punti che, dopo essere stati scoperti, hanno bisogno di una
dimostrazione per essere inseriti nel sistema formale.
Si tratta di risutati semplici ed eleganti, che non si trovano sui comuni libri di geometria,
ma che possono stimolare i ragazzi, in quanto la sorpresa generalmente porta attenzione e
curiosità.
Lavoro in classe: Esistenza dei punti notevoli
Teorema : Gli assi dei lati di un triangolo passano per uno stesso punto, equidistante dai
vertici, detto circocentro.
Dimostrazione:
Dato il triangolo ABC, si costruiscano gli assi dei lati AB e AC: tali assi dovranno
incontrarsi in un punto K perchè sono perpendicolari a due segmenti non adiacenti.
Essendo K sull’asse di AB sarà KA ≅ KB; ma K sta pure sull’asse di AC e perciò KA ≅
KC, ossia il punto K è equidistante dai vertici del triangolo e apparterrà di conseguenza
anche all’asse del lato BC.
Teorema: Le tre altezze di un triangolo passano per uno stesso punto detto ortocentro
Dimostrazione:
Dato il triangolo ABC, si conducano dai vertici le parallele ai lati opposti, che a due a due
si incontrano perché le parallele a due rette che si intersecano, si devono pure intersecare.
Sia allora A’B’C’ il triangolo che in tal modo si viene a costruire.
I vertici A, B, C del triangolo dato sono i punti medi dei lati del triangolo A’B’C’, infatti
AB≅CB’ e AB≅CA’ perchè sono segmenti paralleli compresi tra rette parallele, perciò
CA’≅CB’, ovvero C è il punto medio di A’B’. Questo vale in maniera analoga per gli altri
lati. Ora, poichè ogni perpendicolare ad una retta è perpendicolare ad ogni parallela della
prima, le altezze del triangolo ABC, sono gli assi del triangolo A’B’C’ e, per il teorema
appena dimostrato, si incontreranno in un punto O chiamato Ortocentro.
Teorema: Le bisettrici degli angoli interni di un triangolo si intersecano in un punto
equidistante dai lati, detto incentro.
Dimostrazione
Dato il triangolo ABC, si traccino le bisettrici degli angoli A e B : siccome la somma di
questi due angoli è minore di un angolo piatto (la somma degli angoli interni di un
triangolo è un angolo piatto), anche le rispettive metà avranno per somma un angolo
minore di un piatto e perciò le due bisettrici si incontreranno in un punto I che, dovendo
appartenere gli angoli A e B risulterà interno al triangolo.
Ma, poichè i punti della bisettrice di un angolo ed essi soltanto, sono equidistanti dai lati
dell’angolo, I risulta equidistante dai lati degli angoli A e B, cioè, condotte le perpendicolari
ai lati da I, risulta che IH≅IK≅IT perciò il punto I si trova ad uguale distanza dai lati
dell’angolo C e, in quanto tale, starà pure sulla bisettrice di C.
Teorema: Le mediane di un triangolo si intersecano in un punto detto baricentro, che
divide ciascuna mediana in due parti, di cui quella contenente il vertice è doppia dell’altra.
Per dimostrare questo teorema ci serve una proposizione introduttiva:
Proposizione: In un triangolo qualunque il segmento congiungente i punti medi di due lati
è parallelo al terzo lato e congruente alla sua metà.
Dimostrazione:
Nel triangolo ABC si congiungano i punti di mezzo M e N dei lati AB, AC. Risulta che
MN è parallela a BC, perché, se da M si conduce la parallela a BC questa incontra il lato
AC nel suo punto di mezzo
Infatti la parallela a BC per M dividerà AC nel punto di mezzo, perché, diesegnando la
parallela a BC per A, si ottiene un fascio di rette parallele e per il teorema di Talete N
risulta il punto medio di AC. La retta passante per i punti medi dei lati allora risulterà
parallela al terzo lato.
Per dimostrare ora che MN ≅ 12 BC, si conduca da N la parallela ad AB, che tagierà BC nel
punto di mezzo L. Ma MN ≅ BL, perchè segmenti paralleli compresi tra rette parallele;
perciò M ≅ 12 BC.
Passiamo ora a dimostrare il
Teorema: Le mediane di un triangolo si intersecano in un punto detto baricentro, che
divide ciascuna mediana in due parti, di cui quella contenente il vertice è doppia dell’altra.
Dimostrazione
dato il triangolo ABC, si conducano le mediane AN, BM dei lati BC e AC e sia G il loro
punto d’incontro. Dimostriamo che GB è il doppio di GM e GA doppio di GN.
Siano D ed E i punti medi di GA e GB e si congiungano tra loro; allora, per la proposizione
precedente, nel trianolo AGB il segmento DE è parallelo ad AB e congruente alla metà di
esso.
Ma, analogamente, considerando il triangolo ABC, anche MN è parallelo ad AB e
congruente alla sua metà. Quindi MN e DE sono congruenti e paralleli tra loro. Quindi
MNDE è un parallelogramma.
Ma in ogni parallelogramma le diagonali si dimezzano reciprocamente, perciò GM≅GE e
GM ≅GD, ossia GM≅ 12 GB e GN≅ 12 GA.
Ora, poiché le mediane di un triangolo si tagliano in modo che la parte contenente il vertice
è doppia dell’altra, anche la terza mediana dovrà passare per il punto d’intersezione delle
altre due.
Collegamento con la fisica:
Come abbiamo appena dimostrato, il baricentro è in ogni caso un punto interno al
triangolo. Esso, in fisica, è sovente chiamato, centro di gravità. Se prendiamo una lamina
triangolare di materiale omogeneo, possiamo pensare di sospenderla dopo averla fissata ad
un filo in un suo punto.
Se questo punto è il baricentro, essa rimane in equlibrio, mentre se la fissiamo in altri punti
non otteniamo l’equilibrio.
Questo ci permette di concludere che le forze di gravità che pensiamo applicate ad ogni
punto della piastra sono equivalenti ad un’unica forza applicata nel baricentro.
Nota: Osserviamo le costruzioni che abbiamo fatto nella dimostrazione dei 4 teoremi sui
punti notevoli di un triangolo assegnato; in realtà una volta stabilita l’esistenza di questi
punti, per la costruzione di ognuno di essi basta intersecare due dei segmenti o rette che li
definiscono. Ad esempio, per costruire il circocentro del triangolo ABC tracciamo
solamente gli assi a e b; il circocentro K è la loro intersezione.
Risultati successivi
Dopo aver notato che il circocentro K è equidistante dai tre vertici del triangolo e che
quindi esso è il centro del cerchio circoscritto al triangolo, se la classe si dimostra partecipe
e attenta, potrebbe nascere la curiosità di sapere quanto vale il raggio di questo cerchio, in
modo da poterlo ricavare conoscendo le misure dei lati del triangolo. Questi teoremi
possono evidenziare l’importanza dell’approccio deduttivo, in quanto si può supporre che il
raggio del cerchio circoscritto sia legato alle dimensioni dei lati, ma lavorando in
laboratorio non si riesce a trovare questa dipendenza. In questo modo si può sottolineare
come l’abbandono di questo approccio porta ad impoverire la matematica ed a limitarla in
un elenco di risultati avulsi sia dalla realtà che da un sistema formale. I teoremi seguenti
sono esempi di dimostrazioni costruttive dove, partendo dall’osservazione delle figure e
dalla loro scomposizione e ricercandone le similitudini, si ottengono risultati semplici ed
eleganti.
Proposizione: Il raggio del cerchio circoscritto ad un triangolo è 1/4 del rapporto tra il
prodotto dei lati e l’area del triangolo stesso:
R = abc
4S
Dimostrazione
Dato un triangolo ABC, tracciamo gli assi per i punti medi M a , M b , M c determinando il
circocentro K ed il raggio del cerchio circoscritto R
Tracciamo anche l’altezza relativa ad un vertice, per esempio B.
L’area S del triangolo è S = bh b /2
quindi
h b = 2S/b
Notiamo ora la similitudine dei triangoli BH b A e CKM a , entrambi rettangoli e con l’angolo
BAH b uguale all’angolo CKM a , entrambi metà dell’angolo al centro BKC.
Da questa similitudine ricaviamo la proporzione:
EC : AB = CM a : BH b
cioè:
R : c = a/2 : h b
da cui
R = ac = abc
4S
2h b
Analogamente, abbiamo visto che l’incentro è equidistante dai tre lati e quindi è il centro
del cerchio inscritto nel triangolo. Calcoliamo il valore del raggio di questo cerchio.
Proposizione: Il raggio del cerchio inscritto ad un triangolo è pari al doppio del rapporto tra
l’area e la somma dei lati, ovvero è pari al rapporto tra l’area del triangolo e il
semiperimetro. In formule:
2S
r=
= Sp
a+b+c
Dimostrazione
Dato un triangolo ABC, tracciamo le bisettrici agli angoli e troviamo l’incentro I e il raggio
r del cerchio inscritto.
Il traingolo ABC risulta composto da tre triangoli:
- AIB di area S c = cr
2
- BIC di area S a = ar
2
br
- CIA di area S b =
2
L’area S del triangolo è la somma delle tre aree:
S = S a + S b + S c = r a + b + c 
2
da cui:
r= S
p
Nota: Poichè il Teorema Di Erone afferma che la superficie di un triangolo può essere
espressa nella formula: S = pp − ap − bp − c
Si può osservare che il raggio del cerchio inscritto è:
r = p − ap − bp − c/p
La retta di Eulero
Sui punti notevoli del triangolo, Eulero trovò un’intressante correlazione, oggi nota come
”Teorema di Eulero sui triangoli”. Nato a Basilea, in Svizzera nel 1707, e morto a S.
Pietroburgo, in Russia, nel 1783, Eulero, fu senza dubbio il più grande matematico del
XVIII secolo. Sebbene fosse affetto fin dall’età di trent’anni da una malattia che gli causò
una progressiva perdita della vista, Eulero redasse centinaia di opere matematiche e appunti
che provano la sua straordinaria produttività scientifica. Per esempio, la sistematizzazione e
la riformulazione dell’analisi che si trova nelle sue opere è alla base della matematica
moderna e della teoria delle funzioni. Sebbene fosse soprattutto un matematico, Eulero
fornì anche notevoli contributi di astronomia, meccanica, ottica e acustica. Grazie a questa
capacità di affrontare e risolvere problemi in tutti i campi della matematica e delle scienze,
Eulero, nel campo delle scienze esatte, risulta il più prolifico autore della storia e tutto ciò
nonostante abbia dovuto passare gli ultimi diciassette anni della sua vita completamente
cieco. Tra gli innumerevoli risultati di questo grande matematico, vediamo questo che tratta
dei punti notevoli del tringolo:
Teorema (di Eulero): Nel triangolo, ortocentro, baricentro e circocentro sono sempre
allineati, con ortocentro e circocentro da parti opposte rispetto al Baricentro e distanziati in
modo che la distanza ortocentro-baricentro è doppia della distanza baricentro-circocentro.
Dimostrazione:
Nel teorema dell’ortocentro abbiamo visto che il circocentro di un triangolo corrisponde
all’ortocentro del triangolo mediale, quello cioè ottenuto unendone i punti medi. Inoltre il
triangolo mediale, avendo i lati in proporzione 1:2 con il triangolo iniziale, è simile a
questo e ha lo stesso baricentro, perchè le rispettive mediane coincidono. Il triangolo
mediale, risulta anche ruotato di in angolo piatto intorno al comune baricentro G, rispetto al
triangolo iniziale.
Notiamo che la relazione di similitudine tra triangoli (ma in generale tra tutte le figure
geometriche) conserva gli angoli e mantiene il rapporto tra le lunghezze.
Di conseguenza l’ortocentro del triangolo mediale O m è anche esso ruotato di un angolo
piatto rispetto al comune baricentro G, quindi in linea con G e O e distante da G la metà di
quanto dista O m . Ma l’ortocentro del mediale coincide con il circocentro K del triangolo
iniziale, infatti gli assi dei lati del triangolo iniziale sono le altezze del triangolo mediale.
La retta che passa per ortocentro, baricentro e circocentro è detta Retta di Eulero
Nota: Se l’argomento è stato svolto nella classe, si sarebbe potuto ottenere lo stesso
risultato facendo ricorso alle omotetie. Infatti tra un triangolo ed il suo mediale c’è
un’omotetia di centro G e di ragione − 1 .
2
η G,− 12 : Triangolo iniziale → mediale
Nominando i vertici del triangolo iniziale A 1 , A 2 , A 3 e i vertici del mediale M 1 , M 2 , M 3 ,
otteniamo
η G,− 12 : A i
O iniziale
Mi
O mediale = K iniziale
Vista la definizione di Omotetia η Q,λ : QP ′ = λQP
Si ottiene immediatamente :
η G,− 12 : GK = − 1 GO
2
La ricerca della retta di Eulero è una buon esempio di come un ragazzo può essere motivato
alla ricerca di una dimostrazione perché essa, pur trattando concetti già ben conosciuti
come i punti notevoli, mostra come essi siano soggetti a questa proprietà nuova e
assolutamente non evidente. Le motivazioni che muovono uno studente alla ricerca di
dimostrazioni nascono, in questo caso, più dall’incertezza e dal bisogno di convincere se
stessi o un interlocutore dell’affermazione che dalla necessità di inserirla in un sistema
teorico, necessità che in una scuola superiore difficilmente è presente nei ragazzi .
Così gli allievi sono spinti, più che a soddisfare passivamente una richiesta dell’insegnante,
a cercare argomenti per giustificare l’affermazione che è stata congetturata nell’attività di
laboratorio. Questo porta spontaneamente ad inserire il nuovo teorema dell sistema formale
grazie alla ricerca di similitudini all’interno della figura.
Il cerchio dei nove punti
Abbiamo visto che il triangolo mediale è il triangolo ottenuto unendo i punti medi dei lati;
analogamente si può definire il triangolo ortico, quello ottenuto congiungendo i piedi delle
altezze. Come dimostrato da Poncelet e Feuerbach, il cerchio circoscritto al triangolo
mediale, risulta lo stesso circoscritto al tringolo ortico e passa anche per i punti medi dei tre
segmenti congiungenti l’ortocentro con i vertici ed è pertanto detto cerchio dei nove punti
o di Feuerbach.
Karl Wilhelm Feuerbach (1800-1834), fratello del famoso filosofo, nel 1822 pubblicò il
teorema in questione e altri teoremi di geometria. Sebbene sembra essa sia stata scoperta da
Poncelet un anno prima, il fatto che la circonferenza dei nove punti sia nota come
circonferenza di Feuerbach, è giustificato dalle altre interessanti proprietà di tale
circonferenza messe in luce da Feuerbach. Egli dimostrò che il centro della circonferenza
dei nove punti giace sulla retta di Eulero e si trova tra l’ortocentro e il circocentro, a uguale
distanza dall’uno e dall’altro.
Ancor più notevole è la proprietà contenuta in quello che oggi è noto come teorema di
Feuerbach: la circonferenza dei nove punti di qualsiasi triangolo è tangente internamente al
cerchio inscritto e tangente esternamente ai tre cerchi ex-inscritti.
Teorema (cerchio dei 9 punti)
In un triangolo appartengono alla stessa circonferenza:
- I punti medi dei lati
- I piedi delle altezze
- I punti medi tra Ortocentro e vertici
Dimostrazione:
Consideriamo i punti medi dei lati M a , M b , M c e quelli delle congiungenti i vertici con
l’ortocentro, che chiamiamo X,Y,Z
Il segmento M c M b è parallelo al lato BC per il teorema di Talete applicato al triangolo
ABC. Analogamente il segmento YZ è parallelo al lato BC, per il teorema di Talete
applicato al triangolo AOB. Quindi M c M b e BC sono paralleli.
Il segmento M b Z è parallelo ad AO per Talete applicato al triangolo AOC. Analogamente
parallelo ad AO è il segmento M c Y, per Talete applicato al triangolo AOB. Quindi M b Z e
M c Y sono paralleli ed, essendo AO perpendicolare a BC, M b Z e M c Y sono entrambi
perpendicolari ad M c M b e YZ.
Quindi il quadrilatero M c M b ZY è un rettangolo, e quindi i quattro punti stanno sulla
circonferenza di diametri M c Z e M b Y.
La stessa cosa per i quadrilateri M a M c XZ M b M a YZ, anche loro inscritti in un
circonferenze che, condividendo almeno un diametro con le altre, coincidono con quella in
cui è inscritto il primo rettangolo.
Quindi ne segue che M a , M b , M c , X, Y, Z giacciono sulla stessa circonferenza. Resta da
dimostrare che appartengono a questa circonferenza anche i piedi delle altezze. Questo
appare immediato se si considera che il triangolo M a XH a è rettangolo in H a per cui
quest’ultimo appartiene alla circonferenza che ha per diametro l’ipotenusa XM a che è la
nostra circonferenza. Analogamente si può dire per H b e H c
Quindi abbiamo ottenuto la tesi: i piedi delle tre altezze, i punti medi dei tre lati e dei
segmenti congiungenti i tre vertici con l’ortocentro giacciono tutti sulla medesima
circonferenza.
Osservazione: Essendo il cerchio di Feuerbach circoscritto al triangolo mediale ed essendo
questo simile a triangolo iniziale con il rapporto 1:2, il suo raggio è la metà del raggio
circoscritto al triangolo principale:
r f = abc
8S
Osservazione: Un’altra interessante proprietà del cerchio dei nove punti è l’appartenenza
del suo centro alla retta di Eulero, in una precisa posizione. Questo deriva dal fatto che il
triangolo mediale ha la stessa retta di Eulero del triangolo iniziale e dal fatto che il cerchio
di Feuerbach è circoscritto al triangolo mediale. Quindi il centro N del cerchio di
Feuerbach appartiene alla stessa retta di Eulero, dalla parte opposta di K rispetto a G, ad
una distanza da questo che è la metà della distanza da K. Il centro della circonferenza dei
nove punti è allora il punto medio tra circocentro K e ortocentro O.
Nota: Analogamente a prima, si può vedere che N appartiene alla retta di Eulero usando le
omotetie:
Abbiamo visto che il triangolo mediale è legato a quello iniziale dall’omotetia
η G,− 1 : A i
2
Mi
Quindi il cerchio circoscritto C O,R verrà trasformato da η G,− 12 in C N,R/2 .
Quindi GN = − 12 GO, quindi N sta sulla retta di Eulero ed è il punto medio tra O e K.
Le dimostrazioni di questo capitolo sono un po’ più complesse delle precedenti, non tanto
da un punto di vista concettuale, poiché non vengono usati risultati complessi, quanto per i
termini e il formalismo che potrebbe spaventare gli allievi. In casi simili il docente deve
mettersi in gioco stimolando l’attenzione degli studenti in modo particolare.
Innanzitutto anche per questo risultato si potrebbe prevedere un’attività di laboratorio in
modo da condurre i ragazzi alla ricerca di questi nove punti appartenenti alla stessa
circonferenza; in seguito egli dovrebbe fare leva sul fatto che questo risustato sia
particolarmente sorprendente, in quanto la sorpresa solitamente genera attenzione. In
questo modo si portano gli allievi ad incuriosirsi, ad apprezzare il risultato e ad essere ben
disposti verso la successiva dimostrazione. Essa è molto formativa perché riunisce le
conoscenze acquisite come i punti notevoli e la retta di Eulero con una nuova proprietà e
mostra come i la matematica non sia solo un accumulo di conoscenze ma un sistema
formale dove i risultati sono interdipendenti e dipendono dall’insieme di assiomi scelto.
Questo potrebbe portare gli studenti a sviluppare l’attitudine a cercare le conseguenze dalle
premesse fino a fare proprie le dimostrazioni studiate.
Bibliografia
F. ENRIQUES ”Gli elementi di Euclide e la critica antica e moderna”, 1925.
M. GARDNER ”Enigmi e giochi matematici, Vol II”, 1973.
A. PALATINI, V. FAGGIOLI ”Elementi di Geometria”, 1973
P BOIERI, C. DANE’ ”Geometria con Cabri”, 2003
G. LOLLI ”Touring, un romanzo”
M. MARIOTTI ”Introduzione alla dimostrazione all’inizio della scuola secondaria
superiore”, 1998
M.V. DI LEONARDO ”Leggi logiche e schemi di ragionamento”, on line
E. DI RIENZO ”Storia e proprietà del triangolo”, 2002
T. MARINO ” Argomentare, Congetturare, Dimostrare”, on line
H. MAIER ”Apprendimento in matematica. Difficoltà e modalità per superarle”, 1998
L.ROI ”Approfondimenti di Geometria”, on line
UMI ”Ciclo secondario: La matematica per il cittadino”, 2003
E.AGAZZO, D. PALLADINO ”Le geometrie non euclidee e i fondamenti della geometria”
G: POLYA ”La scoperta matematica”, 1961
A. ZANARDO ”Teorie Assiomatiche: I Numeri Naturali”, 2004
B. SCIMEMI Appunti dalle lezioni, AA 2000/2001