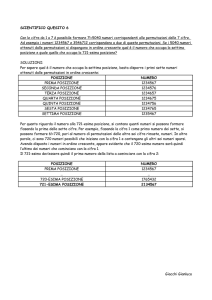
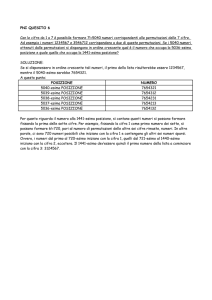
Appunti di Algebra Superiore

Prof.ssa Carla Fiori
Appunti di
Algebra Superiore
Laurea Magistrale in Matematica
Univertisà di Modena e Reggio Emilia
Dipartimento di Matematica Pura e Applicata
Questo documento è stato scritto in LATEX utilizzando l’editor LYX. I diagrammi invece sono stati prodotti utilizzando XY-Pic.
Quest’opera è stata rilasciata sotto la licenza Creative Commons AttribuzioneNon commerciale-Non opere derivate 2.5 Italia. Per leggere una copia della licenza
visita il sito web
http://creativecommons.org/licenses/by-nc-nd/2.5/it/
o spedisci una lettera a Creative Commons, 171 Second Street, Suite 300, San
Francisco, California, 94105, USA.
\
=
$
BY:
Alcuni diritti riservati 2006-2007
This work is licensed under the Creative Commons Attribution-NoncommercialNo Derivative Works 2.5 Italy License. To view a copy of this license, visit
http://creativecommons.org/licenses/by-nc-nd/2.5/it/
or send a letter to Creative Commons, 171 Second Street, Suite 300, San Francisco,
California, 94105, USA.
\
=
$
BY:
Some Rights Reserved 2006-2007
Prefazione
Questi appunti raccolgono le lezioni del corso di Algebra Superiore tenute dalla
Professoressa Carla Fiori presso l’Università di Modena e Reggio Emilia.
L’algebra non é che la geometria scritta;
la geometria non é che l’algebra figurata.
Sophie Germain
i
Indice
Prefazione
i
Capitolo 1. Strutture di incidenza e insiemi di permutazioni
1. Definizioni ed Esempi
2. Insiemi di permutazioni e strutture di incidenza
1
1
4
Capitolo 2. Gruppi e insiemi di permutazioni k-transitivi
1. Definizioni e teoremi
2. Considerazioni finali e problemi aperti
7
7
16
Capitolo 3. Gruppi e insiemi di permutazioni 2-transitivi
1. Definizioni e teoremi
2. Esempi di Quasicorpi associativi non planari
17
17
25
Capitolo 4. Gruppi e insiemi di permutazioni 3-transitivi
1. Introduzione
2. Il gruppo proiettivo lineare P GL(2, K)
3. Il gruppo proiettivo semilineare P ΓL(2, K)
4. Il gruppo proiettivo lineare speciale P SL(2, K)
5. Esempi di insiemi (non gruppi) strettamente 3-transitivi
6. Problemi aperti
28
28
29
30
32
33
34
Capitolo 5. Insiemi e gruppi k-transitivi, k ≥ 4.
35
Capitolo 6. Estensione di gruppi e insiemi di permutazioni k-transitivi
1. Definizioni e Teorema di Witt
2. Estensione di insiemi di permutazioni k-transitivi
3. Estensione di gruppi di permutazioni k-transitivi
36
36
38
41
Capitolo 7. Applicazione dei teoremi di estensione di gruppi e insiemi di
permutazioni k-transitivi
1. Esempi di estensioni di gruppi k-transitivi
2. Esempi di estensioni di insiemi k-transitivi
46
46
51
Capitolo 8. Gruppi e Insiemi k-omogenei.
54
Capitolo 9. Trasformazione di (k,n)-strutture
1. Definizioni e prime proprietà
55
55
ii
INDICE
2. Piani di Moulton
3. Trasformazione di Insiemi di Permutazioni
4. Trasformazione di gruppi di permutazioni strettamente 3-transitivi su
insiemi finiti
iii
59
60
63
CAPITOLO 1
Strutture di incidenza e insiemi di permutazioni
1. Definizioni ed Esempi
Definizione 1.1.1. Siano P e B due insiemi non vuoti tali che P ∩ B = ∅.
Sia I ⊆ P × B. La terna (P, B, I) prende il nome di struttura di incidenza.
Gli elementi di P sono detti punti, gli elementi di B sono detti blocchi, I è detta
relazione di incidenza o semplicemente incidenza.
Un punto p ∈ P è incidente ad un blocco B ∈ B se (p, B) ∈ I.
0
0
Definizione 1.1.2. Due strutture di incidenza (P, B, I) e P , B , = si dicono
isomorfe se esiste una applicazione ϕ tale che:
0
0
(1) ϕ(P) = P , ϕ(B) = B ;
(2) ϕ è biunivoca;
(3) pIB se e solo se ϕ(P ) = ϕ(B) per ogni p ∈ P e B ∈ B.
Considerata una struttura di incidenza (P, B, I), essa é sempre isomorfa ad
una struttura in cui la relazione di incidenza é l’appartenenza 00∈ 00 .
Infatti per ogni B ∈ B sia B ∗ = {p ∈ P | pIB} e sia B ∗ = {B ∗ | B ∈ B}; la
struttura (P, B ∗ , ∈) é banalmente isomorfa alla struttura (P, B, I) nell’isomorfismo
ϕ definito da ϕ (p) = p per ogni p ∈ P e ϕ(B) = B ∗ per ogni B ∈ B.
Di norma una struttura di incidenza è indicata con la coppia (P, B) sottointendendo che la relazione di incidenza è l’appartenenza.
Una struttura di incidenza si dice finita se tali sono P e B. Ad ogni struttura
di incidenza finita resta associata una matrice ∆ detta matrice di incidenza nel
seguente modo.¯
In P e in B si fissi un ordinamento; sia P = {p1 , ..., pm } e B = {B1 , ..., Bn }, ciò
è sempre possibile perchè P e B sono insiemi finiti. La matrice ∆ è così definita:
(1) ∆ = [Ih,k ] ,
1 ⇔ ph I Bk
h = 1, ..., m
Ih,k =
con
.
0 ⇔ ph 6 I Bk
k = 1, ..., n
1
CAPITOLO 1 - Strutture di incidenza e insiemi di permutazioni
2
Viceversa se si fissano due insiemi P e B rispettivamente di m ed n oggetti ed
un ordinamento in ciascuno di essi, data comunque una matrice ∆ ad m righe ed
n colonne ad elmenti 0 e 1, per (1) rimane definita una incidenza I ⊆ P × B e
quindi una struttura di incidenza (P, B, I).
Lo studio delle strutture di incidenza finite equivale a quello delle
matrici m × n con elementi 0 e 1.
Esempio 1.1.3.
P = {x1 , x2 , x3 , x4 , x5 , x6 }, B = {y1 , y2 , y3 }
I = {(x1 , y2 ), (x1 , y3 ), (x2 , y3 ), (x4 , y2 ), (x4 , y3 ), (x6 , y1 ), (x6 , y2 ), (x6 , y3 )}
x1
x2
x3
x4
x5
x6
y1 y2 y3
0 1 1
0 0 1
0 0 0
0 1 1
0 0 0
1 1 1
Esempio 1.1.4.
P 6= ∅, B 6= ∅, I = P × B. Nel caso P e B siano finiti, fissati in essi un
ordinamento, la matrice di incidenza è costituita tutta da elementi 1.
Esempio 1.1.5.
P 6= ∅, B 6= ∅, I = ∅.
Nel caso P e B siano finiti, fissato in essi un ordinamento, la matrice di incidenza
associata è costituita tutta da elementi 0.
Esempio 1.1.6.
Sia Q un quadrato del piano euclideo, P l’insieme dei vertici del quadrato e B
l’insieme dei lati e delle diagonali di Q. Diremo che un punto x ∈ P è incidente
a un blocco y ∈ B, se il punto x appartiene alla retta y. (P, B, I) è una struttura
di incidenza. E’ immediato verificare che in tale struttura ogni punto è incidente
a tre blocchi distinti, fissato comunque un blocco esistono esattamente due punti
incidenti ad esso.
CAPITOLO 1 - Strutture di incidenza e insiemi di permutazioni
3
?x1
x2
??


??

?? 
??
??
 ???

??

?


x4
x3
(P, B, I) è un esempio di struttura di piano affine finito. Ci possiamo proporre
di costruire la matrice di incidenza di questa struttura. Ordinati i punti e i blocchi
in modo che x1 , x2 , x3 , x4 siano i vertici consecutivi di Q, yi sia il lato di Q di
vertici xi , xi+1 (i = 1, 2, 3), y4 quello di vertici x4 , x1 ed inoltre y5 e y6 le diagonali
di vertici rispettivamente x1 , x3 e x2 , x4 , la matrice di incidenza risulta essere la
seguente:
y1 y2 y3 y4 y5 y6
x1 1 0 0 1 1 0
x2 1 1 0 0 0 1
x3 0 1 1 0 1 0
x4 0 0 1 1 0 1
Osserviamo che in tale matrice ogni riga possiede esattamente tre elementi uguali
ad 1, il che equivale a dire che ogni punto è incidente esattamente a tre rette.
Inoltre ogni colonna ha esattamente due elementi 1, il che equivale a dire che ogni
retta è incidente a due punti. Ancora, fissate comunque due righe distinte, esiste
una sola colonna che le interseca ambedue nell’elemento 1 e ciò equivale a dire che
due punti sono incidenti a una sola retta.
Esempio 1.1.7.
Sia K un campo qualsiasi. Sia P = K 2 ,
B = {r | r : ax + by + c = 0 ,
a, b, c ∈ K
;
a, b non entrambi nulli}
l’insieme delle equazioni di 1◦ grado a due incognite a coefficienti in K. Definiamo
I ⊆ P × B: (x, y) ∈ K 2 è incidente ad un blocco r ∈ B se la coppia (x, y) soddisfa
l’equazione espressa da r.
(P, B, I) è una struttura di incidenza.
Questa è una struttura di piano affine.
Se K è il campo delle classi resto modulo 2, si ottiene l’esempio 1.1.6 .
CAPITOLO 1 - Strutture di incidenza e insiemi di permutazioni
4
2. Insiemi di permutazioni e strutture di incidenza
Definizione 1.2.1. Sia G un insieme di permutazioni su un insieme E. La
coppia (E, G) individua una struttura di incidenza.
Definiamo punti gli elementi dell’insieme P = E × E. Per ogni α ∈ G definiamo blocco l’insieme Bα = {(x, α(x)) | x ∈ E} e definiamo blocchi della struttura
l’insieme B = {Bα | α ∈ G}.
La struttura (P, B) così determinata è detta struttura di incidenza associata all’insieme di permutazioni G, essa viene solitamente indicata con
(E 2 , G).
Oltre ai blocchi, nella struttura (E 2 , G) rimangono determinati particolari
insiemi di punti fra cui i seguenti.
Per ogni a ∈ E siano
[a]1 = {(a, y) | y ∈ E} ,
[a]2 = {(x, a) | x ∈ E} ,
G1 = {[a]1 | a ∈ E} , G2 = {[a]2 | a ∈ E} .
Gli elementi di G = G1 ∪ G2 sono detti generatori.
Definizione 1.2.2. Sia G un insieme di permutazioni su un insieme E. Nella
struttura di incidenza (E 2 , G) due punti p, q ∈ E 2 si dicono dipendenti se appartengono allo stesso generatore, in caso contrario si dicono indipendenti. Più
punti p1 , p2 ..., ph ∈ E 2 si dicono indipendenti se sono a due a due indipendenti.
La struttura (E 2 , G) e le famiglie G1 e G2 di generatori, godono di alcune
proprietà di immediata verifica:
(1) Due elementi distinti di G1 (rispettivamente G2 ) sono disgiunti ed hanno
la stessa cardinalità, che è la cardianlità di E.
(2) Gli elementi di G1 (rispettivamente G2 ) formano una partizione di P, le
cui classi sono i generatori di G1 (rispettivamente G2 ). Per la proprietà (1)
le classi della partizione hanno la stessa cardinalità, che è la cardinalità
di E.
(3) Ogni punto appartiene esattamente ad un generatore di G1 ed ad un
generatore di G2 .
(4) Ogni blocco ha la stessa cardinalità di ogni generatore, che è la cardinalità
di E.
(5) Ogni blocco ha in comune con ogni generatore esattamente un punto.
Queste sono proprietà che caratterizzano l’insieme G, ossia se valgono queste proprietà allora rimane determinato un insieme G di permutazioni. Infatti vale il
seguente teorema.
CAPITOLO 1 - Strutture di incidenza e insiemi di permutazioni
5
Teorema 1.2.3. Sia (P, B) una struttura di incidenza tale che esistono due
partizioni G1 e G2 dei punti e si abbia:
(1) |g| = |h|
per ogni g, h ∈ G1 ∪ G2 ;
(2) |g ∩ h| = 1 per ogni g ∈ G1 , per ogni h ∈ G2 ;
(3) |B ∩ g| = 1 per ogni B ∈ B, per ogni g ∈ G1 ∪ G2 .
Allora esistono un insieme E e un insieme G di permutazioni su E tali che (P, B)
è la struttura (E 2 , G) associata a G.
Dimostrazione. Per la (2) ogni elemento di G1 interseca un elemento di G2
in esattamente un punto e pertanto per ogni g ∈ G1 si ha |g| = |G2 |. Analogamente
per ogni h ∈ G2 si ha |h| = |G1 |. Per la (1) segue pertanto
|G1 | = |g| = |h| = |G2 |.
Sia E un insieme di indici tale che |E| = |G1 |; indichiamo gli elementi di G1
con A1 , A2 , .... , Ai , ... con i ∈ E e indichiamo con B1 , B2 , ..., Bj , ... con j ∈ E gli
elementi di G2 .
Gli elementi di P risultano in corrispondenza biunivoca con gli elementi di
E × E, infatti per ogni p ∈ P basta porre p = (i, j) se p ∈ Ai ∩ Bj . A partire da
ogni blocco B ∈ B definiamo l’applicazione αB : E → E, αB (x) = y se (x, y) ∈ B.
Per come definita, αB è una applicazione biunivoca (permutazione) di E in sè.
Sia G = {αB | B ∈ B} ; la struttura (P, B) è isomorfa alla struttura (E 2 , G). Esempio 1.2.4.
Sia E = {1, 2, 3}. Consideriamo
G = {α = id., β = (123), γ = (12), δ = (13)} .
Definiamo P = E × E insieme dei punti. Inoltre a partire dalle permutazioni che
sono elementi di G definiamo:
Bα = {(1, 1), (2, 2), (3, 3)} ,
Bβ = {(1, 2), (2, 3), (3, 1)} ,
Bγ = {(1, 2), (2, 1), (3, 3)} ,
Bδ = {(1, 3), (3, 1), (2, 2)} .
Definiamo B = {Bα , Bβ , Bγ , Bδ } insieme dei blocchi. (P, B) è la struttura di
incidenza associata all’insieme di permutazioni G. Solitamente è indicata con
(E 2 , G).
Generatori:
1 ∈ E ⇒ [1]1 = {(1, y) | y ∈ E} = {(1, 1), (1, 2), (1, 3)}
2 ∈ E ⇒ [2]1 = {(2, y) | y ∈ E} = {(2, 1), (2, 2), (2, 3)}
3 ∈ E ⇒ [3]1 = {(3, y) | y ∈ E} = {(3, 1), (3, 2), (3, 3)} .
G1 = {[1]1 , [2]1 , [3]1 } , è un insieme di generatori che è una partizione di P ossia
due generatori distinti di G1 sono disgiunti e inoltre l’unione dei generatori di G1
ricopre l’insieme P.
Analogamente si definisce l’insieme di generatori G2 = {[1]2 , [2]2 , [3]2 }, dove
CAPITOLO 1 - Strutture di incidenza e insiemi di permutazioni
6
[1]2 = {(x, 1) | x ∈ E} = {(1, 1), (2, 1), (3, 1)}
[2]2 = {(x, 2) | x ∈ E} = {(1, 2), (2, 2), (3, 2)}
[3]2 = {(x, 3) | x ∈ E} = {(1, 3), (2, 3), (3, 3)} .
• Preso un blocco e un generatore, qual’è la loro intersezione?
Esempio: Bγ ∩ [1]2 = {(2, 1)} .
Più in generale possiamo scrivere
Bϕ ∩ [a]1 = {(a, ϕ(a))}
Bϕ ∩ [b]2 = (ϕ−1 (b), b) .
• A partire da un qualunque blocco della struttura (E 2 , B) si costruisce una
permutazione.
Esempio: consideriamo il blocco Bδ = {(1, 3), (3, 1), (2, 2)}, definiamo
φBδ : E → E
1 7−→ 3
2 7−→ 2
3 7−→ 1
φBδ risulta un’applicazione biettiva perchè per ogni x ∈ E esiste ed è
unico l’elemento di Bδ appartenente a [x]1 (e pertanto φBδ è applicazione);
inoltre per ogni (x, y) ∈ Bδ esiste ed è unico [y]2 con Bδ ∩ [y]2 = {(x, y)}
(e pertanto φBδ suriettiva, anzi φBδ biettiva).
Esempio 1.2.5.
Siano P = R × R, B = {r | r : y = mx + n , m ∈ R∗ , n ∈ R} .
A partire dal blocco y = mx + n rimane definita la permutazione
α : R → R, α(x) = mx + n.
(P, B) è una struttura di incidenza.
Quali sono i generatori?
[a]1 = {(a, y)|y ∈ R}
[b]2 = {(x, b)|x ∈ R}.
CAPITOLO 2
Gruppi e insiemi di permutazioni k-transitivi
1. Definizioni e teoremi
Definizione 2.1.1. Sia G un insieme di permutazioni su un insieme E e sia
k ∈ N∗ . G si dice k-transitivo su E se per ogni (x1 , ..., xk ), (y1 , ..., yk ) con xi , yi ∈ E
tali che xi 6= xj , yi 6= yj se i 6= j esiste α ∈ G tale che α(xi ) = yi con i = 1, ..., k.
Se α è unica, G si dice strettamente k-transitivo. Gli insiemi strettamente
1-transitivi sono anche detti regolari .
L’insieme G si dice transitivo su E se è almeno 1-transitivo su E.
Esempio 2.1.2.
Sia R il campo dei numeri reali, per ogni a ∈ R sia αa : R → R , αa (x) = 2x + a
e sia G = {αa | ∈ R} . G é un insieme strettamente 1-transitivo su R.
Infatti comunque presi r, s ∈ R esiste (ed é unica) la permutazione αs−2r ∈ G tale
che αs−2r (r) = s.
Gli insiemi di permutazioni strettamente k-transitivi su un insieme E, finito o no, hanno una particolare importanza perchè rappresentano strutture
geometriche fondamentali.
Nota 2.1.3. Sia G un insieme di permutazioni strettamente k-transitivo su
un insieme E finito, |E| = n. Si possono contare gli elementi di G, infatti fissata
una k-upla (a1 , a2 , ..ak ) di elementi distinti di E, per la stretta k-transitività, gli
elementi di G sono tanti quante sono le possibili immagini di (a1 , a2 , ..ak ), basta
quindi contare le k-uple di elementi distinti di E. Risulta pertanto
|G| = Dn,k = n(n − 1) · ... · (n − k + 1).
In particolare se G è regolare su E si ha
|G| = |E| = n.
7
CAPITOLO 2 - Gruppi e insiemi di permutazioni k-transitivi
8
Teorema 2.1.4. Sia G un insieme di permutazioni su un insieme E. Fissata
α ∈ G, l’insieme α−1 G è ancora un insieme di permutazioni su E e pertanto
rimangono determinate le strutture (E 2 , G) e (E 2 , α−1 G). Si ha che (E 2 , G) è
isomorfo a (E 2 , α−1 G) ed inoltre id ∈ G oppure id ∈ α−1 G.
Dimostrazione. Sia ϕ : (E 2 , G) −→ (E 2 , α−1 G) così definita:
ϕ(x, y) = (x, α−1 (y)) per ogni (x, y) ∈ E 2
.
ϕ(β) = α−1 β
per ogni
β∈G
E’ di immediata verifica che ϕ è un isomorfismo di (E 2 , G) in (E 2 , α−1 G) perché ϕ
é una applicazione biettiva, inoltre se G non contiene l’identità si ha che α−1 α ∈
α−1 G e pertanto l’identità appartiene ad α−1 G.
Il teorema 2.1.4 assicura che, senza ledere in generalità, nello studio di una
struttura di incidenza (E 2 , G) si può sempre supporre id ∈ G.
si dicono dipendenti se appartengono allo stesso generatore, in caso contrario
si dicono indipendenti. Più punti p1 , p2 ..., ph ∈ E 2 si dicono indipendenti se sono
a due a due indipendenti.
Teorema 2.1.5. Sia G un insieme di permutazioni strettamente k-transitvo
su un insieme E e sia (E 2 , G) la struttura ad esso associata. Se p1 , p2 , ..., pk ∈ E 2
sono punti indipendenti allora esiste ed è unico il blocco che li contiene.
Dimostrazione. Siano pi = (xi , yi ), i = 1, ..., k, punti indipendenti di E 2 .
Siccome i punti sono indipendenti, per i 6= j risulta xi 6= xj , yi 6= yj . Per
la stretta k-transitività di G esiste ed è unica la permutazione α ∈ G tale che
α(xi ) = yi , i = 1, ..., k, e pertanto in (E 2 , G) α é il blocco cercato.
Nota 2.1.6. La relazione fra gli insiemi di permutazioni strettamente k-transitivi e le strutture di incidenza associate è un legame fra l’algebra e la geometria che permette di affrontare lo studio di strutture geometriche con l’algebra e
viceversa permette di dare una lettura geometrica di problemi algebrici.
Un notevole esempio è la relazione tra insiemi di permutazioni e piani affini.
Richiamiamo la definizione di piano affine.
Definizione 2.1.7. La struttura di incidenza (P, R) è detta piano affine se:
(1) comunque presi p, q ∈ P, p 6= q, esiste ed è unico R ∈ R tale che p, q ∈ R;
(2) per ogni p ∈ P, per ogni R ∈ R con p ∈
/ R, esiste ed è unico S ∈ R tale
che p ∈ S e S ∩ R = ∅;
(3) esistono almeno 3 punti non appartenenti ad uno stesso elemento di R.
Un piano affine con un numero finito di punti é detto di ordine n se |R| = n per
ogni R ∈ R.
CAPITOLO 2 - Gruppi e insiemi di permutazioni k-transitivi
9
Teorema 2.1.8. Sia G un insieme di permutazioni strettamente 2-transitivo
su un insieme E finito con |E| = n, n ≥ 2. La struttura (E 2 , G) associata a G
determina un piano affine di ordine n.
Dimostrazione. Si definiscono punti gli elementi dell’ insieme P = E 2 , rette
gli elementi dell’ insieme R dati dai blocchi e dai generatori di (E 2 , G).
(1) Siano (x1 , y1 ), (x2 , y2 ) ∈ P. Se x1 = x2 l’unica retta che li contiene è il
generatore [x1 ]1 .
Se y1 = y2 l’unica retta che li contiene è il generatore [y1 ]2 .
Se x1 6= x2 , y1 6= y2 allora per la stretta 2-transitività c’è un unico blocco
(non generatore) che li contiene.
(2) Per le proprietà delle strutture di incidenza associate agli insiemi di permutazioni, per il teorema 1.2.3 ed essendo G strettamente 2-transitivo, si
ha che:
• se p = (x̄, ȳ) ∈ P, [a]1 ∈ R, a 6= x̄, allora l’unica retta di R passante
per p e disgiunta da [a]1 è la retta [x̄]1 ;
• se p = (x̄, ȳ) ∈ P, [b]2 ∈ R, ȳ 6= b, allora l’unica retta di R passante
per p e disgiunta da [b]2 è la retta [ȳ]2 ;
• se p = (x̄, ȳ) ∈ P, Bα ∈ R, α(x̄) 6= ȳ, allora esiste ed è unico Bγ ∈ R
tale che ȳ = γ(x̄) (ossia p ∈ Bγ ) e Bα ∩ Bγ = ∅.
Per dimostrare questo iniziamo con il contare le rette passanti per p.
Considerato [z]1 con z 6= x̄, su [z]1 ci sono esattamente n − 1 punti
indipendenti da p che individuano altrettante rette per p ( l’unico
punto di [z]1 dipendente da p è (z, ȳ)); oltre a queste rette ci sono
esattamente altre due rette per p, sono le rette-generatori [x̄]1 e [ȳ]2
che sono sicuramente diverse dalle precedenti n − 1 perchè [x̄]1 6= [z]1 .
Si conclude che per p passano esattamente (n − 1) + 2 = n + 1 rette.
Contiamo ora le rette per p intersecanti Bα : sono esattamente n − 2
perchè i punti di Bα indipendenti da p sono esattamente n − 2 ( devo
escludere (x̄, α(x̄)) e (α−1 (ȳ), ȳ)). Si conclude pertanto che le rette
per p non aventi punti in comune con Bα sono (n − 1) − (n − 2) = 1
ossia esiste ed è unica la retta passante per p non avente punti in
comune con Bα .
(3) Poiché |E| ≥ 2 esistono almeno 3 punti non appartenenti ad una stessa
retta.
Del teorema ora dimostrato vale anche il viceversa.
Teorema 2.1.9. Sia π un piano affine di ordine n. Esso individua un
insieme di permutazioni strettamente 2-transitivo su n elementi.
CAPITOLO 2 - Gruppi e insiemi di permutazioni k-transitivi
10
Dimostrazione. Posto E = {1, ... , n} fissiamo due fasci distinti di rette
parallele G1 , G2 . Ciascuno di essi contiene n rette, sia G1 = {A1 , ..., An } e G2 =
{B1 , ...Bn } .
Per ogni p ∈ π esistono e sono unici Ai , Bj , tali che Ai ∩ Bj = {p} ; poniamo
allora p = (i, j).
Fissata una retta R con R ∈
/ G1 e R ∈
/ G2 definiamo
αR : E −→ E ,
αR (x) = y
se (x, y) ∈ R .
Le applicazioni αR sono applicazioni biunivoche di E in sè, sono dunque permutazioni su E, perciò
G = {αR | R ∈ π}
è un insieme di permutazioni sull’insieme E. G è strettamente 2-transitivo su E:
infatti siano (x1 , x2 ) e (y1 , y2 ) due coppie di elementi di E con x1 6= y1 e x2 6= y2 .
Le coppie (x1 , x2 ), (y1 , y2 ) individuano due punti distinti del piano π e pertanto
esiste ed è unica la retta R ∈ π tale che (x1 , x2 ) ∈ R e (y1 , y2 ) ∈ R con R 6∈ G1 ∪ G2
e quindi esiste ed è unica αR ∈ G tale che αR (xi ) = yi con i = 1, 2.
Nota 2.1.10. I teoremi 2.1.8 e 2.1.9 valgono per E insieme finito. Se E non
è finito la stretta 2-transitività non basta più per ottenere un piano affine. Questo
sarà approfondito nel capitolo 3.
Nota 2.1.11. Nel piano affine π di ordine n individuato da un insieme G
strettamente 2-transitvo sull’insieme E, |E| = n, ogni fascio di rette parallele
distinto dai fasci dei generatori è un insieme strettamente 1-transitivo su E. Di tali
fasci ne esistono esattamente n−1 e pertanto esistono n−1 insiemi di permutazioni
regolari e distinti che agiscono su n elementi.
Approfondiamo lo studio dei gruppi e degli insiemi di permutazioni k-transitivi.
Teorema 2.1.12. Sia G un gruppo di permutazioni su un insieme E. G è
strettamente k-transitivo su E se e solo se G è k-transitivo su E e solo l’identità
fissa k elementi comunque scelti in E.
Dimostrazione. Sia G strettamente k-transitivo su E. E’ ovvio che G è
k-transitivo su E; inoltre l’identità appartiene a G essendo questo un gruppo e
l’identità fissa sempre k elementi comunque scelti in E. Infine l’identità è l’unico
elemento di G che fissa k elementi di E perchè per ipotesi G è strettamente ktransitivo.
Viceversa sia G k-transitivo su E e tale che solo l’identità fissa k elementi
comunque scelti in E. Consideriamo due k-uple di elementi distinti di E, siano
CAPITOLO 2 - Gruppi e insiemi di permutazioni k-transitivi
11
(x1 , ..., xk ) e (y1 , ..., yk ) con xi 6= xj , yi 6= yj per i 6= j. Poichè G è k-transitivo
esiste α ∈ G tale che α(xi ) = yi , i = 1, ... , k.
Se esistesse anche β ∈ G tale che β(xi ) = yi , i = 1, ... , k, allora risulterebbe
−1
β α ∈ G con β −1 α(xi ) = xi , i = 1, ... , k e pertanto dall’ ipotesi seguirebbe
β −1 α = identità da cui α = β.
Nota 2.1.13. Il teorema 2.1.12 non vale se G non é un gruppo.
Definizione 2.1.14. Sia G un insieme di permutazioni su un insieme E e sia
a ∈ E. Si chiama stabilizzatore di a l’insieme
Ga = {α ∈ G | α(a) = a} .
Se a1 , a2 , ..., ah ∈ E
si chiama stabilizzatore di a1 , a2 , ..., ah
l’insieme
Ga1 ,...,ah = {α ∈ G | α(ai ) = ai con i = 1, ..., h} .
Nota 2.1.15. Lo stabilizzatore di un elemento dipende dall’insieme di permutazioni G fissato ed ha un ruolo importante nello studio di G.
Nota 2.1.16. Se G è un gruppo lo stabilizzatore di un elemento è un sottogruppo di G e quindi di Sym E.
Teorema 2.1.17. Sia G un insieme di permutazioni k-transitivo su un insieme E e sia a ∈ E. Lo stabilizzatore Ga è un insieme (k-1)-transitivo su
E − {a} .
Dimostrazione. Fissiamo due (k-1)-uple in E − {a} , (x1 , x2 , ..., xk−1 ),
(y1 , ..., yk−1 ) con xi 6= xj e yi 6= yj se i 6= j.
Poichè G è k-transitivo su E esiste α ∈ G tale che
a x1 x2 ... xk−1
α:
a y1 y2 ... yk−1
e siccome α(a) = a si ha α ∈ Ga e pertanto Ga è (k-1)-transitivo su E − {a}.
Nota 2.1.18. Se G è un gruppo k-transitivo su E e a ∈ E allora Ga è un
gruppo (k-1)-transitivo su E − {a} .
CAPITOLO 2 - Gruppi e insiemi di permutazioni k-transitivi
12
Teorema 2.1.19. Sia G un gruppo di permutazioni su un insieme E, G
transitivo su E e sia a ∈ E. Se Ga è (k-1)-transitivo su E −{a} (risp. strettamente
(k-1)-transitivo su E − {a}), allora G è un gruppo di permutazioni k-transitivo su
E (risp. strettamente k-transitivo su E).
Dimostrazione. Siano (x1 , ..., xk ) e (y1 , ..., yk ) due k-uple di elementi di E
con xi 6= xj , yi 6= yj se i 6= j. Poichè G è transitivo su E, esiste α ∈ G tale che
α(x1 ) = a ed esiste β ∈ G tale che β(y1 ) = a. Sia γ ∈ Ga tale che γ(α(xi )) = β(yi )
con i = 2, .., k. La permutazione γ esiste certamente in Ga perchè Ga è (k-1)transitivo su E − {a} ed è α(xi ) 6= a e β(yi ) 6= a per ogni i = 2, ..., k. Essendo
G un gruppo si ha β −1 γα ∈ G e β −1 γα(xi ) = yi per ogni i = 1, ..., k, quindi G è
k-transitivo su E. Inoltre se Ga è strettamente (k-1)-transitivo su E − {a}, l’unico
elemento di G che fissa a, x2 , .., xk è l’identità; infatti poiché G é k-transitivo su E,
esiste δ ∈ G tale che δ(a) = a, δ(xi ) = xi con i = 2, ..., k. La permutazione δ fissa
k-1 elementi di E − {a} e δ ∈ Ga , allora per la stretta (k-1)-transitività di Ga , δ è
l’identità in Ga ossia fissa tutti gli elementi di E − {a} e poiché é anche δ(a) = a
si ha che δ fissa tutti gli elementi di E , cioé é l’identità anche in G, allora per il
teorema 2.1.12 G è strettamente k-transitivo su E.
Corollario 2.1.20. Sia G un gruppo di permutazioni su E e a ∈ E. G é
strettamente k-transitivo su E se e solo se Ga é strettamente (k-1)-transitivo su
E − {a}.
Dimostrazione. Segue dai teoremi 2.1.17 e 2.1.19.
Teorema 2.1.21. Sia G un gruppo di permutazioni su un insieme E, sia G
transitivo su E. Se a, b ∈ E allora Ga è coniugato con Gb .
Dimostrazione. Si deve dimostrare che esiste α ∈ G tale che α−1 Gb α = Ga .
Il gruppo G è per ipotesi transitivo e pertanto esiste α ∈ G tale che α(a) = b.
Le permutazioni αGa α−1 fissano b, infatti per ogni γ ∈ Ga si ha αγα−1 (b) =
αγ(a) = α(a) = b. Risulta pertanto αGa α−1 ⊂ Gb da cui Ga ⊂ α−1 Gb α.
Analogamente le permutazioni di α−1 Gb α fissano a e perciò risulta anche
−1
α Gb α ⊂ Ga .
Resta così provato α−1 Gb α = Ga .
Corollario 2.1.22. Sia G un insieme di permutazioni su un insieme E, sia G
transitivo su E. Se a, b ∈ E allora Ga è isomorfo a Gb .
Dimostrazione. La relazione di coniugio che lega gli stabilizzatori determina
l’isomorfismo.
CAPITOLO 2 - Gruppi e insiemi di permutazioni k-transitivi
13
Teorema 2.1.23. Sia G un gruppo di permutazioni k-transitivo su un insieme E finito, |E| = n. Siano x1 , ..., xk elementi distinti di E. Si ha
|G| = |Gx1 ,...,xk | · n(n − 1) · ... · (n − k + 1)
Dimostrazione. Poichè lo stabilizzatore Gx1 ,...,xk è un sottogruppo di G, basta dimostrare che n(n − 1) · ... · (n − k + 1) è il suo indice in G. G è finito
e perciò l’indice di Gx1 ,...,xk coincide con il numero dei laterali distinti. Fissati
α, β ∈ G, i due laterali αGx1 ,...,xk e βGx1 ,...,xk coincidono se e solo se α(xi ) = β(xi )
con i = 1, ..., k, pertanto i laterali distinti sono tanti quante le possibili k-uple
distinte di elementi distinti di E, ossia sono n(n − 1) · ... · (n − k + 1) da cui segue
la tesi.
Teorema 2.1.24. Sia G un insieme di permutazioni strettamente k-transitivo
su un insieme E tale che 1E ∈ G e αβ ∈ G per ogni α, β ∈ G. Allora G è un
gruppo.
Dimostrazione. Poichè G ⊂ SE , basta dimostrare che G è un sottogruppo
di SE . Per ipotesi αβ ∈ G per ogni α , β ∈ G. Rimane da dimostrare che se
α ∈ G allora anche α−1 ∈ G. Sia α ∈ G e sia α(xi ) = yi , i = 1, ..., k; siccome G è
strettamente k-transitivo, esiste ed è unica β ∈ G tale che β(yi ) = xi , i = 1, ..., k.
Per ipotesi βα ∈ G e risulta βα(xi ) = xi , i = 1, ..., k e pertanto βα = 1E da
cui β = α−1 e perciò α−1 ∈ G.
Teorema 2.1.25. Sia G un insieme di permutazioni k-transitivo su un insieme E tale che 1E ∈ G. Se α β ∈ G per ogni α, β ∈ G e solo l’identità fissa k
elementi distinti di E, allora G è un gruppo strettamente k-transitivo su E.
Dimostrazione. Poichè G per ipotesi è chiuso rispetto al prodotto, per dimostrare che è un gruppo basta dimostrare che ogni elemento di G ha l’inverso
che sta in G. Sia α ∈ G, α(x1 ) = y1 , ..., α(xk ) = yk . Poichè G è k-transitivo esiste
β ∈ G tale che β(y1 ) = x1 , ..., β(yk ) = xk , inoltre per ipotesi βα ∈ G e βα fissa
gli elementi x1 , x2 , ..., xk ; poichè per ipotesi solo l’identità fissa k elementi risulta
βα = 1E da cui α−1 = β ∈ G e pertanto G è un gruppo.
Dimostriamo ora che G è strettamente k-transitivo.
Per ipotesi G è k-transitivo, supponiamo per assurdo che esistano α, β ∈ G tali
che α(x1 ) = β(x1 ) = y1 , ... , α(xk ) = β(xk ) = yk , allora β −1 α ∈ G e β −1 α fissa gli
elementi x1 , ..., xk perciò per l’ipotesi fatta risulta β −1 α = 1E da cui α = β.
Teorema 2.1.26. Sia G un insieme di permutazioni su un insieme E. Se G
è transitivo su E e se αβ = βα per ogni α, β ∈ G allora G è un gruppo abeliano e
regolare su E.
CAPITOLO 2 - Gruppi e insiemi di permutazioni k-transitivi
14
Dimostrazione. Da inserire.
Esempio 2.1.27.
Sn è strettamente n-transitivo su E.
Segue dalla definizione di Sn .
Esempio 2.1.28.
Sn è strettamente (n-1)-transitivo su E.
Infatti fissate due (n-1)-uple (x1 , ..., xn−1 ), (y1 , ..., yn−1 ) di elementi distinti di
E, la permutazione che trasforma gli xi negli yi muta anche l’unico elemento di
E diverso dagli xi nell’unico elemento di E diverso dagli yi e pertanto questa
permutazione è unica.
Esempio 2.1.29.
An è strettamente (n-2)-transitivo su E.
Infatti siano x1 , ..., xn−2 e y1 , ..., yn−2 due (n-2)-uple
Rimangono determinate le due n-uple (x1 , ..., xn−2 , a, b)
Sn esistono α e β tali che
x1 ... xn−2 a b
x1 ...
α:
β:
y1 ... yn−2 c d
y1 ...
di elementi distinti di E.
e (y1 , y2 , ..., yn−2 , c, d). In
xn−2 a b
yn−2 d c
e queste sono le uniche permutazioni di Sn che trasformano x1 , ..., xn−2 in y1 , ..., yn−2 .
Inoltre una sola tra le permutazioni α e β è di classe pari perchè α−1 β è una trasposizione (e quindi di classe dispari). Dunque in An esiste un’unica permutazione
che trasforma gli xi negli yi perciò An è strettamente (n-2)-transitivo su E.
Per i gruppi di permutazioni k-transitivi su n elementi, i casi k = n,
k=
n − 1,
k = n − 2 sono considerati “banali”. Nel caso più generale in cui G sia
un insieme non gruppo, si ha il seguente teorema.
Teorema 2.1.30. Sia G un insieme di permutazioni su un insieme finito E,
|E| = n ≥ 3. Se G è strettamente (n-2)-transitivo su E, allora G = An oppure
G = S n − An .
Dimostrazione. La dimostrazione si suddivide in due casi a seconda che la
permutazione identitá 1E appartenga oppure no all’insieme G.
Ricordiamo che An è un sottogruppo di indice due in Sn e i due laterali sono
A n e S n − An .
CAPITOLO 2 - Gruppi e insiemi di permutazioni k-transitivi
15
(1) Sia 1E ∈ G. Si dimostra per induzione che G = An .
Sia n = 3, allora G è strettamente 1-transitivo e perciò |G| = 3 e gli
elementi di G diversi dall’identità non fissano nessun elemento pertanto
risulta
1 2 3
1 2 3
G = 1E ,
,
2 3 1
3 1 2
ossia G = An .
Sia n > 3; l’ipotesi induttiva è che ogni insieme di permutazioni strettamente ((n-1)-2)=(n-3)-transitivo su n-1 elementi contenente l’identità è
il gruppo An−1 .
Osserviamo che se G è strettamente (n-2)-transitivo su n elementi
si ha |G| = n(n − 1) · ... · (n − (n − 2) + 1) = n!2 , ossia |G| = |An |. Per
dimostrare che G coincide con An basta quindi provare che G non contiene
permutazioni di classe dispari. Per assurdo supponiamo che esista σ ∈ G
di classe dispari; scriviamo σ come prodotto di cicli disgiunti σ = σ1 ·...·σh .
Poichè σ è di classe dispari almeno uno dei cicli σi (o comunque un numero
dispari di essi) è di classe dispari. I cicli sono disgiunti e quindi permutabili
e pertanto non è restrittivo supporre che sia σ1 di classe dispari. Sia σ1 =
(x1 x2 ...x2k ). Consideriamo il ciclo τ1 = (x1 x2 ...x2k−1 ) e la permutazione
τ = τ1 σ2 ...σh .
La permutazione τ è di classe pari e fissa almeno l’elemento x2k (perchè
non compare in τ1 nè in σi , i = 2, ..., h) e pertanto τ ∈ An−1 .
Lo stabilizzatore Gx2k è strettamente (n-3)-transitivo su E − {x2k }
e contiene l’identità; perciò, per l’ipotesi induttiva, si ha Gx2k = An−1 .
Allora τ ∈ An−1 = Gx2k ⊂ G da cui τ ∈ G e quindi τ ∈ G, σ ∈ G.
Ciò è assurdo in quanto τ e σ agiscono allo stesso modo sugli elementi
di E − {x2k−1 , x2k } perchè differiscono solo nei cicli τ1 e σ1 i quali hanno
azioni diverse solo sugli elementi x2k−1 e x2k . Le permutazioni τ e σ sono
distinte e agiscono allo stesso modo su (n − 2) elementi di E, ma ciò è
assurdo per la stretta (n-2)-transitività di G.
(2) Sia 1E ∈
/ G. Si dimostra che G = Sn − An .
Sia α ∈ G; si ha α−1 G insieme di permutazioni su E con 1E = α−1 α ∈
α−1 G e perciò per il caso (1) si ha α−1 G = An , G = αAn . Non può essere
αAn = An perchè si avrebbe G = An da cui 1E ∈ G contro l’ipotesi.
Dunque αAn 6= An e pertanto αAn = Sn − An ossia G = Sn − An .
CAPITOLO 2 - Gruppi e insiemi di permutazioni k-transitivi
16
2. Considerazioni finali e problemi aperti
(1) Tutti i gruppi finiti strettamente k-transitivi, k ≥ 2, sono noti. Per K ≥ 4
sono noti anche tutti i grupi strettamente k-transitivi non finiti.
(2) Per k = 2 e per k = 3 esistono esempi di insiemi di permutazioni G, finiti
e non finiti, contenenti la permutazione identitá i quali sono strettamente
k-transitivi e non sono gruppi.
(3) Per k ≥ 4 non vi è alcun esempio di insieme strettamente k-transitivo,
contenente la permutazione identitá che non sia un gruppo.
(4) A.Bonisoli, P.Quattrocchi hanno dimostrato che per qualunque k ≥ 4, se
G è un insieme strettamente k-transitivo finito contenente la permutazione identitá e tale che α−1 ∈ G per ogni α ∈ G allora G è un gruppo. Esso
è il gruppo simmetrico oppure il gruppo alterno oppure il gruppo M4,11
oppure il gruppo M5,12 . (“Each Invertible Sharply d-transitive Finite Permutation set with d ≥ 4 is a group”. Journal of Algebraic Combination,
12, (2000 Olanda), p.p. 239-248.)
(5) Nel lavoro di Bonisoli-Quattrocchi sopra citato si dimostra anche che:
• un insieme di permutazioni su 11 elementi strettamente 4-transitivo
contenente la permutazione identità è necessariamente il gruppo di
Mathieu M4,11 .
• Un insieme di permutazioni su 12 elementi strettamente 5-transitivo
contenente la permutazione identitá è necessariamente il gruppo di
Mathieu M5,12 .
• Per k ≥ 6 non esistono insieme strettamente k-transitivi su un insieme finito con almeno k + 3 elementi.
(6) Problema aperto: un insieme G strettamente 3-transitivo finito contenente
la permutazione identitá e tale che α−1 ∈ G per ogni α ∈ G é un gruppo?
CAPITOLO 3
Gruppi e insiemi di permutazioni 2-transitivi
1. Definizioni e teoremi
I gruppi strettamente 2-transitivi finiti sono tutti noti. Oltre ai gruppi ”banali” S2 , S3 , A4 esistono infinite famiglie di gruppi strettamente 2-transitivi che sono
state classificate da Zassenhaus nel 1936. I gruppi strettamente 2-transitivi non
banali sono dati dalle trasformazioni affini su un quasicorpo associativo planare
oppure su uno pseudocorpo; i primi (quelli su un quasicorpo associativo planare) determinano un piano affine ed inoltre non occorre l’ipotesi di planarità se il
quasicorpo associativo è finito.
Iniziamo con il dare un esempio di gruppo strettamente 2-transitivo.
Esempio 3.1.1.
Sia K un campo, finito o no; per ogni a, b ∈ K, a 6= 0, l’applicazione definita da
αa,b : K −→ K, αa,b (x) = ax+b è una permutazione. Sia G = {αa,b | a ∈ K∗ , b ∈ K}.
L’insieme G così definito è un gruppo di permutazioni strettamente 2-transitivo
su K, sottogruppo di Sym K.
(1) G è un gruppo
• se αa,b , αc,d ∈ G allora si ha αa,b αc,d = αh,k con h = ac 6= 0, k = ad+b
e pertanto αa,b αc,d ∈ G;
• α1,0 : x −→ x è elemento neutro per G;
• se αa,b ∈ G allora αa−1 ,−a−1 b ∈ G è la sua inversa.
(2) G è transitivo
Per ogni x ∈ K esiste in G una permutazione che trasforma 0 in x,
infatti basta considerare un’applicazione del tipo αa,x con a 6= 0.
Comunque presi x, y ∈ K, si considerino le permutazioni α, β ∈ G
tali che α(0) = x, β(0) = y, allora risulta βα−1 (x) = y con βα−1 ∈ G e
pertanto G è transitivo su K.
(3) G0 è strettamente 1-transitivo su K − {0}
Gli elementi di G0 sono tutte e sole le permutazioni del tipo αa,0 . Per
ogni x, y ∈ K∗ esiste ed è unica la permutazione α ∈ G0 tale che α(x) = y,
essa è la permutazione αyx−1 ,0 ; pertanto lo stabilizzatore G0 è strettamente
1-transitivo su K∗ .
17
CAPITOLO 3 - Gruppi e insiemi di permutazioni 2-transitivi
18
Per il teorema 2.1.19 rimane dimostrato che G è strettamente 2-transitivo essendo
verificate(2) e (3).
Il gruppo G dell’esempio 3.1.1 è indicato con AG(1, K) ed è detto gruppo delle
affinità sulla retta affine.
Definizione 3.1.2. Sia G un insieme di permutazioni strettamente 2-transitivo
su E. L’insieme G è detto planare se comunque presi a, b ∈ E e comunque preso
β ∈ G con β(a) 6= b, esiste una ed una sola permutazione α ∈ G tale che α(a) = b
e α(x) 6= β(x) per ogni x ∈ E.
Il gruppo G = AG(1, K) é un esempio di gruppo strettamente 2-transitivo
planare. La proprietá di planaritá non vale per tutti gli insiemi strettamente 2transitivi ma vale sempre nel caso in cui l’insieme sia finito.
Teorema 3.1.3. Se G è un insieme strettamente 2-transitivo su un insieme
E finito allora G è planare.
Dimostrazione. Sia |E| = n, siano a, b ∈ E, a 6= b, e sia β ∈ G tale che
β(a) = c 6= b. Per la stretta 2-transitività, in G esistono esattamente n − 1
permutazioni α tali che α(a) = b perchè fissato un qualunque elemento a ∈ E −{a}
le permutazioni di G che trasformano (a, a) in (b, y) sono tante quante sono le
possibilità di scelta per y ossia sono n − 1 essendo y ∈ E − {b}.
Sia β −1 (b) = d, ovviamente d 6= a per l’ipotesi β(a) 6= b e pertanto una
permutazione γ ∈ G tale che γ(a) = b può avere la stessa azione di β solo su x
tale che x ∈ E − {a, d}.
Per la stretta 2-transitività di G, per ogni x ∈ E − {a, d} esiste una ed una
sola permutazione che trasforma (a, x) in (b, β(x)) e pertanto le permutazioni γ
tali che γ(a) = b e γ(x) = β(x) sono n − 2. Rimane così dimostrato che in G vi è
esattamente 1 = (n − 1) − (n − 2) permutazione che trasforma a in b e non ha la
stessa azione di β su alcun elemento di E.
I prossimi risultati mettono in evidenza alcune proprietà di particolari elementi
di un gruppo G strettamente 2-transitivo (non necessariamente planare).
Definizione 3.1.4. Sia G un gruppo di permutazioni su E, una permutazione
j ∈ G si dice textbfinvoluzione se j 2 = 1E , j 6= 1E .
Nota 3.1.5. Se α é una involuzione, da α2 = 1E segue che α(y) = x implica
α(x) = y ossia α é una simmetria.
CAPITOLO 3 - Gruppi e insiemi di permutazioni 2-transitivi
19
Teorema 3.1.6. Le involuzioni di un gruppo G strettamente 2-transitivo
sono a due a due coniugate.
Dimostrazione. Ricordiamo anzitutto che due elementi g1 e g2 di un gruppo
H si dicono coniugati se esiste x ∈ H tale che g2 = x−1 g1 x.
Siano j1 e j2 ∈ G involuzioni distinte, e sia
a b ...
a c ...
j1 =
, j2 =
b a ...
c a ...
con b 6= c; queste involuzioni esistono certamente perchè G è strettamente
2-transitivo.
Per la stretta 2-transitività di G, esiste γ ∈ G tale che
a c ...
γ=
a b ...
e si ha γ −1 j1 γ = j2 .
Nota 3.1.7. Sia G un gruppo strettamente 2-transitivo, allora:
• in G esiste almeno una involuzione, basta prendere g ∈ G tale che g(a) =
b, g(b) = a con a 6= b;
• una involuzione j ∈ G ha al più un punto fisso perchè se ne avesse più di
uno agirebbe come l’identità;
• se G è su E con |E| = n dispari allora ogni involuzione di G ha esattamente
un punto fisso.
Teorema 3.1.8. Sia G un gruppo strettamente 2-transitivo, si possono avere
due casi:
(1) tutte le involuzioni di G hanno un elemento fisso;
(2) tutte le involuzioni di G sono prive di elementi fissi.
Dimostrazione. Sia j1 ∈ G una involuzione con un elemento fisso, j1 (x) = x.
Ogni altra involuzione j2 ∈ G è coniugata a j1 tramite una opportuna permutazione
γ ∈ G; posto j2 = γ −1 j1 γ si ha che j2 fissa l’elemento γ −1 (x). Si conclude pertanto
che in G o tutte le involuzioni fissano un elemento o nessuna involuzione fissa un
elemento.
Esempio 3.1.9.
Sia G = AG(1, K).
(1) Se K ha caratteristica 2 allora le involuzioni di G sono prive di punti fissi.
Infatti in questo caso le involuzioni sono le applicazioni g(x) = x + b con
b ∈ K∗ e queste sono prive di punti fissi.
CAPITOLO 3 - Gruppi e insiemi di permutazioni 2-transitivi
20
(2) Se K ha caratteristica diversa da 2, le involuzioni sono le applicazioni
h(x) = −x + b con b ∈ K e queste hanno tutte un punto fisso, è l’elemento
x = b(2u)−1 dove u è l’unità del campo K.
Teorema 3.1.10. Sia G un gruppo di permutazioni strettamente 2-transitivo
sull’insieme E e tale che tutte le involuzioni hanno un elemento fisso. Allora per
ogni x ∈ E esiste ed è unica l’involuzione j ∈ G tale che j(x) = x.
Dimostrazione. Iniziamo con il dimostrare l’esistenza: sia x ∈ E e sia j ∈ G
una involuzione, per ipotesi j fissa un elemento di E, sia j(a) = a. Consideriamo
γ ∈ G tale che γ(x) = a, risulta γ −1 jγ(x) = γ −1 j(a) = γ −1 (a) = x con γ −1 jγ
involuzione di G.
Dimostriamo ora l’unicità: supponiamo per assurdo che esistano due involuzioni distinte j1 e j2 che fissano x ∈ E. Sia a ∈ E, a 6= x, sia j1 (a) = b, j2 (a) = c; per la
stretta 2-transitività di G ed essendo j1 (x) = j2 (x) = x, si ha b 6= c, a 6= b, a 6= c. Le
involuzioni j1 e j2 sono tra loro coniugate tramite γ ∈ G tale che γ(a) = a, γ(b) = c,
ossia j2 = γ −1 j1 γ. Risulta j2 (x) = γ −1 j1 γ(x) = x da cui j1 (γ(x)) = γ(x) e perciò
deve essere γ(x) = x essendo j1 6= id; ma allora γ ∈ G, γ(a) = a, γ(x) = x e
pertanto per la stretta 2-transitività di G risulta γ = 1E ma ciò è assurdo perchè
γ(c) = b con c 6= b.
Teorema 3.1.11. Sia G un gruppo di permutazioni strettamente 2-transitivo
su un insieme E. Il prodotto di due involuzioni distinte di G è una permutazione
di G priva di punti fissi.
Dimostrazione. Siano j1 , j2 ∈ G due involuzioni, j1 6= j2 ; ovviamente j1 j2 ∈
G. Supponiamo per assurdo che sia j1 j2 (x) = x con x ∈ E; allora risulta j1 (x) =
j2 (x). Sia j1 (x) = j2 (x) = y, per il teorema 3.1.10 deve essere x 6= y ma allora
j1 (x) = j2 (x) = y e j1 (y) = j2 (y) = x e pertanto j1 = j2 poichè le permutazioni
agiscono allo stesso modo su due elementi diversi; ciò è assurdo per la stretta
2-transitivitá di G e per l’ipotesi j1 6= j2 .
Nota 3.1.12. Il prodotto di due involuzioni di G è un elemento di G ma non
è detto sia ancora una involuzione di G.
Il seguente teorema richiama la condizione che caratterizza la condizione di planarità per i gruppi ma non assicura tale proprietà perchè non assicura la condizione
di unicità.
CAPITOLO 3 - Gruppi e insiemi di permutazioni 2-transitivi
21
Teorema 3.1.13. Sia G un gruppo di permutazioni strettamente 2-transitivo
su un insieme E. Comunque presi a, b ∈ E, a 6= b, esiste α ∈ G tale che α(a) = b
e α(x) 6= x per ogni x ∈ E.
Dimostrazione. Siano a, b ∈ E, a 6= b; dividiamo la dimostrazione in due
casi:
(1) Sia G tale che tutte le involuzioni hanno un elemento fisso. Per il teorema
3.1.10 esiste ed è unica l’involuzione j1 ∈ G tale che j1 (a) = a. Poichè G
è strettamente 2-transitivo, esiste ed è unica l’involuzione j2 ∈ G tale che
j2 (a) = b, j2 (b) = a. Allora risulta j2 j1 ∈ G, j2 j1 (a) = b e j2 j1 (x) 6= x per
ogni x ∈ E per il teorema 3.1.11.
(2) Sia G tale che tutte le involuzioni sono prive di punti fissi.
Sia j ∈ G tale che j(a) = b, j(b) = a; per la stretta 2-transitività di G
la permutazione j esiste, è unica, è una involuzione e per l’ipotesi fatta si
ha j(x) 6= x per ogni x ∈ E.
I seguenti teoremi permettono di approfondire lo studio dei gruppi strettamente
2-transitivi planari.
Teorema 3.1.14. Sia G un gruppo di permutazioni strettamente 2-transitivo
planare su un insieme E e tale che tutte le involuzioni sono prive di punti fissi.
Allora si ha:
(1) Ogni elemento di G privo di punti fissi è una involuzione.
(2) Detto J l’insieme delle involuzioni e detto A = J ∪ {1E }, A è un
sottogruppo di G, abeliano, normale in G, regolare su E.
Dimostrazione.
(1) Sia α ∈ G, α(x) 6= x per ogni x ∈ E e sia α(a) = b con a 6= b. Sia j ∈ G
tale che j(a) = b, j(b) = a; la permutazione j è una involuzione e per
l’ipotesi fatte j(x) 6= x per ogni x ∈ E. Poichè G è planare, in G esiste ed
è unica la permutazione che manda a in b e che non fissa nessun elemento
di E e pertanto deve essere α = j ossia α è una involuzione.
(2) Sia A = J ∪ {1E }.
• A è un sottogruppo di G. Infatti A è chiuso rispetto al prodotto perchè
j j = 1E ∈ A per ogni j ∈ A, inoltre se j1 6= j2 la permutazione j1 j2
è priva di punti fissi e per quanto provato al punto (1) è allora una
involuzione e pertanto j1 j2 ∈ A. Infine se j ∈ A anche j −1 = j ∈ A.
• A è abeliano. Infatti siano j1 , j2 ∈ A, si ha j1 j2 = j3 ∈ A perchè A
è sottogruppo e perciò j3 = j3−1 , allora j1 j2 = j3 = j3−1 = (j1 j2 )−1 =
j2−1 j1−1 = j2 j1 .
CAPITOLO 3 - Gruppi e insiemi di permutazioni 2-transitivi
22
• A è normale in G. Infatti sia γ ∈ G, j ∈ A. Se j = 1E allora γ −1 1E γ = 1E ∈ A; se j 6= 1E allora γ −1 jγ è la permutazione
coniugata di una involuzione e quindi γ −1 jγ ∈ A.
• A è regolare su E. Infatti siano a, b ∈ E. Se a = b allora l’unico
elemento di A che fissa il punto a è l’identità 1E . Se a 6= b allora in
A esiste l’involuzione j tale che j(a) = b, j(b) = a e per la planarità
di G la permutazione j è unica.
Teorema 3.1.15. Sia G un gruppo di permutazioni strettamente 2-transitivo
planare su un insieme E e tale che tutte le involuzioni hanno un punto fisso. Sia
A l’insieme costituito dall’identità e da tutti e soli gli elementi di G privi di punti
fissi; sia J l’insieme di tutte le involuzioni di G e sia j1 ∈ J una qualunque
involuzione. Allora si ha:
(1) A = j1 J = J J ;
(2) A è un sottogruppo di G, abeliano, normale in G, regolare su E.
Dimostrazione.
(1) Per il teorema 3.1.11 si ha j1 J ⊂ A; dimostriamo che A ⊂ j1 J . Sia
α ∈ A; se α = 1E allora α = j1 j1 ∈ j1 J ; se α 6= 1E sia α(a) = b con
a, b ∈ E, a 6= b. Sia j ∈ J tale che j(a) = j1 (b) da cui j1 j(a) = b, inoltre
da a 6= b segue j1 j 6= 1E , j1 6= j e pertanto per il teorema 3.1.11 si ha
j1 j(x) 6= x per ogni x ∈ E. Poichè G è planare, in G esiste ed è unica
la permutazione che manda a in b e non fissa nessun elemento di E e
quindi j1 j = α da cui α ∈ j1 J . Rimane così provato che A = j1 J ; questa
uguaglianza non dipende dalla scelta di j1 ∈ J e pertanto
[
ji J = J J .
A=
ji ∈J
(2)
• A è un sottogruppo di G. Infatti A è chiuso rispetto al prodotto perchè
j1 j2 · j1 j3 = j4 j3 ∈ J J = A (si ricordi che j1 j2 j1 è una involuzione
perchè è una permutazione coniugata di una involuzione).
Inoltre se j1 j2 ∈ A si ha (j1 j2 )−1 = j2−1 j1−1 = j2 j1 ∈ J J = A.
• A è abeliano. Infatti siano j1 j2 , j1 j3 ∈ A, si ha j1 j2 · j1 j3 ∈ A e perciò
j1 j2 · j1 j3 = j1 j4 = j1 j4−1 = j1 (j2 j1 j3 )−1 = j1 j3−1 j1−1 j2−1 = j1 j3 · j1 j2 .
• A è normale in G. Infatti sia γ ∈ G, j1 j ∈ A; si ha γj1 jγ −1 =
γj1 γ −1 γjγ −1 = j2 j3 ∈ J J = A perchè γj1 γ −1 e γjγ −1 sono involuzioni essendo coniugate di involuzioni.
• A è regolare su E. Infatti siano a, b ∈ E. Se a = b allora l’unico
elemento di A che fissa a è l’identità 1E = j1 j1 ∈ J J = A. Se a 6= b
sia j ∈ J l’involuzione tale che j(a) = j1 (b); risulta j1 j(a) = b con
j1 j ∈ J J = A e inoltre j1 j è unica per la planarità di G.
CAPITOLO 3 - Gruppi e insiemi di permutazioni 2-transitivi
23
Corollario 3.1.16. Sia G un gruppo strettamente 2-transitivo planare su E.
In G esiste un sottogruppo A che risulta abeliano, normale in G, regolare su E.
Dimostrazione. Segue dai teoremi 3.1.14 e 3.1.15
Quali sono le strutture algebriche che caratterizzano i gruppi strettamente 2-transitivi? Si dimostra che:
(1) i gruppi strettamente 2-transitivi sono caratterizzati dalla struttura algebrica di pseudocorpo;
(2) i gruppi strettamente 2-transitivi planari sono caratterizzati dalla struttura algebrica di quasicorpo associativo planare.
Come risulta dalla definizione di pseudocorpo e di quasicorpo associativo di
seguito riportate, la struttura di pseudocorpo è più debole di quella di quasicorpo
associativo.
Non si conoscono esempi di pseudocorpi che non siano quasicorpi associativi
mentre sono noti quasicorpi associativi non planari.
Probema aperto: esistono pseudocorpi che non siano quasicorpi associativi?
Richiamiamo le definizioni delle strutture algebriche sopra citate.
Definizione 3.1.17. Sia E un insieme non vuoto e “ +” una operazione binaria
interna ad E. La struttura (E, +) si dice cappio se:
(1) Esistono e sono unici x, y ∈ E tali che a + x = b, y + a = b per ogni
a, b ∈ E.
(2) Esiste 0 ∈ E tale che 0 + a = a + 0 = a per ogni a ∈ E.
Definizione 3.1.18. Sia E un insieme non vuoto e siano “ +” e “” due
operazioni binarie interne ad E. La struttura (E, +, ) si dice pseudocorpo se:
(1) (E, +) è un cappio, sia 0 l’elemento neutro;
(2) per ogni a, b, c ∈ E si ha (a + b) + c = hb,c a + (b + c) con hb,c ∈ E e
dipendente solo da b e da c (questa proprietà è detta pseudoassociativa);
(3) (E ∗ , ) è un gruppo, E ∗ = E − {0};
(4) 0 a = 0 per ogni a ∈ E;
(5) a (b + c) = a b + a c per ogni a, b, c ∈ E.
CAPITOLO 3 - Gruppi e insiemi di permutazioni 2-transitivi
24
Definizione 3.1.19. Sia E un insieme non vuoto e siano “+” e “” due operazioni binarie interne ad E.
La struttura (E, +, ) si dice quasicorpo associativo se:
(1) (E, +) è un gruppo abeliano, sia 0 l’elemento neutro;
(2) (E ∗ , ) è un gruppo, E ∗ = E − {0};
(3) 0 a = 0 per ogni a ∈ E;
(4) a (b + c) = a b + a c per ogni a, b, c ∈ E.
Definizione 3.1.20. Sia E un insieme non vuoto e siano “ +” e “” due
operazioni binarie interne ad E. La struttura (E, +, ) si dice quasicorpo associativo
planare se:
(1) (E, +, ) è un quasicorpo associativo.
(2) Per ogni a, b, c ∈ E, a 6= b, esiste x ∈ E tale che a x = b x + c.
Valgono i seguenti teoremi di cui non riportiamo la dimostrazione.
Teorema 3.1.21. Ogni quasicorpo associativo finito è planare.
Teorema 3.1.22. Sia G un gruppo di permutazione strettamente 2-transitivo
su un insieme E. Si possono definire in E due operazioni “+” e “” tali che (E, +, )
risulti uno pseudocorpo e gli elementi di G si possono rappresentare nella forma
x −→ a x + b, a ∈ E ∗ , b ∈ E.
Viceversa sia (E, +, ) uno pseudocorpo, sia E ∗ = E − {0} e sia
G = {α | α(x) = a x + b, a ∈ E ∗ , b ∈ E} .
G è un gruppo di permutazioni strettamente 2-transitivo su E.
Teorema 3.1.23. Sia G un gruppo di permutazioni su E, G strettamente
2-transitivo e planare. Si possono definire in E due operazioni “+” e “ ” tali che
(E, +, ) risulti un quasicorpo associativo planare e gli elementi di G si possono
rappresentare nella forma
x −→ a x + b, a ∈ E ∗ , b ∈ E.
CAPITOLO 3 - Gruppi e insiemi di permutazioni 2-transitivi
25
2. Esempi di Quasicorpi associativi non planari
Concludiamo il capitolo riportando tre esempi di quasicorpi associativi non
planari.
Esempio 3.2.1.
L’esempio è dovuto a Helmut Karzel.
Consideriamo il campo dei numeri reali (R, +, ·) e fissiamo un suo ampliamento
trascendente
a0 + a1 t + ... + an tn
R(t) =
| n, m ∈ N, bi non tutti nulli .
b0 + b1 t + ... + bm tm
A partire dal campo (R(t), +, ·) costruiamo una famiglia di quasicorpi associativi
non planari deformando l’operazione di moltiplicazione.
Notiamo che se x ∈ R(t)∗ allora x può essere rappresentato nella forma
x=
a0 + a1 t + ... + an tn
p(t)
=
q(t)
b0 + b1 t + ... + bm tm
con an , bm 6= 0
e con p(t), q(t) 6= 0 e primi fra loro. Definiamo allora
x=
|an |
.
|bm |
Se consideriamo l’applicazione ϕ : (R(t)∗ , ·) −→ (R∗ , ·) tale che ϕ(x) = x essa è un
omomorfismo di gruppi perchè banalmente ϕ(x1 x2 ) = ϕ(x1 )ϕ(x2 ), inoltre ϕ è un
isomorfismo se e solo se restringiamo l’immagine a (R+ , ·). Fissiamo a ∈ R+ , a 6= 1;
per ogni x ∈ R(t) definiamo 0 ◦ x = 0 e per ogni x ∈ R(t)∗ , per ogni y ∈ R(t)
definiamo
f1 (t) g1 (t)
f1 (t) g1 (t + lga x)
x◦y =
◦
=
·
.
f2 (t) g2 (t)
f2 (t) g2 (t + lga x)
Proviamo che la struttura (R(t), +, ◦) è un quasicorpo associativo non planare.
(R(t), +, ◦) è un quasicorpo associativo. Infatti:
(1) (R(t), +) è un gruppo perché l’operazione di addizione non è stata modificata.
(2) Per le proprietà dei logaritmi si ha che (R(t)∗ , ◦) è un gruppo:
• ◦ è una operazione binaria interna;
• esiste l’elemento neutro ed è il polinomio costante 1;
• esiste l’elemento inverso:
f1 (t)
f2 (t − lga x)
allora x−1 =
;
per ogni x ∈ R(t)∗ se x =
f2 (t)
f1 (t − lga x)
• vale la proprietà associativa.
(3) Dalla definizione posta si ha che per ogni x ∈ R(t) risulta 0 ◦ x = 0.
(4) Vale la proprietà distributiva a sinistra, come si può facilmente verificare.
CAPITOLO 3 - Gruppi e insiemi di permutazioni 2-transitivi
26
Il quasicorpo (R(t), +, ◦) non è planare. Per dimostrarlo basta determinare un’equazione del tipo
b ◦ x = c ◦ x + d con b, c, d ∈ R(t) e b 6= c
che non ammette soluzioni in R(t).
Una tale equazione è ad esempio 2t ◦ x = x + 1.
Essa è a coefficienti in R(t), inoltre 2t 6= 1 perchè t è un elemento trascendente
su R quindi t 6= 21 ∈ Q.
Per assurdo supponiamo che l’equazione 2t ◦ x = x + 1 ammetta soluzione in
R(t), sia
p(t)
p(t)
2t ◦
=
+1
q(t)
q(t)
allora è
p(t + lga 2)
p(t)
2t ·
=
+1
q(t + lga 2)
q(t)
cioè
(2t)p(t + lga 2)q(t) − q(t)q(t + lga 2) = p(t)q(t + lga 2)
da cui
q(t)((2t)p(t + lga 2) − q(t + lga 2)) = p(t)q(t + lga 2).
Ne segue che q(t) divide p(t)q(t+lga 2), ma q(t) non divide p(t) perciò q(t) divide
q(t + lga 2) e poiché q(t) e q(t + lga 2) hanno lo stesso grado si ha q(t) = λq(t + lga 2)
con λ costante.
Inoltre q(t) e q(t + lga 2) hanno il medesimo coefficiente per il termine di grado
massimo, quindi λ = 1. Perciò q(t) = q(t + lga 2) = costante.
Allora se confrontiamo i gradi dei due membri dell’uguaglianza
(2t)p(t + lga 2)q(t) − q(t)q(t + lga 2) = p(t)q(t + lga 2)
ottenuta in precedenza abbiamo 1 + deg(p) = deg(p) e ciò è assurdo.
(R(t), +, ◦) individua una famiglia di quasicorpi associativi non planari; al
variare di a in R+ , a 6= 1, otteniamo infiniti esempi.
Osservazione
La non planarità è determinata dalla deformazione della moltiplicazione, ma come vedremo nei prossimi esempi è indipendente dalla scelta dell’uso del logaritmo.
Esempio 3.2.2.
Sia K un campo di caratteristica zero e sia K(t) un suo ampliamento trascendente
a0 + a1 t + ... + an tn
K(t) =
| n, m ∈ N, bi non tutti nulli .
b0 + b1 t + ... + bm tm
CAPITOLO 3 - Gruppi e insiemi di permutazioni 2-transitivi
27
(t)
Per ogni x ∈ K(t)∗ con x = ff21 (t)
sia ix = (deg(f1 ) − deg(f2 )) ∈ Z.
Definiamo in K(t) una operazione “◦” nel seguente modo.
Per ogni x ∈ K(t) definiamo 0 ◦ x = 0. Fissato h ∈ K∗ ; per ogni x ∈ K(t)∗ , e
per ogni y ∈ K(t)∗ definiamo
f1 (t) g1 (t)
f1 (t) g1 (t + hix )
x◦y =
◦
=
·
.
f2 (t) g2 (t)
f2 (t) g2 (t + hix )
La struttura (K(t), +, ◦) è un quasicorpo associativo non planare; un’equazione
che non trova soluzione in K(t) è ad esempio
t ◦ x = x + 1.
La dimostrazione è analoga a quella dell’esempio 3.2.1 .
Osservazione
Se scegliamo h = 1 ritroviamo l’esempio 3.2.1 .
Esempio 3.2.3.
Sia K un campo di caratteristica zero e sia K(t) un suo ampliamento trascendente
a0 + a1 t + ... + an tn
| n, m ∈ N, bi non tutti nulli .
K(t) =
b0 + b1 t + ... + bm tm
Per ogni x ∈ K(t)∗ con x = ff12 (t)
sia ix = (deg(f1 ) − deg(f2 )) ∈ Z.
(t)
Definiamo in K(t) una operazione “◦” nel seguente modo. Per ogni x ∈ K(t)∗
definiamo 0 ◦ x = 0. Sia fissato k ∈ K∗ tale che k n 6= 1 per ogni n ∈ Z∗ ; per ogni
x ∈ K(t)∗ e per ogni y ∈ K(t)∗ definiamo
f1 (t) g1 (t)
f1 (t) g1 (tk ix )
◦
=
·
.
f2 (t) g2 (t)
f2 (t) g2 (tk ix )
La struttura (K(t), +, ◦) è un quasicorpo associativo non planare; un’equazione
che non trova soluzione in K(t) è ancora
t ◦ x = x + 1.
La dimostrazione è analoga a quella dell’esempio 3.2.1 .
CAPITOLO 4
Gruppi e insiemi di permutazioni 3-transitivi
1. Introduzione
Sono esempi di gruppi strettamente 3-transitivi i gruppi S3 , S4 , A5 .
Tutti gli altri esempi di gruppi e insiemi strettamente 3-transitivi noti che
agiscono su un insieme E sono tali che |E| = pn + 1, p primo, n ∈ N − {0}. Sono
tutti esempi ottenuti a partire da un campo K con |K| = pn e pertanto richiamiamo
alcune proprietà dei campi finiti.
(1) Se K è un campo finito allora |K| = pn con p primo, n ∈ N − {0}.
(2) Per ogni p primo e n ∈ N − {0} esiste uno ed uno solo campo con pn
elementi indicato con GF (pn ).
n
(3) GF (pn ) è il campo di spezzamento del polinomio xp − x ∈ Zp [x].
(4) Il gruppo moltiplicativo
(K∗
, ·) di un campo finito K è ciclico:
∗
pn −1
K =< σ >= 1, σ, ..., σ
.
(5) Se K = GF (pn ) allora il gruppo Aut K degli automorfismi di K è ciclico
di ordine n, un generatore è l’automorfismo σ : K −→ K, σ(x) = xp detto
automorfismo di Frobenius; AutK =< σ >
Definizione 4.1.1. Sia (K, +, ·) un campo; un elemento x ∈ K∗ = K − {0} è
detto quadrato se esiste y ∈ K∗ tale che x = y 2 .
Si osservi che anche lo zero di K può essere considerato un quadrato, ma quelli
che interessano sono i quadrati non nulli perchè questi formano un sottogruppo di
(K∗ , ·).
Per i campi finiti vale il seguente teorema.
Teorema 4.1.2. Sia K = GF (pn ) un campo finito. Se K ha caratteristica
p = 2 allora tutti gli elementi sono quadrati. Se K ha caratteristica p 6= 2 allora il
sottogruppo moltiplicativo dei quadrati ha indice 2 in K∗ .
Dimostrazione. Sia p = 2, gli elementi del campo soddisfano l’equazione
n−1
x = x da cui x = (x2 )2 e pertanto x è un quadrato per ogni x ∈ K.
Sia p 6= 2 e sia σ il generatore del gruppo ciclico (K∗ , ·). I quadrati del campo
sono tutte e sole le potenze di σ ad esponente pari. Infatti σ 2h è il quadrato di σ h ,
2n
28
CAPITOLO 4 - Gruppi e insiemi di permutazioni 3-transitivi
29
inoltre se supponiamo per assurdo che esista σ 2h+1 = a2 con a ∈ K∗ , si ha a = σ t
da cui σ 2h+1 = (σ t )2 = σ 2t e pertanto deve essere (2h + 1) − 2t ≡ 0 mod (pn − 1)
ossia 2(h − t) + 1 ≡ 0 mod (pn − 1) e ciò è assurdo perchè 2(h − t) + 1 è dispari
mentre pn − 1 è pari. Dunque il sottogruppo H dei quadrati di K∗ è costituito da
tutte e sole le potenze di σ ad esponente pari perciò gli unici lateralin di H rispetto
al gruppo (K∗ , ·) sono H e σH ossia H ha indice 2 in K∗ e |H| = p 2−1 .
Prima di passare alla costruzione di insiemi e gruppi strettamente 3-transitivi,
osserviamo che per noti teoremi non esistono insiemi di permutazioni abeliani e
transitivi che non siano gruppi strettamente 1-transitivi e pertanto la ricerca di
gruppi e insiemi strettamente 3-transitivi va condotta in ambiti non
commutativi.
2. Il gruppo proiettivo lineare P GL(2, K)
Sia K un campo qualsiasi e sia ∞ 6∈ K. Posto E = K ∪ {∞} sia
ax + b
G = α | α(x) =
, a, b, c, d ∈ K, ad − bc 6= 0
cx + d
l’insieme delle applicazioni di E in E ottenute estendendo le operazioni del
campo K all’elemento ∞ in modo tale che
∞ −→
a
c
se c 6= 0, ∞ → ∞ se c = 0,
d
(− ) −→ ∞.
c
L’insieme G risulta essere un sottogruppo di Sym E strettamente 3-transitivo
su E; viene indicato con P GL(2, K) ed è detto gruppo proiettivo lineare di grado
2 sul campo K.
L’elemento ad − bc ∈ K∗ si dice il determinante della permutazione; se α ∈
P GL(2, K) il suo determinante è indicato con det(α).
Per il teorema 2.1.19, dividiamo nelle seguenti tre parti la dimostrazione che
G = P GL(2, K) è un gruppo strettamente 3-transitivo su E = K ∪ {∞} .
(1) P GL(2, K) è un gruppo;
(2) P GL(2, K) è transitivo su E;
(3) G∞ , stabilizzatore di ∞ ∈ E, è strettamente 2-transitivo su K = E−{∞} .
Dimostrazione.
CAPITOLO 4 - Gruppi e insiemi di permutazioni 3-transitivi
30
(1) G = P GL(2, K) è un sottogruppo di Sym E.
Siano α, β ∈ G, per le proprietà dei determinanti risulta det(αβ) =
det(α)det(β) e poichè det(α) 6= 0, det(β) 6= 0 e K privo di divisori dello zero, risulta det(αβ) 6= 0 e pertanto αβ ∈ G. Inoltre per ogni α ∈ G
1
poichè det(α−1 ) = det(α)
si ha che α−1 ∈ G. Rimane così provato che
G = P GL(2, K) è un gruppo.
(2) G = P GL(2, K) è transitivo su E.
Iniziamo con il dimostrare che per ogni y ∈ E esiste α ∈ G tale che
α(∞) = y. Se y = ∞ ogni α ∈ G, α(x) = ax + b, a ∈ K∗ , è tale che
α(∞) = ∞. Se y 6= ∞ ogni α ∈ G, α(x) = yx+b
, b ∈ K∗ , è tale che
x
α(∞) = y.
Comunque presi x, y ∈ E siano α, β ∈ G tali che α(∞) = x, β(∞) = y;
risulta βα−1 (x) = y con βα−1 ∈ G perchè G è un gruppo e pertanto
G = P GL(2, K) è transitivo su E.
(3) G∞ è strettamente 2-transitivo su K.
Dalla definizione di G, segue che G∞ = {α | α(x) = ax + b, a ∈ K∗ } è il
gruppo affine AG(1, K) che è strettamente 2-transitivo su K come dimostrato nel capitolo 3.
Rimane pertanto dimostrato che G = P GL(2, K) è un gruppo strettamente 3-transitivo su E = K ∪ {∞}.
3. Il gruppo proiettivo semilineare P ΓL(2, K)
Sia K un campo qualsiasi, ∞ ∈
/ K, E = K ∪ {∞}. Per ogni automorfismo
σ ∈ Aut K prolunghiamo l’azione di σ a tutto E ponendo σ(∞) = ∞.
Sia
aσ(x) + b
Γ = x −→
, a, b, c, d ∈ K, ad − bc 6= 0, per ogni σ ∈ Aut K =
cσ(x) + d
= {ασ | α ∈ P GL(2, K),
per ogni σ ∈ Aut K}
l’insieme delle applicazioni di E in E ottenute estendendo le operazioni del
campo K all’elemento ∞ in modo tale che
a
d
se c 6= 0, ∞ → ∞ se c = 0, (− ) −→ ∞.
c
c
L’insieme Γ risulta essere un sottogruppo di Sym E 3-transitivo su E (non strettamente); viene indicato con P ΓL(2, K) ed è detto gruppo proietivo semilineare.
∞ −→
CAPITOLO 4 - Gruppi e insiemi di permutazioni 3-transitivi
31
L’elemento ad − bc ∈ K∗ si dice determinante della permutazione; se γ ∈
P ΓL(2, K) il suo determinante è indicato con det(γ).
Dimostriamo che:
(1) Γ è un gruppo;
(2) Γ è 3-transitivo su E.
Dimostrazione.
(1) Dimostriamo che Γ è un sottogruppo di Sym E.
Siano α = ασ, β = βτ ∈ Γ con α, β ∈ P GL(2, K) e σ, τ ∈ Aut K.
Si osservi che poichè gli automorfismi di un campo formano un gruppo,
se σ, τ ∈ Aut(K) allora στ ∈ Aut K. Inoltre per ogni α ∈ P GL(2, K),
indicato det(α) = ∆, risulta det(σα) = σ(det(α)) = σ(∆) e pertanto per
le proprietà degli automorfismi, se ∆ 6= 0 anche σ(∆) 6= 0 da cui σα ∈ Γ
e quindi, oltre a ασ ∈ Γ, si ha anche σα ∈ Γ.
x+b2
x+b1
Se dunque ασ = θ, α(x) = ac11x+d
, β(x) = ac22x+d
, risulta
1
2
ασ · βτ : x −→
a3 θ(x) + b3
c3 θ(x) + d3
con a3 , b3 , c3 , d3 ∈ K, a3 d3 − b3 c3 ∈ K∗ e pertanto ασ · βτ ∈ Γ.
Sia ora ασ ∈ Γ, si ha α−1 ∈ P GL(2, K) e perciò per le osservazioni
precedenti si ha (ασ)−1 = σ −1 α−1 ∈ Γ.
Rimane così provato che Γ = P ΓL(2, K) è un gruppo.
(2) Poichè Aut K è un gruppo, sia 1K l’automorfismo identico su K la cui
azione è stata estesa a tutto E. In P ΓL(2, K) esistono le applicazioni
α1K con α ∈ P GL(2, K) e pertanto P GL(2, K) ⊂ P ΓL(2, K). Abbiamo dimostrato che P GL(2, K) è strettamente 3-transitivo ed essendo P GL(2, K) 6= P ΓL(2, K), P GL(2, K) ⊂ P ΓL(2, K) si conclude che
Γ = P ΓL(2, K) è 3-transitivo su E ma non strettamente 3-transitivo.
Teorema 4.3.1. Sia K un campo qualsiasi e sia ∞ ∈/ K. Posto E = K∪{∞}
si ha P GL(2, K) sottogruppo normale di P ΓL(2, K).
Dimostrazione. P GL(2, K) è un gruppo e poichè per ogni α ∈ P GL(2, K)
si ha α1K ∈ P ΓL(2, K) con 1K automorfismo identità, risulta P GL(2, K) sottogruppo di P ΓL(2, K).
Siano α ∈ P GL(2, K) e βσ ∈ P ΓL(2, K), si ha (βσ)α(βσ)−1 = βσασ −1 β −1 .
Ma σ e σ −1 , essendo automorfismi di K, modificano solo i coefficienti di α, mentre
gli effetti degli automorfismi sull’incognita si annullano e pertanto (βσ)α(βσ)−1 ∈
P GL(2, K) ossia P GL(2, K) è normale in P ΓL(2, K).
CAPITOLO 4 - Gruppi e insiemi di permutazioni 3-transitivi
32
Evidenziamo ora un importante sottogruppo di P GL(2, K) (e quindi di P ΓL(2, K))
fondamentale nella costruzione e nello studio dei gruppi e degli insiemi strettamente 3-transitivi noti.
4. Il gruppo proiettivo lineare speciale P SL(2, K)
campo qualsiasi e sia ∞ 6∈ K. Posto E = K ∪ {∞}, sia J =
Sia K unax+b
α | α(x) = cx+d , a, b, c, d ∈ K, ad − bc quadrato di K∗ } l’insieme delle applicazioni di E in E definite estendendo le operazioni del campo K all’elemento ∞ in
modo tale che per ogni α ∈ J sia
α(∞) =
a
c
se c 6= 0, α(∞) = ∞ se c = 0, α(− dc ) = ∞ .
L’insieme J è contenuto nel gruppo P GL(2, K) e poichè in K∗ il prodotto di due
quadrati è un quadrato e l’inverso di un quadrato è un quadrato, si ha che J è
un gruppo indicato con P SL(2, K) e detto gruppo proiettivo lineare speciale sul
campo K. Ovviamente P SL(2, K) è sottogruppo di P GL(2, K) ed è sottogruppo
di P ΓL(2, K).
Il gruppo P SL(2, K) è sottogruppo normale di P ΓL(2, K).
Infatti siano α ∈ P SL(2, K) e βσ ∈ P ΓL(2, K), si ha (βσ)α(βσ)−1 = βσασ −1 β −1 .
Posto det(β) = ∆1 e det(α) = ∆2 si ha σ(∆2 ) quadrato perchè ogni automorfismo
trasforma quadrati di K∗ in quadrati di K∗ , inoltre risulta
det((βσ)α(βσ)−1 ) = det(β)det(σασ −1 )det(β −1 ) =
= det(β)det(σασ −1 )det(β −1 ) = ∆1 σ(∆2 )∆−1
1 = σ(∆2 )
quadrato di K∗ .
Si conclude pertanto (βσ)α(βσ)−1 ∈ P SL(2, K) e quindi P SL(2, K) sottogruppo normale in P ΓL(2, K).
Nota 4.4.1. P SL(2, K) non è 3-transitivo su E = K∪{∞} perchè è contenuto
propriamente in P GL(2, K) che è strettamente 3-transitivo. Se K è finito allora
P SL(2, K) è un gruppo di indice due in P GL(2, K),
CAPITOLO 4 - Gruppi e insiemi di permutazioni 3-transitivi
33
5. Esempi di insiemi (non gruppi) strettamente 3-transitivi
Sia K = GF (pn ) un campo finito e sia ∞ ∈
/ K; sia H = {x2 | x ∈ K∗ } il
sottogruppo moltiplicativo dei quadrati di K∗ . Sia σ ∈ Aut K, E = K ∪ {∞},
estendiamo l’azione di σ a tutto E ponendo σ(∞) = ∞.
Sia G l’insieme delle permutazioni su E così definito:
ax + b
n
se ad − bc ∈ H;
G = G(p , σ) = α | α(x) =
cx + d
aσ(x) + b
∗
α(x) =
se ad − bc ∈ K − H; per ogni a, b, c, d ∈ K
cσ(x) + d
ossia G = P SL(2, pn ) ∪ {βσ | β ∈ P GL(2, pn ), detβ ∈ K∗ − H} .
L’insieme G è strettamente 3-transitivo su E.
Dimostrazione. Notiamo innanzitutto che σP GL(2, pn ) = P GL(2, pn )σ perchè P GL(2, pn ) è sottogruppo normale di P ΓL(2, pn ) e inoltre σ ∈ P ΓL(2, pn )
perché σ : x −→ 1·σ(x)+0
.
0σ(x)+1
Siano (x1 , x2 , x3 ), (y1 , y2 , y3 ) due terne di elementi distinti di E. Poichè P GL(2, pn )
è strettamente 3-transitivo su E, esiste ed è unica α ∈ P GL(2, pn ) tale che α(x1 ) =
0, α(x2 ) = 1, α(x3 ) = ∞ ed esiste ed è unica β ∈ P GL(2, pn ) tale che β(0) =
y1 , β(1) = y2 , β(∞) = y3 .
La permutazione βα ∈ P GL(2, pn ) è tale che βα(xi ) = yi per i = 1, 2, 3.
Consideriamo ora la permutazione
βσα ∈ P GL(2, pn )σP GL(2, pn ) = P GL(2, pn )σ,
essa è tale che βσα(xi ) = yi per i = 1, 2, 3. Le due permutazioni βα e βσα
agiscono dunque allo stesso modo su x1 , x2 , x3 ma una ed una sola appartiene a
G = G(pn , σ) perchè esse hanno lo stesso carattere quadratico ossia det(βα) ∈ H
se e solo se det(βσα) ∈ H.
Infatti k e σ(k) sono entrambi quadrati o entrambi non quadrati e perciò detto
det(α) = r, det(β) = s si ha det(βα) · det(βσα) = srsσ(r) = s2 rσ(r) ∈ H
e dunque det(βα) e det(βσα) sono entrambi quadrati o entrambi non quadrati
perchè, essendo K finito, H è un sottogruppo di indice 2 in K∗ .
Rimane così provato che G = G(pn , σ) è un insieme strettamente 3-transitivo.
Nota 4.5.1. L’esempio appena visto è ottenuto a partire da un automorfismo
σ fissato arbitrariamente.
Al variare di σ in Aut K si ottengono insiemi strettamente 3-transitivi, non
sempre identificabili fra loro. In particolare si evidenziano i seguenti casi:
CAPITOLO 4 - Gruppi e insiemi di permutazioni 3-transitivi
34
(1) Se σ = 1E allora G = G(pn , σ) = P GL(2, pn ).
(2) Se p = 2 allora H = K∗ e G = G(2n , σ) = P SL(2, 2n ) = P GL(2, 2n ).
(3) G = G(pn , σ) è un gruppo se e solo se σ 2 = 1E .
Teorema 4.5.2. Se G è un insieme di permutazioni strettamente 3-transitivo
su un insieme E finito, contenente la permutazione identitá e tale che |E| = n +
1, n ≡ 0 mod2, allora si ha n = 2h con h ∈ N∗ e G = P GL(2, 2h ).
Dimostrazione. Vedi P. Quattrocchi 00 Sugli insiemi di sostituzioni strettamente 3-transitivi finiti00 , Atti del Seminario Matematica e Fisica dell’Universitá
di Modena, vol. XXIV, 1975, 279-289.
6. Problemi aperti
(1) Sia G strettamente 3-transitivo su E, G contenente la permutazione identità e sia |E| = n + 1, n ≡ 1 mod 2. Risulta n = ph ?
(2) Tutti gli esempi di insiemi strettamente 3-transitivi finiti noti sono quelli
descritti nel paragrafo 5 e dunque sono tutti contenuti in P ΓL(2, pn ) e
contengono tutti P SL(2, pn ).
Esistono insiemi strettamente 3-transitivi non contenuti in P ΓL(2, pn )?
(3) Si è avanzata la seguente congettura. Se G è un insieme di permutazioni
strettamente 3-transitivo su E = GF (pn ) ∪ {∞} contenente la permutazione identità e tale che G ⊂ P ΓL(2, pn ) allora G ⊃ P SL(2, pn ).
(4) Sia G un insieme finito strettamente 3-transitivo su E tale che 1E ∈ G e
αβ ∈ G per ogni α, β ∈ G. G é un gruppo?
CAPITOLO 5
Insiemi e gruppi k-transitivi, k ≥ 4.
In fase di completamento.
35
CAPITOLO 6
Estensione di gruppi e insiemi di permutazioni k-transitivi
Nel teorema 2.1.17 si é dimostrato che da un insieme k-transitivo, k ≥ 2, é
possibile passare ad un insieme (k-1)-transitivo considerando lo stabilizzatore di
un elemento. In generale é possibile costruire insiemi di permutazioni che non sono
k-transitivi ma che contengono stabilizzatori (k-1)-transitivi. Il passaggio inverso,
cioé estendere un insieme G k-transitivo ad un insieme G∗ (k+1)-transitivo, é
vero quando G é un gruppo infatti se G é un gruppo transitivo allora G é ktransitivo se e solo se Ga é (k-1)-transitivo. Rimane aperto il problema di stabilire
sotto quali condizioni sia possibile estendere un insieme k-transitivo a un insieme
(k+1)-transitivo.
1. Definizioni e Teorema di Witt
Definizione 6.1.1. Sia G un insieme di permutazioni su un insieme E. Considerato un elemento ∞ ∈
/ E e posto E ∗ = E ∪ {∞}, un insieme G∗ si dice
estensione di G nel senso di Witt se:
• G∗ è un insieme di permutazioni su E ∗ ;
• G∗∞ , nella sua azione su E, coincide con G.
Teorema 6.1.2. Sia G un gruppo di permutazioni k-transitivo su un insieme
E, k ≥ 2. Fissato a ∈ E e considerata una qualunque permutazione δ ∈ G − Ga
risulta
G = Ga ∪ Ga δGa .
Dimostrazione. Poichè G è un gruppo risulta G ⊃ Ga ∪ Ga δGa .
Dimostriamo che G ⊂ Ga ∪ Ga δ Ga . Sia α ∈ G. Se α ∈ Ga allora α ∈
Ga ∪Ga δ Ga . Se α ∈ G − Ga dimostriamo che α ∈ Ga δ Ga . Poichè α−1 (a) 6= a
e δ −1 (a) 6= a, essendo G k-transitivo su E con k ≥ 2 esiste λ ∈ G tale che λ(a) = a
e λ(δ −1 (a)) = α−1 (a); pertanto α λ δ −1 ∈ Ga ossia α ∈ Ga δ λ−1 con λ−1 ∈ Ga e
dunque α ∈ Ga δ Ga .
Rimane così provato che G = Ga ∪ Ga δ Ga .
36
CAPITOLO 6 - Estensione di gruppi e insiemi di permutazioni k-transitivi
37
Teorema 6.1.3. Sia G∗ un gruppo di permutazioni (k+1)-transitivo su un
insieme E ∗ , k ≥ 2. Fissato ∞ ∈ E ∗ e posto E = E ∗ − {∞} sia G = G∗∞ e siano
a, b ∈ E con a 6= b. Allora esistono α ∈ G∗ e β ∈ G tali che
(1)
(2)
(3)
(4)
(5)
α(∞) = a, α(a) = ∞,
β(a) = b, β(b) = a;
(βα)3 ∈ G, α2 ∈ G;
αGa α = Ga ;
G∗ = G ∪ GαG.
α(b) = b;
Dimostrazione. La (1) è vera perchè G∗ è almeno 3-transitivo. La (2) è vera
perchè G è almeno 2-transitivo. La (3) è vera perchè (βα)3 (∞) = ∞ e α2 (∞) = ∞.
Dimostriamo ora la (4); per ogni γ ∈ Ga si ha γ(∞) = ∞ perchè Ga ⊂ G e
quindi αGa α ⊂ Ga e anche α−1 γα−1 (a) = a da cui α−1 γα−1 ∈ Ga , γ ∈ αGa α e
quindi Ga ⊂ αGa α. Rimane dunque provato che αGa α = Ga . Infine (5) è vera per
il teorema 6.1.2 che assicura G∗ = G∗∞ ∪ G∗∞ αG∗∞ = G ∪ GαG.
Teorema 6.1.4. Teorema di estensione di Witt (1938)
Sia G un gruppo di permutazioni k-transitivo su un insieme E, k ≥ 2. Sia
E ∗ = E ∪ {∞} con ∞ ∈
/ E e sia σ(∞) = ∞ per ogni σ ∈ G. Siano a, b ∈ E, a 6= b.
Se esistono α ∈ Sym E ∗ e β ∈ G tali che:
(1)
(2)
(3)
(4)
G∗∞
α(∞) = a, α(a) = ∞,
β(a) = b, β(b) = a;
(βα)3 ∈ G, α2 ∈ G;
αGa α = Ga ;
α(b) = b;
allora G∗ = G ∪ GαG è un gruppo di permutazioni (k+1)-transitivo su E ∗ e
= G.
Dimostrazione. Dimostriamo che G∗ è un gruppo. Per provare che G∗ è
chiuso rispetto al prodotto distinguiamo tre casi:
(1) Siano δ, τ ∈ G; essendo G un gruppo si ha δτ ∈ G∗ perchè δτ ∈ G ⊂ G∗ .
(2) Sia δ ∈ G e τ ∈ GαG; esistono γ1 , γ2 ∈ G, tali che τ = γ1 αγ2 e poichè
δγ1 ∈ G si ha δτ = δγ1 αγ2 = γ3 αγ2 ∈ GαG ⊂ G∗ , dunque δτ ∈ G∗ .
Analogamente si prova δτ ∈ G∗ se δ ∈ GαG e τ ∈ G.
(3) Siano δ, τ ∈ GαG. Iniziamo con il dimostrare che αGα ⊂ G∪GαG; poichè
α2 (∞) = ∞, α2 (a) = a si ha α2 ∈ G ∩ Ga = Ga , α2 Ga = Ga α2 = Ga ,
ma per l’ipotesi (4) si ha αGa = Ga α−1 e pertanto αGa = Ga α−1 =
Ga α2 α−1 = Ga α ossia
αGa = Ga α.
(I)
CAPITOLO 6 - Estensione di gruppi e insiemi di permutazioni k-transitivi
38
Per l’ipotesi (3) si ha (βα)3 = βαβαβα ∈ G, αβα ∈ β −1 α−1 β −1 G =
β −1 α−1 G e, per l’ipotesi (3), β −1 α−1 G = β −1 α−1 α2 G = β −1 αG ossia
αβα ∈ β −1 αG.
(II)
Tenendo conto del teorema 6.1.2 , di (I), di (II) e dell’ipotesi(4) possiamo
affermare che
αGα = α(Ga ∪ Ga βGa )α = αGa α ∪ αGa βGa α = Ga ∪ Ga αβαGa ⊂
Ga ∪ Ga β −1 αGGa = Ga ∪ (Ga β −1 )α(GGa ) ⊂ Ga ∪ GαG ⊂ G ∪ GαG.
Se dunque δ, τ ∈ GαG si ha δτ ∈ (GαG)(GαG) = GαGαG ⊂ G(G ∪ GαG)G =
GGG ∪ GGαGG = G ∪ GαG = G∗ ossia
δτ ∈ G∗ .
Rimane così completamente dimostrato che comunque presi δ, τ ∈ G∗ risulta
δτ ∈ G∗ . Per dimostrare che per ogni δ ∈ G∗ si ha δ −1 ∈ G∗ , distinguiamo due
casi.
(1) Se δ ∈ G. Essendo G un gruppo segue δ −1 ∈ G ⊂ G∗ .
(2) Sia δ ∈ GαG. Posto δ = λαµ, λ, µ ∈ G risulta δ −1 = (λαµ)−1 =
µ−1 α−1 λ−1 ; essendo G un gruppo e α2 , λ−1 ∈ G si ha che esiste γ ∈ G
tale che α2 γ = λ−1 e pertanto δ −1 = (λαµ)−1 = µ−1 α−1 α2 γ = µ−1 αγ ∈
GαG ⊂ G∗ .
Dimostriamo che il gruppo G∗ è transitivo su E ∗ . Essendo G∗ gruppo basta
provare che per ogni x ∈ E ∗ esiste τ ∈ G∗ tale che τ (∞) = x. Se x = ∞ allora ogni τ ∈ G ⊂ G∗ è tale che τ (∞) = ∞. Se x 6= ∞ sia σ ∈ G tale che
σ(a) = x, σ esiste perchè G è k-transitivo. Considerata τ = σα si ha τ (∞) = x
e τ = σα = σα1E ∈ GαG ⊂ G∗ ossia τ ∈ G∗ .
Dimostriamo che G∗∞ = G. Ogni elemento di G fissa ∞.
Se per assurdo esistesse γ1 αγ2 ∈ GαG tale che γ1 αγ2 (∞) = ∞, poichè γ2 (∞) =
∞, γ1−1 (∞) = ∞ si avrebbe α(∞) = ∞ e ciò è assurdo perchè α(∞) = a ∈ E e
∞∈
/ E.
Per il teorema 2.1.19 rimane così provato che G∗ è un gruppo (k+1)-transitivo
su E ∗ e G∗∞ = G.
2. Estensione di insiemi di permutazioni k-transitivi
Nel 1986 P.Quattrocchi e P.Sisi hanno generalizzato il Teorema di Witt determinando delle condizioni sufficienti per estendere gli insiemi di permutazioni
(non necessariamente gruppi) k-transitivi. Nel 1977 G.Rinaldi e S.Spaggiari hanno
CAPITOLO 6 - Estensione di gruppi e insiemi di permutazioni k-transitivi
39
migliorato le condizioni sufficienti trovate da Quattrocchi e Sisi, dimostrando il
teorema seguente.
Teorema 6.2.1. Sia G un insieme di permutazioni k-transitivo su un insieme
E con k ≥ 1 , |E| ≥ 3. Sia E ∗ = E ∪ {∞} con ∞ ∈
/ E e sia γ(∞) = ∞ per ogni
γ ∈ G. Se esistono α ∈ Sym E ∗ e G ⊂ G tali che:
(1) α(∞) 6= ∞;
(2) G è transitivo su E;
(3) GαG = GαG;
(4) GG ⊂ G , GG ⊂ G;
(5) αGα ⊂ G ∪ GαG;
allora G∗ = G ∪ GαG è un insieme di permutazioni (k+1)-transitivo su E ∗ e
G∗∞ = G.
Se G è strettamente k-transitivo su E allora G∗ è strettamente (k+1)-transitivo
su E ∗ .
Dimostrazione. Siano a e b ∈ E non necessariamente distinti, tali che
α(∞) = b e α(a) = ∞.
Iniziamo con l’ossevare che G∗∞ = G ossia dimostriamo che le sole permutazioni di
G∗ = G ∪ GαG che fissano ∞ sono quelle di G; infatti per definizione se γ ∈ G
si ha γ(∞) = ∞ mentre se γ ∈ GαG si ha γ = γ1 αγ2 con γ1 , γ2 ∈ G e risulta
γ(∞) 6= ∞ perché γ(∞) = γ1 αγ2 (∞) = γ1 (∞) ∈ E.
Siano (x1 , x2 , ..., xk+1 ), (y1 , y2 , ..., yk+1 ) due (k+1)-uple di elementi distinti
di E ∗ ; dimostriamo che esiste una permutazione g ∈ G∗ tale che g(xi ) = yi ,
i = 1 , . . . , k + 1.
Distinguiamo due casi.
1◦ caso: Se k = 1 e x1 = ∞, y2 = ∞, siano β1 , eβ2 ∈ G con β1 (b) = y1 e
β2 (x2 ) = a; risulta allora β1 αβ2 (∞) = y1 e β1 αβ2 (x2 ) = ∞ con β1 αβ2 ∈
G∗ . Analogamente se k = 1 e x2 = ∞, y1 = ∞, esiste in G∗ una permutazione che trasforma (x1 , ∞) in (∞, y2 ).
2◦ caso: Se k = 1 e non si verifica il 1◦ caso oppure se k ≥ 2, esiste r ∈
{1, 2, . . . , k + 1} tale che xr 6= ∞, yr 6= ∞. Siano σ e τ ∈ G tale che
σ(xr ) = a e τ (b) = yr . Per ogni i ∈ {1, 2, . . . , k + 1} - {r} si ha ασ(xi ) ∈
E e α−1 τ −1 (yi ) ∈ E e pertanto, per la k-transitività di G, esite β ∈ G
tale che βασ(xi ) = α−1 τ −1 (yi ), per ogni i ∈ {1, 2, . . . , k + 1} − {r} e
βασ(xr ) = ∞ = α−1 τ −1 (yr ) e quindi τ αβασ(xi ) = yi , per ogni i ∈
{1, 2, . . . , k + 1}. Proviamo che τ αβασ ∈ G∗ , infatti τ αβασ ∈ GαGαG
allora, tenedo conto delle ipotesi 3), 4), 5) si ha:
CAPITOLO 6 - Estensione di gruppi e insiemi di permutazioni k-transitivi
40
τ αβασ ∈ GαGαG ⊂ G(G ∪ GαG)G ⊂ GGG ∪ GαGG ⊂ G ∪ GαGG =
G ∪ GαGG ⊂ G ∪ GαG ⊂ G ∪ GαG. Abbiamo così provato l’esistenza di
un elemento g ∈ G∗ tale che g(xi ) = yi , i = 1, 2, . . . , k + 1, quindi G∗ è
(k+1)-transitivo su E ∗ .
Dimostriamo infine che se è G stretamente k-transitivo su E allora g è unica
cioè G∗ è strettamente (k+1)-transitivo su E ∗ . Supponiamo esistano g, h ∈ G∗
tali che g(xi ) = yi , h(xi ) = yi , i = 1, 2, . . . , k + 1. Distinguiamo tre casi.
1◦ caso: Sia g che h appartengono a G. Per la stretta k-transitività di G
segue necessariamente g = h.
2◦ caso: Sia g che h appartengono a GαG. Se k = 1 e x1 = ∞, y2 = ∞,
siano β 1 , β 2 ∈ G con β 1 (y1 ) = a allora β 2 αβ 1 g(∞) = β 2 αβ 1 h(∞) = ∞ e
β 2 αβ 1 g(x2 ) = β 2 αβ 1 h(x2 ) = β 2 (b) 6= ∞. Inoltre questi sono elementi di
G∗ perchè appartengono a GαGGαG ⊂ GαGαG ⊂ GGG ∪ GGαGG ⊂
G ∪ GαG = G∗ e poichè stabilizzano ∞ essi sono elementi di G avendo
dimostrato che G = G∗∞ . Inoltre, poichè entrambe le permutazioni hanno
lo stesso effetto su x2 , per la stretta 1-transitività di G si ha che β 2 αβ 1 g =
β 2 αβ 1 h da cui g = h. (Si procede in modo analogo se k = 1 e con x2 = ∞
e y1 = ∞). Per k = 1 e non è x1 = ∞, y2 = ∞ oppure per k = 1 e
non è x2 = ∞, y1 = ∞ oppure per k ≤ 2, sia r ∈ {1, 2, . . . , k + 1} tale
che risulti xr 6= ∞ e yr 6= ∞, siano β 1 , β 2 , β 3 ∈ G tale che β 1 (b) = xr e
β 3 (yr ) = a; ricordando che abbiamo supposto g ∈ GαG si osservi che:
αβ 3 gβ 1 αβ 2 ∈ G ∪ GαG infatti gβ 1 αβ 2 ∈ GαGGαG = GαGGαG ⊂
GαGαG ⊂ GGG ∪ GGαGG ⊂ G ∪ GαGG = G ∪ GαGG ⊂ G ∪ GαG
e poichè gβ 1 αβ 2 (∞) = yr 6= ∞, esso è un elemento di GαG. Allora
αβ 3 gβ 1 αβ 2 ∈ αGGαG ⊂ αGαG ⊂ GG ∪ GαGG ⊂ G∗ . Analogamente si dimostra che αβ 3 hβ 1 αβ 2 ∈ G∗ . Si osservi che αβ 3 gβ 1 αβ 2 (∞) =
αβ 3 hβ 1 αβ 2 (∞) = ∞, (quindi sono elementi di G) e che hanno la stessa
azione sui k elementi (β 1 αβ 2 )−1 (xi ), per ogni i ∈ {1, 2, . . . , k + 1} - {r},
allora la stretta k-transitività di G implica che αβ 3 gβ 1 αβ 2 = αβ 3 hβ 1 αβ 2
da cui g = h.
3◦ caso: Sia g ∈ GαG e h ∈ G (o viceversa). in questo caso un elemento
r ∈ {1, 2, . . . , k + 1} tale che xr 6= ∞ e yr 6= ∞, esiste sicuramente (anche
quando k=1 essendo h(∞) = ∞). Prendendo β 1 , β 2 , β 3 come sopra, si
ha che αβ 3 hβ 1 αβ 2 ∈ G∗ infatti:
αβ 3 hβ 1 αβ 2 ∈ αGGGαG ⊂ αGGαG ⊂ αGαG ⊂ GG ∪ GαGG ⊂ G∗ .
Procedendo come nel 2◦ caso, si ottiene g = h e questo è assurdo essendo
G ∩ GαG = ∅.
CAPITOLO 6 - Estensione di gruppi e insiemi di permutazioni k-transitivi
41
Nota 6.2.2. Il teorema precedente è più generale del teorema di Witt perchè
si applica agli insiemi e non solo ai gruppi di permutazioni, inoltre esso vale anche
per k = 1 e non solo per k ≥ 2. Inoltre, come verrà dimostrato nel prossimo
paragrafo, se G è gruppo e k ≥ 2 il teorema equivale al Teorema di Witt.
3. Estensione di gruppi di permutazioni k-transitivi
A conclusione di questo capitolo dimostriamo un teorema che fornisce una
generalizzazione del teorema di Witt per l’estensione dei gruppi di permutazioni.
Teorema 6.3.1. Sia G un gruppo di permutazioni k-transitivo su un insieme
E, k ≥ 1, |E| ≥ 3. Sia E ∗ = E∪{∞}, ∞ ∈
/ E, e sia α ∈ Sym E ∗ con α(∞ =
6 ∞).
∗
G = G ∪ GαG è un gruppo di permutazioni (k+1)-transitivo su E ∗ e G∗∞ = G se
e solo se αGα ⊂ G ∪ GαG. Inoltre G∗ è strettamente (k+1)-transitivo se e solo
se G è strettamente k-transitivo.
Dimostrazione. Siano a e b ∈ E non necessariamente distinti, tali che
α(∞) = b e α(a) = ∞. Sia G un gruppo e sia αGα ⊂ G ∪ GαG, allora prendendo
G = G sono soddisfatte le condizioni del teorema 6.1.6 e pertanto G ∪ GαG = G∗
è un insieme di permutazioni su E ∗ (k+1)-transitivo con G∗∞ = G. Dimostriamo
ora che G∗ è un gruppo; dimostriamo dapprima che α−1 ∈ GαG. Sia β ∈ G
con β(b) = a, allora αβα ∈ G∗ e αβα(∞) = ∞ cioè αβα = β1 ∈ G da cui
segue α−1 = β1−1 αβ ∈ GαG. Proviamo ora che comunque presi g, h ∈ G∗ si ha
gh−1 ∈ G∗ . Distinguiamo 4 casi.
1◦ caso: g, h ∈ G. Poichè G è un gruppo, si ha gh−1 ∈ G e pertanto
gh−1 ∈ G ∪ GαG = G∗ .
2◦ caso: g ∈ G, h ∈ GαG. Si ha h−1 ∈ Gα−1 G e poichè α−1 ∈ GαG e G
gruppo, si ha che Gα−1 G ⊂ GαG, allora h−1 è un elemento di GαG e
pertanto gh−1 ∈ GGαG = GαG ⊂ G∗ .
3◦ caso: g ∈ Gα G, h ∈ G. Si ha h−1 ∈ G perchè G è gruppo e gh−1 ∈
GαGG = GαG ⊂ G∗ .
4◦ caso: g , h ∈ GαG. Si ha gh−1 ∈ GαGGα−1 G = GαGGGαGG =
GαGαG ⊂ G(G ∪ GαG)G = G ∪ GαG = G∗ .
CAPITOLO 6 - Estensione di gruppi e insiemi di permutazioni k-transitivi
42
Viceversa se G∗ = G ∪ GαG è un gruppo allora α ∈ G∗ e pertanto αGα ⊂ G∗ ;
inoltre G∗∞ = G.
Infine, poichè G∗ è un gruppo di permutazioni su E ∗ (k+1)-transitivo e G∗∞ =
G; per il corollario 2.1.21 segue che G∗ è strettamente (k+1)-transitivo su E ∗ se
e solo se G∗∞ , cioè G, è strettamente k-transitivo su E ∗ − {∞} cioè su E.
Nota 6.3.2. IL teorema 6.3.1 generalizza il Teorema di Witt perchè vale anche
per k = 1 mentre per k ≥ 2 è equivalente al Teorema di Witt.
Teorema 6.3.3. Sia G un gruppo di permutazioni k-transitivo su un insieme
E, k ≥ 1. Sia E ∗ = E ∪ {∞} con ∞ ∈
/ E e sia λ(∞) = ∞ per ogni λ ∈ G. Se
∗
esistono α ∈ Sym E e G ⊂ G tali che:
(1) α 6∈ G, α2 ∈ G;
(2) G transitivo su E;
(3) αGα ⊂ G ∪ GαG.
allora risulta GαG = GαG = GαG.
Dimostrazione. Sia α(∞) = 0 ∈ E; poichè α2 ∈ G si ha α(0) = ∞.
Iniziamo con il dimostrare che αG ⊂ GαG.
Poichè G è un gruppo, per ogni g ∈ G esiste g1 ∈ G tale che g = g1 α2 da cui
αg = αg1 αα.
(I)
Distinguiamo due casi:
• αg1 α = g2 ∈ G; in tal caso si ha αg = g2 α e considerata g ∈ G tale che
g(0) = 0 risulta anche αg = g2 α = g2 αg −1 g. Poichè G è un gruppo esiste
g3 ∈ G tale che g3 α2 = g −1 e quindi g2 αg −1 g = g2 αg3 ααg. Per l’ipotesi
(3) è αg3 α ∈ G ∪ GαG, ma g3 = g −1 α−2 e perciò risulta αg3 α ∈ G perchè
αg3 α(∞) = αg3 (0) = αg −1 α−2 (0) = αg −1 (0) = α(0) = ∞.
Risulta dunque αg = g2 αg3 ααg = g2 g4 αg = g5 αg ∈ GαG con g4 =
αg3 α ∈ G e g5 = g2 g4 ∈ G.
• αg1 α ∈ GαG; in tale caso si ha αg1 α = g2 αg 2 con g2 ∈ G e g 2 ∈ G e per
la (I) possiamo scrivere αg = g2 αg 2 α. Poichè g2 αg 2 (0) = αg1 α(0) = 0 e
0 6= ∞ si ha g 2 (0) 6= 0 da cui αg 2 α(∞) 6= ∞. Da αg 2 α ∈ G ∪ GαG e
αg 2 α(∞) 6= ∞ segue αg 2 α ∈
/ G e quindi αg 2 α ∈ GαG e si può scrivere
αg = g2 αg 2 α = g2 g3 αg 4 con g3 ∈ G, g 4 ∈ G da cui αg ∈ GαG.
Sia nel primo che nel secondo caso si ha dunque
αG ⊂ GαG.
CAPITOLO 6 - Estensione di gruppi e insiemi di permutazioni k-transitivi
43
(II)
Dalla (II) si ottiene GαG ⊂ GGαG = GαG e anche GαG ⊂ GGαG =
GαG; d’altra parte da G ⊂ G si ha GαG ⊂ GαG; si conclude pertanto
GαG = GαG.
Proviamo ora che è Gα = GαG.
Sia g ∈ G; G è transitivo su E e perciò esiste g ∈ G tale che g(0) =
g(0), inoltre G è un gruppo e pertanto esiste g1 ∈ G tale che g = gg1 . Si
ha gα = gg1 α = gα2 g2 α = gααg2 α con g2 ∈ G tale che g1 = α2 g2 .
Poichè αg2 α ∈ G ∪ GαG e αg2 α(∞) = αg2 (0) = αα−2 g1 (0) =
α−1 g1 (0) = α−1 g −1 g(0) = α−1 (0) = ∞ si ha αg2 α = g3 ∈ G. Dunque
gα = gααg2 α = gαg3 ∈ GαG e pertanto
(III)
Gα ⊂ GαG.
Dalla (III) si ottiene GαG ⊂ GαGG = GαG e poichè si è già dimostrato che GαG = GαG, si ha
GαG = GαG ⊂ GαG ⊂ GαG.
Rimane pertanto dimostrato che GαG = GαG = GαG.
Teorema 6.3.4. Sia G un gruppo di permutazioni k-transitivo su un insieme
E con k ≥ 1. Sia E ∗ = E ∪ {∞} con ∞ ∈
/ E e sia λ(∞) = ∞ per ogni λ ∈ G. Se
∗
esiste α ∈ Sym E tale che :
(1) α 6∈ G, α2 ∈ G;
(2) αGα ⊂ G ∪ GαG;
allora G∗ = G ∪ GαG è un gruppo di permutazioni (k+1)-transitivo su E ∗ e G∗∞ =
G. Il gruppo G∗ è strettamente (k+1)-transitivo su E ∗ se e solo se G è strettamente
k-transitivo su E.
Dimostrazione. Considerato G = G, per il teorema 6.1.6 G∗ è un insieme
di permutazioni (k+1)-transitivo su E ∗ e G∗∞ = G. Dimostriamo che G∗ è un
gruppo. Siano β, γ ∈ G∗ = G ∪ GαG; per dimostrare che βγ ∈ G∗ distinguiamo
quattro casi:
• β, γ ∈ G. Poichè G è un gruppo risulta βγ ∈ G ⊂ G∗ .
• β ∈ G, γ ∈ GαG. Si ha βγ ∈ GGαG = GαG ⊂ G∗ .
• β ∈ GαG, γ ∈ G. Si ha βγ ∈ GαGG = GαG ⊂ G∗ .
• β, γ ∈ GαG. Sia β = g1 αg2 e γ = g3 αg4 , si ha βγ = g1 αg2 g3 αg4 =
g1 αg5 αg4 con g5 = g2 g3 ∈ G. Per ipotesi αg5 α ∈ G ∪ GαG; se αg5 α ∈ G
CAPITOLO 6 - Estensione di gruppi e insiemi di permutazioni k-transitivi
44
allora βγ ∈ GGG = G ⊂ G∗ , se αg5 α ∈ GαG allora βγ ∈ GGαGG =
GαG ⊂ G∗ .
Rimane così provato che G∗ è chiuso rispetto al prodotto.
Dimostriamo ora che se β ∈ G∗ allora β −1 ∈ G∗ .
Se β ∈ G allora è ovvio che β −1 ∈ G ⊂ G∗ .
Se β ∈ GαG allora β −1 = g2−1 α−1 g1−1 = g2−1 αα−2 g1−1 = g2−1 αg3 con g3 =
α−2 g1−1 ∈ G perchè α2 , g1 ∈ G; risulta dunque β −1 ∈ GαG.
Rimane così completamente dimostrato che G∗ è un gruppo.
Infine se G∗ è strettamente (k+1)-transitivo su E ∗ allora è ovvio che G è
strettamente k-transitivo su E. Viceversa sia G strettamente k-transitivo su E,
lo stabilizzatore di (k+1) elementi di E ∗ di cui uno è ∞ risulta l’identità per la
stretta k-transitività di G, allora poichè G∗ è (k+1)-transitivo su E ∗ , per il teorema
6.1.10??? si ha che G∗ è strettamente (k+1)-transitivo su E ∗ .
Il teorema ora dimostrato generalizza le condizioni sufficienti di Witt; con il
seguente teorema si generalizzano anche le condizioni necessarie.
Teorema 6.3.5. Sia G∗ un gruppo di permutazioni (k+1)-transitivo su un
insieme E ∗ e sia ∞ ∈ E ∗ . Se G = G∗∞ allora esiste α ∈ G∗ − G tale che α2 ∈ G
e G∗ = G ∪ GαG.
Dimostrazione. Sia 0 ∈ E ∗ con 0 6= ∞; poichè G∗ è almeno 2-transitivo su
E esiste α ∈ G∗ tale che α(∞) = 0, α(0) = ∞; risulta α2 (∞) = ∞ e peratnto
α2 ∈ G.
Sia g ∈ G∗ − G; esiste g1 ∈ G∗ tale che g1 (∞) = ∞ e g1 (0) = g −1 (∞) e
pertanto gg1 α−1 (∞) = ∞ da cui gg1 α−1 ∈ G, g ∈ Gαg1 ⊂ GαG; rimane
così provato che G∗ − G ⊂ GαG. Risulta dunque G∗ ⊂ G ∪ GαG e poichè è
ovviamente G ∪ GαG ⊂ G∗ , si ha che G∗ = G ∪ GαG.
∗
Nota 6.3.6. Nell’ipotesi del teorema 6.3.3 ora dimostrato segue anche αGα ⊂
G ∪ GαG perchè αGα ⊂ G∗ .
Nota 6.3.7. Nel caso k ≥ 2 i teoremi 6.3.2 e 6.3.3 sono equivalenti al teorema
di Witt, ma lo generalizzano perchè valgono anche nel caso k = 1. Si veda l’esempio
1 nel capitolo 7.
A conclusione di questo capitolo, riportiamo l’enunciato di un teorema che
fornisce indicazioni circa l’esistenza di insiemi strettamente k-transitivi che non
siano gruppi.
CAPITOLO 6 - Estensione di gruppi e insiemi di permutazioni k-transitivi
45
Teorema 6.3.8. Sia G∗ un insieme strettamente (k+1)-transitivo di permutazioni su E ∗ , k ≥ 2, |E ∗ | ≥ 5, G∗ non necessariamente finito. G∗ è un gruppo se
e solo se esiste un elemento ∞ ∈ E ∗ tale che
• G∗∞ è un gruppo;
• G∗∞ αG∗∞ ⊂ G∗ con α ∈ G∗ , α(∞) 6= ∞, α fissa (k-1)elementi di E ∗ .
CAPITOLO 7
Applicazione dei teoremi di estensione di gruppi e insiemi di
permutazioni k-transitivi
In questo capitolo si riportano esempi di estensioni di gruppi e di insiemi di
permutazioni k-transitivi nel senso di Witt.
1. Esempi di estensioni di gruppi k-transitivi
Esempio 7.1.1.
Sia K un campo finito o no, K∗ = K − {0}; fissato a ∈ K∗ sia πa : K∗ −→ K∗
l’aplicazione biunivoca definita da πa (x) = ax per ogni x ∈ K∗ . L’insieme G =
{πa | a ∈ K∗ } risulta un gruppo di permutazioni strettamente 1-transitivo su K∗ .
Estendiamo il gruppo G a un gruppo strettamente 2-transitivo su K = K∗ ∪{0}
utilizzando il teorema 6.3.1.
Prolunghiamo l’azione di G a tutto K = K∗ ∪ {0} ponendo πa (0) = 0 per ogni
πa ∈ G. Sia α ∈ Sym K definita da α(x) = −x + 1 per ogni x ∈ K.
Risulta αGα ⊂ G ∪ GαG; infatti si ha απa α(x) = ax − a + 1. Se a = 1
allora απa α = 1K∗ ∈ G ⊂ G ∪ GαG. Se a 6= 1 consideriamo r, s ∈ K∗ tali che
−a
r = −a + 1, s = −a+1
; si ha che απa α = πr απs ∈ GαG ⊂ G ∪ GαG.
Poichè le condizioni del teorema 6.3.1 sono verificate, si conclude che G∗ = G ∪
GαG è un gruppo strettamente 2-trasitivo su K; G∗ è il gruppo affine AG(1, K) =
{g|g(x) = ax + b, a, b ∈ K, a 6= 0}.
Esempio 7.1.2.
Dimostriamo che il gruppo strettamente 3-transitivo P GL(2, K) si ottiene come
estensione, nel senso di Witt, del gruppo strettamente 2-transitivo AG(1, K).
Sia K un campo, finito o no, e sia G = AG(1, K) il gruppo affine su K che,
come noto, è strettamente 2-transitivo su K; sia ∞ ∈
/ K e E = K ∪ {∞}.
Sia α ∈ Sym E definita da α(0) = ∞,
alpha(∞) = 0, α(x) = x1 per ogni x ∈ E − {0, ∞}.
Dimostriamo che αGα ⊂ G ∪ GαG.
1◦ caso : Sia β ∈ G, β(x) = ax. Allora αβα ∈ G perchè agisce su x come gli
elementi di G e pertanto αβα ⊂ G ∪ GαG.
46
CAPITOLO 7 - Applicazione dei teoremi di estensione di gruppi e insiemi di permutazioni
47
2◦ caso : Sia β ∈ G, β(x) = ax + b, b 6= 0. Consideriamo γ, δ ∈ G definite
a
1
da γ(x) = − x + , δ(x) = bx + a; si ha αβα = γαδ e γαδ ∈ GαG e pertanto
b
b
αβα ∈ G ∪ GαG.
Per il teorema 6.3.1. si ha pertanto che G∗ = G∪GαG è un gruppo strettamente
3-transitivo su E e G∗∞ = G.
Verifichiamo infine che G∗ = P GL(2, K).
Risulta G∗∞ = G ⊂ P GL(2, K) perchè gli elementi di G sono permutazioni α
del tipo α(x) = ax + b, a 6= 0, che appartengono a P GL(2, K).
Siano ora γ1 , γ2 ∈ G con γ1 (x) = a1 x + b1 , γ2 (x) = a2 x + b2 , a1 , a2 ∈ K∗ , risulta
1 b2 +a1
γ1 αγ2 (x) = b1 a2ax+b
con detγ1 αγ2 = −a1 a2 6= 0 e pertanto γ1 αγ2 ∈
2 x+b2
P GL(2, K). Rimane così provato che G∗ = G ∪ GαG ⊂ P GL(2, K).
Sia ora α ∈ P GL(2, K); siano x1 , x2 , x3 elementi distinti di K ∪ {∞} e sia
α(xi ) = yi , i = 1, 2, 3.
Per la sua stretta 3-transitività, in G∗ esiste β tale che β(xi ) = yi , i = 1, 2, 3,
e poichè G∗ ⊂ P GL(2, K) si ha β ∈ P GL(2, K), ma P GL(2, K) è strettamente
3-transitivo e pertanto β = α ∈ G∗ e quindi P GL(2, K) ⊂ G∗ .
Rimane così dimostrato che G∗ = P GL(2, K).
Esempio 7.1.3.
m
Sia K = GF (p2m ), p 6= 2, H = {x2 | x ∈ K∗ } , σ ∈ AutK, σ(x) = xp ; fissati
a, b ∈ K, a 6= 0, sia ϕa,b : K −→ K la permutazione definita da ϕa,b (x) = ax + b
se a ∈ H, ϕa,b (x) = aσ(x) + b se a ∈ K∗ − H.
L’insieme G = {ϕa,b | a, b ∈ K, a 6= 0} risulta un gruppo di permutazioni strettamente 2-transitivo su K.
Estendiamo il gruppo G al gruppo strettamente 3-transitivo G(p2m , σ). Ricordiamo che in GF (p2m ), si ha −1 ∈ H perchè p2m ≡ 1 mod4, inoltre σ 2 =
identità.
Sia ∞ ∈
/ K, E = K ∪ {∞}; prolunghiamo l’azione di G su tutto E ponendo
γ(∞) = ∞ per ogni γ ∈ G. Sia α ∈ Sym E definita da α(0) = ∞, α(∞) =
0, α(x) = −1
per ogni x ∈ E − {0, ∞}.
x
Dimostriamo che αGα ⊂ G ∪ GαG.
1◦ caso : Sia β ∈ G, β(x) = ax + b con a quadrato.
• Se b = 0, αβα ∈ G ⊂ G ∪ GαG perchè agisce su x come gli elementi di G
del tipo x → ax + b con a un quadrato e con b = 0.
1
a
a
• Se b 6= 0 consideriamo γeδ ∈ G tali che γ(x) = 2 x − , δ(x) = x − .
b
b
b
Si ha αβα = γαδ ∈ GαG ⊂ G ∪ GαG.
m
2◦ caso : Sia β ∈ G, β(x) = axp + b con a non quadrato.
• Se b = 0, αβα ∈ G perchè agisce su x come gli elementi di G del tipo
m
x → axp +b con a non quadrato e con b = 0, allora αβα ∈ G ⊂ G∪GαG.
CAPITOLO 7 - Applicazione dei teoremi di estensione di gruppi e insiemi di permutazioni
• Se b 6= 0 consideriamo γeδ ∈ G tali che γ(x) =
pm
x−
a pm
1
x − ,
2
b
b
48
δ(x) =
a
; risulta αβα = γαδ ∈ GαG ⊂ G ∪ GαG.
bpm
Per il teorema 6.3.1 si ha che G∗ = G ∪ GαG.
G∗ risulta il gruppo delle permutazioni su K ∪ {∞} definite da:
ax + b
, ad − bc ∈ H; a, b, c, d ∈ K
x→
cx +
d
m
axp + b
, ad − bc ∈ K∗ − H; a, b, c, d ∈ K.
x → pm
cx + d
Inoltre il gruppo G∗ = G ∪ GαG ⊂ G(p2m , σ) e poichè |G∗ | = |G(p2m , σ)| =
(p2m + 1)p2m (p2m − 1) si conclude che G∗ = G(p2m , σ).
Esempio 7.1.4.
Con questo esempio si descrive il gruppo di Mathien M4,11 strettamente 4-transitivo
su 11 elementi, come estensione del gruppo G(32 , σ) strettamente 3-transitivo su
GF (32 ) ∪ {∞}.
Per maggiore chiarezza iniziamo con il descrivere il campo GF (32 ).
Sia GF (3) = {0, 1, 2}; consideriamo il polinomio x2 + 1 ∈ GF (3)[x] irriducibile
in GF (3).
Detta i una radice del polinomio, il campo di spezzamento di x2 + 1 è il campo
GF (32 ) = {a + ib | a, b ∈ GF (3)}.
Sia dunque K = GF (32 ) = {0, 1, 2, i, 2i, 1 + i, 1 + 2i, 2 + i, 2 + 2i};ricordando
che i2 + 1 = 0 si ottengono in K le seguenti tavole per le operazioni di “+” e di “·”
che rendono K un campo:
+
0
1
2
i
2i
1+i
1 + 2i
2+i
2 + 2i
0
1
2
i
2i
1 + i 1 + 2i 2 + i 2 + 2i
0
1
2
i
2i
1 + i 1 + 2i 2 + i 2 + 2i
1
2
0
1 + i 1 + 2i 2 + i 2 + 2i
i
2i
2
0
1
2 + i 2 + 2i
i
2i
1 + i 1 + 2i
i
1+i 2+i
2i
0
1 + 2i
1
2 + 2i
2
2i
1 + 2i 2 + 2i
0
i
1
1+i
2
2+i
1+i 2+i
i
1 + 2i
1
2 + 2i
2
2i
0
1 + 2i 2 + 2i
2i
1
1+i
2
2+i
0
i
2+i
i
1 + i 2 + 2i
2
2i
0
1 + 2i
1
2 + 2i
2i
1 + 2i
2
2+1
0
i
1
1+i
CAPITOLO 7 - Applicazione dei teoremi di estensione di gruppi e insiemi di permutazioni
·
1
2
i
2i
1+i
1 + 2i
2+i
2 + 2i
49
1
2
i
2i
1 + i 1 + 2i 2 + i 2 + 2i
1
2
i
2i
1 + i 1 + 2i 2 + i 2 + 2i
2
1
2i
i
2 + 2i 2 + i 1 + 2i 1 + i
i
2i
2
1
2 + i 1 + i 2 + 2i 1 + 2i
2i
i
1
2
1 + 2i 2 + 2i 1 + i 2 + i
1 + i 2 + 2i 2 + i 1 + 2i
2i
2
1
i
1 + 2i 2 + i 1 + i 2 + 2i
2
i
2i
1
2 + i 1 + 2i 2 + 2i 1 + i
1
2i
i
2
2 + 2i 1 + i 1 + 2i 2 + i
i
1
2
2i
I quadrati di K∗ sono gli elementi del gruppo H = {1, 2, i, 2i}.
Sia ∞ ∈
/ K = GF (32 ), E = K ∪ {∞} , σ ∈ AutK definito da σ(∞) = ∞, σ(x) = x3
per ogni x ∈ K. L’insieme
ax + b
aσ(x) + b
∗
2
G = G(3 , σ) =
se ad − bc ∈ H,
se ad − bc ∈ K − H; perogni a, b, c, d ∈ K
cx + d
cσ(x) + d
è un gruppo di permutazioni stretamente 3-transitivo su E.
Consideriamo in G le permutazioni λ(x) = x + 1, γ(x) = ix, τ (x) = (1 + i)x3 e
sia Γ =< λ, γ, τ > il gruppo generato da λ, γ, τ .
Dimostriamo che Γ = G∞ .
Si ha Γ ⊂ G∞ perché lambda(∞) = γ(∞) = τ (∞) = ∞ e poichè G∞ è
strettamente 2-transitivo su K per dimostrare che Γ = G∞ basta dimostrare che
Γ è 2-transitivo su K.
Iniziamo con il dimostrare che Γ è transitivo su K; poichè Γ è un gruppo basta
dimostrare che per ogni x ∈ K esiste ϕ ∈ Γ tale che ϕ(0) = x.
Le permutazioni 1K , λ, λ2 , γλ, γλ2 , τ λ, τ λ2 , λγλ2 , λτ λ sono elementi di Γ e trasformano l’elemento 0 rispettivamente negli elementi 0, 1, 2, i, 2i, 1 + i, 2 + 2i, 1 +
2i, 2+i che sono tutti e soli gli elementi di K; rimane così provato che Γ è transitivo
su K.
Dimostriamo ora che Γ0 è 1-transitivo su K∗ .
Consideriamo il gruppo ∆ =< γ, τ > generato da γ e τ ; ∆ è 1-transitivo su
∗
K perchè per ogni x ∈ K∗ esiste ψ ∈ ∆ tale che ψ(1) = x, infatti le permutazioni
1K∗ , γ, γ 2 , τ, τ γ, γ 3 , γτ, γ 2 τ sono elementi di ∆ e trasformano l’elemento 1 rispettivamente negli elementi 1, i, 2, 1 + i, 1 + 2i, 2i, 2 + i, 2 + 2i che sono tutti e soli gli
elementi di K∗ . Poichè γ(0) = τ (0) = 0 si ha ∆ ⊂ Γ0 ed essendo ∆ 1-transitivo su
K∗ risulta anche Γ0 1-transitivo su K∗ .
Per il terema 2.1.19 rimane così provato che Γ è 2-transtivo su K∗ e pertanto
Γ = G∞ .
Estendiamo il gruppo G = (32 , σ) applicando il teorema di Witt.
CAPITOLO 7 - Applicazione dei teoremi di estensione di gruppi e insiemi di permutazioni
50
Sia ∞0 ∈
/ E, E ∗ = E ∪ {∞0 } = K ∪ {∞, ∞0 }; prolunghiamo l’azione di G a
tutto E ∗ ponendo ρ(∞0 ) = ∞0 per ogni ρ ∈ G. Sia α ∈ Sym E ∗ definita da
α = (i, 2 + 2i)(2, 1 + i)(1 + 2i, 2 + i)(∞, ∞0 ) e sia β ∈ G tale che β(x) = x1 .
Verifichiamo che ∞, ∞0 , 0, G, α, β soddisfano le condizioni del teorema di Witt.
Si ha:
(1) α(∞0 ) = ∞, α(∞) = ∞0 , α(0) = 0;
(2) β(0) = ∞, β(∞) = 0;
(3) (βα)3 = 1E ∈ G e α2 = 1E ∈ G;
(4) αG∞ α = G∞ .
Le condizioni (1), (2), (3) seguono immediatamente dalle definizioni poste. Dimostriamo la (4). Per ogni γ ∈ G∞ ⊂ G risulta αγα(∞) = ∞ e perciò αG∞ α ⊂ G∞
da cui αG∞ α = G∞ perchè sono insiemi finiti e |αG∞ α| = |G∞ |.
Essendo verificate le ipotesi del teorema di Witt si ha che G∗ = G ∪ GαG è un
gruppo di permutazioni strettamente 4-transitivo su 11 elementi, esso è il gruppo
di Mathieu M4,11 .
Nota 7.1.5. Il gruppo P GL(2, 32 ) non è estendibile ad un gruppo strettamente
4-transitivo su 11 elementi.
Esempio 7.1.6. Con questo esempio si descrive l’estensione del gruppo di
Mathieu M4,11 al gruppo strettamente 5-transitivo su 12 elementi detto gruppo di
Mathieu M5,12 .
Sia E ∗ = GF (32 ) = {∞, ∞0 } , ∞00 ∈
/ E ∗ , E ∗∗ = E ∗ ∪ {∞00 } = GF (32 ) ∪
{∞, ∞0 , ∞00 }.
Sia Γ = M4,11 il gruppo di Mathieu strettamente 4-transitivo su E ∗ ; prolunghiamo l’azione di Γ a tutto E ∗∗ ponendo γ(∞00 ) = ∞00 per ogni γ ∈ Γ. Sia
α ∈ Sym E ∗∗ definita da α(∞0 ) = ∞00 , α(∞00 ) = ∞0 , α(∞) = ∞, α(x) = x3 per
ogni x ∈ GF (32 ). Sia β ∈ Γ definita da β(∞) = ∞0 , β(∞0 ) = ∞, β(a + ib) = a − ib
per ogni a + ib ∈ GF (32 ) con riferimento alla notazione usata nell’esempio 7.1.4
per il campo GF (32 ).
Verifichiamo che ∞00 , ∞0 , ∞, Γ, α, β soddisfano le condizioni del teorema di
Witt. Si ha:
(1) α(∞0 ) = ∞00 , α(∞00 ) = ∞0 , α(∞) = ∞;
(2) β(∞) = ∞0 , β(∞0 ) = ∞;
(3) (βα)3 = 1E ∗ , α2 = 1E ∗ ∈ Γ;
(4) αΓ∞0 α = Γ∞0 .
Le condizioni (1), (2), (3) seguono immediatamente dalle definizioni poste.
Dimostriamo la (4). Per quanto visto nell’ esempio 7.1.4 si ha Γ∞0 = G(32 , σ) e
dunque occorre dimostrare che αG(32 , σ)α = G(32 , σ) e poichè α è di periodo 2
basta verificare che αG(32 , α)α ⊂ G(32 , α). Sia g ∈ G(32 , σ),
CAPITOLO 7 - Applicazione dei teoremi di estensione di gruppi e insiemi di permutazioni
51
3
3
x+b
g(x) = ax+b
con ad−bc quadrato di GF (32 )∗ ; si ha αgα(∞) = ∞ e αgα(x) = ac3 x+d
3
cx+d
con a3 d3 − b3 c3 = (ad − bc)3 quadrato di GF (32 )∗ e perciò αgα ∈ G(32 , σ).
3 +b
con ad − bc non quadrato di GF (32 )∗ ; si ha
Sia g ∈ G(32 , σ), g(x) = ax
cx3 +d
3 3 +b3
3 3
3 3
= (ad − bc)3 non quadrato di
αgα(∞) = ∞ e αgα(x) = ac3 xx3 +d
3 con a d − b c
2 ∗
2
GF (3 ) e perciò αgα ∈ G(3 , σ).
Essendo verificate le ipotesi del teorema di Witt si ha che Ω = Γ ∪ ΓαΓ è
un gruppo di permutazioni strettamente 5-transitivo su E ∗∗ , |E ∗∗ | = 12; esso è il
gruppo di Mathieu M5,12 .
Nota 7.1.7. Il gruppo M5,12 non è estendibile ad un gruppo strettamente
6-transitivo su 13 elementi.
2. Esempi di estensioni di insiemi k-transitivi
Applichiamo il Teorema 6.2.1 per ottenere gli insiemi di permutazioni strettamente 3-transitivi, a noi noti, come estensione di insiemi di permutazioni strettamente 2-transitivi.
Esempio 7.2.1.
Sia K = GF (pn ), H = {x2 | x ∈ K∗ } , σ ∈ AutK; fissati a, b ∈ K, a 6= 0, sia ϕa,b :
K −→ K la permutazione definita da ϕa,b (x) = ax + b se a ∈ H, ϕa,b (x) = aσ(x) + b
se a ∈ K∗ − H.
L’insieme G = {ϕa,b |a, b ∈ K, a 6= 0} è un insieme di permutazioni strettamente
2-transitivo su K.
Sia ∞ ∈
/ K, E ∗ = K ∪ {∞}, estendiamo l’azione di σ e di G a tutto E ∗
ponendo σ(∞) = ∞ e γ(∞) = ∞ per ogni γ ∈ G. Sia α ∈ SymE definita da
α(0) = ∞, α(∞) = 0, α(x) = − x1 per ogni x ∈ K∗ . Per ogni b ∈ K sia τb : K −→ K
la permutazione definita da τb (x) = x + b e sia G = {τb |b ∈ K}.
Verifichiamo che α, G, G, soddisfano le condizioni del terema 6.2.1, ossia verifichiamo che valgono le seguenti cinque condizioni.
(1) α(∞) 6= ∞;
(2) G è 1-transitivo su K;
(3) GαG = GαG;
(4) GG ⊂ G; GG ⊂ G;
(5) αGα ⊂ G ∪ GαG.
Infatti:
(1) Dalla definizione di α segue α(∞) = 0 6= ∞.
CAPITOLO 7 - Applicazione dei teoremi di estensione di gruppi e insiemi di permutazioni
52
(2) E’ G ⊂ G e G risulta 1-transitivo su K, infatti, comunque presi x1 , y1 ∈
K, in G esiste ed è unica la permutazione γ tale che γ(x1 ) = y1 : è la
permutazione definita da γ(x) = x + (y1 − x1 ).
(3) Per dimostrare che GαG = GαG sia γ ∈ G tale che γ(x) = x + b e
distinguiamo due casi.
i) Sia γ ∈ G, γ(x) = ax + b0 , a, b0 ∈ K, a ∈ H; risulta γαγ(x) =
, detγαγ = a ∈ H.
x+b
Siano γ 1 ∈ G, γ 1 (x) = x + b0 e γ1 ∈ G, γ1 (x) = a−1 x + ba−1 , a−1 ∈ H
perchè a ∈ H; risulta γαγ = γ 1 αγ1 .
b0 x+bb0 −a
ii) Sia γ ∈ G, γ(x) = aσ(x)+b0 , a, b0 ∈ K, a ∈ K∗ −H; risulta γαγ(x) =
, detγαγ = a ∈ K∗ − H.
σ(x)+σ(b)
Siano γ 1 ∈ G, γ 1 (x) = x+b0 e γ1 ∈ G, γ1 (x) = a−1 σ(x)+σ(b)a−1 , a−1 ∈
K∗ − H perché a ∈ K∗ − H; risulta γαγ = γ 1 αγ1 .
Rimane così provato che GαG ⊂ GαG; analogamente si dimostra che
b0 σ(x)+b0 σ(b)−a
GαG ⊂ GαG e pertanto si ha GαG = GαG.
(4) Per come definiti G e G segue che GG ⊂ G e GG ⊂ G.
(5) Per dimostrare che αGα ⊂ G ∪ GαG distinguiamo due casi.
−x
i) Sia γ ∈ G, γ(x) = ax + b, a, b ∈ K, a ∈ H; risulta αγα(x) = bx−a
.
−1
Se b = 0 allora detαγα = a ∈ H e αγα ∈ G; se b 6= 0 allora αγα(∞) =
α(b) 6= ∞ e perciò αγα ∈
/ G ma esistono γ 1 ∈ G, γ(x) = x − ab−1 , e
γ1 ∈ G, γ1 (x) = ab−2 x − b−1 , tali che αγα = γ1 αγ 1 ∈ GαG.
ii)sia γ ∈ G, γ(x) = aσ(x) + b, a, b ∈ K, a ∈ K∗ − H; risulta αγα(x) =
Se b = 0 allora detαγα = a−1 ∈ K∗ − H e αγα ∈ G; se b 6= 0
allora αγα(∞) = α(b) 6= ∞ e perciò αγα ∈
/ G ma esistono γ 1 ∈ G, γ 1 (x) =
−1
−1
−2
x − σ (ab ), e γ1 ∈ G, γ1 (x) = ab σ(x) − b−1 , tali che αγα = γ1 αγ 1 ∈
Gαγ 1 ∈ GαG.
−σ(x)
.
bσ(x)−a
Le ipotesi del teorema 6.2.1 sono dunque verificate e pertanto G∗ =
G ∪ GαG è un insieme strettamente 3-transitivo su E ∗ = K ∪ {∞}.
Verifichiamo infine che G∗ = G(pn , σ).
Dimostriamo che G∗ ⊂ G(pn , σ); si ha G∗∞ = G ⊂ G(pn , σ), inoltre
anche GαG ⊂ G(pn , σ) perchè considerata γ ∈ G, γ(x) = x + b; si possono
avere due casi:
i) γ ∈ G, γ(x) = ax + b0 , a, b0 ∈ K, a ∈ H;
ii) γ ∈ G, γ(x) = aσ(x) + b0 , a, b0 ∈ K, a ∈ K∗ − H;
CAPITOLO 7 - Applicazione dei teoremi di estensione di gruppi e insiemi di permutazioni
53
ma in entrambi i casi risulta γαγ ∈ G(pn , σ). Dunque G∗ ⊂ G(pn , σ).
Poichè |G∗ | = |G(pn , σ)| = (pn + 1)pn (pn − 1) si ha G∗ = G(pn , σ).
CAPITOLO 8
Gruppi e Insiemi k-omogenei.
in fase di completamento.
54
CAPITOLO 9
Trasformazione di (k,n)-strutture
In questo capitolo si illustra un procedimento mediante il quale da una (k,n)struttura se ne costruisce un’altra non necessariamente isomorfa. Questo procedimento è dovuto a P.Quattrocchi e L.A.Rosati 00 Trasformation of design and other
incidence structures00 , Geometriae Dedicata, 44 (1992), 233-240.
Trasformare una (k,n)-struttura di incidenza permette:
• di ottenere nuove strutture;
• di trasportare una dimostrazione da una struttura ottenuta per trasformazione alla struttura di partenza, o viceversa.
1. Definizioni e prime proprietà
Definizione 9.1.1. Siano k ed n due numeri cardinali con k finito. Si definisce
(k,n)-struttura ogni struttura di incidenza che gode delle seguenti proprietà:
• k punti distinti P1 , P2 , . . . , Pk incidono ad un unico blocco;
• l’insieme dei punti incidenti ad un qualunque blocco ha cardinalità n.
Se (P, B, I) è una (k,n)-struttura denoteremo con < P1 , P2 , . . . , Pk > il blocco
incidente i punti P1 , P2 , . . . , Pk e denoteremo con BI = {P ∈ P | P IB} l’insieme
dei punti che incidono il blocco B ∈ B.
Definizione 9.1.2. Sia (P, B, I) una (k,n)-struttura, F ⊂ B una famiglia di
blocchi e f una permutazione sull’insieme P dei punti. Si dice che la struttura di
incidenza (P, B, I) è trasformabile e che {F, f } è un sistema di trasformazione
per (P, B, I) se e solo se, comunque presi k punti distinti, P1 , P2 , . . . , Pk , si ha che
< P1 , P2 , . . . , Pk >∈ F se e solo se < f (P1 ), f (P2 ), . . . , f (Pk ) >∈ F.
Osservazione 9.1.3.
Se f ∈ Sym P ha periodo finito la condizione a) implica la condizione b), con
a) < P1 , P2 , . . . , Pk >∈ F ⇒ < f (P1 ), f (P2 ), . . . , f (Pk ) >∈ F
55
CAPITOLO 9 - Trasformazione di (k,n)-strutture
56
b) < f (P1 ), f (P2 ), . . . , f (Pk ) >∈ F ⇒ < P1 , P2 , . . . , Pk >∈ F.
Infatti se f ha periodo finito, esiste r ∈ N tale che f r è l’identità e pertanto
applicando ripetutamente la condizione a) si ottiene b).
In particolare se la struttura di incidenza (P, B, I) è finita, certamente f ha periodo
finito perchè il gruppo Sym(P) è di ordine finito, dunque nel caso finito a) implica
sempre b).
Definizione 9.1.4. Sia (P, B, I) una (k,n)-struttura e {F, f } un sistema di
trasformazione per (P, B, I). Definiamo una nuova relazione di incidenza J tra i
punti ed i blocchi nel seguente modo:
se B ∈
/ F allora P J B se e solo se P IB,
se B ∈ F allora P J B se e solo se f (P )IB.
La struttura (P, B, J ) è detta struttura trasformata di (P, B, I) tramite il
sistema di trasformazione {F, f }.
Inoltre per ogni b ∈ B si definisce BJ = {P ∈ P | P J B}.
Si noti che dalla definizione posta segue che l’incidenza J trasforma un blocco
di F in un blocco di F mentre trasforma un blocco di B − F in sé stesso (non è
detto punto per punto).
Osservazione 9.1.5.
B Se B ∈
/ F si ha P J B se e solo se P IB, ossia BJ = BI .
B Se B ∈ F si ha P J B se e solo se f (P )IB, ossia BJ = f −1 (BI ) infatti
BJ = {P ∈ P | P J B} = {P ∈ P | f (P )IB} ed essendo f biunivoca si ha BI =
= {P ∈ P | P IB} = {f (P ) ∈ P | f (P )IB} = {Q ∈ P | f −1 (Q)J B}.
Teorema 9.1.6. Sia (P, B, I) una (k,n)-struttura. Se (P, B, J )è la struttura
trasformata di (P, B, I) tramite il sistema di trasformazione {F, f } allora (P, B, I)
è la struttura trasformata di (P, B, J ) tramite {F, f −1 }.
Dimostrazione. Sia B l’unico blocco cui sono J -incidenti P1 , P2 , . . . , Pk ; se
B ∈ F si ha Pi J B se e solo se f (Pi ) IB per i = 1, 2, . . . , k, ossia se e solo se
B =< f (P1 ), . . . , f (Pk ) >∈ F. Poichè {F, f } è un sistema di trasformazione si ha
anche B 0 =< P1 , . . . , Pk >∈ F.
Siano Qi ∈ P tali che f (Qi ) = Pi per i = 1, 2, . . . , k; poichè B 0 ∈ F si
ha che Qi = f −1 (Pi )J B 0 per i = 1, 2, . . . , k, quindi l’unico blocco di (P, B, J )
J -incidente f −1 (P1 ) , f −1 (P2 ) , . . . , f −1 (Pk ) appartiene ad F.
Analogamente si dimostra che se l’unico blocco J -incidente f −1 (P1 ), . . . , f −1 (Pk )
appartiene ad F allora anche l’unico blocco di (P, B, J ) J -incidente P1 , . . . , Pk
appartiene ad F. Quindi {F, f −1 } è un sistema di trasformazione di (P, B, J ).
Sia (P, B, I 0 ) la struttura di incidenza trasformata di (P, B, J ) mediante {F, f −1 }.
I 0 è così definita:
CAPITOLO 9 - Trasformazione di (k,n)-strutture
se B ∈
/F
se B ∈ F
allora P I 0 B
allora P I 0 B
57
⇔ P J B ⇔ P IB;
⇔ f −1 (P )J B ⇔ f (f −1 (P )) = P IB.
Dunque, poichè I = I 0 , la struttura trasformata di (P, B, J ) mediante {F, f −1 }
è (P, B, I).
D’ora in avanti con < P1 , P2 , . . . , Pk > indichiamo il blocco incidente i punti
P1 , P2 , . . . , Pk secondo la relazione I.
Teorema 9.1.7. La struttura trasformata di una (k,n)-struttura è ancora
una (k,n)struttura.
Dimostrazione. Sia B ∈ B. Se B ∈
/ F allora P J B se e solo se P BI e perciò
l’insieme dei punti J -incidenti B ha cardinalità n perchè sono esattamente i punti
I-incidenti B. Se B ∈ F allora P J B se e solo se f (P )IB; siano Q1 , . . . , Qn i punti
I-incidenti B e siano P1 , . . . Pn i punti tali che F (Pi ) = Qi con i = 1, 2, . . . , n, allora
i punti J -incidenti B sono esattamente n punti P1 , P2 , . . . , Pn .
Consideriamo ora k punti distinti: P1 , P2 , . . . Pk e sia B =< P1 , P2 , . . . , Pk >
l’unico blocco passante per essi nella struttura di partenza. Se B ∈
/ F allora
B è l’unico blocco in B − F che è J -incidente P1 , P2 , . . . Pk . Inoltre non esiste
nessun blocco C ∈ F tale che Pi J C, per i = 1, 2, . . . , k perchè in caso contrario
si avrebbe C =< f (P1 ), . . . , f (Pk ) > ∈ F da cui B =< P1 , . . . , Pk > ∈ F contro
l’ipotesi. Dunque B è l’unico blocco J -incidente P1 , P2 , . . . , Pk .
Analogamente si dimostra che se B =< P1 , . . . , Pk > ∈ F allora considerati i
punti Qi = f (Pi ), i = 1, 2, . . . , k, si ha che < Q1 , Q2 , . . . , Qk > è l’unico blocco
J -incidente P1 , P2 , . . . , Pk .
Nota 9.1.8. Un piano affine (finito o no) è una (2,n)-stuttura e pertanto questo
procedimento di trasformazione può essere applicato in particolare ai piani affini.
È importante osservare che se il piano affine è finito allora esso viene trasformato in
un piano affine perchè l’assioma di Euclide è conseguenza dell’ipotesi di finitezza
mentre se il piano affine è di ordine non finito il suo trasformato è ancora una
(2,n)-struttura ma non è detto che questa sia un piano affine perchè può non
valere l’assioma di Euclide come mostra il seguente esempio.
Esempio 9.1.9. Sia π il piano affine costituito sul campo Q dei numeri razionali ossia P = Q×Q è l’insieme dei punti, B = {r | r : ax + by + c = 0 a, b, c ∈ Q,
a, b non entrambi nulli } è l’insieme delle rette.
Si consideri l’applicazione σ : Q → Q definita da:
(
2
− , per −2 < x < −1
σ(x) =
x
x + 3 per
x ≤ −2
o x ≥ −1
CAPITOLO 9 - Trasformazione di (k,n)-strutture
58
σ è biunivoca e strettamente crescente.
Sia f la permutazione dei punti di π definita da f (x, y) = (σ(x), y). Sia F
la famiglia delle rette di π di equazione ax + by + c = 0 con ab > 0. La coppia
{F, f } è un sistema di trasformazione per π. Infatti:
(1) f è una permutazione sui punti di π.
Dimostrazione. f è una applicazione biettiva perché definita a partire da σ e identità che sono entrambe applicazioni biettive.
(2) Comunque presi due punti distinti P ed R, la retta P R ∈ F se e solo se
la retta f (P ) f (R) ∈ F.
Dimostrazione. Siano P = (x1 , y1 ) e R = (x2 , y2 ) due punti distinti. La retta P R ha equazione (y1 − y2 )x − (x1 − x2 )y + x1 y2 − x2 y1 = 0
e P R ∈ F se e solo se (y1 − y2 ) (x1 − x2 ) > 0. La retta f (P ) f (R) ∈ F
ha equazione (y1 − y2 )x − (σ(x1 ) − σ(x2 ))y + σ(x1 )y2 − σ(x2 )y1 = 0 e
f (P ) f (R) ∈ F se e solo se (y1 − y2 )(σ(x1 ) − σ(x2 )) > 0. Pertano dimostrare che P R ∈ F se e solo se f (P ) f (R) ∈ F equivale a dimostrare che
(x1 − x2 ) e (σ(x1 ) − σ(x2 )) hanno lo stesso segno; poiché σ è strettamente
cresente si ha (x1 − x2 ) > 0 se e solo se x2 > x1 se e solo se σ(x1 ) > σ(x2 )
se e solo se σ(x1 ) − σ(x2 ) > 0.
Rimane dunque provato che {F, f } è un sistema di trasformazione
per π.
Verifichiamo ora che la (2, n)-struttura π ∗ trasformata di π non è un
piano affine. Consideriamo in π la retta t : 3x − 2y + 3 = 0, poiché
3 (−2) < 0 si ha t ∈
/ F e pertanto i punti J -incidenti t sono tutti e
soli i punti I-incidenti t e quindi in π ∗ la retta t è rappresentata ancora
dall’equazione 3x − 2y + 3 = 0.
Analogamente la retta r : 3x − 2y − 1 = 0 è rappresentata dalla
stessa equazione sia in π che in π ∗ perché r ∈
/ F. Inoltre r è J -incidente
il punto P = (−1, −2) ed è J -parallela a t.
Consideriamo ora la retta s che in π ha equazione s : x + y = 0;
s ∈ F e perciò in π ∗ è rappresentata dall’equazione σ(x) + y = 0 e on π ∗
il punto P è J -incidente s. Inoltre in π ∗ le rette t ed s sono J -parallele
infatti t ed s sono J -incidenti in un punto se e solo se il sistema:
3x −2y +3 = 0
σ(x) +y = 0
ammette una soluzione razionale ossia se esiste x ∈ Q tale che 3x+2σ(x)+
3 = 0. Distinguiamo due casi:
CAPITOLO 9 - Piani di Moulton
59
(a) x ∈ (−∞, −2] ∪ [−1, +∞). Si ha σ(x) = x + 3 e l’equazione diventa
−9
3x + 2x + 6 + 3 = 0 che ammette come unica soluzione x =
,
5
−9
questo valore è però non accettabile perché
∈ (−2, −1).
5
(b) x ∈ (−2, −1).
2
4
Si ha σ(x) = − e l’equazione diventa 3x − + 3 = 0 che ammetx
x √
√
−3 + 57
−3 − 57
te come soluzioni x =
e x =
entrambe non
6
6
accettabili perché non razionali.
In π ∗ esistono dunque due rette, r ed s, entrambe J parallele alla
retta t ed entrambe J -incidenti il punto P , ne consegue che π ∗ non
è un piano affine perché in esso non vale l’assioma di Euclide.
Più in generale, in analogia a quanto dimostrato nell’esempio 9.1.9, si dimostra
la seguente proposizione.
Teorema 9.1.10. Sia K un sottocampo del campo R dei numeri reali e sia
π il piano affine costruito su K. Sia σ : K → K un’applicazione strettamente
crescente, f la permutazione sui punti di π definita da f (x, y) = (σ(x), y) e sia F
la famiglia di rette di π aventi equazione ax + by + c = 0 con a b > 0.
(1) La coppia {F, f } è un sistema di trasformazione per π.
(2) Se K = R allora la struttura trasformata di π è sempre un piano affine.
2. Piani di Moulton
In questo paragrafo mostriamo come si possono ottenere i piani di Moulton
applicando il metodo di trasformazione delle (k,n)-strutture. Poiché i piani di
Moulton sono non desarguesiani mentre i piani affini da cui si ottengono per trasformazione sono desarguesiani, questo è un ulteriore esempio che una (k,n)-struttura
e la sua trasformata possono essere non isomorfe.
Sia G = AG(1, K) il gruppo affine e sia π il piano affine associato a G.
Sia h ∈ R+ , h 6= 0, 1 , e sia σ : R → R definita da
x se x ≤ 0
σ(x) =
;
hx se x > 0
l’applicazione σ è biettiva e strettamente crescente.
CAPITOLO 9 - Trasformazione di gruppi di permutazioni strettamente 3-transitivi
60
Sia f ∈ Sym K2 definita da f (x, y) = (σ(x), y) e sia
F = {r : ax + by + c = 0 | a, b, c ∈ R, ab > 0}
la famiglia di rette del piano affine π aventi coefficiente angolare negativo (sono
quindi esclusi gli assi). Per la proposizione 8.1.9 la coppia {F, f } è un sistema di
trasformazione per π.
Considerata l’aplicazione σ sopra definita, al variare di h si ottengono altrettanti sistemi di trasformazione che applicati a π determinano una famiglia di piani
affini π ∗ . In questa trasformazine si ha che:
(1) le rette di π con coefficiente angolare positivo e le rette parallele agli assi
cartesiani non vengono modificate e perciò sono le stesse di π ∗ ;
(2) le rette di π con coefficiente angolare negativo non vengono modificate nei
punti di ascissa negativa mentre vi è una diffrazione nei punti di ascissa
positiva;
(3) la diffrazione 00 devia00 le rette verso il basso se 0 < h < 1, verso l’alto se
h > 1.
I piani π ∗ ottenuti dalla trasformazione di π sono i piani di Moulton e risultano essere piani affini non desarguesiani mentre π è un piano affine desarguesiano.
Ricordiamo che un piano affine è detto desarguesiano se in esso vale il teorema
di Desargues.
Teorema 9.2.1 (Teorema di Desargues). In un piano affine π, considerati i triangoli ABC e A0 B 0 C 0 , se AC k A0 C 0 , AB k A0 B 0 , BC k B 0 C 0 allora
AA0 k BB 0 k CC 0 .
3. Trasformazione di Insiemi di Permutazioni
Come noto ad un insieme di permutazioni strettamente k-transitivo su E, |E| =
n, rimane associata in modo naturale una struttura di incidenza che è una (k, n)
- struttura. A partire dal metodo di trasformazione delle (k,n) - strutture, si
può pertanto stabilire sotto quali ipotesi è possibile trasformare un insieme di
permutazioni su E strettamente k-transitivo su E (finito o no), in un insieme di
permutazioni su E ancora strettamente k-transitivo su E.
Teorema 9.3.1. Sia G un insieme di permutazioni strettamente k-transitivo
su un insieme E, finito o no, tale che 1E ∈ G. Sia G1 ⊂ G, 1E ∈ G1 , G2 = G − G1
e sia σ ∈ SymE. Se valgono le seguenti condizioni:
(1) g2−1 g1 ∈ G per ogni g1 ∈ G1 e per ogni g2 ∈ G2 ;
CAPITOLO 9 - Trasformazione di gruppi di permutazioni strettamente 3-transitivi
61
(2) comunque presi x1 , x2 , ..., xk ∈ E distinti, esiste g1 ∈ G1 tale che g1 (xi ) =
σ(xi ) per i = 1, 2, ..., k;
allora G1 ∪ G2 σ è un insieme di permutazioni su E strettamente k-transitivo e
contenente la permutazione identità.
Dimostrazione. A partire dall’insieme G definiamo una opportuna struttura
d’incidenza nel seguente modo. Sia A = {(x1 , x2 , ..., xk )|xi ∈ E, xi 6= xj sei 6=
j; i, j = 1, .., k} l’insieme delle k-uple di elementi distinti di E; definiamo insieme
dei punti l’insieme P = A × A. Nel seguito se P ∈ P scriveremo P = (x, y) con
x = (x1 , ..., xk ), y = (y1 , y2 , ..., yk ). Inoltre per ogni g ∈ G scriveremo g(x) = y se
g(xi ) = yi per i = 1, 2, ..., k.
A partire da g ∈ G definiamo blocco Bg l’insieme dei punti (x, g(x)) ossia
Bg = (x, g(x)) | x ∈ A. Sia B = {Bg | g ∈ G} l’insieme dei blocchi.
Per ogni P = (x, y) ∈ P diciamo che (x, y)IBg se e solo se g(x) = y; in questo
caso useremo anche la notazione P I Bg .
La struttura (P, B, I) così definita è una struttura di incidenza. In particolare
(P, B, I) è una (1, |A|)-struttura per la stretta k-transitività di G e per come definiti
i blocchi.
Determiniamo ora un sistema di trasformazione per (P, B, I). Se P = (x, y) ∈
P definiamo f (P ) = (σ(x), y) e poniamo F = {Bg | g ∈ G2 }. Indichiamo con
< P > l’unico blocco I-incidente il punto P ∈ P; inoltre osserviamo che da (1),
essendo 1E ∈ G1 , segue che per ogni g2 ∈ G2 risulta g2−1 ∈ G2 e quindi da (1)
segue anche g1−1 g2 ∈ G2 per ogni g1 ∈ G1 e per ogni g2 ∈ G2 .
Dimostriamo che {F, f } è un sistema di trasformazione ossia che
<P >∈F
se e solo se
< f (P ) > ∈ F.
Sia P = (x, y).
• Se P ∈ F allora < f (P ) > ∈ F. Infatti da < P > ∈ F segue che esiste ed
è unico g2 ∈ G2 tale che y = g2 (x), inoltre per la stretta k-transitività di G
esiste ed è unico g ∈ G tale che y = g(σ(x)) e pertanto g2 (x) = gσ(x). Per
(2) esiste g1 ∈ G1 tale che g1 (x) = σ(x) e perciò gg1 (x) = gσ(x) = g2 (x)
da cui g1 (x) = g −1 g2 (x). Se g ∈ G1 allora g −1 g2 ∈ G2 ma ciò è assurdo
perchè G è strettamente k-transitivo e g −1 g2 = g1 ∈ G1 . Allora g ∈ G2 e
pertanto < f (P ) > ∈ F.
• Se < f (P ) > ∈ F allora < P > ∈ F. Infatti esiste g2 ∈ G2 tale che
y = g2 σ(x). Per la (2) esiste g1 ∈ G1 tale che g1 (x) = σ(x) e quindi
g2 g1 (x) = g2 σ(x) = y. Ricordando che g2−1 ∈ G2 per ogni g2 ∈ G2 , per la
(1) si ha g2 g1 ∈ G2 e dunque < P >∈ F.
Rimane pertanto dimostrato che {F, f } è un sistema di trasformazione e la
struttura trasformata di (P, B, I) mediante questo sistema è una (1, |A|)-struttura
(P, B, J). Ciò significa che per ogni x, y ∈ A esiste una ed una sola permutazione
β ∈ G tale che (x, y)JBβ e si ha
CAPITOLO 9 - Trasformazione di gruppi di permutazioni strettamente 3-transitivi
62
• β(x) = y se β ∈ G1 ;
• βσ(x) = y se β ∈ G2 .
Perciò G1 ∪ G2 σ è un insieme di permutazioni strettamente k-transitivo su E
contenente la permutazione identità 1E .
Se consideriamo un gruppo G strettamente k-transitivo su E, allora l’ipotesi
(1) del teorema 9.3.1 è soddisfatta se e solo se G1 è un gruppo, mentre l’ipotesi
(2) equivale a richiedere che se g2 ∈ G2 allora g2 e σ agiscono allo stesso modo su
al più (k − 1) elementi distinti. Valgono infatti i seguenti teoremi.
Teorema 9.3.2. Sia G un gruppo di permutazioni strettamente k-transitivo
su E, finito o no. Sia G1 ⊂ G, 1E ∈ G1 , G2 = G − G1 e sia σ ∈ SymE. Risulta
g2−1 g1 ∈ G2 per ogni g1 ∈ G1 e per ogni g2 ∈ G2 se e solo se G1 è un gruppo.
Dimostrazione. Sia g2−1 g1 ∈ G2 per ogni g1 ∈ G1 e per ogni g2 ∈ G2 ; dimostriamo che G1 è un gruppo provando che per ogni g1 , h1 ∈ G1 si ha g1 h−1
1 ∈
G1 .
Supponiamo per assurdo che sia g1 h−1
∈ G2 ; allora per l’ipotesi fatta si ha
1
−1
anche (g1 h−1
)
g
∈
G
ossia
h
∈
G
e
ciò
è
assurdo.
1
2
1
2
1
Viceversa sia G1 un gruppo. Dimostriamo che g2−1 g1 ∈ G2 per ogni g1 ∈ G1 e
per ogni g2 ∈ G2 . Siano g1 ∈ G1 e g2 ∈ G2 , essendo G gruppo si ha g2−1 g1 ∈ G;
supponiamo per assurdo che sia g2−1 g1 ∈ G1 . In questo caso è anche g1 (g2−1 g1 )−1 ∈
G1 ossia g2 ∈ G1 e ciò è assurdo.
Teorema 9.3.3. Sia G un insieme di permutazioni strettamente k-transitivo
su un insieme E, finito o no, tale che 1E ∈ G. Sia G1 ⊂ G, 1E ∈ G1 , G2 = G − G1
e sia σ ∈ SymE. Allora comunque presi x1 , x2 , ..., xk ∈ E distinti, le seguenti due
condizioni sono equivalenti:
(1) esiste g1 ∈ G1 tale che g1 (xi ) = σ(xi ), i = 1, 2, ..., k;
(2) non esiste g2 ∈ G2 tale che g2 (xi ) = σ(xi ), i = 1, 2, ..., k.
Dimostrazione. Supponiamo valga la (1); non può esistere g2 ∈ G2 che
agisce come σ su k elementi distinti di E perchè risulterebbe contraddetta la stretta
k-transitività di G.
Supponiamo valga la (2); presi x1 , x2 , ..., xk ∈ E distinti, per la stretta ktransitività di G esiste g ∈ G tale che g(xi ) = σ(xi )i = 1, 2, ..., k. Per la (2) la
permutazione g 6∈ G2 e pertanto g ∈ G1 .
CAPITOLO 9 - Trasformazione di Insiemi di Permutazioni
63
4. Trasformazione di gruppi di permutazioni strettamente 3-transitivi
su insiemi finiti
Nel capitolo 4 sono stati descritti gli insiemi di permutazioni strettamente 3transitivi su insiemi finiti contenenti la permutazione identità finora noti. Questi
insiemi possono essere ritrovati applicando opportunamente il metodo di trasformazione introdotto in questo capitolo.
Sia K = GF (pm ) il campo finito di ordine pm e sia E = K∪{∞} con ∞ 6∈ K. Sia
G = P GL(2, pm ), G1 = P SL(2, pm ), G2 = G − G1 e σ ∈ Aut(K) un automorfismo
di K per il quale poniamo σ(∞) = ∞.
Applichiamo il Teorema 9.3.1 di trasformazione.
(1) L’ipotesi (1) del teorema 9.3.1 è verificata perchè G e G1 sono gruppi e
per le proprietà dei determinanti e dei quadrati di un campo.
(2) Dimostriamo che vale l’ipotesi (2) del teorema 9.3.1. Anzittutto notiamo
che per ogni g ∈ G esiste ḡ ∈ G tale che gσ = σḡ e g −1 ḡ ∈ G1 . Infatti
ax + b
se g(x) =
, posto ā = σ −1 (a), b̄ = σ −1 (b), c̄ = σ −1 (c), d¯ = σ −1 (d),
cx + d
aσ(x) + b
σ(ā)σ(x) + σ(b̄)
āx + b̄
si ha gσ(x) =
=
¯ = σ c̄x + d¯ = σḡ(x) dove
cσ(x) + d
σ(c̄)σ(x) + σ(d)
āx + b̄
ḡ(x) =
.Inoltre da ad − bc è un quadrato se e solo se ād¯ − b̄c̄ =
c̄x + d¯
σ(ad − bc) è un quadrato e pertanto o g, ḡ ∈ G1 oppure g, ḡ ∈ G2 ; in
entrambi i casi g −1 ḡ ∈ G1 perchè G1 è gruppo di indice 2 in G.
Siano x1 , x2 , x3 ∈ E distinti. per la stretta 3-transitività di G esiste ed
è unico g ∈ G = G1 ∪ G2 tale che g(xi ) = σ(xi ), i = 1, 2, 3. Dimostriamo
che g ∈ G1 ; per quanto dimostrato sopra esiste ḡ ∈ G tale che gσ = σḡ
e g −1 ḡ ∈ G1 . Per la stretta 3-transitività di G, esiste h ∈ G tale che
h(x1 ) = 0, h(x2 ) = 1, h(x3 ) = ∞; sia h̄ ∈ G tale che hσ = σ h̄ con h−1 h̄ ∈
G1 . Poichè per ogni x ∈ E è ḡ(x) = σ −1 g −1 σ(x) e h̄(x) = σ −1 hσ(x), si ha
h̄ḡ(x) = σ −1 hg −1 σ(x) per ogni x ∈ E e, ricordando che σ(0) = 0, σ(1) =
1, σ(∞) = ∞, risulta h̄ḡ(x1 ) = σ −1 h(x1 ) = 0, h̄ḡ(x2 ) = σ −1 h(x2 ) =
1, h̄ḡ(x3 ) = σ −1 h(x3 ) = ∞ e pertanto, per la stretta 3-transitività di G,
si ha h = h̄ḡ ossia ḡ = h̄−1 h. Poichè h−1 h̄ ∈ G1 e G1 è gruppo, si ha
(h−1 h̄)−1 = h̄−1 h = ḡ ∈ G1 da cui anche g ∈ G.
Rimane così provato che sussiste l’ipotesi (2) del teorema 9.3.1.
Applicando il teorema 9.3.1 a G, G1 , G2 , σ, si ha che l’insieme G1 ∪ G2 σ è
strettamente 3-transitivo su E ed è un gruppo se e solo se σ 2 = 1E . Al variare di σ
in Aut(K) si ottengono tutti gli insiemi ed i gruppi di permutazioni strettamente
3-transitivi finiti contenenti la permutazione identità noti.
CAPITOLO 9 - Trasformazione di Insiemi di Permutazioni
64
Nota 9.4.1. Se la caratteristica del campo K è pari, tutti gli elementi di K
sono quadrati e pertanto G = P GL(2, K) = P SL(2, K). In questo caso applicare
il teorema 9.3.1 a G considerando G1 = P SL(2, K) non è significativo.