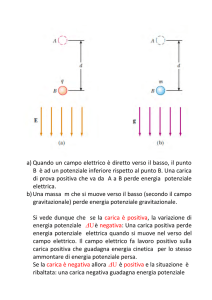
Lezione XXXI Teorema di Gauss

Lezione XXXI
Teorema di Gauss
1
Flusso di un campo vettoriale
Portata di un condotto Riprendiamo l’analogia tra il campo elettrico ele
sue linee di flusso e il campo di velocità di un fluido incomprimibile.
Il concetto di flusso di un campo vettoriale viene dall’estensione del concetto
di portata, una grandezza che misura la quantità di fluido che attraversa una
sezione di un condotto nell’unità di tempo
Supponiamo dapprima di avere un tubo cilindrico percorso da un fluido a
velocità costante, uniforme e parallela all’asse del cilindro: ogni elemento di
volume del fluido possiede cioè una velocità netta ~v uguale a quella qualunque
altro elementino. Le linee di flusso sono dunque rette parallele all’asse del
cilindro.
Se vogliamo calcolare la portata del tubo, dobbiamo stabilire quanto fluido
attraversa una sezione del tubo che prendiamo perpendicolare all’asse, e che
avrà area S. La quantità di fluido che attraversa la superficie S nell’intervallo
di tempo infinitesimo dt corrisponde al volume del cilindretto che ha come base
S e come altezza un tratto lungo dz = v dt, dove v = |~v |.
S !
v
v dt Figura 1: Nel tempo dt la sezione S è attraversata da un volume di fluido
dV = Sv dt.
Se definiamo la portata Q ≡
dV
dt
otteniamo
Q = Sv
Se la sezione del tubo non è perpendicolare alla velocità, troviamo che di
nuovo il volume del fluido è dato dal volume del cilindretto obliquo che ha come
1
base S, ma come altezza dh = dz cos θ = v dt cos θ, dove θ è l’angolo tra la
velocità e la direzione perpendicolare alla superficie S considerata. Otteniamo
pertanto
Q = Sv cos θ
n̂
S θ
!
v
v dt n̂
S’ θ
!
v
v dt Figura 2: Nel caso in cui la superficie S non sia perpendicolare alla velocità del
fluido, nel tempo dt sarà attraversata da un volume di fluido dV = Sv dt cos θ =
S 0 v dt
Notiamo che possiamo interpretare il risultato ottenuto come
Q = S cos θ v = S 0 v
(1)
dove S 0 = S cos θ è la proiezione della superficie S sul piano perpendicolare
a ~v .
Possiamo scrivere, più formalmente
Q = S n̂ · ~v
dove n̂ è il versore perpendicolare alla superficie S diretto in verso “uscente”
dal tubo.
Nel caso in cui la velocità del fluido nel condotto che ci interessa non è uniforme, ossia varia da un punto all’altro, si può calcolare quanto fluido attraversa
la superficie considerata (che non è necessariamente piana) suddividendola in
tanti elementini infinitesimi piani, tali che su ogni elemento di area la velocità
del fluido si possa considerare uniforme, e sommare.
La somma nel limite in cui l’area dei singoli elementini diventa nulla si chiama
integrale di superficie e si scrive
Z
Q=
~v · n̂ dA
(2)
S
2
n̂
dA !
v
Figura 3: Nel caso più generale, il volume che attraversa una superficie nell’unità di tempo si calcola suddivididendola in piccoli elementi dA e applicando a
ciascuno il risultato trovato sopra. La somma è un integrale di superficie.
Un integrale di superficie come quello della 2 è detto flusso del campo
vettoriale ~v (~r) attraverso la superficie S.
Osserviamo che, dato un elementino di superficie dA, il versore normale
n̂ può avere due versi opposti, che danno al flusso un contributo ±~v · n̂ dA
Di conseguenza, dato un campo vettoriale ~v (~r) e una superficie S, il flusso
di ~v attraverso S è fissato in modulo, ma può avere segno opposto secondo
l’orientazione che si sceglie per il versore normale.1
Se la superficie considerata è una superficie chiusa, le due scelte possibile di orientazione della normale corrispondono considerare il flusso uscente o
entrante rispetto al volume racchiuso dalla superficie.
1.1
Flusso del campo elettrico di una carica puntiforme
Consideriamo una carica puntiforme q che per comodità poniamo nell’origine
degli assi del sistema di coordinate. Il campo elettrico prodotto sarà
~ r) =
E(~
q r̂
4π0 r2
(3)
Consideriamo ora una superficie sferica S, di raggio R, centrata nell’origine.
~ uscente da S.
Ci proponiamo di calcolare il flusso del campo E
Prendiamo un punto sulla sfera, di coordinate (R, θ, φ) Consideriamo un
elemento di superficie in corrispondenza di quel punto, individuato spostandosi
lungo un meridiano da θ a θ + dθ, e lungo un parallelo da φ a φ + dφ.
1 Naturalmente una volta scelto il verso della normale per un elementino qualunque della
superficie, questo è automaticamente fissato per gli elementini adiacenti e dunque per tutti
gli altri elementini, nelle superfici semplici che consideriamo (lasciando perdere casi come il
nastro di Moebius o altre superfici “patologiche”).
3
L’elemento di superficie cosı̀ intercettato è approssimabile a un rettangolo
infinitesimo che ha come base un arco di parallelo (di raggio R sin θ e sotteso dall’angolo dφ e pertanto lungo R sin θ dφ) e come altezza un arco di meridiano (di
raggio R e sotteso dall’angolo dθ, dunque lungo R dθ. L’elemento di superficie
ha dunque area dA = R2 sin θ dθ dφ.
Notiamo che per ottenere l’elemento di area abbiamo “affettato” la superficie
sferica con due piani a φ costante (piani meridiani passanti per l’asse verticale),
e con due coni a θ costante, ciascuno dei quali taglia la superficie sferica lungo
un parallelo.
Rdθ
Rsin θ dϕ
Figura 4: Elemento di area di una superficie sferica di raggio R centrata
nell’origine, individuato dagli incrementi angolari dθ e dφ.
Calcoliamo il flusso del campo elettrico dell’eq.3 attraverso l’elemento di
superficie dA. Notiamo che il versore normale a dA in direzione uscente dalla
~
r
sfera è proprio il versore r̂ ≡ R
. Scegliendo questo come verso, abbiamo che
~ · n̂dA = E · r̂dA =
dΦ ≡ E
q 1
q
dA =
sin θ dθ dφ
4π0 R2
4π0
L’elemento di flusso non dipende dalla distanza a cui si trova l’elementino
di superficie sferica, ma solo dall’angolo solido sotteso2 dΩ ≡ sin θ dθ dφ.
~ su tutta la sfera dobbiamo semplicemente integrare
Per ottenere il flusso di E
in dφ da 0 a 2π, e in dθ da 0 a π. Otteniamo che il flusso del campo elettrico
uscente da una superficie sferica centrata nell’origine vale
~ ≡
Φ(E)
I
~ · n̂ dA =
E
q
4π0
2 si
Z
π
Z
sin θ dθ
0
2π
dφ =
0
q
0
(4)
definisce angolo solido sotteso da una data porzione di superficie sferica il rapporto
tra l’area della porzione data e il quadrato del raggio della sfera, in analogia all’angolo piano
definito dal rapporto tra la lunghezza di un arco di cerchio e il raggio.
4
H
indipendentemente dal raggio della sfera considerata. (Il simbolo indica che
l’integrale è eseguito su una superficie chiusa)
Prendiamo ora il caso di una superficie qualunque, e consideriamo il contributo al flusso dovuto a un elementino di superficie ottenuto – come sopra
– affettando la superficie con due piani meridiani che individuano l’incremento
angolare azimutale dφ e con i due coni a θ costante che individuano l’incremento
angolare polare dθ.
In questo caso l’elemento di superficie non è, in generale, perpendicolare al
versore r̂, ha cioè un versore normale che non è parallelo a r̂.
~ · n̂ dA si
Ma abbiamo visto nella formula 1 che l’elemento di flusso dΦ = E
può anche interpretare come
dΦ = ±EdA0
dove dA0 è la proiezione dell’elemento di area sul piano perpendicolare al vettore
di cui si vuole calcolare il flusso (il segno positivo o negativo dipende dall’orien~ è
tazione scelta per la normale). Nel nostro caso il piano perpendicolare a E
(il piano tangente al)la superficie sferica centrata nell’origine che passa per il
punto considerato, e dunque
dA0 = R2 sin θ dθ dφ
esattamente come nel caso della sfera considerato in precedenza.
Figura 5: L’elemento di area di una superficie qualunque a distanza R centrata
nell’origine, individuato dagli incrementi angolari dθ e dφ ha come proiezione
sulla sfera di raggio R l’area infinitesima trovata sopra: R2 sin θdθdφ
Dunque vale che in generale
~ = ±EdA0 = ±
dΦ(E)
5
q
sin θ dθ dφ
4π0
(5)
dove, come già detto, il segno dipende dall’orientazione scelta per la normale
all’elementino di superficie.
1.2
Teorema di Gauss
Diamo ora una dimostrazione semi-formale del Teorema di Gauss.3
Nella situazione descritta sopra (carica puntiforme q posta nell’origine delle
coordinate) consideriamo una superficie chiusa tale che il volume di cui essa
rappresenta il bordo contenga l’origine. Per il momento consideriamo il caso
semplice in cui tale volume sia convesso: in questo caso ogni semiretta che parte
dall’origine incontrerà la superficie di bordo una sola volta, e questo avverrà per
qualunque valore degli angoli θ e φ. Il flusso totale del campo elettrico si ottiene
sommando gli elementi di flusso 5 e la somma è estesa su tutti i valori possibili
dell’angolo θ e dell’angolo φ.
Dunque anche in questo caso, molto più generale della sfera concentrica,
~ =
Φ(E)
I
~ · n̂ dA =
E
q
4π0
Z
π
Z
sin θ dθ
0
2π
dφ =
0
q
0
Figura 6: Flusso del campo di una carica puntiforme attraverso una superficie
chiusa che la contiene.
Consideriamo ora il caso di una superficie chiusa che non contiene la carica
puntiforme. Anche in questo caso prendiamo per comodità il caso più semplice
3 Non
si tratta cioè di una dimostrazione rigorosa, che sarebbe troppo pesante dal punto di
vista matematico, bensı̀ di una discussione a metà tra il formale e l’intuitivo, che però si può
rendere matematicamente ineccepibile.
6
di un volume convesso: osserviamo che ogni semiretta che parte dall’origine
intersecherà la superficie in due punti, o in nessun punto.4
Dunque ogni elemento di angolo solido individuato dagli incrementi angolari
dθ, dφ o non intercetta la superficie chiusa, o la intercetta in due elementini.
Poiché come abbiamo visto il contributo elementare al flusso dipende (in modulo) solo dall’elemento di angolo solido intercettato, i due contributi avranno lo
stesso valore assoluto, ma avranno segno opposto se consideriamo per ciascuno
il verso della normale uscente dalla superficie chiusa (vedi figura 7).
Figura 7: Flusso del campo di una carica puntiforme attraverso una superficie
chiusa che non la contiene.
La somma degli elementi di flusso su tutta la superficie sarà dunque nulla.
Abbiamo concluso che
il flusso uscente da una qualunque superficie chiusa del campo
elettrico generato da una carica puntiforme q vale5
~ =
• Φ(E)
q
0
se la carica è contenuta nel volume racchiuso dalla superficie.
~ = 0 se la carica è esterna.
• Φ(E)
4 in realtà anche in un punto solo, se la semiretta risulta tangente alla superficie. Ma in
questi punti - che costituiscono comunque un insieme di misura nulla - il contributo al flusso
zero, perché il campo è parallelo alla superficie.
5 In realtà abbiamo “dimostrato” il risultato solo per superfici semplici, bordi di volumi
convessi. Tuttavia è abbastanza facile generalizzare il risultato a superfici più complicate,
osservando che ogni semiretta che parte dal’origine intercetta la superficie in un numero dispari
di punti se la superficie racchiude l’origine, e in un numero pari in caso contrario. Un altro
modo è ricondursi al caso precedente suddividendo il volume in tanti volumi più contigui, e
osservando che la somma algebrica dei flussi uscenti da ciascun sottovolume è il flusso uscente
dalla superficie esterna del volume totale (il flusso attraverso le superfici di separazione tra un
sottovolume e l’altro viene contato una volta con un segno e una volta con il segno opposto).
7
A questo punto facciamo ricorso al principio di sovrapposizione. Consideriamo infatti un generico campo elettrico generato da N cariche puntiformi
q1 , . . . , qN . Il campo elettrico totale sarà la somma dei campi generati dalle
singole cariche qi :
~ =E
~1 + E
~2 + · · · + E
~N
E
~ uscente
Consideriamo ora una qualunque superficie chiusa S. Il flusso di E
da tale superficie sarà dato, per linearità dell’integrale, dalla somma dei flussi
dei singoli campi:
I
I
I
I
~ =
~ · n̂ dA =
~ 1 · n̂ dA +
~ 2 · n̂ dA + · · · +
~ N · n̂ dA
Φ(E)
E
E
E
E
S
S
S
S
qi
0
se qi è contenuta
Sappiamo che ciascuno degli addendi contribuirà con
nel volume V delimitato dalla superficie S, con 0 se è esterna. Dunque
~ =
Φ(E)
X qi
Qint
=
0
0
qi ∈V
dove Qint è la carica interna al volume racchiuso da S.
In sintesi, il teorema di Gauss afferma che
Il flusso del campo elettrico attraverso una qualunque superficie chiusa è
proporzionale alla carica interna alla superficie e vale Qint /0
In formula
H
S
~ · n̂ dA =
E
Qint
0
(6)
Nel caso di distribuzioni continue di carica, la carica interna è data dall’integrale della densità di carica ρ(~r) esteso al volume racchiuso dalla superficie
chiusa
Z
Qint =
ρ dV
V
1.3
Flusso e linee di campo
Torniamo per un attimo a quanto detto a proposito delle linee di campo: avevamo scritto che non è sempre vero che “dove le linee di campo sono più fitte,
l’intensità del campo è maggiore”. Questo infatti è vero solo nelle regioni di
spazio in cui non c’è carica elettrica, e dunque il flusso uscente da qualunque
superficie chiusa è nullo.
Per convincercene, consideriamo una regione di spazio in cui le linee di campo
non sono parallele, ma “divergono” (o convergono) e prendiamo una porzione
di superficie A perpendicolare alle linee di campo per esempio nella zona in cui
sono più “fitte”. Consideriamo la linea chiusa che rappresenta il bordo di A.
Se per ogni punto della linea chiusa bordo della superficie tracciamo la linea
di campo che passa da quel punto, otteniamo un cosiddetto “tubo di flusso”
(sempre in analogia al caso dei fluidi, in cui il campo rappresenta la velocità del
8
fluido in un punto, e il flusso la portata) . Prendiamo ora una nuova superficie
perpendicolare alle linee di campo, nella regione di spazio in cui queste sono
meno fitte (il tubo di flusso si allarga) e consideriamo la porzione A0 che si
ottiene intersecandola con il tubo di flusso. Abbiamo ottenuto una superficie
chiusa costituita dal tubo di linee di campo compreso tra i due “tappi” A e
~ uscente dalla superficie chiusa: esso
A0 . Consideriamo il flusso totale Φu (E)
sarà dato dalla somma degli integrali di superficie sui due tappi e sulla parete
laterale del tubo e, per il teorema di Gauss, sarà nullo se nella regione di spazio
considerata non ci sono cariche.
A’ A Figura 8: Flusso del campo attraverso due sezioni A e A0 dello stesso “tubo di
flusso”
La somma degli elementi di flusso su tutta la superficie sarà dunque nulla.
~ = ΦuA + ΦuA0 + Φutubo = 0
Φu (E)
Il contributo al flusso della parete laterale Φutubo é nullo perché, per costru~ è tangente alla
zione, sulla superficie generata dalle linee di campo, il vettore E
~ · n̂ = 0.
superficie, dunque in ogni punto E
Dunque
ΦuA + ΦuA0 = 0
ossia
|ΦuA | = |ΦuA0 |
Se abbiamo preso entrambe le superfici abbastanza piccole da poter considerare il campo uniforme su entrambe, e in entrambi i casi il campo è perpendicolare alla superficie, abbiamo
~ A |A = |E
~ A0 |A0
|E
cioè
~ A0 |
|E
A
= 0
~
A
|EA |
9
L’intensità del campo risulta inversamente proporzionale all’area della superficie, ossia alla “sezione” del tubo di flusso: se questo si allarga (le linee di
campo si diradano) l’intensità del campo diminuisce, e viceversa.
Notiamo che è fondamentale l’ipotesi di assenza di carica nella regione di
spazio considerata!
2
Esempi di uso del teorema di Gauss
Il teorema di Gauss per il campo elettrico vale sempre, per qualunque campo
elettrico e per qualunque superficie chiusa si consideri. Tuttavia è solo in casi
molto particolari che si riesce a sfruttarlo per calcolare il campo elettrico prodotto da una data distribuzione di carica. Si tratta di casi a elevata simmetria in
cui il flusso del campo elettrico attraverso certe superfici si riesce a scrivere come
prodotto di un’area per il valore di un campo (o come semplice combinazione
di espressioni simili), permettendo di calcolare il valore del campo stesso.
La simmetria del problema è fondamentale per stabilire le caratteristiche
del campo prima di scegliere la superficie opportuna a cui applicare il teorema.
Vediamo alcuni esempi
2.1
Distribuzione di carica a simmetria sferica
Una configurazione spaziale si dice a simmetria sferica se esiste un punto (detto
centro di simmetria) tale che ruotando la configurazione (o, che è lo stesso,
ruotando gli assi coordinati) di qualunque angolo rispetto a un qualunque asse
passante per il centro di simmetria, la configurazione rimane indistinguibile
rispetto a prima della rotazione. Una sfera è chiaramente un sistema a simmetria
sferica, ma lo è anche un guscio sferico, un sistema di sfere concentriche ecc.
Un sistema di due sfere non concentriche non è a simmetria sferica, e lo stesso
vale per una sfera con distribuzione di carica qualunque. Nel seguito useremo
preferenzialmente le coordinate sferiche per descrivere la posizione di un punto.
In generale una distribuzione di carica è a simmetria sferica (rispetto all’origine delle coordinate) se la densità ρ(~r), che in generale dipende dalle tre
coordinate sferiche r, θ, φ, non dipende dalle coordinate angolari θ e φ ma solo
dalla distanza r dal centro di simmetria (dunque è una funzione di una sola
variabile anziché di tre):
ρ(~r) = ρ(r)
Dalla legge di Coulomb che esprime il campo elettrico come una funzione
lineare della distribuzione di carica si può dimostrare con semplici passaggi formali che se quest’ultima è a simmetria sferica, anche la funzione campo elettrico
~ r) lo sarà, dunque anche la configurazione del campo non deve cambiare ruoE(~
tando il sistema di un qualunque angolo rispetto a qualunque asse passante per
il centro. In formula
~ r) = E(r)
~
E(~
Come abbiamo visto in precedenza per il caso del campo di un anello carico,
quando la distribuzione ha un asse di simmetria (cilindrica) rispetto al quale
10
rimane invariata per qualunque rotazione, il campo elettrico nei punti dell’asse deve essere diretto lungo l’asse stesso, per rispettare la simmetria. In una
configurazione a simmetria sferica tutte le rette passanti per il centro sono assi
di simmetria. Dunque in qualunque punto dello spazio il campo elettrico deve
essere diretto come la congiungente tra il punto e il centro di simmetria. In altre
parole deve avere solo la componente radiale parallela al versore r̂.
In conclusione
~ r) = E(r)r̂
E(~
~ r), che in generale va da R3 → R3 , grazie alla simmetria
Dalla funzione E(~
siamo passati a dover determinare una funzione E(r) : R → R
Il flusso di un campo simile uscente da una superficie sferica di raggio r
centrata nell’origine è molto facile da calcolare. Infatti in ogni punto della
superficie sferica il versore normale uscente n̂ coincide con il versore radiale r̂.
Dunque
~ r) · n̂ dA = E(~
~ r) · r̂ dA = E(r)r̂ · r̂ dA = E(r) dA
dΦ = E(~
dove abbiamo usato che r̂ · r̂ = 1.
Poiché r è costante su tutta la superficie, il valore E(r) non dipende dal
punto scelto sulla superficie, e dunque può essere portato fuori dall’integrale:
I
I
I
~
~
(7)
Φ(E) ≡ E(~r) · n̂ dA = E(r) dA = E(r) dA = E(r) 4πr2
Consideriamo alcuni casi particolari in cui questo torna utile.
Guscio sferico vuoto Vogliamo calcolare il campo generato da un guscio
sferico di spessore trascurabile, di raggio a e di carica totale Q (o di densità superficiale di carica uniforme σ = Q/4πa2 ). Si tratta di un caso particolarmente
facile di simmetria sferica.
Prendiamo come superficie di Gauss una superficie sferica di raggio r qualunque. La 7 unita al teorema di Gauss ci dice che
~ = E(r) 4πr2 =
Φ(E)
da cui
E(r) =
Qint
0
Qint
4π0 r2
Abbiamo due casi, secondo che r sia maggiore o minore di a.
Per r < a abbiamo Qint = 0, mentre per r > a, Qint = Q = 4πa2 σ. Ne
deduciamo che
E(r) = 0
r<a
E(r) =
Q
σ
=
2
4π0 r
0
Notiamo che:
11
r>a
1. i punti all’interno del guscio sferico “non vedono” le cariche sul guscio, i
cui effetti si annullano in tutti i punti interni;
2. il campo all’esterno del guscio è ovunque identico a quello di una carica
puntiforme di carica uguale a quella del guscio sferico, e posta nel suo
centro. Questo senza bisogno di essere molto lontani: immediatamente
fuori dal guscio il campo è lo stesso che si avrebbe se tutta la carica fosse
concentrata nel centro. Si noti che (sempre grazie al teorema di Gauss)
questo è vero per qualunque distribuzione di carica a simmetria sferica
confinata entro un raggio massimo a. Fuori dalla zona in cui c’è carica,
tutto funziona come se la carica fosse concentrata nel centro di simmetria.
!
E
Figura 9: Campo elettrico all’esterno di una sfera uniformemente carica, e
superficie di Gauss usata per calcolarlo.
Sfera con distribuzione di carica uniforme Vogliamo calcolare il campo
generato da una sfera di raggio a all’interno della quale è presente una densità
di carica uniforme ρ = 4Q/3πa3 ).
Come prima, usando una superficie di Gauss sferica concentrica alla sfera
data, abbiamo
E(r) =
Qint
4π0 r2
dove, come prima Qint = Q = 43 a3 ρ per r > a, mentre per r < a la carica
interna vale
4
Q(r) = r3 ρ
3
Otteniamo quindi
E(r) =
ρ
r
30
r<a
E(r) =
Q
ρa3
=
2
4π0 r
30 r2
r>a
Il campo all’interno della sfera risulta lineare in r, mentre fuori dalla sfera ancora una volta è uguale al campo di una carica puntiforme concentrata
nell’origine.
12
2.2
Simmetria cilindrica: Campo del filo indefinito uniforme
Consideriamo il campo generato da un filo rettilineo indefinito (cioè di lunghezza
molto maggiore delle distanze a cui misuriamo il campo) con densità lineare di
carica λ ≡ dq
d` uniforme. Prendiamo per comodità un sistema di coordinate
cilindriche in cui il filo giace lungo l’asse z.
Questa configurazione di carica gode di due simmetrie fondamentali: la simmetria per traslazione lungo l’asse z, e la simmetria (cilindrica) per rotazione
~ r) deve godeattorno allo stesso asse. Questo significa che anche la funzione E(~
re delle stesse proprietà, ossia non deve variare per una qualunque traslazione
degli assi (o del sistema) lungo z, o per una qualunque rotazione degli assi (o
~ r) non può dipendere dalla
del sistema) attorno all’asse z. Di conseguenza E(~
coordinata cilindrica z (in caso contrario ci accorgeremmo di una sua traslazione), né dall’angolo azimutale φ: dovrà dipendere solo dalla coordinata cilindrica
radiale r (che in questo caso rappresenta la distanza dall’asse e non dal centro
come nel caso sferico).
~ r) = E(r)
~
E(~
~ sopravvivono, semCome prima, notiamo che non tutte le componenti di E
pre grazie alla simmetria: come abbiamo dimostrato in precedenza, infatti, se
una configurazione possiede un piano di simmetria, nei punti del piano il campo
elettrico deve giacere sul piano stesso. Il filo indefinito uniformemente carico
possiede infiniti piani di simmetria: tutti i piani passanti per il filo stesso, e
tutti i piani perpendicolari al filo. È immediato vedere che questo implica che
il campo in ogni punto dello spazio debba essere diretto perpendicolarmente al
filo, ossia lungo il versore radiale cilindrico r̂:
~ r) = E(r)r̂
E(~
!
E
Figura 10: Campo elettrico di un filo rettilineo infinito uniformemente carico, e
superficie di Gauss cilindrica usata per calcolarne il valore.
Per calcolare il campo usando il teorema di Gauss, prendiamo come superficie
chiusa un cilindro coassiale al filo, di raggio r generico e di altezza h qualunque.
13
Il flusso uscente dalla superficie cilindrica ha tre contributi: quello uscente
dalla superficie laterale, e i due flussi uscenti dalle basi. Questi ultimi sono nulli
perché in tutti i punti di ciascuna base il campo, che è perpendicolare al filo, è
~ · n̂ = 0. Al flusso contribuisce
parallelo alla superficie in questione, dunque E
solo la superficie laterale del cilindro, sui punti della quale notiamo che, come nel
caso della sfera trattato sopra, il campo è sempre perpendicolare alla superficie,
in quanto n̂ = r̂. Dunque anche in questo caso
~ · n̂ dA = E(r) dA
dΦ = E
Poiché r è costante su tutta la superficie laterale E(r) si porta fuori dall’integrale nella definizione di flusso, e si ottiene, come nei casi precedenti
~ = E(r)A = E(r)2πrh
Φ(E)
La carica interna alla superficie cilindrica considerata è data dal tratto di
filo intercettato dal cilindro, e vale
Qint = λh
Imponendo il teorema di Gauss otteniamo
E(r)2πrh =
da cui
E(r) =
λh
0
λ
2π0 r
lo stesso risultato che si ottiene integrando la legge di Coulomb.
2.3
Simmetria piana: Campo della lastra piana indefinita
Consideriamo infine il caso di una lastra piana infinita (ossia di dimensioni
trasversali molto maggiori rispetto alle distanze in gioco) uniformemente carica,
con densità superficiale di carica σ, che faremo per comodità coincidere con il
piano cartesiano z = 0.
Si tratta dell’esempio più semplice di configurazione a simmetria piana , cioè
invariante per qualunque traslazione lungo le coordinate x e y. Il fatto che il
campo debba godere della stessa simmetria significa che esso può solo dipendere
dalla coordinata z:
~ r) = E(z)
~
E(~
Notiamo adesso che qualunque piano perpendicolare al piano z = 0 è un
piano di simmetria. Dato un punto generico di coordinate (x, y, z), dal fatto che
su ogni piano di simmetria il campo elettrico deve giacere nel piano deduciamo
che il piano deve giacere nell’intersezione di tutti i piani perpendicolari al piano
(x, y) che passano per quel punto, cioè deve essere parallelo all’asse z. Alla
stessa conclusione si arriva osservando che tutte le rette perpendicolari al piano
infinit dato sono assi di simmetria rotazionale per il sistema e, come abbiamo
già visto, nei punti dell’asse di simmetria di un sistema il campo elettrico deve
essere diretto lungo l’asse.
14
!
E
z !
E
Figura 11: Campo elettrico di un piano infinito uniformemente carico, e
superficie di Gauss cilindrica usata per calcolarne il valore.
Dunque
~ r) = E(z)ẑ
E(~
e ancora una volta ci riduciamo a determinare una funzione R → R.
Notiamo infine che il piano z = 0 è un piano di simmetria, e quindi il campo
nella regione di spazio z > 0 è legato a quello nella regione z < 0 da una
riflessione “speculare” rispetto al piano z = 0. Ne deduciamo che la funzione
E(z) deve essere una funzione dispari
E(−z) = −E(z)
Come superficie di Gauss per calcolare E(z) prendiamo una superficie cilindrica che abbia le basi di area data A in posizione simmetrica rispetto al piano,
rispettivamente a distanza ±z dal piano z = 0.
Notiamo innanzitutto che le pareti verticali del cilindro sono parallele al
campo, e quindi non contribuiranno al flusso. La base superiore (z > 0) invece
~ · n̂ =
ha come versore normale uscente dal cilindro proprio il versore ẑ, dunque E
E(z). Poiché z non varia sulla superficie considerata, nel calcolare il flusso
possiamo portare fuori E(z) dal segno di integrale e otteniamo che il contributo
al flusso della base superiore vale ΦA = AE(z).
La base inferiore ha come versore normale uscente −ẑ, ma anche il campo
~ · n̂ avrà lo stesso segno rispetto al caso
elettrico cambia di segno . Dunque E
della base superiore, e le due basi contribuiscono con lo stesso valore al flusso
totale, che sarà
~ = 2E(z)A
Φ(E)
(con z > 0).
La carica contenuta nel volume individuato dal cilindro è quella del disco di
area A intercettato dal cilindro sul piano, e vale Qint = Aσ
Imponendo il teorema di Gauss troviamo
15
E(z) =
σ
20
E(z) = −
z>0
σ
20
z<0
ritrovando il risultato calcolato a partire dal campo del disco carico sul suo
asse.
16