Geometria Analitica

GEOMETRIA ANALITICA
La geometria analitica consente di studiare e rappresentare per via algebrica informazioni di tipo
geometrico. Lo studio favorisce una più immediata visualizzazione di informazioni, associate a
fenomeni della realtà quotidiana, per via grafica.
Il Piano cartesiano
Il piano cartesiano è lo strumento sul quale è possibile rappresentare oggetti tramite una serie di
convenzioni.
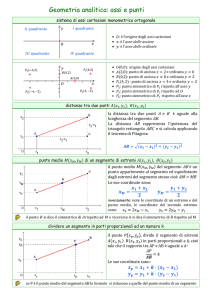
Il Piano Cartesiano è costituito da due assi perpendicolari che si intersecano nell'Origine. L'asse X
(orizzontale) è anche chiamato asse delle ascisse, l'asse Y (verticale) è anche detto asse delle
ordinate.
Gli assi sono orientati e, su di essi, sono presenti suddivisioni che ne indicano la graduazione in
base ad una arbitraria unità di misura.
Sul piano cartesiano è possibile rappresentare e studiare vari oggetti.
Il Punto
Ogni punto del piano cartesiano è individuato da una coppia ordinata di numeri che ne definiscono
la posizione.
La prima componente della coppia prende il nome di ascissa ed individua lo spostamento
orizzontale (positivo o negativo) del punto rispetto l'origine.
La seconda componente della coppia prende il nome di ordinata ed individua lo spostamento
verticale (positivo o negativo) del punto rispetto l'origine.
Il punto A ha coordinate (3;2) infatti il suo spostamento rispetto l'origine è di 3 unità in orizzontale
e 2 unità in verticale.
Osservazione:
Gli assi cartesiani dividono il piano in 4 quadranti. Il segno delle coordinate cartesiane indica
univocamente in quale quadrante è posizionato il punto:
Ascissa
Ordinata
Posizione
+
+
Alto - Destra
+
-
Basso - Destra
-
+
Alto - Sinistra
-
-
Basso - Sinistra
Casi Particolari:
• Se l'ascissa vale 0 (zero) allora il punto è posizionato sull'asse Y.
• Se l'ordinata vale 0 (zero) allora il punto è posizionato sull'asse X.
• L'Origine ha coordinate (0;0)
E' importante saper posizionare e saper individuare punti sul piano cartesiano visto che essi
rappresentano i vertici di una qualsiasi figura geometrica.
Il segmento
Un segmento è una parte di retta delimitata da sue punti detti estremi del segmento. Fissati due
punti sul piano cartesiano costruiremo un segmento semplicemente unendoli in linea retta.
La lunghezza del segmento non è altro che la distanza tra i suoi estremi; di conseguenza è molto
importante saper misurare analiticamente la distanza tra due punti, in quanto, tale misura, ci
consente di calcolare la lunghezza del segmento che li unisce.
In relazione alla posizione dei suoi estremi un segmento può essere:
• Orizzontale:
se i suoi estremi hanno stessa ordinata.
• Verticale:
se i suoi estremi hanno stessa ascissa.
• Obliquo:
se i suoi estremi non hanno né stessa ascissa, né stessa ordinata.
Il segmento AB è orizzontale visto che l'ordinata dei suoi estremi A e B è la stessa (1).
Il segmento CD è verticale visto che l'ascissa dei suoi estremi C e D è la stessa (1).
Il segmento EF, invece, è obliquo.
Calcolo della misura di un segmento
Segmenti orizzontali
Nel caso in cui il segmento da misurare sia orizzontale, la sua lunghezza coincide con la differenza
delle ascisse dei suoi estremi.
Esempi:
A = (2;1) e B = (6;1)
A = (5;1) e B = (3;1)
A = (3;1) e B = (-2;1)
AB = 6 – 2 = 4
AB = 5 – 3 = 2
AB = 3 – (–2) = 3 + 2 = 5
Osserviamo cosa sarebbe accaduto invertendo l'ordine della sottrazione negli esempi precedenti:
A = (2;1) e B = (6;1)
A = (5;1) e B = (3;1)
A = (3;1) e B = (-2;1)
AB = 2 – 6 = –4
AB = 3 – 5 = –2
AB = (–2) – 3 = –5
Una lunghezza non può mai essere negativa per cui, visto che la sottrazione non è un'operazione
commutativa, è opportuno utilizzare il valore assoluto che mi consente di ignorare il segno e
prendere in considerazione solo il modulo.
In definitiva per calcolare la misura di un segmento orizzontale posso applicare la seguente formula:
AB = | XB – XA |
XB è l'ascissa dell'estremo B
XA è l'ascissa dell'estremo A
Segmenti verticali
Quanto affermato per i segmenti orizzontali vale anche per i segmenti verticali con l'unica
differenza che, essendo fissa l'ascissa degli estremi, la misura del segmento si calcola con la
seguente formula:
CD = | YD – YC |
YD è l'ordinata dell'estremo D
YC è l'ordinata dell'estremo C
Segmenti Obliqui
Per determinare la formula del calcolo della misura di un segmento obliquo è necessario osservare
attentamente la figura.
L'esempio vuole calcolare la misura del segmento obliquo AB di cui conosciamo le coordinate dei
vertici A e B.
Per raggiungere tale risultato osserviamo che il punto (G) di incontro delle proiezioni di A e B sugli
assi è allineato orizzontalmente con A e verticalmente con B per cui possiamo affermare che:
XG = XB
e
YG = YA
(1)
Inoltre
•
•
AG = XG – XA in quanto AG è un segmento orizzontale
BG = YB – YG in quanto BG è un segmento verticale
Sostituendo le relazioni (1) in queste due espressioni otteniamo:
•
•
AG = XB – XA in quanto AG è un segmento orizzontale
BG = YB – YA in quanto BG è un segmento verticale
(2)
(3)
Il triangolo AGB è rettangolo: i lati AG e BG prendono il nome di CATETI, mentre il lato AB si
chiama IPOTENUSA. In base al teorema di Pitagora sappiamo che la misura dell'ipotenusa può
essere calcolata una volta conosciute le misure dei cateti secondo la formula:
AB2 = AG2 + BG2
da cui deriva che:
AB= AG 2BG 2
Sostituendo le relazioni (2) e (3) in quest'ultima formula avremo:
AB=  X B − X A 2Y B−Y A2
(4)
Esempio: Si vuole calcolare la misura del segmento AB i cui estremi hanno coordinate A = (2;1) e
B = (6;3).
Il segmento AB è obliquo per cui è necessario applicare la formula (4) sostituendo opportunamente
le coordinate degli estremi A e B, ed eseguendo i calcoli.
XA = 2
XB = 6
YA = 1
AB=  X B − X A 2Y B−Y A2
AB= 6−223−12
AB= 4222
AB= 164
AB= 20 = 4,47
YB = 3
GEOMETRIA ANALITICA
Le coordinate del punto medio di un segmento
Per trattare e risolvere problemi di geometria attraverso la geometria analitica, oltre ai concetti di
punto e segmento precedentemente espressi, è necessario conoscere il concetto di punto medio di un
segmento, e saperne calcolare le coordinate cartesiane una volta note le coordinate degli estremi del
segmento stesso.
L'obiettivo è quello di definire le coordinate del punto M, conoscendo le coordinate dei punti A e B.
Lavorando in termini generici possiamo supporre che i punti A e B abbiano rispettivamente
coordinate:
A = (XA;YA)
B = (XB;YB)
inoltre essendo C, D ed E le proiezioni dei punti A, M e B sull'asse delle X avremo:
XC = XA
XD = XM
XE = XB
(1)
Il Punto M è, per ipotesi, il punto medio del segmento AB, per cui sarà:
AM = MB
Il teorema di Talete afferma che un fascio di rette parallele taglia segmenti trasversali in parti
proporzionali.
Data la costruzione in figura, tale teorema ci consente di affermare che il punto D è il punto medio
del segmento CE. Per cui avremo che:
CD = DE
CD e DE sono due segmenti orizzontali dei quali è possibile calcolare la misura utilizzando le
formule studiate la scorsa lezione:
CD = XD - XC
DE = XE - XD
Queste due lunghezze, come visto precedentemente, sono uguali in quanto D è punto medio di CE
per cui avremo:
XD - XC = XE - XD
XD + XD = XE + XC
2XD = XE + XC
X D=
X E X C
2
(2)
Se sostituiamo le relazioni (1) nella formula (2) otterremo:
X M=
X B X A
2
Tale formula dice che l'ascissa del punto medio M di un segmento di estremi A e B si può calcolare
sommando le ascisse degli estremi e dividendo tutto per due.
Una analoga dimostrazione ci porta a definire l'ordinata del punto M.
Y M=
Y BY A
2
Tale formula dice che l'ordinata del punto medio M di un segmento di estremi A e B si può
calcolare sommando le ordinate degli estremi e dividendo tutto per due.
Formule inverse
Come visto è possibile calcolare le coordinate del punto medio se si conoscono le coordinate degli
estremi del segmento. Utilizzando le stesse formule e qualche passaggio algebrico è possibile
calcolare le coordinate di un estremo (B) del segmento se si conoscono le coordinate del suo punto
medio (M) e dell'altro estremo (A).
X B=2X M − X A
Y B=2Y M −Y A
I TRIANGOLI
Si dice triangolo il poligono convesso con tre lati e tre vertici non allineati.
Ogni triangolo, oltre i lati e gli angoli, ha altri elementi notevoli:
• Bisettrice: si dice bisettrice relativa ad un angolo interno la semiretta che divide in parti uguali
l’angolo.
• Mediana: si dice mediana relativa ad un lato del triangolo il segmento che unisce un vertice con
il punto medio del lato opposto.
• Altezza: si dice altezza relativa ad un lato del triangolo il segmento che unisce in modo
perpendicolare un vertice con il lato opposto.
Ogni triangolo ha tre bisettrici, tre mediane e tre altezze.
Mediane
Altezze
Bisettrici
Osservazione
per come sono state definite è utile notare che mentre mediane e bisettrici sono sempre interne al
triangolo, le altezze possono anche cadere in un punto esterno al triangolo stesso.
Misure
Perimetro = somma dei lati
Area =
Base∗Altezza
2
Classificazione dei triangoli
I triangoli possono essere suddivisi in categorie secondo due modi differenti:
Classificazione secondo i lati:
EQUILATERO:
se ha tutti i lati uguali
Possiamo osservare che in ogni triangolo equilatero le altezze, mediane e bisettrici coincidono tra
loro. Per verificare che un triangolo è equilatero è necessario calcolare le misure dei lati e constatare
che sono tutte uguali.
ISOSCELE:
se ha due lati uguali (detti lati obliqui) ed uno diverso (detto base)
Possiamo osservare che in ogni triangolo isoscele l'altezza relativa alla base è anche mediana e
bisettrice. Per verificare che un triangolo è isoscele è necessario calcolare le misure dei lati e
constatare che due sono uguali ed il terzo diverso.
SCALENO:
se ha tutti i lati diversi
Possiamo osservare che in ogni triangolo scaleno le altezze, mediane e bisettrici non coincidono tra
loro. Per verificare che un triangolo è scaleno è necessario calcolare le misure dei lati e constatare
che sono tutte diverse
Classificazione secondo gli angoli:
RETTANGOLO:
se ha un angolo retto (90 gradi)
Per verificare che un triangolo è rettangolo è necessario calcolare le misure dei lati e constatare che
soddisfano il teorema di Pitagora.
ACUTANGOLO:
se ha tutti gli angoli acuti (minori di 90 gradi).
SCALENO:
se ha un angolo ottuso (maggiore di 90 gradi)
Da ricordare che la somma degli angoli di un qualsiasi triangolo è sempre 180 gradi.
I QUADRILATERI
Si dice quadrilatero il poligono convesso formato da 4 lati e 4 angoli.
A parte i trapezi che non tratteremo, i quadrilateri possono essere così raggruppati:
Poligono
Lati opposti
Diagonali
Angoli opposti
Parallelogramma
Paralleli ma
diversi
diverse
Uguali ma non retti
Rettangolo
Paralleli ma
diversi
uguali
Uguali e retti
Rombo
Paralleli ed uguali diverse
Uguali ma non retti
Quadrato
Paralleli ed uguali uguali
Uguali e retti
Da rilevare che in tutti i tipi di quadrilatero le diagonali si incontrano esattamente nel loro punto
medio.