Algoritmi e diagrammi di flusso Un algoritmo può essere descritto come una sequenza finita ed ordinata di operazioni che descrivono la soluzione di un problema. Per sequenza finita si intende che un algoritmo ha sempre un inizio ed una fine, dunque non ci sono infinite operazioni da compiere. Per sequenza ordinata si intende che l’ordine con il quale si eseguono le operazioni è importante. In realtà, abbiamo a che fare con degli algoritmi non soltanto nel campo dell’informatica, ma anche nella vita di tutti i giorni: lavarsi i denti, preparare una torta, preparare il caffè, sono tutte attività che richiedono una sequenza finita ed ordinata di operazioni, e quindi un algoritmo. Ad esempio, consideriamo l’algoritmo per lavarsi i denti: 1. Prendi lo spazzolino. 2. Prendi il dentifricio. 3. Metti il dentifricio sullo spazzolino. 4. Posa il dentifricio. 5. Apri l’acqua. 6. Bagna lo spazzolino. 7. Chiudi l’acqua. 8. Porta lo spazzolino alla bocca. 9. Spazzolare. 10. Controlla se i denti sono puliti. a. Se i denti non sono ancora puliti, ritorna all’operazione 9. b. Se i denti sono puliti vai all’operazione 11. 11. Posa lo spazzolino. 12. Apri l’acqua. 13. Sciacqua la bocca. 14. Chiudi l’acqua. Da quanto possiamo notare sono verificate le due caratteristiche degli algoritmi, ossia l’algoritmo è una sequenza finita ed ordinata di operazioni: • L’algoritmo è finito: inizia con l’operazione 1 e termina con l’operazione 14. • L’algoritmo è ordinato: se cambiassi l’ordine di alcune operazioni, potrei ottenere: 1. Posa il dentifricio. 1 2. Spazzolare. 3. Chiudi l’acqua. 4. Posa lo spazzolino. 5. Prendi il dentifricio. 6. Metti il dentifricio sullo spazzolino. 7. Apri l’acqua. 8. Bagna lo spazzolino. 9. Chiudi l’acqua. 10. Porta lo spazzolino alla bocca. 11. Controlla se i denti sono puliti. 12. Prendi lo spazzolino. a. Se i denti non sono ancora puliti, ritorna all’operazione 11. b. Se i denti sono puliti vai all’operazione 13. 13. Apri l’acqua. 14. Sciacqua la bocca. Da come possiamo osservare, le operazioni restano le stesse, benché l’ordine sia variato, ma sicuramente con questo algoritmo non potremmo dire di aver lavato i denti correttamente. In informatica le operazioni vengono dette istruzioni, che possono essere di vario tipo : • Azioni: “calcola il valore x”. • Controllo: “se si verifica A allora calcola x… altrimenti calcola y”. • Comunicazione: “leggi il valore x”; “stampa il valore y”. • *Salto: “se si verifica A allora prosegui… altrimenti salta ad un’altra istruzione”. • … I software (programmi) che noi utilizziamo tutti i giorni non sono nient’altro che l’implementazione (la realizzazione) degli algoritmi mediante linguaggi di programmazione. Anche con Excel (che è un programma) è possibile scrivere altri programmi (mediante i fogli di calcolo) che altro non sono che l’implementazione di determinati algoritmi (ad esempio l’algoritmo per stabilire se un numero è pari o dispari). Gli algoritmi, però, possono anche essere rappresentati graficamente, mediante i diagrammi di flusso (flow diagrams), prima di essere realizzati sul calcolatore, al fine di avere una migliore visione di tutte le istruzioni necessarie per l’implementazione dell’algoritmo. Tali diagrammi utilizzano forme geometriche diverse per rappresentare istruzioni di tipo differente; la sequenzialità delle istruzioni viene rappresentata con delle frecce che collegano nell’ordine la varie istruzioni tra loro: Forma utilizzata Descrizione Rappresenta l’inizio dell’algoritmo. Inizio
2 Rappresenta la fine dell’algoritmo. Fine
Rappresenta un’istruzione di comunicazione. Ad esempio la lettura di un dato. I
Comunicazione
Rappresenta un’istruzione di comunicazione. Ad esempio la scrittura di un dato. O
Comunicazione
Rappresenta un’azione. Ad esempio il calcolo di una determinata funzione che restituisce un risultato, come la somma di N numeri. Azione
V
F
Controllo
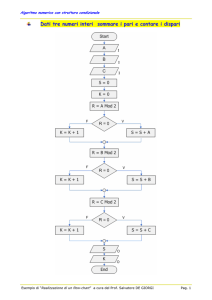
Rappresenta un’istruzione di controllo. Ad esempio il controllo se un valore risulta pari o dispari. Di seguito vengono mostrati alcuni esempio di algoritmi rappresentati mediante diagramma di flusso. Consideriamo l’algoritmo che determini se, dati due numeri, la somma di questi due (senza che venga effettuata) sia pari o dispari. Per determinare se la somma di due numeri sarà pari o dispari bisogna individuare una regola generale: in questo caso la regola è la seguente: • Se i due numeri sono entrambi pari o entrambi dispari, allora la somma sarà pari. • Se i due numeri sono uno pari e l’altro dispari, allora la somma sarà dispari. Infatti, consideriamo i seguenti casi: Numero A Numero B Somma Pari o Dispari ? 1 7 8 Pari 1 4 5 Dispari 3 4 4 3 6 7 10 Dispari Pari Di seguito viene mostrato il diagramma di flusso: Infatti, per determinare se un numero è pari o dispari basta dividere il numero per 2 ed analizzare il suo resto: • Se il resto è uguale a 0, allora il numero è pari. • Se il resto è uguale ad 1, allora il numero è dispari. 4 Quindi, dati i numeri A e B, calcoliamo i resti delle divisioni di A e B per 2 e li “memorizziamo”, rispettivamente, in R_A ed R_B. A questo punto possiamo lavorare direttamente su R_A ed R_B. In Excel, supponendo che A, B, R_A ed R_B siano delle celle, come A1, A2, A3 e A4, possiamo calcolare il resto come segue: A3 = RESTO(A1;2) A4 = RESTO(A2;2) In questo modo, abbiamo svolto già la prima parte dell’algoritmo, ossia la seguente: A questo punto, possiamo passare al resto, ossia a determinare se la somma sarà pari o dispari: A5 = SE(E(A3=0;A4=0);”Pari”; SE(E(A3=1;A4=1);”Pari”; “Dispari”)) In questo modo, abbiamo terminato l’algoritmo, svolgendo la restante parte, ossia la seguente: 5