DEFINIZIONE ASSIOMATICA DEL PRIMO E DEL SECONDO PRINCIPIO
DELLA TERMODINAMICA
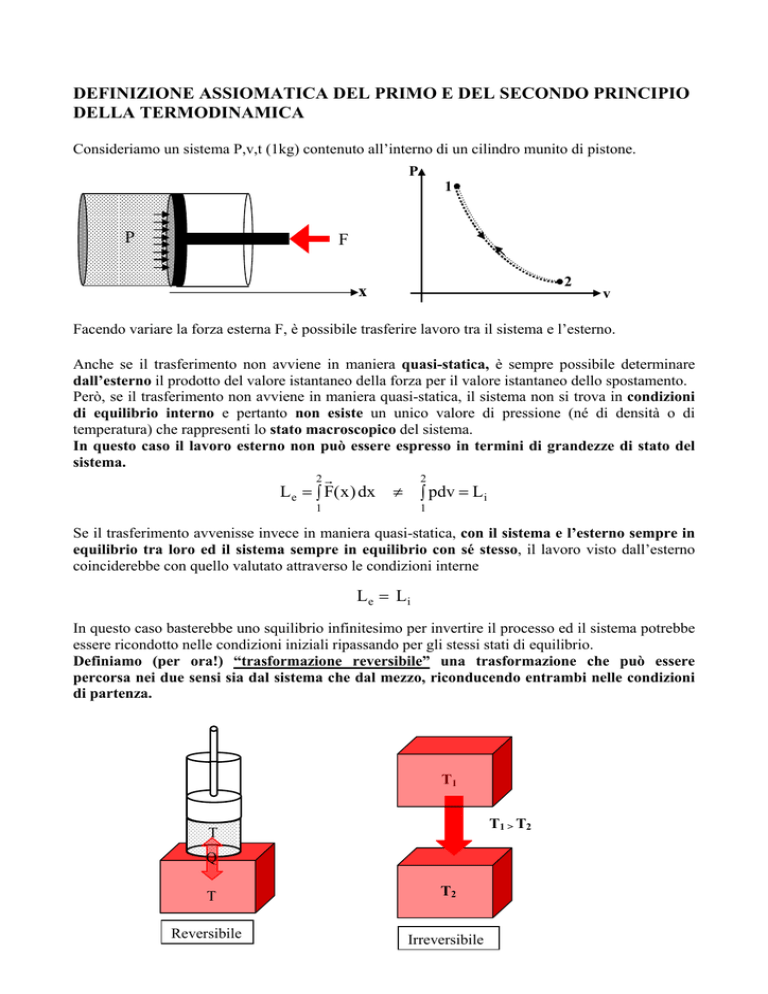
Consideriamo un sistema P,v,t (1kg) contenuto all’interno di un cilindro munito di pistone.
P
1
P
F
2
x
v
Facendo variare la forza esterna F, è possibile trasferire lavoro tra il sistema e l’esterno.
Anche se il trasferimento non avviene in maniera quasi-statica, è sempre possibile determinare
dall’esterno il prodotto del valore istantaneo della forza per il valore istantaneo dello spostamento.
Però, se il trasferimento non avviene in maniera quasi-statica, il sistema non si trova in condizioni
di equilibrio interno e pertanto non esiste un unico valore di pressione (né di densità o di
temperatura) che rappresenti lo stato macroscopico del sistema.
In questo caso il lavoro esterno non può essere espresso in termini di grandezze di stato del
sistema.
2r
L e = ∫ F( x ) dx
2
≠
∫ pdv = Li
1
1
Se il trasferimento avvenisse invece in maniera quasi-statica, con il sistema e l’esterno sempre in
equilibrio tra loro ed il sistema sempre in equilibrio con sé stesso, il lavoro visto dall’esterno
coinciderebbe con quello valutato attraverso le condizioni interne
L e = Li
In questo caso basterebbe uno squilibrio infinitesimo per invertire il processo ed il sistema potrebbe
essere ricondotto nelle condizioni iniziali ripassando per gli stessi stati di equilibrio.
Definiamo (per ora!) “trasformazione reversibile” una trasformazione che può essere
percorsa nei due sensi sia dal sistema che dal mezzo, riconducendo entrambi nelle condizioni
di partenza.
T1
T1 > T2
T
Q
T
Reversibile
T2
Irreversibile
Il I° Principio della termodinamica può essere enunciato in diverse maniere, ma tutti questi
enunciati si riducono in un modo o nell’altro ad affermare il principio di conservazione
dell’Energia.
Il II° Principio invece può essere enunciato in moltissimi modi tra loro equivalenti, cioè
dimostrabili l’uno a partire dall’altro, ciascuno dei quali mette in luce una delle diverse basilari
implicazioni di questa legge fondamentale della natura.
Assiomi del I° Principio della Termodinamica
1) Esiste una forma di Energia, nota come Energia Interna, che è una proprietà intrinseca di ogni
sistema ed è legata funzionalmente alle grandezze misurabili che caratterizzano il sistema.
Per un sistema chiuso, non in movimento, le variazioni di questa proprietà sono date dalla relazione:
δQ = dU + δL
2) L’Energia Interna totale di ogni sistema e di ciò che lo circonda, considerati assieme, rimane
costante
Assiomi del II° Principio della Termodinamica
1) Esiste una proprietà nota come Entropia, che è una proprietà intrinseca di ogni sistema ed è
legata funzionalmente alle grandezze misurabili che caratterizzano il sistema.
Le variazioni di questa proprietà possono essere determinate per mezzo di un processo ausiliario
reversibile mediante la relazione:
⎛ δQ ⎞
dS = ⎜
⎟
⎝ T ⎠ rev
T è la Temperatura Termodinamica Assoluta , sempre positiva, che verrà meglio definita nel
seguito
2) La variazione di Entropia di ogni sistema e di ciò che lo circonda, considerati assieme, è positiva
e tende a zero per tutti i processi che approssimano le condizioni di reversibilità.
∆Stot ≥ 0
Quest’ultima relazione costituisce l’espressione del II° Principio della Termodinamica che verrà
utilizzata in questo corso.
Accettando il precedente enunciato del II° Principio, tutte le altre implicazioni, che potevano essere
usate come enunciati alternativi, devono essere dimostrate a partire dal fatto (non dimostrato, ma
accettato appunto come principio) che l’Entropia di un sistema isolato non può diminuire.
TH
Q?
Due termostati rispettivamente alla temperatura TH e TC si scambiano la
quantità di calore Q, pertanto |QH| = - |Qc|
Ipotesi: TH > TC
Ricordando la convenzione fatta in precedenza (il Calore è positivo quando
entra nel sistema), ci chiediamo : quale serbatoio riceve il calore Q?
TC
Si osservi che, ciascuno dei due termostati è (per definizione di termostato) in equilibrio termico
con sé stesso e pertanto la variazione di entropia di ciascuno dei serbatoi può essere calcolata
tramite la relazione (con il segno del calore riferito al serbatoio) :
∆S = (Q/T)rev
Valutiamo ora la variazione di Entropia totale dell’Universo (come sistema isolato); dobbiamo
calcolare tutte le variazioni di Entropia connesse con questo scambio, e cioè quelle dei due
termostati.
Per il termostato H)
∆SH =
QH
Q
= − C
TH
TH
Per il termostato C)
∆SC =
QC
TC
∆STot = ∆SH + ∆SC = −
QC
Q
+ C
TH
TC
=
⎛ T − TC ⎞
⎟⎟ ≠ 0 essendo TH ≠ TC
QC ⎜⎜ H
T
T
⎝ H C ⎠
Poiché lo scambio di calore avviene sotto una differenza finita di Temperatura, la variazione totale
di Entropia è certamente non nulla, quindi deve essere positiva. Si ha allora :
∆STot > 0
ed essendo TH e TC entrambi positivi, con TH > TC si conclude:
|QC| (TH - TC) > 0
e quindi QC > 0 ossia il calore è ricevuto dal termostato a temperatura più bassa.
Questo risultato dimostra una delle forme più diffuse con le quali viene introdotto il secondo
principio della termodinamica:
Enunciato di Clausius del II° Principio:
Il calore fluisce spontaneamente da una sorgente a temperatura più elevata verso una a
temperatura più bassa.
Nicolas Léonard Sadi Carnot nasce a Parigi nel 1796
da Lazare Carnot che era membro del Direttorio e
sarebbe divenuto ministro della guerra con Napoleone
nel 1799.
Nel 1812, all'età (minima) di 16 anni viene ammesso
all' École Polytechnique dove ebbe come maestri
Poisson, Ampère e Arago.
Nel 1814, dopo la sconfitta di Lipsia, ancora studente,
prende parte alla difesa di Vincennes, combattendo
senza fortuna contro le truppe della sesta Coalizione
che invadono la Francia, giungendo alle porte di
Parigi.
Questa esperienza segna profondamente la vita di
Nicolas che, diplomatosi, si iscrive alla Scuola del
Genio Militare di Metz.
Nel 1815, insieme al padre, appoggia Napoleone
tornato dall'isola d'Elba e lo segue nell'avventura dei
cento giorni fino alla disfatta di Waterloo.
Durante la restaurazione Nicolas continua a prestare
servizio nel Genio Militare ed ha occasione di studiare
alcuni modelli di macchine a vapore.
Nicolas Léonard Sadi Carnot
1796 - 1832
Si convince che queste macchine hanno un'importanza strategica nello sviluppo economico delle
nazioni ed il suo obiettivo diventa quello di progettare la macchina più efficiente possibile.
Il vapore era infatti già utilizzato in molte applicazioni: estrarre l'acqua dalle miniere, scavare
canali, lavorare il ferro, macinare il grano e muovere i telai, ma in maniera assai poco efficiente.
Con la fine delle guerre napoleoniche e l'importazione in Francia dei modelli inglesi più recenti
Nicolas è certo di avere trovato nella supremazia tecnologica dell'Inghilterra la spiegazione della
sua supremazia militare. Lo irrita in particolare il fatto che i progressi inglesi siano dovuti al genio
di pochi tecnici privi di una formale educazione scientifica e si propone di utilizzare la grande
massa di dati sperimentali disponibili sul funzionamento dei diversi modelli di macchine a vapore
per gettare le basi una teoria scientificamente valida sulla trasformazione del calore in lavoro
meccanico.
Nel 1824 Nicolas pubblica il suo lavoro più importante (ed anche l'unico ad essere pubblicato)
"Réflexions sur la puissance motrice du feu et sur les machines propres à développer cette
puissance" che include la prima descrizione del Ciclo di Carnot.
Fervente repubblicano, appoggia la rivoluzione del Luglio 1830 ma, la vittoria del partito
monarchico che sostituisce il Borbone Carlo X con Luigi Filippo d’Orléans, lo spinge ritirarsi dalla
politica ed a tornare ad occuparsi di problemi scientifici.
Muore a Parigi a soli 36 anni, vittima di un'epidemia di colera.
LA MACCHINA DI CARNOT
Supponiamo di avere un cilindro munito di pistone contente 1 kg di una sostanza qualsiasi e due
termostati aventi temperature T1 e T2 misurate in una scala qualsiasi (T1 > T2); per comodità di
rappresentazione grafica sul piano di Clapeyron supporremo ancora - almeno per il momento - che
si tratti di un sistema (P,v,T) o, meglio ancora, di un gas perfetto.
Fase 1) Posto il sistema in contatto con il termostato a temperatura T1 si effettua una espansione
reversibile isoterma A→B con assorbimento del calore Q1 e produzione di una equivalente quantità
di lavoro meccanico L1 (fornito dal sistema = positivo)
L1
p
A
Q1
+
B
Q1
T1
L1
T2
Termostato T1
v
Fase 2) Il sistema viene isolato termicamente e si ottiene una ulteriore quantità di lavoro meccanico
L2 mediante l’espansione reversibile adiabatica B→C. La produzione del lavoro meccanico L2
(fornito dal sistema = positivo) è ottenuta a spese dell’Energia Interna del sistema che si raffredda
L’espansione prosegue finché il sistema non si sia portato alla temperatura T2 del secondo
termostato.
p
L2
B
T1
C
L2 +
T2
v
Fase 3) Posto il sistema in contatto con il termostato a temperatura T2 si effettua una compressione
reversibile isoterma C→D con la cessione del calore Q2 al termostato ed assorbimento di una
equivalente quantità di lavoro meccanico L3 (entrante nel sistema = negativo)
La compressione viene arrestata nel punto D che è individuato dall’adiabatica passante per A
L3
p
A
D
Q2
L3
-
T1
C
T2
Q2
v
Termostato T2
Fase 4) Il sistema viene isolato termicamente e si spende una ulteriore quantità di lavoro meccanico
L4 nella compressione reversibile adiabatica D→A. Il lavoro meccanico L4 (fornito al sistema =
negativo) è convertito tutto in Energia Interna del sistema che si riscalda ritornando alla temperatura
T1 del primo termostato
p
L4
A
D
-
T1
L4
T2
v
Ciclo bitermico reversibile realizzato mediante un ciclo Isotermo-Adiabatico
Carnot).
(Ciclo di
p
Applicando il Primo Principio alla Macchina
di Carnot si ha:
∑i Qei = ∆U + ∑i Lei
A
Essendo:
∑i Qei = |Q1| + |Q2| = Q1 - Q2
Q1
∑i Lei = Ltot (Area del Ciclo) = Q1 - Q2
B
+
D
T1
Q2
C
T2
v
η=
Definendo Rendimento η del ciclo il
rapporto tra il lavoro ottenuto in totale ed il
calore speso, ossia il calore prelevato dalla
sorgente ad alta temperatura, si ha:
L tot Q1 − Q 2
Q
=
= 1− 2
Q1
Q1
Q1
Vogliamo sottolineare il fatto che i calori Q1 e Q2 sono i calori scambiati dal sistema con
l’esterno, particolare che, pur sembrando qui ovvio perché la Macchina di Carnot (essendo
bitermica) scambia calore solo con due sorgenti esterne in maniera reversibile, assumerà un
significato molto importante nel seguito.
In particolare, avendo supposto che il sistema lavorante sia un gas perfetto, possiamo scrivere:
⎛v
Q1 = L1 = R ' T1 ln ⎜⎜ B
⎝ vA
⎞
⎟⎟
⎠
,
⎛v ⎞
Q 2 = L 3 = R ' T2 ln ⎜⎜ C ⎟⎟
⎝ vD ⎠
e poiché v B e v C , v D e v A s tan no sulle stesse adiabatiche :
v kB−1 T1 = v Ck −1 T2
vB vC
=
vA vD
da cui :
;
v kA−1 T1 = v kD−1 T2
Q 2 T2
=
Q1 T1
si ha :
e per tan to :
ηC = 1 −
T2
T1
Per il momento questa relazione può essere considerata valida solo per una Macchina di Carnot
che utilizza come fluido lavorante un gas perfetto e le temperature che in essa figurano sono legate
alla scala del gas perfetto. Dimostreremo in seguito che questa relazione ha una validità assai più
ampia.
Teorema dell’inesistenza della macchina monoterma
Sia M una macchina monoterma, capace cioè di trasformare in
lavoro tutto il calore estratto dalla sorgente TH. Per ipotesi la
TH
macchina operi in maniera ciclica e non sia soggetta al vincolo della
reversibilità. Pertanto la macchina M, assorbendo in ogni ciclo il
|QM|
calore QM, produce il lavoro LM = QM.
|QH|
Scelta quindi una Macchina di Carnot che lavori tra le temperature
|LM|
TH e TC, essendo TC una temperatura qualsiasi ma inferiore a TH,
M
poiché la Macchina di Carnot è reversibile, è possibile utilizzare il
lavoro LM prodotto dalla macchina monoterma per estrarre il calore
|QC| dalla sorgente TC scaricando il calore |QH| = |QC| + |LM| nel
|QC|
serbatoio a tempertura |TH|.
Si ha pertanto: |QH| - |QC| = |LM| = |QM|
Tc
Si noti l’uso del simbolo di valore assoluto, necessario per
confrontare tra loro i calori ed il lavoro, che assumono segno
diverso a seconda della macchina e/o del serbatoio cui sono riferiti.
Si supponga quindi di fare compiere un ciclo alle due macchine accoppiate e di valutare il bilancio
di energia per ciascuno dei due serbatoi.
C
TH
Serbatoio TH : + |QH| - |QM| ; +|QH|-( |QH|-|QC| ) = + |QC|
Serbatoio TC : -|QC|
Le due macchine sono ritornate nelle condizioni iniziali, pertanto un
osservatore, non potendo dedurre dallo stato delle macchine se esse
abbiano lavorato o no, è costretto ad ammettere che la quantità di
calore |QC| è andata “senza altri effetti” o “spontaneamente” dal
serbatoio a temperatura più bassa verso quello a temperatura più
alta. Poiché ciò contrasta con uno degli enunciati del Secondo
Tc
Principio (in particolare con il cosiddetto postulato di Clausius), non
è possibile ammettere l’esistenza di una macchina monoterma ossia
di una macchina capace di produrre lavoro (ciclico!) utilizzando il calore estratto da una sola
sorgente (moto perpetuo di seconda specie).
?
|QC|
Enunciato di Kelvin-Planck : Non esiste alcun processo ciclico il cui solo risultato sia
l’estrazione di calore da un serbatoio e la produzione di una equivalente quantità di lavoro
Superiorità della Macchina di Carnot rispetto a tutte le
macchine bitermiche.
TH
|Q’1|
L
|Q1|
M’ C
|Q2|
|Q’2|
Tc
L
Sia M’ una macchina bitermica ma non soggetta al vincolo della
reversibilità e che esibisca un rendimento superiore a quello di
una macchina C di Carnot quando si trovi a lavorare tra le stesse
temperature.
Perché ciò sia possibile occorre e basta che la macchina M’
produca lo stesso lavoro L prodotto dalla macchina di Carnot,
utilizzando “meglio” la sorgente TH, ossia estraendo da TH un
calore |Q’1| < |Q1| producendo lo stesso lavoro L e scaricando di
conseguenza nel serbatoio TC un calore |Q’2| < |Q2|.
Si avrebbe infatti:
ηC =
Q1 − Q 2
L
=
Q1
Q1
ηM' =
Q'1 − Q'2
L
=
Q'1
Q'1
ηM' > ηC
|Q1|
Poiché la macchina M’ non è reversibile, mentre quella di
Carnot lo è, proviamo a far funzionare quest’ultima da pompa di
calore utilizzando come sorgente di lavoro la macchina M’.
Si supponga quindi di fare compiere un ciclo alle due macchine
accoppiate e di valutare il bilancio di energia per ciascuno dei
due serbatoi.
Serbatoio TH : + |Q1| - |Q’1| ; Serbatoio TC : + |Q’2| - |Q2|
Ed essendo:
|Q2|
|Q’1| - |Q’2| = |L| = |Q1| - |Q2| si ha: |Q1| - |Q’1| = |Q2| - |Q’2|
TH
|Q’1|
L
M’
C
|Q’2|
Si noti che |Q1| > |Q’1| e |Q2| > |Q’2|
Tc
TH
?
|Q1| - |Q’1|
=
Tc
|Q2| - |Q’2|
Le due macchine sono ritornate nelle condizioni iniziali, pertanto un
osservatore, non potendo dedurre dallo stato delle macchine se esse
abbiano lavorato o no, è costretto ad ammettere che la stessa quantità
di calore |Q1| - |Q’1| = |Q2| - |Q’2| è andata “senza altri effetti” o
“spontaneamente” dal serbatoio a temperatura più bassa verso
quello a temperatura più alta.
Poiché ciò contrasta con uno degli enunciati del Secondo Principio
(in particolare con il cosiddetto postulato di Clausius), non è
possibile ammettere l’esistenza di una macchina bitermica, ancorché
non reversibile che, lavorando tra le stesse temperature, abbia un
rendimento superiore a quello della macchina di Carnot.
Dovrà essere dunque :
ηC > ηM’
Se poi la macchina M’, oltre che bitermica fosse anche reversibile (MBR), si potrebbe ripetere il
ragionamento fatto sopra scambiando tra loro la macchina di Carnot e la macchina MBR giungendo
alla conclusione che deve essere contemporaneamente: ηC ≤ ≥ ηMBR.
Quindi non può che essere:
ηC = ηMBR
Tutte le macchine bitermiche reversibili che lavorano tra le stesse temperature devono avere
lo stesso rendimento (Teorema di Carnot).
Lo stesso enunciato si applica ovviamente ad una stessa macchina Bitermica Reversibile in cui si
usino sostanze lavoranti diverse:
Tutte le macchine bitermiche reversibili che lavorano tra le stesse temperature devono avere
lo stesso rendimento, indipendentemente dalla sostanza lavorante.
Le dimostrazioni dei teoremi che abbiamo enunciato sopra sono state condotte con un metodo
che è peculiare della Termodinamica Classica (o Macroscopica) e che si basa sull’impossibilità
del verificarsi di una data ipotesi o di un dato evento pena la negazione di un principio (e/o delle
sue conseguenze) che è stato assunto come vero, ma non dimostrato.
Il Principio che è stato assunto come vero in questo Corso afferma che l’Entropia di un sistema
isolato non può diminuire. In base a questo principio abbiamo potuto dimostrare le affermazioni di
Clausius e di Kelvin-Planck, ciascuna delle quali potrebbe essere a sua volta posta come enunciato
del II° Principio.
Pertanto, se si accettasse (p.es.) l’enunciato di Kelvin-Planck, si potrebbe dimostrare il postulato di
Clausius ed il comportamento dell’Entropia in un sistema isolato.
In realtà, qualunque affermazione che coinvolga in qualche modo il II° Principio può essere usata
come suo enunciato e tutte le altre affermazioni essere dimostrate in base ad essa.
In ciò consiste la “circolarità” degli enunciati del II° Principio, in base alla quale ogni affermazione
può dimostrare le altre purché essa stessa sia accettata senza dimostrazione.
Esistono pertanto svariate decine di formulazioni alternative del II° Principio, una delle più note
delle quali è certamente quella formulata da C. Carathéodory : Nell’intorno di uno stato qualsiasi di
un sistema (avente un numero n di coordinate termodinamiche) esistono stati che non possono
essere raggiunti per mezzo di una trasformazione adiabatica.
A titolo di esempio dimostreremo che, accettato per vero l’enunciato di Kelvin-Planck, è possibile
dimostrare il “postulato” di Clausius.
TH
|QH|
|QC|
|LC|
C
M
|QC|
|QC|
Tc
Supponiamo pertanto che il postulato di Clausius non sia vero e
che sia possibile costruire una macchina che, operando per cicli,
sia capace di spostare una certa quantità di calore |QC| dal
termostato TC a quello TH (con TC < TH).
Dato che, dopo ogni ciclo, la macchina M è tornata allo stato
inziale, lo spostamento avviene “spontaneamente” ossia senza
altri effetti.
Scelta (ed è sempre possibile farlo) una macchina di Carnot
capace di scaricare nel serbatoio TC una quantità di calore pari a
|QC| sarà possibile creare un “cortocircuito” tra le due macchine
che rende inutile la presenza del serbatoio TC.
E’ evidente che, in questa nuova configurazione, la macchina di
Carnot è divenuta una macchina monoterma.
TH
|QH|
|QC|
C
M
|QC|
|LC|
Possiamo concludere pertanto che negare il postulato di Clausius
conduce ad affermare l’esistenza della macchina monoterma, e
quindi a negare l’enunciato di Kelvin-Planck.
M












