cos - DIR

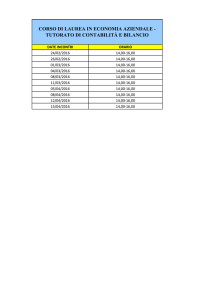
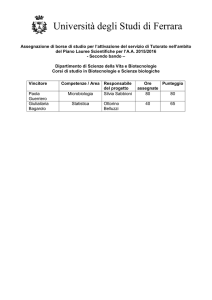
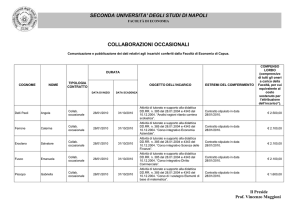
Funzioni goniometriche
tutorato
Misura degli angoli
Gradi e radianti
Radianti
Un radiante è la misura di un angolo con vertice
il centro di una circonferenza (angolo al centro)
che sottende un arco lungo quanto il raggio
della circonferenza.
L’ampiezza a di un angolo, espressa in radianti, è data dal
rapporto tra la lunghezza dell’arco AB e il valore del raggio della
circonferenza
tutorato
g : 360   : 2

Circonferenza
misura 2πr
Angolo giro
misura 360
°
Angolo giro
misura 2π
tutorato
Funzioni goniometriche o circolari
α
PH
 sen 
OP
OH
 cos 
OP
Dipendono solo
dall’ampiezza
dell’angolo
Circonferenza goniometrica
OP=1
PH  sen 
α
OH  cos 
Seno
α
PH
 sen
OP
1  sen  1
Coseno
α
OH
 cos 
OP
1  cos   1
Il teorema di Pitagora, applicato al triangolo
OHP, ove OP=1
ci consente di ricavare la relazione
cos   sen   1
2
2
tutorato
Periodo
I valori delle funzioni seno e coseno si ripetono
sistematicamente ogni intervallo di ampiezza 2π.
Nessun intervallo più piccolo gode di tale
proprietà. In altri termini 2π è il periodo delle
funzioni seno e coseno.
sinx  sin(x  2k )
cosx  cos(x  2k )
tutorato
Funzioni seno e coseno
tutorato
y  senx
tutorato
sinx  sin(x  2k )
tutorato
tutorato
y  cos x
Problema
Date le funzioni definite sui reali f(x)=cos(x) e
g(x)=1/2. Per quali valori di x , f(x)>g(x)?
Problema
Date le funzioni definite sui reali f(x)=cos(4x) e
g(x)=1. Per quali valori di x, f(x)=g(x)?
Circonferenza goniometrica
OP=1
• Mettere grafico con tang
Se cos   0
sen
 tg
cos 
tutorato
Il periodo della tangente è π.
La tangente non è definita per
tutorato
x

2
 k
cos 0 = 1
cos
cos
cos


4

6
2
=0
=
1
2
=
3
2
cos  = –1
sin 0 = 0

sin
sin
2

sin
4

6
=1
cos
1
2
cos
=
=
1
2
3
=0
2

3
=
1
2
tan 0 = 0
tutorato
sin  = 0
sin
sin
3
= 1
2

=
3
tan

4
3
2
=1
Cotangente
1
ctg 
tg
tutorato
Secante e cosecante
1
sec  
cos 
1
cosec  
sen
tutorato
Alcune formule trigonometriche
sin(   )  sin cos   cos  sin 
cos(   )  cos  cos   sin sin 
sin(   )  sin cos   cos  sin 
cos(   )  cos  cos   sin sin 
tutorato
Alcune formule trigonometriche

1  cos 
sin( )  
2
2

1  cos 
cos( )  
2
2
tutorato
Esercizi
sin 120  
tan 15  
tutorato
Funzioni inverse
Arcoseno: f(x)= arcsinx
Arococoseno: g(x)= arccosx
Arcotangente: h(x)= arctgx
tutorato
Esercizi
arcsin  0  
1
arcsin( ) 
2
3
)
2
2
arccos( ) 
2
arcsin(
arccos  1  
tutorato
Risolvere le seguenti equazioni
3 sin x  3cos x  0
sin x  cos x  1
tutorato