CALCOLO DEGLI ELEMENTI UTILI PER TRACCIAMENTO
RETTA D’ALTEZZA CON LA POLARE
La stella Polare descrive attorno al Polo celeste Nord un piccolo
parallelo di declinazione (dista da questo meno di 1°), e pertanto
ricordando la definizione di latitudine in senso astronomico, ossia
altezza del polo celeste elevato sul piano dell’orizzonte vero, se ne
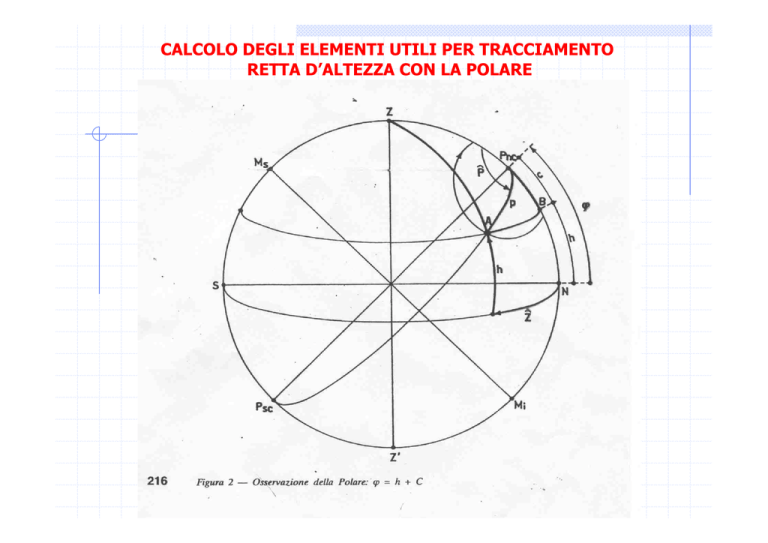
deduce che ϕ ≅ h
e come si vede in figura la latitudine
dell’osservatore può essere ricavata semplicemente con la relazione:
ϕ = h + c.
Ricordando inoltre che la stella Polare indica al navigante la
direzione del Nord, l’azimut è prossimo a 0°.
1° METODO
Scrivendo la relazione ϕ = h + c per l’osservatore che si trova nella posizione
stimata Ps si avrà:
ϕs = hs + (c1 + c2 + c3) – 1°
Per cui l’altezza stimata vale hs = ϕs + 1° – (c1 + c2 + c3)
dove le tre correzioni c1, c2 e c3 si trovano tabulate nelle pagine colorate delle
Effemeridi Nautiche (latitudine con osservazione di Polare):
ts
c1
ho
ts
c2
mese
ts
c3
L’azimut (o meglio l’angolo azimutale stimato Zs) si trae sempre dalle stesse
tavole in funzione di ts ed ho. Pertanto:
ZsE/W = α° ⇒ as = ZsE oppure as = 360° − ZsW
∆h = hv − hs
2° METODO
Ma ancora più facilmente può essere valutata la latitudine vera ϕv con
l’osservazione della Polare:
ϕv = hv + (c1 + c2 + c3) – 1°
Per cui la differenza di latitudine vale ∆ϕ = ϕv − ϕs e l’azimut in questo caso
è sempre Nord (a = 0°): retta d’altezza sistemata esattamente per parallelo.
N.B.1 Le tre correzioni c1, c2 e c3, si trovano come illustrato nel 1° metodo.
N.B.2 L’altezza istrumentale hi deve essere corretta, nel modo classico, con
le correzioni c1 e c2 (con le tabelle delle Effemeridi Nautiche per le stelle).
3° METODO
Nelle Effemeridi Nautiche troviamo elencate tra le principali 66 stelle usate in
nautica anche la Polare (Polaris). Quindi basta considerare tale astro come
una qualsiasi stella.












