Ellisse e Iperbole

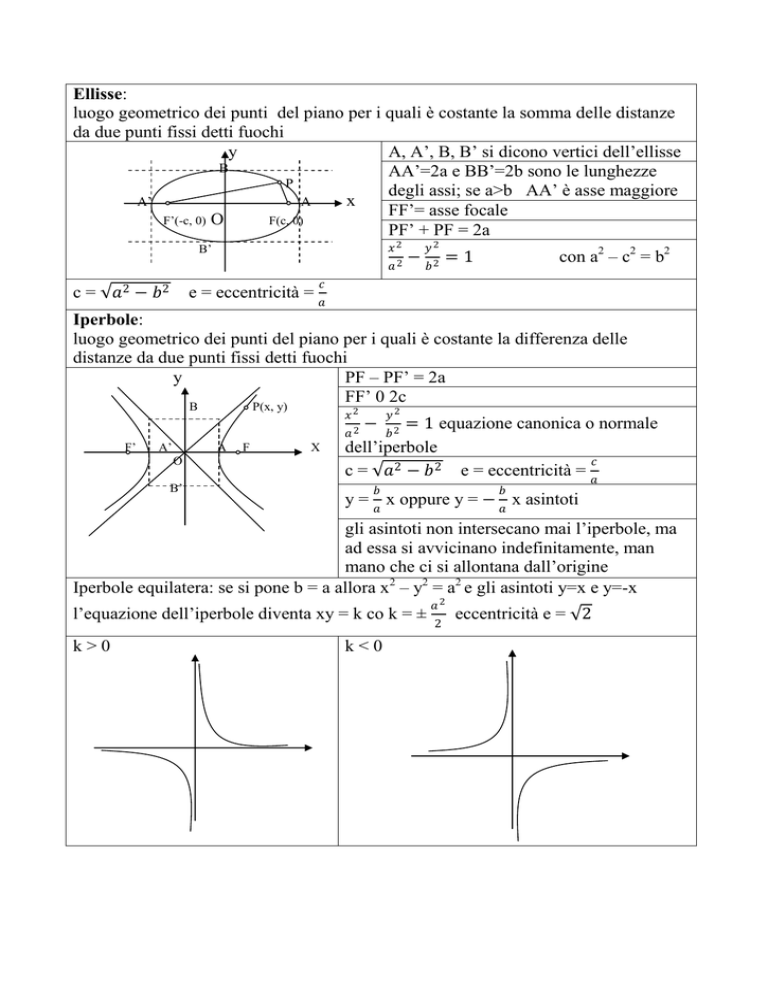
Ellisse:
luogo geometrico dei punti del piano per i quali è costante la somma delle distanze
da due punti fissi detti fuochi
y
A, A’, B, B’ si dicono vertici dell’ellisse
B
AA’=2a e BB’=2b sono le lunghezze
P
degli assi; se a>b AA’ è asse maggiore
A’
A
x
FF’= asse focale
F’(-c, 0) O
F(c, 0)
PF’ + PF = 2a
B’
c = 𝑎2 − 𝑏 2
e = eccentricità =
𝑥2
𝑦2
𝑎
𝑏2
−
2
=1
con a2 – c2 = b2
𝑐
𝑎
Iperbole:
luogo geometrico dei punti del piano per i quali è costante la differenza delle
distanze da due punti fissi detti fuochi
y
PF – PF’ = 2a
FF’ 0 2c
B
F’
A’
P(x, y)
A
O
B’
F
𝑥2
X
𝑦2
− 2 = 1 equazione canonica o normale
𝑎2
𝑏
dell’iperbole
𝑐
c = 𝑎2 − 𝑏 2 e = eccentricità =
𝑏
𝑏
𝑎
𝑎
𝑎
y = x oppure y = − x asintoti
gli asintoti non intersecano mai l’iperbole, ma
ad essa si avvicinano indefinitamente, man
mano che ci si allontana dall’origine
Iperbole equilatera: se si pone b = a allora x2 – y2 = a2 e gli asintoti y=x e y=-x
l’equazione dell’iperbole diventa xy = k co k = ±
k>0
k<0
𝑎2
2
eccentricità e = 2