caricato da
common.user2496
Presentazione su Sistemi, Componenti e Circuiti Elettrici

INDICE
Terza
quarta
QUINTA
TERZA
•
•
•
•
•
•
•
•
•
•
•
•
modelli e sistemi
proprietà dei componenti
sistemi lineari
componenti elettrici
circuiti rc e rl
diodi e bjt
arresto e marcia di un motore
circuiti di interfaccia
laboratorio: tutto sui rele
pilotare un relè con arduino
555
laboratorio 555
• il pc: input e output, il c e la programmazione
• gli algoritmi
• la programmazione
MODELLI
DEFINIZIONE: un modello è una rappresentazione approssimata del sistema reale.
Un modello serve per trasmettere informazioni, per definire e risolvere problemi
NB: il grado di approssimazione dipende dal fine per cui il modello è costruito.
CLASSIFICAZIONE:
•Modello FISICO: consiste in una riproduzione in scala del sistema
•Modello SIMBOLICO: consiste nella rappresentazione del sistema mediante simboli
•GRAFICO: Es: schema a blocchi interconnessi
•MATEMATICO: stabilisce una relazione quantitativa tra le variabili del sistema
•Formula (Espressione analitica)
•Tabella
•Caratteristica: legame grafico tra due variabili
Modelli
Nel dominio del tempo il modello matematico di un sistema continuo è spesso fornito mediante
la rappresentazione ingresso/uscita, cioè dalle sue equazioni differenziali.
Per un sistema del 1° ordine:
E’ comodo studiare la risposta nel tempo ricorrendo anche alla
rappresentazione ingresso/uscita
nel dominio di Laplace, cioè
alla schematizzazione del sistema con blocchi e relative funzioni
di trasferimento:
SISTEMI
DEFINIZIONI
SISTEMA: insieme di elementi, parti, che interagiscono coordinati per svolgere una deteminata funzione.
COMPONENTI: parti di cui il sistema è costituito.
PARAMETRI: grandezze che esprimono delle proprietà specifiche di un sistema o di un componente.
VARIABILI: grandezze fisiche misurabili presenti nel sistema,
•di INGRESSO: indicano la quantità di energia, materia, informazione fornita al sistema
•di STATO: indicano la quantità di energia, materia, informazione accumulata nel sistema
•di USCITA: indicano la quantità di energia, materia, informazione ceduta dal sistema
STATO di un sistema: è definito dalla quantità e dalla distribuzione di energia, materia, informazione
presenti nel sistema (lo si deduce dal valore delle variabili di stato).
NB: non tutti i sistemi sono caratterizzato di uno stato.
SISTEMI LINEARI
Si hanno più modi per definire la linearità di un sistema:
- uscita proporzionale all’ingresso:
- rapporto tra l’uscita e l’ingresso (esauriti i transitori) è costante:
- caratteristica ingresso – uscita è una retta passante per l’origine:
Si hanno diversi tipi di non linearità nella relazione ingresso – uscita:
- Il valore dell’uscita dipende non solo da quello dell’ingresso, ma anche dalla tendenza di
quest’ultimo ad aumentare o diminuire.
- Sono presenti zone in cui nonostante rilevanti variazioni dell’ingresso, l’uscita resta
costante.
’- presente una zona di insensibilità dell’uscita alle variazioni dell’ingresso, superata tale
zona l’uscita segue l’ingresso, ma a questo punto con un certo ritardo.
L’effetto fondamentale della presenza di non linearità nel sistema consiste nella distorsione
armonica, cioè nella comparsa di armoniche non presenti nel segnale d’ingresso.
VARIABILI
Le variabili si possono classificare secondo criteri diversi.
Le variabili che descrivono le cause dei fenomeni sono dette di tipo POTENZIALE
Le variabili che descrivono l’effetto finale sono dette di tipo QUANTITA’.
Le variabili che descrivono il passaggio dalla causa all’effetto sono dette di tipo FLUSSO.
Differenza di
potenziale
Flusso
Quantità
Tensione
Corrente
Carica
Forza
Velocità
Spostamento
Termico
Differenza di
temperatura
Flusso termico
Calore
Idraulico
Differenza di
pressione
portata
Volume
SISTEMA
Elettrico
Meccanico
PROPRIETA’ ELEMENTARI DEI COMPONENTI
SISTEMI ELETTRICI
Il comportamento di un componente, o sistema, è normalmente descritto da più parametri.
I parametri elementari più importanti sono:
RESISTENZA: cioè l’attitudine del componente, sottoposto a una differenza di potenziale, di opporsi
alla formazione della variabile flusso.
In termini matematici:
CAPACITA’: cioè l’attitudine di un componente ad accumulare la quantità.
In termini matematici:
INDUTTANZA (o INERZIA): cioè l’attitudine di un componente di opporsi alle variazioni del
flusso nel tempo.
In termini matematici:
SISTEMI ELETTRICI
SISTEMI MECCANICI
SISTEMI LINEARI
Si hanno più modi per definire la linearità di un sistema:
• uscita proporzionale all’ingresso: y k x
• il rapporto tra l’uscita e l’ingresso (esauriti i transitori) è costante:
y
k/x
• la caratteristica ingresso – uscita è una retta passante per l’origine:
Una retta passante per l’origine ha equazione:
y kx
Una retta non passante per l’origine ha equazione :y k x q
il rapporto: y = k/x
non è costante.
y
Costante risulta invece il rapporto: x k
In questo caso il sistema è LINEARE ALLE VARIAZIONI
Si hanno diversi tipi di non linearità nella relazione ingresso – uscita:
Il valore dell’uscita dipende non solo da quello
dell’ingresso, ma anche dalla tendenza di quest’ultimo ad
aumentare o diminuire.
Sono presenti zone in cui nonostante rilevanti variazioni
dell’ingresso, l’uscita resta costante.
E’ presente una zona di insensibilità dell’uscita
alle
variazioni dell’ingresso, superata tale zona l’uscita segue
l’ingresso, ma a questo punto con un certo ritardo.
L’effetto fondamentale della presenza di non linearità nel
sistema consiste nella distorsione armonica,
cioè nella comparsa di armoniche non presenti nel segnale
ingresso.
VARIABILI
Le variabili si possono classificare secondo criteri
diversi. Un modo è il seguente.
I fenomeni hanno delle cause.
Le variabili che descrivono queste cause sono dette di
tipo POTENZIALE e la causa è data dalla differenza di
potenziale.
Le variabili che descrivono l’effetto finale sono dette di
tipo QUANTITA’.
Le variabili che descrivono il passaggio dalla causa
all’effetto sono dette di tipo FLUSSO.
COMPONENTI E SISTEMI ELETTRICI
Differenza di potenziale V : Tensione elettrica
Flusso I :
Corrente elettrica
Quantità Q:
Carica elettrica
DEFINIZIONE: componente la cui proprietà principale è quella di opporsi alla formazione della corrente
elettrica, quando ai suoi terminali è applicata una tensione elettrica.
Il suo parametro principale è quindi la resistenza:
La resistenza si misura in Ohm:
Un resistore presenta una resistenza di 1 quando, sottoposto alla tensione di 1 V, permette lo scorrimento di
una corrente di 1 A
POTENZA DISSIPATA
Nei resistori non si accumula energia. Al passaggio della corrente, al loro interno avviene una
trasformazione energetica, in cui parte della potenza elettrica transitante è convertita in potenza
termica: il conduttore si scalda.
Il fenomeno fu studiato fin dalle origini dei circuiti elettrici, e nel 1837 J. P. JOULE lo quantificò con
la seguente formula: p(t) = R * i(t)2
riscaldamento di un conduttore per effetto del passaggio della corrente elettrica è noto come effetto
Joule.
il calore non è un’essenza della materia, bensì una manifestazione del lavoro meccanico.
vale la relazione: 1 cal = 4.187 J,
termico del lavoro
equivalente meccanico del calore 1 J = 0.239 cal, equivalente
L’energia è legata alla potenza secondo la seguente relazione:
Energia = Potenza x Tempo [ J ] = [ W ] *[ s ]
DERATING DELLA POTENZA
La potenza nominale di un resistore è riferita a una data temperatura ambiente. Se
questa è maggiore, il resistore
ha una maggiore difficoltà di raffreddamento, per cui occorre diminuire l’effetto Joule che
in esso ha luogo.
Ciò comporta una riduzione della corrente che si può far fluire nel resistore.
Per consentire il calcolo i costruttori forniscono un grafico di declassamento della
potenza del resistore in funzione della temperatura ambiente:
Esempio:
Resistore da 330 ohm, e 0.5 W a 70 °C
Se ne deduce una IMAX:
Tuttavia il resistore è inserito in un circuito la cui
temperatura ambiente raggiunge i 105 °C. Dal grafico del
costruttore si deduce che l’effetto Joule sopportabile scende al 38%
del valore nominale: 0.5·0.38 = 0.19 W.
La corrente massima risulta allora:
DEFINIZIONE: componente in grado di accumulare carica elettrica.
Il suo parametro principale è quindi la capacità, definita dalla legge del condensatore:
La capacità rappresenta quindi la carica
elettrica accumulata per un volt di tensione.
Si misura in Farad:
La corrente elettrica che carica e scarica un condensatore è desumibile dalla legge del
condensatore:
• Osservazioni:
• i(t) tanto maggiore quanto più velocemente varia v(t)
• pericoloso collegare il condensatore direttamente a un generatore di tensione (variazione
istantanea della vc(t))
Accumulando carica elettrica, il condensatore accumula energia elettrostatica:
NB: sia la carica che la tensione sono variabili di stato.
CARICA DEL CONDENSATORE
Se un condensatore viene collegato con una
batteria
attraverso fili ideali con resistenza nulla, il condensatore si
carica immediatamente, cioè in un tempo zero. Quando però nel
circuito è presente una resistenza la carica del condensatore viene
rallentata
Con il condensatore scarico e il deviatore
in posizione B, nel circuito non circola corrente e le tensioni su R e
su C sono nulle
Supponiamo ora di chiudere il
deviatore in A.
A questo punto il condensatore C è collegato alla batteria
E attraverso la resistenza R e nel circuito passa
corrente fino a quando il condensatore si carica ad una tensione pari a E
Immediatamente dopo la chiusura del deviatore
la tensione sul
condensatore è ancora nulla in quanto legata alla carica accumulata
sulle armature
Applicando la legge di K. alla maglia
E = VR + VC
- VC(t) =
E(1 + e-t/RC)
Nel momento della chiusura del tasto VC è zero, mentre VR ha un valore non nullo.
Siccome R è sottoposto a tensione, nel circuito passa, all'istante iniziale, una corrente I che può essere
calcolata con la legge di Ohm:
I = VR/R che carica il condensatore provocando una diminuzione della tensione sulla resistenza quando
C
è
completamente carico, la tensione VC raggiunge la tensione di batteria E, la tensione VR arriva a zero e la corrente si annulla
Un valore importante del circuito RC è la costante di tempo indicata con la
lettera greca tau (τ). La costante di tempo del circuito si calcola facendo il
prodotto della resistenza per la capacità:
τ = R.C
Più piccolo è il valore della τ più in fretta (in meno tempo) si carica il condensatore. Osserviamo subito che
il tempo di carica cresce all'aumentare di C e di R
Si dimostra che dopo un tempo pari a una costante di tempo la tensione sul
condensatore ha superato il 63% del proprio valore finale. Dopo un tempo circa
uguale a 5τ (cinque volte la costante di tempo) il condensatore si è caricato a più del
99% del valore finale.
SCARICA DEL CONDENSATORE
VC(t) = K e-t/RC = E e-t/RC
Corrente I, tensione VC
e tensione VR
durante la scarica hanno
tutte lo stesso andamento,
τ = R.C
ESERCIZIO
a) Determinare la tensione ai capi di un condensatore di 4 mF quando è caricato con 5 mC.
b) Trovare la carica accumulata su un condensatore di capacità pari a 50 pF quando si applica una tensione di 2KV.
a) C = 4 mF = 4*10-6 F
Q = 5 mC = 5*10-3 C
V = Q/C = (5*10-3)/(4*10-6) = (5*103)/4 = 1250 V = 1.25 KV
b) C = 50 pF = 50*10-12 F
V = 2KV = 2000 V
Q =C*V = (50*10-12 )* 2*103 = 10*10-8 = 0.1 mC
ESERCIZIO 1)
Si calcoli la costante di tempo di un circuito RC in cui C=100 mF e R = 220 K ed il tempo che esso impiega a caricarsi
fino al 50% della differenza di potenziale massima (f) fornita dalla batteria.
= RC = (200*103)*(100*10-6) s = 22 s
Posto Q(t) = f*C*(1-e-t/RC) pari al 50% del suo valore massimo:
f*C*(1-e-t/RC) = 0.5*f*C e-t/RC = 0.5
t = -RC ln(0.5) = -22*(-0.693) s = 15.2 s
Per la proprietà dei logaritmi:
e-A/B = C ln(e-A/B) = ln C -A/B = ln C A = -B *(ln C)
ESERCIZIO 2)
Un circuito consiste di un resistore collegato in serie con un condensatore di 0.5 mF ed ha una costante di tempo di
12 ms. Determinare il valore del resistore e la tensione ai capi del condensatore 7 ms dopo averlo collegato ad una
batteria di 10V.
Ricaviamo R dalla costante di tempo:R = /C = (12*10-3)/(0.5*10-6) = 24 k
sappiamo che durante il processo di carica la tensione varia come V(t)=f*(1-e-t/).
Occupiamoci dapprima della parte esponenziale:
Quindi:
V= 10*(1-e-0.583) = 10*(1-0.558) = 4.42 V
-t/ = -(7*10-3)/(12*10-3) = -0.583
Studiare il comportamento di un sistema equivale a esaminare
come varia il suo stato in funzione degli ingressi, cioè come
variano le sue variabili di stato.
Il modello matematico deve quindi legare le variabili di stato
agli ingressi.
Il punto di partenza sono le leggi fisiche.
circuito è formato da due componenti, uno dei quali in grado di
accumulare energia: il condensatore. Come variabile di stato si
assume normalmente la tensione vC(t), e il circuito si considera
alimentato mediante la tensione e(t).
La legge fisica che lega la vC(t) alla e(t) è la legge di Kirchhoff alla maglia:
Le variabili presenti nel modello devono rappresentare ingressi e variabili di stato (o uscite). Nell’equazione di Kirchhoff
occorre quindi scrivere i(t) in funzione di e(t) e/o vC(t):
Dalla legge del condensatore:
Sostituendo, e dopo pochi passaggi:
Equazione differenziale
Osservazioni:
• l’incognita, cioè vC(t), è una funzione; la soluzione quindi non è un numero, bensì una formula
• l’incognita compare con le sue variazioni nel tempo (per via della presenza
dell’accumulatore di energia), e per questo l’equazione è detta differenziale
• l’esistenza di un solo serbatoio di energia fa si che vi sia una sola variabile di stato, vC(t), e
per questo il circuito è
detto del 1° ordine
• l’incognita compare sempre con esponente 1, si tratta quindi di una equazione lineare (da cui:
circuito lineare)
• i parametri R e C sono costanti nel tempo, per cui i, circuito è stazionario
• tutti i termini rappresentano una tensione, per cui il prodotto RC deve avere le dimensioni di
un tempo; è chiamato costante di tempo.
SOLUZIONE NUMERICA
La soluzione numerica consiste nella trasformazione dell’intervallo infinitamente piccolo dt in un intervallo
finito t (passo di integrazione):
Osservazione: l’errore di calcolo è tanto più piccolo quanto minore è il passo di integrazione.
ESEMPIO:
R = 40 ohm , C = 50 mF, e(t) = 12 V.
Per la scelta del passo di integrazione t si segue il seguente criterio: una frazione della
costante di tempo.
Soluzione:
Δt = (1/5)
vc (V)
i (A)
12
0.00
0.300
0.4
12
2.40
0.240
0.4
0.8
12
4.32
0.4
1.2
12
0.4
1.6
0.4
t
e(t)
0.0
0.4
Δt = (1/10)
t
e(t)
vc(t)
i (A)
0.0
12
0.00
0.300
0.2
0.2
12
1.20
0.270
0.192
0.2
0.4
12
2.28
0.243
5.86
0.154
0.2
0.6
12
3.25
0.219
12
7.08
0.123
0.2
0.8
12
4.13
0.197
2.0
12
8.07
0.0983
0.2
1.0
12
4.91
0.177
0.4
2.4
12
8.85
0.0786
0.2
1.2
12
5.62
0.159
0.4
2.8
12
9.48
0.0629
0.2
1.4
12
6.26
0.143
0.4
3.2
12
9.99
0.0503
0.2
1.6
12
6.83
0.129
0.4
3.6
12
10.4
0.0403
0.2
1.8
12
7.35
0.116
0.4
4.0
12
10.7
0.0322
0.2
2.0
12
7.82
0.105
SOLUZIONE ANALITICA
Nel caso di una tensione di alimentazione e(t) = E = costante, l’equazione differenziale presenta la
seguente soluzione:
NB: la corrente ha un andamento opposto a quello della vC(t):
Osservazione:
i(t) ha un picco massimo quando vC(t) è minima;
il picco di i(t) viene prima quello di vC(t).
NB: i(t) può essere calcolata (conoscendo vC(t) )
anche facendo riferimento alla legge di Ohm.
Negli istanti di discontinuità della e(t) occorre
distinguere tra un momento immediatamente
prima
- t0 e un momento immediatamente dopo
t0+:
ESERCIZIO: proprietà filtrante rispetto alle brusche variazioni di tensione
1808: il prof (ad Halle: chimico, fisico e matematico) Johann
Schweigger nota che inprossimità di un conduttore percorso da
corrente l’ago magnetico viene deviato.
1820: Schweigger costruisce una bobina mobile con indicatore per
rilevare il
passaggio di corrente. Seebek lo chiamò
“moltiplicatore”.
1825: William Sturgeon costruisce il primo elettromagnete
(conduttore avvolto su ferro, non isolato).
1827: Joseph Henry potenzia l’elettromagnete con più spire isolate.
1830: Legge dell’induzione elettromagnetica
CIRCUITO RL SERIE: CHIUSURA
Quando l’interruttore S chiude o (apre) il circuito: l’L
impedisce
alla
corrente
di
aumentare
(o diminuire)
istantaneamente, perché la variazione di i genera una
f.e.m. indotta che si oppone alla variazione della corrente
stessa.
1) Consideriamo il caso in cui il circuito venga chiuso Ossia:
t= 0 i = 0
i
R
(1 e
Rt
L
)
L L / R
Durante la fase transitoria si ha un altra
corrente, detta extracorrente di chiusura
CIRCUITO RL SERIE: APERTURA
Dove i0=R La resistenza passa da R ad R’(>> R) costante durante il transitorio
t
R t
i e L e
L
R
R
' L L / R '
iL
L
i(t)
R
extracorrente di apertura, diversa da zero x un tempo molto bretve
ESEMPIO:
R = 1.5 ,
L = 3 H, e(t) = 20 V,
i(0) = 0 A.
Per la scelta del passo di integrazione t si segue il seguente criterio: una frazione della costante di tempo.
Soluzione:
DIODO RADDRIZZATORE
• Il diodo raddrizzatore a giunzione (o semplicemente diodo) è un
componente elettronico a due terminali (bipolo), la cui funzione è quella di
permettere il flusso di corrente elettrica in un verso e di bloccarla
nell'altro. Il simbolo circuitale del diodo esprime chiaramente questa
funzione: il triangolo indica la freccia di direzione in cui il flusso di
corrente è possibile. I due terminali del diodo vengono detti anodo
(A) e catodo (K).
• La figura qui sotto mette a confronto il simbolo circuitale del diodo con
l'aspetto tipico di un diodo reale. Si noti che il catodo viene di solito
marcato sul componente per mezzo di una fascia di differente colore:
Si osservi attentamente quanto segue:
v2 = 0 V
v1 = E = 9 V i2 = 0 A
i1 = E/R1 = 9/300 = 30 mA i3 = i1 = 30 mA
i1=i2= E / (R1+R2) = 9/900 = 10 mA
v1 = i1 * R1 = 10 mA * 300 Ω = 3 V
v2 = vd = i2 * R2 = 600 Ω * 10 mA = 6 V
in polarizzazione diretta è nota la tensione ai
capi del diodo (vale zero), mentre la corrente nel
diodo dipende dal circuito in cui il diodo è inserito;
in polarizzazione inversa è nota la corrente nel
diodo (vale zero), mentre la tensione ai capi del
diodo dipende dal circuito in cui il diodo è inserito.
TENSIONE DI SOGLIA
Affinche il diodo conduca
soglia.
occorre che la tensione applicata superi un valore non nullo, detto tensione di
Il valore della tensione di soglia è diverso a
seconda
del
materiale
a semiconduttore con cui è
stato realizzato il diodo. Per i diodi al silicio il valore è tipicamente compreso fra 0,6 e 0,8 V. I diodi al
germanio hanno invece una tensione di soglia più bassa, intorno agli 0,2-0,4 V.
Quando E supera la tensione di soglia, il diodo entra in zona di polarizzazione diretta e comincia a
condurre corrente, in questa zona la tensione rimane pressoché costante e sempre uguale alla tensione di
soglia Vs
Possiamo sostituire il diodo con un generatore di tensione equivalente di valore pari alla tensione di
soglia sul diodo. Supponendo Vs = 0,7 V per il nostro diodo, abbiamo:
V2 = Vs = 0,7 V
i2 = V2/R2 = 0,7 V/ 600 Ω = 1,16 mA
i1 = v1/R1 = 8,3/300 = 27,6 mA
v1 = E - V2 = 9 - 0,7 = 8,3 V
MISURA DELLA CARATTERISTICA INGRESSO- USCITA DEL
(TRANSCARATTERISTICA)
resistenza di protezione Rp fra
il
diodo e il generatore.
Tale resistenza ha il compito di
assorbire la tensione in eccesso,
limitando
l’assorbimento
di
corrente del diodo
DIODO
In corrispondenza di una certa V la corrente
inversa nel diodo aumenta molto rapidamente;
tale valore
limite viene
detto tensione di
breakdown o di rottura, in quanto
porta
generalmente
alla distruzione del componente
(intorno a – 100 V)
Si evidenzia il comportamento non lineare del diodo
TRANSISTOR BJT NPN E PNP
Iltransistor
a giunzione bipolare è un componente a tre morsetti denominati con base
(B),
collettore (C) ed emettitore (E) . Ci sono due tipi di BJT: il BJT npn e il BJT pnp. Essi differiscono per il
simbolo elettrico e per il versi dei parametri elettrici
Per trovare l’mettitore conviene fare riferimento ai fogli tecnici del
componente
(datasheet)
oppure usare un multimetro. La figura
seguente mostra
l'uso
di
un
multimetro
in configurazione
ohm-metro
per determinare qual è il collettore e qual è l'emettitore
di un BJT npn:
La
misura
si
basa
sul principio che ha la resistenza misurata fra il collettore e la base e fra
l’emettitore e base in un NPN e molto
elevata; Viceversa la resitenza misurata con i terminali al contrario e
molto bassa
LE TRE ZONE DI FUNZIONAMENTO DI UN BJT
Il BJT può lavorare in tre zone
di funzionamento
principali (regions of operation), dette
rispettivamente:
zona di interdizione (cutoff region)
zona attiva
(o
lineare
o amplificazione, forward active region)
zona di saturazione (saturation region)
Nel
seguito
esamineremo dettagliatamente il comportamento del BJT nelle tre zone e i metodi
di calcolo da usare per determinare in quale zona sta funzionando il BJT.
In zona di interdizione non BJT non conduce correnti
n zona attiva il BJT si comporta come un amplificatore di corrente: la corrente di collettore Ic è legata
alla corrente di base Ib e aumenta al crescere di quest'ultima;
In zona di saturazione i lBJT si comporta come
un
conduttore
quasi ideale (un filo) collegato fra collettore ed emettitore: in queste condizioni la tensione Vce è molto
bassa (idealmente zero) e non vale più la relazione di proporzionalità fra Ib e Ic.
ESEMPIO: Controllo marcia/arresto di un motore
.
Quando la bobina:
• richiede una alimentazione > 5 V, oppure
• assorbe una corrente > 40 mA
È necessario interporre tra Arduino e bobina uno stadio di interfaccia.
Descrizione:
Transistor BJT npn (2N1711)
BJT ON
bobina eccitata,
motore in marcia
Per accensione BJT necessaria : (VBE )SAT ∼ 0.9 - 1.3 V
Tensione di controllo fornita da Arduino: 5 V, quindi
IB ∼ (5 – 0.9) / 1k = 4.1 mA < 40 mA
NB: IBOBINA < (IBJT)MAX = 500 mAdc per 2N1711)
(
BJT OFF
bobina diseccitata, motore fermo
(NB :
VBOBINA <(VBJT_CE_OFF)MAX
= 80 Vdc 2N1711)
Diodo (1N4007)
Ha funzione protettiva (per BJT e bobina) contro la sovratensione provocata dalla bobina
al momento dello spegnimento del BJT (e = - dV/dt)
Bobina
Rappresenta l’interfaccia di potenza. Occorre prestare attenzione alla corrente assorbita
dal motore, che deve essere sopportabile dal contatto di potenza del relé.
Motore
Può essere sia DC che AC.
circuiti di interfaccia
Interfacciamento con Motori
Il transistor NPN viene utilizzato come interruttore ON-OFF per fornire la corrente
desiderata alla
bobina del relè. È necessario il diodo di ricircolo
in quanto la corrente
che attraversa la
bobina induttiva quando viene diseccitata non viene istantaneamente ridotta a zero. Quando l'ingresso
alla base è impostato a livello ALTO, il transistor è acceso "ON". La corrente passa attraverso la bobina
del relè e suoi contatti e si ha il pilotaggio del motore.
Quando l'ingresso alla base transistori è BASSO, il transistor è spento "OFF" e il motore si arresta con i
contatti del relè aperti. Qualsiasi forza contro-elettromotrice generata disattivando la bobina scorre
attraverso il diodo di ricircolo e lentamente decade a zero prevenendo danni al transistore. Inoltre, il
MOSFET essendo isolatonon viene influenzato da alcun rumore o picchi di tensione generati dal
funzionamento del motore.
circuiti di interfaccia
INTERFACCIAMENTO IN INGRESSO
l tipo più semplice e più comune di interfacciamento di imput
è l'interruttore a
pulsante in cui
l'operatore può cambiare lo stato di un ingresso semplicemente azionando un interruttore, premendo
un pulsante o muovendo un magnete sul sensore reed.
interfacciamento con
un singolo interruttore
Un resistore di pull-up è necessario per tenere il livello
di tensione di uscita al valore desiderato (in questo
esempio, + 5v) quando l'interruttore è aperto e ad
evitare il
corto circuito dell'alimentazione quando
è chiuso.
La dimensione del resistore di pull-up dipende dalla
corrente del circuito quando l'interruttore è aperto
Se assumiamo una porta logica TTL digitale
che richiede in input
60 micro-amp (60uA),
questa provoca una caduta di tensione attraverso il resistore di: 60uA x 10k = 0,6 V , producendo un
ingresso di tensione "livello alto« di 5,0-0,6 = 4.4V , che è ben entro le specifiche di ingresso di una
porta TTL digitale standard.
Invertendo il resistore con l'interruttore si ha la configurazione di pull-down
Diversamente dal resistore di pull-up che viene utilizzato per limitare la corrente, lo scopo principale di un
resistore di pull-down è di mantenere il terminale di uscita, V OUT a 0V . in questo caso si può utilizzare
una resistenza molto più piccola con l'inconveniente che a quando l'interruttore è chiuso si può avere un
elevata dissipazione di potenza nella resistenza
Sensori / traduttori
interfacciamento con DIP switch
Poiché i contatti degli interruttori meccanici sono progettati per aprire e chiudere rapidamente si
hanno transitori di chiusura
che possono produrre una
serie di impulsi o picchi di tensione
prima della chiusura definitiva dell'interruttore
Ci sono diversi modi che consentono di risolvere il rimbalzo dell'interruttore
1) Carica e scarica con un condensatore
antirimbalzo con porte NAND
con porte NOR
interfacciamento ottico
circuiti di interfaccia
Per isolare elettricamente un circuito da un altro si puo ricorrere agli isolatori ottici che forniscono
un elevato grado di isolamento elettrico tra i terminali di ingresso e di uscita,
che richiedono una
minima di corrente di ingresso (in genere solo 5mA) e che possono essere gestiti da una qualsiasi
porta logica un isolatore ottico è costituito da un LED che produce luce infrarossa e da un
dispositivo fotosensibile a semiconduttore che viene utilizzato per rilevare il fascio infrarossa
emessa.
Poiché l'ingresso è un LED una resistenza serie, R S è necessaria per
limitare la corrente del LED
Gli isolatori opto-triac consentono il comando di carichi fino a 400 v
con un assorbimento di corrente di 100 mA
Questo tipo di configurazione
a
optoisolatore
costituisce la base di un'applicazione del relè a stato
solido che può essere usato per controllare qualsiasi
rete AC direttamente dall'interfaccia di uscita di un
mico-controllore, PIC o circuito digitale, rotella del
mouse, ecc.
LABORATORIO: TUTTO SUI RELE
RELE’ è un dispositivo elettromeccanico in grado di azionare dei contatti
elettrici di potenza (cioè, di chiudere o aprireun circuito mediante lo
spostamento di uno o più contatti elettrici)
Relè elettromeccanico
VEDIAMO COME È FATTO UN RELÈ
IL FUNZIONAMENTO
E’ costituito da una bobina ad elevato n° di spire (avvolte su materiale
ferromagnetico) che, se
percorsa da corrente provoca l’attrazione di un
meccanismo (ancora) che determina la chiusura o l’apertura dei contatti.
TIPOLOGIE COSTRUTTIVE
• I relè si dividono in due blocchi fondamentali:
– Lato comando ( o lato eccitazione) costituito dalla:
• Bobina di eccitazione;
• Nucleo magnetico;
• Ancora mobile. (di forma piatta, a cerniera,
girevole e oscillante)
– Lato potenza ( o lato contatti) costituita dai
contatti elettrici di potenza.
LATO COMANDO
•Bobina
di
eccitazione:
realizzata
con filo di rame
smaltato avvolto su un supporto
isolante;
•Nucleo magnetico: di forma
cilindrica o piatta, realizzato in
ferro
dolce
a
struttura
massiccia per DC e laminata
per AC;
•Ancora mobile: realizzata in
ferro dolce o acciaio dolce;
LATO CONTATTI
•Contati: realizzati con argento e oro per basse potenze; leghe di
argento e argento-ossido di cadmio per potenze notevoli
•Molle portacontatti: realizzati in lega di rame-zinco-nichel devono
possedere una elevata elasticità da rimanere invariata anche dopo un
lungo periodo di funzionamento.
PRINCIPIO DI FUNZIONAMENTO
CON ACCENSIONE DA DUE O PIÙ PUNTI
TIPI DI RELÈ
•
Neutro: se il suo funzionamento NON DIPENDE dal verso della corrente nella bobina;
•
Polarizzato: se il suo funzionamento DIPENDE dal verso della corrente nella bobina;
•
Monostabile: se la posizione dei contatti si mantiene
SOLO per la durata dell’eccitazione
della bobina;
•
Bistabile: se la posizione dei contatti si mantiene ANCHE dopo l’eccitazione della bobina ed
occorre una nuova eccitazione per far tornare i contatti nella posizione di partenza.
TIPI DI RELÈ
RELÈ: PARAMETRI CARATTERISTICI
•
Tensione di eccitazione: tensione nominale necessaria per l’eccitazione della bobina del relè;
•
Corrente di eccitazione: corrente assorbita dalla bobina del relè durante la sua eccitazione;
•
Tipo di eccitazione: AC (alternate current);DC (direct current)
•
Durata elettrica: massimo numero di manovre con carico elettrico inserito;
•
Durata meccanica: massimo numero di manovre senza carico elettrico inserito;
• Frequenza di commutazione: numero massimo di commutazioni al secondo
CARATTERISTICHE DEI RELÈ
RELÈ: PARAMETRI CARATTERISTICI
•
Tensione di contatto: massima tensione nominale fra i contatti quando sono aperti;
•
Corrente di contatto: massima corrente che può circolare fra
•
Resistenza della bobina: rapporto tra tensione di eccitazione e la corrente;
i contatti quando sono chiusi;
I contatti possono assumere 3 posizioni di base a seconda del tipo di applicazione cui
sono destinati:
• NC (Normally Closed): i contatti sono chiusi a relè diseccitato; essi si aprono in seguito
all’eccitazione della bobina;
• NO (Normally Open): i contatti sono aperti a relè diseccitato; essi si chiudono in seguito
all’eccitazione della bobina;
• SC (SCambio): a relè diseccitato alcuni contatti sono chiusi e altri aperti; all’eccitazione del
relè i contatti chiusi si aprono e quelli aperti si chiudono.
COMPORTAMENTO IN
CONDIZIONI DI PRESENZA DELLA
TENSIONE DI INGRESSO
2 TIPOLOGIE DI RELÈ
Relè bistabili (detti anche ritenuta o ad impulsi
Nei relè blstabili le posizioni di riposo (per esempio, contatti
aperti) e di lavoro (per esempio, contatti chiusi) ) sono
entrambi stabiliti anche in assenza di alimentazione della
bobina di eccitazione di ciascun intervento di apertura e di
chiusra dei relè è ottenuto alimentandola bobina stessa per
un breve istante (mediante un impulso di corrente).
Il mantenimento del contatti nella posizione di lavoro,
anche al cessare dell'alimentazione, e assicurato da un
sistema di ritenuta dì natura meccanica
IL CIRCUITO DI
COMANDO
RELÈ INTERRUTTORE AD ALIMENTAZIONE
DIRETTA
L’alimentazione della bobina coincide con tensione di rete
RELÈ INTERRUTTORE AD ECCITAZIONE
SEPARATA
L’alimentazione della bobina è a bassa tensione
PILOTARE UN RELÈ CON
ARDUINO
PILOTARE UN RELÈ CON
ARDUINO
PILOTARE UN RELÈ CON
ARDUINO
PILOTARE UN RELÈ CON
ARDUINO
PILOTARE UN RELÈ CON
ARDUINO
PILOTARE UN RELÈ CON
ARDUINO
PILOTARE UN RELÈ CON
ARDUINO
PILOTARE UN RELÈ CON
ARDUINO
CALCOLO DELLA RESISTENZA SULLA
BOBINA
CALCOLO DELLA RESISTENZA SULLA
BOBINA
IL CIRCUITO
IL CIRCUITO
IL CIRCUITO
IL CIRCUITO
IL CIRCUITO
IL CIRCUITO
IL CIRCUITO
IL CIRCUITO
IL CIRCUITO
IL CIRCUITO
IL CIRCUITO
IL CIRCUITO
IL CIRCUITO
IL CIRCUITO
IL CIRCUITO
IL CIRCUITO
IL CIRCUITO
IL CIRCUITO
IL CIRCUITO
IL CIRCUITO
IL CIRCUITO
IL CIRCUITO
IL PROGRAMMA
ESERCITAZIONI PROPOSTE
NE555
CIRCUITO INTEGRATO 555
L’integrato 555 ideato nei primi anni ‘70 è un temporizzatore di estrema precisione, versatile e di grande
semplicità di utilizzo.
Trova impiego in svariate applicazioni dell’elettronica analogica.
Il suo nome è dovuto alla presenza al suo interno di tre resistenze da 5 kW.
CIRCUITO INTEGRATO 555
Lo schema a blocchi dell’integrato a tecnologia bipolare è costituito da:
3 resistori da 5 kW,
due comparatori,
un flip-flop del tipo SR,
un BJT
un buffer di uscita, in grado di erogare una corrente massima di 200 mA.
I tre resistori realizzano un partitore resistivo in grado di fornire le tensioni di riferimento 2/3 di Vcc e
1/3 di Vcc, rispettivamente al comparatore 1 e al comparatore 2.
Le uscite dei comparatori sono collegate agli ingressi di Reset e di Set del flip-flop, la cui uscita
complementare pilota la base del BJT.
555 come astabile
Supponiamo che inizialmente il condensatore C sia scarico: gli ingressi dei due comparatori sui
piedini 2 e 6 si trovano a livello basso.
Il comparatore 1 dà in uscita un livello basso, quindi il reset del flip-flop è a livello basso; il
comparatore 2 dà in uscita un livello alto, settando il flip-flop e portando l'uscita Q a 1 e Q negato a
0.
Sul piedino 3 si ha Vout = H.
Il BJT è interdetto, quindi il piedino 7 si trova isolato da massa.
C inizia a caricarsi attraverso la serie di Ra ed Rb.
Quando Vc raggiunge il valore di 1/3 di Vcc, il comparatore 2 commuta e si porta a livello basso
(S=0) ma il flip-flop non commuta perché anche R=0, ed il condensatore continua a caricarsi.
Quando Vc raggiunge i 2/3 di Vcc, il comparatore 1 commuta, portando la sua uscita a livello alto
resettando il flip-flop (R=1) e portando l’uscita negata a livello alto, che satura il transistor.
Sul piedino 3 si ha ora Vout=L.
Il piedino 7 risulta collegato a massa e il condensatore si scarica attraverso la resistenza Rb.
Quando Vc scende al di sotto di 1/3 di Vcc, il comparatore 2 commuta, settando il flip flop, portando la
sua uscita a livello H e l’uscita negata a livello L.
Ora si ha Vout=H e il BJT risulta quindi interdetto, il piedino 7 risulta non più a massa, permettendo a
C di ricaricarsi, ripetendo il ciclo precedente.
• 555 come monostabile
• In condizioni di riposo l’ingresso positivo (V+) del comparatore 1 è mantenuto a + Vcc tramite la
resistenza Ra, mentre l’ingresso negativo (V-) è posto a (2/3)Vcc.
• L’uscita del comparatore 1 è alta e resetta il flip-flop, portando l’uscita negata del flip-flop a livello alto.
• L’ingresso negativo del comparatore 2 viene mantenuto, mediante un segnale di ingresso, ad un valore di
tensione maggiore di 1/3 di Vcc.
• L’uscita del comparatore è quindi Low.
• In queste condizioni si ha quindi il reset del flip-flop a livello alto e il set a livello basso, saturando il BJT.
• Nell’istante in cui all’ingresso negativo del comparatore 2 si ha una tensione negativa, inferiore a 1/3
di Vcc, la sua uscita va H, settando il flip-flop e interdicendo il BJT, permettendo al condensatore C di
caricarsi.
• Il condensatore inizia quindi a caricarsi attraverso la resistenza Ra.
Appena Vc che è anche quella del piedino positivo del primo comparatore, raggiunge i 2/3 di Vcc, l’uscita
del comparatore va H facendo condurre il transistor.
C si scarica rapidamente attraverso la bassa resistenza di uscita del BJT, restando scarico fino all’arrivo
del nuovo impulso.
LABORATORIO
555-astabile
555-monostabile
ASTABILE
ASTABILE
1)
ν= 25Hz, T=40ms
2)
C=10µF
3)
R2=1430Ω
4)
R1=2860Ω
∆t_off=10ms, ∆t_on=30ms
Ton = 0.693 (R1+R2)C
Toff = 0.693*R2C
∆t_on ∆t_of
T
MONOSTABILE
ASTABILE
MONOSTABILE
T=1.1*R*C=1.1*(20kΩ)*(1µF)~22ms
T
Il BJT Q1 in conduzione (saturazione) possiamo supporlo
equivalente ad una resistenza di bassissimo valore (2 ohm) ,
mentre quando non è in conduzione (interdizione) il suo
valore possiamo ritenerlo equivalente ad un resistenza di alto
valore >(10 Kohm).
Durante la conduzione del BJT
l’induttanza a regime si
comporta come un corto circuito, per cui la I = 12V/(118 +
2 OHM) = 100mA .
Il diodo ,polarizzato inversamente, non conduce corrente
Vce =1 * + 2Ω = 100 mA* 2 = 0.2 v
Nell’istante in cui il BJT commuta e va in interdizione, la sua resistenza equivalente sarà di 10 KΩ.
L’induttanza della bobina mantiene la stessa corrente di prima della commutazione ,diminuendo il
suo valore gradualmente con costante di tempo L / R, per cui ,almeno istantaneamente, sarà la VCE
=VR = R x I =10 K * 100mA = 1000 Volt.
Questa sovratensione, presente ai capi del BJT lo danneggerebbe, ma il diodo essendo adesso
polarizzato direttamente, entra in conduzione istantaneamente e con la sua VD = 0,5 Volt, impone
un abbassamento immediato della tensione VCE = 1000 Volt ad un valore a regime Vce = Vcc /(118
+10KΩ)*10KΩ = 11,86 Volt
Possiamo quindi affermare che la funzione del diodo D1 è quella di proteggere il transistore dalla
presenza di una elevata sovratensione presente tra il suo collettore ed emettitore ( VCE )
nell’istante della commutazione saturazione → interdizione
In questo caso il diodo è in polarizzazione diretta e quando il BJT è in conduzione avremmo nel
ramo una corrente
I= Vce/Rbce = Vce –VdRbce = 12 – 0.2/2 5,75 A
Sia il diodo che il BJT potrebbero non sopportare questo alto valore di corrente e danneggiarsi.
Oltretutto il diodo non avrebbe più la funzione di protezione contro la sovratensione (1000Volt)
dovuta all’induttanza della bobina durante la commutazione ON ®OFF
Per VIN > VCC il diodo D3 è polarizzato direttamente, quindi è in conduzione.
Sarà
quindi VIN - VCC = VR8 + VD3 ®
(Vin –Vcc) = (Vin –V2) + (V2 – Vcc)
(Vin –Vcc) = (Vin –V2 – Vd3)
(V2 = = (Vcc +Vd3)
(V2 = = (Vcc +0.5)
Per VIN < 0Volt (valori della tensione d’ingresso
negativi) è invece polarizzato direttamente il diodo
D4 che sarà quindi in conduzione.
Si avra
-Vin = -Vre –Vd4
-Vin = (-Vin –(-V2) – Vd4)
-Vin = -Vin +V2 _Vd4
V2 = -0.5 v
In questo caso lo stato d’uscita ON del timer viene determinato dal tempo necessario al
condensatore C7 a raggiungere un valore di 9,6 Volt , diverso dal valore precedente di 8 Volt
(2/3 Vcc),con un’alimentazione Vcc=12 Volt e senza la resistenza R1 aggiunta.
Conseguenza di ciò avremmo un tempo ON del timer diverso (maggiore) da quello definito dalla
espressione T = 1,09(R2+ R3)*C7
7. Quali sarebbero i tempi massimi e minimi con un condensatore C7 da 1 μF?
T = 1.09´ (R2 + R3) ´C7
Tmax= 1,09*10^6 *10^5*10^-6 = 1,199 sec
Tmin 1,09*(10^5* 10^-6 = 0.109 sec
8. Che cosa succede se si scambiano R4 e il pulsante S1?
La V2 =2,9V è minore dei 4 volt presenti all’ingresso + del comparatore B ,per cui il FFsarebbe
sempre attivo all’ingresso S (start) e l’uscita del timer sarebbe sempre ON.
Finito un ciclo ON, il FF si verrebbe a trovare con i due ingressi S=1 e R=1; condizione di blocco per
il funzionamento del FF.
Viceversa ,premendo il pulsante, il pin 2 sarebbesempre agganciato alla Vcc e l’uscita del timer
sarebbe sempre OFF
9. Che cosa succede se non si salda il condensatore C5 ?
Il pin 4 del reset sarebbe sempre disattivato perché agganciato a Vcc ed il timer all’accensione non
avrebbe momentaneamente l’uscita forzata a 0 ma uno stato ON o OFF casuale.
10. Con l’uscita del 555 (pin 3) è possibile pilotare una porta logica TTL ? A quali condizioni?
Si a condizione che la Vcc= 5 Volt oppure si inserisca in uscita (pin 3) un partitore
resistivo che limiti la Vout a 5 Volt.
11. Dove altrimenti sarebbe possibile collegare il diodo LED di segnalazione?
Avendo un diodo led in conduzione una corrente Imax= 20 mA , può essere pilotato direttamente in uscita
(pin 3), potendo quest’uscita pilotare carichi fino a 100 mA.
12. Dire almeno un caso in cui è indispensabile la presenza del relè
L’uso del relè è indispensabile quando si devono pilotare carichi che prevedono unassorbimento di corrente
oltre i 100mA (sia in tensione continua che alternata), quando ecessitano di una tensione d’alimentazione
in alternata (per qualsiasi valore); peresempio l’uso del timer per l’accensione delle luci delle scale in un
condominio;
13. Che cosa succederebbe se al posto di R8 saldassimo una resistenza da 10 Kohm?
La V2 = 6 V sarebbe sempre superiore ai 4 V ( 1/3 Vcc) presen
all’ingresso V+ del comparatore B e di conseguenza non
avrebbe mai la commutazione dell’uscita del suddet
comparatore , necessaria per attivare lo stato d’uscita ON d
timer.
14. Quali sono i valori corretti di tensione da applicare al pin 2 del 555 per avviare la temporizzazione? Perché?
La commutazione dell’uscita del timer da OFF a ON avviene quando il valore della V2 ( pin 2 del 555 ) scende sotto il
valore di riferimento di 4 Volt (1/3 Vcc) , quindi per valori che vanno do 0 Volt a 4 Volt ,perché solo in queste condizioni il
comparatore B può commutare e dare all’ingresso S (start ) del FF l’impulso necessario per la commutazione dello stato
logico d’uscita ( Q ). Quindi per 0V <V2<Vcc
15. Cosa potrebbe accadere se non ci fosse il resistore R3 in serie al trimmer R2 ?
Il resistore R3 in serie al trimmer R2, oltre ad regolare il tempo in cui l’uscita del timer è ON funge da
resistenza di carico per il BJT interno all’Ic 555.Nel caso in cui il trimmer fosse cortocircuitato R2 = 0 ohm (
Tmin ), senza la R2 il BJT si verrebbe a trovare con una resistenza di carico Rc = 0 danneggiandosi perché
attraversato da un’alta corrente Icarico.
16. Che cosa succede se si scambiano fra di loro R6 e C5 ?
Per essere attivo il reset, il pin 4 deve essere a potenziale 0 Volt. Con la configurazione seguente,
all’accensione del circuito, inizialmente il C5 è scarico (cortocircuito ) ( Vc = 0 ), la V4 sarà a potenziale Vcc e
quindi il reset non è attivo.
Di conseguenza l’ OUT del timer può assumere uno stato ON o OFF casuale.
Quando il condensatore si sarà caricato non permetterà il passaggio di corrente
e di conseguenza la caduta di tensione nella R6 sarà VR6 = 0 Volt e quindi il
reset sarà da questo istante in poi sempre attivo e bloccherà l’OUT del timer
sempre a 0 Volt.
17. Dire almeno un caso in cui sarebbe stato possibile pilotare un carico senza relè
Per alimentare ed attivare per un tempo T , l’accensione di lampade o semplici
apparecchiature elettriche o elettroniche che non richiedono una corrente superiore a 100 mA ( lettori mp3, diodi Led,
piccoli motorini in corrente continua, lampeggiatori in bassa tensione continua, ecc.. )
18. Che cosa accade se D4 viene invertito?
Il diodo D4 in questo caso risulta polarizzato direttamente ed in
conduzione tramite la R5.
La VD4 = 0,5 Volt impone questo valore all’ingresso del pin 2 ( V2 =
0,5 Volt) , interpretatodal Ic 555 come un livello (V2<4Volt) atto
a provocare lo start ( livello ON in uscita ) che simanterrà in
modo ripetitivo indipendentemente dallo stato del pulsante.
Oltretutto il D4 nonesplicherà più la sua principale funzione di
protezione dell’ingresso da valori di tensione negativi ( Vin < -0,5
Volt )
19. Perché C1 e C2 sono stati utilizzati in parallelo anziché uno solo dei due?
C1 ( 0,1 uF ) serve a filtrare disturbi di alta frequenza presenti nella linea di alimentazione :
C2 ( 100 uF ) ha una funzione di filtro di livellamento della Vcc.
20. Se la linea che collega il pulsante all’ingresso del circuito è abbastanza lunga ,quali problemi
potrebbero sorgere? Come risolverli?
Se il pulsante di start è posto in posizione remota rispetto al circuito, con percorsi adiacenti a quelli della rete
elettrica ogni qualvolta si accende un elettrodomestico (Aspirapolvere, lavatrice , ecc.. ) i disturbi provocati
dalle spazzole dei motori elettrici ,captati per induzione dai fili del pulsante sono sufficienti ad attivare il timer
rendendolo quindi poco affidabile.
Per esempio , una Zin = 1K (impedenza d’ingresso dell’apparecchiatura) attraversata da una corrente indotta
(disturbo) di 1 mA , avrebbe ai suoi capi una Vin= Zin*I = 1K*1mA = 1 Volt , ma se la Zin = 100K la Vin
=100K * 1mA = 100 Volt. E’ importante quindi, al fine di ridurre l’effetto dei disturbi di linea che la Zin sia la più
bassa possibile. A tal fine si è realizzato uno stadio d’ingresso a bassa impedenza costituito da R4, C3, seguito
da un filtro passivo composto da R5, C4.
IL PC: INPUT E OUTPUT
Generalità
architettura a BUS
Classificazione delle memorie
Porte seriali
architettura del software
Linguaggi di programmazione
Il linguaggio C
Gli algoritmi
LA PROGRAMMAZIONE
GENERALITA
Nel 1946 fu costruito l’ENIAC, primo calcolatore elettronico, realizzato interamente a valvole.
Tuttavia l’organizzazione era sostanzialmente la stessa del MARK 1.
John von Neumann (1903 – 1957), matematico di origine ungherese, naturalizzato americano,
aveva visto funzionare il Mark 1 a Los Alamos nel 1944, dove veniva utilizzato per i calcoli
necessari per la bomba atomica. Neumann non rimase soddisfatto del funzionamento del Mark 1
per :
• dati e istruzioni non venivano inseriti attraverso le stesse unità di ingresso e non
venivano memorizzati nella stessa memoria
• l’esecuzione di un programma richiedeva la continua presenza di operatori umani.
Nel 1946 von Neumann pubblicò un articolo in cui proponeva una macchina alternativa, in cui:
• dati e istruzioni dovevano essere immessi attraverso le stesse unità di ingresso e
dovevano essere memorizzati nella stessa memoria
• per l’esecuzione di un programma, si doveva caricarlo interamente in memoria.
Nel 1947 era stato costruito il primo transistor, ma il primo calcolatore a transistor risale al 1959, realizzato dall’IBM.
Negli anni ’60 l’integrazione dei componenti elettronici su un unico chip di silicio divenne molto grande, tanto che nel
1971 si arrivò a costruire il primo microprocessore (μP, CPU) nei laboratori della Intel per opera di Federico Faggin.
Il μP racchiudeva diversi blocchi dell’architettura di von Neumann:
NB:
la piccola parte di memoria incorporata nel μP è denominata ‘cache’.
Nel 1975 fu costruito il primo calcolatore con μP. Si costruirono grandi calcolatori destinati ai centri
di ricerca e a grandi utenze in generale (unico calcolatore con molti terminali: multiplazione a
divisione di tempo).
Nell’agosto del 1981 l’IBM presentò sul mercato un piccolo calcolatore destinato all’uso
personale: il PC. I PC , in quanto macchine economiche, nacquero con due difetti che li
caratterizzano tuttora: non sono
• deterministici: non garantiscono un tempo massimo in cui la routine sarà eseguita;
• real time: velocità di risposta (esecuzione routine) non all’altezza di quella del processo
esterno da controllare.
ARCHITETTURA A BUS
Il bus è un canale di comunicazione formato da più linee condivise da tutti i componenti del sistemi.
Hard disk
Caratteristiche:
• è possibile un solo trasmettitore (Tx) per volta: in caso contrario, nella più innocua delle ipotesi, il livello
logico della linea potrebbe essere incerto
• sono possibili più ricevitori (Rx) contemporaneamente; esiste un limite massimo al numero dei Rx
dipendente dal fan-out del trasmettitore
• il grande vantaggio del bus è la sua espandibilità, cioè la possibilità di aggiungere ulteriori componenti nel
sistema mantenendo inalterato il circuito esistente.
Il bus può essere diviso in tre parti funzionali:
• address bus: linee che portano l’informazione dell’indirizzo del componente
• data bus: linee su cui viaggiano i dati che i componenti del sistema si scambian
• control bus: linee su cui viaggiano i segnali di comando che gestiscono l’accesso al bus.
L’accesso al bus dei componenti, come Tx o come Rx, è gestito dal master (spesso un μP).
In generale si hanno due tecniche di accesso al bus:
•
Polling: il master sonda periodicamente, in sequenza, lo stato di tutti i componenti, se
qualcuno ha bisogno di impegnare il bus, viene accontentato.
Vantaggio: semplicità hardware
Svantaggio: possibili tempi lunghi di attesa di accesso.
• Interrupt: il componente che deve impegnare il bus invia una comunicazione al PIC (es: 8259),
il quale esamina tutte le richieste e invia al master la richiesta con priorità più alta; il master, sulla
base delle proprie esigenze interne può accogliere o meno la richiesta; nel caso la accolga chiede
al PIC il codice del componente che ha chiesto l’impegno del bus e invia i relativi segnali di comando.
CLASSIFICAZIONE DELLA MEMORIA in un PC
Classificazione per tipologia secondo:
• il tipo di accesso:
• sequenziale: nastri, alcuni registri
• casuale (RAM): dischi (magnetici e ottici), chip seminconduttori
• l’uso:
• solo lettura (ROM): chip sminconduttori, CD-ROM
• lettura/scrittura: dischi (magnetici e ottici), chip seminconduttori
• la conservazione dei dati dopo aver tolto l’alimentazione:
• non volatile: chip semiconduttori, dischi, nastri
• volatile:
• statica (SRAM): più veloce e più costosa,
• dinamica (DRAM): bisogno di continuo rinfresco, maggiore integrazione
cache: è chiamata di 1° livello.
buffer memory: memoria tampone (SRAM), disposta vicina al μP,
lavora a una frequenza più alta di quella di lavoro (cache di 2° livello).
working memory: memoria di lavoro (DRAM), memoria in cui è
caricato il programma per l’esecuzione.
bulk memory: memoria di massa (dischi), per la funzione di
archivio.
PORTE seriali e parallela in un PC
Trasmissione parallela: tutti i bit del dato sono trasmessi contemporaneamente, ciascuno sulla
propria linea.
Es: RS 232, la cui massima
velocità di trasmissione nei PC
è in genere di 115 200 baud (bit
al secondo: bps oppure b/s)
NB: a fronte di un disturbo, solo la linea di segnale può variare il suo potenziale (la linea di
ritorno è vincolata a 0 V) e ciò potrebbe alterare il valore del bit.
8
Porte in un PC - USB
Es: USB (Universal Serial Bus), nuovo standard, che nei PC sta sostituendo sia le vecchie porte sia parallele che seriali.
I nuovi chip e la trasmissione differenziale consentono velocità molto alte:
USB 1.0 1.5 Mb/s
1.1 12 Mb/s
2.0 480 Mb/s
3.0 4.8 Gb/s
Vantaggio della trasmissione differenziale: un disturbo elettromagnetico colpisce in ugual misura i
due conduttori (entrambi liberi di variare il loro potenziale) per cui la differenza dei potenziali non
cambia.
ARCHITETTURA SOFTWARE di un PC
Il software di un PC è organizzato su più livelli:
FIRMWARE (BIOS per PC IBM compatibili):
consiste in programmi
(routine, cioè procedure) fornite dal costruttore del PC. All’atto
dell’avviamento le routine del firmware programmano i chip del sistema,
testano la memoria e caricano in memoria il sistema operativo.
SISTEMA OPERATIVO: consiste in una collezione di programmi utili alla
gestione delle risorse del computer, che dispensano l’utente dalla fatica di
dover scriverli in proprio. Si tratta di programmi scritti facendo ricorso
alle routine del firmware.
PACCHETTI SOFTWARE APPLICATIVI: i programmi messi a disposizione
dal sistema operativo (es: editor di testo) sono spesso poveri di
funzionalità. Facendo ricorso alle routine del firmware e del sistema
operativo si sono costruiti quindi dei programmi molto più ricchi, già
pronti per l’utente.
SOFTWARE DI SVILUPPO:
sono linguaggi di programmazione, che
permettono la creazione di applicazioni nuove. Spesso infatti le esigenze
degli utenti non possono essere soddisfatte dai pacchetti applicativi già
esistenti.
LINGUAGGI DI PROGRAMMAZIONE
Il primo linguaggio di programmazione è stato il linguaggio macchina: codice operativo e dati
erano rappresentati da sequenze di 0 e 1.
Esempio: per μP compatibili con l’8086 della Intel l’operazione ‘metti il numero 4 nel registro
AX’ costringeva i programmatori a scrivere il seguente codice:
1011 1000 0000 0100
Con il conseguente problema di frequenti errori di scrittura e scarsa leggibilità
La soluzione fu trovata nella codifica esadecimale: B 8 0 4
Si producevano meno errori, ma permaneva la scarsa leggibilità.
Con la codifica esadecimale, dopo aver scritto il programma (codice sorgente) si rende
necessaria una decodifica in binario del codice esadecimale.
Il passo successivo fu la creazione di linguaggi di programmazione con codici
mnemonici (assembly): MOV AX, 4
L’istruzione diveniva più chiara: il codice operativo MOV esprime chiaramente il senso dell’operazione
(mnemonico).
I linguaggi assembly sono definiti di basso livello, in quanto richiedono comunque la piena
conoscenza del microprocessore da programmare.
La trasformazione del codice sorgente (estensione .asm) in binario è svolta da un programma
chiamato assembler, il quale si occupa anche di controllare la sintassi. L’assembler crea un file binario
con estensione .obj (file oggetto). Se il programma sorgente è formato da più file, l’assembler
esamina un file per volta. E’ successivamente compito di un altro programma, il linker, collegare i vari
file oggetto e aggiungere il codice delle librerie utilizzate.
Il linker crea il file eseguibile (.exe) senza fissare un indirizzo assoluto cui il programma sarà caricato
nella memoria RAM. Si è voluto lasciare al sistema operativo la libertà di caricare il file eseguibile
nella zona di memoria al momento più conveniente. Un programma che permette questo al sistema
operativo si dice rilocabile.
Difficoltà presenti nella programmazione in
assembly:
• la realizzazione di programmi complessi
rende molto impegnativa la programmazione
• l’obbligo per il programmatore della piena
conoscenza del μP che dovrà eseguire Il
programma.
Per superare le difficoltà proprie della programmazione assembly sono stati creati linguaggi di programmazione
evoluti (detti anche di alto livello: Basic, C, Pascal, …).
Presentano il vantaggio
• di consentire la programmazione anche a utenti senza alcuna conoscenza dell’hardware del computer
• di implementare istruzioni compatte (facendo ricorso a librerie) che riducono il lavoro del programmatore.
Questi vantaggi sono ottenuti al costo di uno sfruttamento meno ottimale delle risorse del computer (per la
caratteristica di essere one-to-many e per la presenza di codice superfluo).
La traduzione del file sorgente in eseguibile può essere realizzata con programmi:
I programmi
interpreti sono ottimizzati per una veloce fase di messa a punto del programma che
si sta scrivendo (debugging) , ma ogni volta che occorre eseguire un file sorgente lo si deve
trasformare in eseguibile. Sul disco non resta alcun file oggetto o eseguibile. I linguaggi di
programmazione i cui programmi sono eseguiti per mezzo di un interprete sono detti linguaggi
interpretati (es: Basic, Html).
I programmi compilatori sono invece ottimizzati per l’avviamento veloce dell’esecuzione dei file
eseguibili, in quanto memorizzano su disco sia i file oggetto (.obj) che quelli eseguibili (.exe),
sono però più lenti in fase di messa a punto. I linguaggi di programmazione i cui programmi sono
eseguiti per mezzo di un compilatore sono detti linguaggi compilati.
Per il linguaggio di programmazione C, si sono costruiti normalmente solo compilatori per cui lo
si considera un linguaggio compilato.
Confronto Interprete – Compilatore:
L’esecuzione di un programma sorgente mediante un interprete è meno efficiente, poiché
impegna più memoria ed è meno veloce in quanto il codice macchina è generato durante
l’esecuzione stessa.
L’esecuzione tramite un compilatore parte invece da un codice già in linguaggio macchina,
che viene caricato e immediatamente eseguito.
Tuttavia un interprete consente una maggiore flessibilità nella fase di scrittura e prova di un
programma.
Negli ultimi anni si è sviluppato un approccio ibrido: software di sviluppo che consentono sia
l’interpretazione che la compilazione del codice sorgente.
IL LINGUAGGIO
La prima versione del linguaggio C fu realizzata nel 1972, da Dennis Ritchie, presso i Bell
Laboratories (AT&T). Ritchie si fondò su lavori precedenti, costruendo un linguaggio capace di
implementare molti più tipi di dati (interi, reali, caratteri, strutture).
Il C pur essendo un linguaggio di programmazione di alto livello conservò la prerogativa dei
linguaggi assembly, che interagivano direttamente con l’hardware della macchina (per questo
fu spesso indicato come di medio livello). Molte istruzioni in C (es: incremento e decremento)
sono direttamente traducibili in singole istruzioni di linguaggio macchina. Il C fu pensato come
un linguaggio di programmazione per esperti.
Il C si rivelò un linguaggio potente, efficiente, con sintassi compatta e fu molto apprezzato
in ambito industriale e scientifico.
Col C fu riscritto il sistema operativo Unix.
Il proliferare di più versioni del C, con conseguenti problemi di portabilità, fece si che nel 1990
fu definito lo standard ANSI C.
Nel 1998 fu definito uno standard ISO/IEC del C++.
1
IL COMPILATORE DEV-C++
Il compilatore Dev-C++ consente la programmazione anche secondo il C standard (ANSI C). All’apertura del programma
(icona
) si presenta la seguente finestra:
Il nuovo file è automaticamente nominato “Untitled1”: lo si può salvare subito assegnandogli il nome
desiderato, oppure al momento della compilazione.
E’ utile evidenziare il numero di riga. Per farlo: dal menu
Tools Editor Options Display
A questo punto spuntare l’opzione Line Numbers e chiudere con OK.
STRUTTURA DI UN PROGRAMMA
Un programma in C è diviso in due parti:
• sezione dichiarativa: in cui il programmatore indica i sottoprogrammi (librerie) e i dati che
intende utilizzare
• Chiamate a librerie esterne (#include): il preprocessore (precompilatore), prima
di avviare la fase della compilazione vera e propria sostituisce la riga con l’intero
contenuto del file.
#include
#include
<stdio.h>
“stdio.h”
la ricerca del file è effettuata all’interno della cartella standard
la ricerca del file è effettuata prima nella stessa cartella del file sorgente, poi in
quelle standard
• Definizione delle costanti (#define):
#define
•
•
MAX 100
il preprocessore sostituisce il valore di MAX (cioè 100) in tutti i
punti del programma in cui è presente
Dichiarazione delle variabili:
int x;
float y;
le variabili dichiarate in questa sezione hanno validità globale
•sezione esecutiva: in cui viene scritto il codice degli algoritmi che si intende far eseguire. Si tratta
della scrittura di funzioni. In tutti i programmi deve essere presente la funzione main().
NB: le variabili dichiarate all’interno delle funzioni hanno validità solo in ambito locale e si
sovrappongono e annullano le variabili globali con lo stesso nome.
Il programma precedente, scritto senza commenti risulta:
NB: è importante ricordare che con le istruzioni di assegnamento:
a = b;
z = x + y;
si carica nella variabile indicata a sinistra il valore dell’espressione a destra.
Il programma può essere mandato in esecuzione anche con i seguenti comandi:
• Menu Execute -- Compile & Run
• Da tastiera: F9
•
7
TIPI DI DATI
Quando il C fu scritto si decise di non fissare con
uno standard l’impegno di memoria dei tipi di
dati. Questa flessibilità consente di sfruttare al
meglio le caratteristiche dei diversi compilatori e
sistemi operativi.
NB: in C non sono definite variabili booleane. Per
le condizioni di VERO e FALSO si ricorre alle
variabili intere:
0 FALSE
0 TRUE
Programmare significa determinare quali operazioni eseguire e in quale sequenza per raggiungere la
soluzione
Perché il programmatore possa istruire il calcolatore sulle operazioni da fare serve un linguaggio noto ad entrambi che
sia da interfaccia fra i due operatori sapendo che:
Il calcolatore comprende solo sequenze di zeri e
uno (ad es. la sequenza 1001001 potrebbe significare, per un
ipotetico
calcolatore, “fai la somma”): linguaggio macchina
Il programmatore comprende le parole “fai la somma” (mentre 1001001 non significa nulla per lui): linguaggio umano
L’interfaccia « traduttore» è un linguaggio di programmazione ad alto livello (HLL) che può essere definito con:
Interprete: Le istruzioni del codice sorgente vengono ad
una ad una tradotte in linguaggio macchina e subito
eseguite dalla CPU
compilatoreTutto il codice sorgente viene tradotto in linguaggio macchina e memorizzato in un file detto programma
(o file o codice) eseguibile
In un HLL il programmatore non ha necessità di programmare le operazioni di base (ad es. leggere un numero dalla
tastiera, calcolare la radice quadrata, visualizzare una parola, ecc.) che sono programmate e compilate dal produttore
del traduttore e sono a disposizione del programmatore sotto forma di funzioni
I codici eseguibili (quindi già tradotti in linguaggio macchina) che realizzano queste operazioni vengono raggruppati in
file detti librerie (collezioni di funzioni di base)
Il processo di creazione di un eseguibile a partire dai sorgenti (build) è composto da 2 fasi:
- La compilazione che traduce il codice C in linguaggio macchina ottenendo il file oggetto:
- il linking: il file oggetto e le librerie vengono unite (collegate – link) in modo da ottenere un unico file eseguibile
Il compilatore verifica la correttezza del codice C e produce due tipi di errori:
Error: errori sintattici, impediscono la generazione del codice eseguibile
Warning: errori non sintattici che non impediscono la generazione del codice eseguibile; segnalano un possibile
problema che il compilatore risolve in base a regole generiche che potrebbero non essere quella corrette
Gli algoritmi
ALGORITMI, PROGRAMMI E DATI
Algoritmo = insieme di istruzioni che indicano come svolgere operazioni complesse su dei dati attraverso successioni di
operazioni elementari
Programma = algoritmo in un linguaggio
“comprensibile” dal computer.
Dato = informazione da elaborare rappresentata in un formato che consenta al programma di operare su di essa
Controllo del programma
L’ordine con cui le diverse operazioni devono essere eseguite è specificato da particolari costrutti linguistici, detti strutture di
controllo.
Si hanno tre strutture fondamentali:
sequenza
selezione (o scelta)
iterazione (o ciclo)
La sequenza indica una successione di operazioni che devono essere eseguite una dopo l’altra,
La selezione (o scelta) permette a un programma di proseguire secondo uno tra due (o più) flussi di istruzioni alternative
L’iterazione (o ciclo, o loop) consiste nella ripetizione di una o più istruzioni,.
I diagrammi a blocchi
• Il linguaggio dei diagrammi a blocchi è un possibile formalismo per la descrizione di algoritmi
• Il diagramma a blocchi, o flowchart, è una rappresentazione grafica dell’algoritmo
• Un diagramma a blocchi descrive il flusso delle operazioni da eseguire per realizzare la trasformazione,
definita nell’algoritmo, dai dati iniziali ai risultati
• Ogni istruzione dell’algoritmo viene rappresentata all’interno di un blocco elementare, la cui forma grafica è
determinata dal tipo di istruzione
• I blocchi sono collegati tra loro da linee di flusso, munite di frecce, che indicano il susseguirsi di azioni
elementari
I diagrammi a blocchi
• L’insieme dei blocchi elementari che descrivono un algoritmo deve soddisfare le
seguenti condizioni:
ciascun blocco di azione o di lettura/scrittura ha una sola freccia entrante ed una sola freccia
uscente
ciascun blocco di controllo ha una sola freccia entrante e due frecce uscenti
ciascuna freccia entra in un blocco oppure si innesta in un’altra freccia
ciascun blocco è raggiungibile dal blocco iniziale
il blocco finale è raggiungibile da qualsiasi altro blocco
Diagramma a blocchi per la selezione, in un mazzo
di chiavi, di quella che apre un lucchetto
ESERCIZI DI SVILUPPO DI ALGORITMI ORIENTATI ALLA PROGRAMMAZIONE
•
•
•
•
Partiamo dall’analisi del problema
Scriviamo la specifica funzionale
Introduciamo i contenitori di dati necessari e le relative operazioni elementari
Scriviamo l’algoritmo che opera su tali dati con un diagramma di flusso
Problema: telefonata
Descrizione:
vogliamo chiamare un abbonato con il telefono.
Requisiti, in cui prevediamo i diversi casi:
la telefonata viene eseguita con successo
messaggio “telefonata riuscita”
la telefonata non può essere portata a termine
messaggio “telefonata non riuscita”
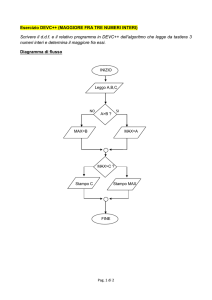
A) PROBLEMA MAGGIORE
• Descrizione: vogliamo il maggiore tra due numeri interi, x e y.
• Requisiti in cui prevediamo i diversi casi:
– se x - y > 0, il maggiore è x
– se x - y < 0, il maggiore è y
– se x - y = 0, x e y sono uguali
Esempio: lati di un triangolo. Come esempio di selezioni binarie in cascata si può considerare il seguente
PROBLEMA: “scrivere un algoritmo che consenta di stabilire se tre numeri, a, b, c possono essere i lati di un triangolo”.
ALGORITMO: come è noto, in un triangolo la somma di due lati qualsiasi è maggiore del terzo
Perciò dovranno essere contemporaneamente soddisfatte le tre condizioni:
a + b > c
a + c > b
b + c > a
LA PSEUDOCODIFICA
La pseudocodifica è un linguaggio per la descrizione di algoritmi secondo le regole della programmazione
strutturata
•
La descrizione di un algoritmo in pseudocodifica si compone di due parti...
la dichiarazione delle variabili usate nell’algoritmo
la descrizione delle azioni dell’algoritmo
• Tipo delle variabili
Il tipo di una variabile indica l’insieme dei valori che possono essere assegnati a quella variabile
Su costanti e variabili di un tipo è possibile effettuare le operazioni che sono proprie di quel tipo e
tutte le operazioni di confronto
Sono permessi i seguenti 4 tipi: integer, real, boolean, stringq
Per realizzare i cicli la maggior parte dei linguaggi (tra cui il C) dispone dei tre costrutti specifici
for , while , do-while
il cui uso costituisce uno dei fondamenti della cosiddetta programmazione strutturata che consentono di evitare
l’istruzione di salto, sconsigliata dai principi della programmazione strutturata
Iterazione enumerativa (for). Applicata ad una somma
for esamina il valore di una espressione di controllo o condizione, e se la trova diversa da zero (o “vera”) esegue una o più
istruzioni, altrimenti esce dal ciclo.
Le istruzioni vengono eseguite un numero prefissato di volte, dopo di che si ha l’uscita dal ciclo..
Iterazione. Affinché l’iterazione sia costituita da un numero finito di passi è necessario che nella linea di collegamento
sia inserito un simbolo di decisione che contenga la condizione di uscita dal ciclo.
Tale blocco di controllo si dice guardia, e si può trovare prima /dopo del gruppo di istruzioni che costituiscono il ciclo
Esempio: Somma dei primi n numeri naturali. Le pseudo istruzioni sono le seguenti:
leggi n;
somma = 0;
for (i=1; i<=n;
i=i+1)
somma = somma + i;
Il costrutto while inizia esaminando il valore di una espressione di controllo o
condizione.
Se essa è diversa da zero (ossia è vera) le istruzioni del ciclo vengono eseguite, altrimenti si ha
l’uscita dal ciclo.
Dopo le istruzioni del ciclo ne viene eseguita una che altera il valore dell’espressione di controllo, e
quando questa risulta uguale a zero si ha l’uscita del ciclo.
Iterazione con guardia alla fine (do-while). Il ciclo do-while inizia con la parola do, seguita dalla o
dalle istruzioni da eseguire, e termina con la parola while seguita dalla condizione che deve
essere verificata per la ripetizione del ciclo.
Esso realizza il diagramma di flusso già visto
LA PROGRAMMAZIONE
Introduzione
funzioni di Imput/output
variabili, dati e costanti, input e output
il controllo di flusso
Strutture iterative
Vettori
stringhe e caratteri
sottoprogramma
esercizi
AMBIENTE DI SVILUPPO: GEANY 1) NUOVO -- SCRITTURA FILE DI TESTO
2) SALVA COME ESTENSIONE .c, .cpp, .pas ec
3) compila compila esegui
Programmare significa determinare quali operazioni eseguire e in quale sequenza per raggiungere la
soluzione
Perché il programmatore possa istruire il calcolatore sulle operazioni da fare serve un linguaggio noto ad entrambi che
sia da interfaccia fra i due operatori sapendo che:
Il calcolatore comprende solo sequenze di zeri e
uno (ad es. la sequenza 1001001 potrebbe significare, per un
ipotetico
calcolatore, “fai la somma”): linguaggio macchina
Il programmatore comprende le parole “fai la somma” (mentre 1001001 non significa nulla per lui): linguaggio umano
L’interfaccia « traduttore» è un linguaggio di programmazione ad alto livello (HLL) che può essere definito con:
Interprete: Le istruzioni del codice sorgente vengono ad
una ad una tradotte in linguaggio macchina e subito
eseguite dalla CPU
compilatoreTutto il codice sorgente viene tradotto in linguaggio macchina e memorizzato in un file detto programma
(o file o codice) eseguibile
In un HLL il programmatore non ha necessità di programmare le operazioni di base (ad es. leggere un numero dalla
tastiera, calcolare la radice quadrata, visualizzare una parola, ecc.) che sono programmate e compilate dal produttore
del traduttore e sono a disposizione del programmatore sotto forma di funzioni
I codici eseguibili (quindi già tradotti in linguaggio macchina) che realizzano queste operazioni vengono raggruppati in
file detti librerie (collezioni di funzioni di base)
Il processo di creazione di un eseguibile a partire dai sorgenti (build) è composto da 2 fasi:
- La compilazione che traduce il codice C in linguaggio macchina ottenendo il file oggetto:
- il linking: il file oggetto e le librerie vengono unite (collegate – link) in modo da ottenere un unico file eseguibile
Il compilatore verifica la correttezza del codice C e produce due tipi di errori:
Error: errori sintattici, impediscono la generazione del codice eseguibile
Warning: errori non sintattici che non impediscono la generazione del codice eseguibile; segnalano un possibile
problema che il compilatore risolve in base a regole generiche che potrebbero non essere quella corrette
STRUTTURA DI UN PROGRAMMA
Un programma in C è diviso in due parti:
• sezione dichiarativa: in cui il programmatore indica i sottoprogrammi (librerie) e i dati che
intende utilizzare
• Chiamate a librerie esterne (#include): il preprocessore (precompilatore), prima
di avviare la fase della compilazione vera e propria sostituisce la riga con l’intero
contenuto del file.
#include
#include
<stdio.h>
“stdio.h”
la ricerca del file è effettuata all’interno della cartella standard
la ricerca del file è effettuata prima nella stessa cartella del file sorgente, poi in
quelle standard
• Definizione delle costanti (#define):
#define
•
•
MAX 100
il preprocessore sostituisce il valore di MAX (cioè 100) in tutti i
punti del programma in cui è presente
Dichiarazione delle variabili:
int x;
float y;
le variabili dichiarate in questa sezione hanno validità globale
•sezione esecutiva: in cui viene scritto il codice degli algoritmi che si intende far eseguire. Si tratta
della scrittura di funzioni. In tutti i programmi deve essere presente la funzione main().
NB: le variabili dichiarate all’interno delle funzioni hanno validità solo in ambito locale e si
sovrappongono e annullano le variabili globali con lo stesso nome.
ESEMPIO ; Programma che evidenzia alcune opzioni di visualizzazione dei numeri reali
Funzioni di I/O per numeri
Per utilizzare le funzioni di Input/Output bisogna includere il file di intestazione (header file) denominato <stdio.h>
<stdio.h> contiene la sintassi d’uso di varie funzioni e la definizione di alcune costanti simboliche (#define), (EOF) usata da
alcune funzioni per segnalare la fine dell’input o del file
Sintassi:
---------------------------------------------------------------------------------------------------------scanf(stringa di formato, lista di variabili)
scanf("%d", &i);
Legge valori dalla tastiera e li assegna alle variabili indicate nella lista di variabili &i
Per ciascuna variabile c’è il corrispondente tipo nella stringa di formato scanf("%d%d",&a, &b);
Input da tastiera : scanf("%d", &i) Notare che
- la variabile i è preceduta dal carattere &
- La funzione precedente "%d", assegna alla variabile i il valore intero letto dalla tastiera
-----------------------------------------------------------------------------printf(stringa di formato, lista di espressioni)
printf("valore digitato: %d", i);
Visualizza il testo indicato nella stringa di formato con i valori elencati nella lista di espressioni a, b
Ciascun valore della lista di espressioni viene visualizzato sostituendolo alla corrispondente direttiva di conversione nella stringa di
formato printf("Lat: %d, Lon: %d\n", a, b);
Output su video printf("%d", i) notare che:
- la variabile i non è preceduta dal carattere &
- la funzione precedente «d» visualizza un numero intero: contenuto nella variabile i
In conclusione per rappresentare una o piu variabili si deve prenotare la posizione che le variabili devono occupare all’interno
del messaggio per mezzo di specificatori di formato
Lo specificatore di formato è un
simbolo, (d: intero, f: float, c: char, ecc) preceduto da % associato al tipo di variabile da
rappresentare in funzione delle esigenze del programmatore
d: specificatore di formato, i: variabile
scanf("%d", &i);
L’esecuzione di questa istruzione fa
sì che il sistema attenda in input un
dato da parte dell’utente.
LETTURA E STAMPA
#include <stdio.h>
#include <stdlib.h>
int main()
{
int i; // istruzione dichiarativa
// istruzioni operative
printf("digita un numero ");
scanf("%d", &i); //legge i
printf("valore digitato: %d\n", i);
/* istruzione di ritorno al sistema operativo */
return EXIT_SUCCESS;
}
Il primo esperimento Si vuole scrivere un programma in linguaggio C che chieda all’utente di introdurre da tastiera due
numeri interi e visualizzi il valore della loro somma sul video
premessa
I numeri richiesti vengono immagazzinati nella memoria centrale del calcolatore (RAM)
Ciascun numero sarà immagazzinato in una piccola porzione di memoria detta variabile costituita da un certo numero di
byte
A ogni variabile il programmatore dà un nome per potersi riferire ad essa
Anche il risultato della somma dovrà essere immagazzinato nella memoria del calcolatore in una variabile, quindi avremo:
1.Chiedere il primo numero e metterlo in una variabile di nome A
2.Chiedere il secondo numero e metterlo in una variabile di nome B
3.Calcolare la somma di A e B e mettere il risultato in una variabile di nome S
4.Visualizzare il contenuto della variabile
Assegnazioni di variabili
Assegnare un valore ad una variabile significa memorizzare in essa un valore
Per assegnare un valore si usa il simbolo ‘=’:
X = 12
Il valore può essere il risultato di un calcolo:
S = A+B
questo indica che in Sviene memorizzato il valore risultante dal calcolo A+B
Il segno = significa “prende il valore di”:
S prende il valore del risultato di A+B
Ogni volta che si assegna un valore ad una variabile, il contenuto precedente viene perso
Definizione delle variabili
Tutte le variabili utilizzate nel programma devono essere definite
Le definizioni vanno collocate tutte insieme
prima delle istruzioni eseguibili:
int A, B, S // intindica che A, Bed Ssono variabili adeguate a contenere valori interi
scanf("%d", &A);
scanf("%d", &B);
S = A + B;
printf("%d", S);
IL PRIMO ESPERIMENTO
Le istruzioni che costituiscono il programma devono essere racchiuse tra parentesi graffe per formare un blocco. Se questo è l’unico
presente, deve essere chiamato main:
Per far terminare il programma, si usa l’istruzione return (seguita da un numero, in genere 0) collocata alla fine del blocco main
Per utilizzare le funzioni di input/output (I/O) è necessario che all’inizio del file C sia indicato il nome del file di intestazione che le
descrive (stdio.h) con la direttiva #include:
#include <stdio.h>
main()
{
int A, B, S;
scanf("%d", &A);
scanf("%d", &B);
S = A + B;
printf("%d", S);
return 0;
}
Sebbene non obbligatorio secondo lo standard, molti compilatori segnalano un errore se main non è preceduto da int
#include <stdio.h>
int main()
Miglioramento input
Quando il programma parte, non informa l’utente di essere in attesa che egli introduca due valori da sommare
E’ utile far precedere ciascuna scanf da un’istruzione printf che informi l’utente su che cosa egli debba fare:
printf("Introduci 1o valore: ");
scanf("%d", &A);
printf("Introduci 2o valore: ");
scanf("%d", &B);
IL PRIMO ESPERIMENTO:
Miglioramento output
Il risultato del calcolo viene mostrato a video come semplice numero, ma è preferibile aggiungere una scritta che ne specifichi
il significato
Si può aggiungere tale scritta tra le virgolette della stessa printfche visualizza S:
printf("La somma vale: %d", S);
Soluzione finale
#include <stdio.h>
int main()
{
int A, B, S;
printf("Primo valore? ");
scanf("%d", &A);
printf("Secondo valore? ");
scanf("%d", &B);
S = A + B;
printf("La somma vale: %d", S);
return 0;
}
/* LISTATO 1.5 Calcolo area rettangolo */
#include <stdio.h>
int base, altezza, area;
main()
{
printf("AREA RETTANGOLO\n\n");
printf("Valore base: ");
scanf("%d", &base);
printf("Valore altezza: ");
scanf("%d", &altezza);
area = base*altezza;
printf("Base: %d\n", base);
printf("Altezza: %d\n", altezza);
printf("Area: %d\n", area);
}
APPROFONDIMENTI printf
#define BASE 3
Grazie a questa istruzione, all’interno del programma potremo utilizzare BASE al posto del valore intero 3.
La definizione stessa di costante implica che il suo valore non può essere modificato: BASE può essere utilizzata
in un’espressione a patto che su di essa non venga mai effettuato un assegnamento.
Il programma del paragrafo precedente potrebbe quindi essere trasformato in quello del Listato 1.4
/* LISTATO 1.4: Calcolo area rettangolo, prova utilizzo
costanti */
#include <stdio.h>
#define BASE 3
#define ALTEZZA 7
main()
{
int area;
area = BASE * ALTEZZA;
printf("Base: %d\n", BASE);
printf("Altezza: %d\n", ALTEZZA);
printf("Area: %d\n", area);
}
Per fare in modo che il programma precedente calcoli l’area del
rettangolo con base 102 e altezza 34, è sufficiente modificare le
linee dov’è presente l’istruzione define:
#define BASE 102
#define ALTEZZA 34
Per lasciare una linea vuota si deve inserire un ulteriore \n nell’istruzione printf all’interno di doppi apici:
printf("AREA RETTANGOLO\n\n").
Il primo \n fa andare il cursore a linea nuova dopo la visualizzazione di AREA RETTANGOLO, il secondo \n
lo fa scorrere di un ulteriore linea.
se si vuole lasciare una linea prima della visualizzazione si fa precedere \n ad AREA RETTSANGOLO
printf("\nAREA RETTANGOLO\n\n\n");
E possibile inserire il salto in qualsiasi posizione all’interno dei doppi apici, come nel seguente esempio:
printf("AREA \nRET\nTAN\nGOLO");
che provoca in fase di esecuzione la visualizzazione:
AREA RET TAN GOLO
Si possono stampare più variabili con una sola printf, indicando prima tra doppi apici i formati in cui si
desiderano le visualizzazioni e successivamente i nomi delle rispettive variabili.
L’istruzione
printf("%d %d %d", base, altezza, area);
inserita alla fine del programma precedente stamperebbe, se i dati immessi dall’utente fossero ancora 10
e 13:
10 13 130
Per raffinare ulteriormente l’uscita di printf, si possono naturalmente inserire degli a capo a piacere:
printf("%d\n%d\n%d", base, altezza, area);
che hanno come effetto
10
13
130
All’interno dei doppi apici si possono scrivere i commenti che devono essere stampati. Per esempio, se la
visualizzazione della terza variabile deve essere preceduta da Area:, l’istruzione diventa la seguente:
printf("%d\n%d\nArea: %d", base, altezza, area);
10
13
Area: 130
Analogamente si può procedere con le altre variabili:
che darà in uscita
printf("Base: %d\nAltezza: %d\nArea: %d", base, altezza, area);
Si tratta dunque di inserire i vari messaggi che devono apparire sul video tra doppi apici, prima o dopo i simboli che
descrivono i formati degli oggetti da visualizzare.
Così come \n effettua un salto a linea nuova, la sequenza \t provoca l’avanzamento del cursore di uno spazio di
tabulazione:
printf("Base: %d\tAltezza: %d\tArea: %d", base, altezza, area); produce come uscita
E possibile inserire nella printf, al posto delle variabili, delle espressioni, di tipo specificato dal formato
10*13);
printf("Area: %d",
Il %d ci indica che il risultato dell’espressione è di tipo intero; l’istruzione stamperà 130. Un’espressione può
naturalmente contenere delle variabili: printf("Area: %d", base*altezza);
Si può definire all’interno di una istruzione printf anche il numero di caratteri riservati per la visualizzazione
di un valore, nel seguente modo:
printf("%5d%5d%5d", base, altezza, area);
Il %5d indica che verrà riservato un campo di cinque caratteri per la visualizzazione del corrispondente valore,
che sarà sistemato a cominciare dall’estrema destra di ogni campo:
Inserendo poi un carattere - dopo il simbolo di percentuale e prima della lunghezza del campo il valore viene
sistemato a cominciare dall’estrema sinistra della maschera.
L’istruzione printf("%-5d%-5d%5d", base, altezza, area);
Scrivere un programma che chieda di introdurre 3 numeri A, B e C dalla tastiera e successivamente visualizzi il risultato dei
seguenti calcoli:
1) A–B
2) A–B+C
3) A–B–C
2. Scrivere un programma che chieda due numeri e li memorizzi nelle variabili A e B. Il programma deve ora scambiare il contenuto di
A e di B (es. se inizialmente A contiene 12 e B 27, dopo lo scambio A contiene 27 e B 12).
#include <stdio.h>
int main()
{
int A, B, C, X, Y, Z;
printf("Primo valore? ");
scanf("%d", &A);
printf("Secondo valore? ");
scanf("%d", &B);
printf("Terzo valore? ");
scanf("%d", &C);
X = A-B;
printf("Risultato 1 = %d\n", X);
Y = A-B+C;
printf("Risultato 2 = %d\n", Y);
Z = A-B-C;
printf("Risultato 3 = %d\n", Z);
return 0;
}
#include <stdio.h>
int main()
{
int A, B, Temp;
printf("Primo valore? ");
scanf("%d", &A);
printf("Secondo valore? ");
scanf("%d", &B);
Temp = A;
A = B;
B = Temp;
printf("%d\n", A);
printf("%d\n", B);
return 0;
}
La soluzione con 2 variabili temporanee è
meno efficiente (usa una variabile in più
ed
esegue
un’operazione
di
assegnamento in più) e non è quindi
preferibile:
TempA = A;
TempB = B;
A = TempB;
B = TempA;
SEQUENZE DI ESCAPE
• le funzioni di output (come printf) hanno il compito di
stampare a video (o, a seconda dei casi, in uno specifico
stram) la STRINGA racchiusa tra parentesi tonde.
Una stringa è una sequenza di CARATTERI racchiusa tra
virgolette.
Si definiscono caratteri:
- lettere (a, X, é...)
- cifre (0, 1, 2...)
- simboli (+, £, *...)
- sequenze di escape (o di controllo)
In particolare, le sequenza di escape sono sequenze di
caratteri che provocano particolari comportamenti della
funzione printf. Ad esempio, la sequenza 'n' fa sì che il
cursore si posizioni nella posizione iniziale della riga
successiva dello schermo.
Riporto qui di seguito l'elenco completo delle sequenza di
escape
•
•
La programmazione per moduli: file HEADER
La scrittura delle funzioni all’interno dello stesso file che le richiama non consente ad altri file il loro utilizzo.
Per ovviare a questo inconveniente si sposta il codice della funzione in altro file: il file header.
Si tratta di file con estensione … .h.
ESEMPIO:funzione potenza()
In alternativa si può lasciare nel file header le direttive al preprocessore e la dichiarazione
dei prototipi delle funzioni, e spostare in altro file c la definizione delle funzioni.
ESEMPIO precedente:
LA PROGRAMMAZIONE IN LINGUAGGIO C
1. VARIABILI
2. DATI E COSTANTI
3. IMPUT E OUTPUT DI DATI
La
Tipi di dati di base
variabile è una porzione di memoria dove collocare il dato
In C esistono diversi tipi di variabili, che servono per rappresentare tipi di dato diversi, dai grossi numeri ai testi. Alcuni linguaggi permettono
la dichiarazione di variabili generiche, ma poter assegnare a ciascun dato il tipo di variabile adeguato, consente anche una migliore
gestione della memoria (alla fonte).
Nella tabella seguente sono mostrati i vari tipi, la parola chiave C che li identifica (char per carattere, int per intero, etc.), la tipologia di
informazioni che rappresentano ed il numero di byte necessari per la loro rappresentazione in C:
Specicatori di tipo delle variabili:
I void: tipo di dato indefinito, ovvero non specificato,
I char: rappresenta i caratteri nel set a disposizione sul calcolatore,
I int: rappresenta numeri interi,
I float: numeri in virgola mobile (decimali) a precisione singola,
I double: rappresenta numeri virgola mobile a precisione doppia.
Modicatori di tipo: modicano il range di valori ammissibili
per il tipo
I short: riduce il numero di valori memorizzabili,
I long: aumenta il numero di valori memorizzazabili,
I signed: il tipo di dato e dotato di segno,
I unsigned: il tipo di dato non e dotato di segno.
Modificatori
del tipo di accesso: const volatile
I
- una variabile di tipo const, e non può essere modificata dal
programma, ma gli si può assegnare un valore iniziale che sarà
mantenuto per tutta la durata dell'esecuzione del programma.
const int x = 5;
- Il modificatore volatile viene utilizzato per indicare al compilatore
che il valore di una variabile può essere modificato in modo non
esplicitamente specificato dal programma.
In C il char è considerato un intero per cui
int j
J = ‘A ‘+ ‘B2 ‘= IN ASCII = 65 + 66
I tipi di dati primari, eccetto il tipo void, ammettono dei modificatori di tipo. Tali
modificatori (signed, unsigned, long, short) sono impiegati per adattare con
maggiore precisione i tipi di dati fondamentali alle esigenze del programmatore
che influiscono sull’economia complessiva del programma (velocita,occupazione
di memoria, tempo di esecuzione)
Esempio
Si vogliono memorizzare 2 milioni di valori interi compresi tra 0 e 100. I valori sono compatibili (ossia nel range) di tutti i tipi di dati
visti, dai char (arrivano almeno fino a 127) ai long double, ad esempio si considerino le due soluzioni seguenti:
si usa il tipo char: si occupano 2 MB e i calcoli sono veloci
si usa il tipo double: si occupano 16 MB e i calcoli sono molto più lenti (senza alcun vantaggio rispetto al caso
precedente)
Inizializzazione delle variabili
L’assegnazione esplicita del valore iniziale alle variabili contestualmente alla definizione è detta inizializzazione
I valori usati per inizializzare possono essere espressioni che utilizzano variabili già inizializzate
int x = 12,
y = 27*3*x;
double pigreco = 4.0*atan(1.0);
atan = arctg
const double Pi = 3.141592653;
const double Pi = 4.0*atan(1.0);
const può essere messo prima o dopo il nome di tipo a cui si riferisce. const int x = 12; o int const x = 12;
ESEMPIO
/* Programma che acquisisce da tastiera due numeri, li somma e visualizza il risultato su monitor */
#include <stdio.h>
#include <stdlib.h> float
x, z;
int y;
int main()
{ printf(“\aInserisci un valore per la variabile x: ");
/* Con \a si fa emettere un beep */
scanf("%f", &x); /* funzione che acquisisce da tastiera un numero reale e lo pone all'indirizzo della variabile x. */
printf(“\aInserisci un valore per la variabile y: ");
scanf("%d", &y);
z = x + y;
printf(“La somma risulta z = x + y = %f", z);
system(“pause”);
}
CONVERSIONE di TIPO delle variabili
Il compilatore del C non esegue alcun controllo sul tipo dei dati: se si attribuisce un numero
reale ad una variabile intera si commette un errore che il compilatore non segnala.
Esempi:
int x = 2;
int x =
2.4;
in x viene correttamente caricato il valore 2
in x viene caricata solo la parte intera: 2; la parte decimale 4 non viene
presa in considerazione
float x = 2;
float x =
2.7;
in x viene correttamente caricato il valore 2
in x viene correttamente caricato il valore 2.7;
L’assenza di controllo sul tipo di dati può creare qualche problema in alcune operazioni aritmetiche.
Occorre tenere presente che il compilatore C opera sempre con la seguente sequenza:
• prima di eseguire l’operazione , esamina gli operandi, che devono essere dello stesso tipo, se
non lo sono converte il tipo minore nel tipo maggiore e solo dopo esegue l’operazione;
• il risultato dell’operazione è fornito con lo stesso tipo degli operandi.
Esempi:
int x = 3; float
y = 5.6; int
z = x + y;
Gli operandi sono di tipo diverso: il tipo minore (int) viene convertito
nel tipo maggiore(float), la somma si svolge quindi con due valori float,
il risultato però è caricato in una variabile tipo intero z, e ciò comporta
la perdita della parte decimale: in z risulta memorizzato il numero 8.
NB: Per risolvere il problema, la variabile z deve essere dichiarata float.
int x = 7;
int y = 2;
float z = x / y;
Gli operandi (x e y) sono dello stesso tipo: intero. Il compilatore C
fornisce il risultato come intero: 3 invece che 3.5 e nella variabile z, pur
essendo di tipo float, viene caricato il numero 3.
Per far si che la divisione fornisca il risultato con la virgola (tipo float), i
suoi operandi devono essere variabili (o numeri) reali.
NB: una possibile soluzione è la seguente: float z = (1.0 * x) / y;
prima si esegue la moltiplicazione, per cui il compilatore trasforma il contenuto della x da
valore intero a valore float (da 7 a 7.0) e fornisce il risultato come float (7.0);
successivamente deve essere eseguita una divisione tra un float e un int , per cui prima il valore
int (2) è convertito in float (2.0); il risultato (3.5) è quindi fornito come float e nella variabile z
viene correttamente memorizzato il valore 3.5.
In alternativa si deve operare una conversione esplicita in float di uno dei due operandi:
esempio:
float z = (float) x / y;
In questo caso: x è prima convertito in float e poi reso disponibile per la divisione.
NB: x è convertito in float solo per quella istruzione, nelle istruzioni successive resta int.
ESEMPIO: programma che esegue una divisione tra una costante tipo intero e una variabile tipo intero
#include <stdio.h>
#include <stdlib.h>
const x = 7;
/* la variabile x è dichiarata costante , cioè di sola lettura (solo per i tipi
int e char) il tentativo di modificarla provoca un messaggio di errore */
int y, z;
float w, q;
int main()
{ printf("Inserire un valore per y: ");
scanf("%d", &y);
z = x/y; w
= x/y;
q = (float)x/y;
/* float davanti alla costante x converte quest’ultima in variabile reale */
printf(“Risultati della divisione:\nz = %d \nw = %f
system(“pause”);
}
\nq = %f \n\n”, z, w, q);
Direttiva
#define
Con la direttiva #define si assegna un valore a un simbolo. Il preprocessore, nella fase
preliminare alla compilazione, sostituisce il simbolo presente nel codice della funzione main con il
valore assegnato.
La direttiva #define non occupa memoria.
Esempi di direttive #define:
#define MAX 20
NB: l’alternativa con const MAX = 20 avrebbe richiesto un impegno di memoria.
#define MAX 31.4 Definizione di costanti reali
#define x 24*1.5
Il simbolo x indica una moltiplicazione
#define messaggio printf(“Sistema pronto!”)
Il simbolo messaggio indica la visualizzazione di un testo
#define TEST0(x) printf(“\nValore di x: %d, x”)
#define avviso “Si è verificato un errore!”
#define pari(x)
x%2 == 0
Controllo sull’uguaglianza a zero di x ; ma è più sicuro scrivere: ((x)%2 == 0)
ESEMPIO : Applicazione di macro realizzate con la direttiva #define
#include <stdio.h>
#include <stdlib.h>
#define testo1 “Inserire un numero intero:
” carica(x) scanf(“%d”, &x)
#define
#define testo2(x) printf(“\nNumero inserito: x = %d\n”, x)
int a;
int main()
{ printf(testo1);
carica(a);
testo2(a);
system(“pause”); }
ESEMPIO: programma che utilizza la scrittura compatta degli operatori aritmetici
L’esecuzione del programma genera la seguente finestra:
OSSERVAZIONI
• Sono possibili assegnazioni multiple: x = y =9;
• Istruzione da evitare: x = x++; è indefinita e il programma smette di funzionare
• Gli operatori aritmetici (+, -, *, /) e di confronto hanno precedenza rispetto agli operatori logici
Il NOT logico ha precedenza rispetto all’AND logico, il quale ha precedenza rispetto all’OR logico
Approfondimenti: Enumerazioni
Un’enumerazione serve per definire una lista di identificatori aventi valori costanti di tipo int
Sintassi:
enum [nome] {cost1, cost2, ...};
enum boolean {FALSE, TRUE);
definisce le due costanti:
FALSE (con valore 0)
I nomi delle costanti vengono in genere scritti in maiuscolo
Al primo identificatore viene assegnato il valore 0, al secondo identificatore 1, e così via
I valori delle costanti possono ripetersi, anche nella stessa numerazione
enum a {A=1, B=1, C=2, D=2, ecc.};
Costanti simboliche
E’ possibile dare un nome (un identificatore) ad una quantità costante, questo nome è detto simbolo (per convenzione in
maiuscolo)
Prima della compilazione, il preprocessore cerca i simboli definiti con direttive #define:
#define nome sequenza_di_caratteri
e sostituisce ogni occorrenza del simbolo nome con la corrispondente sequenza_di_caratteri
#define TRUE
1
Esempi
#define
#define
FALSE 0
DIM
80
Nell’esempio il preprocessore cerca ogni occorrenza di DIM e la sostituisce con 80 (i due caratteri 8 e 0), quindi una riga
di codice come la seguente:
int vett[DIM];
viene trasformata in:
int vett[80];
prima della compilazione vera e propria
Esercizi
Scrivere un programma che chieda 4 numeri double e ne calcoli la media (double) con 2 decimali.
2. Scrivere un programma che chieda un valore double e lo visualizzi con le 3 specifiche di conversione %f, %e e %g.
1.
#include <stdio.h>
int main()
{
double a, b, c, d;
double media;
printf("Primo valore: ");
scanf("%lf", &a);
printf("Secondo valore: ");
scanf("%lf", &b);
printf("Terzo valore: ");
scanf("%lf", &c);
printf("Quarto valore: ");
scanf("%lf", &d);
media = (a+b+c+d)/4;
printf("La media e': %.2f\n",
media);
return 0;
}
#include <stdio.h>
int main()
{
double x;
printf("Introduci un valore: ");
scanf("%lf", &x);
printf("Visualizzazione con %%f: %f\n",
x);
printf("Visualizzazione con %%e: %e\n",
x);
printf("Visualizzazione con %%g: %g\n",
x);
return 0;
}
Listato 1.6: programma completo che utilizza
la funzione abs().
/* LISTATO1.6: Esempio utilizzo di abs() */
#include <stdio.h>
#include <math.h>
main()
{
int a, b, segmento, lunghezza;
printf("\n\nLUNGHEZZA
SEGMENTO\n");
printf("Primo estremo: ");
scanf("%d", &a);
printf("Secondo estremo: ");
scanf("%d", &b);
segmento = a-b;
lunghezza = abs(segmento);
printf("Lunghezza
segmento:
lunghezza);
%d\n",
Un esempio di funzione C predefinita è
abs(i), che prende il nome da
absolute: se dopo la parola abs(),
all’interno delle parentesi tonde, viene
inserito un numero intero, la funzione
abs()
ne restituisce il
valore assoluto, che è quindi possibile
catturare assegnandolo a una variabile o
utilizzandolo
direttamente all’interno
di un’espressione.
Se quindi w e j sono variabili di tipo
intero, l’istruzione
w =
abs(j); assegna a w il valore
assoluto di j. All’interno delle parentesi
tonde può essere inserito direttamente un
valore, come nel caso
w = abs(3);
che assegna a w il valore 3, o come nel
caso
w = abs(-186); che assegna a w il
valore 186.
per poter utilizzare tale funzione si deve
dichiarare esplicitamente nel programma,
prima del main, l’inclusione del
riferimento a tale libreria.
#include <math.h>
math.h
Espressioni e funzioni matematiche
ESPRESSIONI NUMERICHE
somma
sottrazione
moltiplicazione
divisione
resto della divisione intera
+
*
/
%
Operatori unari: un solo operando
x
x
x
x
x
=
=
=
=
=
2
a + b;
a - b;
a * b;
a / b;
a % b;
La divisione tra interi produce risultato intero con
troncamento della parte frazionaria
Il resto può essere calcolato solo con operandi di
tipo intero (non floating-point)
Precedenza degli operatori
1
3
Le regole di precedenza (o priorità) specificano in
quale ordine vengono eseguiti i calcoli
Raggruppati in livelli di priorità decrescente:
1.
+ –
2. ()
3. * / %
4. + –
segno
somma e sottrazione
Esempi
x = a+b*c;
x = (a+b)*c;
x = a + -b;
prima la moltiplicazione
prima la somma
a + (-b)
Operatori di assegnamento
La forma di assegnamento: variabile op= espressione essendo op un operatore del C, equivale a:
variabile = variabile op espressione x += 5;
equivale a x = x + 5;
Operatori ++ e ––
Incrementano/decrementano di 1 una variabile: ++a;
++a incrementa a di 1 prima che a venga utilizzata nel calcolo (incremento prefisso)
a++ incrementa a di 1 dopo che a è stata utilizzata nel calcolo (incremento postfisso)
––a e a–– decrementano a di 1
Esempi:
a = 5;
x = ++a;
ora a vale 6 e x vale 6
a = 5;
x = a++;
ora a vale 6 e x vale 5
Funzioni matematiche
Richiedono che venga indicato il file di intestazione (header file) <math.h> che ne descrive la sintassi
Se i valori passati non sono di tipo double, vengono automaticamente promossi a tale tipo (per effetto del
prototipo <math.h>)
Le funzioni trigonometriche usano i radianti (180o = rad)
Valori casuali
La funzione rand ogni volta che viene chiamata produce un diverso valore intero compreso tra 0 e RAND_MAX (estremi
inclusi) con distribuzione uniforme
x=rand()
Valori logici
Il valore 0 equivale a falso, Ogni valore 0 equivale a vero
Quindi nelle espressioni relazionali scrivere
!=0 è opzionale:
if (trovato) ... equivale a if (trovato != 0) ...
Operatori logici: Operatori (in ordine di priorità
decrescente):
NOT, ha priorità superiore agli operatori relazionali e
aritmetici If( !(a>b) )...
AND, ha priorità inferiore agli operatori relazionali e
Espressioni logiche:Si possono usare le parentesi
per cambiare l’ordine di valutazione delle operazioni
aritmetici if ( a>b && c!=0 ) ...
OR, ha priorità inferiore agli operatori relazionali e
aritmetici if ( a>b || c!=0 ) ...
Esempi
if ( a>b || c<d && a!=0 ) ... equivale a:
if (trovato == 0)
... equivale a:
e quindi, essendo il !=0 sopprimibile, a:
if ( a>b ||
(c<d && a!=0) ) ...
if ( !(trovato != 0) )... Il valore 0 equivale a falso,
Ogni valore 0 equivale a vero
if (!trovato)...
Attenzione: è errato scrivere una condizione come a < b < c, occorre spezzarla come a<b && b<c
Valutazione minima di && e ||
Gli operatori &&e ||vengono valutati sempre da sinistra a destra
La valutazione delle espressioni termina non appena è possibile
stabilire se la condizione è complessivamente vera o falsa:
if (cond1 && cond2 && cond3 && ...) ...
Se cond1 è falsa (0), non si valutano le condx successive e complessivamente la condizione dà 0 (falso)
if (cond1 || cond2 || cond3 || ...) ...
Se cond1 è vera (!=0), non si valutano le condx successive e complessivamente la condizione dà 1 (vero)
Espressioni relazionali
Confrontano due valori, I valori possono essere espressioni
Se il risultato è vero danno risultato 1 (non un generico valore diverso da 0), se falso danno 0
Operatori: == uguale
!= diverso
maggiore
>= maggiore o uguale
<
Hanno priorità inferiore alle operazioni aritmetiche
prima calcola le espression
i
a-5e 12*x
poi
minore
if (a-5 >= 12*x)...
ne fa il confronto
Hanno priorità maggiore degli operatori di assegnamento
x = 5 > 2;
prima fa il confronto tra 5 e 2 poi
<= minore o uguale
ne assegna il risultato
int x;
a x
>
Scrivere un programma che chieda 4 numeri int, ne calcoli la media,
la memorizzi in una variabile float e la visualizzi con 2 decimali.
1.
Scrivere un programma che chieda un valore double di temperatura in
gradi Fahrenheit e calcoli i valori delle corrispondenti temperature in
gradi Celsius e Kelvin (entrambi con parte frazionaria).C 5/9 *(F 32), K
C 273.15
#include <stdio.h>
int main()
{
double f, c, k;
printf("Temperatura in gradi Fahrenheit: ");
scanf("%lf", &f);
c = 5.0/9.0 * (f-32);
k = c + 273.15;
printf("Celsius: %f\nKelvin: %f\n", c, k);
return 0;
}
/* Considerazioni: c = 5/9 * (f-32);
da' sempre 0 perche' 5 e 9 sono interi e la divisione tra
interi da' risultato intero con troncamento (appunto 0)
c = (f-32) * 5/9; con il float il risultato ò è corretto,*/
#include <stdio.h>
int main()
{
int a, b, c, d;
float media;
printf("Primo valore: ");
scanf("%d", &a);
printf("Secondo valore: ");
scanf("%d", &b);
printf("Terzo valore: ");
scanf("%d", &c);
printf("Quarto valore: ");
scanf("%d", &d);
media = (a+b+c+d)/4.0F;
printf("La media e': %.2f\n", media);
return 0;
}
/* Considerazioni: media = (a+b+c+d)/4.0; media = (float)(a+b+c+d)/4;
media = (float)(a+b+c+d)/4.0F; media = ((float)a+b+c+d)/4; */
IL CONTROLLO DI FLUSSO
STRUTTURE
Il C è un linguaggio di programmazione strutturato, nel senso che il flusso delle operazioni da
eseguire è gestito mediante strutture, tra le quali molto importanti sono:
Strutture SELETTIVE:
• IF … ELSE
• SWITCH
Strutture ITERATIVE (RICORSIVE):
• Ciclo WHILE
• Ciclo FOR
18
Struttura IF … ELSE
Quando l’esecuzione di un certo codice è subordinata a una condizione, si ricorre alla struttura
else. La struttura può essere utilizzata in più modi:
if (condizione)
{
………
Se la condizione è vera viene eseguito il codice compreso tra le parentesi graffe
}
ESEMPIO:
programma che esegue un controllo rispetto a una soglia
#include <stdio.h>
#include <stdlib.h>
const soglia = 10; /* la variabile soglia è dichiarata costante , cioè di sola lettura; il tentativo di
modificarla provoca un messaggio di errore */
int y;
int main()
{ printf("Inserire un valore per y: ");
scanf("%d", &y);
if(y > soglia)
{ printf("Valore non valido. Supera quello della soglia! \n"); }
system(“pause”);
}
if …
Struttura alternativa
if (condizione)
Se la condizione è vera si esegue il codice immediatamente seguente
{
………
altrimenti si esegue il codice che segue ‘else’
}
else
{
………
}
ESEMPIO: programma che verifica un valore rispetto a una soglia.
#include <stdio.h>
#include <stdlib.h> int soglia = 10, y;
int main()
{ printf("Inserire un valore per y: "); }
scanf("%d", &y);
if(y > soglia)
{ printf("Valore non valido. Supera quello della soglia!"
}
else
{ printf("Valore valido.");
}
system(“pause”);
}
Struttura alternativa
Struttura alternativa
if (condizione1)
………
{
}
ESEMPIO: programma che esegue un controllo con più condizioni else if (condizione2)
{………
}
#include <stdio.h>
#include <stdlib.h> int main(){
if (condizione1)
{
………
}
else if (condizione2)
{
………
}
else
………
{
}
unsigned int y;
printf("Inserire un valore intero per y: "); scanf("%d", &y);
if(y < 6 && y >= 1)
/* per maggiore chiarezza: if((y < 6) && (y >= 1)) */
{printf("Profitto INSUFFICIENTE!\n"); }
else if (y == 6)
{printf("Profitto SUFFICIENTE!\n"); }
else if (y >=7 && y <= 10)
{printf(“AVANTI COSI!\n"); }
else
{printf(“Valore al di fuori del range consentito!\n"); }
system(“pause”);
}
ESERCIZIO:
scrivere un programma che acquisisce due
numeri interi da tastiera se entrambi maggiori di 13, calcola e
visualizza la media aritmetica altrimenti individua e visualizza
il numero maggiore
ALGORITMO
ALGORITMO: Sequenza di passi per ottenere la
soluzione di un problema o classe di problemi.
Introduzione
La scrittura di un programma non deve avvenire di getto, perché bisogna sempre approfondire prima la
problematica che il programma deve risolvere.
In generale la risoluzione di un generico problema mediante l’uso del calcolatore passa per tre fasi
fondamentali:
• Analisi del problema
• definizione completa del problema
• ricerca di eventuali algoritmi già esistenti
• individuazione delle variabili (ingresso, intermedie, uscita)
• valutazione dell’opportunità di ricorrere al calcolatore
• Definizione dell’algoritmo per la soluzione automatica
L’algoritmo deve contemplare tutti i casi che con i dati di ingresso possono presentarsi.
Un modo comodo e chiaro per descrivere la sequenza di passi che costituiscono l’algoritmo è dato
dai
diagrammi di flusso (flow charts).
NB: possono esistere più algoritmi che risolvono lo stesso problema, ma con efficienza diversa.
• Implementazione dell’algoritmo su calcolatore
Consiste nella traduzione di un algoritmo in sequenza di istruzioni appartenenti a un determinato
linguaggio di programmazione.
ESECUZIONE CONDIZIONALE
Le selezioni condizionali permettono di decidere l’attivazione di parti (diverse) di codice, in base al valore di un’espressione
Costrutto if-else
Costrutto if
Permette l’esecuzione di un blocco di
codice solo se si verifica una certa
Il flow-chart corrispondente è:
Selezione a più rami
condizione
SE (condizione è vera)
ALLORA esegui istruzioni
// maggiore fra due
numeri
#include <stdio.h>
int main()
{
int a, b;
scanf("%d",&a);
scanf("%d",&b);
Esempio
if (a > b)
Programma che chiede un numero e
printf("%d",a);
se è positivo scrive “positivo”
altrimenti nulla.
else
scanf("%d",&n);
printf("%d",b);
if (n > 0)
return 0;
{
printf("positivo\n");
}
}
scanf("%d", &n);
if (n > 0)
printf("positivo\n");
else
if (n < 0)
printf("negativo\n");
Costrutto
if interno
else
printf("nullo\n");
printf("FINE\n");
Quando n > 0 non valuta l’altro controllo
I blocchi di istruzioniQualsiasi istruzione può essere sostituita
da un blocco di istruzioni
Un blocco di istruzioni deve essere contenuto all’interno di
parentesi graffe: il corpo di una funzione è un caso particolare
di blocco di istruzioni
Per eseguire in modo condizionale
più di una singola istruzione è (necessario e) sufficiente
racchiudere l’insieme di istruzioni in un blocco
LISTATO N. 3
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
main()
{
double num;
printf("introdurre un numero non negativo: ");
scanf("%lf", &num);
/* Lo specificatore %lf indica un tipo double */
if (num<0)
printf("errore nei dati di ingresso: il numero è negativo.
\n");
else
printf("la radice quadrata è:%f \n", sqrt(num));
printf("il quadrarto di %lf è: %lf \n", num, num*num);
printf("il cubo di %lf è: %lf \n", num, num*num*num);
exit(0);
}
Scrivere un programma che legge un carattere,
stampandolo se è una lettera dell’alfabeto, ignorandolo in
caso contrario
Note:
Esiste la funzione di libreria isalpha() che restituisce un valore
diverso da 0 se l’argomento è una lettera dell’alfabeto
L’uso di una chiamata di funzione come espressione condizionale
è comune in C
LISTATO N. 2
#include <stdio.h>
#include <stdlib.h>
#include <ctype.h> /* incluso per la funzione
isalpha */
main()
{
char ch;
printf("introdurre un carattere: ");
scanf("%c", &ch);
if (isalpha(ch))
printf("%c", ch);
else
printf("%c non è un carattere alfabetico|n", ch);
exit(0);
}
ISTRUZIONI IF INNESTATE
• Una singola istruzione if permette al programma di scegliere fra due alternative. Talvolta è necessario specificare
alternative successive: dopo aver preso la decisione_1, è necessario valutare la decisione_2, la decisione_3, etc.
• Questa tipologia di controllo del flusso richiede un costrutto if innestato (o annidato)
• Esempio ealizzare una funzione che, dati tre interi, ne determina il massimo/minimo
• Nelle istruzioni if annidate sorge il problema di far corrispondere ad ogni clausola else l’opportuna istruzione if
• Regola: Una clausola else viene sempre associata all’istruzione if più vicina fra quelle precedenti ad ogni
istruzione if può corrispondere una sola clausola else
• Per facilitare la programmazione, è opportuno indentare correttamente i vari if:
Una clausola else dovrebbe sempre essere posta allo stesso livello di indentazione dell’if associato
#include <stdio.h>
int main()
{
int a, b, c;
scanf("%d%d%d",&a,&b,&c);
if (a > b)
if (a > c)
printf("%d",a);
else
printf("%d",c);
else
if (b > c)
printf("%d",b);
else
printf("%d",c);
return 0; }
int min(a, b, c)
int a, b, c;
{
if (a<b)
if (a<c)
return a;
else
return c;
else if (b<c)
return b;
else
return c;
}
/* LISTATO 4: CALCOLA LE RADICI DI UN'EQUAZIONE DI SECONDO GRADO. */
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
int main()
{
float a, b, c, delta;
printf ("scrivi a, b, c: ");
scanf ("%f %f %f", &a, &b, &c);
delta = b*b - 4*a*c;
if (delta == 0)
{
/* radici coincidenti */
printf ("radici coincidenti: x0 = x1 = %f", -b/(2*a));
}
else
{
if (delta > 0) {
/* radici reali distinte */
printf ("radici reali distinte: x0 = %f, x1 = %f",
(-b + sqrt (delta))/(2*a), (-b - sqrt (delta))/(2*a));
}
else {
/* radici complesse */
printf ("radici complesse coniugate: \n"
"parte reale = %f, parte immaginaria = +/- %f",
-b/(2*a), sqrt (-delta)/(2*a));
} }
return EXIT_SUCCESS;
}
/*Scrivere un programma che richiesto all'utente un
numero intero stabilisca se e' pari o dispari.
Suggerimento: l’operatore modulo, x%y, restituisce il
resto della divisione intera di x per y */
#include <stdio.h>
main()
{
int a;
printf("inserisci numero:");scanf("%d",&a);
if (a%2==0)
printf("numero pari");
else
printf("numero dispari");
getchar();
}
Scrivere un programma che chieda
due numeri da tastiera e dei due
visualizzi il maggiore
#include <stdio.h>
int main()
{
double a, b;
printf("Introduci il primo valore:
");
scanf("%lf", &a);
printf("Introduci il secondo valore:
");
scanf("%lf", &b);
if (a >= b) /* oppure solo > */
printf("%f\n", a);
else
printf("%f\n", b);
return 0;
}
Scrivere un programma che chieda un numero da
tastiera e stampi sul video se è pari o dispari
(consiglio: calcolare il resto).
#include <stdio.h>
int main()
{
int a;
printf("Introduci il valore:
");
scanf("%d", &a);
if (a % 2 == 0)
printf("Pari\n");
else
printf("Dispari\n");
return 0;
}
Scrivere un programma che chieda tre numeri da
tastiera e li stampi in ordine decrescente.
#include <stdio.h>
int main()
{ double a, b, c;
printf("Introduci il primo valore: ");
scanf("%lf", &a);
printf("Introduci il secondo valore: ");
scanf("%lf", &b);
printf("Introduci il terzo valore: ");
scanf("%lf", &c);
if (a > b && a > c) /* verifica se a e' > di entrambi */
if (b > c)
printf("%f %f %f\n", a, b, c);
else printf("%f %f %f\n", a, c, b);
else if (b > c) /* a non e' il piu' grande, o e' b o e' c */
if (a > c)
printf("%f %f %f\n", b, a, c);
else printf("%f %f %f\n", b, c, a);
else
/* non puo' che essere c */
if (a > b)
printf("%f %f %f\n", c, a, b);
else printf("%f %f %f\n", c, b, a);
return 0; }
. Si vogliono dividere gli allievi di un corso in tre squadre denominate
ROSSA, VERDE e BLU secondo il loro numero di matricola. L’assegnazione
avviene con il seguente criterio: l’allievo con matricola 1 va nella squadra
ROSSA, quello con matricola 2 nella VERDE, quello con matricola 3 nella
BLU, quello con matricola 4 nella ROSSA, quello con 5 nella VERDE ecc.
Il programma deve chiedere il numero di matricola dell’allievo e
indicare a quale squadra è assegnato. Usare il costrutto if.
#include <stdio.h>
int main()
{
int matricola;
printf("Introduci il numero di matricola:
");
scanf("%d", &matricola);
if (matricola % 3 == 1)
printf("ROSSA\n");
else if (matricola % 3 == 2)
printf("VERDE\n");
else
printf("BLU\n");
return 0;
}
. Scrivere un programma che chieda da tastiera
di introdurre un numero intero corrispondente
ad
un
voto
e
stampi
a
video
“Insufficiente” se è inferiore a 18,
“Appena sufficiente” (18),
“Basso” (19-20),
“Medio” (21-23),
“Buono” (24-26),
“Alto” (27-29),
“Massimo”
(30)
“Impossibile” (tutti gli altri)
#include <stdio.h>
int main()
{
int voto;
printf("Introduci il voto: ");
scanf("%d", &voto);
if (voto <= 0)
printf("Impossibile\n");
else if (voto < 18)
printf("Insufficiente\n");
else if (voto == 18)
printf("Appena sufficiente\n");
else if (voto <= 20)
/* inutile scrivere
anche voto > 18 */
printf("Basso\n");
else if (voto <= 23)
printf("Medio\n");
else if (voto <= 26)
printf("Buono\n");
else if (voto <= 29)
printf("Alto\n");
else if (voto == 30)
printf("Massimo\n");
else
printf("Impossibile\n");
return 0;
}
#include <stdio.h>
int main()
{
char l;
printf("MENU DI PROVA\n");
printf("a) Per immettere dati\n");
printf("b) Per determinare il maggiore\n");
printf("c) Per determinare il minore\n");
printf("d) Per ordinare\n");
printf("e) Per visualizzare\n");
printf("Scelta: ");
scanf("%c",&l);
fflush(stdin);
switch(l)
{
case ('a'):
{
printf("\nIn esecuzione l'opzione a");
break;
}
case ('b'):
{
printf("\nIn esecuzione l'opzione b");
break;
}
case ('c'):
{
printf("\nIn esecuzione l'opzione c");
break;
}
case ('d'):
{
printf("\nIn esecuzione l'opzione d");
break;
}
L’istruzione switch
case ('e'):
{
printf("\nIn esecuzione l'opzione
e");
break;
}
default:
{
printf("\nOpzione inesistente!");
break;
}
}
getchar();
}
#include <stdio.h>
int main() {
int cost;
char c;
printf("Inserisci il costo del biglietto\n");
scanf("%d",&cost);
fflush(stdin);
printf("Inserisci la tua eventuale condizione particolare:\n");
printf("1.'S'tudente\n2.'P'ensionato\n3.'D'isoccupato\n4.'N'essumo di
questi\n");
scanf("%c",&c);
fflush(stdin);
switch(c) {
case 'S':
printf("L'importo da pagare e' %d",cost-((cost*15)/100));
break;
case 'P':
printf("L'importo da pagare e' %d",cost-((cost*10)/100));
break;
case 'D':
printf("L'importo da pagare e' %d",cost-((cost*25)/100));
break;
default:
printf("L'importo da pagare e' %d",cost);
break;
}
getchar(); }
Su una linea ferroviaria, rispetto alla tariffa piena,
gli utenti pensionati usufruiscono di uno sconto del
10%, gli studenti del 15% e i disoccupati del 25%.
Codificando i pensionati con P, gli studenti con una
S e i disoccupati con una D, scrivere un
programma che richiesto il costo di un biglietto e
l'eventuale condizione particolare dell'utente,
visualizzi
l'importo
da
pagare.
Si vogliono dividere gli allievi di un corso in tre squadre denominate ROSSA,
VERDE e BLU secondo il loro numero di matricola. L’assegnazione avviene
con il seguente criterio: l’allievo con matricola 1 va nella squadra ROSSA,
quello con matricola 2 nella VERDE, quello con matricola 3 nella BLU,
quello con matricola 4 nella ROSSA, quello con 5 nella VERDE
#include <stdio.h>
int main()
{
int matricola;
printf("Introduci il numero di matricola: ");
scanf("%d", &matricola);
switch (matricola % 3)
{
case 1:
printf("ROSSA\n");
break;
case 2:
printf("VERDE\n");
break;
default:
printf("BLU\n");
break;
}
return 0; }
. Scrivere un programma che chieda da tastiera di introdurre un numero intero corrispondente ad
un voto e stampi a video “Insufficiente” se è inferiore a 18, “Appena sufficiente” (18)
“Basso” (19-20), “Medio” (21-23), “Buono” (24-26), “Alto” (27-29), “Massimo” (30)
“Impossibile” (tutti gli altri)
#include <stdio.h>
int main()
{ int voto;
printf("Introduci il voto: ");
scanf("%d", &voto);
switch (voto)
{
case 18:
printf("Appena sufficiente\n");
break;
case 19: case 20:
printf("Basso\n");
break;
case 21:
case 22:
case 23:
printf("Medio\n");
break;
case 24:
case 25:
case 26:
printf("Buono\n");
break;
case 27:
case 28:
case 29:
printf("Alto\n");
break;
case 30:
printf("Massimo\n");
break;
default:
if (voto > 0 && voto < 18)
printf("Insufficiente\n");
else
printf("Impossibile\n"); break;
return 0; }
STRUTTURE ITERATIVE
Ciclo WHILE
Fa eseguire un blocco di codice fintanto
ché una certa condizione è vera
Valuta la condizione prima di
eseguire il blocco
Ciclo FOR
Ciclo DO-WHILE
Il flow-chart corrispondente è il
seguente:
Fa eseguire un blocco di codice fintanto ché
una certa condizione è vera
Valuta la condizione dopo aver eseguito il
blocco
Se la condizione è inizialmente falsa,
il blocco non viene eseguito neppure
una volta
somma = 0;
scanf("%d", &v);
while (v != 0)
{
somma += v;
scanf("%d", &v);
}
printf("Somma:%d", somma);
ciclo FOR:
for (i=0; i<=1000; i++)
printf("%d", i);
fino a quando i, che viene
via via incrementata, è
minore o uguale a 1000 viene
stampata la variabile i
Anche se la condizione è inizialmente falsa,
il blocco viene eseguito almeno una volta
somma = 0;
do
{
scanf("%d", &v);
somma += v;
}while (v != 0);
ESEMPI ITERATIVI: CICLO FOR
Scrivere un programma che calcoli la
media (con parte frazionaria) di 100
valori introdotti dalla tastiera.
.
#include <stdio.h>
#define N 100
int main()
{
int v, somma;
int i;
somma = 0;
for (i=1; i<=N; i++)
{
printf("Inserire il %do valore: ", i);
scanf("%d", &v);
somma += v;
}
printf("Media: %f\n",
(double)somma/N);
return 0;
}
. Scrivere un programma che chieda
quanti
siano i valori che verranno
introdotti dalla tastiera, li chieda tutti e
ne stampi la somma e la media.
#include <stdio.h>
int main()
{
int v, somma;
int i, n;
somma = 0;
printf("Quanti valori? ");
scanf("%d", &n);
for (i=1; i<=n; i++)
{
printf("Inserire il %do valore: ", i);
scanf("%d", &v);
somma += v;
}
printf("Somma: %d\n", somma);
printf("Media: %f\n", (double)somma/n);
return 0;
}
ESEMPI ITERATIVI: CICLO FOR
Scrivere un programma che richieda N numeri da
tastiera e ne calcoli il valore massimo
#include <stdio.h>
int main()
{
int v, max;
int i, n;
printf("Quanti? ");
scanf("%d", &n);
Scrivere un programma che calcola i primi N numeri di Fibonacci,
con N introdotto dalla tastiera. I numeri di Fibonacci sono una
sequenza di valori interi che inizia con i due valori fissi 1 e 1 e
ogni successivo valore è la somma dei due precedenti.
Ad esempio i primi 10 numeri di Fibonacci sono: 1 1 2 3 5 8
13 21 34 55.
#include<stdio.h>
int main()
{
int i, n;
double a, b, c;
printf("Inserire il 1o valore: "); /* chiede il primo valore
*/
scanf("%d", &v);
max = v;
/* il primo valore e' anche l'attuale max */
for (i=1; i<n; i++) /* parte da 1 e non da 0 perche' il
primo */
{
/* e' gia' stato letto */
printf("Inserire il %do valore: ", i+1);
scanf("%d", &v);
if (v>max)
max = v;
}
printf("Massimo: %d\n", max);
/* tipi con ampio range */
printf("Quanti numeri? ");
scanf("%d", &n);
a = 1;
b = 1;
for (i=0; i<n; i++)
{
c = a + b;
printf("%.0f ", a);
a = b;
b = c;
}
printf("\n");
return 0;
}
return 0;
}
Esempi iterativi: ciclo for
/*Scrivere un programma che richiesto all'utente
/*Scrivere un programma che visualizzi * un numero m calcoli la somma dei primi m
il quadrato dei primi 24 numeri
elementi
naturali*/
* della serie armonica (1/k, per k che va da 1 a
#include <stdio.h>
#define DIM 24
main()
{
int i;
for(i=1;i<=24;i++)
printf("%3d al quadrato:
%3d\n",i,i*i);
getchar();
}
m)*/
#include <stdio.h>
int main()
{
int m;
float k,S=0.0;
printf("m: ");
scanf("%d",&m);
fflush(stdin);
for(k=1;k<=m;k++)
S=S+1/k;
printf("sommatoria: %f",S);
getchar();
}
ESEMPI ITERATIVI: WHILE
Si scriva un programma che calcoli il fattoriale di un numero
intero N dato dalla tastiera. Si ricordi che il fattoriale di un
numero n (simbolo n!) viene calcolato con la seguente
formula:
n! = n ·(n–1)·(n–2)· ... ·2 ·1.
fibonacci
#include<stdio.h>
int main()
{
double n, a, b, c;
range, anche n */
printf("Massimo numero? ");
scanf("%lf", &n);
#include<stdio.h>
int main()
{
int n;
double fatt;
a = 1;
b = 1;
if (n>=1)
printf("1 1 ");
c = a + b;
while (c<=n)
{
printf("%.0f ", c);
a = b;
b = c;
c = a + b;
}
printf("\n");
printf("Numero di cui calcolare il fattoriale: ");
scanf("%d", &n);
fatt = 1;
while (n>0) /* n>1 e' ancora meglio: inutile molt. per 1
*/
fatt *= n--;
printf("Fattoriale: %.0f\n", fatt);
return 0;
}
/* tipi con ampio
return 0;
}
Esempi iterativi: while
#include <stdio.h>
int main() {
int n, m, n1, m1; printf("Inserisci due numeri naturali : ");
scanf("%d%d", &n, &m);
n1 = n; m1 = m;
while (n1 != m1) {
if (n1 < m1)
m1 = m1 - n1;
else
n1 = n1 - m1; }
printf("Il massimo comun divisore con il metodo euclideo tra %d e %d e' %d\n", n, m, n1);
return 0; }
#include <stdio.h>
int main()
{
int n, m, t;
printf("Inserisci due numeri naturali : ");
scanf("%d%d",&n,&m);
if (n < m)
t = n;
else
t = m;
while (n % t != 0 || m % t != 0)
t = t - 1;
printf("Il massimo comun divisore tra %d e %d e' %d\n", n, m, t); return 0;
}
ESEMPI ITERATIVI_ DO WHILE
Si scriva un programma dove il calcolatore determini casualmente un numero intero
compreso tra 0 e 99 e chieda all’utente di trovare il numero stesso. Ad ogni input
dell’utente il calcolatore risponde con “troppo alto” o “troppo basso”, finché non
viene trovato il valore corretto. Per generare valori casuali si utilizza la funzione
rand.
#include<stdio.h>
#include<time.h>
#include<stdlib.h>
#define MAXVAL 99
int main()
{
int x, v;
srand(time(NULL));
x = rand() % (MAXVAL+1);
do
{
printf("Introduci un valore intero tra 0 e %d: ", MAXVAL);
scanf("%d", &v);
if (v<x)
printf("Troppo basso!\n");
else if (v>x)
printf("Troppo alto!\n");
}while(x!=v);
printf("Trovato!\n");
return 0;
}
// FATTORIALE
#include <stdio.h>
#include <stdlib.h>
int main()
{
int n, i;
long int nfatt;
printf ("inserisci n: ");
scanf ("%d", &n);
i = 1;
nfatt = 1;
while (i <= n)
{
nfatt = nfatt * i;
i++;
}
printf ("n! = %ld", nfatt);
return EXIT_SUCCESS;
}
getchar() legge dati il cui tipo non è noto a priori e li fornisce sotto forma di char
Quando getchar() raggiunge la fine del file, viene restituito un valore speciale, detto EOF: un nome costante,
definito in stdio.h, che solitamente vale 1
In questo caso, il carattere di fine stringa è \n
#include <stdio.h>
#include <stdlib.h>
/* Conta il numero di spazi contenuti in una stringa
* immessa da terminale */
int main()
{
int ch, numerispazi=0;
printf("introdurre una frase:\n");
ch = getchar();
while(ch!='\n')
{
if(ch==' ')
numerispazi++;
ch = getchar();
}
printf("il numero di spazi è: %d\n",
numerispazi);
#include <stdio.h>
#include <stdlib.h>
/* Conta il numero di spazi contenuti in una stringa
* immessa da terminale */
int main()
{
int ch, numerispazi=0;
printf("introdurre una frase:\n");
ch = getchar();
do {
ch = getchar();
if(ch==' ')
numerispazi++;
ch = getchar();
}
while(ch!='\n');
printf("il numero di spazi è: %d\n", numerispazi);
exit(0);
}
exit(0);
}
I CICLI INNESTATI
• I costrutti iterativi possono essere innestati
a qualunque livello di profondità
• Il ciclo di livello nesimo deve terminare la
propria esecuzione prima che il ciclo al
livello n1 possa riprendere l’iterazione
Lo specificatore di formato %5d forza la
funzione printf() a stampare 5 caratteri
per ogni intero: se il numero richiede
meno di 5 caratteri, viene preceduto da un
numero appropriato di spazi bianchi
#include <stdio.h>
#include <stdlib.h>
/* Stampa una tavola pitagorica mediante cicli
innestati */
int main()
{
int j, k;
printf(" 1 2 3 4 5 6 7 8 9 10\n");
printf("________________________________\n");
for(j=1; j<=10;j++)
{
printf("%5d|",j);
for(k=1; k<=10;k++)
printf("%5d",j*k);
printf("\n");
}
exit(0); }
Le istruzioni break e continue, goto
Le istruzioni break devono essere evitate, quando possibile: producono salti (incondizionati) e rendono il programma di difficile lettura e
comprensione
L’istruzione continue deve essere evitata, quando possibile, perché, come break, altera il flusso di controllo naturale (attraverso un
salto incondizionato
È possibile scrivere cicli con modalità alternative, che non prevedono l’uso di break; break è invece “insostituibile” nel caso di switch
L’istruzione goto ha lo scopo di trasferire il controllo del flusso in un punto particolare, identificato da un’etichetta o label
La label è un nome seguito da “:” e deve essere contenuta nella stessa funzione che contiene il goto che vi fa riferimento
Il goto deve essere
usato solo quando il codice risultante guadagna in efficienza senza perdere troppo in leggibilità
VETTORI
VETTORI
Lavorando con una variabile semplice, ad ogni ripetizione del ciclo il nuovo valore viene sovrascritto sul vecchio,
perdendolo definitivamente. E’ possibile conservare i valori precedenti ricorrendo ai vettori.
I vettori sono un insieme di numeri, ordinato. Ciascun elemento del vettore è individuato da un proprio indirizzo. Il primo
elemento del vettore ha indirizzo 0.
Codice C :
Esempio: il numero 21 risulta essere il 4° elemento (indirizzo 3) del vettore y.
Per utilizzare gli elementi del vettore nelle operazioni è sufficiente richiamarli nel modo
seguente: Esempio: per disporre del valore del 5° elemento del vettore si deve scrivere:
x[4].
NB: I vettori sono molto utili quando si deve memorizzare una grande quantità di numeri.
Memorizzando i numeri in un vettore è possibile utilizzarli per elaborazioni successive col vantaggio di
poter usufruire della struttura dei cicli.
FUNZIONI
Quando si hanno sequenze di istruzioni che possono
• ripetersi nello stesso programma, o
• essere comuni a più programmi
conviene isolare tale codice e identificarlo come sottoprogramma.
In C ciò si realizza mediante la scrittura di funzioni. La sintassi è la seguente:
NomeFunzione (parametri)
{ ………………….
codice
…………………
}
Le variabili si distinguono in globali e locali.
Le variabili globali (dichiarate nella sezione dichiarativa del programma):
• se non definite, sono inizializzate a zero
• possono essere lette e modificate da tutte le funzioni
• conservano il valore, eventualmente modificato, fino al termine del programma.
Le variabili locali (dichiarate all’interno delle funzioni):
• se non definite, hanno inizialmente valore incerto
• possono essere lette e modificate solo all’interno della funzione in cui sono dichiarate
• al termine dell’esecuzione della funzione il loro valore non è più disponibile (se non indicate in return).
•
ESEMPIO: funzione potenza()
NB
E’ possibile indicare con uno stesso nome sia una variabile globale che una locale: non vi è pericolo di
interferenza in quanto quella locale maschera, all’interno della funzione in cui è dichiarata, quella
globale e la funzione lavora con la sola variabile locale.
programma precedente non fornisce una risposta corretta nel caso in cui
•
sia la base che l’esponente sono uguali a zero
•
l’esponente è negativo
Una possibile correzione è la seguente:
Il
In alternativa si può inserire tutto il codice di controllo nella funzione potenza():
ESEMPIO:
funzione CaricaVettore()
Array
Un vettore è una struttura di dati composta da un numero determinato di elementi tutti dello stesso tipo, ognuno
dei quali è individuato da un indice specifico. I vettori si dicono variabili strutturate mentre all’opposto tutte le
variabili semplici siano anche dette non strutturate. Il tipo dei dati contenuti nel vettore viene detto tipo del vettore,
ovvero si dice che il vettore è di quel particolare tipo.
Dunque per il vettore, come per qualsiasi altra variabile, devono essere definiti il nome e il tipo; inoltre si
deve esplicitarne la lunghezza, cioè il numero di elementi che lo compongono.
Una scrittura possibile è perciò la seguente:
int a[6];
Come sempre in C, prima deve essere dichiarato il tipo (nell’esempio int), poi il nome della variabile (a),
successivamente tra parentesi quadre il numero degli elementi (6) che dev’essere un intero positivo. Questa
dichiarazione permette di riservare in memoria centrale uno spazio strutturato come in Figura
Per accedere a un singolo elemento di a si deve specificare il nome del vettore seguito dall’indice dell’elemento
posto tra parentesi quadre. L’array a è composto da sei elementi e l’indice può quindi assumere i valori: 0, 1, 2, 3, 4,
e 5
Le istruzioni a[0] = 71;
a[1] = 4; assegnano al primo elemento del vettore a il valore 71 e al secondo 4.
Se b è una variabile intera (cioè dello stesso tipo del vettore), è possibile assegnare il suo valore a un elemento di a
e viceversa:
a[3] = b;
In generale un singolo elemento dell’array può essere utilizzato esattamente come una variabile semplice.
Nell’espressione
b = b + a[0] * a[5];
il valore di b è sommato al prodotto tra il primo e il sesto elemento di a e il risultato è assegnato a b.
Spesso l’array viene trattato all’interno di iterazioni; infatti risulta semplice far riferimento a suoi elementi
incrementando ciclicamente il valore di una variabile intera e utilizzandola come indice. Esempio di iterazione:
Inizializzazione dell'array
for(i=0; i<=5; i++) {
printf("Inser. intero: ");
scanf("%d", &a[i]);
L’indice
i
dell’array
a
è
/* LISTATO 4.1: Memorizza in un array di interi il punteggio raggiunto da sei
inizializzato a 0 e assume a ogni
studenti e ne determina il maggiore, il minore e la media
*/
iterazione successiva i valori 1, 2,
#include <stdio.h>
3, 4, 5 .
main()
{
int voti[6];
/* Ricerca del maggiore*/
int i, max, min; float media;
max = a[0];
printf("VOTI STUDENTI\n\n");
for(i=1; i<=5; i++)
/* Immissione voti */
if(a[i]>max) max = a[i];
for(i=0; i<=5; i++) {
printf("Voto %dº studente: ", i+1);
: la variabile max
viene inizializzata al valore del
scanf("%d", &voti[i]);
primo elemento del vettore, quello con indice zero.
}
/* Ricerca del maggiore */ max = voti[0];
for(i=1; i<=5; i++) if(voti[i]>max)
max = voti[i];
/* Ricerca del minore */ min = voti[0];
for(i=1; i<=5; i++) if(voti[i]<min)
min = voti[i];
/* Calcolo della media */ media = voti[0];
for(i=1; i<=5; i++)
media = media + voti[i];
media = media/6;
printf("Maggiore: %d\n", max); printf("Minore: %d\n", min); printf("Media: %f\n", media);
}
Il blocco
del
for richiede
all’utente l’immissione di sei valori
che vengono
assegnati
sequenzialmente,
mediante
l’istruzione scanf, agli elementi del
vettore.
Se quindi vengono inseriti in
sequenza i valori 9, 18, 7, 15, 21
e 11, dopo l’esecuzione del ciclo il
vettore si presenterà in memoria
come in Figura
Si noti che la richiesta dei voti all’utente viene fatta evidenziando il numero d’ordine che corrisponde al valore
dell’indice aumentato di una unità.
printf("Voto %dº studente: ", i+1);
Alla prima iterazione appare sullo schermo:
Voto 1º studente:
Considerazioni analoghe a quelle fatte per il calcolo del maggiore valgono per il minimo e la media.
I calcoli potevano essere effettuati all’interno della stessa iterazione con un notevole risparmio di tempo di esecuzione:
/* LISTATO 4.1a
#include <stdio.h>
main() {
int voti[6]; int i, max, min; float media;
/* Immissione voti */
printf("VOTI STUDENTI\n\n");
for(i=0; i<=5; i++) {
printf("Voto %dº studente: ", i+1); scanf("%d", &voti[i]);
}
/* Ricerca maggiore, minore e media */
max =voti[0]; min = voti[0]; media = voti[0];
for(i= 0; i <= 5; i++) { if(voti[i] > max) max = voti[i]; if(voti[i] < min)
min = voti[i];
media = media+voti[i];
}
printf("Maggiore: %d\n", max); printf("Minore: %d\n", min); printf("Media: %f\n", media);
}
✓
NOTA
È importante ricordare che in C l’indice inferiore del vettore è zero e quello superiore è uguale al numero di
elementi meno 1: se si desidera un array di 100 si dichiara voti[100];
ma si deve tenere presente che
l’indice assume valori da 0 a 99.
4.2 Esempi di uso di array
Per determinare la destrezza di n concorrenti sono state predisposte due prove, entrambe con una valutazione che
varia da 1 a 10; il punteggio totale di ogni concorrente è dato dalla media aritmetica dei risultati delle due prove. Si
richiede la visualizzazione di una tabella che contenga su ogni linea i risultati parziali e il punteggio totale di un
concorrente.
/* LISTARTO 4.2: Carica i punteggi di n concorrenti su due prove Determina la classifica */
#include <stdio.h>
#define MAX_CONC 1000 /* massimo numero di concorrenti */
#define MIN_PUN 1 /* punteggio minimo per ogni prova */
#define MAX_PUN 10 /* punteggio massimo per ogni prova */
main()
{
float prova1[MAX_CONC], prova2[MAX_CONC], totale[MAX_CONC];
int i, n;
do {
printf("\nNumero concorrenti: ");
scanf("%d", &n);
}
while(n<1 || n>MAX_CONC);
/* Per ogni concorrente, richiesta punteggio nelle due prove */
// LISTARTO 4.2: SEGUITO
for(i=0; i<n; i++) {
printf("\nConcorrente n.%d \n", i+1);
do {
printf("Prima prova: ");
scanf("%f", &prova1[i]);
}
while(prova1[i]<MIN_PUN ||
prova1[i]>MAX_PUN);
do {
printf("Seconda prova: ");
scanf("%f", &prova2[i]);
}
while(prova2[i]<MIN_PUN ||
prova2[i]>MAX_PUN);
}
/* Calcolo media per concorrente */
for(i=0; i<n; i++)
totale[i] = (prova1[i]+prova2[i])/2;
printf("\n CLASSIFICA\n");
for(i=0; i<n; i++)
printf("%f %f %f \n", prova1[i], prova2[i],
totale[i]);
}
Non conoscendo a priori il numero di concorrenti che
parteciperanno alle gare si fa l’ipotesi che comunque non siano più
di 1000, valore che memorizziamo nella costante MAX_CONC. In
conseguenza di ciò definiamo di lunghezza MAX_CONC gli array
che conterranno i risultati: prova1, prova2 e totale.
Richiediamo all’utente a tempo di esecuzione il numero effettivo dei
concorrenti e verifichiamo che non sia minore di 1 e maggiore di
MAX_CONC: (VERIFICARE)
do {
printf("\nNumero concorrenti: ");
scanf("%d", &n);
}
while(n<MIN_PUN || n>MAX_CONC);
In seguito richiediamo l’introduzione dei risultati della prima e
della seconda prova di ogni concorrente, controllando che tale
valutazione non sia minore di 1 e maggiore di 10, nel qual caso
ripetiamo la richiesta.
Abbiamo memorizzato in MIN_PUN e
MAX_PUN i limiti inferiore e superiore del punteggio assegnabile, in
maniera che, se questi venissero modificati, basterebbe intervenire
sulle loro definizioni perché il programma continui a funzionare
correttamente. Infine calcoliamo il punteggio totale e lo
visualizziamo
4.3 Inizializzazione di variabili
L’inizializzazione di una variabile può essere esplicitata direttamente al momento della sua dichiarazione, come con
int i = 0;
L’istruzione dichiara la variabile i di tipo intero e le assegna il valore zero. Di seguito alla dichiarazione di tipo possono
essere definite e inizializzate più variabili:
int a = 50, b = 30, c, d = 333;
definisce le variabili intere a, b, c e d; inizializza a al valore 50, b a 30, d a 333, c non è inizializzata.
Analogamente si possono assegnare valori agli altri tipi di variabili semplici:
float x = 567.8927;
float y = 7e13;
char risposta = 's’;
Per gli array l’inizializzazione è possibile solamente se sono stati dichiarati come extern o come static;
Le variabili extern sono quelle che vengono definite prima di main. L’inizializzazione si ottiene inserendo I
valori tra parentesi graffe, separati da una virgola: Le variabili di tipo static sono permenenti all'interno della
funzione o del file in cui sono dichiarate.
int voti[6] = {11, 18, 7, 15, 21, 9};
Il compilatore fa la scansione dei valori presenti tra parentesi graffe da sinistra verso destra e genera
altrettanti assegnamenti consecutivi agli elementi del vettore, rispettando la loro posizione; dunque voti[0] assume il
valore 11, voti[1] 18, voti[2] 7 ecc.
Quando tutti gli elementi dell’array vengono inizializzati è possibile omettere l’indicazione del numero di elementi, e
scrivere
int voti[] = {11, 18, 7, 15, 21, 9};
È infatti il compilatore stesso che conta i valori e di conseguenza determina la dimensione del vettore.
Gli array di caratteri, comunemente detti stringhe, possono essere inizializzati anche inserendo il loro contenuto tra
doppi apici:
char frase[] = "Analisi, requisiti";
ESERCIZI
Scrivere un programma che chieda quanti
valori
verranno introdotti dalla tastiera (max 100), li chieda
tutti e successivamente li visualizzi dall’ultimo al primo.
#include<stdio.h>
#define MAXNUM 100
int main()
{
int v[MAXNUM], n, i;
printf("Quanti valori introdurrai (max %d)? ",
MAXNUM);
scanf("%d", &n);
if (n>0 && n<=MAXNUM)
{
for (i=0; i<n; i++)
{
printf("Introduci il %do valore: ", i+1);
scanf("%d", &v[i]);
}
for (i=n-1; i>=0; i--)
printf("%d\n", v[i]);
}
else
printf("Il valore inserito (%d) non e' corretto\n", n);
return 0;
}
Scrivere un programma che chieda quanti valori verranno introdotti dalla tastiera
(max 100), li chieda tutti e successivamente visualizzi prima tutti i valori pari
nell’ordine in cui sono stati inseriti e poi tutti i valori dispari nell’ordine inverso.
#include<stdio.h>
#define MAXNUM 100
int main()
{
int v[MAXNUM], n, i;
printf("Quanti valori introdurrai (max %d)? ", MAXNUM);
scanf("%d", &n);
if (n>0 && n<=MAXNUM)
{
for (i=0; i<n; i++)
{
printf("Introduci il %do valore: ", i+1);
scanf("%d", &v[i]);
}
for (i=0; i<n; i++)
if (v[i] % 2 == 0)
printf("%d ", v[i]); /* PARI */
/* NO ELSE QUI in quanto si vogliono SALTARE i dispari */
for (i=n-1; i>=0; i--)
if (v[i] % 2 == 1)
printf("%d ", v[i]); /* DISPARI */
/* NO ELSE QUI in quanto si vogliono SALTARE i pari */
}
else
printf("Il valore inserito (%d) non e' corretto\n", n);
return 0;
}
#include<stdio.h>
#define MAXNUM 100
int main()
{
int a[MAXNUM], b[MAXNUM], c[MAXNUM], n, i;
printf("Quanti valori introdurrai (max %d)? ",
MAXNUM);
scanf("%d", &n);
if (n>0 && n<=MAXNUM)
{
for (i=0; i<n; i++)
{
printf("Introduci il %do valore di a: ", i+1);
scanf("%d", &a[i]);
}
for (i=0; i<n; i++)
{
printf("Introduci il %do valore di b: ", i+1);
scanf("%d", &b[i]);
c[i] = a[i] + b[i];
}
for (i=1; i<n; i+=2)
printf("%d\n", c[i]);
for (i=0; i<n; i+=2)
printf("%d\n", c[i]);
}
else
printf("Il valore inserito (%d) non e' corretto\n", n);
return 0;
}
Scrivere un programma che definisca 2 vettori A e B di uguali
dimensioni (la dimensione sia chiesta in input, max 100), chieda
in input tutti i valori del primo e successivamente tutti i valori
del secondo (devono comparire sul video richieste come le
seguenti:
il
“Introdurre
il
“Introdurre
e successivamente
“Introdurre il
“Introdurre il
1° valore
2° valore
1°
2°
valore
valore
di A”,
di A” ecc.
di B”,
di B” ecc.
Il programma crea un terzo vettore C della stessa dimensione
di A e B contenente nel 1° elemento la somma del 1o elemento
di A e del 1o elemento di B, nel 2o elemento la somma del 2o
elemento di A e del 2o elemento di B etc.
Alla fine deve visualizzare tutti gli elementi di posizione (non
indice) pari di C (il 2o, il 4o,…) e poi tutti quelli di posizione
dispari (1o, 3o,…).
Esempio: vettori di lunghezza 4, in A sono stati messi i valori: 3
5 2 6 e in B: 3 2 6 3, verranno quindi calcolati e messi in C i
valori: 6 7 8 9 e quindi stampati i valori: 7 9 6 8.
#include<stdio.h>
#define MAXNUM 100
int main()
{
int v[MAXNUM], max, min, somma;
int n, i;
do
{
printf("Quanti valori introdurrai (max %d)? ", MAXNUM);
scanf("%d", &n);
}while(n>MAXNUM || n<=0); /* continua a chiedere un nuovo valore per n fintanto che il
valore non e' minore di MAXNUM */
for (i=0; i<n; i++)
{
printf("Introduci il %do valore: ", i+1);
scanf("%d", &v[i]);
}
max = v[0];
min = v[0];
somma = v[0];
for (i=1; i<n; i++)
{
somma += v[i];
if (v[i]>max)
max = v[i];
else if (v[i]<min)
min = v[i];
}
printf("Massimo: %d\n", max);
printf("Minimo: %d\n", min);
printf("Somma: %d\n", somma);
printf("Media: %f\n", (double)somma/n);
return 0; }
Scrivere un programma che chieda
quanti valori verranno introdotti dalla
tastiera (max 100), li chieda tutti e li
collochi in un vettore.
Successivamente, il programma deve
determinare il massimo, il minimo, la
somma e la media di questi valori.
7 Stringhe / caratteri
Caso particolare: STRINGHE
Le stringhe sono dei vettori i cui elementi sono dei caratteri. Nel codice C le stringhe si possono definire come segue:
char x[6];
stringa di 5 caratteri più il terminatore di stringa \0 (rappresentazione del carattere 0)
charx[ ] = {‘c’, ‘o’, ‘d’, ‘i’, ‘c’, ‘e’, ‘\0’};
stringa di 6 caratteri
char x[ ] = “scuola”; stringa di 6 caratteri (NB: in questo caso il compilatore aggiunge il terminatore di stringa (7°
carattere))
ESEMPIO: Programma che consente solo 3 tentativi per l’inserimento del codice segreto
Struttura iterativa:
ciclo
FOR
Al ciclo while si può sostituire il ciclo for.
for (campo1; campo2;
campo3)
{ …………………...
……………………
……………………
}
campo1: valore iniziale della variabile di
conteggio campo2:
condizione per la
ripetizione
del
codice
campo3:
aggiornamento della variabile di conteggio
ESEMPIO 12: programma che acquisisce 6 numeri interi da tastiera e in contemporanea esegue la somma, al termine calcola la media
#include <stdio.h>
#include <stdlib.h> int x, k, s = 0;
float m;
int main()
{ for(k = 1; k <= 6; k ++)
{ printf("Inserisci il %d numero intero: ", k);
scanf("%d", &x);
s = s + x;
/* aggiornamento della somma */
}
m = s / 6.0; /* calcolo della media */
printf("Il valore della somma risulta %d, e della media %f \n", s, m);
system(“pause”);
}
NB: all’inizio k vale 1, lo si confronta
con 6, se minore si esegue il codice tra
parentesi graffe, poi si incrementa k
di 1 e lo si confronta di nuovo con 6,
se ancora minore si ripete il codice.
6.1 Definizione
Una variabile di tipo char consente di memorizzare un singolo carattere.
Molto spesso, però, è comodo poter trattare come una sola unità un insieme di caratteri
alfanumerici, detto stringa; a questo scopo si possono utilizzaree gli array di char.
La linea di codice
char a[10];
Dichiara un vettore costituito da dieci caratteri.
char frase[] = "Analisi, requisiti ";dichiara invece l’array monodimensionale di
caratteri frase, il cui numero di elementi è determinato dalla quantità di caratteri
presenti tra doppi apici più uno, il carattere null (\0).
Il carattere \0 è il primo del codice ASCII, corrisponde alla notazione
binaria 00000000 e non ha niente a che vedere con il carattere 0 che
corrisponde a 00110000.
È importante osservare la differenza tra le due inizializzazioni:
char d = 'r’;
char b[] = "r";
La prima assegna alla variabile d di tipo char il valore r, la seconda assegna all’array b[] la sequenza di
caratteri r e \0; in quest’ultimo caso si tratta effettivamente di una stringa.
Naturalmente, quando si desidera far riferimento a un carattere si deve inserirlo tra apici singoli:
per esempio
b[2] = 't';
assegna al terzo elemento dell’array b il carattere t.
Il carattere terminatore \0 ci permette di trattare le stringhe senza conoscere a priori la dimensione.
Il programma del Listato 6.1 consente di verificare la corrispondenza tra ogni carattere presente in
una stringa e il suo equivalente valore all’interno del codice ASCII, espresso nei sistema decimale e
ottale.
/* listato 6.1 Visualizzazione caratteri di una stringa */
#include <stdio.h>
char frase[] = "Analisi, requisiti ";
main()
{
int i=0;
while(frase[i]!='\0') {
printf("%c = %d = %o \n", frase[i], frase[i], frase[i]); i++;
}
}
Il ciclo while permette di fare la scansione, uno a
uno, dei caratteri della stringa.
Viene controllato se il carattere in esame è \0, nel
qual caso non ci sono più caratteri da esaminare e
l’iterazione ha termine.
L’istruzione printf visualizza a ogni ciclo un elemento
dell’array, in tre formati differenti:
printf("%c
=
%d
frase[i],frase[i],frase[i]);
=
%o
\n",
Il primo formato, specificato da %c, indica il carattere ASCII stesso,
il secondo e il terzo sono i suoi corrispondenti codici espressi nel sistema decimale (%d) e ottale (%o).
Questo gioco di corrispondenze tra caratteri e numeri interi, definite dal codice ASCII, è sempre valido e
offre grande libertà al programmatore.
Comunque, se si desidera la visualizzazione dell’intera stringa, è possibile usare l’istruzione printf tramite la
specifica del formato %s:
printf("%s", frase);
Tale istruzione, se inserita nel Listato 6.1 , restituirebbe:
Analisi, requisiti
In questo caso è l’istruzione printf stessa che provvede a stampare carattere per carattere la stringa e a
bloccarsi nel momento in cui identifica il carattere \0.
6.2 Esempi di uso delle stringhe
/* LISTAYO 6.2 Copia di una stringa su un'altra */
#include <stdio.h>
char frase[] = "Analisi, requisiti ";
main()
{
int i;
char discorso[80];
for(i=0; (discorso[i]=frase[i])!='\0'; i++);
printf(" originale: %s \n copia: %s \n", frase, discorso);
}
La variabile intera i viene utilizzata come indice degli array, per fare la scansione delle due stringhe carattere per
carattere e per effettuare la copia. Nell’istruzione for viene inizializzato il valore di i a 0:
i = 0;
Successivamente il ciclo assegna a discorso[0] il valore di frase[0] e controlla che tale valore non sia uguale a \0
(marca di fine stringa), nel qual caso il ciclo ha termine. A ogni nuova iterazione il valore di i viene incrementato di
1:
i++;
Viene quindi assegnato
a discorso[i] il valore di
frase[i], (discorso[i]=frase[i])
Se si desidera copiare soltanto alcuni caratteri della prima stringa sulla seconda si deve modificare l’istruzione for
del Listato 6.2. Scrivendo
for(i=0; ((discorso[i]=frase[i])!='\0') && (i<7); i++)
si è inserita la condizione i<7 messa in AND (&&) con la verifica di fine stringa; in questo modo verranno
copiati solamente i primi sette caratteri. L’istruzione printf visualizzerà allora:
originale: Analisi, requisiti copia: Analisi
Il programma del Listato 6.3 permette invece di aggiungere a una variabile stringa i caratteri presenti in
un’altra.
/* LISTATO 6.3: Concatenazione di due stringhe */
#include <stdio.h>
char frase[160] = "Analisi, requisiti ";
main()
{
char dimmi[80]; int i, j;
printf("Inserisci una parola: ");
scanf("%s", dimmi);
for(i=0; (frase[i])!='\0'; i++) ;
for(j=0; (frase[i]=dimmi[j])!='\0'; i++,j++) ;
printf("frase: %s \n", frase);
}
In questo caso indichiamo esplicitamente il numero di elementi
(160) che compongono la variabile frase, poiché desideriamo
definire un array che possa contenere più caratteri di quelli
presenti nella stringa assegnatagli all’inizio (20):
char frase[160] = "Analisi, requisiti ";
In questo modo frase potrà contenere i caratteri che gli
verranno concatenati. La prima istruzione
printfrichiede
all’utente una stringa e scanf la inserisce nell’array di caratteri
dimmi.
In generale non si conosce il numero di caratteri che
attualmente costituiscono la stringa di partenza, per cui si deve
scorrerla fino a posizionare l’indice sul carattere terminatore:
for(i=0; (frase[i])!='\0'; i++);
Alla fine del ciclo i conterrà l’indice dell’elemento del vettore
dov’è presente il carattere \0. Nel caso
specifico, avendo
assegnato a frase la stringa "Analisi, requisiti ", iavrà valore 20.
Adesso dobbiamo assegnare agli elementi successivi di frase il contenuto di dimmi:
for(j=0; (frase[i]=dimmi[j])!='\0'; i++,j++) ;
L’indice j scorre dimmi a partire dalla prima posizione, mentre i scorre frase a partire dal suo carattere
terminatore; alla prima iterazione il carattere \0 di frase viene sostituito dal primo carattere di dimmi. A
ogni ciclo successivo viene assegnato a frase[i] il valore di dimmi[j].
All’ultima iterazione il carattere \0 di dimmi viene posto in frase, così da chiuderla correttamente.
L’istruzione printf visualizza il nuovo contenuto di frase.
printf("frase: %s \n", frase);
Osserviamo di seguito una possibile esecuzione del programma.
Inserisci una parola: funzionali
frase: Analisi, requisiti funzionali
In Figura 6.2, A e B corrispondono agli stati degli array immediatamente prima e dopo l’esecuzione del
secondo fordel programma che effettua la concatenazione.
Figura 6.2 Stato degli array prima e dopo la concatenazione
Un altro modo per memorizzare una stringa è l’uso, all’interno di un ciclo, della funzione getchar, che
cattura il carattere passatole in ingresso (Listato 6.4).
/* Listato 6.4 Immissione di caratteri con getchar()
Concatenazione di due stringhe*/
#include <stdio.h>
char frase[160] = "Analisi, requisiti ";
main()
{
char dimmi[80];
int i, j;
printf("Inserisci una parola: ");
for(i=0; (dimmi[i]=getchar())!='\n'; i++) ;
dimmi[i]='\0';
for(i=0; frase[i]!='\0'; i++);
for(j=0; (frase[i]=dimmi[j])!='\0'; i++,j++);
printf(" frase: %s \n", frase);
}
Il ciclo for che sostituisce l’istruzione scanf inizializza l’indice
i a zero, cattura il carattere passato da tastiera mediante la
funzione getchar e lo inserisce nel primo elemento dell’array
dimmi:
for(i=0; (dimmi[i]=getchar())!='\n'; i++);
A ogni iterazione il valore di i viene incrementato di 1 e il
valore immesso viene inserito nel corrispondente elemento
dell’array. Il ciclo si ripete finché il carattere immesso è
diverso da \n, cioè fino a quando l’utente non batte un Invio.
La stringa memorizzata in dimmi non contiene il carattere terminatore, che va esplicitamente
assegnatogli nella posizione appropriata:
dimmi[i] = '\0';
È chiaro che potremmo decidere d’interrompere l’inserimento al verificarsi di un altro evento; per
esempio, quando l’utente batte un punto esclamativo. In questo modo potremmo memorizzare
più linee nello stesso array: ogni Invio dato dal terminale corrisponde infatti all’assegnamento di
un \n
a un elemento dell’array; evidentemente una successiva visualizzazione dell’array
mostrerebbe la stringa con gli accapo inseriti dall’utente.
NOTA
Nel programma abbiamo definito dimmi di 80 caratteri. Se l’utente ne inserisse un numero maggiore,
come abbiamo già evidenziato, i sovrabbondanti andrebbero a sporcare zone contigue di memoria
centrale. Il C non fa infatti nessun controllo automatico del rispetto dei margini dell’array. È il
programmatore che si deve preoccupare di verificare che gli assegnamenti vengano effettuati su elementi
definiti dell’array, per cui un più corretto ciclo d’inserimento del programma sarebbe:
for(i=0; ((dimmi[i]=getchar())!='\n') && (i<80)) ;i++);
Il ciclo prosegue finché il carattere catturato è diverso da \n e contemporaneamente i è minore di 80.
Scriviamo adesso un programma che confronta due stringhe rivelando se la prima è uguale, maggiore o
minore della seconda (Listato 6.5). L’ordinamento seguito è quello definito dal codice di rappresentazione
dei caratteri, che nella maggior parte delle macchine è il codice ASCII.
/* L NO 6.5:Confronto fra ARRAY DI CHARdue stringhe */
#include <stdio.h>
char prima[160] = "mareggiata";
main()
{
char seconda[80];
int i;
printf("Inserisci una parola: ");
for(i=0; ((seconda[i]=getchar()) != '\n') && (i<80) ;i++) ;
seconda[i]='\0';
for(i=0; (prima[i] == seconda[i]) && (prima[i] != '\0') &&
(seconda[i] != '\0'); i++);
if(prima[i]==seconda[i])
printf("Sono uguali\n"); else
if(prima[i]>seconda[i])
printf("La prima è maggiore della seconda\n"); else
printf("La seconda è maggiore della prima\n");
}
L’istruzione For
for(i=0; (prima[i]==seconda[i]) &&
(prima[i]!='\0') && (seconda[i]!='\0'); i++);
scorre in parallelo gli elementi dei due array e li
confronta;
il ciclo si interrompe quando
prima[i] non risulta essere uguale a seconda[i]
oppure quando finisce una delle due stringhe.
L’if seguente serve a determinare la ragione per
cui il ciclo for si è interrotto; si noti che l’unica
possibilità
per cui prima[i] è uguale a
seconda[i] si presenta quando entrambi sono
uguali a \0, il che significa che le stringhe
hanno la stessa lunghezza e sono uguali.
6.3 Funzioni di libreria
Esistono nella libreria string.h funzioni standard che permettono di effettuare le operazioni che abbiamo
esaminatosulle stringhe e molte altre ancora. Come al solito, è sufficiente dichiarare il riferimento a tale libreria
all’inizio del programma per poter utilizzare le funzioni in essa contenute.
La funzione strcpy consente di copiare stringa2 su stringa1: strcpy(stringa1, stringa2);
La funzione strncpy permette invece di copiare i primi n caratteri di stringa2 in stringa1: strncpy(stringa1,
stringa2, n);
mentre la funzione strcat consente di concatenare stringa2 a stringa1: strcat(stringa1, stringa2);
La funzione strcmp serve a confrontare stringa2 con stringa1 (Listato 6.6): strcmp(stringa1, stringa2);
Se risultano essere uguali viene restituito zero, se stringa1 è maggiore di stringa2 viene restituito un valore
positivo, altrimenti un valore negativo .
/* LISTATO 6.6 Confronto tra due stringhe con strcmp */
#include <stdio.h>
#include <string.h>
char prima[160] = "mareggiata";
main()
{
char seconda[80];
int i, x;
printf("Inserisci una parola: ");
for(i=0; ((seconda[i]=getchar())!='\n') && (i<80); i++);
seconda[i] = '\0';
if( (x = (strcmp(prima, seconda))) == 0)
printf("Sono uguali\n");
else
if(x>0)
printf("la prima è maggiore della seconda\n");
else
printf("la seconda è maggiore della prima\n");
}
ESEMPI
Scrivere un programma che date due
stringhe in input stampi la più lunga.
La prima se sono di uguale
lunghezza.
#include<stdio.h>
#include<string.h>
#define MAXSTR 80
int main()
{
char a[MAXSTR], b[MAXSTR];
printf("Stringa 1? ");
gets(a);
printf("Stringa 2? ");
gets(b);
if (strlen(a) >= strlen(b))
printf("%s\n", a);
else
printf("%s\n", b);
return 0;
}
Scrivere un programma che
date due stringhe in input
stampi la maggiore.
#include<stdio.h>
#include<string.h>
#define MAXSTR 80
int main()
{
char a[MAXSTR], b[MAXSTR];
printf("Stringa 1? ");
gets(a);
printf("Stringa 2? ");
gets(b);
if (strcmp(a,b) >=0 )
printf("%s\n", a);
else
printf("%s\n", b);
Scrivere un programma che
chieda in input una stringa e
calcoli da quanti caratteri è
composta
(senza
usare
la
funzione strlen ma cercando
il carattere '\0’)
#include<stdio.h>
#define MAXSTR 80
int main()
{
char a[MAXSTR];
int cont;
Scrivere un programma che data
una stringa
in input, la
converta tutta in maiuscolo.
#include<stdio.h>
#include<string.h>
#include<ctype.h>
#define MAXSTR 80
int main()
{
char a[MAXSTR];
int i, l;
printf("Stringa? ");
gets(a);
l=(int)strlen(a);
for (i=0; i<l; i++)
a[i] = (char)toupper(a[i]);
printf("%s\n", a);
printf("Stringa? ");
gets(a);
cont=0;
while (a[cont] != '\0')
cont++;
printf("%d\n", cont);
return 0;
}
}
return 0;
return 0;
}
Scrivere un programma che data
una stringa in input verifichi se
essa contiene almeno una ‘A’ tra i
primi 10 caratteri.
#include<stdio.h>
#define MAXSTR 80
int main()
{
char a[MAXSTR];
int i, trovato=0;
printf("Stringa? ");
gets(a);
for (i=0; i<10 && a[i] != '\0'; i++)
/* (1) */
if (a[i] == 'A')
trovato = 1;
if (trovato == 1)
printf("Trovato\n");
else
printf("Non trovato\n");
return 0;
}
Scrivere un programma che richieda in
input una stringa e conti quante
cifre essa contiene.
Esempio
“Ciao2004! C6?” deve dare 5.
#include <stdio.h>
#include<string.h>
#include<ctype.h>
#define MAXSTR 80
int main()
{
char a[MAXSTR];
int i, L, cifre=0;
printf("Introduci la stringa:");
gets(a);
}
L=(int)strlen(a);
for (i=0; i<L; i++)
if (isdigit(a[i]))
cifre++;
printf("Cifre: %d\n", cifre);
return 0;
Scrivere un programma che richieda in
input una stringa e conti di quante
lettere maiuscole, lettere minuscole,
cifre e altri caratteri è composta
#include <stdio.h>
#include<string.h>
#include<ctype.h>
#define MAXSTR 80
int main()
{
char a[MAXSTR];
int i, L, maius=0, minus=0, cifre=0;
printf("Introduci la stringa:");
gets(a);
L=(int)strlen(a);
for (i=0; i<L; i++)
if (isupper(a[i]))
maius++;
else if (islower(a[i]))
minus++;
else if (isdigit(a[i]))
cifre++;
printf("Maiuscole: %d\n", maius);
printf("Minuscole: %d\n", minus);
printf("Cifre: %d\n", cifre);
printf("Altri: %d\n", L-maius-minuscifre);
return 0;
}
IL CODICE ASCII
I caratteri e le stringhe
Per memorizzare i simboli grafici corrispondenti ai caratteri
bisogna associare un numero intero a ciascuno di essi
Contiene i 95 caratteri di base (es. non le lettere accentate)
Ha 4 sezioni importanti:
Spazio (è il carattere visibile di codice più basso)
Cifre (0-9 in ordine crescente)
Maiuscole (A-Z in ordine cresc.)
Minuscole (a-z in ordine cresc.)
Le 4 sezioni sono separate da altri caratteri generici
(punteggiatura, simboli matematici, ecc.)
Alcuni caratteri speciali (caratteri di controllo) non vengono visualizzati,
ma producono un effetto (es. inserire un ritorno a capo, beep)
Caratteri
Per memorizzare un carattere, il C memorizza il numero intero corrispondente al suo codice ASCII ('A' equivale
a 65, '0'a 48, ecc.)
Costanti carattere: indicate tra apici singoli ('A'), oppure indicandone il codice ASCII in: decimale: 65, in ottale:
'\101, in esadecimale: '\0x41'
Le costanti di tipo carattere vengono anche chiamate letterali carattere (character literal )
Essendo numeri interi, i caratteri possono essere usati nelle operazioni:
x = c–'0';
se c contiene il codice ASCII di una cifra, c–'0' ne è il valore corrispondente
Esempio
Se c='7', allora '7'–'0'viene valutato come 55–48, cioè il valore 7 (il risultato è di tipo int per effetto delle
promozioni integrali)
Variabili carattere: variabili di tipo intero su 8 bit, sono definite di tipo char ;y definizione
y = 'A’; assegnazione con carattere y = 65
y ='\0x41’; con cod. ASCII esadecim.
ypuò essere usata sia come numero (65) sia come carattere ('A'):
printf("%c ha valore %d\n", y, y); dove la specifica %c serve per visualizzare il simbolo corrispondente ad un
codice ASCII, mentre la specifica %d visualizza un numero intero, questo visualizza: A ha valore 65
Stringhe
Sono vettori di char terminati da un carattere
di codice ASCII pari a 0 (il terminatore non è il carattere '0' che ha valore 48 nel codice ASCII, ma il carattere
'\0')
Le terminate da uno 0 vengono anche dette stringhe ASCIIZ, il linguaggio C ha solo questo tipo di stringhe
Stringhe costanti: Sono sequenze di caratteri racchiuse da doppi apici, la stringa "ciao ciao" è composta da 9+1
caratteri, l’ultimo è '\0’
Per includere in una stringa i caratteri \ e " è necessario precederli dal carattere di escape \
"vero\\falso" memorizza: vero\falso
"premi \"invio\" per terminare«
memorizza: premi "invio" per terminare
Una stringa costante viene anche chiamata letterale stringa (string literal )
Più stringhe costanti consecutive (separate da
nulla, spazi, Tab o ritorni a capo) vengono concatenate dal
compilatore in una sola:
"ciao" "ciao"
"ciao"
"ciao"
viene memorizzata come fosse scritta così:
"ciaociaociaociao" (17 caratteri)
Una stringa costante è un vettore di char di classe di allocazione static (quindi non modificabile) inizializzato
con i caratteri dati
Le classi di allocazione sono descritte in altro set di slide (puntatori)
Variabili stringa
Sono vettori di char di dim. fissa, l’ultimo carattere deve essere il terminatore '\0'
char nome[15];
definisce una variabile stringa composta di 15 char, può contenere fino a 14 caratteri utili (deve esserci
spazio per il carattere '\0')
Il 1o carattere è nome[0], il 2o nome[1], ecc.
Il terminatore permette di occupare solo parzialmente una stringa (lo spazio relativo ai restanti caratteri
esiste ma è inutilizzato)
Si possono inizializzare le variabili stringa in 2 modi equivalenti:
char s[20]="Ciao";
char s[20]={'C','i','a','o'};
Il carattere di posizione 4 (il 5o) è '\0' in entrambi i casi: infatti, essendo vettori, se l’inizializzazione non
riempie completamente la stringa, i caratteri successivi a quelli indicati sono tutti 0 (cioè '\0')
I singoli elementi della stringa sono caratteri:
s[2] vale 'a'
s[0] = 'M'; modifica s in "Miao"
Per assegnare una stringa NON si può scrivere s="Ciao" ma serve una funzione
I/O di caratteri <stdio.h>
printf("%c", varChar);
manda in output il carattere
scanf("%c", &varChar);
legge 1 carattere (anche spazi e ritorni a capo) e lo mette in varChar, se viene indicata un’ampiezza (es. %4c)
legge esattamente quel numero di caratteri (anche spazi) e li assegna alla STRINGA indicata come parametro,
senza aggiungere il '\0': scanf("%4c", varStringa); per saltare gli spazi iniziali si usi %1s
I/O di caratteri <stdio.h>
putchar(varChar);
manda in output il carattere
varInt = getchar();
getchar restituisce il carattere letto o la costante EOF per segnalare la fine dell’input, varInt deve essere di
tipo int per potervi memorizzare anche EOF che è di tipo int.
EOF è una costante simbolica definita in <stdio.h> con una #define, in genere vale –1
Libreria caratteri <ctype.h>
Le seguenti funzioni danno risultato vero (valore !=0) se il carattere c è del tipo indicato
isdigit(c) cifra decimale
isalpha(c) lettera
isalnum(c) carattere alfanumerico
isxdigit(c) cifra esadecimale
islower(c) lettera minuscola
isupper(c) lettera maiuscola
iscntrl(c) carattere di controllo
isspace(c) white space (' ','\t','\n',...)
isprint(c) char stampabile, incluso lo spazio
isgraph(c) char stampabile, escluso lo spazio
ispunct(c) stampabile, no spazio, no alfanum
Libreria caratteri <ctype.h>
Le seguenti funzioni producono un valore int
contenente il codice ASCII del carattere c eventualmente
convertito, se possibile:
toupper(c) in maiuscolo
tolower(c) in minuscolo
Altrimenti il valore prodotto resta c (invariato)
Se si vuole convertire in maiuscolo/minuscolo tutta una stringa è necessario applicare la funzione a ciascuno
dei caratteri:
for (i=0; i<strlen(s); i++)
s[i] = (char)toupper(s[i]);
notare il cast: toupper produce un int
Funzioni su stringhe <stdlib.h>
varInt = atoi(stringa) converte stringa in int
x=atoi("123"); 123 in complem. a 2
varLong = atol(stringa) converte stringa in long
y=atol("123"); 123 in complem. a 2
varDouble = atof(stringa) converte stringa in double
z=atof("1.23E5"); 1.23×105 in floating point
Confronto tra stringhe
Avviene confrontando i caratteri di posizione corrispondente delle due stringhe secondo i loro codici ASCII ( “< ” significa
“precede”)
“cane”
“cane”
<
>
“gatto”
“Gatto”
“cane”
<
“cavallo”
“cavallo”
<
“cavallone”
“cavallo”
<
“cavallo ”
Libreria stringhe <string.h>
Lunghezza di una stringa, Copia di una stringa, Concatenazione di stringhe
Concatenazione di stringhe, Ricerca in stringhe
ESEMPI
Scrivere un programma che date due
stringhe in input stampi la più
lunga. La prima se sono di uguale
lunghezza.
#include<stdio.h>
#include<string.h>
#define MAXSTR 80
int main()
{
char a[MAXSTR], b[MAXSTR];
printf("Stringa 1? ");
gets(a);
printf("Stringa 2? ");
gets(b);
if (strlen(a) >= strlen(b))
printf("%s\n", a);
else
printf("%s\n", b);
return 0;
}
Scrivere un programma che
date due stringhe in input
stampi la maggiore.
#include<stdio.h>
#include<string.h>
#define MAXSTR 80
int main()
{
char a[MAXSTR], b[MAXSTR];
printf("Stringa 1? ");
gets(a);
printf("Stringa 2? ");
gets(b);
if (strcmp(a,b) >=0 )
printf("%s\n", a);
else
printf("%s\n", b);
Scrivere un programma che
chieda in input una stringa e
calcoli da quanti caratteri è
composta (senza usare la
funzione strlen ma cercando
il carattere '\0’)
#include<stdio.h>
#define MAXSTR 80
int main()
{
char a[MAXSTR];
int cont;
Scrivere un programma che data
una stringa
in input, la
converta tutta in maiuscolo.
#include<stdio.h>
#include<string.h>
#include<ctype.h>
#define MAXSTR 80
int main()
{
char a[MAXSTR];
int i, l;
printf("Stringa? ");
gets(a);
cont=0;
while (a[cont] != '\0')
cont++;
printf("%d\n", cont);
return 0;
}
}
printf("Stringa? ");
gets(a);
l=(int)strlen(a);
for (i=0; i<l; i++)
a[i] = (char)toupper(a[i]);
printf("%s\n", a);
return 0;
return 0;
}
sottoprogramma
7.1 Il concetto di sottoprogramma
Un programma è formato da elementi connessi in modo da raggiungere un determinato scopo. Le istruzioni
possono essere considerate i componenti di un programma.
Un programma non può essere “smontato” oltre il limite delle singole istruzioni, ma è possibile aggregare gruppi
di istruzioni per formare dei “semilavorati” detti sottoprogrammi. Come un personal computer è composto da
tastiera, video, stampante e unità centrale, così un programma per il calcolo degli stipendi potrebbe essere
scomposto nei sottoprogrammi di immissione delle ore lavorate, di calcolo dello stipendio e di visualizzazione e
stampa della situazione contabile di ogni impiegato.
I sottoprogrammi si usano anche per evitare di replicare porzioni di codice sorgente: invocare un
sottoprogramma significa mandare in esecuzione la porzione di codice corrispondente. Se un sottoprogramma è
invocato più volte, la porzione di codice è eseguita più volte, tante quante sono le invocazioni. Il vantaggio dei
sottoprogrammi è appunto di consentire al programmatore di avere tante chiamate ma una sola porzione di
codice.
È possibile poi creare delle librerie, cioè delle raccolte di sottoprogrammi che possono essere utilizzati senza
essere a conoscenza dei dettagli implementativi. È quanto avviene con le funzioni printf() e scanf(), la cui
dichiarazione è contenuta nel file stdio.h.
7.2 Sottoprogrammi C
In C i sottoprogrammi sono detti funzioni: a partire da uno o più valori presi in ingresso, esse ritornano (o
restituiscono) un valore al programma chiamante. Come indicato in Figura 7.1, una funzione può essere
pensata come una scatola nera che a determinati valori in ingresso fa corrispondere un determinato valore
in uscita.
Un esempio di funzione C è abs(i), già utilizzata più volte. Considerando la funzione abs come una scatola
nera, tutto quello che dobbiamo sapere
e in effetti già sappiamo
è che inserendo come argomento i di
tale funzione un numero intero essa ne ritorna il valore assoluto (Figura 7.2).
Prima di esaminare la sintassi di dichiarazione e definizione di una funzione si consideri l’esempio riportato
nel Listato 7.1.
Per
poter
usare
un
identificatore
occorre
innanzitutto
#include <stdio.h>
double cubo(float);
main()
{
float
a; double b;
printf("Inserisci un numero: "); scanf("%f", &a);
b = cubo(a);
printf("%f elevato al cubo è uguale a %f", a, b);
}
double cubo(float c)
{
return (c*c*c);
}
dichiararlo. La dichiarazione: double cubo(float);
che precede main introduce l’identificatore cubo.
Per mezzo di questa dichiarazione si specifica che cubo è il
nome di una funzione che restituisce al programma chiamante
un valore di tipo double. Inoltre si dichiara che la funzione cubo
accetta in ingresso un solo valore come argomento, il cui tipo è
float.
In sostanza
abbiamo dichiarato un nuovo nome, cubo,
abbiamo detto a quale categoria appartiene questo nome.
La definizione della funzione cubo avviene più tardi, dopo
la fine del blocco di istruzioni di main:
double cubo(float c)
{
return (c*c*c); }
e
Oltre al nome della funzione viene definito il numero, il tipo e il nome dei suoi parametri, cioè le variabili su cui
essa agisce. Nel nostro esempio è presente un solo parametro, il cui tipo è float e il cui nome è c.
Il compito svolto da cubo è molto semplice: il valore passato nel parametro c è moltiplicato per se stesso tre
volte (c*c*c) e il risultato di questa espressione è convertito in double e restituito (con return) al programma
chiamante.
Il programma chiamante non ha da fare altro che passare alla funzione cubo un valore. Nell’esempio lo fa
passando a cubo il valore contenuto nella variabile a: cubo(a). Successivamente il valore calcolato da cubo viene
assegnato a una variabile di tipo double. Nell’esempio tale variabile è b e l’assegnazione è b = cubo(a);
Con questo semplice esempio abbiamo messo in luce diversi aspetti della sintassi delle funzioni:
• • la dichiarazione di una funzione:
double cubo(float); (double tipo di ritorno, float tipo di utilizzo)
• • la definizione di una funzione:
double cubo(float c) {...}; nome della funzione
• • il ritorno di un valore:
return(c*c*c);
• • l’invocazione di funzione:
b = cubo(a).
Passiamo ora a considerare in dettaglio ciascuno dei punti evidenziati.
Passiamo ora a considerare in dettaglio ciascuno dei punti evidenziati.
7.3 Dichiarazione di una funzione
In termini generali una funzione viene dichiarata con la sintassi detta prototyping: (prototipazione)
tipo_ritorno nome_funz (tipo_par1, ..., tipo_parN);
La dichiarazione introduce il nome della funzione, che in questo modo può essere utilizzato dal programma, ma
presuppone che da qualche altra parte ne esista la definizione, altrimenti quel nome resterebbe privo di
significato e il compilatore segnalerebbe un errore.
Nella dichiarazione di una funzione si potrebbero specificare anche i nomi dei parametri formali. Per
esempio:
double cubo(float c);
è una dichiarazione valida. Il nome del parametro formale, però, è assolutamente superfluo. Ciò che conta
in una dichiarazione è il tipo, o meglio la lista dei tipi dei parametri formali. Se in una dichiarazione di una
funzione si specificano anche i nomi dei parametri formali il compilatore semplicemente li ignora.
7.4 Definizione di una funzione
In termini generali una funzione viene definita con la sintassi prototyping nel seguente modo:
tipo_ritorno nome_funz (tipo_par1 par1, ..., tipo_parN parN)
{
...
}
La definizione stabilisce il nome della funzione, i valori in ingresso su cui agisce
detti parametri formali ,
il blocco di istruzioni che ne costituiscono il contenuto, e l’eventuale valore di ritorno. Per i nomi delle
funzioni valgono le consuete regole in uso per gli identificatori. Nelle parentesi tonde che seguono il nome
della funzione sono definiti i parametri formali specificandone il tipo e il nome.
Per ogni funzione introdotta nel programma occorre una definizione ( si ricordi che in C non è ammesso che
più funzioni abbiano lo stesso nome)
Nel blocco istruzioni delimitato da parentesi graffe può essere inserita qualunque istruzione, compresa una
chiamata di funzione.
#include <stdio.h>
#include <stdlib.h>
double coefficiente_binomiale(int n, int k);
int fattoriale(int n);
int n, k;
int main()
{
printf("n= "); scanf("%d", &n);
printf("k= "); scanf("%d", &k);
if((n < k) || (k < 0))
printf("dati non validi \n ");
else
printf("n su k =%lf\n", coefficiente_binomiale(n,
k));
return EXIT_SUCCESS;
}
double coefficiente_binomiale(int n, int k)
{
return fattoriale (n) /
(double) fattoriale(k)*fattoriale(n-k); }
int fattoriale (int n)
{
int fatt = 1;
while (n>1)
fatt*= n--;
return fatt; }
/* LISTATO 7.2: DICHIARAZIONE E
DEFINIZIONE DI FUNZIONE*/
#include <stdio.h>
double quad(float); double cubo(float);
double quar(float); double quin(float);
double pote(float, int);
La funzione main richiama la funzione potenza pote passando a essa due
parametri attuali: base ed esponente
ptnz = pote(base, esponente);
main() {
int base, esponente;
double ptnz;
printf(" Inserire base: " );
scanf("%d", &base);
printf(" Inserire esponente (0-5): ");
scanf("%d", &esponente);
ptnz = pote( base, esponente);
if (ptnz == -1)
printf("Potenza non prevista\n");
else
printf("La potenza %d di %d e' %f \n", esponente, base, ptnz); }
La funzione pote, che riceve in ingresso i valori nei
parametri b ed e corrispondenti rispettivamente a base ed
esponente, valuta il valore dell’esponente; dopo di ciò
effettua una delle seguenti azioni:
restituisce il valore 1 per esponente 0, la base stessa b
per esponente 1, invoca la funzione quad
per esponente 2, cubo
per esponente 3, quar
per esponente 4, quin
per esponente 5 oppure restituisce
1 per segnalare la
non disponibilità della potenza richiesta.
double quad(float c)
return(c*c);
}
double cubo(float c)
return(c*c*c); }
double quar(float c)
return(c*c*c*c); }
double quin(float c)
return(c*c*c*c*c);
}
{
{
{
{
double pote(float b, int e) {
switch (e) {
case 0: return (1); case 1: return (b);
case 2: return (quad( b )); case 3: return (cubo( b ));
case 4: return (quar( b )); case 5: return (quin( b ));
default : return (-1);
} }
Se l’esponente è 2, viene dunque invocata la funzione quad, cui la
funzione pote trasmette il parametro attuale b:
case2: return quad( b );
quad lo riceve in ingresso nel parametro formale c (FIGURA 7.2)
La funzione quad calcola il quadrato di c e restituisce il risultato a
pote, la quale a sua volta lo restituisce a main che l’aveva invocata
(Figura 7.3). Il main gestisce tramite if il ritorno del valore negativo
1, usato per segnalare la non disponibilità della potenza richiesta.
7.5 Visibilità
Prima di passare all’elemento sintattico “return”, dobbiamo osservare quanto segue.
Una dichiarazione introduce un nome in un determinato ambito di definizione, detto scope. In altre parole, ciò
significa che un nome può essere usato soltanto -o, come si usa dire, è visibile in una specifica parte del testo
del programma. Per un nome dichiarato all’interno del blocco istruzioni di una funzione (nome locale), la
visibilità si estende dal punto di dichiarazione alla fine del blocco in cui esso è contenuto.
Per un nome definito al di fuori di una funzione (nome globale) la visibilità si estende dal punto di
dichiarazione alla fine del file in cui è contenuta la dichiarazione.
Così, per esempio, in
int x; f()
{
int y;
y = 1;
}
la visibilità della variabile y si estende dal punto di definizione sino alla fine del blocco di appartenenza.
Anche i parametri formali di una funzione hanno un campo di visibilità che si estende dall’inizio alla fine del
blocco istruzioni della funzione; sono quindi considerati a tutti gli effetti variabili locali alla funzione
int x;
g(int y, char z)
{
int k; int l;
...
}
le variabili y e z sono locali alla funzione g e hanno una visibilità che si estende dalla parentesi graffa aperta
{ alla corrispondente parentesi graffa chiusa }. Quindi la definizione di y e z precede all’interno del blocco la
definizione delle altre variabili locali k e l aventi anch’esse una visibilità che va dal punto di definizione
alla fine del blocco . Per questo motivo la funzione:
f(int x)
{ int x; }
è errata: in essa si tenta di definire due volte la variabile locale x nello stesso blocco.
Una dichiarazione di un nome in un blocco può nascondere, o come si dice in gergo, mascherare, la
dichiarazione dello stesso nome in un blocco più esterno o la dichiarazione dello stesso nome globale.
Un nome ridefinito all’interno di un blocco nasconde il significato precedente di quel nome, significato che
verrà ripristinato all’uscita del blocco di appartenenza (Listato 7.3) .
NOTA: È inevitabile che in un programma avvenga il
// 7.3: Esempio di mascheramento dei nomi
mascheramento di nomi e non è infrequente il caso in
int x; /* nome globale */
cui il
programmatore non si accorge di aver
f()
mascherato un nome all’interno di un blocco. È allora
{
consigliato identificare le variabili globali con dei nomi
int x; /* x locale che nasconde x globale */
caratteristici e univoci: usare per variabili globali nomi
x = 1; /* assegna 1 a x locale */
del tipo i, j oppure x significa rischiare mascheramenti
indesiderati.
{
7.6 return
int x; /* nasconde il primo x locale */
x = 2; /* assegna 2 al secondo x locale */
}
x = 3; /* assegna 3 al primo x locale */
}
scanf ("%d", &x); /* inserisce un dato in x globale */
A ogni funzione C è associato un tipo, scelto tra quelli
fondamentali o derivati, che caratterizza un valore.
Questo
valore è detto valore di ritorno della
funzione ed è restituito dalla funzione al programma
chiamante per mezzo
dell’istruzione return. La
sintassi
da
usare
è:return
(espressione);
oppure:
return espressione;
All’interno del blocco istruzioni di una funzione si possono avere più istruzioni return. Nella funzione pote:
double pote( b, e)
float b;
int e; {
switch (e) { case 0: return 1; case 1: return b; case 2: return quad(b); case 3: return cubo(b); case 4:
return quar(b); case 5: return quin(b); default : return -1; } }
a ogni scelta del costrutto switch-case corrisponde un’uscita e la restituzione di un diverso valore. In questo caso
abbiamo usato la forma sintattica del return non inserendo l’espressione di ritorno tra parentesi tonde.
L’invocazione di una funzione, detta anche chiamata di funzione (Paragrafo 7.8), può stare alla destra
dell’operatore di assegnamento, salvo il caso in cui il tipo sia void. Nella funzione cubo del Listato 7.1, per esempio:
b = cubo(a); alla variabile b viene assegnato il valore restituito dalla funzione cubo. Naturalmente il valore di
ritorno può essere utilizzato all’interno di un’espressione:
y = a * cubo(x) + b * quad(x) + c * x + d;
Nel caso in cui non sia esplicitamente definito un tipo di ritorno il linguaggio C assume che esso sia il tipo
fondamentale int.
7.7 Chiamata di una funzione
Una funzione C viene invocata facendo riferimento al nome e passando a essa una lista di parametri conforme in
tipo, numero e ordine alla lista dei parametri formali elencata nella definizione della funzione stessa (Listato 7.4).
//LISTATO 7.4: chiamata di funzione
#include <stdio.h>
double area(float, float, char);
main()
{
float b, h;
double a;
char p;
printf("Inserire poligono
(Triangolo/Rettangolo): ");
scanf("%c", &p);
printf("\nInserire base: ");
scanf("%f", &b);
printf("\nInserire altezza : ");
scanf("%f", &h);
a = area( b, h, p);
printf("Il poligono (b = %f, h = %f) ha area
%f\n", b, h, a);
}
double area(float base, float altezza, char
poligono)
{
switch (poligono) {
case 'T': return (base * altezza/2.0);
case 'R': return (base * altezza);
default : return -1;
}
}
/*LISTATO 7.5: le funzioni come strumento di riutilizzo del
codice*/
#include <stdio.h>
double area(float, float, char); main()
{
float b, h; double tri, ret;
printf("Inserire base: "); scanf("%f", &b); printf("Inserire
altezza: "); scanf("%f", &h);
tri = area(b, h, 'T');
ret = area(b, h, 'R');
printf("Il triangolo (b = %f, h = %f) ha area %f\n", b, h, tri);
printf("Il rettangolo (b = %f, h = %f) ha area %f\n", b, h, ret);
}
double area(float base, float altezza, char poligono)
{
switch (poligono) {
case 'T': return (base * altezza/2.0);
case 'R': return (base * altezza);
default : return -1;
}
}
7.8 Passaggio dei parametri
In questo capitolo abbiamo operato una distinzione
tra due tipi di parametri: i parametri formali e i
parametri attuali.
I parametri formali sono quelli dichiarati per tipo,
numero e ordine nella definizione della funzione. I
parametri attuali sono invece quelli che vengono
passati alla funzione all’atto della chiamata.
In C il passaggio dei parametri avviene sempre e
soltanto per valore. Ciò significa che all’atto
dell’invocazione di una funzione ogni parametro
formale
è
inizializzato
con
il
valore
del
corrispondente parametro attuale.
Ecco perché deve esistere una coerenza di tipo e di
numero tra parametri formali e parametri attuali.
Occorre comunque chiarire che non è necessaria la
perfetta corrispondenza. Infatti, nel trasferimento
di valore da
parametro attuale a parametro
formale possono essere effettuate delle conversioni
implicite di tipo. Per esempio,
nel semplice
programma:
main()
{
double c;
c = cubo( 2 );
}
double cubo(float c);
{
return( c*c*c );
}
L’istruzione c= cubo(2) è perfettamente valida poiché la costante intera 2 viene
convertita nella costante di tipo double 2.0 (si ricordi che non esistono in C le
costanti float).
Poiché con il passaggio dei parametri i valori dei parametri attuali sono travasati
nelle locazioni di memoria corrispondenti ai parametri formali, si ha che la
semantica del passaggio dei parametri è quella delle inizializzazioni di variabile:
come per le inizializzazioni sono previste delle conversioni implicite di tipo.
Più in dettaglio, si ha che nel passaggio dei parametri possono avvenire le
conversioni seguenti.
float I parametri attuali float sono convertiti in double prima di essere passati alla funzione. Di conseguenza tutti i parametri formali float
sono automaticamente trasformati in double.
char Tutti i parametri attuali char e short int, che esamineremo nei capitoli successivi, sono convertiti in
int. Di conseguenza tutti i parametri formali char sono trasformati in int.
Occorre poi osservare che non è consentito il passaggio di parametri di tipo array, proprio perché in C il passaggio dei parametri avviene
esclusivamente per valore. Infatti, se il compilatore si trovasse nella necessità di passare un array di tipo int a[1000], occorrerebbe una
quantità di tempo proporzionale per effettuare il travaso di valori tra due array di 1000 int.
Oltre al passaggio esplicito di parametri, è possibile anche il passaggio implicito. Infatti basta definire una variabile globale sia alla funzione
chiamante sia a quella chiamata per ottenere la condivisione della variabile stessa. Si consideri l’esempio del Listato 7.6, in cui la variabile
globale
char str[] = "Lupus in fabula";
è visibile sia dalla funzione main sia dalla funzione lung_string: quest’ultima fa riferimento a str per calcolarne il numero di caratteri,
mentre la funzione main vi fa riferimento per visualizzarne il contenuto.
/*LISTATO 7.6:Passaggio di
7.8 void
parametri con variabile globale*/
Abbiamo trattato il passaggio di parametri e la restituzione di
#include <stdio.h>
un valore da parte di una funzione. Prendiamo ora in esame
char str[] = "Lupus in fabula";
funzioni che non restituiscono alcun valore, e funzioni che non
int lung_string(void);
hanno parametri. In entrambi i casi il C mette a disposizione
main()
un “tipo” speciale detto void.
{
int l;
l = lung_string();
Tipico esempio di funzioni che non restituiscono alcun
printf("La stringa %s ha %d caratteri\n", str, l);
valore è quello delle funzioni il cui scopo è la
}
visualizzazione di un messaggio o, più in generale, la
int lung_string(void)
produzione di un’uscita su uno dei dispositivi periferici. Queste
{
funzioni sono talvolta conosciute con il curioso nome di
int i;
funzioni “lavandino” ( sink, in inglese) poiché prendono dati
for (i = 0; str[i] != '\0'; i++);
che riversano in una qualche uscita, senza ritornare niente al
return i;
chiamante.
}
Un esempio di funzione “lavandino” è la funzione stampa_bin (Listato 7.7).
La funzione stampa_bin divide ripetutamente per 2 il decimale v e memorizza i resti delle divisioni intere nel
vettore a[], che poi legge a ritroso per visualizzare l’equivalente binario del decimale v. nella dichiarazione
void stampa_bin( int );
sia nella definizione
si usa lo specificatore di tipo void per indicare l’assenza di un valore di ritorno.
void stampa_bin( int v )
Viceversa, quando per una funzione non è specificato il tipo void per il valore di
{
ritorno, nel blocco istruzioni della funzione è logico che sia presente per lo meno
...
una istruzione return.
}
Il tipo void è usato anche per le funzioni che non assumono alcun parametro. Un esempio di funzione che non ha parametri e
che non restituisce alcun valore è rappresentato da mess_err (Listato 7.8).
/*_ LISTATO 7.6: esempio di funzione lavandino*/
#include <stdio.h>
#define DIM_INT 16
void stampa_bin ( int );
main() {
char resp[2];
int num;
resp[0] = 's';
while( resp[0] == 's' ) {
printf("\nInserisci un intero positivo: ");
scanf("%d", &num);
printf("La sua rappresentazione binaria è: ");
stampa_bin( num );
printf("\nVuoi continuare? (s/n): ");
scanf("%s",resp);
}
}
void stampa_bin( int v ) {
int i, j;
char a[DIM_INT];
if (v == 0)
printf("%d", v);
else {
for( i=0; v != 0; i++) {
a[i] = v % 2; v /= 2;
}
for(j = i-1 ; j >= 0; j--) printf("%d", a[j]);
} }
/*_ LISTATO 7.7: funzione senza parametri*/
#include <stdio.h>
void mess_err( void );
main()
{
int a, b, c;
printf("Inserire dividendo:");
scanf("%d", &a);
printf("Inserire divisore:");
scanf("%d", &b);
if (b != 0) {
c = a/b;
printf("%d diviso %d = %d\n", a, b, c);
}
else
mess_err();
}
void mess_err( void )
{
int i;
char c;
for (i = 0; i <= 20; i++) printf("\n");
printf(" ERRORE! DENOMINATORE NULLO");
printf("\n Premere un tasto per continuare\n");
scanf("%c%c", &c, &c);
}
La funzione mess_err non prende parametri e
non restituisce alcun valore; essa ha il solo
compito di visualizzare un messaggio di errore nel
caso di inserimento di un denominatore nullo. In C
una funzione che non prende parametri può essere
anche designata semplicemente dalle sole parentesi
tonde, senza usare la
parola chiave void. Per
esempio:
e
void mess_err();
mess_err();
sono dichiarazioni valide. Nel secondo caso, però,
mess_err viene considerata una funzione il cui
eventuale valore di ritorno è di tipo int, anche se in
realtà non ha nessun valore di ritorno. Non è forse
questo il caso anche della funzione main? Abbiamo
continuato a definirla con:
void main(void)
{
...
}
a indicare il fatto che non ritorna nessun valore
è
quindi di tipo void
e che non assume parametri.
ESEMPI
Si scriva un programma che per 10 volte chieda all’utente
un valore e ne calcoli il logaritmo in base 2.
Per il calcolo del logaritmo si scriva una funzione con
prototipo:
double log2(double a);
che calcoli il valore utilizzando la formula
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#define NUM 10
double log2(double valore);
int main()
{
int i;
double a;
for (i=0; i<NUM; i++)
{
printf("Introdurre un numero: ");
scanf("%lf", &a);
printf("Il log2 di %f vale: %f\n", a, log2(a));
}
return EXIT_SUCCESS;
}
/*--------------------------------------------------------*/
double log2(double x)
{
return log(x)/log(2.0);
}
Si scriva una funzione con prototipo: double media(double v[], int len); che calcoli e
restituisca la media di un vettore di double passato come argomento. Si scriva un programma che
riempia due vettori di lunghezza differente (es. a[8] e b[10], li passi a media e visualizzi il
risultato per ciascuno di essi. La funzione non esegua operazioni di input/output.
#include <stdio.h>
#include <stdlib.h>
#define DIM1 8
#define DIM2 10
double media(double vettore[], int lunghezza);
int main()
{ int i;
double a[DIM1], b[DIM2];
printf("Inserire %d valori per a:\n", DIM1);
for (i=0; i<DIM1; i++)
scanf("%lf", &a[i]);
printf("Inserire %d valori per b:\n", DIM2);
for (i=0; i<DIM2; i++)
scanf("%lf", &b[i]);
printf("La media di a vale: %f\n", media(a,DIM1));
printf("La media di b vale: %f\n", media(b,DIM2));
return EXIT_SUCCESS;
}
/*--------------------------------------------------------*/
double media(double v[], int len)
{ double somma=0;
int i;
for (i=0; i<len; i++)
somma += v[i];
return somma/len;
}
Si scriva la funzione sommaVett che calcoli la somma di due
vettori. Si scriva un main che chieda la dimensione dei
vettori (max 100), ne chieda i valori, li passi alla funzione
e visualizzi il vettore dei risultati. Non si alteri il contenuto
dei due vettori da sommare. La
funzione non faccia
input/output.
Per non usare variabili esterne o variabili locali static, alla
funzione bisogna passare anche il vettore dei risultati (il
contenuto iniziale non è rilevante).
/*--------------------------------------------------------*/
void sommaVett(const int a[], const int b[], int r[], int n)
{
int i;
for (i=0; i<n; i++)
r[i] = a[i] + b[i];
}
/* Note
Il vettore da riempire con il risultato della somma viene
allocato nel chiamante (main) e passato alla funzione, il
contenuto iniziale di questo vettore e' irrilevante.
Per garantire la non modifica dei vettori si puo' usare la
clausola const come indicato.
*/
#include <stdio.h>
#include <stdlib.h>
#define MAXNUM 100
void sommaVett(const int a[], const int b[], int r[], int n);
int main()
{
int x[MAXNUM];
int y[MAXNUM];
int risultato[MAXNUM];
int n;
int i;
do {
printf("Lunghezza dei vettori? ");
scanf("%d", &n);
}while (n<1 || n>MAXNUM);
for (i=0; i<n; i++)
{
printf("x(%d): ", i+1);
scanf("%d", &x[i]);
}
for (i=0; i<n; i++)
{
printf("y(%d): ", i+1);
scanf("%d", &y[i]);
}
sommaVett(x, y, risultato, n);
for (i=0; i<n; i++)
printf("risultato(%d): %d\n", i+1, risultato[i]);
return EXIT_SUCCESS; }
esercizi
SOLUZIONE: Esercizio 1 Dati tre numeri interi, individuare il più grande.
47
SOLUZIONE
Esercizio 2
(Programma che acquisisce 9 numeri interi da tastiera e al termine ne
fa la media aritmetica)
Nel programma occorre organizzare un ciclo che acquisisca i numeri, all’interno del ciclo
organizzare l’esame del numero, se pari incrementare una variabile per il conteggio.
SOLUZIONE
Esercizio 3 (Programma che interrompe un ciclo se la somma dei numeri acquisiti
supera una soglia predefiniti pari a 28)
Rappresentato con il diagramma di flusso, il programma appare con struttura molto semplice e la sua
traduzione in C può realizzarsi in più modi.
SOLUZIONE Esercizio 4 (programma che carica in memoria 8 numeri interi; in seguito ne fa la somma)
#include <stdio.h>
#include <stdlib.h>
int z[5];
/* creazione di un vettore di nome z, di tipo intero e costituito
da 4 numeri interi.
NB: in fase di dichiarazione l'indice in parentesi
quadra indica il numero di elementi che
costituiscono il vettore.
int k = 0, s = 0;
/* variabile di conteggio, deve essere impostata a 0
poichè rappresenterà l'indice degli elementi del
vettore z (e il primo elemento ha indice 0); */
int main()
{ while(k <= 7)
{printf("Inserisci un numero intero per z[%d] = ", k);
scanf("%d", &z[k]);
k++;
}
k = 0;
while(k <= 7)
{ s = s + z[k];
k++;
/* il numero digitato da tastiera viene caricato nel
k-esimo elemento del vettore z */
/* aggiornamento della variabile di conteggio */
/* azzeramento della variabile di conteggio */
// ciclo per la somma
}
printf("\nLa somma degli elementi del vettore risulta %d”, s);
system(“pause”);
}
SOLUZIONE
Esercizio 5 (programma che carica in memoria 6 numeri reali, ma interrompe l’acquisizione
nel caso un numero risulti maggiore di 31.5)
#include <stdio.h>
#include <stdlib.h>
int v[6], k = 0;
int main()
{ while (k < 6)
{ printf("Inserisci un numero intero: ");
scanf("%d", &v[k]);
if (v[k] > 31.5)
{ printf(“\nCiclo interrotto”);
break; }
k++;
}
printf(“\nAcquisizione terminata \n");
system(“pause”);
}
SOLUZIONE Esercizio 7
(Programma che ricerca il numero intero più piccolo tra gli elementi di un
vettore di 5 elementi, da acquisire)
1/2
SOLUZIONE Esercizio 8 (Programma che carica in memoria 5 numeri interi; in seguito verifica se
è presente almeno un valore, tra gli elementi del vettore, che si ripete)
1/2
SOLUZIONE Esercizio 9
(Programma che carica in memoria 9 numeri interi e, in seguito, li ordina in senso crescente)
1/2
SOLUZIONE Esercizio 9 Programma che carica in memoria 9 numeri interi e, in seguito, li ordina in senso crescente)
#include <stdio.h>
#include <stdlib.h>
void main(){
int k = 0, x[7], y, h;
while(k < 7)
2/2
// acquisizione del vettore
{printf("\nInserire un valore per x[%d] = ", k);
scanf("%d", &x[k]);
k++;
}
k = 0;
while(k < 6)
{ h = k + 1;
while(h < 7)
{ if(x[h] < x[k])
{ y = x[k];
x[k] = x[h];
x[h] = y;
}
h++;
}
k++;
// ordinamento in senso crescente
}
printf("\nVettore ordinato:");
k = 0;
while(k < 7)
{printf("\n x[%d] = %d ", k, x[k]);
k++;
}
system(“pause”);
}
// visualizzazione del vettore ordinato
SOLUZIONE:Esercizio 6 (programma che carica in memoria 7 numeri interi e informa su
quanti sono dispari e quanti pari)
#include <stdio.h>
#include <stdlib.h>
int x[7], p = 0, d = 0, k = 0;
float dec ;
int main()
{ while (k <= 6)
{ printf("Inserisci un numero intero: ");
scanf("%d", &x[k]);
dec = x[k] / 2.0 – x[k] / 2;
if (dec == 0)
p++;
else
d++;
k++;
}
printf("\nI numeri pari sono %d", p);
printf("\nI numeri dispari sono %d \n", d);
system(“pause”);
}
SOLUZIONE
Esercizio 7
(Programma che ricerca il numero intero più piccolo tra gli elementi di un vettore di 5
elementi, da acquisire)
#include <stdio.h>
#include <stdlib.h> int k = 0,
x[5], y;
int main()
{ while(n < 5)
{printf("\nInserire un valore per x[%d] = ", k);
scanf("%d", &x[k]);
k++;
}
y = x[0]; k = 1;
while(k < 5)
{ if(x[k] < y)
y = x[k];
k++;
}
printf("\nIl numero più piccolo risulta %d \n", y);
system(“pause”);
}
2/2
SOLUZIONE Esercizio
8 (Programma che carica in memoria 5 numeri interi; in seguito verifica se è
almeno un valore, tra gli elementi del vettore, che si ripete)
#include <stdio.h>
#include <stdlib.h>
void main(){
int n = 0, x[5], y, i = 0; while(n < 5)
{printf("\nInserire un valore per x[%d] = ", n); scanf("%d", &x[n]);
n++;
}
while(i < 4)
{ y = x[i]; n = i + 1;
while(n < 5)
{ if(x[n] == y)
{printf("\nIl valore %d si ripete \n", y); break;
}
n++;
}
i++;
}
printf(‘’Non ci sono numeri che si ripetono’’); system(“pause”);
}
2/2
QUARTA
•
•
•
•
•
•
•
•
AUTOMI
classificazione dei sistemi
automi a stati finiti
caratteristiche di un sistema
sistemi a stati finiti ( automi )
modelli di rappresentazione dei sistemi a stati finiti
diagramma di transizione degli stati
ESEMPI
•
•
•
•
•
•
Il plc
segnali a tempo continuo
schemi a blocchi
comportamento in regime permanente
stabilità dei sistemi
plc
AUTOMI
CLASSIFICAZIONE DEI SISTEMI
SISTEMI CONTINUI
Si tratta di sistemi caratterizzati da variabili continue.
Esempio: Circuito elettrico ohmico - capacitivo
Le variabili evolvono con continuità (Sistemi continui) e sono continuamente osservate, cioè il
tempo è rappresentato da una semiretta continua (a tempo continuo).
esempio: Circuito elettrico ohmico - capacitivo
Le variabili sono continue (Sistemi continui), ma i loro valori non sono rilevati con continuità, bensì
a intervalli di tempo (a tempo discreto).
NB: Rientrano in questa classe tutti i sistemi continui controllati mediante controllori digitali.
SISTEMI DISCRETI
Sono sistemi caratterizzati da variabili discrete.
Esempio: Circuito elettrico ‘Interrotta’
Le variabili interruttore e lampada possono
assumere solo due configurazioni (alto/basso,
on/off, aperto/chiuso,
acceso/spento) (Sistema
discreto).
Le loro configurazioni sono rilevate con continuità
nel tempo (a tempo continuo).
esempio: Circuito elettrico ‘Interrotta’
Le variabili interruttore e lampada sono discrete
(Sistema discreto).
Le loro configurazioni sono rilevate a intervalli di
tempo (a tempo discreto).
NB: La classificazione del sistema come sistema discreto e quindi dei componenti Interruttore e
Lampada come componenti discreti risponde alle necessità di chi realizza o utilizza il sistema.
Ma per l’industria che costruisce gli interruttori e le lampade, questi non sono affatto componenti
discreti. La transizione da
uno stato all’altro non è istantanea, ma è caratterizzata da una
progressione continua di cui tener conto in sede di costruzione del componente.
I sistemi discreti a tempo discreto si dividono in due classi:
COMBINATORI
Sistemi in cui le uscite dipendono dal valore
attuale degli ingressi.
SEQUENZIALI
Sistemi in cui le uscite dipendono dal valore attuale
degli ingressi e dello stato.
Esempio: Comando con pulsanti di Marcia/Arresto di
un motore
Sono rappresentati mediante tavole di verità
I1
I2
L
A
A
OFF
A
C
OFF
C
A
OFF
C
C
ON
NB: sono sistemi in cui non vi è memoria della
configurazione degli ingressi negli istanti precedenti
quello attuale.
I sistemi discreti a tempo discreto sequenziali
vengono chiamati anche SISTEMI A STATI FINITI.
AUTOMA A STATI FINITI
L’automa a stati finiti è un sistema digitale, con un numero finito di ingressi ed uscite digitali e con
un numero finito di stati che, essendo numerabili, possono essere rappresentati con una variabile
ancora digitale.
Ricordiamo che:
a) L’informazione associata ad una grandezza elettrica digitale non è legata al valore della
tensione ma a codici numerici binari costruiti con segnali elettrici del tipo ON/OFF
a) L’ingresso
costituisce una sollecitazione che il sistema subisce dall’ambiente esterno
c) L’uscita
costituisce la risposta che il sistema dà all’ambiente esterno quando è stato sollecitato
da uno o più ingressi
d) Lo
stato è la condizione in cui si trova il sistema in un determinato istante e alla quale è
pervenuto in seguito alla sequenza di sollecitazioni subite negli istanti precedenti: questo
implica un effetto “memoria” dal quale non si può prescindere.
Per un sistema, essere in uno stato piuttosto che in un altro vuol dire dare risposte diverse per
lo stesso ingresso.
Caratteristiche di un automa
Ingressi, uscite e stati
l’attività di un automa si esplica come successione di azioni, secondo una gamma fissa
preregistrata (automa stupido ma utile) oppure in risposta a sollecitazioni esterne (automa
intelligente).
Le azioni si susseguono in sequenza, il sistema evolve da una fase operativa alla successiva;
pertanto l’automa è prima di tutto un sistema dinamico o sequenziale, ovvero un sistema
che modifica il proprio stato con l’avanzare del tempo.
Le azioni non hanno luogo con continuità bensì a scatti; dopo una breve fase di transito da
uno stato al successivo, segue una fase di mantenimento di durata maggiore.
Le azioni sono cioè separate da intervalli di tempo finiti, perciò l’automa è anche un sistema
discreto.
Nel compiere il suo ciclo di lavoro l’automa transita attraverso diverse situazioni interne,
dette stati.
Nel corso di un ciclo si verifica una successione di stati e il passaggio da uno stato all’altro è
imposto sia dalla logica operativa intrinseca della macchina, sia da eventuali sollecitazioni
esterne che condizionano il flusso operativo.
Per poter descrivere il funzionamento di un automa in modo preciso e rigoroso, non è sufficiente
ricorrere all’approccio descrittivo con il quale abbiamo esordito, è necessario rappresentare
simbolicamente gli elementi che ne identificano il comportamento e descrivere le relazioni che li
correlano.
Gli elementi fondamentali sono l’insieme degli ingressi, che influenzano l’evoluzione del sistema,
l’insieme degli stati, che originano le sequenze operative e l’insieme delle uscite, che sono gli
elementi utili.
Un insieme di elementi prende il nome di alfabeto. Gli elementi di questi insiemi vengono de
finiti variabili.
Per economia di scrittura, spesso ci si riferisce a un insieme di variabili con un solo simbolo, anzi
ché enumerarle a una a una.
I simboli compatti sono:
insieme variabili di ingresso: I(t)
insieme variabili di uscita: U(t)
insieme variabili di stato: X(t)
L’evidenziazione di ingressi e uscite non è sufficiente per rappresentare l’automa in quanto
mancano gli stati e le relative transizioni
A tale scopo un automa si puo cosi rappresentare:
sezione di memoria: memorizza lo stato attuale;
•sezione logica: prepara lo stato futuro.
•sezione di temporizzazione (clock): sincronizza
l’evoluzione.
Per poter avanzare attraverso la sequenza dei propri stati, una macchina automatica sequenziale
deve ricordare lo stato nel quale si trova (per esempio un orologio ricorda l’ora indicata) e avere
una logica, una intelligenza, che le permetta di costruire, a partire dalla conoscenza dello stato
attuale, lo stato futuro, cioè quello successivo.
La macchina genera allora le uscite (output) in base alle sollecitazioni di ingresso (input) e allo
stato interno, registrato nella propria memoria.
Affinché il meccanismo sia cadenzato, è necessario poi un segnale che disciplini l’emissione delle
sequenze, cioè blocchi il sistema nel proprio stato per un dato intervallo di tempo, dopodiché dia
via libera alla transizione allo stato successivo.
Il segnale di clock svolge il ruolo di temporizzazione, chiudendo e aprendo il circuito, quindi
bloccando o rilasciando il processo di avanzamento degli stati.
esempio: Orologio digitale
L’orologio può essere senz’altro classificato come automa. È un sistema dinamico, dato che
evolve nel tempo; è discreto perché compie il passaggio da una condizione a quella
successiva a intervalli regolari distanziati da intervalli di tempo finiti. Consideriamo per
semplicità un orologio costituito solo dalle cifre dei minuti, rappresentate simbolicamente
DM = Decine dei Minuti
UM = Unità dei Minuti
DM e UM sono in questo caso le variabili di uscita.
L’orologio potrebbe poi disporre di due pulsanti, con stampigliate le sigle:
AVM: avanzamento veloce minuti
ALM: avanzamento lento minuti
Queste sono le variabili di ingresso.
A queste indicazioni corrisponde allora il blocco
mostrato a fianco come:
Esempio: Apertura a combinazione
Si consideri una cassaforte con apertura a combinazione a 4 cifre. La sequenza numerica vie ne
immessa facendo ruotare alternativamente a destra e a sinistra, in corrispondenza delle tacche
numeriche, la manopola che comanda il congegno di apertura, introducendo una sequenza
numerica prefissata.
Supponendo che la combinazione prefissata sia 1357 per essere sicuri di non scordarsi la
combinazione, ci si può limitare a memorizzare solo il primo numero della sequenza e affidarsi,
per la ricostruzione della sequenza, allo schema logico consistente nel sommare ogni volta 2 alla
cifra precedente.
La funzione di memoria è strettamente correlata con lo stato. È la memoria del sistema a
conservare lo stato, la condizione attuale.
La successione passata degli stati rappresenta la “storia” del sistema; in base a questa storia si
costruiscono gli stati futuri.
Gli stati si indicano simbolicamente con la lettera maiuscola S seguita da un indice numerico
progressivo, ovvero S0, S1, S2 ...
Lo stato presente viene chiamato stato attuale e indicato come S(t), lo stato al passo successivo
viene chiamato stato futuro e indicato come S(t + 1). Si noti che si è parlato di passo e non di
istante di tempo in qaunto Il funzionamento di un automa è indipendente dall’entità del passo
«clock»
stati S1, S2, S3, S4 ----- : 1 ➞ 3 ➞ 5 ➞ 7.
Esempio: Automa che genera la sequenza dei numeri naturali
Questo esempio dovrebbe fare luce su quanto detto ora. Un sistema, per generare
automaticamente la sequenza 0, 1, 2, 3 …, deve possedere una memoria (per conoscere il numero
appena generato) e una logica (per costruire il numero successivo in base al numero appena
generato).
In questo caso la logica è molto semplice e consiste nel sommare 1 al numero appena generato.
La tabella descrive sinteticamente
questo processo.
Conteggio pezzi
Un sistema per imballaggio conta tramite fotocellula delle lattine, prima di confezionarle. Ogni tre
lattine deve terminare il ciclo di conteggio e iniziare quello di imballaggio. Il conteggio avviene alla
rovescia partendo da 3.Rappresentare la sequenza degli stati del ciclo di conteggio.
la numerazione S3, S2, S1, S0 della sequenza
degli stati è convenzionale, ma viene fatta
coincidere con il conteggio per linearità di
ragionamento
Esempio: Serbatoio
Il sistema è costituito da:
a) un serbatoio d’acqua
b) un sensore SH per segnalare il raggiungimento del livello
massimo
c) un sensore SL per segnalare il raggiungimento del livello minimo
d) una elettrovalvola di carico VC
e) una valvola di scarico VS
f) un automa per la gestione delle operazioni secondo le modalità di
seguito indicate
Funzionamento:
Fase di scarico: partendo dalla condizione di serbatoio pieno, la valvola di carico VC è chiusa,
bloccando l’afflusso di acqua nel serbatoio, fino a quando il livello non scende al di sotto del valore
minimo per effetto del deflusso ottenuto manovrando la valvola di scarico VS.
Fase di carico: quando il livello minimo è stato raggiunto, la valvola VC viene aperta e resta aperta
fino a quando il serbatoio non si riempie raggiungendo il livello massimo, dopodiché si riparte con
la fase di scarico.
Nota: è abbastanza intuitivo che, per un buon funzionamento, la portata associata alla valvola di
carico VC sia maggiore di quella associata alla valvola di scarico VS.
Osservazione
Quando il livello dell’acqua è compreso tra quello massimo e quello minimo, i sensori generano per
l’automa lo stesso ingresso, sia durante la fase di carico che durante quella di scarico. E’
importante quindi che il sistema di controllo (automa) abbia una memoria che gli ricordi in quale
fase si trova, consentendogli di reagire con la giusta uscita (apertura o chiusura della valvola VC).
SERBATOIO
Un modo semplice per illustrare il comportamento del sistema di controllo è quello di utilizzare un diagramma
di stato come quello rappresentato nella Fig. 9.
SISTEMI A STATI FINITI
( AUTOMI )
• Gli automi a stati finiti sono sistemi dinamici, stazionari, con ingressi, stato, uscite e tempo
• discreti
• Sono dinamici i sistemi dotati di memoria (Es: flip-flop JK).
• La memoria è costituita dallo stato del sistema.
• Definizione: lo stato rappresenta una situazione in cui il sistema si trova per
effetto delle configurazioni degli ingressi negli istanti precedente
• Sono stazionari i sistemi i cui parametri restano costanti nel tempo.
•
NB: i sistemi a stati finiti sono una classe di sistemi molto importante in cui rientrano la
logica di controllo delle macchine utensili,
• il funzionamento di un sistema operativo per PC
• Il funzionamento di una lavatrice
• ……………………………………..
AUTOMA DI MEALY
Nel modello di Mealy l’uscita dipende dalla elaborazione,
da parte di una rete combinatoria, degli ingressi e dello
stato attuale.
Le uscite commutano durante la transizione dallo stato
attuale allo stato futuro (sia per i sistemi sincroni che
asincroni).
AUTOMA DI MOORE
Nel modello di Moore l’uscita dipende
dalla
elaborazione,da parte di una rete combinatoria,
del solo stato attuale.
MODELLO DI HUFFMAN
E un modello generale per rappresentare un
automa: un unico sottosistema combinatorio
retroazionato con elementi di memoria.
Gli elementi di memoria sono dei flip flop
(sincroni o asincroni): uno per ogni variabile
di stato.
CONFRONTO TRA L’AUTOMA DI MEALY E L’AUTOMA DI MOORE
La sintesi di un sistema a stati finiti può essere realizzata sia con il modello di Mealy che con
quello di Moore.
Tuttavia cambiano la complessità e le prestazioni del sistema costruito.
Automi di Mealy
•Sono più veloci, gli ingressi giungono
direttamente sul circuito delle uscite.
• Hanno un minor numero di stati, potendo
associare le uscite alle transizioni
Sono possibili uscite spurie transitorie
dovute a percorsi diversi, con differenti
ritardi di propagazione, cui gli ingressi sono
soggetti.
Automi di Moore
•Sono meno veloci, gli ingressi causano
direttamente solo il cambiamento dello
stato; le uscite si aggiornano dopo che il
nuovo stato si è stabilizzato.
•Hanno un maggior numero di stati, dovendo
associare le uscite agli stati
•Si
ottiene
un
maggior
controllo
sull’evoluzione
della macchina, grazie
all’aggiornamento delle uscite subordinato
al raggiungimento del nuovo stato
.
•Sono più facilmente testabili
MODELLI DI RAPPRESENTAZIONE DEI SISTEMI A STATI FINITI
Il funzionamento di un automa può essere illustrato (descritto) mediante:
• TABELLA di transizione degli stati e TABELLA delle uscite
• DIAGRAMMI di transizione degli stati
ESEMPIO: riconoscitore di sequenza per sblocco meccanismo
Descrizione: il sistema deve riportarsi allo stato iniziale ogni volta che riceve in ingresso un
carattere non valido.
Configurazioni valide per l’ingresso: {A, B, C, D, E, F}
Configurazioni previste per l’uscita: {blocco, sblocco}
Sequenza valida: BDA
La corrispondenza della logica di controllo (sistema) al modello di Mealy oppure di Moore è spesso
una scelta del progettista.
AUTOMA DI MEALY
La tabella di transizione degli stati descrive l’evoluzione dello stato del sistema in funzione dello
stato attuale e dell’ingresso:
Poiché le uscite dipendono oltre che dallo stato, anche dagli ingressi, per la loro indicazione si deve
costruire la tabella delle uscite:
AUTOMA DI MOORE
Poiché le uscite sono definite in corrispondenza degli stati, esse sono indicate nelle stesse
celle degli stati futuri.
DIAGRAMMA DI TRANSIZIONE DEGLI STATI
Il funzionamento di un automa può essere descritto anche con i diagrammi di transizione degli
stati (o grafi).
•A ogni nodo è associato uno stato ( x )
• A ogni arco è associato un ingresso, la freccia
indica la direzione della transizione di stato
causata dall’ingresso specificato
•Autoanello: transizione che parte e giunge sullo
stesso stato
• Lo stato iniziale
doppio cerchio.
viene
rappresentato
con
un
Esercizio precedente:
PASSI (Algoritmo) PER LO STUDIO DEGLI AUTOMI
Descrizione del sistema:
• Definizione degli ingressi, degli stati e delle uscite (attribuzione dei
configurazioni possibili)
simboli e esame delle
• Individuazione di uno stato iniziale da cui cominciare la costruzione
diagramma
della tabella o del
• Costruzione della tabella o del diagramma.
NB: si può cominciare da uno stato iniziale qualsiasi, normalmente si sceglie quello più comodo.
Il sistema di controllo, descritto mediante diagramma di transizione degli stati o mediante tabelle
di transizione, può essere implementato (realizzato) con
• hardware cablato per la specifica applicazione
• hardware programmabile, scrivendo uno specifico software di controllo.
• Il linguaggio di programmazione è il C ANSI, con compilatore Dev-C++.
ESEMPIO Comando di marcia / arresto di un motore
Descrizione del sistema
Il sistema di controllo è molto semplice: mediante due pulsanti si comanda la marcia e
l’arresto di un motore.
NB: occorrerebbe prevedere un terzo pulsante che ponga termine al controllo.
Definizione degli ingressi
Gli ingressi sono due pulsanti normalmente aperti (Marcia, Arresto), che possono assumere
solo due configurazioni (P: premuto, R: a riposo).
Definizione degli stati
Lo stato del sistema può essere rappresentato dal contatto di potenza oppure dalla
condizione del motore: F = fermo, M = in marcia.
Definizione delle uscite
L’uscita è rappresentata dal comando (COM) che si vuole esercitare sul motore. E’ un segnale
a due livelli (avvio motore, arresto motore).
Può essere associato allo stato: uscite = stato. Di conseguenza: modello di Moore.
Individuazione stato iniziale
Si deve decidere se cominciare con il motore fermo o in marcia. Ipotesi: motore fermo.
Scrivere il software di controllo.
Schema generale
Descrizione della logica di controllo mediante: diagramma di transizioni degli stati.
Automa di Moore.
Il software di controllo presenta fondamentalmente due sezioni:
• sezione di inizializzazione: in cui scrivere il codice da eseguire una sola volta, all’inizio
• sezione sotto scansione ciclica: in cui si scrive il codice di controllo, la cui esecuzione è
ripetuta ciclicamente.
Esempio di software di controllo:
ESEMPIO: COMANDO PUNTO LUCE: MEDIANTE RELE’ INTERRUTTORE
Descrizione del sistema
Il sistema è costituito da due pulsanti, un relè interruttore (con due posizioni di lavoro),
una lampada.
Premendo indifferentemente uno dei due pulsanti lo stato dei contatti del relè
interruttore commuta, e di conseguenza commuta anche lo stato della lampada.
Definizione degli ingressi
Gli ingressi sono due pulsanti normalmente aperti (S1, S2), che possono assumere solo
due configurazioni (P: premuto, R: a riposo).
(su scheda Velleman: Rilasciato = lettura 0)
Definizione degli stati
Lo stato del sistema può essere rappresentato dal contatto del relè oppure dallo stato della
lampada: contatto aperto = Lampada spenta, contatto chiuso = Lampada accesa. Simbolo L
= (ON, OFF).
Definizione delle uscite
L’uscita della logica di controllo è rappresentata da un comando impulsivo COM, che fa
commutare il relè.
Individuazione stato iniziale
Si deve decidere se cominciare con il contatto aperto o chiuso. Ipotesi: contatto aperto.
Schema generale
Soluzione
Costruzione del diagramma di transizione degli stati
Occorre scegliere quale rappresentazione utilizzare: Mealy o Moore?
Il sistema è molto semplice; l’uscita (il contatto di potenza) può essere fatta
corrispondere allo stato. In questo caso la rappresentazione è quello di Moore.
ESEMPIO: CONTROLLO TRAPANO AUTOMATICO
Descrizione del sistema
Premendo il pulsante S0 si alimenta il motore M1.
Il carrello porta utensile scende alla velocità v1.
L’attivazione del finecorsa S2 modifica la velocità di discesa del carrello
v2 < v1 e attiva il motore M2.
L’attivazione del finecorsa S3 disattiva il motore M2 a fa salire alla
velocità v1 il carrello.
L’attivazione del finecorsa S1 arresta il motore M1.
Schema generale
Definizione degli ingressi
Gli ingressi sono costituiti dal pulsante S0 e dai finecorsa S1, S2, S3.
Si tratta di segnali che possono assumere solo due configurazioni:
Pulsante: S0 = Rilasciato, Premuto
(su scheda Velleman: Rilasciato = lettura 0)
Finecorsa: S1, S2, S3= Rilasciato, Premuto
soluzione: Diagramma di transizione degli stati
NB: si dovrebbero assumere opportune precauzioni per evitare l’invio di comandi contraddittori
(interblocco)
ESEMPIO: MISCELATORE
Descrizione del sistema
Il sistema miscela due liquidi. Componenti:
•pulsanti S1, S2 normalmente aperti
•elettrovalvole M1, M2, M3 normalmente chiuse
•sensori di livello B0, B1, B2 normalmente aperti (asciutti), si chiudono in
presenza del liquido
• motore M0
Premendo S1 si avvia il ciclo, previa verifica di serbatoio vuoto (altrimenti
provvedere allo svuotamento).
Fasi del ciclo:
•con serbatoio vuoto (B0, B1, B2 asciutti) , elettrovalvole M2 e M3 chiuse,
motore fermo: si fa entrare il 1° liquido aprendo l’elettrovalvola M1;
• durante il riempimento si attiva B0: nessun intervento del controllo
•attivazione di B1: chiusura di M1, apertura di M2 (entrata del 2° liquido) e
avvio del motore
• attivazione di B2: chiusura di M2 e apertura di M3 (inizio scarico)
• disattivazione di B2: nessun intervento di controllo
• disattivazione di B1: arresto motore M0
• disattivazione di B0: chiusura M3 e ripetizione del ciclo.
NB: con serbatoio vuoto, premendo S2 il sistema si porta allo stato iniziale di riposo.
Definizione degli ingressi
Gli ingressi sono rappresentati dal pulsante S1 normalmente aperto e i tre sensori di livello
normalmente aperti.
Definizione degli stati
L’identificazione degli stati dipende dal modello:
• Moore: ad ogni uscita diversa occorre associare uno stato
• Mealy: possibile accorpare più stati
Definizione delle uscite
Le uscite rappresentano i comandi che il sistema di controllo deve emettere: il motore e le
tre elettrovalvole.
Individuazione stato iniziale
Si deve prevedere uno stato di attesa, da cui uscire con l’attivazione del pulsante S1.
Soluzione: modello di Moore
Soluzione: modello di Mealy
Esempio di software di controllo:
MISCELATORE: MOORE
Soluzione : modello di Mealy
Esempio di software di controllo:
MISCELATORE: MEALY
ESEMPI0:
Distributore di bibite
Costo della bibita: 40 €cent
Monete utilizzabili: 10 €cent , 20 €cent
Il sistema, oltre alla parte che gestisce l’automa, prevede:
a) una gettoniera che generi un codice numerico binario per ognuna delle due monete e per
la condizione di riposo (nessuna moneta)
b) un dispositivo che, su comando dell’automa, sganci la bibita
c) un dispositivo che, su comando dell’automa, sganci il resto
Si noti che per l’ingresso occorrono due bit, perché sono da codificare 3 condizioni diverse, e
quindi due linee (X1 e X0). I comandi per lo sgancio, invece, richiedono un bit ciascuno
perché ognuno di loro prevede solo due condizioni (sganciare o non sganciare): necessita
quindi una sola linea per ogni comando (B e R).
In situazioni diverse, dove ci siano più tipi di monete oppure più tipi di bibite oppure più
possibilità di resto, cresce il numero di condizioni da considerare e quindi cresce anche il
numero di bit e con esso il numero di linee.
Formalizziamo le variabili utilizzate.
Ingressi X1 X0 (binari):
Nessuna moneta (00); Moneta da 10 €cent (01); Moneta da 20 €cent (10).
Totale: 2 linee di ingresso (2 bit).
Uscite (binarie):
Comando per lo sgancio della bibita B (0/1); Comando per lo sgancio del resto R (0/1).
Totale: 2 linee di uscita (2 bit), una per il sottosistema di sgancio della bibita ed una per il
sottosistema di sgancio del resto.
Come per gli ingressi, è possibile fondere insieme le due uscite utilizzando una sola variabile a 2
bit. ( Es.: BR = 00 né bibita né resto; 01 non ammesso; 10 solo bibita, 11 bibita + resto ).
Stati:
Gli stati corrispondono alla somma di volta in volta accumulata con l’introduzione delle monete.
Risultano 5 stati: 0 €cent, 10 €cent, 20 €cent, 30 €cent.
In questo caso non servono variabili ma una locazione di memoria
Diagramma degli stati
Per descrivere le evoluzioni nel tempo del sistema, ovvero come esso passi da uno stato all’altro
quando viene sottoposto alle sollecitazioni degli ingressi esterni, vengono utilizzati i diagrammi di
stato.
La rappresentazione viene fatta utilizzando per ogni stato un cerchio (nodo) che porta indicato al
proprio interno il nome dello stato (S0 , S1 , …. oppure A, B, ….), e collegando i vari nodi con degli
archi orientati che indicano l’evoluzione da uno stato all’altro. Per completare i diagrammi,
vengono aggiunte le indicazioni sugli ingressi che generano l’evoluzione da uno stato all’altro e
sulle uscite corrispondenti a tale evoluzione.
Modello di Mealy:
in tale modello, nello stato terminale di una evoluzione non è possibile conoscere l’uscita se non
si conosce contemporaneamente anche l’ingresso che ha portato l’automa in quello stato (uno
stesso stato
possibilità di più uscite).
Per tale motivo, accanto agli archi orientati corrispondenti alle evoluzioni generate dagli
ingressi, vengono indicati sia gli ingressi stessi che le uscite (separati da una barra).
Modello di Moore:
in tale modello, noto lo stato raggiunto, è nota l’uscita corrispondente (uno stato una uscita). Per
tale motivo gli ingressi vengono indicati accanto agli archi orientati corrispondenti alle evoluzioni
che essi generano, mentre l’uscita viene indicata accanto al nome dello stato, all’interno del cerchio
rappresentativo dello stato stesso.
Per meglio comprendere la differenza tra modello di Mealy e modello di Moore, scegliamo di
utilizzare inizialmente il primo tipo; successivamente, con qualche piccola modifica al diagramma
ottenuto, passeremo all’altro tipo. Scopriremo che il modello di Moore, pur avendo di norma più
stati, consente una semplificazione del software.
La Fig. 6 illustra una prima stesura del diagramma di stato (automa di Mealy); una seconda stesura
si otterrà per passare al modello di Moore (Fig. 7); una terza ed ultima stesura (Fig. 8) si renderà
necessaria per risolvere alcuni problemi legati all’implementazione fisica dell’automa.
1) automa di Mealy)
Prima di procedere con la descrizione del diagramma di figura, occorre chiarire che lo schema
rappresentato indica tutte le possibili situazioni che possono presentarsi nella realtà.
Ad esempio, con una sequenza costituita da una moneta da 20c seguita da un’altra moneta da
20c, la macchina, partendo dallo stato di riposo “0c” passa prima allo stato “20c” e poi da questo
salta allo stato di riposo “0c”, dopo aver dato la bibita senza resto (Uscita “1/0c”).
Ancora, con una sequenza costituita da una moneta da 20c seguita da un’altra da 10c e ancora da
un’altra da 20c la macchina, partendo dallo stato di riposo “0c” passa prima allo stato “20c”, poi
allo stato “30c” e infine allo stato di riposo “0c”, dando la bibita con un resto di 10c (Uscita
“1/10c”).
E così via.
Ovviamente, se non viene raggiunto o superato il valore della bibita, l’automa resta in uno stato
intermedio con le uscite bloccate a “0/0c”.
a) Lo stato “0c” è lo stato di riposo; quello cioè in cui si trova la macchina quando è in attesa
di un nuovo ciclo per l’acquisto della bibita.
L’uscita è “0/0c” perché non devono essere dati né la bibita né il resto.
Con 10c si passa allo stato “10c”, mentre se la moneta introdotta è da 20c si passa allo stato
“20c”.
Quando l’ingresso è “0c” (nessuna moneta introdotta), la macchina rimane sullo stesso stato.
Da notare che i nomi degli stati rappresentano anche l’ammontare di moneta introdotta. Per
tutti gli ingressi fin qui citati non devono essere dati né la bibita né il resto, non avendo
raggiunto una somma pari al valore della bibita (Uscita 0/0c).
b)Quando
la macchina è nello stato “10c” l’introduzione di una moneta da 10c la porta nello stato
“20c”, già visto; se la moneta , invece, è da 20c la macchina va nello stato “30c”.
Ancora una volta, non essendo stato raggiunto il valore della bibita, la macchina non deve dare
niente in uscita (Uscita 0/0). Quando l’ingresso è “0c” (nessuna moneta introdotta), la macchina
rimane sullo stesso stato.
C) Nello stato “20c” l’introduzione di una moneta da 10c fa passare la macchina nello stato “30c”,
senza alcuna conseguenza sull’uscita, mentre l’introduzione di una moneta da 20c la fa tornare
nello stato “0c”.
In quest’ultimo caso, avendo raggiunto il valore della bibita, la stessa viene sganciata senza alcun
resto (Uscita “1/0c”). Quando l’ingresso è “0c” (nessuna moneta introdotta), la macchina rimane
sullo stesso stato.
d) Nello stato “30c” l’introduzione di una moneta o da 10c o da 20c fa tornare la macchina nello stato
di riposo “0c”: nel primo caso viene raggiunto esattamente il valore della bibita, per cui viene
sganciata la stessa senza resto (Uscita 1/0c); nel secondo caso, invece, viene superato il valore della
bibita, per cui vengono sganciati bibita e resto da 10c (Uscita 1/10c). Quando l’ingresso è “0c”
(nessuna moneta introdotta), la macchina rimane sullo stesso stato.
Tabelle di transizione di stato e di trasformazione di uscita
Tali tabelle hanno entrambe come indicatori di riga lo stato attuale e come
l’ingresso. Al loro interno riportano, rispettivamente, lo stato futuro e l’uscita.
indicatore di colonna
Nella Tab. a) è possibile conoscere lo stato futuro
incrociando stato attuale ed ingresso.
Analoga cosa vale per la Tab. b), con riferimento
all’uscita.
Come si può controllare anche dal diagramma degli stati, quando, ad esempio, se lo stato attuale è
“30c” e viene introdotta una moneta da 10c, la macchina si porta nello stato di riposo “0c” (stato
futuro) e dà come uscita “1/0c” (bibita senza resto).
Queste tabelle sono fondamentali per il progetto dell’automa in logica cablata, mentre in logica
programmata possono essere utilizzate o meno, a seconda della soluzione scelta.
all’automa di Moore,
Rispetto all’automa di Mealy, l’uscita è legata solo
allo stato cui fa riferimento, per cui
essa viene
direttamente indicata nel cerchietto rappresentativo
dello stato stesso.
Per garantire questa condizione per tutti gli stati, è
stato necessario aggiungere qualche stato in più.
La situazione cambia nel modo seguente:
a) Lo stato “0c” è lo stato di riposo; quello cioè in cui si trova la macchina quando è in attesa di
un nuovo ciclo per l’acquisto della bibita.
L’uscita è “0/0c” perché non devono essere dati né la bibita né il resto.
Con 10c si passa allo stato “10c”, mentre se la moneta introdotta è da 20c si passa allo stato
“20c”.
Quando l’ingresso è “0c” (nessuna moneta introdotta), la macchina rimane sullo stesso stato.
Per tutti gli stati fin qui citati non devono essere dati né la bibita né il resto, non avendo
raggiunto una somma pari al valore della bibita (Uscita 0/0c).
Quando la macchina è nello stato “10c” l’introduzione di una moneta da 10c la porta nello stato
“20c”, già visto; se la moneta , invece, è da 20c la macchina va nello stato “30c”. Ancora una
volta, non essendo stato raggiunto il valore della bibita, la macchina non deve dare niente in
uscita (Uscita 0/0c). Quando l’ingresso è “0c” (nessuna moneta introdotta), la macchina rimane
sullo stesso stato.
b)Nello stato “20c” l’introduzione di una moneta da 10c fa passare la macchina nello stato “30c”,
mentre l’introduzione di una moneta da 20c la fa passare nello stato “40c”.
In quest’ultimo caso, avendo raggiunto il valore della bibita, la stessa viene sganciata senza alcun
resto (Uscita “1/0c”).
Quando l’ingresso è “0c” (nessuna moneta introdotta), la macchina rimane sullo stesso stato.
c) Nello stato “30c” l’introduzione di una moneta da 10c fa passare la macchina nello stato “40c”,
mentre l’introduzione di una moneta da 20c la fa passare nello stato “50c”.In entrambi i casi viene
quindi raggiunto o superato il valore della bibita: nel primo caso viene sganciata la sola bibita
(Uscita 1/0c); nel secondo vengono sganciati bibita e resto da 10c (Uscita 1/10c). Quando
l’ingresso è “0c” (nessuna moneta introdotta), la macchina rimane sullo stesso stato.
d)Gli stati “40c” e “50c” sono di chiusura per il ciclo di acquisizione della bibita. Nel primo viene
rilasciata solo la bibita, nel secondo la bibita e il resto di 10c.
In entrambi i casi, essendosi chiuso il ciclo per l’acquisizione del prodotto, il sistema si riporta
nello stato di riposo. Si noti che gli ingressi 10c e 20c non avranno mai la possibilità di
presentarsi in questi due stati finali, perché il ritorno a zero dei segnali provenienti dalla
gettoniera, dopo il passaggio dell’ultima moneta (Ingresso “0c”), avrà già resettato la macchina
portandola nello Stato “0c”.
In ultima analisi, nei due stati finali, gli ingressi 10c e 20c rappresentano condizioni di indifferenza
(don’t care) e questo giustifica la X sulle evoluzioni finali che portano allo stato di riposo.
Tabelle di transizione di stato e di trasformazione di uscita
In questo caso, trattandosi di un automa di Moore per il quale l’uscita è legata solo allo stato, la
tabella di trasformazione di uscita non ha l’ingresso come indicatore di colonna (tabella ad una
sola dimensione).
STATO
FUTURO
STATO
ATTUALE
INGRESSO
USCITA
0c
10c
20c
0c
0c
10c
20c
0c
0/0c
10c
10c
20c
30c
10c
0/0c
20c
20c
30c
40c
20c
0/0c
30c
30c
40c
50c
30c
0/0c
40c
0c
0c
0c
40c
1/0c
50c
0c
0c
0c
50c
1/10c
Tab. c) Transizione di stato
Tab. d) Trasformazione di uscita
Come si può controllare anche dal diagramma degli stati, quando, ad esempio, lo stato attuale
è “30c” e viene introdotta una moneta da 10c, la macchina si porta nello stato “40c” (stato
futuro) e dà come uscita “1/0c” (bibita senza resto).
Per concludere, occorre ribadire che se si vuole rendere esecutivo il progetto bisogna
curare attentamente l’interfaccia con l’hardware, per cui può essere necessario in certi casi
apportare qualche correttivo al diagramma degli stati, che non ne cambia la struttura logica
ma semplicemente corregge certe situazioni
prodotte dalla suddetta necessità di
interfacciare l’hardware.
E’ questo il caso degli “Stati trappola”.
L’aggiunta di questi stati al diagramma si rende necessaria quando accade che un ingresso
che porta in uno stato fa anche uscire da quello stato. Il più delle volte succede che il ciclo
di acquisizione del microprocessore legga l’ingresso migliaia di volte per lo stesso stato,
innescando una deriva che porta il sistema ad evolvere velocemente da uno stato all’altro,
come impazzito.
Il problema si risolve inserendo tra due stati un terzo stato che blocchi l’evoluzione tra i
primi due finché l’ingresso non si è di nuovo azzerato: questo è il motivo per cui tale stato
aggiunto è stato qui definito “trappola”. La Fig. 8 riporta il diagramma di stato del
distributore di bibite modificato a questo scopo
Con riferimento alla Fig. 8, si veda ad
esempio quello che succede nello stato
“20c” con un ingresso 10c: il sistema si
porta nello stato “30 bis” e lì rimane
bloccato finché l’ingresso non si azzera;
azzeratosi l’ingresso, l’automa evolve
verso lo stato “30c”.
Si noti che i due stati di chiusura “40c” e
“50c” non sono preceduti da stati
trappola perché essi stessi fungono da
trappola; bisogna solo stare attenti a
sganciare bibita e/o resto una sola volta.
Le nuove tabelle di transizione di stato e di trasformazione
di uscita diventano:
STATO ATTUALE
INGRESSO
0c 10c 20c
0
0
10b 20b
10b
10
20b
20
30b
30
40
50
10
10
20
20
30
30
0
0
10b
20b
20b
30b
30b
40
40
50
10b
30b
20b
40
30b
50
40
50
STATO
FUTURO
USCITA
0
10b
10
20b
20
30b
30
40
50
0/0c
0/0c
0/0c
0/0c
0/0c
0/0c
0/0c
1/0c
1/10c
PLC
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
logica di controllo
Architettura dei istemi di controllo
IL PLC
campo di utilizzo del PLC
controllo del processo
componentistica
funzionamento base dei PLC
Linguaggio di programmazione "ladder"
organizzazione della produzione
installazione- manutenzione - ricerca guasti
considerazioni sulla scelta del PLC
linee di produzione con il PLC
LOGICA DI CONTROLLO
Una automazione può, oggi, essere realizzata secondo due diverse tecnologie.
In passato la logica di controllo era implementata (realizzata) attraverso la tecnologia cablata: i
circuiti di controllo erano realizzati collegando i componenti mediante cavi (cablaggio).
Con questa tecnologia elettromeccanica (relè, temporizzatori) cablata si realizza, ancora oggi, un
controllo:
•rigido (poco flessibile)
•molto ingombrante
•con notevole consumo energetico.
Nel corso del ‘900 lo sviluppo dell’automazione ha reso sempre più complicato il cablaggio dei
quadri di controllo.
Il numero di componenti (relè, temporizzatori) impiegati nella logica cablata è cresciuto
esponenzialmente e la gestione dei quadri di controllo è divenuta molto complessa.
Alla luce dello sviluppo dell’elettronica integrata, nel 1968 la General Motors, allo scopo di ridurre
i costi e le difficoltà derivanti dalla tecnologia cablata, emanò delle specifiche che i nuovi
controllori, fondati sulla tecnologia programmabile e destinati a sostituire i quadri di controllo
(cablati), avrebbero dovuto rispettare.
Dall’applicazione di quelle specifiche nacque il PLC (Programmable Logic Controller). Oggi il più
diffuso controllore programmabile nell’automazione industriale.
Una automazione realizzata con tecnologia programmabile comporta la scrittura di un software
per il controllo.
Ciò consente di modificare il controllo semplicemente riscrivendo il software. Si realizza quindi
un sistema molto flessibile.
Realizzato con tecnologia programmabile elettronica, il controllo consente:
•minori consumi energetici
•minore ingombro.
NB: A parità di tecnologia, un circuito di controllo cablato risulta comunque più veloce di uno
programmabile. Ciò è dovuto all’assenza nel circuito cablato delle fasi di decodifica delle
istruzioni.
Nel 1973 si costruirono i primi PLC in grado di comunicare tra loro. Tuttavia la mancanza di
standard comuni rese incompatibili le reti di costruttori diversi.
Negli anni ’80, ancora la General Motors rese i PLC programmabili tramite Personal Computer
(invece che con tastiera dedicata).
Negli anni ’90 sono stati costruiti PLC con ingombri ridotti e si è proceduto a una parziale
convergenza dei protocolli.
ARCHITETTURA DEI SISTEMI DI CONTROLLO
ARCHITETTURA TRADIZIONALE
Il
PLC è collegato ai sensori e agli
attuatori
attraverso
un
collegamento punto a punto.
Vantaggi
• Affidabilità Svantaggi
•Elevato costo dei cablaggi
• Bassa
flessibilità
(Espandibilità)
3
Flessibilità: capacità di un sistema
di
controllo di configurarsi e
ampliarsi
semplicemente
aggiungendo componenti.
ARCHITETTURA A BUS
Il PLC è collegato ai sensori e agli attuatori
attraverso un bus.
Bus: insieme di linee di collegamento, cui
accedono sia il PLC che i sensori e gli attuatori.
NB: sensori e attuatori devono essere del
tipo intelligente.
Vantaggi:
• Flessibilità (Espandibilità) (possibilità di
aggiungere altri componenti)
• Intelligenza distribuita (decentramento di
funzioni)
Svantaggi:
• Maggior costo dei componenti
• Assenza di standard comuni tra costruttori
(con conseguenti problemi di affidabilità di
funzionamento).
ARCHITETTURA SCADA
(Supervisor Control And Data Acquisition)
Un sistema SCADA è un sistema in cui il software permette una alta possibilità per l’operatore di
interfacciarsi col processo.
Un grande vantaggio è rappresentato dalla Scalabilità: capacità di un sistema di controllo di
adattarsi alle necessità aggiungendo utenti o risorse (proprietà tipiche dei sistemi in rete).
IL PLC
Il
PLC è un dispositivo o sistema digitale elettronico che utilizza una memoria programmabile per
memorizzare informazioni o istruzioni, atte a realizzare specifiche funzioni, finalizzate al controllo di sistemi
combinatori e sequenziali per la gestione di macchine e processi, quali: operazioni logico-aritmetiche,
temporizzazioni, conteggi, comparazioni, codifiche, decodifiche".
i PLC , oltre alle funzioni strettamente logiche (AND,OR,NOT etc.) sono in grado di eseguire conteggi,
temporizzazioni,comparazioni, calcoli numerici, ed altre operazioni di manipolazioni di dati in formato bit, byte, word
(come ad esempio operazioni di SHIFT, TEST su BIT, ed altre).
I più evoluti tra essi oramai possono essere paragonati a dei veri e propri Personal Computer, per cui si potrebbe anche
chiamarli IPC (Personal Computer Industriali).
In altre parole, un PLC può essere definito come uno speciale elaboratore, di tipo industriale, (Avente cioè
caratteristiche ben precise che gli consentono di lavorare con assoluta affidabilità in un ambiente difficile e gravoso, come
può esserlo un ambiente industriale, per la presenza notevole di disturbi elettrici, vibrazioni, ampie variazioni di
temperatura ed umidità, polveri etc.) concepito per risolvere problemi di controllo ed automazione e che si
differenzia dal PC soprattutto per quanto riguarda il linguaggio di programmazione (che non deve essere particolarmente
complesso, per far si che possa essere utilizzato da tecnici che non hanno conoscenze orientate all'elettronica ed
all'informatica) e l'interfacciamento con i dispositivi esterni.
In sintesi: si definisce PLC
•un sistema elettronico a funzionamento digitale
•destinato ad un uso in ambito industriale
•dotato di memoria, in cui archivia il programma da eseguire
•per controllare vari tipi di macchine e processi.
PROGETTAZIONE DEL SOFTWARE DI CONTROLLO
Ogni problema di automazione richiede una corretta progettazione:
• della struttura meccanica
• dei cablaggi elettrici
• del software del sistema di controllo.
NB: Prima di cominciare a scrivere il software sarebbe opportuno stendere una dettagliata
descrizione dell’automazione da realizzare. Il tempo trascorso in questa attività preliminare
non è sprecato, in quanto consentirà di scrivere un software più funzionale e facile da
modificare e adattare ai futuri cambiamenti che le inevitabili riorganizzazioni dei processi
industriali richiederanno.
La descrizione dell’automazione è facilitata dal ricorso alle rappresentazioni grafiche (Ladder,
FBD, SFC).
STRUTTURA
FUNZIONAMENTO
Un programma per PLC è costituito da tre elementi:
•programma utente
•blocco dati (opzionale)
•configurazione CPU (opzionale).
Il programma, scritto con la Unità di Programmazione (anche PC), deve essere caricato nella CPU
del PLC.
La CPU immagazzina il programma nella RAM e questa, a sua volta, lo copia immediatamente
nella EEPROM per la memorizzazione permanente.
NB: Il trasferimento del programma nella
EEPROM fornisce maggiori garanzie di
affidabilità durante l’esecuzione.
Il programma in esecuzione è quello caricato
nella EEPROM.
RAM
- EEPROM
NB: Il PLC non è una macchina di
Von Neumann: la memoria è
divisa in diverse aree.
Condensatore ad alta capacità.
E’ in grado di mantenere la RAM attiva per
diversi giorni dopo che è stata tolta
l’alimentazione.
CAMPO DI UTILIZZO DEI PLC
La necessità dell'industria di produrre a "qualità costante" e sempre più elevata, di rendere
flessibile la capacità produttiva e migliorare la produttività per poter essere competitiva nelle
attuali condizioni di mercato, spinge verso un'automazione che interessa tutti i livelli del
processo produttivo. Si va cioè verso la "fabbrica automatica" ed il PLC sta assumendo in
quest'ultima il ruolo di componente fondamentale.
Non esiste ormai settore di produzione, trasformazione o controllo in cui non si trovano o non
siano possibili applicazioni del controllore a logica programmabile.
I PLC delle ultime generazioni non hanno più soltanto le caratteristiche originali di semplici
"sequenziatori" , ma stanno assumendo quelle di "calcolatori di processo" con compiti di controllo
e supervisione del processo produttivo visto che è possibile dotarli della possibilità di comunicare
con altri PLC e PC ed inoltre presentano delle interfacce utente sempre più sofisticate.
Il PLC presenta una serie di vantaggi, rispetto alla logica cablata realizzata con componenti
elettromeccanici e pneumatici, che lo rendono sicuramente e fortemente competitivo;i più im
portanti di questi vantaggi sono:
maggiore economicità sia nella fase di realizzazione
del sistema di comando sia nella fase di gestione
dello stesso, in particolare riguardo ad eventuali
ampliamenti e/o modifiche.
ampliamenti al sistema di comando possono essere
fatti semplicemente " aggiungendo " i componenti e
limitandosi al loro collegamento fisico senza dover
modificare quello delle altre apparecchiature.
modifiche al ciclo di automazione possono
essere apportate semplicemente intervenendo
sul "programma" e
lasciando inalterati i
collegamenti fisici.
Il tempo per realizzare le modifiche può essere ragionevolmente ridotto al minimo in quanto è
possibile "testare" e mettere a punto il programma eseguendo delle prove "al banco" su uno
stesso PLC dotato di opportuni simulatori.
Il PLC si può intendere come una apparecchiatura "General Purpose" (è l'utente che decide
per quale applicazione specifica verrà utilizzato) con:
- possibilità di Ampliamento
recupero e reimpiego dello stesso PLC qualora non fosse più necessaria l'applicazione a cui era
stato inizialmente destinato.
assenza di parti in movimento e quindi ridotta usura e manutenzione e lunga vita dei
componenti:
possibilità di produrre facilmente la stampa dei programmi
possibilità di autodiagnosi dei guasti
possibilità di inserimento in reti di controllo centralizzate
ingombro ridotto
minimo consumo
maggior sicurezza poichè nella maggior parte dei casi si hanno tensioni di max 30 V e di
conseguenza impossibilità di incidenti folgoranti.
CONTROLLO DI UN PROCESSO CON PLC
Per poter controllare una macchina od un processo il PLC deve acquisirne lo stato istante per istante ed in
base alle istruzioni scritte nella propria memoria, determinare se devono o meno essere apportate delle
modifiche allo stato attuale delle uscite.
Per acquisire lo stato attuale del processo vengono collegati agli "ingressi" del PLC tutte quelle
apparecchiature che possono fungere da "sensori" del sistema ("datori" di segnali) quali ad es. : pulsanti,
finecorsa, fotocellule, interruttori, contatti ausiliari di relè, telerruttori, relè termici, ecc.
Per "attuare" quanto è stato determinato dall'elaborazione del programma, alle uscite del PLC sono collegate
tutte quelle apparecchiature atte a realizzare quanto necessario per l’esecuzione del processo
(attuatori), che possono essere, a seconda di come viene realizzato l'automatismo, di tipo pneumatico,
oleodinamico od elettromeccanico od anche misto, come ad es. :relè, telerruttori, elettrovalvole, lampade di
segnalazione, suonerie, cilindri pneumatici od oleodinamici, valvole elettropneumatiche etc.
Il compito principale di un PLC è quello di acquisire informazioni e dati provenienti dal sistema controllato,
elaborarli in base ad un programma [che quindi non è altro che una serie di istruzioni tramite cui viene definito
come si dovrà comportare la macchina (processo) al verificarsi di eventi o situazioni ben definite] ed emettere,
verso il sistema controllato, il risultato di tale elaborazione che costituisce ciò che va fatto in quel momento da
parte degli organi preposti all'esecuzione del processo.
Per far ciò il PLC è dotato, oltre che di moduli d'ingresso e di uscita (I/O) , di un'unità centrale di elaborazione
(CPU), che costituisce il cuore del sistema e sovrintende a tutte le operazioni necessarie al funzionamento del
sistema, di MEMORIA per memorizzare il cosidetto sistema operativo del PLC, il programma utente ed i risultati
intermedi dell'elaborazione, di un ALIMENTATORE per alimentare tutte le varie parti costituenti il PLC ed infine
di un SISTEMA BUS per permettere i collegamenti fra le varie parti che compongono il sistema.
Oltre a ciò, il PLC deve poter comunicare con il mondo esterno ed è quindi dotato della possibilità di collegarsi
con delle periferiche per permettere il dialogo uomo-macchina, per comunicare con altri PLC, per permettere
l'utilizzo di memorie di massa e per fornire documentazione cartacea.
IL PLC NEL DETTAGLIO
L'ALIMENTATORE
La CPU necessita di alimentazione ad una tensione continua e stabilizzata di pochi volt
(solitamente 5). Altri
circuiti richiedono una tensione di 12 0 24 V sempre in corrente continua.
L'unità centrale di un PLC è equipaggiata pertanto con un alimentatore in cui sono raggruppati tutti i dispositivi
necessari per fornire tale alimentazione quali :
TRASFORMATORI ;
RADDRIZZATORI (Convertitori C.A./C.C.)
STABILIZZATORI.
Si può considerare parte dell'alimentatore anche il dispositivo che commuta sulla batteria
tampone, in assenza di alimentazione dalla rete, per salvare il contenuto della RAM.
Interfaccia uomo-macchina (in inglese Human-Machine Interface, HMI) si riferisce allo strato
che separa un essere umano che sta utilizzando una macchina dalla macchina stessa.
Profibus è l'acronimo di Process Field Bus. Si tratta di un bus di campo (field bus). Le sue applicazioni sono nel
campo dell'automazione industriale di processo.
-LA CPU
La CPU (Central Processing Unit o Unità Centrale) è la parte più importante del PLC di cui costituisce
"l'intelligenza". Essa è l'unità di governo del sistema ed il suo elemento centrale è un componente
integrato denominato Microprocessore.
Il microprocessore racchiude in sè tutte le funzioni di calcolo e controllo del processore centrale di un
normale calcolatore. La sua caratteristica più importante è la programmabilità che ha consentito il grande
passo in avanti dalla logica cablata alla logica programmabile.
Attualmente i microprocessori utilizzati come CPU dei controllori programmabili sono molto vari in quanto
non esiste una qualsiasi forma di standardizzazione.
Ogni costruttore impiega il microprocessore che ritiene più adatto alle prestazioni che vuole fornire al suo
sistema con livellio di potenza diversificati ( da 16 a 64 bit)
IL SISTEMA BUS
Il sistema bus è un insieme di collegamenti interni per la trasmissione e lo scambio di segnali, tensione
d'alimentazione e potenziali di massa.
Lo scambio di segnali tra il microprocessore e le schede d'ingresso e d'uscita avviene quindi tramite il sistema
bus.
Il bus è suddiviso in più gruppi di segnali:
-bus degli indirizzi, tramite il quale si può accedere agli indirizzi delle singole schede;
- bus dati, tramite il quale i dati possono essere letti dalle schede d'ingresso o trasferiti alle schede d'uscita;
-bus di comando, tramite il quale vengono gestiti i segnali di comando e controllo dello svolgimento delle
funzioni all'interno del controllore.
-LA
MEMORIA
Il PLC ha bisogno di memoria sia per il proprio sistema operativo sia per la memorizzazione del
programma utente sia per l'elaborazione dei dati intermedi durante l'esecuzione del programma.
Di solito il costruttore utilizza, per la memorizzazione del sistema operativo, una memoria di tipo ROM (Read
Only Memory), che ha appunto le caratteristiche di essere non volatile e di non poter essere modificata visto
che è una memoria di sola lettura.
Il programma utente , al contrario, deve poter essere modificato in quanto la sua stesura è demandata
all'utente che lo adatterà alle sue esigenze iniziali e, qualora fosse necessario, lo modificherà in seguito a
nuove esigenze.
Lo stesso si può dire riguardo la memoria necessaria per la memorizzazione dei risultati intermedi in quanto
sulla stessa il PLC effettuerà continuamente operazioni di lettura e scrittura.
Quindi, sia per il programma utente che per la memorizzazione dei risultati intermedi, il costruttore fornisce il
PLC di una memoria di tipo RAM (Random Access Memory) che può essere letta e riscritta.
La dimensione della RAM utente è uno dei parametri che caratterizza maggiormente un PLC in quanto da essa
dipende la lunghezza del programma che può essere gestito dal PLC.
Per PLC di piccola taglia, attualmente, si hanno memorie utente che hanno dimensione da tre a quattro
Kbyte, a cui corrisponde la capacità di memorizzare programmi di circa mille istruzioni.
Ovviamente in PLC di taglia superiore la dimensione della RAM varia proporzionalmente con la complessità
del set di istruzioni del linguaggio di programmazione proprio del PLC e con le dimensioni, prevedibilmente
superiori, dei programmi necessari per gestire automatismi complessi.
ASPETTO FUNZIONALE DELLE MEMORIE DEL PLC
In base al loro impiego, le memorie in un PLC si possono distinguere in :
memoria di sistema,
memoria di programma,
memoria dati.
LA MEMORIA DI SISTEMA :
La memoria di sistema serve a conservare tutte quelle particolari istruzioni che servono per la gestione ed
il controllo del funzionamento della CPU e che pertanto costituiscono un vero e proprio SISTEMA
OPERATIVO del PLC.
Dato che il suo contenuto è di primaria importanza per il controllore, vengono utilizzate delle memorie di
tipo ROM, per evitare la sua involontaria cancellazione. Nulla vieta comunque che sia PROM o EPROM,
purchè non accessibile all'utente.
LA MEMORIA DI PROGRAMMA :
È la memoria destinata a contenere le istruzioni che costituiscono il programma eseguibile dal PLC. Per
svolgere tale funzione essa deve essere accessibile all'utente (a cui è demandata la stesura del
programma stesso) e viene quindi realizzata con memorie di tipo RAM.
LA MEMORIA DATI :
È anche detta MEMORIA DI LAVORO e prevede due sezioni distinte: i FLAG ed i REGISTRI
I FLAG (o MERKER)
Si tratta di una certa quantità di memoria in formato WORD o DOUBLE WORD
che
può essere
indirizzataanche in formato BYTE od a singoli BIT e che può
essere
utilizzata dall'utente
per
memorizzare risultati intermedi durante l'elaborazione del programma.
Tali risultati possono essere successivamente utilizzati in altre parti del programma.
I singoli BIT di queste memorie possono essere "SETTATI" (cioè posti
"RESETTATI" (cioè posti al valore logico 0).
al
I REGISTRI
Si tratta di memoria di tipo RAM che viene utilizzata per svolgere determinate
l'esecuzione del programma.
valore
logico 1)
funzioni durante
Solitamente si ha almeno un registro di LAVORO in cui vengono memorizzati i risultati delle singole
operazioni di tipo logico-aritmetico che vengono svolte dalla CPU istruzione dopo istruzione, un registro
AUSILIARIO che interviene solo in particolari situazioni, un registro di STACK che serve per la
memorizzazione di risultati intermedi quando il registro di lavoro deve essere utilizzato per altre
elaborazioni ed infine un registro di STATO.
o
LA SEZIONE DI INPUT/OUTPUT DI UN PLC
La sezione di I/O di un PLC riveste particolare importanza per quanto concerne la valutazione delle
prestazioni dello stesso, è usuale accennare innanzitutto alla quantità di punti di ingresso e di uscita
quando si parla delle caratteristiche di un PLC.
Questo comunque non è l'unico parametro di riferimento per la scelta di un PLC, infatti bisognerà tenere
conto di altre caratteristiche come ad es. la velocità di esecuzione di un ciclo di programma, la possibilità di
eseguire calcoli, la dimensione della RAM utente, ecc.
Non esistono quindi dei parametri di riferimento asfsoluti per valutare la scelta di un PLC rispetto ad un altro,
ma ciò dovrà essere fatto di volta in volta in funzione ovviamente del rapporto PRESTAZIONI/PREZZO in
riferimento alle specifiche dell'impianto da gestire.
UNITÀ D'INGRESSO
Le informazioni provenienti dal processo controllato possono essere semplicemente definite
come
"segnali in ingresso".
Questi segnali sono ovviamente di tipo elettrico e dovranno essere trattati in modo che siano riconoscibili
dalla CPU.
Il compito delle schede d'ingresso (come poi, in senso inverso, faranno anche le schede d'uscita) è quello di
consentire il dialogo tra il PLC ed il gruppo di potenza, o , per essere più precisi, per permettere al PLC di
acquisire i comandi e lo stato degli attuatori del suddetto gruppo.
Tali segnali possono essere sia segnali di tipo binario, caratterizzati dalla possibilità di assumere due soli valori
(" 1 logico" e " 0 logico"), a prescindere dalla natura iniziale del segnale, che potrebbe essere anche di tipo
analogico o comunque un segnale instabile nel tempo, ma lo si vuole trattare come segnale "digitale
binario", caratterizzato quindi da due soli stati possibili : assenza di tensione o presenza di tensione.
I segnali possono essere anche di tipo analogico, quindi variabili nel tempo dentro un prefissato intervallo
di valori, in questo caso devono preventivamente essere trattati da appositi convertitori A/D prima di essere
elaborati dalla CPU o digitali
SCHEDE D'INGRESSO DIGITALI.
Nel caso di segnali da trattare come segnali di tipo ON/OFF le schede d'ingresso devono essere in grado di
"capire" quando il segnale in ingresso è da considerare ON e quando è da considerare OFF, quando si tratta
di un disturbo ed inoltre di isolare galvanicamente la CPU dall'esterno in modo che eventuali sbalzi di
tensione o sovraccarichi od addirittura corto circuiti non danneggino la stessa.
Uno dei compiti svolti dalle schede d'ingresso è quello di adattare il livello e le caratteristiche del segnale.
Infatti, mentre la tensione di funzionamento interna del PLC è una tensione bassa (di solito 5 V), i segnali
possono presentarsi con livelli di tensione diversi ( 24, 48, 110, 220 V ).
La prima operazione svolta dalle schede di ingresso consiste nella messa in forma o squadratura del segnale.
Per determinare con certezza se il segnale è ON oppure OFF, di solito le schede d'ingresso sono costruite in modo che il
segnale esterno viene riconosciuto tale entro un intervallo di valori prefissato.
Ad es. si consideri un segnale a 24 V
Per evitare di acquisire false informazioni dovute a disturbi indotti dal mondo esterno si effettua un filtraggio
delle informazioni parassite, viene cioè valutato non solo il livello logico del segnale, ma anche la sua durata. Tanto
maggiore è questo ritardo tanto più grande risulta l'immunità ai disturbi.
TECNICA DEL MULTIPLEXAGGIO DEGLI INGRESSI IN UN CONTROLLORE PROGRAMMABILE
Spesso si presenta la necessità di collegare agli ingressi di un PLC dei segnali numerici opportunamente
codificati. Uno dei codici più usati per questo scopo è il codice BCD.
Usando questo codice, se si vuole inserire dei valori numerici con un certo numero di cifre, occorreranno un numero
di ingressi digitali pari a quattro per ogni cifra che costituisce il valore numerico da inserire.
Per cui, se si vuole inserire un valore numerico compreso tra 0 e 9999, si devono utilizzare quattro
codificatori ognuno dei quali occupa quattro ingressi (migliaia, centinaia, decine, unità).
In totale servono quindi 16 ingressi da destinare
esclusivamente all'acquisizione del valore da
inserire.
È possibile ridurre questo numero utilizzando una
tecnica di multiplexaggio degli ingressi come
quella indicata in figura, in cui si collegano i 16
segnali
provenienti
dai
codificatori,
disaccoppiandoli con dei diodi, a 4 ingressi del
PLC.
.
Questa soluzione richiede una gestione software un pò più sofisticata, permette però di risparmiare complessivamente
il 50 % di punti di I/O necessari.
Sono infatti necessari 4 ingressi e 4 uscite invece di 16 ingressi
SCHEDE D'INGRESSO ANALOGICHE
Esistono in commercio dei sensori analogici (termocoppie, resolver, ecc.) che forniscono, in relazione al livello di un
liquido in un serbatoio, alla temperatura di un forno, alla pressione in una tubazione etc., un segnale variabile con
continuità entro due limiti.
I valori di questi segnali sono standardizzati; valori tipici sono :
± 50 mV, ± 1 V, ± 5 V, ± 10 V, 0..10 V, 0..20 mA, ± 20 mA, +4..20 mA.
Per rendere possibile l'elaborazione da parte del PLC del valore del segnale in ingresso, qualunque esso sia, bisogna
convertire il segnale analogico variabile in un segnale digitale comprensibile alla CPU.
La precisione del convertitore dipende dal numero di bit che è in grado di
elaborare, cioè dalla sua "risoluzione" ed anche dalla sua "accuratezza".
Il numero di bit solitamente va da un minimo di 8 a 10, 12 bit
Con 8 bit è. possibile elaborare 28 = 256 combinazioni, con 10 bit 210 = 1024
combinazioni e con 12 bit 212 = 4096 combinazioni.
Il PLC ha un'immagine a gradini della grandezza come quella di figura
Se ad es. si ha una temperatura variabile da Tmin a Tmax e si utilizza un sensore che fornisce un valore in tensione da 0 a
10 V ( 0 V = Tmin e 10 V = Tmax ) ed il convertitore è ad 8 bit, si ha una risoluzione di 10/256 = 0.039 V a cui
corrisponderà un valore di temperatura dato da:
(Tmax-Tmin)/256.
Se ad es. l'intervallo di variazione della temperatura è di 100 °C la risoluzione del convertitore analogico/digitale sarà di
100/256=0.39 °C.
Con un ADC a 10 bit la risoluzione sarebbe di 100/1024=0.0976 °C.
Se si avesse un ADC a 12 bit la risoluzione diventerebbe di 100/4096=0.0244 °C.
Maggiore quindi è il numero di bit, maggiore sarà la fedeltà con la quale il convertitore trasformerà il segnale analogico in
segnale digitale.
Le schede analogiche possono avere diversi ingressi, per ridurre i costi si ricorre alla tecnica del multiplexer, che consente di
commutare i diversi ingressi su di un unico convertitore, questo determina però un leggero aumento del tempo di
Acquisizione dati
Anche nelle schede analogiche la CPU riceve i segnali digitali mediante
l'interposizione di optoisolatori.
SCHEDE D'USCITA DIGITALI
I moduli o schede d'uscita rappresentano sostanzialmente la interfaccia tra
l'elaborazione del programma attuata dalla CPU del PLC e gli attuatori che
costituiscono il sistema di comando verso l'impianto controllato.
Per quanto concerne il numero di uscite presenti su ogni scheda di uscita
valgono le stesse considerazioni fatte per le schede di ingresso.
Si definisce "tempo di emissione dell'uscita" l'intervallo di tempo che intercorre tra l'istante cui appare
un'immagine d'uscita nella memoria del PLC e quello in cui viene raggiunta la soglia di tensione a cui corrisponde
l'effettiva attivazione dell'uscita.
Per le uscite a relè questo tempo dipende principalmente dal tempo di salita dei relè, che varia da due a più decine di
millisecondi, mentre per le uscite statiche (a transistor) tale tempo è decisamente più breve.
Le tensioni più frequentemente utilizzate sono 24 o 48 V, si possono comunque avere tensioni diverse. La corrente che ogni
singola uscita è in grado di erogare va da 100 mA a 2 A.
SCHEDE D'USCITA ANALOGICHE
Le schede di uscita analogiche svolgono, in senso inverso, le stesse funzioni delle schede di ingresso analogiche. Operano
cioè una conversione digitale-analogica (D/A) dei valori, elaborati dal PLC così come definito da programma, che devono
essere trasmessi all'attuatore collegato alla scheda, il quale è costruito per ricevere un segnale analogico in tensione od in
corrente.
Vale tutto quanto già detto a proposito delle schede d'ingresso analogiche.
PERIFERICHE
Il controllore programmabile per poter dialogare con il mondo esterno (per essere programmato, per i controlli diagnostici,
per la stampa dei programmi su carta, per l'emissione di segnali d'allarme, per la messa a punto del programma ed altre
funzioni) necessita di particolari apparecchiature denominate unità periferiche, quali ad es. :
consolle di programmazione ;
memorie di massa ;
simulatori ;
programmatori di EPROM ;
interfaccia per stampanti e plotter ;
moduli di collegamento per personal computer ;
unità di servizio (chiavi elettroniche).
:
Sistema di gestione di un impianto per la produzione alimentare
Il sistema permette la gestione di un impianto per
la produzione di prodotti alimentari con controllo
dei tempi, delle temperature e del dosaggio degli
alimentari.
E possibile la gestione in manuale o in automatico
con la registrazione delle ricette per le varie
tipologie di lavorazione richieste
L’operatività e gli stati di funzionamento sono gestiti
da un terminale touch screen
I DISPOSITIVI DI PROGRAMMAZIONE
Il PLC trasmette segnali alle schede d'uscita in funzione dei valori acquisiti dalle schede d'ingresso ed elaborati secondo
le istruzioni contenute nel programma utente che è allocato in memoria.
È quindi indispensabile un'interfaccia che permetta il dialogo tra l'operatore e la macchina in modo da rendere possibile
la immissione del programma elaborato dal programmatore ed una serie di altre funzioni più o meno sofisticate.
Le funzioni fondamentali che un dispositivo di programmazione deve garantire sono
scrittura del programma nella memoria del PLC; lettura del programma già residente in memoria;
modifica del
programma; ricerca di istruzioni del programma; compilazione del programma.
Tra le funzioni superiori dei dispositivi di programmazione rientra ad es. il : Funzionamento ON-LINE ed OFF-LINE
I piccoli modelli possono operare solo ON-LINE, cioè collegati al PLC.
La capacità di operare OFF-LINE, propria delle unità più evolute, consente al programmatore di scrivere e testare i
programmi " al banco ", in condizioni sicuramente migliori di quelle che si avrebbero sull'impianto ed inoltre in tempi
che non dipendono dallo stato di realizzazione dell'impianto, nel caso di un impianto nuovo o comunque, in caso di
modifiche da apportare ad un impianto già in funzione, l'attività di messa a punto del programma non comporta la
fermata dell'impianto
Per mezzo di opportune interfacce è possibile collegare il PLC a calcolatori con i quali potrà scambiare informazioni.
Con un collegamento in rete si possono svolgere per mezzo di un calcolatore funzioni come :
controllo della produzione; raccolta e gestione di dati relativi al processo ;rilevamento degli eventuali guasti;
supervisione e controllo dei processi produttivi mediante sinottici dell'impianto visualizzati su monitor ; forzatura degli
ingressi e delle uscite; controllo e modifica a distanza e del programma e di alcuni parametri come valori di conteggi e
temporizzazioni.
FUNZIONAMENTO BASE DEI PLC
I PLC , così come i computer, è in grado di elaborare solamente informazioni espresse dai due livelli logici 1 e 0. Di
conseguenza tutte le informazioni fornite ad un PLC, siano dati od istruzioni, devono essere espresse tramite
combinazioni di questi due stati o livelli logici.
Spesso il livello logico 1 viene indicato con la lettera H (dall'inglese HIGH cioè livello ALTO) ed il livello logico 0 con la
lettera L (dall'inglese LOW, cioè livello BASSO).
La rappresentazione di dati ed istruzioni in termini di 0 ed 1 logici prende il nome di rappresentazione binaria,
un'informazione, nella forma comprensibile al PLC, si può presentare nella seguente forma :
0011 1010 1100 1110
Come si vede, la precedente espressione binaria è costituita da più bit.
Una sequenza del genere prende il nome di " PAROLA ".
In particolare si tratta di una parola a 16 bit, che si riferirà ad un PLC che opera in parallelismo 16, in grado cioè di
elaborare dati espressi, al massimo, con 16 bit.
-FUNZIONAMENTO SEQUENZIALE
Caratteristica base di tutti i sistemi di elaborazione dati è il funzionamento sequenziale, che è da intendersi come "fare
una cosa alla volta , una dopo l'altra".
Il funzionamento sequenziale dei sistemi a PLC porta a due considerazioni importanti :
1)l'elaborazione
di un programma richiede un certo tempo che può essere più o meno lungo, a seconda del numero e
del tipo di istruzioni che lo compongono.
2)l'elaborazione
sequenziale delle istruzioni comporta anche il fatto che, qualora si abbiano nel programma delle
istruzioni che portano alla elaborazione di risultati in contraddizione fra loro, si possono creare delle situazioni di
incertezza già in fase di programmazione.
-TEMPO DI ESECUZIONE DELLE ISTRUZIONI
Per tempo di esecuzione di un'istruzione si intende il tempo che intercorre tra l'istante in cui l'istruzione stessa viene letta
dalla memoria, sfruttando l'indirizzo che in quel momento è contenuto nel contatore di programma (Program Counter), e
l’istante in cui, dopo che la stessa è stata decodificata ed eseguita, la CPU inizia la fase di lettura dell'istruzione successiva.
Tali durate sono molto varie fra di loro, ad es. la lettura di un ingresso può essere eseguita anche in un solo microsecondo,
mentre caricare un contatore può richiedere anche 600 microsec.
A seconda dei modelli, per una stessa marca di PLC, ed ancora di più per PLC di marca diversa, la stessa istruzione può
richiedere tempi molto diversi per essere eseguita. A volte addirittura in un dato PLC viene eseguita in un tempo fino a
mille volte superiore a quello necessario in altro PLC.
-TEMPO DI CICLO (O DI SCANSIONE)
Per TEMPO DI CICLO si intende il tempo necessario per eseguire tutte le istruzioni che costituiscono il programma.
-TEMPO DI REAZIONE
Supponendo che un ingresso venga esaminato una sola volta per ciclo, per TEMPO DI REAZIONE del PLC si intende la
somma del tempo di ritardo nell'acquisizione della variazione e la durata del ciclo.
Il tempo di reazione è variabile in quanto dipende dal momento in cui si verifica la variazione dell'ingresso.
IL CONCETTO DI CICLO NEI PLC
Una caratteristica fondamentale dei PLC è il funzionamento sequenziale della CPU.
Le istruzioni che costituiscono il programma vengono eseguite una alla volta, una dopo l'altra tranne ovviamente i casi in
cui si incontrano delle istruzioni di salto che impongono una variazione a questa sequenza.
Alla fine del programma, svolte alcune operazioni di sistema, si ricomincia dalla prima istruzione.
TIPI DI CICLI
In relazione ai cicli ed alla gestione dell'input-output i PLC si differenziano sostanzialmente nel fatto che i
valori degli ingressi e delle uscite vengono letti e scritti (aggiornati) direttamente od indirettamente tramite
una memoria.
Nel caso in cui l'accesso è diretto, si ha un modo di funzionamento che si avvicina molto al concetto di
risposta del sistema agli eventi in tempo reale (prendere in considerazione i fenomeni nel momento stesso
in cui avvengono ed agire subito di conseguenza
Nel caso di utilizzo di una memoria intermedia, l'acquisizione dello stato degli ingressi viene fatta
contemporaneamente in un certo istante (ad es. prima di eseguire il ciclo) e questo valore viene mantenuto
invariato in memoria per tutta la durata del ciclo anche se nel frattempo alcuni o tutti gli ingressi hanno
modificato il loro stato.
I costruttori di PLC hanno impostato modalità diverse di attuazione dei cicli in riferimento ai due momenti
fondamentali di "acquisizione degli ingressi" ed "aggiornamento delle uscite".
I tipi di ciclo che si trovano più comunemente sono i seguenti :
-CICLO SINCRONO IN INGRESSO ED IN USCITA
È il ciclo tipico in cui si fa uso dei registri di "immagine degli ingressi" e di "immagine delle uscite".
Il PLC legge tutti gli ingressi contemporaneamente all'inizio del ciclo e crea in memoria (ovvero nel registro a
ciò dedicato) una immagine del processo relativa all'istante in cui è stato acquisito il valore di ogni singolo
ingresso.
Tale immagine rimane invariata per tutta la durata del ciclo anche se, durante l'esecuzione
dello stesso, alcuni ingressi dovessero modificare il loro stato.
Le varie fasi eseguite da un PLC, funzionante con questo tipo di ciclo, sono descritte in figura
- CICLO SINCRONO IN INGRESSO ED ASINCRONO IN USCITA
Come nel ciclo precedente, gli ingressi sono acquisiti contemporaneamente
all'inizio del ciclo, si ha quindi anche in questo caso un registro di immagine degli
ingressi.
Le uscite invece vengono aggiornate non appena viene elaborato un risultato
(ovvero non appena un risultato da assegnare ad un'uscita è disponibile, questo
viene subito emesso all'esterno e l'uscita interessata viene aggiornata)
-CICLO ASINCRONO IN INGRESSO ED IN USCITA
L'organizzazione di questo ciclo è basata sulla elaborazione delle sequenze di istruzioni una per una. Viene letto un
ingresso (o più ingressi se nella sequenza ne compaiono più di uno), lo si usa in una data funzione, si elabora il
valore dell'uscita, viene aggiornata l'uscita ed infine si passa alla sequenza successiva
Il primo tipo di ciclo che abbiamo visto è tipico dei PLC di basso livello. Il secondo è scarsamente
diffuso. Il terzo è adottato da un PLC di buon livello
Comunque sia questa è soltanto una schematizzazione dei tipi di ciclo dei PLC, in commercio si possono trovare
soluzioni le più diverse.
Modulo base S7 - 224
Il
modulo base dispone di I/O integrati:
14 Ingressi (Byte 0 e Byte 1)
10 Uscite (Byte 0 e Byte 1)
LINGUAGGI
DI
PROGRAMMAZIONE
NOTE STORICHE
I linguaggi di programmazione del PLC hanno avuto uno sviluppo diverso da quello dei calcolatori.
Il PLC è stato introdotto inizialmente per sostituire i quadri di comando a relè, per cui dovevano
essere gestiti non da informatici, bensì da elettricisti con scarse conoscenze di informatica.
Gli elettricisti progettavano i quadri di comando con degli schemi a contatto per cui si organizzò un
linguaggio di programmazione del PLC molto simile (LADDER) e oggi molto diffuso. Le industrie
costruttrici di PLC scelsero linguaggi proprietari, con conseguenti problemi di portabilità.
La programmazione a contatti non consente tuttavia di sfruttare al meglio la potenza hardware del
PLC. Per questo e anche per consentire la programmazione a tecnici informatici e elettronici furono
sviluppati in seguito altri due tipi di linguaggi: IL (Instruction List) e FBD (Functional Diagram
Block).
Restava comunque la difficoltà di realizzare una facile ed efficace automazione dei grandi impianti.
Inoltre, a causa della incompatibilità tra i modelli dei diversi costruttori e dell’aumento della
complessità dell’automazione, si è rivelata sempre più critica la manutenzione del software di
controllo.
Nel
tentativo
di
risolvere
questa
problematica
fu
implementato
un
nuovo
linguaggio
di
programmazione, simile a uno di quelli di alto livello per la programmazione del PC e standardizzato,
con sintassi vicina a quella del Pascal: ST (Structured Text).
Un processo di automazione, e quindi la scrittura di un software di controllo, può essere visto come
un automa a stati finiti (DES, Discrete Event System).
La rappresentazione grafica di un DES mediante i tradizionali diagrammi di transizione degli stati
presentava dei limiti che li rendevano incapaci di una descrizione completa dell’automazione.
I diagrammi erano stati di valido aiuto nella:
•descrizione del funzionamento di un automa a stati finiti
•progettazione dell’hardware.
Ma nella progettazione del software di controllo i limiti dei diagrammi emersero a mano a mano che
l’automazione si rendeva sempre più complessa; i diagrammi con consentivano la rappresentabilità
di
•più stati attivi contemporaneamente
•processi paralleli
•funzioni di controllo logiche.
Nel solco di questa problematica, nel 1975 in Francia si cominciò a sviluppare il GRAFCET (Graphe
de
Coordination Etapes Transitions), una rappresentazione del processo di automazione
mediante un diagramma funzionale standardizzato, capace di rappresentare processi sequenziali
(processi il cui
svolgimento avviene a passi e la transizione da un passo al successivo è
Il
subordinato a certe condizioni)
Grafcet:
•era un formalismo che consentiva una buona progettazione del controllo degli impianti
•era indipendente dalla tecnologia con cui il controllo sarebbe stato implementato
•forniva una rappresentazione immediata del processo di automazione.
•Nel corso degli anni ’80 il Grafcet fu ulteriormente sviluppato e il successo fu tale che nel
1987 fu assunto come standard internazionale dall’IEC (Comitato Elettrotecnico
Internazionale).
.
Infine la norma IEC 1131 – 3 del 1993 (recepita in Italia nel 1996), cercando di mettere ordine nei
vari linguaggi di programmazione dei PLC, ha incluso anche il Grafcet tra i linguaggi di
programmazione con la nuova denominazione di Sequential Functional Chart (SFC).
Per la programmazione dei PLC i costruttori possono quindi implementare i seguenti linguaggi:
•IL (Istruction List)
•ST (Structured Text)
•LD (Ladder Diagram)
•FBD (Function Block Diagram)
•SFC (Sequential Functional Chart)
Programmare un PLC significa trasferire in esso una sequenza di istruzioni (programma) in un
linguaggio di programmazione opportunamente codificate tramite delle periferiche dedicate a
questo scopo (unità di programmazione).
Il compito del PLC sarà quello di determinare lo stato delle uscite, ad esso collegate, in funzione
dello stato degli ingressi, secondo le relazioni stabilite dal programma che il PLC esegue.
IL PLC può essere programmato a svolgere una certa sequenza di operazioni, più o meno
complessa, sulla base dell'insieme delle funzioni elementari da esso eseguibili sulla base del SET
di istruzioni di cui è dotato (operazioni logiche, conteggi, comparazioni, temporizzazioni, etc),
Visto che il PLC deve operare in un contesto di automazione industriale, la sua capacità di espressione
funzionale deve essere omogenea con le esigenze di automazione industriale.
Basti pensare che i più elementari problemi da risolvere nell'ambito dell'automazione industriale sono del tipo : "
se il tal contatto è chiuso e contemporaneamente quell'altro contatto è aperto, allora attiva la tal
uscita".
I linguaggi attualmente in uso si possono considerare appartenenti a due categorie ben precise, cioè quella dei
linguaggi grafici e quella dei linguaggi letterali.
La differenza fra questi due tipi consiste essenzialmente nella modalità di rappresentazione visiva delle
combinazioni logiche che costituiscono le varie sequenze in cui è suddiviso un programma : in quelli grafici si fa
uso di simboli grafici mentre in quelli letterali si fa uso di codici letterali mnemonici cui è attribuita una
determinata funzione .
alcuni dettagli del linguaggio LADDER (o KOP
Appartiene alla categoria dei linguaggi grafici perchè si presenta in maniera
simile ad uno schema elettrico funzionale, con delle semplici modifiche
rispetto a quest'ultimo :
flusso di potenza va da sinistra verso destra ;
il flusso logico va dall'alto verso il basso ;
ogni circuito è disegnato in posizione orizzontale invece che verticale.
- le linee che rappresentano l'alimentazione vengono disegnate verticalmente invece che orizzontalmente;
i simboli dei contatti NA, dei contatti NC e delle bobine vengono semplificati come si vede in figura In questo
tipo di linguaggio, per rappresentare lo stato dell’operando, viene valutato il livello logico della funzione e non
il livello fisico del sensore collegato all’operando che è interessato
Cenni sul fup e awl e Ladder
AWL
I linguaggi letterali (o liste d'istruzioni o linguaggi simbolici o AWL) utilizzano una serie di parole (codici letterali
mnemonici) che identificano ognuna una determinata funzione logica (AND, OR, NOT, ecc.), allo stesso modo si possono
rappresentare temporizzatori, contatori, comparatori, ecc.
I due programmi visti precedentemente in FUP ed in KOP, si presentano sotto la seguente forma
- FUP
E’ un linguaggio di tipo grafico, la differenza rispetto al KOP sta nel fatto che i simboli utilizzati per rappresentare le
funzioni logiche, non sono più dei contatti bensì dei blocchi logici.
LINGUAGGIO DI PROGRAMMAZIONE LADDER
E'
il
più
Si basa su simboli di provenienza "elettrica":
Binari di
vecchio linguaggio di programmazione per
potenza (power
PLC
rail), contatti elettrici e avvolgimenti magnetici (coil)
Si articola in linee verticali dette “rung”
Ciascun “rung” può contenere contatti, coil, Function Block e Funzioni
Ciascun "rung" deve essere connesso necessariamente al binario di potenza sinistro (left power rail), mentre il
collegamento con quello destro è opzionale
Elementi di Base del Linguaggio Ladder
Power Rail
Linee Elettriche Orizzontali
Connessioni ai Power Rail
Contatto Normalmente Aperto
Contatto Normalmente Chiuso
Coil (bobine)
Negated Coil
ORGANIZZAZIONE DELLA PRODUZIONE DEL SOFTWARE PER
LA
PROGRAMAZIONE
La prima fase per la programmazione di un PLC che deve gestire un qualunque impianto di automazione industriale od
applicazioni diverse, è quella dell'ANALISI FUNZIONALE del problema da risolvere.
In questa prima fase non interessa quello che sarà il contenuto del programma, il quale deve essere visto come una
scatola nera di cui interessa sapere ciò che vi entra, le elaborazioni che deve effettuare e ciò che ne dovrà uscire.
In pratica bisogna definire :
Qual'è il punto di partenza, cioè quanti, quali e di che tipo sono i segnali in ingresso, con quali caratteristiche, con
quale durata e con quale significato ;
L'esatta definizione e descrizione del funzionamento dell'impianto anche nei minimi particolari, perchè in base a
ciò si dovrà definire le elaborazioni che il PLC (ovvero il programma che deve essere scritto) dovrà svolgere.
Qual'e' il punto di arrivo vale a dire i segnali che dovranno essere forniti al processo : come , quando, in che forma,
con quale durata.
A queste fasi segue quella della definizione della " Lista di Occupazione degli I/O " ; questa lista è importante per il
programmatore perchè gli permette di sapere in quale determinato ingresso è collegato il tal sensore ed in quale uscita
è collegato il talaltro attuatore.
Subito dopo la lista di occupazione degli I/O si può eventualmente fare anche una lista di assegnazione delle variabili
interne (memorie a disposizione dell'utente) che si intende utilizzare per scopi particolari o comunque definibili già prima
di iniziare la stesura del programma, come per es. quali memorie si utilizzeranno per memorizzare dei valori di conteggio,
quali per memorizzare situazioni particolari del processo ecc.
E' importante inserire dei commenti e delle osservazioni che rendano il programma più chiaro e leggibile
Il modo di come si descrive il funzionamento dell'impianto può essere diverso a seconda di come ognuno è abituato
a lavorare, cioè si può ricorrere ad es. ad uno o più diagrammi di flusso, se il processo è costituito da più fasi di
lavorazione,
Dopo avere scritto il programma si può analizzare le possibilità di ottimizzarlo e minimizzarlo per renderlo il più
efficiente possibile.
TEST E SIMULAZIONE
Dopo che il programma è stato sviluppato, bisogna passare alla fase di correzione e messa a punto dello stesso.
Ciò può essere fatto trasferendo il programma nella memoria del PLC ed eseguendolo simulando l'azionamento dei
sensori tramite un opportuno simulatore.
La simulazione permette di analizzare il comportamento del PLC di fronte alle varie situazioni che si possono
presentare nella realtà e verificare quindi se il programma è rispondente con quanto si vuole fare.
Dopo di chè si può passare alla fase successiva che è quella della documentazione dei programmi comprendente
1. Descrizione di massima dell'impianto
E' necessario quantomeno redigere uno schema completo dei collegamenti completandolo con una descrizione del
funzionamento dell'impianto
.
2. Lista di occupazione I/O
Da questa lista deve essere possibile ricavare tutte le informazioni che riguardano i sensori e gli attuatori collegati al PLC
ed anche informazioni riguardo le unità di funzione (memorie, contatori, registri, ecc.) utilizzati all'interno del programma.
Per compilare questa lista e documentarla, è sufficiente l'uso di una tabella organizzata su più colonne come quella
dell'esempio in fig. 18
3.Listato del programma :
Il listato del programma deve essere completo di commenti esplicativi che ne facilitano la comprensione, altrimenti
risulterebbe del tutto insufficiente qualunque sia il linguaggio di programmazione utilizzato.
Le unità di programmazione più diffuse permettono ormai con facilità sia la programmazione che la stampa dei programmi
nei diversi linguaggi disponibili per quel tipo di PLC.
4. Cross reference :
Per cross reference s'intende una lista di riferimento che consente di indicare, per ogni operando (ingresso, uscita,
memoria) tutti i punti del programma in cui viene utilizzato, consentendo quindi una ricerca a colpo d'occhio del punto di
programma in cui bisogna eventualmente intervenire.
INSTALLAZIONE - MANUTENZIONE - RICERCA GUASTI
Per l'installazione di un PLC bisogna distinguere tra l'installazione dell'HARDWARE e l'installazione del SOFTWARE.
INSTALLAZIONE DELL'HARDWARE :
Si ricorda che per l'installazione di un PLC, bisogna attenersi alle norme CEI 44-5 (1985) fasc. 729: "Equipaggiamenti
elettrici di macchine industriali. Parte 1: norme generali".
E' necessario considerare diversi aspetti, come la corretta installazione, la protezione contro i disturbi di natura elettrica,
ed infine le caratteristiche ambientali, allo scopo di garantire un corretto funzionamento, la sicurezza del personale e
dell'impianto stesso.
E' sempre importante leggere il manuale d'installazione fornito con il PLC, in quanto vi possono essere delle prescrizioni
particolari che tengono conto delle caratteristiche tipiche del controllore che si sta installando.
I controllori programmabili devono essere protetti dalle sovratensioni che possono generarsi sia negli ingressi che nelle
uscite.
Le unità d'ingresso sono munite al loro interno di accoppiatori ottici (optoisolatori) , i quali evitano che una sovratensione
possa danneggiare i circuiti interni del PLC.
Per quanto riguarda le uscite, se queste non sono già protette dai cortocircuiti, bisogna prevedere l'installazione di fusibili
extrarapidi sulle stesse.
Inoltre è da considerare sempre qual'è la potenza elettrica massima che una unità di uscita è in grado di comandare,
sommando le potenze dei singoli carichi (relè, contattori, ecc.) ed individuando nel ciclo della macchina qual'è il numero
massimo di uscite che si trovano ad essere attivate contemporaneamente.
Se il valore di potenza così ottenuto supera quello massimo ammissibile dal PLC occorrerà prevedere l'utilizzo di contattori
o relè di potenza per amplificare la potenza massima erogabile dal PLC. Bisogna sempre predisporre un dispositivo
d'emergenza per togliere tensione ai carichi d'uscita in caso di necessità ed un dispositivo per togliere tensione alle
macchine non in funzione, per interventi sulle stesse, tramite dei sezionatori a relè.
MANUTENZIONE E RICERCA GUASTI
Oltre ad una corretta installazione, è necessario che venga fatta periodicamente una adeguata manutenzione.
Tutti i PLC , pur con certe differenze, hanno delle funzioni di test ed autodiagnosi dei guasti o mal funzionamenti (test
sul funzionamento del microprocessore, sulla memoria, sul livello della batteria, ecc.) che permettono una ricerca dei
guasti guidata e quindi di individuare l'anomalia più velocemente.
La funzionalità degli I/O si può controllare tramite i led indicatori per ogni punto di I/O.
Nelle apparecchiature più sofisticate è possibile visualizzare sulle unità di programmazione un insieme di informazioni
sulla natura dello specifico guasto.
La manutenzione ordinaria, che di norma dovrebbe essere fatta con frequenza almeno semestrale o maggiore se
le condizioni ambientali lo impongono, serve a prevenire una serie di guasti soprattutto per quanto riguarda la parte
relativa alle circuiterie di collegamento dei sensori e degli attuatori, ponendo cura ad es. ai seguenti punti :
- controllo delle viti di fissaggio ;
-verifica del corretto inserimento dei cavi di collegamento nei rispettivi morsetti e che le viti degli stessi siano
correttamente serrate ;
-controllare la carica della batteria che a seconda del tipo che viene usato ha una durata che varia da due anni a
cinque anni (batterie al litio).
E' utile riportare su di una apposita targhetta la data in cui la stessa dovrà essere sostituita.
E' consigliabile tenere a magazzino delle unità di I/O di ricambio, che sono le parti del PLC più soggette a guasti
semprechè il PLC sia costruito in modo da permetterne la rapida sostituzione.
Per le eventuali misure di controllo che si dovessero rendere necessarie, è opportuno l'uso di un multimetro, digitale od
analogico che sia, dotato di una elevata impedenza d'ingresso.
A volte le cause di guasto o di anomalie di funzionamento, possono essere la temperatura o l'umidità, per cui è
opportuno disporre di un igrometro ed un termometro
-
MISURE PER LA PROTEZIONE DAI DISTURBI ELETTRICI
Per garantire la protezione dai disturbi elettrici, che non agiscono sull'hardware ma sul software e possono determinare
mal funzionamenti del controllore, è opportuno fissare il PLC su di una piastra metallica collegata a terra.
Per quanto riguarda il cablaggio dei conduttori, deve essere realizzato separando i conduttori di alimentazione
del controllore e del circuito di potenza dai conduttori dei segnali di I/O, prevedendo la loro sistemazione in canaline
separate oppure, se ciò non è possibile, schermando singolarmente i cavi in corrente alternata.
La stessa cosa va fatta per i conduttori di collegamento dei segnali analogici rispetto ai segnali digitali: se sono
alloggiati nella stessa canalina, si dovranno schermare i cavi di collegamento dei segnali analogici.
Bisogna procurarsi un unico punto di riferimento di massa per il collegamento al morsetto di massa sul PLC.
Occorre anche separare il cablaggio per corrente alternata da quello per corrente continua ed evitare di collocare i
conduttori vicino a disturbi elettrici particolarmente forti.
Vanno rispettate la sezione e la lunghezza massima dei conduttori che è indicata nei manuali del controllore.
Se nell'armadio in cui è alloggiato il PLC vi sono dei contattori o dei relè con bobine comandate da contatti
elettromeccanici, si può rendere necessaria l'installazione di gruppi RC spegniarco in parallelo alle bobine.
E' da evitare l'installazione di lampade fluorescenti all'interno dell'armadio.
L'installazione del software richiede procedure diverse a seconda dell'unità di programmazione che è stata usata per la
programmazione e che si usa per l'immissione del programma sul PLC.
Si tratta di operazioni semplici da effettuare, sia che si eseguano da unità di programmazione, sia da PC; in entrambi
i casi si dispone di un menù di comandi di facile comprensione ed utilizzo.
LA SCELTA ED IL DIMENSIONAMENTO DEL CONTROLLORE PROGRAMMABILE
Bisogna considerare diversi fattori per arrivare a definire qual'è, tra i PLC presenti in commercio, quello che soddisfa
maggiormente le proprie esigenze.
E' opportuno considerare i seguenti punti :
numero e tipo di segnali che si devono elaborare (cioè numero di I/O)
tipo e volume dell'elaborazione che deve svolgere il PLC (Kbyte memoria RAM utente e dati)
tempo di ciclo del PLC
tipo di sensori ed attuatori
tipo di morsettiere e cablaggi
tipo di memorie installabili
caratteristiche ambientali
possibilità di dialogo con altri PLC o con PC
assistenza tecnica, vita operativa
linguaggi di programmazione
costo delle apparecchiature, costo delle interruzioni del funzionamento dell'impianto.
Vi sono alcuni criteri di massima che è possibile seguire per individuare il prodotto che meglio si adatta alle proprie
esigenze, tra questi possiamo distinguere criteri funzionali,(quantità delle funzioni che il PLC può svolgere) tecnologici
(le caratteristiche dei sensori, elettronici od elettromeccanici) , operativi (possibilità di ampliamento)ed infine criteri
economici
CONSIDERAZIONI SULLA SICUREZZA NEL CAMPO DEI PLC
Una prima distinzione da fare è quella tra guasti attivi e guasti passivi.
Un guasto è passivo se non si manifesta subito, attivo invece quando si manifesta subito. Entrambi possono essere pericolosi
o non pericolosi.
Un guasto attivo e pericoloso è ad esempio il cortocircuito tra i conduttori di un pulsante di marcia (o in genere di un
sensore che ha il compito di abilitare l'attivazione di un'uscita) che provoca l'azionamento non voluto dell'uscita.
Un guasto passivo non pericoloso è l’interruzione di un conduttore di collegamento di un pulsante di marcia che impedirà di
.
avviare il motore ma nella stragrande maggioranza dei
casi non crea situazioni di pericolo.
Sia il cortocircuito tra due conduttori di collegamento di un sensore, sia l’interruzione di un conduttore possono provocare dei
guasti attivi e/o passivi entrambi pericolosi o non pericolosi a seconda che si verifichino sui conduttori di collegamento di un
contatto NA o NC. Altro fattore importante ai fini della sicurezza è l'isolamento dei conduttori.
Si pensi ad un cortocircuito sullo stesso conduttore, che pur essendo di solito scarsamente considerato, è un guasto che può
provocare situazioni di pericolo : nel caso in cui un difetto d'isolamento su di un conduttore provochi il cortocircuito di un
contatto NA, se in conseguenza di ciò si ha l'attivazione di una lampada o di un segnale acustico per quanto sia sgradito non
è sicuramente pericoloso, ma se viene cortocircuitato un pulsante di marcia, ciò determinerà l'azionamento indesiderato del
motore corrispondente con ovvio pregiudizio della sicurezza.
Nel primo caso si avrebbe un guasto attivo ma non pericoloso nel secondo un guasto attivo pericoloso. Si ritiene che
l’interruzione di un conduttore (ad es. per un morsetto allentato) si possa verificare con maggiori probabilità rispetto al
cortocircuito tra due conduttori, ragion per cui nella scelta dei contatti da utilizzare (NA o NC) si dovranno adottare gli
accorgimenti che danno maggior garanzie di sicurezza.
Un'importante regola che è assolutamente da rispettare ai fini della sicurezza contro le interruzioni dei
conduttori di collegamento delle apparecchiature di comando è quella di usare sempre dei contatti NA per la
apparecchiature che hanno il compito di attivare delle uscite (abilitare dei movimenti) e dei contatti NC per le
apparecchiature che hanno il compito di disattivare le uscite (arresto di movimenti).
Per quanto il PLC possa essere considerato un'apparecchiatura che elabora delle informazioni, agisce comunque in ambiente
industriale ed i guasti che possono creare situazioni di pericolo è indifferente che avvengano all'interno od all'esterno dello
stesso.
Un errore di trasmissione dati all'interno del PLC potrebbe provocare l'attivazione di un'uscita invece di un'altra, bisogna
adottare particolari accorgimenti perchè il sistema di controllo soddisfi le prescrizioni normative in termini di sicurezza.
− I comandi che riguardano i circuiti di sicurezza devono agire su componenti elettromeccanici indipendenti dal PLC.
In generale, per effettuare un'installazione che garantisca un elevato grado di sicurezza, occorre
considerare i seguenti punti.
• Le apparecchiature collegate ad un PLC dovrebbero comprendere dispositivi di comando interbloccanti ed interruttori
di sicurezza che impediscano il funzionamento durante un guasto dell'impianto.
• L'alimentazione dell'equipaggiamento elettronico deve essere sempre derivata da un trasformatore d'isolamento,
collegato a valle dell'interruttore generale, ed utilizzato anche per gli altri circuiti ausiliari della macchina o dedicato
esclusivamente alla componente elettronica.
• Occorre provvedere all'interruzione delle uscite ritenute critiche, ai fini della sicurezza, quando la macchina non è in
funzione o quando si deve intervenire all'interno della macchina stessa (messa a punto, manutenzione, ecc.). Il circuito
di tali uscite deve essere interrotto da un contatto pulito di un interruttore o di un relè e non da un dispositivo a
semiconduttore (transistor, Triac).
• Ogni modulo o circuito di uscita va collegato ad un solo carico ed in conformità alle specifiche del costruttore (per ciò
che attiene, per esempio, alla potenza massima assorbita e alla sopportabilità in termini di potenza reattiva).
• Bisogna escludere il controllo dal PLC con una predisposizione esterna e realizzare un comando ad impulsi esterno per
la messa a punto della macchina o per il caricamento del programma; in caso di guasto del PLC, devono rimanere
efficaci i dispositivi di emergenza e gli interruttori di sicurezza. Questi dispositivi di sicurezza devono agire direttamente
sugli organi attuatori nella parte di potenza del comando.
• In presenza di comandi a distanza, la cui attivazione potrebbe produrre sulla macchina situazioni di pericolo, è
necessario prevedere un dispositivo di esclusione a chiave, che consenta ai manutentori ed agli operatori di porsi,
all'occorrenza, in situazioni di sicurezza contro avvii o consensi intempestivi provenienti da zone remote.
Linee di produzione
Uno degli impieghi più importanti per i controllori programmabili è nelle linee di assemblaggio (le cosi dette “catene di
produzione”).
Nelle linee ci sono più PLC, ciascuno governa un macchinario, un robot o parte della linea. Questi comunicano fra loro
tramite una rete. Di solito c'è un PLC “Master” e uno o più “Slave”.
Il “Master” invia pacchetti di dati agli “Slave” che eseguono la lavorazione di conseguenza; La comunicazione è del tipo
a bus (detto “Bus di campo:unica connessione tra i diversi PLC).
Il “Master” individua lo “Slave” con cui deve comunicare tramite un indirizzo (detto “Stazione”). Il “Bus di campo” è
fisicamente realizzato con due o quattro fili, oppure con una vera e propria rete ethernet.
In alcuni reti è necessario disporre di più PLC “Master”, perchè non c'è una vera è propria linea di
produzione, ma piuttosto diverse stazioni di lavorazioni indipendenti.
In questo caso una tecnica molto usata è di fare comunicare i PLC tra loro in modo sequenziale. Cioè una sorta di catena,
in cui ciascun PLC trasmette in rete un pacchetto di dati seguito da un “Token” (come il testimone nella staffetta).
Questo “Token” contiene il numero della stazione destinataria del pacchetto. Ciascun PLC riceve e verifica se il “Token”
punta la propria stazione, in caso contrario lo ritrasmette al PLC successivo. Cosi via, di solito a catena chiusa, cioè con
l'ultimo PLC collegato al primo della catena.
SEGNALI A TEMPO CONTINUO
SEGNALI CANONICI
TRASFORMATA DI LAPLACE
ANTITRASFORMATA DI LAPLACE
TEOREMA DEL VALORE INIZIALE E FINALE
ESERCIZI
LAPLACE: POLI COMPLESSI CONIUGATI
LAPLACE: SOLUZIONE DI EQUAZIONI DIFFERENZIALI
SEGNALI CANONICI
Tipicamente nei controlli automatici per testare un sistema dinamico si utilizzano dei segnali detti
canonici o di saggio, utilizzati come funzioni elementari in combinazione delle quali è scomposto il
generico ingresso. Infatti, assumendo che il sistema sia lineare, il principio di sovrapposizione
degli effetti permette di studiare separatamente l’effetto di tali segnali.
Inoltre l’ipotesi di linearità assicura che l’uscita del sistema si componga unicamente dei modi
elementari «andamenti temporali “elementari” associati ai poli della fdt, rappresentano per cui
dinamiche proprie del sistema indipendenti dal particolare ingresso. e dei modi dell’ingresso.
come si vedrà nell’analisi di stabilità dei sistemi lineari.
Pertanto le caratteristiche dinamiche dell’uscita di un sistema sono analoghe in corrispondenza di
diversi ingressi, a meno dei modi introdotti da questi ultimi
segnale a gradino
• Ingresso a impulso
NB:
non
sempre
è
possibile
ricavare
sperimentalmente
la
risposta
del
sistema
all’impulso, in quanto l’impulso deve fornire
l’energia sufficiente al sistema per provocarne la
risposta. La trasformata di laplace del segnale
impulsivo è pari a 1
Nel dominio del tempo viene rappresentato
da u (t). La trasformazione di Laplace del
gradino unitario è 1 / s
SEGNALI CANONICI
Segnale a rampa :
Nel dominio del tempo viene rappresentato
da r (t). La trasformazione di Laplace del
segnale a rampa è 1 / s 2
segnale parabolico :
Nel dominio del tempo viene rappresentato da t 2 / 2.
La trasformazione di
Laplace
del segnale
3
parabolico è 1 / s
segnale sinusoidale:
Nel dominio del tempo viene rappresentato da sin
(ωt) . la Laplacetrasformazione della sinusoide è
ω / (s 2 + ω 2)
segnale cosinusoidale:
Nel dominio del tempo viene rappresentato da
cos (ωt). Latrasformazione di Laplace del coseno
è ω / (s 2 + ω 2 )
SEGNALI CANONICI
La risposta del sistema è la somma di due contributi.
Il primo è indipendente dalle condizioni iniziali e dipende solo dall’ingresso (risposta forzata): si
ottiene quando al sistema è applicato un ingresso e le condizioni iniziali sono nulle.
Il secondo è indipendente dal segnale forzante e dipende solo dalle condizioni iniziali (risposta
libera): è l’evoluzione dinamica del sistema privo di ingresso con condizioni iniziali non nulle.
Le radici del polinomio a numeratore della funzione di trasferimento G(s) ( RAPPORTO FRA USCITA
E INGRESSO) sono dette zeri del sistema (in numero pari a m), mentre le radici del polinomio a
denominatore della funzione di trasferimento G(s) sono dette poli del sistema ( in numero pari a
n).
Gli zeri e i poli di un sistema possono essere o reali o complessi e coniugati a coppie.
TRASFORMATA DI LAPLACE
Per descrivere l’evoluzione di un sistema in regime transitorio, ossia durante il passaggio delle
uscite da un regime stazionario ad un altro, è necessario ricorrere ad un modello più generale
rispetto al modello statico, detto modello matematico dinamico.
Tale modello è costituito da una o più equazioni differenziali che legano non solo le variabili
incognite di uscita (effetti) con quelle note di ingresso (cause), ma anche le loro derivate
rispetto al tempo.
Oltre ai metodi classici derivati dall'analisi matematica, per risolvere una equazione
differenziale lineare a coefficienti costanti, quale quella descritta precedentemente, si può
utilizzare l’operatore di trasformazione secondo Laplace.
Si tratta di un procedimento che presenta numerosi vantaggi rispetto alle tecniche classiche
dell’analisi. In particolare, esso trasforma equazioni integro-differenziali in equazioni
algebriche, di più semplice risoluzione.
La trasformata di Laplace è una trasformazione funzionale. Tale trasformazione stabilisce una
corrispondenza biunivoca tra funzioni oggetto (funzioni del tempo) e funzioni immagine della
variabile complessa s.
Lo studio dei transitori dei sistemi viene effettuato attraverso l’applicazione della trasformata di
Laplace che consente di trasformare equazioni
differenziali complesse di cui sono note le
costanti in semplici
polinomi. le trasformate di Laplace possono essere utilizzate solo per
risolvere le equazioni differenziali complesse con costanti note .
TRASFORMATA DI LAPLACE
L'operazione di trasformazione a partire dalla sua definizione matematica può risultare abbastanza
complicata, ma nella pratica viene in genere eseguita facilmente consultando delle tabelle, che
mettono in relazione le principali funzioni nel dominio del tempo con le corrispondenti funzioni nel
dominio della frequenza, e/o applicando delle semplici regole di trasformazione.
La frequenza complessa S è definita come S = σ + j ω.
La trasformata di Laplace è un operatore
che associa ad una funzione del tempo f(t)
definita per t≥0 una funzione F(s) a valori
complessi definita per valori della variabile
complessa s.
L’utilizzo delle trasformate di Laplace consente di
semplificare notevolmente i calcoli nella risoluzione
di equazioni differenziali: operazioni di derivazione
ed integrazione nel dominio del tempo corrispondono
ad operazioni di tipo algebrico nel dominio delle
trasformate.
ANTITRASFORMATA DI LAPLACE
Data una funzione di Laplace F(s), si definiscono:
- zeri di F(s) i valori di s che annullano il numeratore
- poli di F(s) i valori di s che annullano il denominatore.
Antitrasformazioni immediate:
F(s) = 6/ s
f (t) = 6
F(s) = 5 s^3
f (t) = 5 ⋅t2^2
F(s) = 6/S+2
f (t) = 6⋅e−2⋅t
Una funzione razionale (rapporto tra polinomi) può essere scomposta in somma di fratti semplici:
da cui è immediata la antitrasformazione:
Da cui è immediata la antitrasformazione:
f (t) = R1 ⋅e^(s1⋅t) +R2 ⋅e^(s2⋅t)
ANTITRASFORMATA DI LAPLACE
La risposta impulsiva di
un sistema può essere
ricavata
applicando
in
ingresso un segnale che
approssimi l’impulso di
Dirac e misurando l’uscita
corrispondente.
L’impulso
di
Dirac
è
un’astrazione
matematica
che
può
solo
essere
approssimata.
In molti casi non è
possibile né conveniente
applicare al sistema una
sollecitazione
impulsiva
per non danneggiare il
sistema
a
causa
dell’elevata
ampiezza
dell’impulso.
TRASFORMAZIONI
Le trasformazioni in matematica sono spesso utilizzate per aggirare le rilevanti difficoltà che si
presentano nello svolgere direttamente i calcoli richiesti. Per esempio:
nella esecuzione di calcoli come prodotti e divisioni
nella risoluzione di equazioni come quelle biquadratiche e differenziali.
Un prodotto è convertito in somma mediante la trasformazione Logaritmo. Il percorso della
trasformazione è più lungo, ma meno difficoltoso.
Una equazione biquadratica è risolvibile con una semplice sostituzione:
Una equazione differenziale lineare si può risolvere più facilmente con delle opportune trasformazioni.
Se le variabili di ingresso sono sinusoidali e interessa la soluzione a regime si può ricorrere alla
trasformazione di Steinmetz: (proposta per risolvere i circuiti elettrici in corrente alternata)
Osservazioni: questa trasformazione
non fornisce informazioni sul funzionamento durante il transitorio in quanto
presuppone che l’ingresso sinusoidale sia applicato da talmente tanto tempo da essersi
esauriti tutti i transitori
ha permesso, se non la comparsa, certamente una migliore gestione del concetto di
impedenza (che non esiste nel dominio del tempo).
Per le variabili di ingresso che hanno andamenti generici e sono nulle per t <= 0 è stato
elaborato un procedimento noto col nome di Trasformata di Laplace
Osservazione:
La soluzione descrive il funzionamento del
circuito a partire da t = 0, comprendendo quindi
oltre al regime, anche il transitorio (in quanto si
segue
l’ingresso
sin
dalla
sua
prima
applicazione al sistema: cioè per t >= 0).
TEOREMA DEL VALORE INIZIALE/FINALE
teorema del Valore iniziale
Ci permette di trovare il valore iniziale al tempo t = (0 + ) per una data funzione (Laplace)
senza ricorrere alla f (t), che richiede un processo molto noioso .
poi teorema Valore iniziale è dato da
Applicazioni
Trovare il valore iniziale per la funzione
dal teorema del valore iniziale
il valore iniziale è 5.
TEOREMA DEL VALORE INIZIALE/FINALE
Esempio 2: trovare il valore iniziale della funzione trasformata
dal teorema valore iniziale
Esempio 3:
Trovare il valore iniziale di
Valore iniziale teorema non è applicabile in quanto il polinomio del numeratore deve essere
inferiore del polinomio denominatore.
TEOREMA DEL VALORE INIZIALE/FINALE
esempio 4
Risolvere l'equazione utilizzando trasformata di Laplace
questo può essere risolto utilizzando frazioni parziali, che è più facile che risolvere nella
sua forma precedente. In primo luogo, il denominatore deve essere fattorizzato.
i coefficienti A e B devono essere trovati
Sostituendo nell'equazione:
Quindi, utilizzando la tabella l'equazione può essere riconvertito in forma normale.
TEOREMA DEL VALORE INIZIALE/FINALE
teorema del valore Finale
E 'molto interessante scoprire che possiamo trovare il primo valore o l'ultimo valore di f (t) ,
senza dover studiare la funzione intera f (t).
Ci permette di trovare il valore finale al tempo t = (0 - ) per una data funzione
esempi
trovare i valori finali di F(s) senza calcolare esplicitamente f (t)
Risposta
TRASFORMATA DI LAPLACE: esercizi
TRASFORMATA DI LAPLACE CON POLI COMPLESSI CONIUGATI
Antitrasformazione in presenza di poli complessi coniugati:
Se i poli sono complessi coniugati, tali risultano anche i residui:
TRASFORMATA DI LAPLACE:SOLUZIONE EQUAZIONI DIFFERENZIALI
TRASFORMATA DI LAPLACE:SOLUZIONE EQUAZIONI DIFFERENZIALI
TRASFORMATA DI LAPLACE:SOLUZIONE EQUAZIONI DIFFERENZIALI
ALGEBRA DEGLI SCHEMI A BLOCCHI
ALGEBRA DEGLI SCHEMI A BLOCCHI
ESERCIZI
ALGEBRA DEGLI SCHEMI A BLOCCHI
Nei controlli automatici spesso il legame fra due variabili viene indicato con un blocco, ad
esempio con il simbolo
si vuole intendere che la variabile y(t) è dipendente dalla variabile x(t). Ù
Se il legame tra tali grandezze è lineare, tempo invariante e statico, ossia espresso da un
guadagno G, il blocco è puramente algebrico, e istante per istante vale la relazione y=Gx e il
blocco viene indicato come in figura.
Esaminiamo ora una serie di regole che consentono di trasformare uno schema a blocchi in un
nuovo diagramma equivalente al primo ma più semplice e compatto.
per risolvere schemi a blocchi comunque complicati si devono rispettare le seguenti condizioni:
- sistemi lineari
- semplificazione a partire dal blocco interno
- blocchi concentrici , non si devono intersecare
ALGEBRA DEGLI SCHEMI A BLOCCHI
punto di diramazione (collegamento parallelo)
Blocchi in parallelo
Le relazioni espresse nello schema sono:
y1=G1x
y2=G2x
y=y1+y2
Considerando simultaneamente le equazioni si ha:
y=y1+y2=(G1+G2)x=Gx, con G=G1+G2
Perciò lo schema di partenza si può trasformare in uno più
semplice
ALGEBRA DEGLI SCHEMI A BLOCCHI
2) Blocchi in cascata o serie
Consideriamo lo schema
Si ha:
y=G2z=G1G2x
quindi il diagramma equivalente è:
Si conclude che la serie o cascata di due o più blocchi è equivalente ad un unico blocco il
cui guadagno è pari al prodotto dei guadagni dei blocchi componenti.
3) Scambio di giunzioni sommanti
Lo schema:
indica l’operazione:
z=(x+y)+w
ALGEBRA DEGLI SCHEMI A BLOCCHI
ALGEBRA DEGLI SCHEMI A BLOCCHI
Reazione negativa/positiva
esprime le relazioni:
y=Ge,
e=x-z=x-Hy
quindi
y=Gx-GHy,
ossia
Y = x* G/(G+H)
ESERCIZI
ESERCIZI
ESERCIZI
COMPORTAMENTO IN REGIME TRANSITORIO
RISPOSTA NEL DOMINIO DEL TEMPO
RISPOSTA LIBERA E FORZATA
TRANSITORIO E REGIME
SISTEMI DEL 1 ORDINE
SISTEMI DEL 2 ORDINE
ESEMPI APPLICATIVI
Poli dominanti
Risposta nel dominio del tempo
In un sistema possono essere presenti più accumulatori di energia, quindi più variabili di stato, ossia più poli nelle
funzioni di trasferimento.
Ad ogni polo corrisponde una costante di tempo.
Le costanti di tempo più grandi determinano la durata complessiva del transitorio. Quando sono molto più grandi,
il transitorio è di fatto determinato da esse.
Alle costanti di tempo più grandi corrispondono i poli più piccoli (in valore assoluto). Questi poli sono chiamati
dominanti.
Se nel sistema sono presenti poli dominanti, gli altri poli si possono trascurare.
Consideriamo un generico sistema
Se il segnale d’ingresso e(t) subisce brusche variazioni, il segnale d’uscita (risposta del sistema) è
costituito dalla somma di una risposta transitoria ed una risposta permanente (o risposta a regime).
Per determinare il segnale d’uscita u(t), si procede nel seguente modo:
1.Si determina la G(s)G(s) = U(s)/E(s)
2.Si determina la E(s), facendo uso delle tabelle delle Td.L
3.Si calcola l’uscita U(s) =G(s)*E(s)
4.Si antitrasforma la U(s) per risalire alla u(t)
16
RISPOSTA FORZATA E RISPOSTA LIBERA
Classificazioni dei sistemi per ordine
La classificazione per ordine di un sistemi viene fatto in relazione al numero di poli della sua
f.d.t.
Un sistema quindi dicesi di:
- ordine zero quando la sua f.d.t. non presenta poli
- ordine uno quando la sua f.d.t. presenta un polo (denominatore della f.d.t. è un polinomio di primo
grado)
- ordine due quando la sua f.d.t. presenta 2 poli (denominatore della f.d.t. è un polinomio di secondo
grado)
La risposta di un si può scomporre in: y(t) = yFORZATA (t) + yLIBERA (t)
Componente FORZATA: csistemaomponente della risposta che dipende direttamente dall’azione
forzante, cioè dall’ingresso (corrisponde alla risposta del sistema quando quest’ultimo è, nell’istante
iniziale, allo stato zero)
Componente LIBERA: componente della risposta che non dipende direttamente dall’ingresso (è la
risposta che il sistema produce nonostante l’ingresso sia nullo; è diversa da zero solo se il sistema ha
accumulato energia in precedenza)
Esempio: circuito RC, ingresso e(t) = k
Esempio: circuito RL, ingresso x(t) = e(t) = k
Transitorio e Regime
La risposta di un sistema può essere scomposta in componente transitoria yT(t) e componente di
regime yR(t) :
y(t) = y (t) + y r(t)
La componente transitoria è formata da tutti quei termini che si annullano per il tempo che tende a
infinito.
La componente di regime è formata da tutti quei termini che invece non si annullano, cioè:
y R (t) = lim y(t)
tinf
NB: nei sistemi lineari la componente di regime assume la stessa forma
d’onda dell’ingresso.
• Nel dominio del tempo le variabili sono esaminate secondo la loro evoluzione temporale
• Normalmente si esamina la risposta del sistema a un segnale di prova canonico, cioè si sollecita il
sistema con un:
.
ingresso a gradino
ingresso a impulso
NB: non sempre è possibile ricavare sperimentalmente la risposta del sistema
all’impulso, in
quanto l’impulso deve fornire l’energia sufficiente al sistema per provocarne la risposta.
SISTEMI DEL 1° ORDINE
Un sistema del 1° ordine è un sistema con un solo accumulatore di energia. Ossia un
sistema il cui comportamento è descrivibile con una sola variabile di stato.
NB: si assume come uscita del sistema la variabile di stato y(t)
y(t)
y(t)
Risposta all’impulso:
Risposta al gradino:
t
t
Le prestazioni di un sistema (non solo del 1° ordine) nel dominio del tempo sono spesso
fornite
con l’indicazione di alcuni tempi caratteristici definiti nella risposta al gradino.
tD : tempo di ritardo (delay time)
Fornisce l’indicazione della prontezza di risposta del sistema
tR : tempo di salita (rise time)
Fornisce l’indicazione della accelerazione di y(t)
tS : tempo di assestamento (setting time. Fornisce l’indicazione della
durata del transitorio. Corrisponde al
tempo impiegato dalla
risposta y(t) per portarsi entro la fascia +/- Δ%
SISTEMI DEL 2° ORDINE
Un sistema del 2° è un sistema il cui comportamento è descritto da due variabili di stato, sono
cioè sistemi con due accumulatori di energia:
La risposta nel tempo dipende dai poli della funzione di trasferimento. Per meglio descriverle si
introducono due parametri:
• δ = coefficiente di smorzamento
• ωn = pulsazione naturale [rad/s]
E si
eseguono le seguenti sostituzioni:
a1 = 2·δ·ωn,
a0 = ω2n
SISTEMI DEL 2° ORDINE
La risposta al gradino presenta un transitorio che dipende solo dai poli della funzione di trasferimento.
I tre poli di Y(s) risultano
NB: s1 e s2 sono i poli della funzione di trasferimento; possono
essere reali o complessi in funzione di .
Sistema sovrasmorzato
Ipotesi:
I poli
y(t)
1
Im
s t
y(t) K 0 K 1 e s1t K 2 e 2
della fdt sono reali distinti
>1
•
•
s2
s1
•
Re
s0
t
Sistema a smorzamento critico
y(t)
Ipotesi:
Im
1
I poli
=1
sono reali coincidenti
y(t) K 0 K t e
st
•
s1 = s2
•
s0
Re
t
SISTEMI DEL 2° ORDINE
Sistema sottosmorzato
Ipotesi:
1
s
I poli sono complessi coniugati
0
y(t) K 2 K e cos(t )
t
1,2
j
n
n
12
NB: ωn rappresenta la pulsazione alla quale
oscillerebbe la risposta del sistema nel caso
assenza di smorzamento ( = 0).
di
SISTEMI DEL 2° ORDINE
Relazioni tra i poli della funzione di trasferimento e i parametri e ωn
Dall’espressione dei poli della funzione di trasferimento:
s 1,2 n jn
1 2
risultano le seguenti corrispondenze:
n
n 1 2
s 2 2 n
Da cui: (prescindendo dal segno di )
cos
n
n
1 2
,
sotituendo
dopo alcuni calcoli risulta
:
,
n
n
2 2
SISTEMI DEL 2° ORDINE
Relazione tra massima sovraelongazione e
Nei sistemi del 2° ordine senza zeri, con poli complessi coniugati (delta < 1), la massima
sovraelongazione SMAX dipende solo dal coefficiente di smorzamento :
SMAX%
y(t)
yMAX
SMAX
yR
t
SISTEMI DEL 2° ORDINE
Esercizio: Circuito RLC serie, calcolo e ωn in funzione dei parametri del circuito
La tensione e(t) rappresenta l’ingresso. Come uscita è assunta la tensione sul condensatore.
Si deve manipolare la funzione di trasferimento
in modo da porre uguale a 1 il coefficiente del termine con s2
:
Osservando la funzione di traferimento, risulta:
Da cui:
1
2
R
C
L
n
1
LC
NB: un aumento di R comporta un aumento di ,,
mentre non influisce su ωn.
Sistema del 2° ordine, la cui funzione di trasferimento possiede uno zero
SISTEMI DEL 2° ORDINE
La presenza di uno zero:
• altera la pendenza con cui la risposta si avvia: non più con tangente orizzontale.
• altera SMAX, che non dipende più solo da
• non altera la pulsazione di oscillazione ω
X(s)
k bs 1
s 2 a 1s a
Y(s)
0
Nel sistema è presente uno zero:
s
1
b
NB: con zero positivo il sistema presenta una risposta che
si avvia in direzione opposta.
SISTEMI DEL 2° ORDINE
Esaminando la risposta nel tempo, è possibile stimare i parametri della funzione di trasferimento.
Esempio: sistema del 2° senza zeri (ricavare k, , ωn)
X0
X(s)
t
k
2
s 2 s 2
n
Y(s)
n
Per il calcolo del valore di regime yR è conveniente ricorrere
al teorema del valore finale:
Calcolo :
Dal grafico della risposta si legge yMAX e yR, con essi si calcola SMAX e
per via grafica si ricava .
Calcolo ωn:
Dal grafico della risposta si legge il periodo T, con esso si calcola la
pulsazione di oscillazione ω = 2 / T, e quindi: n
2
1
Calcolo k:Applicando il teorema del valore finale si ottiene:
SISTEMI DEL 2° ORDINE: ESEMPI APLICATIVI
5RISPOSTA
AL GRADINO DI AMPIEZZA E DI UN SISTEMA DEL 2°
ORDINE CON >1, (POLI REALI ISTINTI E NEGATIVI)
La risposta al gradino è aperiodica
RISPOSTAAL GRADINO DI AMPIEZZA E DI UN SISTEMA DEL 2° ORDINE CON =1, (POLI REALI CCOINCIDENTI E NEGATIVI)
La risposta al gradino è aperiodica
SISTEMI DEL 2° ORDINE: ESEMPI APPLICATIVI
RISPOSTA AL GRADINO DI AMPIEZZA E DI UN SISTEMA DEL 2° ORDINE CON <1, (POLI COMPLESSI E CONIUGATI CON
PARTE REALE NEGATIVA )
La risposta al gradino è oscillatoria smorzata
Studio della riposta del sistema retroazionato
Calcolo della f.d.t. del sistema retroazionato W(s)
Il circuito retroazionato è equivalente al circuito in figura
con H(s)=1
SISTEMI DEL 2° ORDINE: ESEMPI APPLICATIVI
SISTEMI DEL 2° ORDINE: APPLICATIVI
La risposta si ricava antitrasformando la U(s), facendo uso delle tabelle
delle T.d.L.
SISTEMI DEL 2° ORDINE: ESEMPI APPLICATIVI
Il sistema descritto dallo schema a blocchi è sottoposto ad un
gradino di ampiezza 5
Determinare:
a) il valore a regime
b) il tempo di salita
c) il tempo a cui avviene l’overshoot
d) il valore dell’overshoot
e) il valore max del segnale d’uscita
f) il tempo di assestamento al 2%
Soluzione
Calcolo della risposta U(s)
Il circuito retroazionato è equivalente al circuito in figura con H(s)=1
Confrontiamo la nostra fdt con quella standard
SISTEMI DEL 2° ORDINE: ESEMPI APPLICATIVI
Il comportamento dei sistemi di controllo in regime permanente
CLASSIFICAZIONE DEI SISTEMI DI CONTROLLO
ERRORE STATICO
CALCOLO DELL'ERRORE A REGIME
CONSIDERAZIONI SUL SEGNALE D'INGRESSO
COMPORTAMENTO DEI SISTEMI DI CONTROLLO TIPO 0
COMPORTAMENTO DEI SISTEMI DI CONTROLLO TIPO 1
COMPORTAMENTO DEI SISTEMI DI CONTROLLO TIPO 2
TABELLA RIASSUNTIVA
ESERCIZI
DISTURBI ADDITIVI
ESERCIZI
CLASSIFICAZIONE DEI SISTEMI DI CONTROLLO AD ANELLO CHIUSO
La classificazione dei sistemi ad anello chiuso per tipo, viene fatto in relazione al numero di poli nell’origine della f.d.t. ad anello
aperto. Il tipo del sistema indica il numero dei poli che la G(s)H(s) presenta nell’origine
N. dei poli nulli della G(s)H(s)
classificazione
0
1 (s al denominatore )
2 (s2 al denominatore )
sistema di tipo zero
sistema di tipo uno
sistema di tipo due
Nel progetto di un sistema di controllo ad anello chiuso occorre tener conto, della precisione e della sensibilità ai disturbi additivi e
parametrici .
ERRORE A REGIME
La precisione rappresenta la capacità di un sistema di produrre una risposta la più simile possibile a quella desiderata, ma in un
sistema di controllo reale l’uscita non è mai esattamente quella desiderata ma è affetto da errore
La precisione di un sistema è evidenziata dall’errore statico, cioè
l’errore permanente o a regime. Esso è definito come differenza tra
il valore d’uscita desiderata u0 (t )e il valore realmente ottenuto u(t )
a transitorio esaurito, quando vengono applicati in ingresso i segnali
tipici: gradino; rampa; parabola
ERRORE STATICO
Alimentazione di potenza
X(s)
E(s)
YRET(s)
Y(s)
G(s)
H(s)
Per errore statico si intende lo scostamento, a regime, della variabile controllata Y(s) dal valore
desiderato.
Tale scostamento è in relazione con il segnale errore E(s) uscente dal nodo di confronto: essi hanno
lo stesso valore percentuale.
E’ allora possibile svolgere i calcoli sul segnale errore E(s).
E(s) X (s) X RET (s) X (s) H (s) Y (s) X (s) H (s) X (s)
G(s)
X (s)
1 G(s) H (s) 1 G(s) H (s)
CALCOLO DELL’ERRORE A REGIME
Il calcolo dell’errore a regime richiede il calcolo del limite
dove è richiesta la conoscenza della funzione e(t), cioè della antitrasformata di E(s).
E’ possibile evitare la antitrasformazione ricorrendo al teorema del valore finale:
er lim e(t) lim s E(s)
t s0
e sostituendo l’espressione di E(s):
er lim s
s0
X(s)
X(s)
lim s
1 G(s) H(s) s0 1 L(s)
Osservazioni: la precisione statica dipende quindi dal
Valore del segnale di ingresso X(s)
Guadagno d’anello G(s)•H(s)
Il comportamento dei sistemi di controllo in regime permanente
Considerazioni sul GUADAGNO D’ANELLO
L(s) = G(s)•H(s)
In assenza di ritardi finiti, le funzioni di trasferimento sono razionali, cioè si presentano come rapporto tra polinomi:
L(s) G(s) H(s)
1 N(s)
s n D(s)
I sistemi con retroazione sono classificati in tipi, in funzione del numero di poli nulli presenti nel guadagno d’anello:
n =0
n =1
n =2
………
sistema tipo 0
sistema tipo 1
sistema tipo 2
Ai fini del calcolo dell’errore statico conviene porre:
L' (s)
N(s)
D(s)
LST = valore statico del guadagno d’anello
Considerazioni sul SEGNALE DI INGRESSO
Le prestazioni a regime dipendono anche dalla forma del segnale d’ingresso. In alcuni sistemi il segnale di ingresso non ha
una forma prestabilita, per cui si caratterizza la precisione statica considerando segnali con forma standard (canonica).
Ingresso a gradino
Ingresso a rampa
X0
X(s)
s
x(t) X 0
X(s)
x(t) X0 t
X0
s2
X0
t
X0 t
t
Ingresso a parabola
x(t) X 0 t
2
2X0
X(s)
s3
X0 t 2
t
Il comportamento dei sistemi di controllo in regime permanente TIPO 0
e r lim s
SISTEMA TIPO 0
s0
n =0
X(s)
1 L(s)
Guadagno d’anello: L(s) N(s)
D(s)
Calcolo dell’ERRORE a regime:
Ingresso a gradino
Errore di posizione
X0
X0
X0
e r lim s s
s0
1 L(s) 1 lim N(s) 1 L ST
s0 D(s)
Ingresso a rampa
Errore di velocità
X0
2
X0
s
e r lim s
lim
s0
s0
1 L(s)
s s L(s)
Ingresso a parabola
Errore di accelerazione
2 X0
3
2 X0
s
e r lim s
lim 2
2
s0
s0
s
s
L(s)
1 L(s)
Il comportamento dei sistemi di controllo in regime permanente TIPO 0
Ingresso a rampa
SISTEMA TIPO 0
Errore di velocità
Errore assoluto sull’uscita del sistema si ricava dividendo quello
sul nodo di confronto er per il guadagno statico della fdt di
retroazione H0:
e
yr
r
H0
Il comportamento dei sistemi di controllo in regime permanente TIPO 1
e r lim s
SISTEMA TIPO 1
n=1
Guadagno d’anello:
Calcolo dell’ERRORE
Ingresso a gradino
Errore di posizione
Ingresso a rampa
Errore di velocità
Ingresso a parabola
Errore di accelerazione
s0
L(s)
X(s)
1 L(s)
1 N(s)
s D(s)
X0
X0
s
e r lim s
0
s 0
1 L(s) 1 lim 1N(s)
s0 s D(s)
X0
X0
X
s 2 lim
er lim s
0
s0
1 L(s) s0 s s N(s)
LST
s D(s)
2X 0
3
X0
s
e r lim s
lim
s0
s0
1N(s)
1 L(s)
s2 s2
s D(s)
Il comportamento dei sistemi di controllo in regime permanente TIP0 1
Ingresso a rampa
SISTEMA TIPO 1
Errore assoluto sull’uscita del sistema si ricava
dividendo quello sul nodo di confronto er per il
:
guadagno statico
della fdt di retroazione H0
yr
Ingresso a gradino
Errore di posizione
Errore di velocità
Errore assoluto
sull’uscita del sistema
y r
X0
LST H 0
er
H0
0
Ingresso a parabola
Errore di accelerazione
Il comportamento dei sistemi di controllo in regime permanente tipo 2
SISTEMA TIPO 2
n =2
Guadagno d’anello:
L(s)
1 N(s)
s 2 D(s)
Calcolo dell’ERRORE
Ingresso a gradino
Errore di posizione
Ingresso a rampa
Errore di velocità
Ingresso a parabola
Errore di accelerazione
X0
X0
s
e r lim s
0
s0
1 L(s) 1 lim 1 N(s)
s0 s2 D(s)
X0
s2
e r lim s
lim
s0
1 L(s) s0
X0
0
1 N(s)
s s 2
s D(s)
2X 0
2X 0
X0
s3 lim
e r lim s
s0
1 L(s) s0 s 2 s 2 1 N(s)
LST
2
s D(s)
Il comportamento dei sistemi di controllo in regime permanente: tipo 2
Ingresso a rampa
SISTEMA TIPO 2
Errore assoluto sull’uscita del sistema si ricava dividendo quello
sul nodo di confronto er per il guadagno statico della fdt di
retroazione H0:
yr
Ingresso a gradino
Errore di posizione
Errore di velocità
0
er
H0
0
Ingresso a parabola
Errore di accelerazione
Errore assoluto
sull’uscita del sistema
y r
2 X 0
LST H 0
RIEPILOGO
TABELLA RIASSUNTIVA
NB: le espressioni che appaiono in tabella si riferiscono ai valori assoluti calcolati
rispetto al segnale errore er :
RIEPILOGO
ESERCIZIO
1) Dimensionare il ramo di retroazione
2) Calcolare il guadagno A0 del convertitore di potenza in modo da avere un errore a regime al 5%
3) Verificare la stabilità del sistema ricorrendo al metodo di Routh, nell’ipotesi che il convertitore sia caratterizzato
da una risposta istantanea.
Soluzione
1) Dimensionare il ramo di retroazione
Si calcola il valore statico di H(s):
H0
XRIF 4 0.0465
YID
86
2) Calcolare il guadagno statico A0 del convertitore di potenza in modo da avere un errore a regime al 5%
L’incognita A0 è nascosta all’interno dell’espressione dell’errore a regime e precisamente nella costante LST.
Il sistema è di tipo 0, l’ingresso è un gradino, dalla specifica risulta
er
La costante LST risulta:
X0
er MAX
1 L ST
LST lim L'(s) A 0 10 H 0 A 0 0.465
s0
mentre l’errore massimo ammissibile è :
e r MAX 0.05 4 0.2
Per il calcolo di A occorre dunque
0 risolvere ladisequazione:
La cui soluzione conduce a A0 40.9
4
0.2
1 A0 0.465
Soluzione
3) Verificare la stabilità del sistema ricorrendo al metodo di Routh
Occorre valutare il comportamento dinamico del ramo di retroazione e del convertitore di potenza.
Si ipotizza che siano entrambi privi di fenomeni dinamici, cioè che presentino una risposta immediata.
• H(s) = H0
• A(s) = A0
Si deve calcolare l’equazione caratteristica dell’intero sistema, ma prima occorre assegnare un valore
al guadagno A0 del convertitore:
Ipotesi A0 = 41.
L’equazione risulta:
Tabella di Routh:
1
6
5
20.1
1.98
20.1
s3 5s 2 6 s 20.1 0
Non essendoci variazioni di segno nella prima colonna, il sistema risulta stabile.
Infatti le soluzioni risultano: S1 = - 4.639
S2 = - 0.181 + j 2.072 S3 = - 0.181 – j 2.072
Esercizio
Il comportamento dei sistemi di controllo in regime permanente
Sapendo che l’errore a transitorio esaurito vale 1,5 per un segnale d’ingresso a parabola unitaria, determinare il valore di k
Soluzione
Il
sistema è di tipo 2, poiché nella della f.d.t. ad anello aperto compaiono due poli nulli.
L’errore a regime è uguale a
e() lim s
s0
Per un segnale a parabola unitaria
R(s)
H0 1G(s)H0
r(t) = t2
2
e R(s) =
s3
questo errore è:
Il comportamento dei sistemi di controllo in regime permanente
Esercizio
Ricavare il valore di k affinché l’errore a regime sia minore del 2% per un segnale d’ingresso a gradino unitario.
Soluzione
Il sistema è di tipo 0, poiché la f.d.t. ad anello aperto non ha poli nell’origine .
G(s)H(s) =
L’errore a regime è uguale a
e() lim s
s0
0,4k
s2 0,4s 0,04
R(s)
H0 1G(s)H0
Per un segnale a gradino unitario r(t) = 1 e R(s) = 1/s questo errore è:
p= e() lim s
s0
1
s 1
1
0,4k
s2 0,4s 0,04
1
0,4k
= lim
s0 1
s2 0,4s 0,04
=
1
0,4k
1
0,04
Posto p < 2/100 si ricava k
2 1 0,4k 50 0,4k 49
1
<
0,04
0,04
1 0,4k 100
0,04
k
49 0,04
0,4
k 4,9
DISTURBI ADDITIVI: GENERALITÀ
I disturbi additivi sono segnali indesiderati che entrano nel sistema e si sommano al segnale utile
Ad esempio in un sistema di riscaldamento la variazione della temperatura esterna è un disturbo additivo che provoca una
variazione non desiderata del valore della grandezza fisica. Per valutare l’effetto prodotto da uno o più disturbi sulla risposta si
applica il principio di sovrapposizione degli effetti.
ESERCIZI - EFFETTI DEI DISTURBI ADDITIVI
Esercizio 1 – Disturbo sul blocco di andata - Risposta a regime
Determinare la risposta a regime del sistema in figura sollecitato da un segnale a gradino unitario. Il disturbo ha ampiezza 0,1.
Soluzione
Per determinare l’uscita applichiamo e il principio di sovrapposizione degli effetti: considerando l’uscita
come somma dell’uscita U1(S) dovuta al segnale R(s), e U2(s), dovuta al disturbo.
Consideriamo agente solo il segnale R(s) poniamo 1(s) =0
Riducendo i due blocchi in cascata ad un solo blocco con fdt G1G2 si ha
W1
G1 G 2
1 G1 G 2 H
U1 W R
Soluzione
Avendo in ingresso un gradino di ampiezza unitaria
R(s)=1/s :
8
1
(uscita complessa in assenza del disturbo)
U1(s)
s s3 6s2 11s 38
1 8
= 0,21 (valore a regime)
Uf1 = lim s U1(s) = s
s s3 6s2 11s 38
s0
Consideriamo ora, agente solo il disturbo 1(s) poniamo R(s)= 0
Lo schema è equivalente
Riducendo i due blocchi in cascata ad un solo blocco si ha
Soluzione
W2
G2
1 G2 G1 H
U2 W2 1
8
8
8(s 3)
(s 1)(s 2)
W2 (s 1)(s 2)
= W2
32
(s 1)(2)(s 3) 32 (s 1)(s 2)(s 3)
1
(s 1)(s 2)(s 3)
(s 1)(s 2)(s 3)
8(s 3)
=
s3 6s2 11s 38
Avendo in ingresso un disturbo di ampiezza 0,1 1(s)=0,1/s sostituendo si ha :
(uscita complessa dovuta al solo disturbo)
U2 (s) 0,1 8(s 3)
s s3 6s2 11s 38
8(s 3)
Uf 2 = lim s U2 (s) = lim s 0,1 8(s 3)
= lim
3
2
3
s s 6s 11s 38 s0 s 6s2 11s 38
s0
s0
Uf 2 =
2,4
= 0,063 (valore a regime dovuto al solo disturbo)
38
La risposta complessiva a regime è
Uf Uf1 Uf 2 = 0 , 21 +0 , 06 3 = 0,273
ESERCIZIO
Esercizio 2 – Disturbo all’ ingresso e sul blocco di andata - Risposta a regime
Determinare la risposta a regime del sistema in figura sollecitato da un segnale a gradino unitario. I disturbi hanno entrambi
ampiezza 0,1 Per determinare l’uscita applichiamo e il principio di sovrapposizione degli effetti: considerando
l’uscita come somma dell’uscita U0(S) dovuta al segnale R(s), U1(s), dovuta al disturbo 1(s) e U2(s) , dovuta al disturbo 2 (s)
Consideriamo agente solo il segnale R(s), poniamo 0(s) =0 e 1(s) =0
10
(s
1)(s
5)
W0 (s)
=
50
1
(s 1)(s 2)(s 5)
10(s 2)
=
s3 8s2 17s 60
10
10(s 1)(s 5)
(s 1)(s 5)
=
=
(s 1)(s 2)(s 5) 50 (s2 3s 2)(s 5)
(s 1)(s 2)(s 5)
SOLUZIONE
U0 (s) W1(s) R(s)
Avendo in ingresso un gradino di ampiezza unitaria
U0 (s) = 1 10(s 2)
s s3 8s2 17s 60
Uf 0
(uscita complessa in assenza dei disturbi)
= lim s U0 (s) = s 1 10(s 2)
s0
R(s)=1/s, sostituendo si ha:
s s3 8s2 17s 60
= 20
=
0,333
( valore a regime)
60
Consideriamo ora agente solo il disturbo 1(s) =0, poniamo R(s) e 1(s) =0
W1(s) W0 (s) =
10(s 2)
s3 8s2 17s 60
; U1(s) W1(s) 1(s)
Avendo in ingresso un disturbo di ampiezza 0,1 1(s)=1/s, sostituendo si ha:
(uscita complessa dovuta al disturbo 1 )
U1(s) 0,1 10(s 2)
s s3 8s2 17s 60
0,1 10(s 2)
Uf1 = lim s U0 (s) = s
= 20 = 0,033 (valore a regime )
s s3 8s2 17s 60 60
s0
SOLUZIONE
Consideriamo infine agente solo il disturbo 1(s) =0, poniamo R(s) e 0(s) =0
(uscita complessa dovuta al disturbo 1 )
U2 (s) 0,1 (s 2)(s 5)
s s3 8s2 17s 60
0,1 (s 2)(s 5)
= 1 = 0,017 ( valore aregime)
U f 2 = lim s U0(s) = s
s s3 8s 2 17s 60
60
s0
Nota
:
L’effetto del disturbo che si introduce nel blocco di andata è minore di quello all’ingresso.
Uf = Uf 0 + Uf1 + Uf 2 = 0,333+0,033+0,017 = 0,383
STABILITA DEI SISTEMI LINEARI
STABILITA DEI SISTEMI LINEARI
CRITERIO DI ROUTH-HURWITZ
RETROAZIONE NEGATIVA E VELOCITà DI RISPOSTA
STABILITA DEI SISTEMI LINEARI
• Introduzione
• Definizione: lo stato di un sistema è rappresentato dalla quantità e distribuzione dell’energia all’interno del sistema,
ed è riassumibile col valore assunto dalle variabili di stato.
• Lo studio del comportamento di un sistema si effettua esaminando l’evoluzione del suo stato.
• Quando il sistema permane in un determinato stato, cioè le sue variabili di stato permangono nei loro valori, lo stato è
definito ‘stato di equilibrio’.
• Lo stato di equilibrio può essere:
• instabile:
Il disturbo temporaneo fa
cambiare stato al sistema.
• stabile: Il disturbo temporaneo provoca variazioni limitate dello
stato (temporanee o permanenti).
STABILITA DEI SISTEMI LINEARI
Stabilità dei sistemi lineari
Nei controlli industriali si pretende però che, col venir meno della perturbazione, lo stato ritorni a quello di partenza, in
quanto diversamente la variabile controllata verrebbe a dipendere oltre che dall’ingresso di controllo, anche dalle
perturbazioni presentatesi in passato.
Nei sistemi la variabile controllata deve dipendere solo dall’ingresso di controllo (ingresso forzante), deve cioè essere
descritta dai soli termini della componente forzata. Solo così il controllore può controllare la variabile d’uscita del sistema.
Ciò equivale a pretendere che il sistema di controllo sia caratterizzato da una risposta libera che tenda ad estinguersi in
seguito alla scomparsa della perturbazione.
Esempio:
Risposta libera
che si estingue
t
Risposta
libera che si
estingue
Esempio:
y(t)
x(t)
Sistema
t
t
Comparsa
del disturbo
Esempio:
Scomparsa
del disturbo
y(t)
x(t)
Sistema
t
Risposta libera
che si estingue
t
STABILITA DEI SISTEMI LINEARI
Nei sistemi lineari la stabilità dell’intero sistema è garantita dalla stabilità di un singolo stato di equilibrio, in
quanto se la risposta libera si estingue a partire da uno stato si estingue a partire da qualsiasi altro stato di
equilibrio.
Ciò non è vero per i sistemi non lineari. Per essi lo studio della stabilità dell’intero sistema richiede lo studio della
stabilità di ogni singolo stato di equilibrio, che, in questi sistemi, dipende dall’ampiezza del disturbo.
Esempio:
STABILITA DEI SISTEMI LINEARI
Metodo di Routh - Hurwitz
a n s n a n1 s n1 ............ a1 s a 0 0
Data la seguente equazione caratteristica:
Condizione necessaria, ma non sufficiente, affichè tutte le radici siano a parte reale negativa è che i coefficienti abbiano
tutti lo stesso segno.
Il metodo permette la determinazione del segno delle radici senza risolvere l’equazione caratteristica: si costruisce la
seguente tabella:
n
an
an-2
an-4
…
n-1
an-1
an-3
an-5
…..
n-2
b1
b2
……
…..
…..
c1
…..
…..
….
0
….
b1
c1
a n1 a n2 a n a n3
a n 1
b2
a n1 a n4 a n a n5
a n1
b1 a n3 a n1 b 2
b1
Regola: ad ogni variazione di segno tra i termini consecutivi della prima colonna presentano corrisponde
una radice con parte reale positiva, ad ogni permanenza una radice con parte reale negativa.
STABILITA DEI SISTEMI LINEARI
ESEMPIO:
+
_
1
A
s 2 s 5 s 1
3
2
1)
Verificare la stabilità per A = 40.
2)
Calcolare il valore limite di A per cui il sistema si mantiene stabile.
0.1
Soluzione: occorre calcolare l’equazione caratteristica del sistema:
1)
3
1
s3 2 s 2 5 s 1 A 0.1 0
5
Non essendoci variazioni di segno nella prima colonna le
2)
2
2
1+4
1
2.5
0
0
5
soluzioni hanno parte reale negativa e quindi il sistema è
stabile.
3
1
5
2
2
1 + A·0.1
1
4.5 - A·0.05
0
0
1 + A·0.1
Per la stabilità non devono esserci variazioni di segno nella prima colonna:
4.5 A 0.05 0
1 A 0.1 0
A 90
A 10
Il guadagno negativo non ha significato pratico, per cui:
A < 90.
STABILITA DEI SISTEMI LINEARI
ESEMPIO:
+
_
1
s 2s 3
A
Calcolare il valore dell’intervallo di A per cui il sistema si mantiene stabile.
0.1
Soluzione: equazione caratteristica del sistema:
2
1
1
1
0
-6 + A·0.1
s 2 s 6 A 0.1 0
-6 + A·0.1
Per la stabilità deve essere:
6 A 0.1 0
Da cui:
A 60
NB: in questo esempio il sistema complessivo è tanto più stabile quanto maggiore è il guadagno. La causa è da ricercarsi nell’instabilità del blocco del
ramo diretto: la retroazione, unita a un alto guadagno, stabilizza il sistema.
Retroazione negativa e velocitò di risposta
La retroazione negativa modifica la larghezza di banda del sistema e quindi la sua velocità di risposta.
Come esempio si consideri il seguente sistema del 1° ordine:
k
s 1
X(s) X 0
Y(s) X(s)
k
s 1
Il valore di regime risulta:
YR X k
0
Se si introduce un ramo di retroazione: h
X(s) X 0
+
Y(s) X(s)
k
s 1
_
k
s 1 k h
Sono evidenti due conseguenze:
• diminuzione della costante di tempo:
h
• diminuzione del valore di regime:
Il calo del valore di regime dell’uscita può essere affrontato
preamplificando il segnale di ingresso:
X(s) X 0
1 k h
+
_
k
s 1
h
YR X 01 k h
'
1 k h
YR X 0
k
1 k h
k
X 0 k
1 k h
Retroazione negativa e velocitò di risposta
Con retroazione e
preamplificazione
Retroazione negativa e velocitò di risposta
QUINTA
RISPOSTA IN FREQUENZA
STABILITÀ DEI SISTEMI DI CONTROLLO
CONTROLLORI
ESERCIZIO: CONTROLLO DI UN MOTORE IN CC
ESERCIZIO: CONTROLLO DI SPESSORE
CONTROLLO DIGITALE
ARCHITETTURA DI UN SISTEMA DI CONTROLLO
Risposta in frequenza
CONTENUTO ARMONICO
RISPOSTA IN REGIME SINUSOIDALE
DIAGRAMMI DI BODE
TRACCIAMENTO DEI DIAGRAMMI DI BODE
GRAFICI DELLE FUNZIONI ELEMENTARI
RETI CORRETTRICI A SELLA, ANTICIPATRICE, RITARDATRICE
SISTEMI DEL 2° ORDINE CON POLI COMPLESSI CONIUGATI
ESEMPI
DIAFRAMMI DI NYSQUITS
ESEMPI
Risposta in frequenza
CONTENUTO ARMONICO
Il concetto di contenuto armonico di una funzione è connesso alla possibilità di rappresentarla come somma di
termini trigonometrici (seno, coseno).
.
Nel 1807 Jean Baptiste Fourier, fisico e matematico francese, pubblicò uno scritto Sulla Propagazione del Calore, in
cui espose la possibilità di rappresentare una funzione come somma di sinusoidi.
Armonica
f (t) A 0
A
n1
n
cosn 0 t n
0
2
T0
La serie di Fourier permette di scomporre una funzione, anche discontinua, purché periodica, in una somma
infinita di termini trigonometrici (continui).
Esempio:
Risposta in frequenza
Esempio:
Segnale periodico: è sempre scomponibile come somma di infinite sinusoidi (Teorema di Fourier)
Risposta in frequenza
Spettro delle ampiezze An
Spettro delle fasi ρn
Distribuzione delle ampiezze lungo l’asse delle pulsazioni
Distribuzione delle ampiezze lungo l’asse delle pulsazioni
A1
0
A2
A0
1
2
NB: spettri discreti
ω
ω
Segnale non periodico: una funzione di area limitata è scomponibile in somma di infinite sinusoidi con pulsazioni
infinitamente vicine
Esempio: impulso unitario
A∙ 1 = 1
A
Spettro delle ampiezze continuo
1
A’∙ 2 =1
A’
1
2
t
2
1
2
2
1
ω
Risposta in frequenza
RISPOSTA IN REGIME SINUSOIDALE
In regime sinusoidale si utilizza la variabile complessa immaginaria pura s = jw dove con w si
indica la pulsazione del segnale d’ingresso
Modulo e fase della f.d.t in regime sinusoidale
Il modulo dalla f.d.t.(rapporto fra l’ampiezza della sinusoide d’uscita e l’ampiezza della sinusoide
d’ingresso) se maggiore di uno rappresenta l’amplificazione del sistema, invece se minore di uno
l’attenuazione.
La fase della f.d.t. rappresenta lo sfasamento della sinusoide d’uscita rispetto alla sinusoide
d’ingresso.
Risposta in regime sinusoidale
Se ad un sistema lineare stabile si applica un segnale sinusoidale, a regime il sistema risponde
ancora con un segnale sinusoidale con la medesima pulsazione w e con ampiezza e fase in
funzione di w
Risposta in frequenza
Esercizio1
Al circuito in figura (R=1K ; C=1microF) è applicato un segnale sinusoidale
vi(t) = 7*sen(1000*t) Determinare il segnale d’uscita calcolando l’ampiezza e lo sfasamento
circuito RC
circuito RC
trasformato
Segnale d’uscita
vi (t) = 7 sen(1000 t)
vo( t)= 4,95 sen( 1000t- 0 , 785)
Risposta in frequenza
RISPOSTA IN FREQUENZA
Per risposta in frequenza si intende: la risposta di un sistema al variare della frequenza f o
pulsazione w quando in ingresso è applicato un segnale sinusoidale.
Per l’analisi della risposta in frequenza di un sistema, vengono utilizzati dei grafici di facile
costruzione:
- i diagrammi cartesiani o di Bode
- i diagrammi polari o di Nyquist.
I diagrammi di Bode sono due e precisamente: un diagramma del modulo e un diagramma della
fase, mentre il diagramma di Nyquist è unico.
Con i diagrammi di Bode è possibile l’analisi in frequenza di un sistema in modo rapido, anche se
approssimato. Ad es. possiamo ricavare facilmente sia l’attenuazione e che lo sfasamento tra il
segnale d’ingresso e quello d’uscita a certe frequenze.
Diagramma del modulo
Il diagramma del modulo è la rappresentazione grafica dell’andamento del modulo della f.d.t.
(attenuazione o amplificazione) di un sistema al variare della pulsazione w
In tale diagramma sull’asse delle ordinate si riporta in scala lineare il modulo della f.d.t. in decibel
G(jω) ()dB = 20 log(G)
mentre sull’asse delle ascisse, in scala logaritmica si riporta la pulsazione w in rad/sec o la
frequenza in Hz
Risposta in frequenza
Vantaggi dell’uso della scala logaritmica
In luogo di moltiplicazioni e divisioni si opera con somme e sottrazioni
Si può approssimare il diagramma, on errori accettabili, con delle semirette di facile tracciamento
È possibile rappresentare ampi campi di variazione di pulsazioni o frequenze
Diagramma della fase
Il diagramma della fase è la rappresentazione grafica dell’andamento dello sfasamento
(argomento) della f.d.t. di un sistema al variare della pulsazione w.
Sull’asse delle ordinate si riporta in scala lineare gli sfasamenti in gradi della f.d.t. mentre sull’asse
delle ascisse, in scala logaritmica, si riporta la pulsazione w in rad/sec o la frequenza in Hz
TRACCIAMENTO DEI DIAGRAMMI DI BODE
I diagrammi di Bode sia per il modulo che per la fase, si possono ottenere sommando i diagrammi
approssimati delle funzioni elementari.
Dimostrazione
Consideriamo un generico sistema la cui f.d.t. in forma normale è:
Risposta in frequenza
Per il modulo
I quattro termini che compaiono della [2] rappresentano le funzioni elementari.
Dalla [2] si evince che il diagramma di Bode relativo al modulo lo si può ottenere tracciando
singolarmente i diagrammi di dette funzioni elementari per poi sommarli.
Per la fase
L’argomento di
G(jω), <(ω∠jG ) la somma degli argomenti dei singoli fattori della [1]
∠jG(jw) = ∠k + ∠ (1+jωτ)+∠ G(jω)^ ∠-( 1 +jωp)+
Anche per l’argomento il diagramma di Bode lo si può ottenere tracciando singolarmente i
diagrammi delle funzioni elementari per poi sommarli.
Risposta in frequenza
GRAFICI DEI DIAGRAMMI DI BODE DELLE FUNZIONI ELEMENTARI
Costante moltiplicativa G(j) = K
Diagramma del modulo
G(jω)db = 20 log K
fig. 1
fig. 2
Diagramma della fase
0
Gj = arctg
K
0
180
per
K 0
per
K 0
Risposta in frequenza
Polo nell’origine G(s) = 1/s
G j
1
j
Diagramma del modulo
Gjω
1
= 20 log 20log
dB
Per disegnare il diagramma troviamo dei punti:
Gjω
= -20log
dB
0,1
+20 dB
0 dB
-20 dB
Si tratta di una retta con pendenza –20 dB/dec
che interseca l’asse delle ascisse nel punto
fig. 7
fig. 8
Da notare:
Se il polo nell’origine ha molteplicità g
Il diagramma del modulo sarà ancora una retta, che interseca l’asse delle ascissenel punto ma con pendenza – 20g
Il diagramma della fase sarà ancora una retta parallela all’asse delle ascisse ma di valore –90°g
Risposta in frequenza
Zero nell’origine G(s) = s
G j j
Diagramma del modulo
Gjω
= 20log
dB
Per disegnare il diagramma troviamo dei punti:
Gjω
= -20log
dB
0,1
-20 dB
0 dB
+20 dB
Si tratta di una retta con pendenza + 20 dB/decade
che interseca l’asse delle ascisse nel punto
fig. 9
Diagramma della fase
Gj j Gj = arctg = arctg = +90°
0
Da notare:
Se lo zero nell’origine ha molteplicità g
G j jg
Il diagramma del modulo sarà ancora una retta, che interseca l’asse delle ascissenel punto ma con pendenza +20g
Il diagramma della fase sarà ancora una retta parallela all’asse delle ascisse ma di valore +90°g
Risposta in frequenza
Diagramma del modulo
Zero reale e negativo G(s)=1+s
G(j)=1 + jz
l massimo errore che si commette nella appresentazione asintotica si ha per =z e vale3 dB, infatti:
Risposta in frequenza
Diagramma della fase
Per disegnare il grafico troviamo i punti più significativi:
0
Fase
fase
approssimat
a
Gj
arctg 0 = 0°
0°
0,1 z arctg 0,1 = 0,7°
0°
z
10z arctg 10 = 84,3°
arctg = 90°
45°
arctg 1 = 45°
90°
90°
Risposta in frequenza
Polo reale e negativo G(s) = 1/1+s
1
Gj
1 j p
Il diagramma può essere tracciato per tratti in modo approssimato (diagramma asintotico), pertanto consideriamo i due casi: << p e >> p
Risposta in frequenza
il massimo errore che si commette nella rappresentazione asintotica si ha per =p e vale -3 dB, infatti:
f
Diagramma della fase
per disegnare il grafico troviamo i punti più significativi
Risposta in frequenza
Esercizio – Tracciare i diagramma di Bode del circuito in figura (filtro passa alto)
R= 1K
C= 1 mF
Soluzione
= RC = 1K 1 mF = 10 +3 10 -6 = 0,001 sec
Diagramma del modulo
la f.d.t. presenta uno zero nell’origine e un polo reale ( p=1000 rad/sec)
Contributo dello zero
Contributo del polo
Per costruire il diagramma del modulo basta sommare i diagrammi
elementari relativi ad uno zero nell’origine ed un polo reale ( p=1000 rad/sec)
Nota:
In pratica la somma viene effettuata sommando le pendenze: pendenze
uguali ed opposte si annullano reciprocamente, producendo un
andamento costante.
Risposta in frequenza
Per costruire il diagramma della fase basta sommare i diagrammi elementari relativi ad uno zero nell’origine ed un polo
reale
Elementi per la costruzione del diagramma del polo
Risposta in frequenza
Tracciare i diagramma di Bode di un sistema la cui f.d.t. è la seguente
Diagramma del Modulo
Poli
La f.d.t. presenta due poli non nell’origine, in corrispondenza di ciascun polo la pendenza varia –20dB/dec,
(1+s10 -3 ) = 0 = p1 = - 103
p1 103 rad /sec
(1+s10 -4 ) = 0 = p2 = - 10 -4
p2 104
Costante
K=
lim
s 0
10
=10
rad /sec
KdB =20log10 = 20dB
(2 s 103)(1 s 104 )
Il diagramma asintotico del modulo si costruisce nel seguente modo: si traccia
una semiretta parallela all’asse di ordinata 20 dB fino a p1 da p1 aw p2 il
diagramma scende con pendenza di – 20 db/dec da p2 il diagramma scende invece
con pendenza –40dB/dec
Risposta in frequenza
Diagramma della fase
Si
tracciano i diagrammi approssimativi dei singoli termini e poi si sommano
Costante
1° Polo
□ 0,1 p1= 10 2 rad/sec ( 0°)
■ 10p1 =104 ( -90°)
2° Polo
0,1p2=103 rad/sec ( 0°)
10p2 =105 ( -90°)
0°
Contributo 1° polo
Contributo 2° p olo
Risposta in frequenza
Diagrammi di Bode di una rete ritardatrice
Risposta in frequenza
Diagramma della fase
G(s)=
1 sT
1 s
G( j)
1 jT
1 j
Risposta in frequenza
Diagrammi di Bode di una rete anticipatrice
Risposta in frequenza
Risposta in frequenza
Diagrammi di Bode di una rete a sella
Risposta in frequenza
osserva
che
il
circuito
agisce
contemporaneamente
da
ritardatore
e
anticipatore, ma in due Bode di pulsazioni
diverse
Si
Risposta in frequenza
SISTEMI DEL 2° ORDINE
Sistema del 2° ordine senza zeri.
X(s)
k
2
s 2 s 2
n
t
Y(s)
n
t
Poli della funzione di trasferimento:
s1,2 n n 2 1
NB: s1 e s2 sono soluzioni dell’equazione caratteristica;
possono essere reali o complesse in funzione di .
Risposta in frequenza
IF(j)IdB
Ipotesi:
1
Le soluzioni sono
s1
s1,2 n n 1
2
Ipotesi:
1
Le soluzioni sono
reali coincidenti:
•s
•
reali distinte:
2
log10
IF(j)IdB
s1,2 n
•
s1 = s2
log10
Risposta in frequenza
Ipotesi:
1
s1, 2 n jn 1 2
Le soluzioni sono complesse coniugate:
=0
IF(j)IdB
0 < < 0.707
=0
y(t)
< 0.5
0.5 < < 0.707
MR
0.707 < < 1
0.707 < < 1
= 1
= 1
•
n
log10
t
Risposta al gradino nel dominio del tempo
Risposta in frequenza
7Grafici dei diagrammi di Bode di un sistema del 2° ordine
con poli complessi coniugati (<1)
Diagramma del modulo
Il diagramma del modulo per < n e > n è uguale a quello di un sistema del secondo ordine
+40dB/decade)
con polo doppio ( pendenza retta
Risposta in frequenza
Nell’intorno di wn, esso subisce delle modificazioni che dipendono da
L’analisi matematica mette in evidenza l’esistenza di un massimo della curva per
Da notare:
Nel caso in cui = 0,7 la risposta è quella di un filtro LPF a banda piatta con
pulsazione di taglio n e pendenza di –40dB/dec. (filtro alla Butterworth de 2° ordine)
Risposta in frequenza
Dimostrazione che per < n e > n
il diagramma del modulo è quello di un sistema del secondo ordine con polo doppio.
2
2
GjωdB = 20 log 1
n
n
2
Per << n
2
Risposta in frequenza
Esercizi - Diagrammi di Bode di sistemi del 2° ordine con poli complessi e coniugati
Risposta in frequenza
Risposta in frequenza
DIAGRAMMI DI NYQUIST
A differenza dei diagrammi di Bode le informazioni sul modulo e la fase della f.d.t. si ricavano da un
unico diagramma. Il diagramma di Nyquist è la rappresentazione nel piano di Gauss del modulo e
della fase della f.d.t al variare della pulsazione w.
Il diagramma polare1, si ottiene congiungendo i vertici dei vettori della f.d.t. del sistema G(jw) per w
variabile tra 0 e infinito.
Esempi di tracciamento dei diagrammi di Nyquist
Il diagramma di Nyquist può essere tracciato in due modi: per via numerica, quando si ha ha disposizione un
elaboratore o per via qualitativa grafica.
Esempio di tracciamento per via numerica del diagramma di Nyquist di un sistema di tipo 0 con un
solo polo
con Excel
UN grafico di tipo polare è un grafico le cui coordinate sono
un vettore e un angolo
1
Risposta in frequenza
Esempio di tracciamento del diagramma di Nyquist per via qualitativa grafica di un sistema di tipo 0
con un solo polo
G(s) 10
1 s0.01
Gj
10
1 j0.01
Da notare:
Ogni punto P del diagramma di Nyquist è individuato dalle
coordinate polari (modulo; fase)
P1( = (10; 0°)
P2 ( ) = (0 ; 0°)
P3 ( ) = (7; -45°)
Risposta in frequenza
Esercizio 2 - Sistemi di tipo zero con due poli reali
G(s)
G(j)
G(j)
7
(1 s0.1)(1 s0.01)
7
(1 j0.1)(1 j0.01)
7
2
2
1 1
10
100
p1 = - 10 ; p2 = -100
Risposta in frequenza
Esercizio 3 - Sistemi di tipo zero con tre poli
G(s)
G(j)
7
(1 s0.2)(1 s0.1)1 0.01s
p1 = - 5 ; p2 = - 10 ; p3 = - 100
7
(1 j0.2)(1 j0.1)1 0.01j
Risposta in frequenza
Esercizio 4 - Sistemi di tipo uno con tre poli
G(s)
20
s1 0,1 s(1 0,01s)
G(j)
p1 = 0 ; p2 = -10 ; p3 = -100
1
j1 0,1 j(1 0,01j)
G jω =
20
1 0,12 1 (0,01)2
;
Risposta in frequenza
Esercizio 5 - Sistemi di tipo due con tre poli
20
G(s)
p1 = 0 ; p2 = 0 ; p3 = -10
s2 1 0,1 s
G(j)
1
j j 1 0,1 j
Gjω =
20
2 1 0,12
;
Stabilità dei sistemi di controllo
GENERALITA
CRITERIO GENERALE DI STABILITA
CRITERIO DI BODE
MARGINE DI FASE
CRITERIO GENERALE DI STABILITA
CRITERIO SEMPLIFICATO
RIDUZIONE DEL GUADAGNO AD ANELLO
SPECIFICHE DEI SISTEMI RETROAZIONATI
CRITERIO DI NYSQUITS
MARGINE DI AMPIEZZA E DI FASE
CRITERIO DI STABILITA DI NYSQUITS
RETI CORRETRICE
TECNICHE DI STABILIZZAZIONE
RETI RITARDATRICE, ANTICIPATRICE A SELLA
Stabilità dei sistemi di controllo
GENERALITÀ
La stabilità di un sistema non dipende dal segnale d’ingresso, ma dipende solo dalla f.d.t. del
sistema
f.d.t. =
U(s)
E(s)
Un sistema lineare tempo invariante si dice stabile semplicemente se risponde ad un ingresso
limitato con una uscita limitata, invece se risponde con una uscita che tende a zero il sistema
dicesi stabile asintoticamente.
Esempio di risposta:
Stabilità dei sistemi di controllo
Un sistema lineare tempo invariante si dice instabile se risponde ad un ingresso limitato con una
uscita non limitata (divergente)
Esempio di risposta:
CRITERIO GENERALE DI STABILITÀ
Il criterio generale di stabilità permette di determinare la stabilità di un sistema di controllo quando
si conoscono i poli della f.d.t. ad anello chiuso.
W(s) = f.d.t. ad anello chiuso
G(s) H(s) = f.d.t. ad anello aperto.
Stabilità dei sistemi di controllo
Un sistema lineare è stabile se e solo se la f.d.t. del sistema ha tutti i poli a parte reale non positiva
e gli eventuali poli a parte reale nulla siano semplici.
Un sistema lineare è asintoticamente stabile se è solo se ha tutti i poli a parte reale negativa.
Esercizio 1
Uno stabilimento utilizza, per la cottura di merendine, un sistema di controllo di temperatura a
catena chiusa. Sapendo che le funzioni di trasferimento del
regolatore, del circuito di
comando, del forno e del circuito di reazione (termocoppia e circuito di condizionamento)
sono rispettivamente:
Stabilità dei sistemi di controllo
Determinare la f.d.t. complessiva del sistema
Soluzione
Stabilità dei sistemi di controllo
Il criterio di stabilità di Bode
La funzione d'anello
Per verificare la stabilità di un sistema ad anello chiuso bisogna studiare il comportamento
della funzione d'anello
G(S) · H(S)
al variare della frequenza.
Infatti la funzione di anello, funzione della variabile complessa S, è una grandezza complessa e
quindi ha una parte reale ed una parte immaginaria. Come tutte le grandezze complesse è
pertanto caratterizzata da un modulo e da una fase.
Stabilità dei sistemi di controllo
Il segnale di ingresso “x” viene quindi amplificato (oppure attenuato) e sfasato, dalla
funzione di anello. Tale segnale, così modificato, viene riportato al nodo sommatore e da
questo cambiato di segno, con un ulteriore sfasamento di 180° (introdotto dal nodo
sommatore stesso). Pertanto, il segnale rischia di essere riportato in ingresso al blocco di
andata in fase con il segnale originario (sfasamento complessivo pari a 360°) e amplificato
con modulo del
guadagno maggiore o uguale a 1. In tal caso, eventuali oscillazioni
introdotte dal segnale originario “x”, anche in sua assenza, si autoalimenterebbero, dando
luogo ad instabilità del sistema
Il criterio di Bode
Per garantire la stabilità di un sistema a catena chiusa, bisogna studiare i diagrammi di
bode del modulo e della fase della funzione di anello. Il sistema è stabile solo se non
esistono frequenze a cui, ad uno sfasamento di 180° corrisponde un guadagno di anello
maggiore o uguale a 1.
Il diagramma della fase
Il diagramma
di BODE della
fase
viene
ricavato dal diagramma
di BODE dell’ampiezza
tenendo presente i seguenti criteri:
Ad una pendenza di n · 20 dB/decade corrisponde una fase di n · 90° , per i valori di frequenza lontani almeno
una decade dai punti critici (poli o zeri) più vicini.
Nei campi di frequenze in prossimità dei punti critici, i tratti di curva vengono raccordati linearmente.
Stabilità dei sistemi di controllo
Un esempio: la funzione d'anello
Consideriamo ad esempio il caso in cui G(S) e H(S) siano entrambe f.d.t. del primo ordine, del
tipo:
G(S) = Gst / [1 + τ1 · S]
H(S) = Hst / [1 + τ2 · S]
La funzione d'anello è data allora da:
G(S) · H(S) = Gst · Hst / [(1 + τ1 · S) (1 + τ2 · S)]
I diagrammi di Bode
Si tratta di una f.d.t. del secondo ordine, con due poli reali e distinti.
Supponiamo che i poli si abbiano in corrispondenza delle pulsazioni wp1 = 103 s-1, wp2 = 106 s-
1
e
che il guadagno statico complessivo sia pari a Gst · Hst = 1000.
Qui sotto sono riportati i diagrammi di Bode del modulo e della fase corrispondenti alle condizioni
ipotizzate.
Stabilità dei sistemi di controllo
Dall'analisi dei diagrammi si osserva che esistono delle frequenze in cui viene effettivamente
raggiunto uno sfasamento di 180° (per valori di w superiori a 107 s-1). Questo però avviene
quando il guadagno risulta comunque di valore ben
inferiore a 1 (al di sotto dell'asse
corrispondente a 0 dB). Non esistono quindi apparentemente rischi di instabilità.
Stabilità dei sistemi di controllo
Il margine di fase
In realtà, la modellizzazione del comportamento di un sistema tramite i diagrammi di Bode è una modalità di
rappresentazione abbastanza approssimata (come del resto sono tutti i modelli). Quelle tracciate sono infatti curve
ideali: quelle reali dovrebbero avere un andamento più "smussato". Inoltre non è sempre facile conoscere con molta
precisione i valori dei poli, degli zeri e del guadagno statico dei "sistemi reali".
Per tali motivi si preferisce utilizzare il Criterio di Bode con un certo margine di sicurezza. A tale scopo si prende in
considerazione il valore di frequenza in cui il guadagno risulta pari a 1 (0 dB) e si individua il valore di fase
corrispondente (nel nostro esempio questo si verifica in corrispondenza della pulsazione di valore pari a 106 s-1). Viene
detto allora margine di fase la differenza fra tale valore di fase ed il valore critico di 180°. Nel nostro caso il margine di
fase, evidenziato nel diagramma con un segmento orientato di colore rosso, risulta esattamente pari a 45°.
Proprio questo viene in genere indicato come valore minimo del margine di fase, necessario per garantire la sicura
stabilità del sistema. Risulta infatti evidente che, per frequenze più vicine a quelle che determinano lo sfasamento
critico di 180°, il guadagno scende rapidamente, al di sotto del valore unitario, scongiurando il rischio di instabilità.
Il Criterio di Stabilità di Bode Semplificato
Cosa succede al variare del guadagno statico
Dall'analisi dell'esempio precedente, risulta che un sistema con due poli, di cui il secondo in corrispondenza
dell'asse 0 dB, ha il margine di fase minimo (45°) sufficiente per dichiarare il sistema "sicuramente stabile".
Stabilità dei sistemi di controllo
Aumentando il valore del guadagno statico oltre i 60 dB il secondo polo si sposterebbe al di sopra
dell'asse 0 dB e la curva del guadagno taglierebbe l'asse con pendenza pari a -40 dB/decade. La
frequenza corrispondente al guadagno unitario aumenterebbe di valore. In tal caso il margine di
fase diventerebbe insufficiente e non si potrebbe dichiarare il sistema "sicuramente stabile". Al
contrario, diminuendo il valore del guadagno statico sotto i 60 dB, il secondo polo si sposterebbe
al di sotto dell'asse 0 dB e la curva del guadagno taglierebbe l'asse con pendenza pari a -20
dB/decade. La frequenza corrispondente al guadagno unitario diminuirebbe di valore. In questo
caso il margine di fase aumenterebbe garantendo con sicurezza ancora maggiore la stabilità del
sistema.
Il criterio di stabilità semplificato
Dalle considerazioni precedenti si deduce il seguente criterio di stabilità semplificato, che si
applica utilizzando esclusivamente il diagramma di Bode del modulo della funzione d'anello. Un
sistema è "sicuramente stabile" solo se la funzione d'anello non presenta pendenze di valore
uguale o superiore, in valore assoluto, a 40 dB/decade al disopra dell'asse 0 dB.
Conflitti
Un basso valore di guadagno statico della funzione d'anello è garanzia di stabilità del sistema.
Pero, come vedremo nelle lezioni successive, ci possono essere motivi validi per cercare di
elevare il guadagno statico quanto più sia possibile. Infatti, un guadagno statico elevato assicura
una migliore precisione ed una maggiore immunità ai disturbi del sistema. Un guadagno statico
elevato migliora inoltre il comportamento alle frequenze elevate, aumentando la velocità di
risposta del sistema.
Stabilità dei sistemi di controllo
C'è pertanto conflitto tra la stabilità e le altre prestazioni che caratterizzano la qualità di un
sistema di controllo ad anello chiuso. Caso per caso, sarà compito del progettista del sistema di
controllo trovare il compromesso migliore tra le opposte esigenze ed adottare particolari
strategie che
permettono talvolta di conciliarle, senza sacrificare troppo le prestazioni
desiderate
CRITERIO GENERALE DI STABILITÀ DI BODE
Consideriamo un sistema ad anello chiuso
Il criterio di stabilità di Bode permette di determinare la stabilità quando è nota la funzione f.d.t.
ad anello aperto cioè la L(s) = G(s)*H(s).
Un sistema a catena chiusa è stabile: se lo sfasamento della f.d.t. ad anello aperto calcolato in
corrispondenza della pulsazione critica è inferiore in valore assoluto a 180°
Esempio: consideriamo un sistema ad anello chiuso i cui diagrammi di Bode della f.d.t. ad anello
aperto siano i seguenti
Stabilità dei sistemi di controllo
Stabilità dei sistemi di controllo
CRITERIO SEMPLIFICATO DI STABILITÀ DI BODE
Un sistema ad anello chiuso è stabile se il diagramma del modulo del guadagno ad anello aperto
interseca l’asse delle ascisse con una pendenza di – 40dB/dec. Se la pendenza è maggiore o uguale
a –60dB/dec il sistema è sicuramente instabile; con una pendenza di –40dB/dec il sistema potrebbe
essere instabile e si deve ricorrere al criterio generale di stabilità
ESERCIZI - CRITERIO SEMPLIFICATO DI STABILITÀ DI BODE
L’attraversamento dell’asse delle ascisse avviene con una pendenza di – 20dB/dec, pertanto il sistema è stabile
Stabilità dei sistemi di controllo
L’attraversamento dell’asse delle ascisse avviene con una pendenza di – 60dB/dec, pertanto il sistema
è instabile
Stabilità dei sistemi di controllo
Esercizio 3
Verificare la stabilità del sistema ad anello chiuso
L’attraversamento dell’asse delle ascisse avviene con una pendenza di – 40dB/dec, il criterio
semplificato di Bode non ci permette di valutare la stabilità.
Stabilità dei sistemi di controllo
STABILIZZAZIONE PER RIDUZIONE DEL GUADAGNO DI ANELLO
Esercizio 1
Analizzare la stabilità del sistema dell’esercizio N.3, ma con guadagno K minore di 35dB
La curva del modulo ha lo stesso andamento della figura dell’esercizio N.3, ma parte non più da
50dB, ma da 20dB. L’attraversamento dell’asse delle ascisse avviene ora prima del secondo polo
con una pendenza di – 20dB/dec, per il criterio semplificato di Bode il sistema è stabile.
Stabilità dei sistemi di controllo
Esercizio 2
Stabilizzare il sistema dell’esercizio N.2 riducendo il guadagno d’anello
E’ sufficiente fare in modo che quando
arriva il secondo polo la curva attraversi
l’asse delle ascisse. Quindi bisogna
imporre che alla pulsazione di
100
rad/sec il guadagno
L’attraversamento dell’asse delle ascisse ora avviene con una
pendenza di – 20dB/dec, per il criterio semplificato di Bode il
sistema è stabile.
Nota:
Da questi esempi si evince:
che la stabilità oltre al guadagno d’ anello dipende dal
numero dei poli della L(s), in quanto ogni polo
incrementa ulteriore la pendenza di 20dB/dec
che con la riduzione del guadagno di anello K, si migliora
la stabilità del sistema.
Questo metodo di stabilizzazione in genere non è seguito, perché il sistema di controllo diviene più
lento, meno preciso e più sensibile ai disturbi.
.
Stabilità dei sistemi di controllo
ESERCIZI: CRITERIO GENERALE DI STABILITÀ DI BODE
Osservazioni
Rispetto al criterio di Nyquist, il criterio di Bode ha il vantaggio di servirsi dei diagrammi di Bode
più agevoli da tracciare.
La pulsazione critica può essere ricavata con buona approssimazione dal diagramma di Bode
asintotico del modulo, a condizione che non vi siano cambiamenti di pendenza nelle vicinanze
della pulsazione critica
La fase critica invece conviene calcolarla analiticamente.
Esercizio 1
Discutere la stabilità con il criterio di Bode.
Stabilità dei sistemi di controllo
- La fase critica può essere calcolata analiticamente Φc
=)L(jcω∠= -2⋅arctg 3 = 144°
Nota:. Φc ricavato dal diagramma asintotico ha un valore
minore.
Poiché lo sfasamento in corrispondenza della pulsazione
critica è 144° < 180° il sistema ad anello chiuso per il
criterio di Bode è stabile
Esercizio 2
Discutere la stabilità con il criterio di Bode.
Stabilità dei sistemi di controllo
Stabilità dei sistemi di controllo
Esercizio 3
Uno stabilimento utilizza, per la cottura di merendine, un sistema di controllo di temperatura a
catena chiusa. Sapendo che le funzioni di trasferimento del regolatore, del sistema di comando, del
forno e del blocco di reazione (termocoppia e circuito di condizionamento) sono rispettivamente:
Soluzione
Analizzare la stabilità del sistema
Stabilità dei sistemi di controllo
La f.d.t. ad anello aperto è stabile in quanto i poli della f.d.t. sono reali e negativi ( p1= -1/500;
p2= -1/50), pertanto per determinare la stabilità del sistema ad anello chiuso si può applicare
il criterio di Bode.
Stabilità dei sistemi di controllo
SPECIFICHE DEI SISTEMI REAZIONATI NEL DOMINIO DELLA FREQUENZA
Nota:
Per determinare la stabilità si poteva in alternativa applicare il criterio semplificato di Bode.
Dal grafico si nota che l’attraversamento dell’asse delle ascisse avviene con una pendenza di –
20dB/dec, pertanto per il criterio semplificato di Bode il sistema è stabile
Per la progettazione dei sistemi ad anello chiuso si tengono conto nel dominio della frequenza delle
seguenti specifiche
Larghezza di banda
La larghezza di banda è l’intervallo delle frequenze tale che il modulo della f.d.t. ad anello chiuso
W(s), non è mai minore di 3dB del valore che esso assume quando omega =0
Per il calcolo della larghezza di banda per sistemi ad anello chiuso si utilizza la f.d.t. ad anello
aperto.
L(s) = G(s)*H(s)
La larghezza di banda (B) di un sistema ad anello chiuso è approssimativamente uguale alla
pulsazione critica B = wca
Picco di risonanza e Pulsazione di risonanza
Per i sistemi ad anello chiuso del 2°ordine con poli complessi e coniugati ζ <= 0.7
Stabilità dei sistemi di controllo
Pulsazione critica wC = pulsazione alla quale il modulo della funzione di trasferimento ad anello aperto vale 0dB
Stabilità dei sistemi di controllo
IL CRITERIO DI NYQUIST
• Il criterio di Nyquist consente di stabilire se un sistema, del quale si conosce la risposta armonica ad
anello aperto, sia stabile o meno una volta chiuso in retroazione:
• Per la sua natura sostanzialmente grafica, esso risulta di notevole ausilio per il progettista perchè,
oltre a fornire indicazione sulla stabilità del sistema in retroazione costituisce anche un’utile guida
per giudicare dell’efficacia di possibili interventi che migliorino il comportamento dinamico del
sistema in retroazione.
• Criterio di Nyquist: sistemi stabili ad anello aperto. Nell’ipotesi che la funzione guadagno di
anello F(s) abbia tutti i poli a parte reale negativa, eccezion fatta per un eventuale polo nullo
semplice o doppio, condizione necessaria e sufficiente perche il sistema in retroazione sia
asintoticamente stabile `e che il diagramma polare completo della funzione F (jω) non circondi n´e
tocchi il punto critico −1+j0.
Stabilità dei sistemi di controllo
• Il criterio di Nyquist fa riferimento ai diagrammi polari “completi, cio`e tracciati per ω variabile da −∞
a +∞. Essendo
F (−jω) = F ∗(jω)
il diagramma per pulsazioni negative si ottiene per ribaltamento intorno all’asse delle ascisse di
quello tracciato per pulsazioni positive.
Nel caso di un sistema di tipo 0, il diagramma polare competo `euna curva chiusa;
• Nei casi di sistemi di tipo 1 o di tipo 2 (che presentano rami all’infinito) si conviene di completare i
diagrammi, rispettivamente, con una semicir- conferenza e con una circonferenza all’infinito percorsa
in senso orario che parte da ω = 0− ed arriva ad ω = 0+
Stabilità dei sistemi di controllo
• Il precedente enunciato del criterio di Nyquist `equello che copre la maggior parte dei casi di interesse. Si puo
dare tuttavia il seguente enunciato piu` generale, che si applica anche al caso in cui il sistema in esame sia
instabile ad anello aperto.
• Criterio di Nyquist: sistemi instabili ad anello aperto, con un eventuale polo nell’origine semplice o
doppio. Nell’ipotesi che la funzione guadagno di anello F (s) non presenti poli immaginari,
eccezion fatta per un eventuale polo nullo semplice o doppio, condizione necessaria e sufficiente
perch´e il sistema in retroazione sia asintoticamente stabile `e che il diagramma polare completo della
funzione F (jω) circondi il punto critico −1+j0 tante volte in senso antiorario quanti sono i poli di
F(s) con parte reale positiva.
Ogni giro in meno in senso antiorario o ogni giro in piu in senso orario corrisponde alla presenza,
nel sistema in retroazione, di un polo con parte reale positiva.
• Esempio Si consideri un sistema in retroazione:
Stabilità dei sistemi di controllo
Se il punto critico viene circondato (due volte in senso antiorario), il che avviene per valori elevati
della costante K, il sistema in retroazione e` stabile, dato che il guadagno di anello presenta due poli
con parte reale positiva. Se invece il punto critico non viene circondato, il che avviene per valori
relativamente bassi della costante K, il sistema in retroazione e` instabile.
Stabilità dei sistemi di controllo
MARGINI
DI AMPIEZZA E
DI
FASE
Quando il diagramma di Nyquist di un sistema in retroazione ha un andamento regolare, con ampiezza funzione
monotona decrescente della pulsazione si può dedurre da esso informazione non solo sulla stabilità del sistema, ma
anche sulla sua maggiore o minore criticità o tendenza all’instabilità.
• `E infatti evidente che, quanto pi`u il diagramma di Nyquist di un sistema tabile ad anello aperto si svolge lontano
dal punto critico, tanto piu lontano dall’instabilità `e il sistema: la vicinanza del diagramma di Nyquistal punto critico
`e normalmente associata ad un comportamento dinamico
non soddisfacente.
• Per quantificare la “distanza di G(jw) dal punto critico −1, si utilizzano due parametri, detti margini di stabilità,
che misurano la cosiddetta“stabilita relativa” dei sistemi in retroazione:
Stabilità dei sistemi di controllo
- Margine di ampiezza MA: `e l’inverso del modulo del guadagno di anello alla pulsazione corrispondente
alla fase − 3.14
– Margine di fase MF : `e l’angolo che occorre sottrarre alla fase (normalmente negativa) del guadagno di
anello alla pulsazione corrispondente al valore unitario del modulo (detta pulsazione di intersezioneo di
incrocio) per ottenere il valore − 3.14.
Margini di ampiezza e fase nei diagrammi di Bode
Stabilità dei sistemi di controllo
CRITERIO DI STABILITÀ DI NYQUIST
Il criterio di stabilità di Nyquist permette di determinare la
stabilità del sistema ad anello chiuso.
Esso si basa sul tracciamento del diagramma di Nyquist della
funzione f.d.t. ad anello aperto cioè L(s) = G(s)⋅H(s). per
ωvariabile da – ∞ a + ∞ 1
Enunciato del criterio di stabilità di Nyquist
Il criterio afferma che un sistema ad anello chiuso è stabile se e solo se il numero di giri (N) in
senso antiorario compiuti dal diagramma di Nyquist della f.d.t. ad anello aperto intorno al punto –
1 è uguale al numero dei poli (P) a parte reale positiva (cioè non presenta poli nel semipiano
destro)
Riassumendo
P = N ⇒ sistema stabile
P ≠ N ⇒ sistema instabile
Nota
Se P=0, cioè la f.d.t. ad anello aperto non presenta poli a parte reale positiva. Il sistema ad anello
chiuso è stabile, se il diagramma di Nyquist non compie nessun giro intorno al punto –1 (N=0)
Stabilità dei sistemi di controllo
ESERCIZI - CRITERIO DI STABILITÀ DI NYQUIST
Stabilità dei sistemi di controllo
modulo parte da 10 e decresce, la fase parte da 0 e decresce fino a 180°
Il diagramma di Nyquist non compie nessun giro intorno al punto –1, pertanto il sistema ad anello
chiuso è stabile.
Stabilità dei sistemi di controllo
Stabilità dei sistemi di controllo
Stabilità dei sistemi di controllo
MARGINE DI FASE E MARGINE DI GUADAGNO
Il margine di fase e il margine di guadagno permettono di valutare il grado di stabilità di un sistema
ad anello chiuso.
Margine di fase
dove:
fc (sfasamento critico) è lo sfasamento della f.d.t. ad anello aperto in corrispondenza della pulsazione
alla quale il modulo della funzione di trasferimento ad anello aperto vale 1.
Stabilità dei sistemi di controllo
dove:
OQ è il modulo della fdt ad anello aperto in corrispondenza di uno sfasamento della f.d.t. ad anello
aperto di 180°
Stabilità dei sistemi di controllo
RETI CORRETTRICI
Si sono visti in precedenza alcuni criteri, tramite i quali si può valutare la stabilità di un sistema a
spira chiusa; qui in particolare ci riferiamo al criterio di Bode che considera la funzione di
trasferimento ad anello aperto .
Si studia il diagramma del modulo di questa funzione e si cerca di individuare la pulsazione
di taglio( pulsazione di attraversamento dell'asse a 0dB ).
Questo metodo, afferma che il sistema è stabile se la fase della funzione Gloop calcolato
corrispondenza della pulsazione di taglio è inferiore a 180°; è instabile se superiore a 180°.
in
Si è inoltre fatto notare, che se l'attraversamento avviene con una pendenza maggiore ai
20dB/dec il sistema è fortemente indiziato di instabilità. E' stato, inoltre introdotto un parametro:
il margine di fase
nel quale appare φt=fase della Gloop alla pulsasione di taglio.
Per avere un buon grado di stabilità, il sistema deve presentare margine di fase positivo non
inferiore a 40°, quindi γ≥40°.
Stabilità dei sistemi di controllo
Con questi pochi elementi da ricordare, cerchiamo di considerare alcuni sistemi instabili
vedere se c'è un modo di ripristinarne la stabilità.
per
TECNICHE DI STABILIZZAZIONE
Il modo più semplice e immediato di rendere stabile un sistema è quello di ridurre
opportunamente il guadagno statico di anello.
L'effetto che in tal modo si ottiene risulta immediato se si osserva il diagramma polare del
sistema in esame.
Infatti se si ha ad esempio un sistema la cui funzione di trasferimento ad anello aperto vale:
Stabilità dei sistemi di controllo
dove le tre costanti di tempo T1, T2 e T3 sono positive; ipotizzando di far variare
statico ( il guadagno in continua ) da K a K',
il
guadagno
il diagramma polare subirà la modificazione illustrata a fianco.
Si nota che per K il sistema appare instabile, in quanto il diagramma abbraccia il punto
-1+j0.
Se però riduce il guadagno statico K al valore di K' il diagramma polare si rimpicciolisce e può
risultare come quello disegnato, in cui il punto -1+j0 si trova all'esterno del diagramma polare
(sistema formalmente stabile).
Stabilità dei sistemi di controllo
La stessa variazione rappresentata sul piano cartesiano viene qui illustrata.
si ottiene un diagramma simile al precedente ma traslato verso il basso Il nuovo diagramma
risulta aver un valore minore ω't<ωt della pulsazione di taglio e quindi anche del
corrispondente sfasamento φt.
Questa opzione è poco consigliabile, perchè si peggiorano le caratteristiche statiche del sistema e
si riduce anche la rapidità di risposta;si ottiene cioè un sistema più lento e meno preciso.
Si preferisce seguire altre strade, che consistono nell'alterare la configurazione poli-zeri del
sistema.
Stabilità dei sistemi di controllo
Sul diagramma di Bode, si effettua lo spostamento delle costanti di tempo T al
denominatore della funzione di trasferimento del sistema. Considerando la funzione di
prima:
L'alterazione avviene introducendo nella funzione di trasferimento una coppia polo- zero,cioè
inserendo in cascata sulla linea di andata un elemento che abbia funzione di trasferimento:
ottenendo una funzione corretta
di fatto, si ha lo spostamento della costante di tempo T1.
Stabilità dei sistemi di controllo
Si ha un diagramma delle attenuazioni che ha ancora, una pulsazione di taglio ω't e uno sfasamento
φ't poco maggiore del precedente ,con un guadagno statico del sistema ancora pari a K.
Stabilità dei sistemi di controllo
Cioè la stabilizzazione avviene solo a spese delle prestazioni dinamiche del sistema,senza alterare
quelle statiche. Si è cioè ottenuto, una funzione di trasferimento
del tutto simile alla
precedente,ma con costante di tempo T al posto di T1.
Un altro modo per migliorare la stabilità del sistema è quello di spostare una o più delle costanti
di tempo minori, ( pulsazioni angolari più elevate e distanti dall'origine ) in modo da renderle più
piccole riducendo così il loro contributo allo sfasamento in corrispondenza di ωt .
Questa operazione può essere eseguita ponendo ancora in cascata sulla linea di andata
elemento con funzione di trasferimento del tipo visto con T < T3 .
un
Si ottiene un sistema del tutto simile al precedente,ma con la costante di tempo più piccola
diminuita ( e costante d'angolo corrispondente aumentata). Si può naturalmente ottenere sia
l'aumento della costante di tempo maggiore,sia la diminuzione delle costanti di tempo più
piccole.
Se queste ultime sono ridotte in modo tale che le corrispondenti pulsazioni d'angolo siano
almeno 3÷4 volte maggiori della pulsazione di taglio ωt si ottiene un diagramma di Bode che
scende con una pendenza di -20dB/decade fino a valori di ω molto maggiori di ωt e il sistema
risulta sicuramente stabile con un conveniente grado di stabilità (margine di fase di 50° 60°).
Stabilità dei sistemi di controllo
Per ottenere questo risultato in un sistema a reazione, bisogna inserire nella linea di andata e
più precisamente fra i vari stadi amplificatori del segnale differenza,delle reti elettriche che
abbiano funzione di trasferimento con le caratteristiche indicate .
R ETE R I T A R DA T R I C E
Una rete ritardatrice è un circuito RC secondo lo schema riportato qui a fianco.
La sua funzione di trasferimento si può ottenere con la regola del partitore
in pratica
risulta
e il diagramma di Bode delle attenuazioni appare come in figura seguente (ad es.)
Stabilità dei sistemi di controllo
Stabilità dei sistemi di controllo
Come si può notare il diagramma coincide con l'asse a zero dB per ω<ωt= 1/T, essendo la
costante numerica K=1,
poi scende con pendenza -20dB/dec fino a valori di ω=ω2=1/τ oltre
il quale diventa una retta parallela all'asse delle ascisse.
Lo sfasamento φ risulta negativo entro un certo intervallo di frequenza al di fuori del quale è
nullo,da cui il nome rete ritardatrice o lag in quanto dà luogo a uno sfasamento sempre in ritardo.
Per quanto detto basta far coincidere la costante τ con una costante di tempo del sistema,per
provocare una compensazione polo-zero descritta in precedenza.
RETE ANTICIPATRICE
Una rete anticipatrice è un circuito RC secondo lo schema riportato qui a fianco.
Anche la sua funzione di trasferimento si può ottenere con la regola del partitore
Stabilità dei sistemi di controllo
con una funzione di trasferimento:
Con risulta
il diagramma di Bode delle attenuazioni e degli sfasamenti sono (ad es.):
Stabilità dei sistemi di controllo
Stabilità dei sistemi di controllo
Come si può notare il diagramma delle attenuazioni coincide con l'asse zero dB per ω>ω2 mentre
per ω<ω1 il diagramma è una retta parallela all'asse delle ascisse di ordinata a < 1
perciò la
rete anticipatrice determina una riduzione del guadagno statico del sistema.
Per ovviare all'inconveniente si può porre in cascata alla rete suddetta un amplificatore di guadagno:
ottenendo un diagramma del modulo così modificato
Stabilità dei sistemi di controllo
In tal caso il complesso amplificatore-rete anticipatrice risulta avere funzione di trasferimento:
Lo sfasamento introdotto dalla rete,come si può notare dai diagrammi è sempre in anticipo da
cui il nome rete anticipatrice o lead.
Facendo coincidere la costante τ con una delle costanti di tempo minori del sistema si ottiene la
riduzione di questa costante di tempo che verrà sostituita da T < τ.
RETE A SELLA
Spesso accade che per rendere sufficientemente stabile un sistema occorre eseguire ambedue le
operazioni precedentemente descritte,cioè aumento della costante di
tempo maggiore della
funzione di trasferimento A(s)B(s) del sistema e diminuzione di una delle costanti di tempo
minori. In tal caso è opportuno disporre in cascata ad un amplificatore della linea di andata una
rete a sella avente funzione di trasferimento:
con:
e
Stabilità dei sistemi di controllo
Una rete che realizza questo tipo di funzione di trasferimento è quella disegnata qui a fianco.
E' una combinazione della rete ritardatrice con quella anticipatrice. La sua funzione di trasferimento
vale:
da cui risulta:
e se è
è anche:
Stabilità dei sistemi di controllo
Il diagramma di Bode relativo alla funzione di trasferimento della rete a sella è il seguente:
Se ora si fa coincidere τ1 con la costante di tempo di A(s)B(s) che si vuole aumentare τ2 con quella che
si vuole ridurre,la funzione di trasferimento complessiva presenterà al posto delle due costanti di
tempo in questione la T' e la T'' rispettivamente. Così si avrà una funzione di trasferimento corretta:
Stabilità dei sistemi di controllo
se si pone:
si ha:
Occorre considerare che:
1.Nella determinazione delle reti stabilizzatrici i rapporti fra le costanti di tempo T' τ1 τ2 e T" in tutti i
tipi di reti viste, non devono essere scelti di valore molto elevato per
realizzabilità.
questioni di pratica
E' difficile realizzare reti stabilizzatrici con circuiti RC in cui i rapporti suddetti superino il valore di
10÷15. Nel caso che fossero richiesti per una buona stabilizzazione rapporti maggiori è consigliabile
usare due reti in cascata separate da una amplificatore disaccoppiando i circuiti RC.
E' in pratica impossibile che ci possa essere una compensazione perfetta fra le costanti di tempo
numeratore della rete stabilizzatrice e quella a denominatore della funzione di trasferimento del
sistema dato,che si intende aumentare o ridurre.
In pratica risulterà sempre una differenza fra esse e questo fatto darà luogo ad un diagramma di
Bode leggermente deformato.
3. Le reti in cascata possono essere inserite solo a monte di amplificatori ad elevate
d'ingresso, perchè non venga alterata la loro funzione di trasferimento.
impedenza
Controllori
CONTROLLO ON/OFF
PID
PID PROPORZIONALE
PID INTEGRATIVO
PID DERIVATIVO
PID TOTALE
PWM
RISPOSTA IN FREQUENZA
REGOLATORE PI
TEORIA DEL CONTROLLO
Controllori
Generalita
I controllori, in base alle informazioni ricevute dall'organo di riferimento (o dal
regolatore
dell'anello immediatamente più esterno) e dall'organo di misura «segnale retroazionato»,
forniscono dei segnali utili a correggere qualsiasi allontanamento, causato da variazioni funzionali
del sistema o da variazioni delle variabile di processo dal loro valore di riferimento.
Il loro scopo è infatti fare in modo cioè che la variabile di processo segua più strettamente
possibile il
valore di
riferimento indipendentemente dalla presenza
o meno di disturbi.
garantendo in questo modo la stabilità
I controllori standard largamente utilizzati in campo industriale sono caratterizzati da una rete di
retroazione che ha una struttura fissa (di tipo P, I, PI, PD, PID) e da parametri che, dimensionati
per una certa condizione di lavoro, restano fissi durante il funzionamento
La regolazione è dunque relativa ad una determinata condizione di funzionamento; pertanto se ci si
allontana sensibilmente da tale condizione si possono verificare smorzamenti non più soddisfacenti
e anche instabilità.
In questi casi può essere opportuno ricorrere a controllori adattativi, in cui o i parametri o la
struttura della rete di retroazione sono variabili in relazione alle condizioni di funzionamento del
sistema controllato, in modo che il circuito di regolazione risulti sempre stabilizzato in maniera
ottimale
Controllori
E’ chiamato anche controllo a
tutto o niente.
CONTROLLO ON / OFF
CARATTERISTICA del controllore ON/OFF
Si tratta di un controllore:
• con uscita a due posizioni
• con isteresi.
I controllori ON/OFF presentano i seguenti parametri
regolabili:
• Set Point
• Ampiezza del ciclo di isteresi
Set Point
Imposta il valore desiderato della variabile controllata.
Ampiezza del ciclo (differenziale)
Non è possibile fissare la variabile controllata al valore stabilito
mediante il SP. Bisogna stabilire quindi una fascia, intorno al SP, di valori
tollerabili.
Ciò che si imposta è il valore del differenziale .
Controllori
Azioni di controllo: ON/OFF
OSSERVAZIONI
• PRECISIONE
Alla variabile controllata è consentita una
escursione entro la banda impostata attraverso
il differenziale. Ciò fa si che la precisione risulti
tanto maggiore quanto minore è il differenziale.
• E’ dunque possibile aumentare la precisione
riducendo il differenziale.
Tuttavia la riduzione del differenziale comporta un più frequente
intervento degli organi di commutazione e degli attuatori con
conseguente maggiore usura e riduzione della vita media.
Controllori
Azioni di controllo: ON/OFF
• COSTANTI DI TEMPO
Sistemi con costanti di tempo piccole comportano
un più
frequente intervento degli organi di
commutazione e degli attuatori.
La conseguenza è una maggiore
usura e una
riduzione della vita media dei componenti il sistema
di controllo, se di tipo meccanico.
Controllori
Azioni di controllo: ON/OFF
• INERZIA
Nei sistemi in cui è presente una
notevole inerzia si può verificare una
fuoriuscita della variabile controllata
dalla fascia consentita.
La conseguenza è una precisione
minore di quella impostata con il
differenziale.
CONCLUSIONI
• Si tratta di un controllo semplice ed economico
• Ma poco preciso
Controllori
Azioni di controllo: PID
GENERALITA’
Generalmente la ricerca di buone prestazioni a regime comporta la realizzazione di sistemi che presentano un cattivo
comportamento in transitorio. Succede infatti che l’alto valore del guadagno d’anello necessario per le buone
prestazioni a regime sia spesso anche la causa di notevoli e prolungati pendolamenti della variabile controllata
durante il transitorio.
I regolatori sono composti fondamentalmente da tre parti:
• un generatore del segnale di riferimento
• un nodo di confronto
.• una rete di elaborazione ed amplificazione
8
Controllori
Azioni di controllo: PID
AZIONI DI CONTROLLO
Le azioni di controllo nei controllori PID sono tre:
• AZIONE PROPORZIONALE
L’azione di controllo risulta proporzionale
al segnale errore:
y(t) K P e(t)
• AZIONE INTEGRALE
L’azione di controllo risulta proporzionale all’integrale del segnale errore:
y(t) K I e(t) dt
• AZIONE DERIVATIVA
L’azione di controllo risulta proporzionale alla derivata del segnale errore:
y(t) K D
de(t)
dt
Controllori
Azioni di controllo: PID - Proporzionale
e
AZIONE PROPORZIONALE
Circuiti di
elaborazione ed
amplificazione
Il circuito di elaborazione ed amplificazione produce una uscita proporzionale all’ingresso:
I parametri caratteristici sono:
• Campo proporzionale
• Banda di azione
• Banda proporzionale
y
y(t) K P e(t)
Controllori
Azioni di controllo: PID - Proporzionale
La Banda proporzionale è definita dal rapporto:
B%
e
100
y
Essa rappresenta il valore % dell’ingresso che produce un incremento unitario sull’uscita.
Esempio: Un controllore con B = 25% sviluppa un incremento unitario dell’uscita in
corrispondenza di un incremento di 0.25 dell’ingresso.
OSSERVAZIONI
• Un controllore con B piccola risulta avere
• maggiore sensibilità
• maggiore rapidità di risposta
• rischio pendolamento uscita
• Nel caso di riferimento costante e sistema Tipo 0 il controllo proporzionale risulta soddisfacente se il
sistema controllato è caratterizzato da:
• variazioni di carico piccole
• variazioni di carico poco frequenti.
Controllori
Azioni di controllo: PID - Proporzionale
Esempio:
Nei sistemi Tipo 0 occorre intervenire con un riassetto manuale del riferimento per annullare l’errore a regime. Ma in
presenza di una successiva variazione permanente del carico permane un errore (offset) sulla grandezza controllata.
NB: L’inconveniente dell’offset è tanto più sopportabile quanto minore e poco frequente è la variazione di carico permanente.
Controllori
Configurazione standard deL Controllore P (proporzionale).
f.d.t(s) =Vout/Vrif-Vmis = - R1/Rr = k
- Retroazione negativa
- Sommatore con Rm e Rr uguali
Questo controllore fornisce una risposta rapida e
permette un controllo fine della variabile di processo
poiché la sua uscita varia proporzionalmente allo
scarto di ingresso. Esso però non è in grado di
mantenere nullo il segnale di errore (può solo ridurlo
aumentando il guadagno), in quanto quando lo scarto
di ingresso si annulla la sua uscita si azzera e ciò
causa l'allontanamento della variabile di processo dal
riferimento desiderato
Quindi il sistema non si stabilizza mai, ma fluttua attorno al riferimento. Un aumento del guadagno
proporzionale comporta una diminuzione del
tempo di salita, ma anche più elevate sovra
elongazioni.
Controllori
Azioni di controllo: PID - Integrale
e
AZIONE INTEGRALE
Il circuito di elaborazione ed amplificazione produce una
uscita proporzionale all’integrale dell’ingresso:
Circuiti di
elaborazione ed
amplificazione
y
y(t) K I e(t) dt
INTEGRALE
E’ un operatore matematico con cui si calcolano delle aree.
L’uscita y(t)
risulta dalla somma algebrica dell’area
delimitata dalla variabile e(t) con l’asse dei tempi.
L’uscita di controllo y(t) è costante solo quando il segnale
errore e(t) è nullo.
L’azione integrale consente quindi un flusso di potenza
verso il sistema controllato anche in presenza di errore
nullo.
La costante KI rappresenta la costante di integrazione. Attraverso essa è possibile rafforzare o indebolire l’azione di
controllo integrale quale risulta dal solo integrale dell’errore.
Controllori
Azioni di controllo: PID - Integrale
Il circuito di elaborazione ed amplificazione nel dominio di Laplace è descrivibile con la seguente funzione di
trasferimento:
OSSERVAZIONI
• L’operatore integrale introduce nel sistema un polo nullo, alzando di uno il tipo del sistema. Ciò comporta
le seguenti conseguenze:
•Miglioramento della sensibilità del sistema (il contributo degli errori piccoli è sommato nel tempo e l’uscita
y(t) finisce col raggiungere valori che possono influire sull’azione di controllo).
•Miglioramento delle prestazioni a regime (Esempio: nei sistemi Tipo 0 si annulla l’errore a regime rispetto ad
un ingresso a gradino).
• Aumento del rischio di pendolamento della variabile controllata.
• Poiché l’azione di controllo dipende dal valore dell’integrale (area), negli istanti iniziali essa è di debole
intensità in quanto occorre del tempo per la formazione di tale area.
Ciò comporta un aumento dei tempi di risposta del sistema.
Controllori
Azioni di controllo: PID - Integrale
ESEMPIO:
NB: Il degrado delle prestazioni dinamiche è tale da sconsigliare l’uso dell’azione integrale da sola. Occorre sempre
abbinarla all’azione proporzionale.
Controllori
Configurazione standard deL Controllore I (integrativo): ILl circuito di retroazione é costituito da un
condensatore C1 ; pertanto dalla configurazione generale che segue si deduce la seguente f.d.t.:
f.d.t(s) = - 1/(sRrC1) = 1/s*τi
Questo controllore ha il compito di ridurre l'errore statico a regime e di mantenerlo nullo in
presenza di disturbi costanti sulla variabile d'uscita, in quanto, essendo la rapidità di variazione
del segnale di uscita proporzionale al segnale di ingresso, quando l'ingresso si annulla l'uscita
mantiene il valore che aveva all'istante di annullamento del segnale di ingresso (tiene conto cioè
della ''storia passata'' del sistema).
dSu/dt = K Si
----Si = 0
----
Su non varia
Controllori
Dal punto di vista dinamico l'azione integrale porta ad un peggioramento dei margini di stabilità
in quanto per w 0 il modulo della f.d.t tende all’infinito rendendo il regolatore fortemente
instabile (lavora in saturazione)
E raramente usato da solo a causa della sua scadente velocità di risposta, è molto usato in
unione con un controllore P.
Controllori
AZIONE PROPORZIONALE – INTEGRALE ( CONTROLLORE PI )
Il controllore PI sviluppa contemporaneamente sia l’azione proporzionale che quella integrale:
E’ possibile scrivere la funzione di trasferimento anche nei seguenti termini:
Controllori
Azioni di controllo: PID - Proporzionale-Integrale
Il peso delle due azioni di controllo si modifica nel corso dell’esercizio del controllo.
Il significato di TI si può desumere dai grafici Ia lato:
nell’ipotesi di errore costante, T
rappresenta il
tempo impiegato dall’azione integrale per uguagliare
(ripetere) l’azione proporzionale.
Il reciproco 1/TI rappresenta il numero di volte che l’azione
integrale ripete quella proporzionale in un secondo.
Nella fase iniziale prevale l’azione proporzionale, ma col
trascorrere del tempo questa si mantiene costante mentre
si rafforza quella integrale.
Con l’abbinamento delle due azioni si:
• Migliora il comportamento a regime, grazie all’azione integrale che alza di uno il Tipo di sistema.
• Migliora la prontezza di risposta, grazie all’azione proporzionale.
OSSERVAZIONE:
L’azione integrale aggrava il fenomeno della sovracorrezione per cui, nei sistemi con spontanea
tendenza al pendolamento della risposta, può risultare destabilizzante.
Controllori
Configurazione standard deL Controllore PI (proporzionale integrativo)
In questo controllore, in cui si completano le caratteristiche di risposta rapida del controllore P e di
errore nullo a regime del controllore I, il circuito di retroazione è costituito da un condensatore C1 in serie
ad una resistenza R1 , si ha pertanto
Z1(s) = R1+1/Sc1
e quindi
f.d.t.(s) = Vu/Vr = [(1+sR1C1)/sRrC1] = (1+s*τn)/s*τi
Per il dimensionamento del regolatore PI
- si determinano i valori delle costanti di tempo Tn e Ti , che devono essere tali da
assicurare che il circuito di regolazione sia stabile e ben smorzato;
- si scelgono poi i valori di R e Rr (10-100 kohm), tenendo conto del carico
di misura
- dalle costanti di tempo si ricavano i valori di R1 e C1
ammissibile per gli organi
Controllori
Azioni di controllo: PID - Derivativa
AZIONE DERIVATIVA
e
Circuiti di
elaborazione ed
amplificazione
y
Il circuito di elaborazione ed amplificazione produce una uscita proporzionale alla derivata dell’ingresso:
y(t) K D
de(t)
dt
DERIVATA
E’ un operatore matematico con cui si calcolano le tangenti.
L’uscita y(t) risulta proporzionale alla tangente all’errore in
quell’istante.
Con errore costante l’azione derivativa è nulla. L’azione derivativa
è quindi nulla a regime.
Il controllo mediante l’azione derivativa lavora di anticipo
sull’evoluzione dell’errore. Nel tratto iniziale l’azione si indebolisce
ben prima che cominci a ridursi l’errore, esercitando così una
azione frenante sull’evoluzione futura dell’errore.
La costante KD rappresenta la costante di derivazione. Attraverso essa è possibile rafforzare o indebolire l’azione di
controllo derivativa quale risulta dalla sola derivata dell’errore.
Controllori
Azioni di controllo: PID - Derivativa
Il circuito di elaborazione ed amplificazione nel dominio di Laplace è descrivibile con la seguente funzione di trasferimento:
Y(s)
K D s
E(s)
E(s)
KD = costante di derivazione
K D s
Y(s)
OSSERVAZIONI
• L’operatore derivata lavora di anticipo sull’evoluzione dell’errore (riducendo la potenza quando l’errore sta ancora
salendo e aumentandola quando sta ancora diminuendo). Ciò comporta:
• Aumento della velocità di risposta del sistema, che abbinato all’anticipo consente un
• forte contrasto alle sovracorrezioni che il sistema spontaneamente tenderebbe a
produrre, con conseguenti
• migliori prestazioni dinamiche, cioè forte riduzione del pendolamento della risposta (l’azione correttrice
è tanto più energica quanto più velocemente varia l’errore)
• Complessivamente si ottiene un effetto stabilizzante sull’intero sistema.
• Poiché a regime l’errore è costante, la derivata è nulla. Ne consegue che a regime l’azione derivativa è del tutto assente.
Controllori
Configurazione standard del Controllore derivativo (D).
Nei casi in cui il sistema, in relazione alla sua inerzia, risponda lentamente, il controllore deve
sviluppare un segnale correttivo elevato, che se rimane elevato sovracompensa l'errore e porta
il sistema in oscillazione.
Serve quindi nei confronti dei bruschi disturbi un'azione correttiva inizialmente elevata che
diminuisce nel tempo, ottenibile con un controllore derivativo, la cui uscita è proporzionale alla
velocità di variazione del suo ingresso.
L'azione derivativa migliora i margini di stabilità in quanto introduce un anticipo
3.14/2 e fornisce una correzione che anticipa l'andamento dell'errore nel tempo.
L’inconveniente è che risponde solo a variazioni del
segnale errore, per cui se il sistema presenta un
errore a regime non interviene. Inoltre l'aumento
della banda passante porta ad amplificare i segnali
con contenuto armonico a frequenze elevate (come il
rumore sovrapposto al segnale utile).
di fase pari a
Controllori
Per tali motivi negli azionamenti elettrici, il controllore
utilizzano quasi esclusivamente regolatori di tipo PI.
derivativo non viene impiegato e si
Controllori
AZIONE PROPORZIONALE – DERIVATIVA ( CONTROLLORE PD )
Il controllore PD sviluppa contemporaneamente sia l’azione proporzionale che quella derivativa:
Nel dominio di Laplace:
Y(s)
K P K D s
E(s)
E(s)
KP K D s
Y(s)
E’ possibile scrivere la funzione di trasferimento anche nei seguenti termini:
Controllori
Azioni di controllo: PID - Proporzionale-Derivativo
Così come è stata scritta la funzione di trasferimento non corrisponde ad alcun componente fisicamente realizzabile.
Occorre immaginare la presenza di almeno un polo. Si può immaginare un polo la cui costante di tempo sia molto più
piccola di TD, in modo da rappresentare un transitorio molto più veloce e quindi ininfluente:
Y(s)
TDs
K P 1
T
E(s)
1 D s
N
Costante di tempo N volte più piccola di TD, il
valore di N è normalmente compreso tra 10 e 100.
Il peso delle due azioni di controllo si modifica nel corso dell’esercizio del controllo.
Il significato di TD si può desumere dai grafici a lato:
nell’ipotesi di un aumento lineare dell’errore, TD rappresenta
il tempo impiegato dall’azione proporzionale per uguagliare
(ripetere) l’azione derivativa.
Nella fase iniziale prevale l’azione derivativa, ma col trascorrere
del tempo questa si mantiene costante mentre si rafforza quella
proporzionale.
Controllori
ESEMPIO:
Con Controllore KP = 3
Azioni di controllo: PID - Proporzionale-Derivativo
KD = 0.4
NB: all’avviamento l’azione derivativa è molto brusca e potrebbe imprimere al sistema accelerazioni dannose.
Controllori
Con l’abbinamento delle due azioni:
Azioni di controllo: PID - Proporzionale-Derivativo
• Migliora il comportamento in transitorio, grazie all’azione derivativa che interviene di anticipo e riduce il
pendolamento
• L’effetto stabilizzante consente di diminuire la banda proporzionale dell’azione proporzionale, con
conseguente riduzione dell’errore a regime.
OSSERVAZIONI:
• Come ingresso all’azione derivativa viene spesso applicato il segnale di retroazione. Il
segnale errore presenta infatti delle discontinuità (a causa di discontinuità sul segnale di riferimento) che
farebbero impennare il valore della derivata, facendo saturare gli amplificatori e provocando di fatto la perdita
del controllo.
• Ulteriori miglioramenti del comportamento a regime richiedono l’aggiunta dell’azione integrale.
• Nei processi in cui sono presenti disturbi casuali e di breve durata, l’azione derivativa può causare dannosi
pendolamenti e se ne sconsiglia pertanto l’uso.
Controllori
Controllore proporzionale - derivativo (PD).
Nelle applicazioni industriali più diffuse, anche l’azione derivativa viene associata all’azione proporzionale così
da creare i cosiddetti controllori PD i quali possono essere utilizzati nei sistemi in cui si hanno improvvise
variazioni di carico.
Alcune tipologie di tali impianti possono essere sistemi di controllo per servomotori, oppure sistemi che non
presentano problemi di stabilità e di prestazioni statiche ma che, invece, richiedono una buona velocità di
risposta o un allargamento della banda passante
Con questo regolatore l’azione con cui è modificata la variabile manipolata è proporzionale alla velocità di
cambiamento dell’errore.
Controllori
AZIONE PROPORZIONALE – INTEGRALE - DERIVATIVA ( CONTROLLORE PID )
E(s)
Circuiti di
elaborazione ed
amplificazione
Y(s)
Il controllore PID sviluppa contemporaneamente le tre azioni di controllo:
La legge di controllo è quindi composta da:
• un’azione proporzionale all’errore;
• un’azione Integrale sull’errore;
• un’azione Derivativa sull’errore
Nel dominio di Laplace:
Y(s)
K
1
K P I K D s K P 1
TD s
E(s)
s
TI s
Il controllore PID permette l’adattamento del controllo al sistema da controllare. Impostando i parametri KP, TI, TD
(oppure KP, KI, KD) è possibile far si che siano soddisfatte sia le specifiche a regime che quelle in transitorio.
Controllori
Tra le ragioni del vastissimo utilizzo dei regolatori PID nella pratica dell’automazione industriale (i
PID sono anche detti regolatori industriali), ricordiamo:
• semplicità di realizzazione in diverse tecnologie (elettronica, idraulica, pneumatica);
• efficacia per la regolazione di un’ampia gamma di processi industriali;
• standardizzazione con i relativi vantaggi in termini di affidabilità e economicità;
- semplicità di taratura dei parametri;
• possibilità di taratura automatica dei parametri, per mezzo di semplici esperimenti
ESEMPIO:
Azioni di controllo: PID - Proporzionale-Integrale-Derivativo
351.2
0.5s2 0.8s 1
Sistema
controllato
G(s)
Ramo di
retroazione
H(s) 0.1
Controllori
Azioni di controllo: PID - Proporzionale-Integrale-Derivativo
Il controllore PID può essere messo a punto empiricamente
variando uno o più valori dei guadagni e osservando come
si modifica la risposta del sistema.
Si pongono uguali a zero i guadagni integrale e derivativo e
si aumenta il guadagno proporzionale fino a che il sistema
risponde bene a variazioni del punto di regolazione senza
eccessive sovraelongazioni.
Scelto un ragionevole valore del guadagno proporzionale si
aumenta quindi
lentamente il guadagno integrale per
forzare a zero l'errore del sistema.
Nella maggior parte dei casi è richiesto un piccolo valore del
guadagno integrale, in quanto se abbastanza grande, può
sopraffare l'azione del termine proporzionale, rallentare la
risposta globale e far oscillare il sistema attorno al punto
di regolazione.
In tale caso il problema si risolve
usualmente
riducendo
il guadagno
integrale
ed
aumentando il guadagno proporzionale.
Nel controllo dei motori normalmente il guadagno derivativo del controllore PID è mantenuto nullo
(il termine derivativo viene infatti implementato solo nel caso di carichi con inerzia molto elevata).
Schema di un controllore PID REALE
Controllori
il componente attivo è l’amplificatore operazionale IC1 connesso nella
configurazione invertente. La rete composta da R4, R5, R6 e P1
costituisce una resistenza equivalente Req che varia tra 11MΩ e
231MΩ. Questa rete è stata adottata per poter avere valori così grande
di resistenza usando resistenze di valore normalmente reperibili in
commercio.
L’azione proporzionale svolta dal controllore è realizzata tramite le
resistenze R1 e Req: variando il valore di P1, si aumenta il guadagno e
di conseguenza diminuisce l’errore. Però se un guadagno maggiore
migliora le prestazioni di precisione e di velocità, comporta anche un
minore margine di stabilità.
La parte integrale del controllore viene svolta dalle resistenze R1 e R7
e dai condensatori C4, C5 e C6.
I tre condensatori possono essere inseriti singolarmente o in combinazione tra loro permettendo
ampi margini di regolazione: infatti variando la capacità varia la costante di tempo del regolatore
integrale. Integrando il segnale di ingresso (errore) varia la propria uscita fino a quando il segnale di
errore non è nullo. La parte derivativa del controllore è formata dalle resistenze R2 e Req e dai
condensatori C1, C2 e C3.
Anche in questo caso i condensatori possono essere utilizzati singolarmente o in combinazione tra
loro consentendo ampi margini di regolazione. L’azione derivativa ha il grosso problema di dare
uscita nulla in presenza di errore costante e diverso da zero: per questo motivo non viene mai usata
da sola ma sempre affiancata dal controllo integrale o da quello proporzionale o da una loro
combinazione.
Controllori
Viene però usata perché il suo effetto è positivo per il margine di stabilità: infatti può rendere
stabile un sistema divenuto instabile a causa dell’adozione di guadagni troppo elevati o azioni
integratrici troppo grandi Controllori adattativi.
Le caratteristiche funzionali dei controllori standard sono determinate dalla struttura del loro
circuito di retroazione e dai valori assunti delle relative resistenze e capacità.
Nel caso di sensibili variazioni delle condizioni di funzionamento ipotizzate nella fase di
progettazione del controllore dell'azionamento e qualora si richiedono al sistema controllato
prestazioni elevate, é necessario fare ricorso a controllori adattativi
Questi sono essenzialmente di due tipi:
- a struttura fissa e parametri variabili;
- a parametri fissi e struttura variabile.
I controllori adattativi a
struttura fissa e parametri variabili si ottengono inserendo
nel loro circuito di retroazione uno o più moltiplicatori mentre quelli a parametri fissi e
struttura variabile consentono di passare da una struttura proporzionale-integrativa ad una
struttura proporzionale grazie all’inserimento di elementi attivi (mosfet, diodi)
Controllori
Considerazioni sulla scelta e sul dimensionamento del controllore.
Negli azionamenti elettrici il sistema elettromeccanico da regolare, anche se ordine elevato,
presenta un comportamento dinamico simile a quello di un sistema del secondo ordine;.
Esso possiede infatti normalmente: due costanti di tempo dominanti
(meccanica τm e elettrica τa),
che rallentano la dinamica del sistema, e una serie
di piccole costanti di tempo τpk (e/o di piccoli
ritardi) prodotti da organi
di comando, filtri
e circuiti ausiliari di regolazione, il cui
effetto si estingue rapidamente La loro f.d.t é quindi del tipo:
f.d.t= K / (1+s*τm) (1+s*τa) *(1+s*τp) )
con K guadagno statico
τp= piccola costante di tempo equivalente a tutti i ritardi del sistema
E' pertanto necessario utilizzare uno o più controllori in cascata, al fine di compensare le costanti
di tempo dominanti del sistema da regolare e inserire un polo nell'origine, la cui assenza
comporta un errore a regime nella risposta a gradino.
Con
scelte adeguate delle costanti di tempo del controllore il sistema si rende stabile e la rapidità
di regolazione non dipende piú dalle caratteristiche del motore o della macchina azionata ma solo
dalla piccola costante di tempo equivalente τp
Controllori
PWM
Amplificazione PWM
PRINCIPIO DI FUNZIONAMENTO
La amplificazione presenta le seguenti caratteristiche:
• una uscita istantanea a due posizioni
• un periodo degli impulsi costante
• un duty cycle proporzionale all’ingresso:
• un valore medio nel periodo funzione di TON:
Per la dipendenza del valore medio dell’uscita dal segnale di ingresso, la amplificazione PWM è detta anche a tempo proporzionale
Controllori
Amplificazione PWM
La alta frequenza di commutazione fa si che il carico veda (risulti sensibile) solo il valore medio.
Il controllo PWM realizza quindi un più efficiente controllo proporzionale, ma conserva il limite intrinseco dell’azione
proporzionale: un errore di offset in caso di variazione permanente del carico o comparsa di disturbi permanenti.
Con una frequenza di commutazione degli IGBT di ~ 18 - 20 kHz, si ha un periodo di 55.6 - 20 ms, per cui la risposta
dell’amplificatore può essere considerata istantanea, ossia la sua funzione di trasferimento come una costante (cioè non
contenente termini con la variabile s).
Controllori
RISPOSTA IN FREQUENZA
Regolatore PI
Il controllore PI è caratterizzato dalla seguente funzione di trasferimento:
F(s)
s k p k i
s
In
cui sono presenti:
• uno zero: s = - ki/kp
• un polo: s = 0
Dai diagrammi di Bode si possono trarre le seguenti osservazioni:
• il modulo presenta un andamento tipo passa basso e, nel caso kp < 1, introduce una attenuazione verso le
pulsazioni maggiori
• il controllore introduce un ritardo di fase, maggiore verso le basse pulsazioni
• un aumento del peso dell’azione integrale (ki) comporta (a parità di kp) uno spostamento a destra dello zero, con
conseguentemente ampliamento dell’intervallo di pulsazioni dove maggiore è il ritardo di fase.
Controllori
REGOLATORE PI
L’azione proporzionale, associata all’azione integrale, ha un parziale effetto stabilizzante. Se si riporta la risposta in
frequenza al variare di kp, si può osservare come all’aumentare del peso dell’azione proporzionale si riduce l’intervallo
di pulsazioni con forti ritardi, ma tende ad aumentare la banda passante del complesso degli apparati in cascata.
L’introduzione di un controllore PI in un controllo con retroazione ha delle conseguenze che dipendono dalle
caratteristiche del sistema, tenuto conto che si introduce comunque un ritardo di fase.
6
Controllori
Controllore PI introdotto in un sistema molto stabile
APPLICAZIONE
Sistema senza controllore PI
+
200
s 2 6 s 5
+ _
0.04
Sistema con controllore PI
Ipotesi:
kP 2
k I 1.6
+
+ _
s kP kI
s
200
s 2 6 s 5
0.04
Controllori
Controllore PI introdotto in un sistema molto stabile
Osservazioni:
risultano evidenti:
• il forte aumento del guadagno d’anello alle basse frequenze
• l’estensione della banda passante (kp è > 1)
Controllori
Controllore PI introdotto in un sistema molto stabile
Il sistema senza controllore è caratterizzato da un MG infinito e da un MF pari a 117°.
Dopo l’introduzione del controllore PI il MG resta infinito, mentre il MF si riduce a 65°, un valore ancora rilevante e
soddisfacente.
NB: al di là del posizionamento dello zero del controllore, quest’ultimo introduce comunque un ritardo di fase che riduce
il MF, ed ha, quindi, comunque un effetto destabilizzante.
Controllori
Controllore PI introdotto in un sistema molto stabile
NB
: L’azione proporzionale pesa il 25% in più rispetto all’azione integrale.
Controllori
Controllore PI introdotto in un sistema poco stabile
Il sistema senza controllore è caratterizzato da un MG pari a 23.2 dB e da un MF pari a 31.3°.
Con l’introduzione del controllore PI i margini divengono entrambi negativi e denotano un anello chiuso instabile.
Valori diversi di kp e ki mantengono il sistema stabile, ma i margini sono così ridotti da rendere del tutto inaccettabile
il transitorio (es: kp = 3, ki = 0.4, cioè kp 6.5 volte ki, risultano MG = 8.71 dB e MF = 6.7°).
NB: si ricordi che un aumento di kp ha effetto stabilizzante, ma al prezzo di un aumento dell’ampiezza delle
sovraelongazioni.
RIEPILOGO
Controllori
Un sistema di controllo ad anello chiuso deve soddisfare le specifiche assegnate nel dominio della
frequenza e quelle assegnate nel do-minio del tempo. Queste ultime si suddividono in specifiche del
comportamento a regime (errore a regime, sensibilità ai disturbi additivi e para-metrici) e in
specifiche del comportamento in regime transitorio ( tempo di salita, sovraelongazione, tempo di
assestamento, velocità della rispo-sta).
Le specifiche definite nel dominio della frequenza sono la banda passante, la stabilità, il margine di
fase e il margine di guadagno. In particolare se il sistema non è stabile, o se il suo margine di fase e il
suo margine di guadagno non corrispondono a quelli richiesti, è necessario intervenire sul sistema,
modificarlo in modo che risponda ai requisiti richiesti senza alterare, nei limiti del possibile, le altre
caratteristiche quali la velocità della risposta e la precisione.
La stabilizzazione, ad esempio, di un sistema instabile mediante la riduzione del guadagno di anello è
consigliabile solo in casi particolarmente semplici perché tale tecnica provoca, come si è visto,
l'aumento dell'errore a regime.
Nei casi più
complessi, quando cioè il progettista deve soddisfare le specifiche assegnate, è
necessario modificare la configurazione del sistema introducendo, in punti opportuni della catena, reti
elettriche di tipo passivo o di tipo attivo al fine di migliorare le prestazioni statiche e dinamiche del
sistema.
Se si desidera stabilizzare il sistema senza diminuire il guadagno del sistema e allora possibile usare
una rete ritardatrice.
Controllori
La rete ritardo-anticipo, infatti, permette di sfruttare i pregi di entrambe le reti correttrici,
consente di stabilizzare sistemi assolutamente instabili (ovvero sistemiche, se chiusi in
retroazione
con un semplice regolatore proporzionale, sono instabili in anello chiuso per
qualsiasi valore del guadagno), senza un eccessivo aumento della larghezza di banda.
Inoltre, poiche la rete ritardo-anticipo ha guadagno statico unitario, non varia la precisione a
regime.
Elementi del circuito di controllo.
Negli azionamenti elettrici il tipo di controllo del moto di gran lunga più diffuso è quello in cascata
o gerarchico, che è caratterizzato dalla presenza di più anelli sovrapposti, in ognuno dei quali la
variabile di stato ha una dinamica molto più rapida di quella relativa alla variabile di stato
dell'anello immediatamente più esterno.
Regolatore di posizione: non presente
Controllori
Regolatore di corrente: dipende dal tipo di motore
Regolatore di velocità: dipende dal tipo di carico
Regolatore di posizione: dipende dal tipo si carico
e si posiziona nell’anello esterno
Le caratteristiche salienti del controllo in cascata sono:
- relativa semplicità nella scelta e nel dimensionamento dei vari controllori (uno per ogni
variabile controllata); il transitorio della variabile di un anello inizia solo dopo che è terminato
quello della variabile relativa all'anello sovrastante per cui si può prendere in esame una sola
parte del sistema per volta. Nel caso dell'azionamento di figura si dimensiona il controllore
dell'anello di corrente, quindi quello di velocità e infine quello di posizione
- notevole flessibilità, in quanto é possibile, partendo da un dato azionamento,
ottenere
facilmente il controllo di ulteriori variabili aggiungendo altri anelli;
- elevata protezione del sistema, in quanto ogni variabile intermedia può essere controllata
limitando il relativo valore di riferimento.
In un circuito di controllo si possono distinguere:
Controllori
a. organi di riferimento
Forniscono una grandezza di riferimento regolabile espressa per mezzo
di una tensione
continua (di valore massimo pari a 10-15V). L'elemento più
semplice e più usato é il
potenziometro
b. organi di controllo
La funzione dell'organo di controllo è quella
fornire, in base ai valori della tensione di
comando (Vcm) fornita dal regolatore
di corrente e delle
tensioni di riferimento ricavate
dalla rete di alimentazione(Vr) le sequenze degli impulsi di gate per gli SCR controllando gli
istanti di innesco e quindi il valore medio della tensione ai suoi morsetti in uscita
c. Organi di misura
I sensori sono insiemi di uno o più trasduttori con relativa circuiteria per l'elaborazione del
segnale, la cui funzione è convertire una generica grandezza fisica in ingresso in un segnale
elettrico (generalmente in una tensione continua) in uscita interfacciabile con il sistema di
controllo.
I sensori si dividono in assoluti o incrementali, in analogici e digitali, in intelligenti (se
interagiscono con un computer di controllo per la manipolazione dei dati) e non intelligenti (se
forniscono al computer dei semplici dati).
Controllo del motore in continua a magnete permanente
Dal punto di vista elettrico, il motore può essere assimilato al seguente circuito
Definendo con:
Ke costante di velocita,
R resistenza di armatura,
L induttanza di armatura
E = Ke*w(t)
va= R*i+ L*(di(t)/dt)+ E
Trasformando nel dominio di Laplace e ipotizzando I(0)=0 si ottiene
V(s) = Ke*wm(s) + (R +L*s)*i(s)
per un motore in corrente continua possiamo scrivere
C = coppia del motore = Kt *i(t)
Kt costante di coppia del motore Es = Ke*w
Per la parte meccanica, supponendo che la trasmissione del moto venga effettuata mediante un albero
ed un giunto di tipo rigido, in modo che la velocità dell'asse lato-motore e lato-carico sia la stessa, la
coppia generata Cm dal motore dovrà essere uguale alla somma della coppia resistente Cr applicata
all'albero del motore e della coppia inerziale (inerzia dovuta alla parte meccanica e al carico, trascurando
la coppia di attrito)
Cm –Cr = Cj = J*(dw/dt)
w = (1/Js)*(Cm – Cr)
d θ(t)/dt =w(t)
θ = (1/s)*w
Schema a blocchi del
senza carico )
motore comprensivo del
controllo del moto
controllo di posizione
carico (che coincide, nel caso in esame, con quello
Funzione di trasferimento. Per lo studio della funzione di trasferimento, si deve tenere presente che
la coppia resistente Cr, che la coppia motoria Cm deve vincere, è somma di più termini:
Detto J il momento di inerzia complessivo del motore e del carico, At il coefficientedi attrito viscoso
complessivo del motore e del carico, e Cu la coppia resistente del carico, si può quindi scrivere:
In questo schema a blocchi sono considerate come entrate la tensione di armatura e la coppia resistente del carico, e
come uscita la velocità angolare: si tratta di un sistema a retroazione negativa, pertanto il motore tende ad
autocompensarsi, ovvero a mantenerecostante la sua velocità (con Va costante).
Se si suppone che siano trascurabili gli attriti, la funzione di trasferimento del motore,valutata rispetto alla tensione di
alimentazione, risulta:
Si tratta di una funzione di trasferimento con due poli; questo motore è
quindi un sistema del secondo ordine. I poli si ricavano dalle radici del
denominatore:
poli possono risultare reali negativi (distinti o coincidenti), o complessi coniugati a parte reale
negativa.
In ogni caso, quindi, il sistema è asintoticamente stabile; in presenza di una sollecitazione a gradino
della tensione di ingresso, se i poli sono reali la velocità del motore raggiunge il valore a regime in
modo aperiodico, mentre con poli complessila raggiunge tramite un’oscillazione smorzata.
Due parametri caratteristici del motore sono la costante di tempo elettrica e e la costante di tempo
meccanica m
Si potrebbe facilmente dimostrare che, qualora risulti Tm >= 4Te, i poli risultano reali (risposta aperiodica); in
particolare qualora risulti Tm >= 10T e i due poli coincidono, a meno del segno, con l’inverso delle due costanti
di tempo e, ovviamente, esiste un polo dominante determinato da Tm
Da queste premesse può proseguire lo studio calcolando
la f.d.t equivalente al
comportamento desiderato della macchina e del sistema (a vuoto, oppure quando viene
impressa una variazione brusca della coppia resistente).
Si studiano successivamente le risposte ai vari segnali d’ingresso, determinandone le
condizioni di stabilità tenendo presente che Il motore in continua è caratterizzato da due
parametri particolarmente importanti,
la costante di tempo elettrica
τe= La/Ra
la costante meccanica τm = Ra*J /KeKt,
dove j è il momemto di inerzia complessivo del motore collegato al carico.
Se, come normalmente succede,
τm>>τe la funzione di trasferimento del motore F (s) =
w (s)/Va(s), che lega la velocità di rotazione alla tensione di armatura, espresse mediante la
trasformata di Laplace, viene a presentare due poli distinti, in valore assoluto sostanzialmente
coincidenti con l'inverso delle costanti di tempo.
La frequenza di taglio del sistema viene pertanto ad essere determinata dal polo corrispondente
alla costante meccanica del motore
Si potrebbe facilmente dimostrare che, qualora risulti Tm >= 4Te, i poli risultano reali (risposta aperiodica); in particolare
qualora risulti Tm >= 10T e i due poli coincidono, a meno del segno, con l’inverso delle due costanti di tempo e,
ovviamente, esiste un polo dominante determinato da Tm
Dinamo tachimetrica
I motori in corrente continua sono delle macchine dal funzionamento reversibile, ovvero, ponendo in rotazione la
macchina, è possibile prelevare una tensione di armatura. La macchina, in questo modo, si comporta da
generatore in continua e viene detta dinamo. In particolare, per la la forza elettromotrice di armatura risulta
direttamente proporzionale alla velocità: se tra i terminali dell’avvolgimento non viene applicato un carico
significativo, ovvero la tensione Va viene prelevata praticamente a vuoto, risultando trascurabile la c.d.t. su Ra,
per cui si può considerare
Va =E
Una macchina di questo tipo, strutturalmente equivalente a un piccolo motore in DC a magnete permanente,
viene detta dinamo tachimetrica e viene usata come trasduttore di velocità angolare, calettandola su un asse di
rotazione di cui si vuole va-lutare la velocità di rotazione. Le dinamo tachimetriche devono presentare come
caratteristiche peculiari una limitata inerzia e poche perdite meccaniche, in modo da non alterare le
caratteristiche del carico meccanico applicato all’asse di rotazione. Mediamente, queste dinamo presentano una
sensibilità di 0,1÷1 V per 100 giri/min. Vediamo alcuni limiti di questi trasduttori:
la tensione di uscita presenta una certa ondulazione residua: La presenza del collettore permette poi di prelevare
un segnale raddrizzato a onda intera. Per ridurre l’ondulazione, si deve aumentare il numero dei settori del
collettore (fig. 3);
◗
la linearità è abbastanza limitata (difficilmente l’errore di linearità è inferiore al 10%);
◗
l’inerzia meccanica e l’attrito non sono sempre totalmente trascurabili;
◗
presentano una limitata velocità massima, a causa delle vibrazioni delle spazzole;
◗
le spazzole sono soggette a usura.
Motori a eccitazione indipendente :
caratteristica meccanica
E = K*
Φ *Ω
(1)
Cm = K * Φ *I
Caratteristica meccanica del motore
con
U = E +Ri*Ii
(2)
I = U – E /Ri = (U – K*Φ*Ω)/Ri
(3)
eccitazione indipendente e flusso costante
la velocità è:
- direttamente proporzionale alla tensione alle spazzole,
- inversamente proporzionale al flusso risultante in cui sono immersi
conduttori d’indotto
La variazione di velocità può quindi ottenersi con la variazione della
tensione, con la variazione del flusso o con entrambe le variazioni
Lo schema a blocchi coincide con quello a magneti permanenti
Operando a flusso costante, per variare la velocità si agisce sulla tensione di armatura e si opera,
come d’altronde nei motori a magnete permanente, a coppia motrice costante. Infatti, per la , o per la ,
al variare di Va varia anche E e, quindi, la differenza rimane costante e tale risulta anche la Ia e, per la o
la , la Cm.
Al variare della velocità, a flusso costante, essendo Ia costante, la potenza assorbita dall’armatura
cresce linearmente con la Va.
Facendo ancora riferimento alla figura , quando la velocità del motore supera il valore nominale, se
non si vuole sovraccaricare lo stesso in modo eccessivo, non è più possibile aumentare la velocità
agendo sulla tensione di armatura. Mantenendo costante la tensione di armatura, si può variare la
velocità agendo sul flusso. In questo modo, però, per aumentare la velocità si deve ridurre il flusso;
infatti per la , se si suppone E Va, si vede che la velocità è inversamente proporzionale al flusso.
Riducendo il flusso, si vede che, per la , diminuisce la coppia motrice; in conseguenza deve ridursi
anche la coppia resistente e tende a risultare costante la Pa.
Per lo studio della funzione di trasferimento, se si opera a flusso costante, rimane valido quanto
esposto per i motori a magnete permanente.
Si osservi, infine, che in questo tipo di motore, per invertire il verso di rotazione, è possibile agire sia
sul verso della tensione di armatura che su quella di eccitazione
ESERCIZIO: CONTROLLO DI SPESSORE
SCHEMA DI PRINCIPIO
SCHEMA A BLOCCHI
Alimentazione di potenza
Circuiti di retroazione
Il ritardo finito viene inserito nel ramo diretto in quanto il ramo di retroazione comincia con la lettura
della variabile d’uscita da parte del sensore.
CONVERTITORE
DI POTENZA
Svolge la funzione della amplificazione della potenza ed è caratterizzato da un guadagno A0:
Ao = Va/e
La velocità di risposta dipende dalla tecnologia con cui sono realizzati.
Se introduce un ritardo la sua funzione di trasferimento è dipendente dalla variabile di Laplace ‘s’.
Ipotesi:
risposta istantanea
Funzione di trasferimento
A(s) = A0
SERVOMOTORE ELETTRICO
Svolge la funzione di attuatore: converte la potenza elettrica in potenza meccanica.
La sua funzione di trasferimento dipende dalla tecnologia con cui è realizzato.
Ipotesi: Motore a collettore in corrente continua a magneti permanenti
Funzione di trasferimento: costituisce un sistema del 2° ordine
VITE A RICIRCOLO DI SFERE
Svolge la funzione di attuatore (insieme al servomotore): converte il movimento rotatorio in traslatorio.
Il suo parametro fondamentale è il passo:
Dal passo si ricava il Rapporto di trasformazione:
traslazione della chiocciola per un giro della vite
In questo esempio la Funzione di trasferimento non corrisponde al Rapporto di trasformazione, in quanto:
RITARDO FINITO (1/3)
E’ un ritardo dovuto alla collocazione fisica del sensore che misura lo spessore della lamiera: è posto alla distanza
d dagli assi dei cilindri
Lo si calcola attraverso la relazione:
Nel dominio di Laplace si rappresenta con il termine
NB: si tratta di una funzione di trasferimento di tipo trascendente, occorre trovare una funzione razionale che ne
rappresenti una buona approssimazione.
RITARDO FINITO (2/3)
Una funzione esponenziale può essere approssimata con diverse funzioni. Per piccoli valori dell’esponente le
diverse rappresentazioni sono equivalenti.
RITARDO FINITO (3/3)
In questo sistema:
Approssimante di Padé (1° ordine):
Approssimante di Padé (2° ordine):
CIRCUITI DI RETROAZIONE
• Il ramo di retroazione è costituito da:
-Sensore, per la misura della variabile controllata
-Circuiti di elaborazione, per il condizionamento del segnale elettrico fornito dal sensore
• Il dimensionamento del guadagno è determinato da:
-valore desiderato della variabile controllata (xd)
-valore del segnale di retroazione Vret uguale all’ingresso di riferimento (Vrif)
Più in generale:
ESEMPIO NUMERICO (1/6)
CONVERTITORE DI POTENZA
Il guadagno risulta posto pari a:
SERVOMOTORE
VITE A CIRCOLAZIONE DI SFERE
Esempio numerico (2/6)
RITARDO FINITO
Il sensore è collocato alla distanza d = 10 cm
La lamiera avanza con la velocità di vl = 0.2 m/s
Funzione di trasferimento: Approssimante di
Padé del 1° ordine:
CIRCUITI DI RETROAZIONE
La lamiera deve essere laminata allo spessore di
Il segnale di riferimento è posto a Vrif = 5 V
x = 12 mm
Ipotesi: i circuiti forniscono una risposta istantanea, ciò consente di scrivere la funzione di trasferimento come
una costante pura
Esempio numerico (3/6)
VERIFICA DELLA STABILITA’
Metodo di Routh
Calcolo della funzione di trasferimento del ramo diretto:
G(s) AM (s) Rv(s) RF (s)
Esempio numerico (4/6)
I coefficienti dell’equazione soddisfano la condizione necessaria.
Si costruisce la tabella:
I coefficienti
della prima colonna non presentano variazioni di segno per cui il sistema risulta
stabile: 4 soluzioni reali negative e/o complesse coniugate con parte reale negativa.
Le soluzioni dell’equazione caratteristica risultano infatti:
s1 = - 3.90
s2 = - 2.99
s3 = - 0.057 + j 0.25
s4 = - 0.057 - j 0.25
Esempio numerico (5/6)
NUOVA IPOTESI
un problema sul controllo della velocità della lamiera provoca un rallentamento del nastro facendo salire
il ritardo t0 a 5 s
Se il problema di controllo si prolunga nel tempo potrebbero presentarsi fenomeni di instabilità.
E in questo caso, ricalcolando il segno delle soluzioni dell’equazione caratteristica, si scopre che il
sistema è divenuto instabile.
Equazione caratteristica:
soluzioni:
10 s4 34 s3 17 s2 0.023s 0.79 0
s1 = - 2.79
s2 = - 0.69
s3 = 0.037 + j 0.20
s4 = 0.037 - j 0.20
Esempio numerico (6/6)
controlli digitali
MOTORE PASSO PASSO
MOTORE A RILUTTANZA VARIABILE
TECNICHE DI PILOTAGGIO
CARATTERISTICA MECCANICA
INTEGRATO L298
controlli digitali
MOTORE PASSO PASSO
Proprietà
E’ un motore alimentato con forme d’onda impulsive: ad ogni impulso corrisponde una rotazione del motore di un
angolo fisso (passo, step).
Vantaggi:
•
adatti per controllo di posizione e/o velocità in sistemi con catena aperta (senza retroazione)
•
•
affidabili e robusti (non necessitano di manutenzione periodica)
facile controllo via computer (forme d’onda impulsive) Svantaggi:
• bassa potenza specifica
• basso rendimento energetico
• necessità di scheda di alimentazione elettronica
• funzionamento irregolare a basso regime
• bassa velocità massima
controlli digitali
TECNOLOGIA di realizzazione del rotore
• Magneti permanenti (MP)
• Riluttanza variabile (RV)
• Ibridi
NUMERO DI FASI presenti sullo statore
• Bifase
• Polifase
SENSO DI CIRCOLAZIONE della corrente negli avvolgimenti di ciascuna fase statoriche
• unipolare: un solo senso di percorrenza della corrente nell’avvolgimento
• bipolare: è possibile invertire il verso della corrente nell’avvolgimento
Un parametro molto importante è quello della RISOLUZIONE, esprimibile come:
• angolo (passo, step) di cui ruota il rotore per ogni impulso
Risoluzione =360
Numero di passi
• numero di passi per giro
NB: la risoluzione deriva dalle caratteristiche costruttive del motore, ma può essere modificata
attraverso la scheda elettronica di pilotaggio.
controlli digitali
Motore step a Magnete Permanente
Motore step ibrido
controlli digitali
Motore a Magneti Permanenti, Bifase, Bipolare
Magneti Permanenti: il rotore è formato da magneti permanenti (magnetizzazione radiale).
Nell’esempio è presente una sola coppia polare.
Bifase: si hanno due fasi A-C e B-D
Bipolare: l’assenza di una presa centrale nelle fasi lascia intendere che deve essere possibile
l’inversione della corrente nelle fasi.
Funzionamento:
Alimentando il motore dal terminale A, si genera un flusso magnetico che ha un nord in 1 e
un sud in 3 (fig. a). Considerando la situazione di partenza del rotore, il nuovo flusso lo fa
girare di 90° in senso orario (fig. b). Una successiva alimentazione dal terminale B (nord in 2
e sud in 4) induce una ulteriore rotazione di 90° (fig. c).Alimentando ulteriormente da C e poi
da D si fa completare al rotore un giro.
controlli digitali
Il rotore compie un giro completo
in
4 T (T = durata di un
impulso). Spesso la cadenza dei
passi viene indicata con la
frequenza:
f
Se il moto è continuo, è possibile
calcolare una velocità media di
rotazione
2
4T
1
T
rad
s
Dove 2 / 4 rappresenta l’angolo per passo.
NB:
questa modalità di alimentazione (tecnica di
pilotaggio) è chiamata One Phase-On (oppure
Wave Drive Mode)
controlli digitali
Motore a Magneti Permanenti, Bifase, Unipolare
Unipolare: la presenza della presa centrale nelle fasi
lascia intendere che la corrente nelle fasi può avere
un solo senso.
Funzionamento:
La corrente entra da un terminale ed esce dalla
presa centrale.
Alimentando in sequenza i terminali A – B - C – D
si fa fare un giro completo al motore.
NB: i motori unipolari sono pilotati con le stesse tecniche dei motori bipolari.
controlli digitali
Confronto Bipolari - Unipolari
• I motori unipolari richiedono una scheda di controllo più semplice poiché non richiedono
l’inversione del verso della corrente nelle fasi
• I motori bipolari forniscono una coppia maggiore a parità di volume esterno in quanto
l’intero avvolgimento è percorso da corrente, quando la fase è eccitata (negli unipolari
invece solo metà avvolgimento per volta può essere percorso da corrente)
controlli digitali
Motore a Riluttanza Variabile
Funzionamento: il rotore non è magnetizzato; la coppia motrice si forma per l’anisotropia del rotore:
•Alimentando la bobina 2 si crea un polo magnetico in 2,
•che induce un polo opposto in y’,
•i due poli si attraggono e nasce la coppia motrice.
NB: se il rotore fosse un cilindro (isotropo) il punto y’ si troverebbe sull’asse 2 – 2’ e non
nascerebbe alcuna coppia.
Il fenomeno può essere descritto anche in termini di riluttanza: la coppia motrice nasce in
quanto il circuito magnetico nel tratto 2 – 2’ presenta riluttanza minima su un percorso che
non è quello diretto, più breve, tra i denti di statore. Le forze di attrazione tra i poli magnetici
indotti non giacciono sulla stessa linea d’azione e formano quindi una coppia.
Essendo il rotore non magnetizzato, l’inversione del senso di
rotazione non può avvenire invertendo le polarità magnetiche
sullo statore (come in quelli a MP).
Occorre modificare la sequenza di alimentazione degli
avvolgimenti.
Per questo motivo gli avvolgimenti hanno una presa centrale.
Statore e rotore devono avere numero di denti diverso per evitare
un loro allineamento.
CONFRONTO
controlli digitali
MP - RV
MOTORI a MP:
• Grazie al rotore magnetizzato, presentano una coppia residua, in assenza di alimentazione.
• Sono costruibili solo a bassa risoluzione, in quanto, per ragioni meccaniche, non si può
aumentare più di tanto il numero di poli magnetici del rotore.
• Per via dell’alta inerzia del MP del rotore la frequenza di alimentazione deve essere piuttosto
bassa.
Il profilo b corrisponde a un maggior momento
d’inerzia, che frena la
accelerazione e ritarda il raggiungimento della posizione finale da parte del
rotore.
Il profilo a consente di dimezzare la durata degli impulsi (raddoppia la
frequenza), impossibile per il motore dal profilo b.
Motori a RV
• Non manifestano alcuna coppia residua.
• Realizzano risoluzioni molto alte.
• Raggiungono velocità maggiori
• Presentano fenomeni di risonanza che generano oscillazioni
dell’asse intorno alla posizione diequilibrio.
controlli digitali
Motore Ibrido
Il rotore è formato da due corone dentate poste agli estremi di un cilindro
che contiene un magnete permanente (magnetizzazione assiale).
I denti delle due corone sono sfasati di 1/2 passo polare (passo polare =
distanza angolare tra due denti).
Sullo statore sono presenti espansioni polari con denti dello stesso passo
di quelli di rotore.
Quando i denti di rotore sono allineati con quelli di una espansione
polare,
essi risultano sfasati di 1/4 di passo da quelli dell’altra
espansione polare.
La tecnologia ibrida è complessa e costosa, ma consente di raggiungere
alte risoluzioni (480 passi per giro).
I motori ibridi esaltano i vantaggi delle altre due tecnologie:
• disponibilità di una coppia residua (grazie al magnete permanente)
• alta risoluzione (grazie sagomatura del rotore per generare percorsi
a riluttanza diversa).
controlli digitali
TECNICHE DI PILOTAGGIO
• Le seguenti tecniche si applicano a tutti i tipi di motori:
• FULL STEP (Passo intero)
• Wave Drive Mode (One Phase-On): alimentazione di una fase per volta
• Normal Drive Mode (Two Phase-ON): alimentazione di due fasi per volta
• HALF STEP (Mezzo passo), mediante alternanza One Phase-On e Two Phase-On
• MICROSTEPPING (micropassi), mediante modulazione della corrente.
controlli digitali
ESEMPIO: Two Phase-On
Osservazioni: Rispetto alla tecnica One Phase-On
• si modifica la posizione di equilibrio del rotore, ma non
cambia la risoluzione (90° per passo)
• la coppia motrice aumenta di 1.41 volte:
BT
BAC = BDC = B
BAC
BT = 1.41B
BBD
controlli digitali
ESEMPIO:
Half Step
A
B
C
D
t
A
AB
B
BC
C
Osservazioni:
• si raddoppia risoluzione (45° per passo)
• la coppia motrice non è costante: quando sono alimentate due fasi
aumenta di 1.41 volte. Si supera il problema aumentando la
corrente quando si alimenta un solo avvolgimento.
controlli digitali
ESEMPIO:
Microstepping
Consiste nell’alimentare due fasi per volta,
ma regolando la corrente nelle diverse fasi.
Se si dimezza la corrente nella fase B-D:
Consiste nell’alimentare due fasi per volta,
ma regolando la corrente nelle diverse fasi.
controlli digitali
Esempi di collegamenti
Si tratta di motori a 2 fasi, ma con diverse bobine e
collegamenti esterni.
cavi per i
Non esiste uno standard nella designazione dei colori dei cavi.
controlli digitali
Circuiti di alimentazione
2 bobine ( 4 cavi ) : Bipolare
4 bobine ( 8 cavi ) : Unipolare
Motore con 5 fasi
controlli digitali
Principali grandezze nominali
DATI DI TARGA
Angolo di passo
[°]
Angolo di cui ruota il rotore ad ogni passo
Tensione di fase
[V]
Tensione di alimentazione delle fasi
Corrente di fase
[A]
Corrente assorbita da una fase quanto alimentata alla tensione di fase
Resistenza di fase [ Ω ]
Induttanza di fase [ L ]
Resistenza elettrica di una fase
Induttanza di una fase
Coppia di mantenimento (Holding Torque) [ Nm ] Coppia sviluppata dal motore quando
alimentato e fermo
Coppia residua (Detent Torque) [ Nm ] Coppia sviluppata dal motore quando non alimentato e fermo
Momento d’inerzia [ kg m2 ]
Momento d’inerzia del rotore
NB: nel caso dal motore fuoriescano un numero di conduttori tale da consentire funzionamenti sia
come unipolare che bipolare e il costruttore fornisca i dati di targa senza specificare a quale
configurazione si riferiscano, essi sono normalmente da attribuirsi alla configurazione bipolare.
controlli digitali
NB:
CH = Coppia di mantenimento (coppia di stallo) (Holding Torque): il motore è alimentato ed è
fermo. In questa circostanza assorbe la corrente massima (di fase).
A bassa velocità (frequenza) il motore ha normalmente un funzionamento instabile, per cui si evita
di tracciare la caratteristica.
All’aumentare della velocità la coppia generata diminuisce (con la corrente assorbita). Oltre un
limite massimo di velocità (frequenza) il motore perde il passo e si blocca.
controlli digitali
Normalmente il motore parte da fermo e viene alimentato immediatamente con impulsi alla frequenza
desiderata.
Durante l’avviamento la coppia motrice deve vincere oltre alla coppia resistente del carico anche la
coppia d’inerzia, che si manifesta in conseguenza della accelerazione:
La coppia d’inerzia (Ci) si oppone alla accelerazione, per cui non tutta la coppia di pull-out (Cpo) è
disponibile per il carico.
Si definisce coppia di pull-in (Cpi) la coppia di carico che il motore riesce ad avviare senza perdere
passi. Essa dipende quindi dal
• carico (per via dell’inerzia) e dalla frequenza
(per via della coppia motrice CPO)
controlli digitali
Motore Passo Passo Caratteristica meccanica
Start-Stop Range: per coppie di carico interne a quest’area il motore è in grado di
avviare, fermare e invertire il movimento del carico senza perdere passi.
Slew Range: per coppie di carico interne a quest’area il motore riesce ad avviare o arrestare
il carico, senza perdere passi, solo se la frequenza di alimentazione varia lentamente.
controlli digitali
Formule
TP = intervallo di tempo tra due passi (nella modalità One phase-On: durata dell’impulso) [ s ]
f = frequenza dei passi, passi per secondo
[ Hz ] ω = velocità
angolare [ rad/s ]
α = angolo corrispondente ad un passo [ rad ]
Il motore deve raggiungere la velocità (ω) corrispondente alla frequenza di alimentazione nel
tempo TP di un passo.
controlli digitali
Esercizio
Verificare se è possibile avviare con frequenza di 500 Hz, un carico caratterizzato da un JC = 22 gcm2 e
una CC = 6 Ncm, col seguente motore:
α = 3.6 ° = 0.06283
rad
IN = 0.80 A
R = 4.5 Ω L
= 5.7 H
CH = 11.4 Ncm
CD = 1.55 Ncm
JM = 15 gcm2
SOLUZIONE
Bisognerebbe verificare se la CC, alla frequenza di 500 Hz, si trovi all’interno della curva di pull-in. Ma non si
dispone della curva di pull-in. Si deve allora calcolare la coppia d’inerzia e verificare che sottraendola alla coppia
di pull-out non dia origine a una coppia inferiore a quella del carico.
Da Curva di pull-out, a 500 Hz: CPO = 10 Ncm
JT = JM + JC = 15 + 22 = 37 gcm2 = 37·10-3·10-4 kgm2
t
f 2 0.06283 5002 15708
C i J T
rad/s 2
3.7 106 15708 0.0581 Nm 5.81 Ncm
t
= 3.7·10-6 kgm2
C pi C po C i 10 5.81 4.19 Ncm
NB: Cpi < CC, quindi il motore non
può avviare a 500 Hz questo carico.
controlli digitali
Esercizio
Con i dati dell’esercizio precedente, calcolare la curva di pull-in.
NB: calcolare la coppia di pull-in per le seguenti frequenze (Hz): 100, 300, 600, 1000, 2000, 4000
α = 3.6 ° = 0.06283
rad
IN = 0.80 A
Curva di
pull-out
R = 4.5 Ω L
= 5.7 H
•
•
CH = 11.4 Ncm
CD = 1.55 Ncm
JM = 15 gcm2
•
SOLUZIONE
f
[ Hz ]
CPO
[ Ncm ]
Δω/Δt
[ rad/s2
]
Ci
[ Ncm ]
Cpi
[ Ncm ]
100
10
628.3
0.23
9.77
300
10
5 655
2.1
7.9
600
9.8
22 619
8.4
1.4
1000
9.5
62 830
23.2
- 13.7
2000
8.2
251 320
4000
5.7
1 005 280
NB: tra 600 Hz e un 1 kHz la coppia
di pull-in si annulla.
controlli digitali
Esercizio
Un carico, con CC = 4 Ncm e JC incognito, è azionato da un motore passo passo. Determinare il JC massimo che il motore
riesce ad avviare alla frequenza di 500 Hz.
Dati motore:
α = 1.8 ° = 0.0314 rad IN
= 0.30 A
R = 24 Ω L
= 30 mH
CH = 13.8 Ncm
CD = 1.75 Ncm
C po Cc 0.07
0.00000892 kgm 2
7850
t
89.2 gcm 2
JT
JM = 17 gcm2
SOLUZIONE
Occorre cercare la max coppia d’inerzia, da cui ricavare il max JC. Il
vincolo è imposto dalla relazione: Cpi ≥ CC da cui:
Ci ≤ CPO – CC = 11 – 4 = 7 Ncm = 0.07 Nm
Δω/Δt = 0.0314·5002 = 7850 rad/s2
controlli digitali
Esercizio
Con i dati dell’esercizio precedente e, considerando un JC = 40 gcm2, calcolare la massima velocità con cui è
possibile avviare il carico.
SOLUZIONE
Il calcolo si riduce alla ricerca della frequenza max di alimentazione.
Occorre:
• costruire la curva di pull-in, fino al primo valore negativo
• tracciare una linea orizzontale al livello CC
• leggere in corrispondenza dell’intersezione la frequenza
JT = 17 + 40 = 57 gcm2 = 5.7·10-6 kgm2
f
[ Hz ]
CPO
[ Ncm ]
Δω/Δt
[ rad/s2 ]
Ci
[ Ncm ]
Cpi
[ Ncm ]
100
10
314
0.18
9.82
200
11
1 256
0.72
10.28
500
11
7 850
4.5
6.5
800
10.6
20 096
11
- 0.4
1000
10
31 400
18
-8
controlli digitali
integrato l298
controlli digitali
MOTORE PASSO PASSO CON UN PONTE H L298
si dovrà scaricare la libreri accedendo al link https://github.com/yohendry/arduino_L298N.
Una volta scaricata la libreria in formato zip si dovrà andare al menu Sketch -> #Include Libreria > Aggiungi libreria da file .ZIP e aggiungere la libreria appena scaricata
/*Programma per testare il comando di un motore stepper tramite un L298N Dual H-Bridge Motor Controller
Vengono utilizzati i seguenti pin
Pin +5V -> Pin laterale del potenziometro
Pin GND
-> Pin GND modulo e pin laterale potenz.
Pin Digital 2
-> Collegato al pin IN1
Pin Digital 3
-> Collegato al pin IN2
Pin Digital 4
-> Collegato al pin IN3
Pin Digital 5
-> Collegato al pin IN4
Pin Analog A0
-> Collagato al centrale del potenziometro
*/
#include <Stepper.h>
const int stepsPerRevolution = 200;
/*cambiare questo per adattare il numero di passi per giro; per il vostro motore da calcolare dividendo
360° con il numero di gradi per passo, Inizializzare la libreria passo-passo su pin da 2 a 5*/
Stepper myStepper(stepsPerRevolution, 2,3,4,5);
int stepCount = 0; // numero di passi del motore
void setup() {
// niente da fare all'interno della configurazione
}
void loop() {
// Legge il valore della tensione fornito dal potenziometro:
int sensorReading = analogRead(A0);
// mappa il valore nel range da 0 a 100:
int motorSpeed = map(sensorReading, 0, 1023, 0, 100);
// Imposta la velocità del motore:
if (motorSpeed > 0) {
myStepper.setSpeed(motorSpeed);
// step 1/100 of a revolution:
myStepper.step(stepsPerRevolution/100);
}
}
I
diodi in contro fase servono per proteggere le uscite
dell’integrato L298N da eventuali sovratensioni generate
durante l’alimentazione delle bobine.
void setup()
{
//i pin 2-3-4-5 sono
//configurati come uscite
pinMode(2, OUTPUT);
pinMode(3, OUTPUT);
pinMode(4, OUTPUT);
pinMode(5, OUTPUT);
//forza le uscite a livello
logico basso
digitalWrite(2, LOW);
digitalWrite(3, LOW);
digitalWrite(4, LOW);
digitalWrite(5, LOW);
}
void loop()
{
//FASE 1
//Alimenta solo la prima
bobina
digitalWrite(2, HIGH);
digitalWrite(3, LOW);
digitalWrite(4, LOW);
digitalWrite(5, LOW);
delay(10);
//FASE 2
digitalWrite(2, LOW);
digitalWrite(3, LOW);
digitalWrite(4, HIGH);
digitalWrite(5, LOW);
delay(10);
//FASE 3
//Alimenta solo
bobina
digitalWrite(2,
digitalWrite(3,
digitalWrite(4,
digitalWrite(5,
delay(10);
//fase 4
//Alimento solo
bobina
digitalWrite(2,
digitalWrite(3,
digitalWrite(4,
digitalWrite(5,
delay(10);
}
la terza
LOW);
HIGH);
LOW);
LOW);
la quarta
LOW);
LOW);
LOW);
HIGH);
controlli digitali
2Un altro modo per pilotare il motore è quello di utilizzare la libreria Stepper.h
#include <Stepper.h> //include la libreria dedicata ai motori
passo passo
#define STEPS 100 // variabile che individua gli step del
motore utilizzato
int val = 0; //setta una variabile per la lettura dell’ingresso
analogico
int previous = 0; //variabile per la lettura precedente
dall'ingresso analogico
Stepper stepper(STEPS, 2, 3, 4, 5); //crea un'instanza della
classe specificando i pin di uscita
void setup()
{
stepper.setSpeed(30); //imposta la velocità del motore a 30
giri al minuto
}
void loop()
{
val = analogRead(0); //legge il valore del potenziometro
stepper.step(val - previous); //sposta il motore di un numero
di passi uguale al cambiamento letto da A0
previous = val; //registra il valore precedente letto dal
sensore
}
#include <Stepper.h>
const int stepsPerRevolution = 200;
Stepper myStepper(stepsPerRevolution,
9,10,11,12); // initialize the stepper
library on pins 9 through 12:
void setup() {
// set the speed at 60 rpm:
myStepper.setSpeed(60);
// initialize the serial port:
Serial.begin(9600);
}
void loop() {
// step one revolution in one direction:
Serial.println("clockwise");
myStepper.step(stepsPerRevolution);
delay(500);
// step one revolution in the other
direction:
Serial.println("counterclockwise");
myStepper.step(-stepsPerRevolution);
delay(500); }
SCHEMA DEI COLLEGAMENTI
ESEMPIO: Programma che gestisce i comandi di base di un motore passo passo
Nel programma è presente codice che va ripetuto più volte. Per una scrittura più efficiente è meglio scrivere questa
parte di codice in dei sottoprogrammi (funzioni) da richiamare all’occorrenza. E’ stato quindi creato un nuovo file.c,
denominato LibreriaMPP.c, con all’interno i sottoprogrammi : intestazioneMPP(), opzioni_iniz(); controllo().
Il programma principale (denominato K8055_MotorePP.c), alla luce della scelta precedente, contiene il seguente
codice:
Il file LibreriaMPP.c risulta:
Contenuto della cartella:
5
ARCHITETTURA DEI SISTEMI DI CONTROLLO
GENERALITA
A ANELLO APERTO
A ANELLO CHIUSO
ESEMPIO
SISTEMA DI CONTROLLO
SISTEMA DI CONTROLLOA MICROPROCESSORE
CLASSIFICAZIONE DEI SISTEMI DI CONTROLLO
F.D.T. NEI SISTEMI DI CONTROLLO
ARCHITETTURA DEI SISTEMI DI CONTROLLO
Per sistema di controllo si intende un qualsiasi sistema in grado di fare assumere alla grandezza
d’uscita un prefissato andamento in funzione della grandezza di
ingresso, anche in presenza di
disturbi (dovuti a fattori esterni al sistema) e parametrici (dovuti al deterioramento parziale dei
componenti del sistema).
I sistemi di controllo possono essere distinti in due categorie: sistemi ad anello aperto e sistemi ad
anello chiuso:
AD ANELLO APERTO
Nei sistemi ad anello aperto l’azione di controllo è indipendente dall’uscita; non si opera nessuna
misura della grandezza d’uscita
Pregi: semplice, stabile
Difetti:
• precisione affidata alla accuratezza del modello matematico dei componenti
• vulnerabile ai fenomeni di usura e invecchiamento dei componenti in quanto non più
fedelmente descritti dai modelli matematici memorizzati
.
• vulnerabile in caso di infiltrazione di disturbi.
ARCHITETTURA DEI SISTEMI DI CONTROLLO
Esempio
Consideriamo un sistema di controllo di temperatura ad esempio di un forno a gas
In questo sistema la temperatura, grandezza da controllare, viene
scelta mediante il
posizionamento di una manopola che regola l’erogazione del gas al bruciatore
In questo sistema non si opera nessun controllo sulla grandezza d’uscita.
Il controllo ad anello aperto presenta lo svantaggio che un’eventuale variazione dell’uscita rispetto
al valore desiderato, dovuta ad es. ai disturbi, non viene percepita in ingresso.
Una più efficacia regolazione della temperatura può essere ottenuta misurando continuamente la
temperatura del forno ed intervenendo di conseguenza sulla manopola, aumentando l’afflusso del
gas se la temperatura è al disotto del valore desiderato oppure diminuendolo in caso contrario
ARCHITETTURA DEI SISTEMI DI CONTROLLO
Compensazione in avanti (feed - forward)
In catena aperta è possibile compensare i disturbi a condizione che siano prevedibili e misurabili, è cioè possibile
annullare gli effetti sull’uscita controllata.
In assenza di disturbo e compensazione:
y A x
In presenza di disturbo, senza compensazione:
y A x d
In presenza di disturbo, con compensazione:
y A x
ARCHITETTURA DEI SISTEMI DI CONTROLLO
AD ANELLO CHIUSO
Se sostituiamo completamento l’intervento dell’uomo con dispositivi appropriati, il sistema
diventa “sistema di controllo automatico di temperatura ad anello chiuso”
Nei sistemi ad anello chiuso detti anche sistemi a retroazione (feedback) l’azione di controllo dipende
dall’uscita.
L’uscita, viene continuamente <<saggiata>> ed il suo valore è confrontato con una grandezza di
riferimento (Vi), in modo da produrre, ogni qualvolta ci sia una diversità fra l’uscita reale e
quella voluta, un azione correttiva che riporti l’uscita al valore desiderato.
Un sistema di controllo ad anello chiuso può essere schematizzato nel seguente modo:
ARCHITETTURA DEI SISTEMI DI CONTROLLO
Blocco di reazione
E’ costituito da un trasduttore che effettua la conversione della grandezza fisica da controllare (temperatura,
velocità, ecc. ) in un segnale elettrico proporzionale e da un blocco di condizionamento che adatta il segnale
generato dal trasduttore per essere confrontato con il segnale di riferimento Nodo sottrattore
Il nodo sottrattore ha il compito di elaborare il segnale di riferimento e quello di reazione e quindi di generare
il segnale errore Ve che opera l’opportuna azione correttrice.
Nei sistemi continui il dispositivo che effettua il confronto (nodo sottrattore) è realizzato con un amplificatone
in connessione differenziale, nei sistemi di controllo On-Off invece con un comparatore.
Controllore
Il controllore ha lo scopo di manipolare il segnale errore, è presente se occorre migliorare il comportamento
dell’intero sistema in termini di velocità, precisione e stabilità, può essere una rete correttrice oppure un
regolatore industriale.
Blocco di comando attuatore
Il segnale proveniente dal nodo sottrattore opportunamente trattato, comanda l’attuatore (riscaldatore,
motore, ecc) per produrre il segnale d’uscita desiderato. Il blocco di comando attuatore in genere è composto
da un preamplificatore e da un amplificatore di potenza.
Nota: per lo studio dei sistemi di controllo a catena chiusa si fa uno dello schema semplificato.
ARCHITETTURA
ARCHITETTURA DEI
DEI SISTEMI
SISTEMI DI
DI CONTROLLO
CONTROLLO
Difetti:
la modalità con cui si decide l’azione di controllo può dare origine a un sistema instabile per via
dei ritardi con cui i segnali si propagano tra i vari blocchi:
1)il blocco di misura impiega del tempo nell’eseguire la misura della variabile
controllata, il cui valore giunge quindi in ritardo sul nodo di confronto
2)l’azione di controllo, che è decisa sulla base di una situazione che è già vecchia,
impiega del tempo per giungere sul sistema controllato e produrre i suoi effetti.
Questi ritardi, sia nel ramo di retroazione che in quello diretto, sono responsabili della
generazione di azioni di controllo eccessive, cioè di sovracorrezioni che provocano il
pendolamento dell’uscita controllata e, nei casi peggiori, l’instabilità del sistema.
I ritardi possono essere:
•
di trasporto: per trasporto di materia, trasmissione meccanica, pneumatica
•
inerziali: dovuti all’accumulo e rilascio di energia (termica, meccanica, elettrica) negli
accumulatori.
ARCHITETTURA DEI SISTEMI DI CONTROLLO
ESEMPIO DI UN SISTEMA DI CONTROLLO AUTOMATICO DI VELOCITÀ DI UN MOTORE IN CORRENTE CONTINUA
Descrizione dei blocchi:
Il sistema di reazione trasduce la velocità di rotazione in tensione (Vr) Il potenziometro fornisce la
tensione di riferimento (Vi)
Il nodo sottrattore confronta la tensione di riferimento (Vi) con quella
trasduzione e produce il segnale errore. ( Ve = Vi-Vr )
proveniente da sistema di
Il controllore ha lo scopo di manipolare il segnale errore; è presente se occorre migliorare il comportamento
dell’intero sistema in termini di velocità, precisione e stabilità, può essere una rete correttrice oppure un
regolatore industriale(PID)
Il blocco di comando (amplificatore), fornisce al motore il valore opportuno di tensione per mantenere
costante la velocità . (Esso rappresenta l’elemento di regolazione)
ARCHITETTURA DEI SISTEMI DI CONTROLLO
Principio di funzionamento.
Fissato tramite il potenziometro il valore della tensione di riferimento Vi (quindi la velocità di
rotazione del motore), se il motore tende a rallentare, diminuirà la tensione proveniente dal blocco
di reazione (Vr), aumenterà l’errore (Ve) e la tensione ai capi del motore, di conseguenza
aumenterà anche la velocità del motore, compensando così la diminuzione di velocità.
ESEMPIO DI UN SISTEMA DI CONTROLLO AUTOMATICO DI TEMPERATURA DI UN FORNO
Descrizione dei blocchi:
Il blocco di reazione trasduce la temperatura in tensione (Vr). È costituito dall’insieme del
trasduttore (ad es. termocoppia) e dal blocco di condizionamento. Il blocco di condizionamento ha
la funzione di adattare i valori di tensione generati dalla termocoppia per il confronto con la
tensione di riferimento.
Il potenziometro fornisce la tensione di riferimento (Vi) ; rappresenta il valore della
temperatura “ideale” che si vuole mantenere nel forno;
Il nodo sottrattore1 confronta la tensione di riferimento (Vi) con quella proveniente da
sistema di trasduzione e produce il segnale errore. ( Ve = Vi- Vr );
ARCHITETTURA DEI SISTEMI DI CONTROLLO
Il controllore ha lo scopo di manipolare il segnale errore; è presente se
occorre
migliorare
il
comportamento dell’intero sistema in termini di velocità, precisione e stabilità, può essere una rete
correttrice oppure un regolatore industriale (PID)
Il blocco di comando è costituito, ad es. da una elettrovalvola proporzionale, in grado cioè di
modulare l’apertura in funzione della tensione di pilotaggio; in uscita si avrà quindi una portata di
combustibile proporzionale alla tensione stessa.
Il forno” è l’impianto da controllare è costituito dall’insieme del bruciatore e del forno vero e
proprio.
Principio di funzionamento.
Fissato tramite il potenziometro il valore della tensione di riferimento Vi (quindi la temperatura del
forno), se la temperatura del forno diminuisce , diminuirà la tensione proveniente dal blocco di
reazione (Vr), aumenterà l’errore (Ve) e quindi la tensione ai capi dell’elettrovalvola , di conseguenza
aumenterà la quantità di combustibile e quindi aumenterà la temperatura del forno, compensando
così la diminuzione di temperatura.Il nodo sottrattore in genere è realizzato con un amplificatore
operazionale.
ARCHITETTURA DEI SISTEMI DI CONTROLLO
SISTEMA DI CONTROLLO
Il sistema di controllo ON/OFF, (a funzionamento intermittente nel tempo), viene usato quando non
si richiede una marcata precisione; esso è economico e semplice da realizzare.
La struttura base è la seguente:
E’ cosi chiamato perché il dispositivo che effettua il confronto (comparatore) tra la grandezza
d’uscita convertita in tensione (Vr), tramite il blocco di reazione e quella di ingresso (Vi), ha
solamente due stati possibili alto (h) o basso (l).
Caratteristica del comparatore:
se Vr <Vi se Ve = “h”
Ve = “l”
Vr > Vi
-
-
Principio di funzionamento del sistema:
Se l’uscita è minore di quella desiderata (impostata tramite Vi), il comparatore venendosi a trovare
allo stato alto, attiva l’attuatore (ad es. riscaldatore, motore, ecc) per mezzo del blocco di comando.
Non appena l’uscita raggiunge il valore desiderato il comparatore commuta allo stato basso,
disattivando così l’attuatore.
ARCHITETTURA DEI SISTEMI DI CONTROLLO
Possibile andamento dell’uscita
di un sistema di controllo on/off
PROGETTAZIONE DI UN SISTEMA DI CONTROLLO AUTOMATICO DI TEMPERATURA ON/OFF , FACENDO USO
DEL TRASDUTTORE AD590
Specifiche: temperatura di set-point 40°C
Questo sistema consente di controllare la temperatura di un
ambiente, mediante l’attivazione di un riscaldatore quando la
temperatura scende al disotto di una soglia prefissata (40°C).
La temperatura di soglia (40°C) viene scelta impostando Vi tramite
il trimmer R2’’.
Calcolo della tensione Vr per una temperatura di soglia di 40°C.
Il trasduttore AD590 trasduce la temperatura
in corrente,
eroga una corrente 1 A per ogni °K. Di temperatura
ARCHITETTURA DEI SISTEMI DI CONTROLLO
Dimensionamento del generatore di tensione di riferimento
Scegliendo:
R1= 4.7K, R2=1.5K
R2 =1k (trimmer multigiri di regolazione)
Regolando il trimmer multigiri R2
si ottiene Vi = 3,13V
ARCHITETTURA DEI SISTEMI DI CONTROLLO
Dimensionamento del blocco di comando
Il relè per essere eccitato necessita di una corrente Il = 12/300 = 40mA che l’operazionale non è in grado di
fornire.
dati relè:
Va=12V ; R=300
dati BjT 2N2222A: h FE( min) = 75; V CE ( s a t ) =0,3V ; V BE ( s a t ) =0,8V
È pertanto necessario ricorrere ad un BJT in funzionamento ON/OFF.
Calcolo della Ib di saturazione
Per portare in saturazione il BJT è necessaria una Ib>Ic/ h FE( min) ,
sostituendo si ha: Ib > 40 / 75 = 0 , 53 m A. Si può scegliere Ib = 2mA
Dimensionamento della Re
Da notare:
Il diodo inserito in parallelo alla bobina del relè, serve per evitare sovratensioni pericolose sul
collettore del BjT nella commutazione in OFF.
Il diodo inserito sul BJT, serve per proteggere la giunzione BE, quando l’uscita del comparatore è a
livello basso (Ve -12V).
ARCHITETTURA DEI SISTEMI DI CONTROLLO
SISTEMA DI CONTROLLO A MICROPROCESSORE
Il sistema di controllo a microprocessore fa uso di un elaboratore o di un sistema
dedicato; ha un funzionamento che dipende dal programma di gestione.
a microP
Vantaggi:
Il vantaggio più evidente è quello della versatilità, infatti se si vuole variale il valore della
grandezza da controllare, basta modificare il programma di gestione senza
intervenire
sull’hardware .
Il blocco di reazione acquisisce la grandezza da controllare e la converte in formato digitale
L’elaboratore legge il dato digitale, lo confronta con il valore di riferimento precedentemente
impostato e invia il risultato dell’elaborazione al convertitore D/A..
Il convertitore D/A lo converte in segnale analogico. e lo invia al blocco di commando
Il blocco di comando fornisce all’attuatore il segnale opportuno dicontrollo.
Note:
Se la grandezza da controllare varia velocemente prima del convertitore A/D, bisogna inserire il
blocco Sample-Hold, per mantenere stabile il segnale durante il processo di conversione.
Nei sistemi di controllo on/off a microprocessore manca il convertitore D/A.
ARCHITETTURA DEI SISTEMI DI CONTROLLO
CLASSIFICAZIONE DEI SISTEMI DI CONTROLLO
I sistemi di controllo a catena chiusa si distinguono in:
regolatori: quando il valore della grandezza controllata deve essere mantenuta costante;
esempi:
- sistema di controllo di velocità di un motore in c.c. (deve essere mantenuta costante la velocità);
- sistema di controllo della temperatura di un forno (deve essere mantenuta costante la temperatura);
servomeccanismi : quando la grandezza controllata di tipo meccanico (posizione, velocità, ecc.) deve
seguire nel tempo le variazioni della grandezza di riferimento;
esempio
- sistema di trasmissione e di ricezione via satellite: l’antenna di ricezione e
trasmissione “insegue
istante per istante il satellite;
a valore programmato: quando la grandezza controllata varia nel tempo secondo un programma
stabilito;
esempio:
- lavatrice automatica: tutte le grandezze di questo sistema (livello e temperatura dell’acqua, verso e
velocità del cestello hanno nel tempo un andamento che è prefissato mediante il programmatore.
- torni a controllo numerico: le azioni compiute dalla macchina sono
controllate da un programma
gestito da un calcolatore o da un sistema amicroP dedicato.
REQUISITI DI UNSISTEMA DI CONTROLLO
Ad un sistema di controllo è richiesto:
- di risentire del minore modo possibile dei disturbi dovuti a cause esterne;
- di rispondere il più prontamente possibile alle sollecitazioni;
- di fornire una risposta la più precisa possibile
ARCHITETTURA
ARCHITETTURA DEI
DEI SISTEMI
SISTEMI DI
DI CONTROLLO
CONTROLLO
LA FUNZIONE DI TRASFERIMENTO DEI SISTEMI DI CONTROLLO REAZIONATI
In molti casi per agevolare lo studio dei sistemi di
controllo reazionati è preferibile utilizzare lo
schema equivalente con retroazione unitaria.