caricato da
common.user2665
Le Grandezze in Chimica
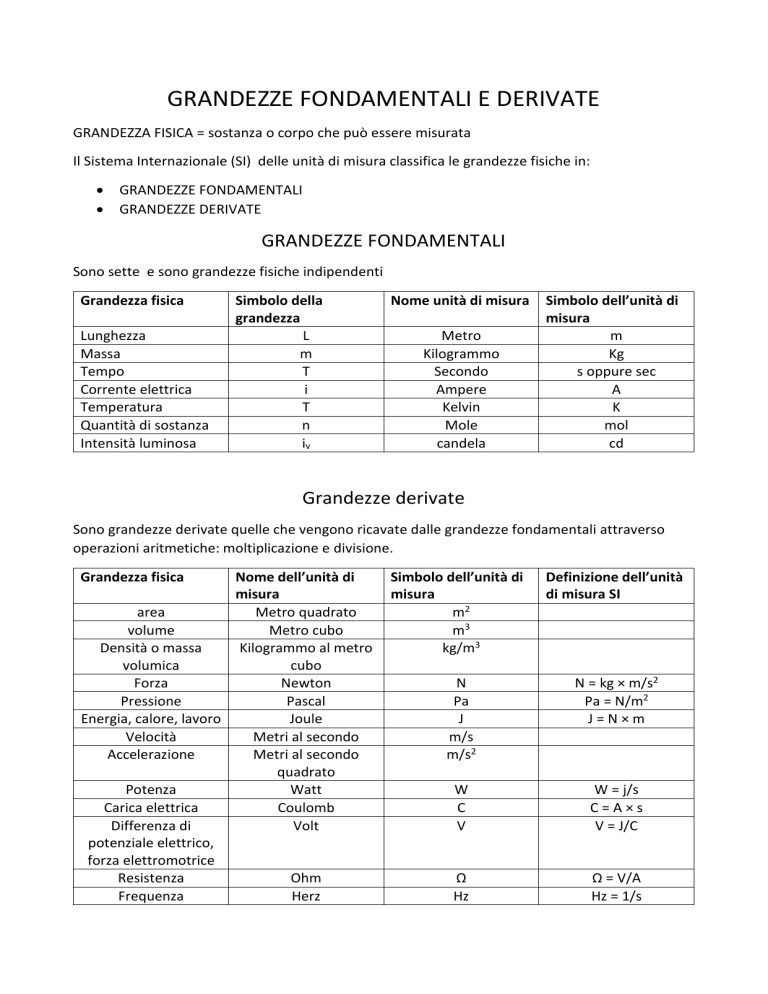
GRANDEZZE FONDAMENTALI E DERIVATE GRANDEZZA FISICA = sostanza o corpo che può essere misurata Il Sistema Internazionale (SI) delle unità di misura classifica le grandezze fisiche in: GRANDEZZE FONDAMENTALI GRANDEZZE DERIVATE GRANDEZZE FONDAMENTALI Sono sette e sono grandezze fisiche indipendenti Grandezza fisica Lunghezza Massa Tempo Corrente elettrica Temperatura Quantità di sostanza Intensità luminosa Simbolo della grandezza L m T i T n iv Nome unità di misura Metro Kilogrammo Secondo Ampere Kelvin Mole candela Simbolo dell’unità di misura m Kg s oppure sec A K mol cd Grandezze derivate Sono grandezze derivate quelle che vengono ricavate dalle grandezze fondamentali attraverso operazioni aritmetiche: moltiplicazione e divisione. Grandezza fisica Nome dell’unità di misura area Metro quadrato volume Metro cubo Densità o massa Kilogrammo al metro volumica cubo Forza Newton Pressione Pascal Energia, calore, lavoro Joule Velocità Metri al secondo Accelerazione Metri al secondo quadrato Potenza Watt Carica elettrica Coulomb Differenza di Volt potenziale elettrico, forza elettromotrice Resistenza Ohm Frequenza Herz Simbolo dell’unità di misura m2 m3 kg/m3 Definizione dell’unità di misura SI N Pa J m/s m/s2 N = kg × m/s2 Pa = N/m2 J=N×m W C V W = j/s C=A×s V = J/C Ω Hz Ω = V/A Hz = 1/s Grandezze intensive ed estensive: Le grandezze fisiche sono classificate in: Grandezze intensive Grandezze estensive Grandezze intensive Sono grandezze intensive della materia quelle grandezze che non dipendono dalle dimensioni del campione. Temperatura di ebollizione ( es dell’acqua, l’acqua bolle sempre a 100° C) Temperatura di fusione Densità (es dell’acqua non dipende dalla quantità) Non varia al variare della posizione del corpo Calore specifico Molarità Normalità Pressione Grandezze estensive Sono grandezze estensive della materia quelle grandezze che dipendono dalle dimensioni del campione. Sono grandezze che si possono sommare es 1 kg (acqua) + 1 kg (acqua) = 2 kg di acqua Massa Volume Lunghezza Area Energia Quantità di calore La massa m La massa di un corpo è la misura della sua inerzia, cioè della resistenza che il corpo oppone a tutte le variazioni del suo stato di quiete e di moto. La massa è la quantità di materia di un corpo, che si misura con la bilancia a due bracci Caratteristiche: non varia al variare della posizione del corpo nello spazio, in qualsiasi luogo rimane la stessa. Non varia al variare della temperatura del corpo. Cioè quando un corpo passa, per riscaldamento, dallo stato solido allo stato liquido o dallo stato liquido a quello gassoso la sua massa rimane sempre la stessa L’unità di misura è il kg Il peso N Il peso di un corpo è la forza con cui il corpo viene attratto dalla terra (forza di gravità). Si chiama forza peso ed è una grandezza proporzionale alla massa m del corpo. Formula del peso P = m × g (P = kg × m/s2 = N) Caratteristiche: la forza peso si misura con il dinamometro Cambia da un luogo all’altro a seconda dell’accelerazione di gravità P = è il peso m = la massa del corpo misurata in kg g = accelerazione di gravità uguale in tutti i corpi nello stesso luogo ma cambia da luogo a luogo (cioè se ci si allontana dalla terra sarà minore) l’unità di misura è il Newton N La densità La densità è il rapporto tra la massa di un corpo e il suo volume Formula d= 𝑚 𝑣 (d = 𝑘𝑔 𝑚³ ) La densità è una proprietà intensiva della materia che dipende dalla temperatura e dalla pressione ( soprattutto per i gas). Per quasi tutti i materiali un aumento di temperatura causa un aumento di volume e quindi una diminuzione del valore della densità. Nel SI Sistema Internazionale la densità si misura in kg/m3 ma vengono usati anche i g/cm3. La densità dei gas si misura in g/L Il volume m3 Formula V= 𝑚 𝑑 Il volume è lo spazio che occupa un corpo, per un gas il volume corrisponde al recipiente che lo contiene Nel SI Sistema Internazionale l’unità di misura è il metro cubo m3 ma vengono usati anche: il litro (L) e il millilitro ( mL) Da ricordare che: 1 L = 1 dm3 1 mL = 1 cm3 Il peso specifico Formula 𝑃 𝑚×𝑔 𝑉 𝑉 Ps = = =d×g Il peso specifico assoluto è il rapporto tra il peso di un corpo P e il suo volume V. L’unità di misura è N/m3 Misure precise e accurate Ad esempio un’asta misura 10 m nel fabbricarla si possono avere delle aste affette da errori Misura precisa: la precisione della misura è data dal livello di vicinanza di una misurazione con l’altra e da quanto le misure risultino raggruppate Misura accurata: ha a che vedere con il livello di vicinanza delle misure rispetto al valore atteso (10 m) Possono quindi esistere: MISURE PRECISE MA NON ACCURATE MISURE ACCURATE MA NON PRECISE MISURE PRECISE E ACCURATE MISURE NON ACCURATE E NON PRECISE Errori sistematici e errori casuali(accidentali) Ogni rilevamento di una misura è soggetto ad errori Errori sistematici: sono quegli errori che influenzano la misura solo in uno dei due sensi: o sempre per eccesso o sempre per difetto. Errori casuali (accidentali): sono quegli errori che influenzano la misura in modo imprevedibile sia per eccesso sia per difetto La media aritmetica Il valore medio di una serie di misure si trova sommando fra loro tutti i valori delle misure della serie e dividendo tale somma per il numero delle misure. XM = 𝑋1+𝑋2+𝑋3 3 L’errore assoluto (indica l’incertezza della misura) È ottenuto calcolando la differenza tra il massimo valore misurato e il valore minimo e dividendo per 2 Ea = 𝑋𝑚𝑎𝑥 −𝑋𝑚𝑖𝑛 2 Questo ci fa capire che l’ultima cifra del valore medio X ottenuto è una cifra incerta e tramite il calcolo dell’errore assoluto capiremo che il valore della misura sarà compreso ± ea Errore relativo (indica la precisione della misura) È dato dal rapporto tra l’errore assoluto e la media aritmetica Er = 𝐸𝑎 𝑋 Cifre significative È un altro modo per indicare l’incertezza della misura Regole: Tutti i numeri diversi da zero si considerano cifre significative Gli zeri che si trovano fra due cifre sono significativi (70,8) Gli zeri sulla sinistra che precedono la prima cifra diversa da zero non sono significativi (0,00708, 0,0708, 0,708) Gli zeri terminali, a destra di una cifra decimale diversa da zero sono cifre significative (8080,0) Calcoli con cifre significative addizione e sottrazione La regola da seguire è questa: il risultato di una addizione e di una sottrazione tra dati sperimentali deve essere espresso con il numero di cifre decimali pari a quelle del dato che ne ha di meno (le cifre decimali sono quelle dopo la virgola) Esempio: 58,6 cm + 13,72 = 73,3 Calcoli con cifre significative moltiplicazione e divisione La regola da seguire è questa: il risultato di una moltiplicazione e di una divisione tra dati sperimentali deve essere espresso con il numero di cifre significative pari a quelle del dato che ne ha di meno Esempio: 36,58 m : 20,4 s = 1,79 m/s








