meccanica applicata alle macchine

1. Composizione dei meccanismi:
Macchina: Sistema di organi disposti in modo tale da compiere, muovendosi sotto
l’azione di forze convenientemente applicate, lavoro d’interesse industriale.
Meccanismo: Dispositivo in grado di trasformare le forzo d’ingresso ed il movimento
in un insieme di forze di uscita e movimento desiderati.
Membri: Organi che compongono una macchina, od un meccanismo.
Elemento cinematico: Membro a contatto con
Coppia cinematica: Insieme di due elementi cinematici a contatto; ha almeno un
grado di libertà. A seconda di dove avviene il moto, varia il numero dei gradi di
libertà, se è piano ho 3 gdl, se è spaziale ho 6 gdl.
Tipologie di coppie:
1) Indipendenti: Permettono un movimento relativo ad un solo gdl.
2) Combacianti: In contatto con porzioni di superficie finita.
3) Elementari: Coppie rigide e combacianti.
3.1) Rotoidale: Moto di rotazione (es. cerniera).
3.2) Prismatica: Moto di traslazione (es. cilindro + pistone).
3.3) Elicoidale: Moto elicoidale (es vite + madrevite).
Catena cinematica: Un dispositivo è tale se suppongo che nessuno dei membri che
lo compongono sia a priori da considerarsi fisso.
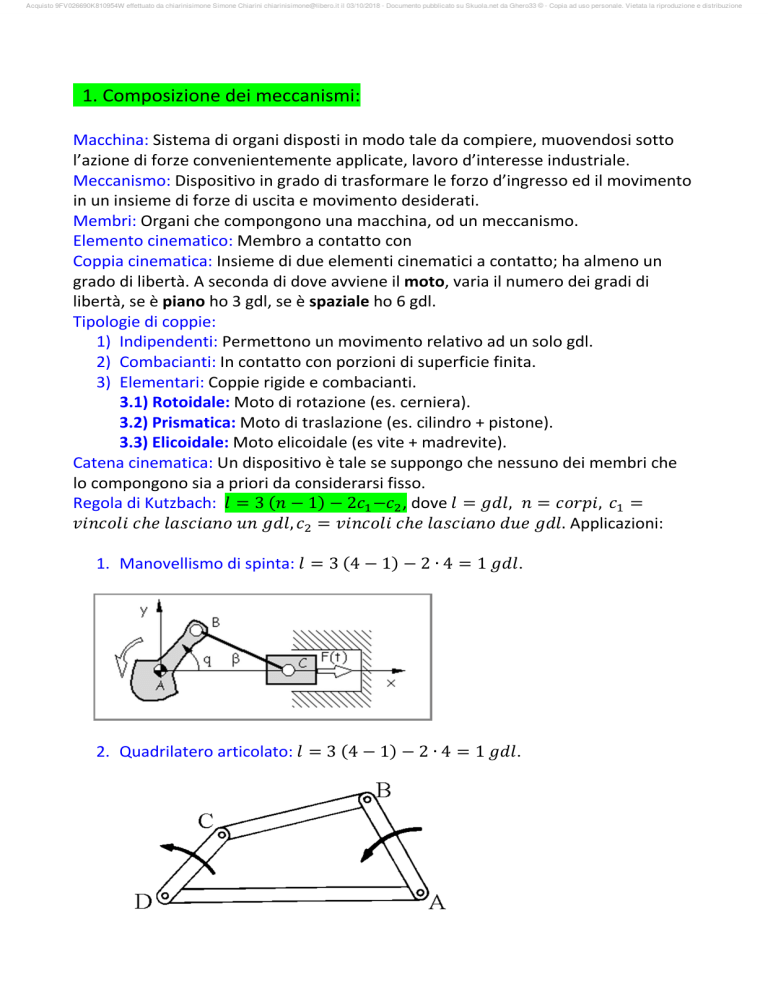
Regola di Kutzbach:
3
1
2
, dove
,
,
. Applicazioni:
,
1. Manovellismo di spinta:
3 4
1
2∙4
1
.
2. Quadrilatero articolato:
3 4
1
2∙4
1
.
3. Camma e punteria:
3 4
1
2∙3
1
1
.
4. Giunto di Oldham:
3 5 1
2∙6 0
, in realtà ha 1 gdl; infatti il
corpo 4 non aggiunge nessun vincolo poiché il punto M descrive una
traiettoria circolare.
2. Forze agenti sulle macchine:
Forze:
Motrice: (Nel movimento della macchina compie lavoro positivo).
Resistente: (Nel movimento della macchina compie lavoro negativo).
Esterne: Derivano dall’azione di corpi esterni alla macchina o dall’azione di campi di
forze.
Interne: Nascono dal contatto fra i membri della macchina. Esempi:
1.Attrito di strisciamento fra superfici asciutte (tra le due superfici in contatto non
molecole/atomi di altre sostanze, come polvere, ossidazione…).
"
Legge di Coulomb: !
, f = coefficiente di attrito, dipende dal materiale, dalla
#
natura delle superfici, dalla temperatura, dalla pressione di contatto, 0,2 ≤ ! ≤ 1,8.
2. Attrito mediato (tra le due superfici in contatto c’è un materiale lubrificante).
Conseguenza dell’attrito tra superfici asciutte è il logoramento, quanto vale?
Ipotesi del Reye: “Il volume di materiale asportato durante il logoramento è
proporzionale al lavoro di attività”.
Esempi:
1) Perno di spinta:
Un albero/disco/geometria cilindrica su un piano è tenuto da una forza assiale,
mantenuta in rotazione con un momento d’attrito μA. Quanto vale per mantenere la
rotazione? Distribuzione di pressione fra superfici di contatto.
Per le ipotesi del Reye: ! ∙ ∙ 2& ∙ '( ≡ 2& ∙
∙ (Lavoro
resistente/dissipato dalle forze di attrito è proporzionale al volume), f=coefficiente
*
di attrito, p=pressione di montaggio, h=usura/riduzione di pattino. Quindi
.
+
Voglio trovare la distribuzione delle pressioni:
̅
-
./
.0
∙ 2& ∙
3̅
4 ./ 5.0
./
2& -
∙
+
⟹
.0
̅
2& 2
2
⟹
(equazione traslazione verticale)
Voglio il momento di attrito da applicare al perno di spinta per mantenere la
rotazione:
./
67
- !∙
67
!
.0
∙ 2&
.0 8./
./
∙
2&! -
&! 2
.0
2
⟹
! 29:;<= (equazione di rotazione).
Nota bene: Se 67 > ! 29:;<= , c’è slittamento.
2) Pattino su superficie piana:
(
+
@0 5@A
B
∙C
( D1
F
+ E G,
B
asportato per effetto dell’usura.
Ipotesi del Reye: C! H
C
E
I I
!! II
Dall’equilibrio:
B
B
C
̅ C
- D1 + E G C
(
̅
+E
(
2
1+E
C
E
@0 5@A
K
+E
Forza necessaria per mantenere l’equilibrio: L
@A
, h è lo spessore del materiale
I
C
!
̅
⟹
B
MB !
J
+E
C
! ̅
K
2
II I
⟹
Porzione dissipata dal punto p:
̅ ∙ C(
E
B
-
(
0 ⇒
C C
èE
B
- NC + E
(
I
E JJ
C
O C
I ⇒ C(
2
, ′
E
2
+E
I
3
⟹ C(
I
I .
2E
3
2+E
1+
3) Ceppo-puleggia (freni a ceppo e tamburo):
Direzione di accostamento –> ho la massima usura.
Descrizione: La puleggia ruotante attorno al proprio asse viene premuta sulla fascia
cilindrica da un ceppo che viene accostato alla puleggia con un movimento di
traslazione. Voglio trovare la distribuzione della pressione nel contatto ceppopuleggia. Affinché il ceppo possa rimanere a contatto con la puleggia nonostante
l’usura, deve subire uno spostamento traslatorio. Lo strato usurato ha pertanto
un’altezza h0 costante secondo la direzione di accostamento; quindi secondo il
raggio della puleggia, lo spessore dello strato varia secondo la legge:
( cos V. Il volume di materiale asportato dall’usura sull’area elementare 2 V
vale: 2 ( cos V V. Il lavoro di attrito corrispondente vale: ! 2 V'(
α( angolo di cui ha ruotato la puleggia . Per le ipotesi del Reye:
Volume del materiale asportato = Lavoro delle forze di attrito:
2 cos V V
! 2
V'( ⟹
V
(
cos V.
Voglio calcolare d=angolo che individua la direzione della risultante delle azioni di
pressione. Per farlo basta osservare che d individua tale direzione ⟺ proiettando
tutte le azioni di pressione in direzione ortogonale a quest’ultima, si ottiene un
valore nullo. Cioè:
g
-
5
g
sin '
d 2 '
g5hij g
g
2 - cos '
5
g
f sin '
d
'
0⟹
tan d tan f
.
g8hij g
Proiettando tutte le azioni di pressione sull’angolo d, devo trovare Fp:
L3
o
/
o
5
/
M
cos '
d 2 '
⋯
2lm cos f
d + sin m cos f + d n.
Calcolo la forza equivalente alle azioni di attrito:
La risultante è p !L3 ed è ortogonale alla direzione individuata da d, inoltre sarà
applicata ad una distanza d da O tale che:
g
m
4 sin
2 cos d.
- ! 2 V !L3 ,
2
g
m + sin m
5
Circonferenza del Romiti:
K=Intersezione delle rette di azione T e Fp.
Al variare di d, il punto K descrive una circonferenza di diametro:
42
hij
o
/
g8hij g
cos d.
(
ssss = braccio di tutte le risultanti delle azioni normali e tangenziali
Se trovo d trovo qr
ssss
che la puleggia ed il ceppo si scambiano. qr
t. hij
o
/
g8hij g
cos d.
Punto P0 = Per questo punto passano le risultanti delle azioni normali e tangenziali
che si scambiano il ceppo e la puleggia.
Utilità del Romiti = Risolvere equilibri freno a ceppo flottanti.
Attrito di rotolamento:
Caso ideale:
Le forze dissipanti (ad esempio l’attrito) sono assenti.
La distribuzione delle pressioni è simmetrica.
Caso reale:
La distribuzione delle pressioni è deformata.
R si sposta in anticipo rispetto al rotolamento della ruota di una quantità u
(=parametro d’attrito volvente, è causato da elasticità imperfetta, elasticità
ritardata, urti tra le asperità).
' ' < 1 , rappresenta la frazione della semicirconferenza c della zona
deformata.
P ed R costituiscono una coppia ⟹ il momento si oppone all’v (= rotazione ruota
sul terreno) ⟹ devo applicare un momento 6 per mantenerlo un moto con
v=costante.
Esempi (parametro d’attrito volvente):
1) Ruota e piano perfettamente elastici:
∁
xy
3+
z
'xy
{ I ,
3+
z
⟹ !+
|
'xy
JJ
3
I
z+
2) Solo la strada è deformabile e la pressione è proporzionale alla deformazione:
}≡ |
}≡
+
•z
@
'x y
•
y
⟹
€+
z
•
⟹ !+
+
€+
z
'x y
•
+
2
≃
€
z+ /
3) Ruota rigida, strada si deforma plasticamente:
} ≡ |,
'
€
'x ⟹ !+
z
'x
€
z+
+
2
⟹
2
Cuscinetti a rotolamento:
Utilità: L’attrito è più basso rispetto ai cuscinetti di strisciamento.
3. Lavoro e rendimento:
Il lavoro di una forza/coppia è una grandezza scalare: ‚
La forza può essere applicata a:
L∙
I E
I .
Parti mobili:
Lavori positivi --> forza motrice
Lavori negativi --> forza resistente
Telaio:
Reazioni movente = membro al quale è applicata la forza motrice.
Reazioni cadente = membro al quale è applicata la resistenza utile.
Forza motrice compie lavoro: ‚ƒ
Resistenza utile compie lavoro: ‚.
Resistenza passiva compie lavoro: ‚€
Teorema delle forze vive:
Δ…
‚ƒ
‚.
‚€ Δ…
J
.
I
E
Se ΔΕ 0 per ogni intervallo di t ⟹ l’energia cinetica è costante ⟹ la macchina si
dice in condizioni di regime assoluto: ‚ƒ ‚. + ‚€ .
L’energia cinetica E è una funzione periodica del tempo t, di periodo T.
Regime:
Assoluto --> L’equazione ‚ƒ ‚. + ‚€ è sempre vera, Δ…
di tempo (esempio: turbine, alternatori).
0 per ogni intervallo
Periodico --> L’equazione ‚ƒ ‚. + ‚€ è verificata solo per intervalli di tempo
che sono multipli del periodo T (esempio: motori alternativi, come motori a pistone,
pompe a pistone, compressori alternativi).
Rendimento per le macchine a regime: ‡
‡<Œ•BŽ•BŽ:=
;ˆ‰
;ˆŠ
; ‡9:;<=
Differenza di perdita: 1
‡
ˆ‰
ˆŠ
ˆ•
ˆ‰
ˆŠ
ΔI
siccome ‚€ ≠ 0 ⟹ ‡ < 1
E
ˆŠ
1) Meccanismi in serie:
Il cadente di ogni meccanismo è il movente del successivo, il rendimento è:
‡
ˆ ‰•
ˆŠ0
ˆ ‰0
ˆŠ/
∙
ˆ ‰/
ˆŠ•
∙ …∙
ˆ‰•’0
ˆŠ•
∙
ˆ ‰•
ˆŠ•“0
‡ ∙ ‡ ∙ … ∙ ‡Ž
2) Meccanismi in parallelo:
Il moto è trasmesso da un movente a più meccanismi differenti, oppure viene
trasmesso da più meccanismi ad un solo cadente, il rendimento vale:
‡
‚+
‚9
‚+0 + ‚+/ + ⋯ + ‚+•
‚90 + ‚9/ + ⋯ + ‚9•
‡ ∙ ‚90 + ‡ ∙ ‚9/ + ⋯ + ‡Ž ∙ ‚9•
‚90 + ‚9/ + ⋯ + ‚9•
3) Espressioni del rendimento:
Considero una macchina in cui:
Forza motrice = P, ‚9 } ∙
Forza resistente = Q, ‚+ ” ∙ •
P, Q rimangono costanti
I E I
I E I
Condizioni ideali: Macchina identica, ma senza resistenze: ‚€A 0
Considero L9=•+<*: un po’ più piccola, non ci sono forze da equilibrare (es: attrito),
dunque }( L → ‚ƒA }( ∙
‚+ + ‚€A
‚9A , E ‚€A
‚9A }( ∙
‚+
‚9
‚9
} ∙ sp
4) Moto retrogrado:
‡
0 ⟹ ‚+
}(
}
‚9A
}( ∙
, il rendimento vale:
Macchina funzionante a regime, ma in condizioni di moto invertito, nel senso che la
forza Q, che prima era resistente, diventa la forza motrice. Per osservarne il moto a
regime, dovremo applicare una forza }K con la stesso retta d’azione di P, che
costituisce la forza resistente della macchina.
‡
K
ˆ˜—
ˆ˜™
€˜ ∙Œ3
š∙Œ3
€˜ ∙Œ3
€˜
€A ∙Œ3
€A
Moto diretto: }(
”, condizioni ideali; }
}( 1
‡
⟶ ‡<1
} x
x ∙ ”, condizioni reali (k>1)
Moto retrogrado: NON lascio la fune ed il peso viene giù con un moto accelerato,
MA: mi deve scendere con
I I ⟹ devo applicare una forza resistente:
}K ∙ x
”
J
E I
I
, L+
E
E
•
,è
)
5) Relazione œ • œK :
1
‡K
‡
‚€
‚ƒ
‡∙ x+1
œ
1
x
‡
‚K€
‚Kƒ
K
‚K€
1
⟹
‚+
1
‡
‡K
‚+ ‚€
∙
‚ƒ ‚K€
‚€
‡∙ K
‚€
‚K€
∶
‚€
x
6) Macchina ad arresto spontaneo:
Avvien quando la macchina si ferma spontaneamente, nel caso che venga a mancare
la forza motrice, senza che inizi il moto retrogrado:
‡K ≤ 0 ⟹ ‡ ≤
x
1+x
è x ≃ 1 ⟹ ‡ ≤ 0,5
E
I
Esempi di rendimento:
I
E
|
E
I .
1) Piano inclinato:
‡
}(
,
}
f ≫ ',
}( sin f
Condizioni reali: } sin f +
Condizioni ideali: }(
‡
}(
⟹ ‡
}
1 + ! cot f
1 + ! cot '
š hij ¡
hij £
sin '
sin ' +
I
” sin '
” sin ' +
∙
sin f +
sin f
:‡
0,5
Condizioni moto retrogrado: }K sin f
⟹}
š hij ¡8¢
hij £8¢
sin ' ∙ sin f cos + sin cos f
sin f sin ' cos + sin cos '
&
f
∨ '
2
” sin '
⟹ }K
š hij ¡5¢
hij £5¢
‡
K
}K
}(
1
1
! cot '
! cot f
I
: ‡K
0
'
2) Coppia rotoidale:
Q=Forza resistente (assegnata), P=Forza motrice(nota solo la retta d’azione), R=Reazione
vincolare passante per il punto H (dall’equilibrio dei momenti) e tangente al circolo
d’attrito (di raggio ¦).
šz8.§
Equilibrio dei momenti intorno al centro del perno: } ∙
”∙|+2∙¦ ⟹}
Equilibrio delle forze usando thr. Carnot: 2
Dal momento che 2 ≃ 2( ho che:
2(
y}( + ”
Dunque:
}
”| + 2¦
”©
2}” cos V
|
”|
Da cui:
‡
}(
}
Mentre:
1 + ¦y
1
+1
©ª
”|
|
2 cos V
¦
|
+ ”© + 1
+
1
1
|
2
cos V
|
« +”
|
2 cos V
¨} + ”
2ª
”|
2}” cos V
« ” cos V
B
‡K
1
¦©
+
1
|
2
cos V
|
3) Coppia prismatica:
Q = Forza resistente (nota); P = Forza motrice (nota retta d’azioni)
} cos ' + f
}
‡
” cos f
cos ' + f
}(
}
” cos f
cos f
cos f
1 ! tan '
1 + ! tan f
4) Coppia elicoidale:
}(
∙
⟹ }( cos '
” cos f
cos '
cos ' +
cos '
” cos f
cos f ∙ cos ' cos
sin ' sin
cos ' ∙ cos f cos + sin f sin
Considero una vita mobile e la madrevite sia fissa. Alla vite applico una forza
resistente Q (nota e diretta secondo l’asse). Sono note anche le caratteristiche
geometriche della vite (cioè: h = passo, rm = raggio medio del filetto, V = angoli che
le generatrici degli elicoidi formano con un piano normale all’asse della vite). È noto
anche = angolo d’attrito tra vite e madrevite. Sia ' = inclinazione dell’elica media.
Voglio trovare Mm = momento necessario a mantenere la vite in moto uniforme.
Considerazioni:
Considero un tratto elementare di elica media, di lunghezza , ed indico con • ∙
la forza su di esso agente; • è dunque la forza unitaria di contatto. La forza • è
scomponibile in una componente normale (indicata con ¬), che forma con l’asse
della vite un angolo, d, ed una componente tangenziale (indicata con -¬), diretta
secondo l’elica media, ossia secondo la direzione dello strisciamento della vite sulla
madrevite.
Per calcolare il momento ®9 si ricorre all’equazione dei lavori, scrivendo che il
lavoro motore, corrispondente ad una certa variazione della vite, è uguale alla
somma del lavoro resistente e del lavoro perduto per spostamenti corrispondenti,
facendo riferimento alla rotazione 2& posso scrivere che:
®9 ∙ 2&
” + ‚3 ‚
I
Il lavoro perduto, come si evince dalla figura, è dovuto unicamente alle forze ! .
Infatti lo spostamento della forza ! , per una rotazione 2& della vite, è pari alla
lunghezza dell’ipotenusa di un triangolo rettangolo di cateti
2& 9 . L’ipotenusa
@
risulta uguale a
. Dunque:
hij ¡
JJ
J
‚3
E
¯
!
sin ' (
I
I
I II
I
E
I
®9
” +
¯
!
M
sin ' (
2&
Voglio calcolare l’integrale, dunque dall’equilibrio delle forze agenti sulla vite alla
traslazione assiale:
¯
¯
” + ! sin ' -
(
Ottengo quindi che:
®9
cos d -
⟹ -
(
”
!
°1 +
2&
sin ' cos d
”
cos d ! sin '
¯
(
! sin '
”
2&
®9A
±
Il rendimento della coppia vale dunque:
®9A
®9
‡
1+
1
1
sin ' cos d
sin ' cos d !
sin ' cos d + !
! sin '
'
'
Voglio calcolare d essendo noti V ed ' (questo può essere calcolato se sono noto il
@
passo h ed il raggio 9 , infatti tan '
). Osservo che ' e d sono le proiezioni su
4+™
due piani ortogonali dell’angolo d, dunque:
I
d
I
'+I
V ⟹ cos d
√1 + I
Dall’espressione del rendimento:
‡
I II
1 ! K tan '
ª
1 + ! K cot '
E I
I
sin ' cos d !
sin ' cos d + !
sin ' cos d
!
K
cos '
!
«
cos d
tan ',
'
'
'+I
sin ' cos '
∙
cos d cos '
cos ' cos '
1+!
∙
cos d sin '
1
E
1
V
!
I
1 !K
tan '
tan ' + ! K
tan ' ∙ cot '
E I
1
I
cos '
1 tan K tan '
tan '
tan ' + tan K
Se il filetto è:
Rettangolare: ' d,
Triangolare: d > ',
K
Rendimento moto retrogrado:
!K
tan
K
K
tan '
tan ' +
I , ‡
‡
K
tan '
tan '
K
ù|
K
4. Richiami di cinematica del corpo rigido:
Un moto rigido può essere sempre considerato determinato dal rotolamento di una
rigata mobile ´K su una rigata fissa ´ ed in pari tempo da uno scorrimento della
prima lungo la generatrice di contatto. Le due rigate sono il luogo delle successive
posizioni dell’asse di moto rispetto al sistema di riferimento fisso e rispetto al corpo
in movimento. Un moto rigido piano è tale che il vettore v
µ, si mantiene sempre
parallelo a se stesso e la velocità di traslazione dei punti sull’asse di moto è nulla,
quindi il moto di tutti i punti avviene sui piani normali ad v
µ; le due rigate diventano
due cilindri aventi lo stesso asse. Un generico piano normale ad v
µ taglia i due cilindri
K
secondo due curve: ¶ (polare fissa / base) e ¶ (polare mobile / rulletta).
Teorema di Chasles: 3̅
̅( + v
µ∧ P O
̅( + ̅€A
v
µ ∧ P O è la velocità che supposto O fisso, il punto P avrebbe se ruotasse
intorno ad O con la v
µ caratteristica di un moto rigido.
Teorema di Rivals: s3 s( + vºµ ∧ } q + v
µlv
µ ∧ } q n s( + s€A
vºµ ∧ } q + v
µlv
µ ∧ } q n è l’accelerazione che, supposto O fisso, il punto P
avrebbe se ruotasse intorno ad O con vºµ e la v
µ caratteristiche di un moto rigido.
Teorema di Eulero-Savary:
c = centro di istantanea rotazione, punto di tangenza;
e K sono a contatto dopo un tempo I ⟶ »
Quanto vale s* ?
s*
*̅
'
*̅
*̅
I
I+ I
I
¼
s*
¼
¼K
»
2
'Δv
,
I
¼K
I+ I
»v
I
'
I
*̅
I
I
I+ I
I J
»
⟹
2K
v ⟹ s*
'
*̅
I
0, è I
I II I
'
Ȼ
Δv
1
2
E |
1
«
2K
K
I
E
I ! E
K
»
⟹ »
Δ
I
'Δ
»
Prendendo sulla normale alle polari un punto S tale che |¾ ¿| ∆
Sfrutto la formula di Rivals, prendendo il polo O coincidente con il centro C di
istantanea rotazione:
s3
s* + vºµ ∧ }
q +v
µ ∧ lv
µ∧ }
s* + v
µ∧ v
µ∧ } ¿
v ¾ ¿
v }
v ¾
vºµ ∧ }
Á
¿
E
I E
¿
v ¾
I I
Âv } º ¿
J
II
q n
E
I
}
v ¾
,
v Á
E E
J
Á +v Á
I
}
}
E
¿,
}
I
II
E
.I
Dunque:
s€
Âvº }
¿ +v ¾
}
Âvº }
¿ +v ¾
Se prendo P coincidente con J } ≡ Á , cosa succede?
Á +v Á
}
La componente tangenziale sarà: sÕ v ¾ Á .
La componente normale sarà: sÃŽ v Á }
0.
Al variare dell’angolo , J lo costruisco sempre nello stesso modo ⟹ data una
direzione trovo su ogni direzione un punto J che ha la componente di accelerazione
normale nulla ⟹ J sta su una circonferenza, che si chiama:
Circonferenza dei flessi:
È il luogo geometrico dei punti che appartengono al piano mobile che hanno
istantaneamente la componente normale di accelerazione nulla:
Ωè
I
Relazione tra:
ssss
ÆÇ
I
s3
I
¦
II
ssss
}¿
Ä
Äv
}Ω
I },
ssss
ÈÇÉ Ì
Ë -ÍÎÏÐÑÌÒÓÍÔ• ÕÓ ÖÐÑ•ÎÍ
ssss
ÊÇ
}
II
K
×ÌØÌÎÙ
Punto P (appartenente al piano mobile);
Punto C (centro d’istantanea rotazione);
Punto J (appartenente alla retta ssss
}¿ e giacente sulla circonferenza dei flessi);
Punto Ω (centro di curva della traiettoria del punto P).
P, C, J, Ω sono allineati.
II
Altra formulazione:
sss
Á}
1
∆
sss + ¿}
ssss
Á¿
ssss
¿}
ssss
Ω}
Ë
Ú
Ë
Û
1
Δ cos
ssss
+ ¿}
∙ cos
ssss
¿}
ssss
¿}
ssss
ssss
Ω¿ + Ω}
∙ cos
ssss
ssss
¿} ∙ ¿Ω
Ë
ÛK
ª
Ë
ssss
ÈÊ
ssss
¿}
⟹ Δ cos
ssss
Ω}
ssss
Ω}
∙ cos
ssss ∙ Ω}
ssss
¿}
ssss
¿}
ssss
Ω}
ssss ⟹
¿}
ssss
ssss
Ω¿ + Ω}
∙ cos
sssss¿}
ssss Ω}
ssss
¿}
Ë
« ÜÝÞ ß ÉÌ -ÍÎÏÐÑÌÒÓÍÔ• ÕÓ ÖÐÑ•ÎÍ
ssss
ÈÇ
×ÌØÌÎÙ
Esistono punti per i quali la componente di accelerazione tangenziale è nulla? Essa
vale:
µv
¿} + ¾Á
vº ssss
¿} + Δ sin v
s* vº ssss
Essa è nulla per i punti del piano situati su una circonferenza detta circonferenza
delle accelerazioni passante per C, avente il centro sulla tangente connessa alle due
àá/
polari, di diametro: º . È il luogo geometrico dei punti del piano mobile che hanno
á
istantaneamente accelerazione tangenziale nulla. Nota bene ¿ ∉ alla circ. delle
accelerazioni, poiché ha accelerazione tangenziale.
K = Polo delle accelerazioni, è il punto appartenente ad entrambe le circonferenze
(accelerazioni e flessi) dunque ha accelerazione totale nulla.
Proprietà di K:
s7Ž
tan '
v ssss
qã; såŽ
s7•
s7Ž
v
vº
v ssss
qæ; s7•
ssss
qã
ssss
qã
vº ssss
qã; så•
v
; tan f
vº
så•
såŽ
v
vº
vº ssss
qæ
ssss
qæ
ssss
qæ
v
⟹ '
vº
f,
è:
1B Il polo delle accelerazioni K, vede le accelerazioni di tutti i punti del piano sotto
lo stesso angolo;
2B Le accelerazioni di tutti i punti del piano mobile sono proporzionali rispetto alla
distanza del punto da K;
çæ
3B L’angolo ãr
d è lo stesso descritto dall’accelerazioni s7 e så .
Esempio: Quadrilatero articolato (catena cinematica, che ha quatto membri collegati
ssss (manovella, vincolata al telaio,
con quattro coppie rotoidali: 1) Telaio (fisso); 2) qã
sssss (bilanciere, vincolata al telaio,
movimento di rotazione rispetto ad O); 3) q′æ
ssss (biella).
movimento di rotazione rispetto ad O’; 4) ãæ
Nota bene 4 membri rigidi ⟹ 4 moti rigidi piani diversi, voglio il moto della biella:
Circonferenza dei flessi della biella, circonferenza delle accelerazioni, circonferenza
ausiliaria:
Come trovo la circonferenza delle accelerazioni?
sssss e trovo C (centro di istantanea rotazione della
Prolungo le direzioni di ssss
qã e q′æ
biella, vede le velocità di A e B sotto un angolo retto).
Teorema di Eulero:
sss
Áã
ssss
¿ã
I
ssss
qã
Á ,
ssss
Á′æ
ssss
¿æ
I
sssss
q′æ
ÁK .
La circonferenza dei flessi passa per J, J’ e C (punti noti).
L’accelerazione di J, essendo sulla curva dei flessi, è tutta tangenziale ed è passante
per il polo dei flessi S. Nota l’accelerazione di A, trovo il punto M, che è il punto
d’incontro dell’accelerazione di J e di A.
Chiamo circonferenza ausiliaria quella che passa per J, A e M. Questa circonferenza
interseca la circonferenza dei flessi in J e nel centro delle accelerazioni K.
La circonferenza delle accelerazioni ha il centro sulla tangente alla circonferenza dei
ssss r”
ssss.
flessi, passa per C e per K ⟹ ”¿
5. Sistemi articolati:
Un sistema articolato è un meccanismo formato da più membri (aste) collegati fra
loro da coppie rotoidali e prismatiche. Si distinguono in:
1) Piani --> Gli assi di tutte le coppie sono paralleli fra loro.
2) Sferici --> Gli assi di tutte le coppie sono incidenti in un punto.
3) Generali --> Gli assi delle coppie sono comunque sghembi.
Il membro fisso costituisce il telaio.
Se il meccanismo ha un solo grado di libertà la relazione fra il numero
numero di coppie rotoidali è la seguente:
2
4
di aste ed il
Esempi di sistemi articolati:
1) Quadrilatero articolato:
È l più semplice sistema articolato. Possiede 4 coppie rotoidali e quindi ha 4 aste.
ssss = Manovella (rotazione di 360°), æé
ssss = Lato fisso (telaio), ã¿
ssss = Bilanciere
ãæ
ssss = Biella. Ci sono tre tipi di quadrilatero articolato:
(oscilla), ¿é
1. A doppia manovella,
2. A doppio bilanciere,
3. A manovella e bilanciere.
Studio cinematico del quadrilatero articolato, due problemi:
1) Problema di sintesi cinematica:
Date delle caratteristiche del moto che voglio ottenere, trovare il meccanismo che
mi consente di ottenere quel moto.
2) problema analisi cinematica:
Ho un sistema articolato, conosco i dati, ̅ , s, voglio trovare la velocità e
l’accelerazione di tutti gli altri punti appartenenti ai membri del meccanismo.
Esempio:
4
Per convenzione la velocità è ruotata di rispetto alla direzione reale ed v
1.
Velocità di B:
̅å
| ̅å |
̅
B
+v
µ∧ æ
ã
̅
7
+ ̅å7
̅
7
0,
èãè
I !
ssss, direz. perpendicolare ad ãæ
ssss , ruoto di 90° → ̅å //ãæ
ssss → ãæ
ssss
v
µãæ
̅å7
| ̅å |
Velocità di C:
̅ì
̅ìå
̅å + ̅ìå
ssss
‚æ
̅ì
ssss
̅ì //¿é
ssss
‚ã
̅ìå
v
µå ∧ ¿
æ
I
90° →
ssss
J. // ¿æ
Velocità di P (generico punto solidale alla biella):
̅€
̅å + ̅€å
in generale:
Voglio le accelerazioni:
̅€å
sssss
®æ
̅€
̅€
sssss
®ã
*̅
+ ̅€ì
̅€ì
ssss
®‚
Accelerazione di B:
så
såŽ + så•
så
v ãæ
så•
vºµ ãæ, E v
ãæ
ssss
æã
I ⟹ vºµ
0 ⟹ så•
0
såŽ
ísî
ssss
7å
Accelerazione di C:
1. sì
Ž
sìå
så + sìå
ìå
ssss
¿æ
ssss
æ‚
ssss
¿æ
Ž
•
så + sìå
+ sìå
ssss v
æï
sìå
v
æ
Ž
ï → sìå
ssss
æï
Infatti dai triangolo ACB e ABL risulta che:
ã¿æ ≡ æ‚® ⟹
ãæ‚
æ®ï ⟹
ssss
ãæ
ssss
æ¿
ssss
æ‚
ssss
ãæ
sssss
ssss
æ®
æ‚
⟹
ssss
ssss
æ‚
æ¿
ssss
sssss
æï
æ®
⟹
sssss
ssss
æ®
ãæ
Unisco le due espressioni:
sssss
æ®
,
ssss
ãæ
ssss
æï
ssss
æ‚
ssss
ssss
æï
æ‚
̅ìå
æ‚ ssss
Ž
ssss
⟹ æï
sìå
ssss
ssss
ssss
ssss
æ¿ æ‚
æ¿
æ¿
•
L’accelerazione sìå
è diretta ortogonalmente alla congiungente ssss
æ¿
v ãæ
sìŽ
2. sì
+
sì• ,
sìŽ
ssss
‚ã
v
ssss
¿é
̅ì
ssss
¿é
2ã
Prendo un punto R su ssss
‚ã tale che sia ssss
Dunque ottengo che:
sìŽ
v
2
ssss/
ˆ7
ssss
ìð
ã
Sia S il punto comune alla normale a ssss
‚ã condotta per R ed alla normale ssss
¿æ condotta
per N, risulta che:
sì
ã ¾
v
Accelerazione del punto P, solidale alla biella:
så
Ž
sìå
•
sìå
såŽ
ssss
æã
ssss
ïæ
ñ sìå
ssss
¾ï
sìŽ
sì•
ssss
¾æ
ssss
2ã
ñ sì
ssss
¾2
ssss
¾ã
B = Polo delle accelerazione, quindi proprietà di K (vedi sopra)
s€
s€
så + s€å
ò s
sì + s€ì €
ssss,
Ӌ
E I
”?
Avevo ipotizzato che v
µ = costante, cosa succede se v
µ ≠ 0/costante:
Per quanto riguarda la velocità non cambia nulla, mentre l’accelerazione så• ≠ 0.
så
såŽ + så• ,
såŽ
vº
ssss
ãæ
v
såŽ
ssss
ãæ
sì
Ž
•
sìå + sìå
+ sìå
sìŽ
ssss
¾ã
så•
̅ìå
ssss
¿æ
ssss
v ãæ
så•
ããK → så
2
sì
sssss
æã′
I
ssss
æ¾
ssss ,
vº ãæ
s*Ž
sìå
J
v
̅ì
ssss
¿é
sssss
2ã′
1, •
:
2) Manovellismo:
Si tratta di un meccanismo composto da 4 membri: Manovella, Biella,
Corsoio/Pistone, Guida/Glifo, che sono collegati tra loro con tre coppie rotoidali ed
una coppia prismatica (glifo). Il manovellismo si dice:
Centrato = La traiettoria rettilinea di P passa per O.
Deviato = La traiettoria rettilinea di P non passa per O.
(Il manovellismo di spinta è circa un quadrilatero articolato, ottenuto facendo
tendere all’infinito la lunghezza delle due bielle / manovelle / biella e manovella.
Velocità:
̅ƒ
̅ìƒ
sssss ,
®q
̅€ƒ
sssss ,
{®
̅ì€
ssss,
‚®
̅€
ssss,
{‚
̅ì
ssss,
‚q
ssss
{q
Accelerazioni:
sƒ
sssss ,
®q
ssss ,
¾q
s€
Ž
s€ƒ
sssss ,
”®
•
s€ƒ
ssss ,
¾”
s€ƒ
sssss
p®
ö
•
Considero la risoluzione analitica:
ssss(
q}
∙
+
1
sin V
+
cos f +
+
1
5Ãô
1 ⟹ cos f
cos V + 1
⟹
õ1
cos V + Â
sin f ⟹ sin f
sin f + cos f
1
ã
cos f
sin V
+
+
sin V, D
¯
¯
¨ 1
1
ã
ö + õ1
sin f ,
¶G ⟹ sin f
sin f
¨ 1
cos V + 1
5Ãô
¶ sin V,
¶ sin V
¨ 1
¶ sin V
:
∙
∙
I
I
¶ 2 sin V cos f
v sin V + v
2 ¨ 1 ¶ sin V
¶
≃ v ªsin V + sin 2V«
2
I
v Nsin V +
¶ 2 sin V cos V
O≃
2 ¨ 1 ¶ sin V
º¶
≃ v cos V + ¶ cos 2V + 2v sın V + sın 2V
Trasmissione delle forze nel quadrilatero articolato:
Q = Forza resistente, nota; P = Forza motrice, nota retta d’azione. Cerco la P tale che
faccia equilibrio con Q in condizioni reali ed ideali.
Q è applicata su CD, cioè un corpo rigido sottoposto a tre forze (Q, reazione del
telaio in D, reazione della biella in C). La biella è un membro rigido sottoposto a due
forze, che per equilibrio costituiscono una coppia di braccio nullo, la cui retta
d’azione è l’asse della biella. Prolungo BC e Q e chiamo il punto d’intersezione K1.
Congiungo D e K1. Il membro 1 è sottoposto a tre forze (R21 nota, P, di cui conosco
solo la retta d’azione e la reazione del telaio su 1).
Condizioni reali, c’è attrito. Abbiamo dimostrato che le reazioni della coppia
rotoidale sono sempre tangenti al circolo d’attrito, però ho quattro possibilità di
tangenza, infatti:
Come scelgo le rette d’azione? Voglio forze tangenti al circolo d’attrito e che
generino una componente di momento che si opponga al moto:
Sono su ② e vedo ③ ruotare in senso orario, affinché R23 mi dia una componente
di momento che si opponga al moto deve essere tangente dalla parte di sotto,
infatti:
Sono su ② e vedo ① ruotare in senso orario, affinché R21 mi dia una componente
di momento che si opponga al moto deve essere tangente dalla parte di sopra,
infatti:
Trasmissione delle forze nel manovellismo di spinta:
La manovella è in equilibrio sotto l’azione di ®+ e di un sistema di forze in grado di
equilibrare ®+ ⟶ cerco una coppia di forze che faccia equilibrio a ®+ .
Condizioni reali:
Cosa succede in corrispondenza del punto morto superiore ed inferiore:
Fenomeno di arresto/impuntamento: condizione per cui le reazioni d’attrito sono in
grado di equilibrare qualunque forza motrice ⟹ se ®. 0, la condizione ® 0
non posso verificarla. Vi sono due archi nei punti dei quali la coppia resistente è
nulla (archi d’arresto). Essi sono definiti dalla condizione in cui tutti e tre i circoli
d’attrito sono alternativamente tangenti ad una stessa retta.
3) Meccanismi a croce:
3.1) Giunto di Oldham:
Si compone di quattro membri collegati da due coppie prismatiche e due coppie
rotoidali.
ssss
ãæ
|
,
¿
I
I
K
I
I J
Tengo ferma la biella:
3 E
1
2
⟹
:
3 4
1
2∙2
2
1
Il cursore A può ruotare intorno ad A ed il cursore B può ruotare intorno a B.
Se prendo un albero uscente solidale al cursore A ed un albero uscente solidale al
ssss e si
cursore B, ottengo una trasmissione tra due alberi. Se si tiene fissa l’asta ãæ
rende mobile la croce i due cursori ruotano rispettivamente attorno ad A e B. Il
meccanismo si presta a collegare fra loro due assi paralleli non coincidenti. Il centro
dell’arco O ruota attorno ad O’ con velocità angolare doppia di quella degli altri. Il
rapporto fra le velocità dei due alberi è costante e pari ad 1.
ãqø æ
4
ãqø æ,
q ãùq
',
q æøq
f,
'
f,
d
La velocità di rotazione della croce è doppia di quella degli altri.
2'
3.2) Giunto di Cardano:
È un meccanismo a croce sferico. Gli assi delle due coppie prismatiche (C, D)
corrispondono a due circonferenze massime, di diametro della sfera. I cursori (A, B)
sono simili a dei “salsicciotti” stondati che percorrono tubi, che hanno una
geometria compatibile con la geometria dell’asse e ci scorrono dentro. Si muovono
su una circonferenza con assi convergenti passanti per il centro della sfera. La biella
ssss è un segmento sferico, geometricamente a forma di arco di circonferenza, la cui
ãæ
caratteristica particolare è che i due perni che l’accoppiano hanno l’asse incidente
nel centro della sfera.
ssss e rendo le due circonferenza libere di muoversi ⟹ se il
Tengo ferma la biella ãæ
punto D (coppia rotoidale) lo rendo solidale ad un albero e faccio lo stesso con C ⟹
il movimento della croce fa si che ci sia un collegamento tra i due alberi in C e D, con
l’asse incidente nel centro della sfera (punto O).
Proprietà: È omocinetico (rapporto di trasmissione costante e pari ad 1 nel tempo)?
Dipende. Considero un triangolo sferico:
cot V K
tan V cos ', derivo nel tempo:
hij/ ô
;ô ˜
;•
cos '
úûh/ ô
;ô
;•
v
K
sin V K
cos 'v
cos V
v cos '
cos V + sin Vsin '
cos '
v
cos V 1 + cot V
v cos '
cos V + sin V 1
v cos '
cos V 1 + tan Vcos '
sin '
1
v cos '
sin Vsin '
Dunque non è omocinetico, lo sarebbe solo se l’angolo di circonferenza tra i due
alberi fosse zero, poiché cos 0
1. Per angoli piccoli le oscillazioni di velocità
úûh (
nono sono significative, invece per alberi grandi lo sono.
Per ottenere un collegamento omocinetico si possono impiegare due giunti di
Cardano ed un albero ausiliario:
v = Albero Motore, vK = Albero intermedio, vKK= Albero di contatto.
' = Angolo di incidenza tra i due alberi, f = Piano che contiene i due assi.
'
'
KK
cos
cos
v
vKK
vKK vK
v
2
2
⟹
∙
1
v
vK v
v K 1 sin V K sin ' v K 1 sin V K sinK '
2
2
Ciò a condizione che gli angoli V K dei due giunti siano uguali misurati a partire dallo
stesso riferimento. Questo comporta che quando un lato della croce giace sul piano
f, lo stesso accada per il lato corrispondente della croce del secondo giunto.
È possibile anche ottenere un collegamento fra assi sghembi, perché si possono
ancora soddisfare le condizioni precedenti. Occorre che in questo caso quando un
lato della croce si trova su d, il lato corrispondente della croce del secondo giunto si
trovi su f.
Esempi di sistemi articolati: Meccanismo di sterzo delle autovetture.
'
Angolo di sterzata della ruota interna;
f
Angolo di sterzata della ruota esterna;
Carreggiata / Distanza tra le due ruote;
‚
Passo del veicolo.
tan '
m
C
C
‚
‚
;
+
; tan f
‚ cot ' ;
‚ cot f
; cot f
cot '
Angolo d’inclinazione dell’asse del glifo rispetto all’asse del veicolo;
Spostamento della barra;
tan m
tan m
sin '
cos m cos m
'
'
tan m + f
sin f
⟹
cos m cos m + '
⟹ sin ' cos m cos f
⟹ sin ' cos f cos m
sin m sin f
sin f cos m cos ' + sin m sin ' ⟹
sin f cos ' cos m
Divido per sin ', cos f, cos m ⟹ cot f
Basta porre:
3
ˆ
tan m
2 tan m
2 sin ' sin f sin m
cot '
6. Meccanismo con sagome e camme:
2 tan m
‚
Eccentrici a camme: Si indicano con questo nome i meccanismi atti a generare
movimenti alternativi o periodici (di traslazione o di rotazione) che si svolgono
secondo una legge determinata.
Punteria = Organo cadente, trasla;
Sagoma = Organo movente, trasla;
Camma = Organo movente, ruota;
Bilanciere = Organo cadente, ruota.
Nel caso della punteria il contatto puntiforme come quello indicato non è in genere
adottato, perché porta forti resistenze di attrito e rapidi logoramento. In genere il
profilo dato al cedente è uno di questi tre:
La coppia cinematica non è divisa; il contatto è assicurato soltanto se la forza mutua
agisce nel senso di premere un elemento sull’altro.
1) Meccanismi a sagoma e punteria:
Il problema cinematico consiste nel determinare il moto della punteria assegnati il
profilo e la velocità della sagoma. Supponiamo che il profilo attivo della punteria sia
costituito da un punto.
Legge di moto (alzata): ü
C I
̅ ,
̅
I
! C I
I
Legge della velocità:
̅
é
ü I
I
̅ I
I
I I J
! C C
I
C
ü I
I
Á r : º
!K C ̅
! C
C
•
ü
I•
̅ ,
•
! C
C•
̅
I
I
̅•
Forme tipiche dei diagrammi: ü I , ̅ I , s I , sº I relativi ad un cadente, il quale
partendo da una posizione di riposo ü 0 inizi il movimento per I 0 e raggiunga
per I p la posizione di fine corsa ü
.
Adesso era nota la geometria / configurazione / sistema e volevo trovare la velocità
e l’accelerazione della punteria.
Problema inverso (più comune): Assegnata la legge del moto ̅ I della punteria e
̅
costante, determinare il profilo della sagoma:
̅ I
;ý
;F
̅ → ü
ís/ •
ís0
̅
costante, I
F
í0
⟹ü C
ís0
F
F
M( ̅ Dís G C
0
Se la punteria è a rotella / a testa sferica il problema non cambia, le curve
considerate costituiscono la traiettoria del centro della rotella. Il profilo effettivo
della sagoma è definito come l’inviluppo di una famiglia di carichi aventi il centro
sulla curva suddetta.
2) Meccanismi con camma e punteria:
Dato il profilo e la velocità di rotazione della camma determinare la velocità ̅ della
punteria.
sssss v e
M = Punto appartenente alla camma ed alla punteria (velocità ̅
q®
sssss þ ̅ ).
direzione tangente al profilo della camma ⟹ q®
Prendo la tangente al profilo della camma e proietto lungo la direzione ortogonale
la componente della velocità ̅ ⇒ ̅
cos ' + V
̅ cos V.
4
'+f+V
.
sssss sin f vq®.
sssss
̅ sin f
̅ cos V vq®
q{ Componente di ̅ e ̅ lungo la normale al profilo della camma in direzione
ssss
7
ssss v.
perpendicolare alla sua direzione e verso reale ⟹ ̅
v
q¿
úûh ô
C = Punto trovato come incontro tra le due rette: 1B Passante per O ed
ortogonale alla punteria, 2B ) Congiungente H e M.
Oppure:
3
̅
ƒ
Oppure:
*
̅
ƒ
+ 7̅ ,
*
̅
ƒ
v
sssss ,
q®
̅.
v
sssss ,
®¿
3
̅
ƒ
̅
ssss ∙ v
q¿
C è il centro di istantanea rotazione del moto relativo della punteria rispetto alla
camma. La velocità assoluta di un punto generico del piano mobile si ottiene
sommando la velocità relativa di questo punto rispetto alla camma più la velocità
dello stesso punto appartenente alla camma. Se questo punto coincide con C la
3
*
ssss ∙ v.
velocità relativa è zero ⟹ *̅
q¿
*̅
Questo stesso risultato si può ottenere ancora per un’altra via utile per il calcolo
grafico dell’accelerazione. Per piccoli movimenti si può sostituire al profilo effettivo
il cerchio osculatore e quindi il meccanismo equivale al manovellismo della figura:
Ne segue che l’accelerazione della punteria può essere calcolata con lo stesso
procedimento grafico valido per il manovellismo:
3) Meccanismi a camma e bilanciere:
Problema cinematico: Dati i profili e la velocità v
µ della camma determinare la
velocità v
µ del bilanciere.
z
̅
ƒ
v
µ
q
®,
v
µ
z
̅
ƒ
v
µ
I
I ,
*
̅
ƒ
v
µ
+
® ∈
z
̅
ƒ
̅.
,
v
µ
v
µ
|
q
® + ®
{
q
Quindi:
ssssss
q
{v
µ
ssssss
q
{v
µ ,
v
µ
ssssss
q{
∙v
µ
ssssss
q {
sssss
q¿
∙v
µ
sssss
q ¿
Per determinare l’accelerazione si può fare ricorso al quadrilatero articolato della
figura:
Eccentrico:
{
Impuntamento delle camme:
In alcune situazioni il momento motore applicato alla camma non è capace di
equilibrare alcuna forza resistente Q applicata alla punteria. Si dice allora che il
meccanismo “si impunta”. L’equilibrio è possibile solo se Q è diretta in senso
opposto, ossia se agisce forza matrice.
7. Ruote dentate:
Studio la statica delle ruote con la statica dei corpi rigidi, osservazioni:
Le ruote non sono rigide, ma si deformano.
Perché si studiano? Poiché ci sono certe osservazioni che mi danno spiegazione a
questi fenomeni.
Le rotaie sono più vicine al modello dei corpi rigidi.
Suddivido tre cassi per la statica delle ruote:
1) Ruota condotta:
p = Forza peso, u = Parametro di attrito volvente, T = Forza di trazione, d = Angolo
della risultante, = Angolo di attrito, ≫ d.
Non ho momenti, ho due forze: Ruota su terreno e Terreno su ruota (costituiscono
una coppia di braccio nullo).
2) Ruota motrice:
v
µ
̅
,
2
®.
+:Œ<Œ•:Ž•:
2z
®9 ,
d≪
Nota bene: Non ha senso trattare il problema della statica della ruota in condizioni
ideali, poiché se sono in condizioni ideali non ha senso parlare di rotolamento della
ruota.
Voglio trovare la forza di trazione da applicare alla ruota per fare equilibrio alle forze
applicate:
2s
µ
®
0
0
Le forze applicate alla ruota costituiscono una coppia non di braccio nullo, poiché c’è
un momento resistente. Due momenti:
10) Resistente, generato dalle azioni che il veicolo applica sulla ruota ed il terreno.
20) Motore, che la ruota deve generare per fare equilibrio ai momenti del numero 1.
d ≤ , se d > ⟹ La ruota non avrebbe più rotolamento, non sarebbe garantita
l’aderenza sul terreno ⟹ la ruota striscerebbe.
3) Ruota frenante:
Voglio mantenere ̅
equilibrio alla ruota.
®
2|
costante ed applicare un ®
+:ŽBŽ•:
tale da garantire
d ≤ , poiché se d > la ruota non rotolerebbe più rispetto al
terreno, ma si bloccherebbe ⟹ striscerebbe.
Profili coniugati:
Dato un moto rigido piano definito mediante le primitive ¶ ¶K si definiscono profili
coniugati due curve che durante il moto si mantengono costantemente in contatto.
Le due polari sono un esempio particolare di profilo coniugato. Dalla definizione
segue che:
La normale comune ai profili coniugati nel punto di contatto passa per il centro di
istantanea rotazione del moto C. Infatti in caso contrario si avrebbe il distacco o la
compenetrazione dei profili. Come si tracciano i profili coniugati? Date le polari
¶ ¶K ed il profilo K , tracciare il profilo coniugato di K .
1 ® I
:
K
Si disegna il profilo K nelle varie posizioni e con questo si genera il profilo
inviluppo delle varie posizioni di K .
2 ® I
E
:
per
3 ® I
K K
sssssss
¿
®
K
sssssss
¿
®
:
Prendiamo una curva ¼ ed un punto P ad essa solidale e facciamo rotolare ¼ una
volta su ¶ ed una volta su ¶K . Durante questo moto P genera due curve e K che
sono due profili coniugati.
KK
ssssss
¿
}
K K ssssss
ssssss
¿
} ¿ KK }
ssssss
ssssss
¿
} ⟹ ¿
}K
ssssss
¿
}
Analogamente se si considera una curva 6 solidale ad ¼, questa durante il
K
rotolamento di ¼ su ¶ ¶K inviluppa due profili conigati
. Questo metodo si due
K
profili qualunque essi risultino coniugati. Infatti
è definita assegnati
K
K
K
¼ ¶ ¶ ; se variamo ¶
¶ si ottiene una nuova curva
, che è ancora
K
.
coniugata di
Trasmissione del moto fra due assi paralleli:
K
Considero due assi fra loro paralleli
e due corpi rigidi rotanti attorno ad essi
con velocità angolare v
µ v
µ K fra loro discordi. Imponendo la condizione
determinare la primitiva del moto.
µ˜
á
I.
µ
á
Determino il moto relativo dell’asse K rispetto ad imponendo a tutto il sistema
una velocità v
µ. Il moto risultante (moto relativo) è ancora una rotazione di
intensità v + vK attorno ad un asse parallelo agli altri due:
sssssK
qq
I
I
⟹
ssss
q¿
K¿
sssss
q
K¿ ⟹
sssss
v
µKq
ssss
v
µq¿
I
I
v
µK
v
µ
I
ssss
q¿
K¿
sssss
q
ssss
J q¿
K¿
sssss
q
.
K
K ¿ . Il moto è
sssss
Le primitive del moto sono due cilindri di assi
e di raggi ssss
q¿ q
piano e può essere studiato in una qualsiasi sezione normale agli assi. La
trasmissione del moto può avvenire materializzando due qualsiasi profili coniugati
definiti dalle due polari che in questo caso sono costituite da due cerchi di raggio
sssss .
ssss
q¿ q′¿
Ruote di frizione:
Se come profili coniugati prendo le due primitive ¶ ¶K ho una coppia cinematica
superiore, detta ruota di frizione. La trasmissione del moto da movente a cedente è
dovuta unicamente all’attrito ed occorre premere con una forza ï le due ruote l’una
contro l’altra affinché queste possano manifestarsi.
In assenza di perdite di rotolamento si ha:
®9A
dove:
!
∙
∙ ï,
!!
I
®+
I
I
∙
II I
E
K
∙ ï ⟹ ®9A
0<
≤ !,
µ
á
µ™
á
•
•
®+
>!
v
µ
∙ ®+
v
µ
∙ ®+
II ,
Nell’esercizio effettivo occorre tener conto della perdita per rotolamento che è
l’unica causa di perdita della coppia.
®+
®9 ï ∙ m + ∙ ï ∙ , ®+
ï∙m+ ∙ï∙
⟹ ï
⟹
∙
m
⟹ ®9
‡
®9A
®9
+m
®
m +
+
m
m
,
®+
¾
+
m
m
ï ¨1 +
®+
m
¨1 +
,
¾
!
J
I
E|
Essendo m piccolo sembra che ‡ sia elevato; in realtà occorrono forti valori di ï con
grosse deformazioni e strisciamenti locali.
Ruote dentate cilindriche ad evolvente:
Per avere una trasmissione sicura e non dipendente dal valore del coefficiente di
attrito, non si può adottare come profili coniugati le primitive del moto. Occorre
dunque rinunciare ad avere un contatto di puro rotolamento. I profili coniugati
comunemente adottati sono generati da una retta 6 solidale ad un’altra retta ¼
(epiciclo) che rotola sulle due primitive. È facile verificare che i profili così generati
sono volventi di cerchio. Infatti se f è l’angolo formato da ¼ e 6, l’angolo che la
4
normale d (retta dei contatti) al profilo forma con ¼ '
f ' = Angolo di
pressione, rappresenta la direzione ortogonale ai profili coniugati nel punto di
tangenza reciproca) è costante e quindi in ogni posizione la retta d mantiene una
distanza costante da q pari a ¦
cos '. Quindi l’evoluta del profilo coniugato è
una circonferenza di centro q e raggio ¦ (circonferenza di base). Analogamente il
profilo ¦ è l’evolvente della circonferenza di centro q e raggio ¦
cos '.
I profili coniugati suddetti possono anche essere generati come traiettoria di un
punto } di d, mentre questa rotola sulla circonferenza di base. Le ruote ad
evolvente dal punto di vista cinematico godono delle seguenti proprietà:
La forza trasmessa dai denti, prescindendo dagli attriti, ha direzione costante,
I profili rimangono coniugati anche se l’interasse varia; cambia solo l’angolo di
pressione ',
La ruota con numero infinito di denti (dentiera) ha superfici dei denti piane.
Definizioni:
Ingranaggio = Accoppiamento di due ruote dentate,
Lavoro esterno = Entrambe le ruote dentate hanno dentatura esterna,
Lavoro interno = Almeno una ruota dentata ha dentatura interna.
Come costruisco le ruote dentate? Problema di proporzionalmente. Faccio
riferimento al modulo come grandezza per il loro dimensionamento:
E
2∙2
,
J
2
EI
I ,
J
=
I
Definizioni:
Passo
: Distanza dall’inizio di un dente a quello successivo
2&
J
&E
Spessore (pieno): Distanza misurata sulla primitiva dei due punti sui fianchi opposti
del dente:
J
Vano (vuoto): Distanza dei due denti contigui:
2
Lina di contatto; arco di azione:
sssss Accesso, il dente della ruota motrice penetra dentro il vano corrispondente
¿ï
della ruota condotta.
sssss
ï
¿ Recesso, il dente della ruota motrice si disaccoppia rispetto al vano della
ruota condotta.
Durante il moto il punto di contatto di due profili descrive un segmento della retta d
detto: arco di ingranamento. Esso è delineato dai punti ï ï intersezioni di d con
le circonferenze di testa delle due ruote. Quando il profilo di contatto si sposta da
ï a ï , le due primitive rotolano di un arco che si chiama: arco di azione.
ã ã
J
.
È importante considerare la lunghezza dell’arco di azione in relazione al passo
4+
&E. Infatti, essendo l’arco su cui rotolano le due primitive durante il
contatto di due profili, se risultasse > vorrebbe dire che per un arco
non
esisterebbe alcun dente in contatto e quindi le due ruote non sarebbero più
vincolate l’una all’altra. Deve risultare quindi:
≥
J
I
I
Ià
è
E I ,
I
è
Ià
E
E I .
Il calcolo della lunghezza dell’arco di azione e dell’arco di ingranamento può essere
effettuato nel modo che segue
sssss
ï
¿;
{‚
æ ¿
{‚
¦
sssss
Il valore del segmento ï
¿
+
+C
1
; æ ¿
cos '
sssss
ï
¿
;
cos '
æ æ
sssssss
ï
ï
cos '
C può essere ottenuto dalla relazione:
&
2C cos D' + G
2
+ C + 2C sin '
La condizione di continuità del moto è in pratica sempre verificata, perché
sussistono condizioni più restrittive di esse ( infatti ↓).
Condizione di non interferenza dei profili:
sssssss
ssssss
ïï ≤p
p
¦
ssssss
q
p, ¦
sssssss
q
p ,
J
:
sssss
sssss
ï¿≤p
¿
sssss
sssss
ï
¿≤p
¿
sssssss
ï
ï I
E
I II
I
I II
I
ssssss
p
p
Si verifica facilmente che nelle dentature ad evolvente il punto di contatto } di due
profili deve essere sempre interno od esterno al segmento ssssss
p p e non può essere in
parte esterno ed in parte interno. Infatti i centri di curvatura dei profili sono i punti
p p e quindi quando è interno i denti debbono essere ambedue convessi,
quando è esterno devono essere uno concavo (quello di curvatura minore) e l’altro
convesso. Un dente non può essere convesso per una parte del profilo e concavo
per la rimanente, segue quindi l’asserto.
ssssss
In particolare nelle ruote esterne sssssss
ï ï è sempre interno al segmento p
p,
nell’imbocco fra una ruota interna ed una esterna è sempre esterno.
sssss ≤ ¿p
sssss
Deve risultare quindi: ¿ï
sssss ≤ ¿p
sssss
¿ï
Per ruote normali aventi uguale addendum prendendo per ruota uno quella di
sssss ≤ ¿p
sssss. Essa impone
diametro maggiore la condizione più gravosa è la prima: ¿ï
un valore massimo all’addendum e per date primitive un valore minimo al numero
∙ ∙+
di denti J:
x∙E
.
Dalla figura risulta che:
⟹
⟹
+
+
9BF
9BF
+2
9BF
sin ' + 2
sin ' ∙
9BF
+¨
+
sin ' ∙
sin '
+2
(perché E è una grandezza discontinua)
x∙
+/
Ž/ ™ •
≤
+¨
+
sin ' ∙
+2
⟹
0 ⟹
≥ x ∙ E9BF
+2
( 9<Ž è il = minimo di denti che dato un accoppiamento di ruote consente di
soddisfare la condizione di interferenza)
9<Ž
≥
+¨
+¨
2∙x
2∙x∙
+
sin ' ∙
+2
2∙x
+ yD G + sin ' ∙ D1 + 2 G
+ sin ' 1 + 2
Per ruote a dentatura interna il calcolo si svolge in modo analogo, il rapporto di
trasmissione τ deve essere cambiato di segno ed il radicale deve essere preso con il
segno negativo:
2∙x
≥
9<Ž
+ ¨ + sin ' 1 + 2
Per
∞ (coppia dentiera-pignone) l’espressione precedente risulta
indeterminata. Applicando i teoremi di De l’Hopital si ha:
9<Ž
≥
2x
sin '
espressione ricavabile anche in modo semplice:
9BF
sssss sin '
¿p
sin ' ⟹
x∙2∙
≤
∙ sin '
Convenzione dei profili sulle ruote dentate per ovviare alla non interferenza.
Se ho che la ruota più piccola ha un J 9<Ž ⟹ la ruota più grande dovrà avere di
conseguenza più denti.
ï = minimo i denti 13 ≤ J9<Ž ≤ 17 (cinematismo), se ho una ruota con 17 denti,
allora la condizione di non interferenza non è verificata
Se J
Se J
12 ⟹ J
20 ⟹ J
Caso di due ruote:
60
100
v
µ+
v
µƒ
⟹
1
5
B¯z:+= *=;=••=
B¯z:+= 9=•=+:
72
100,
I
E
I
ù
E
I
I.
J ,J
=
I
JJ
Descrizione figura:
① I valori sono maggiori J 9<Ž J 9<Ž ⟹ è verificata la condizione di non
interferenza per tutte e due le ruote.
② Una delle due ruote dentate ha un numero minore di denti del numero di denti
consentiti dalla condizione di non interferenza, l’altro maggiore; ma:
J + J ≥ 2J9<Ž
③ J J hanno un numero di denti minore di quanto consentito dalla condizione
di non interferenza, ma tale che:
J + J < 2J9<Ž
Cosa posso correggere:
② Posso effettuare la correzione dei profili ⟹ prendere un utensile e correggere le
posizioni rispetto al centro della ruota dentata da realizzare. Faccio uno
spostamento della primitiva all’utenza in senso positivo o negativo.
Prendo un tratto di evolvente in posizione diverso rispetto a
quello standard. Il dente a secondo di dove lo prendo è più convesso
⟹ Se sono nella zona ②, se è vero che J + J ≥ 2J9<Ž , posso crescere in più la
ruota con denti minori, in meno la ruota con denti maggiori
③ C C dovranno essere diversi anche in modulo, poiché devo correggere
entrambe le ruote.
Pignone (ruota con mento denti) + ruota: = di denti diversi, stesso materiale, ruota
più resistente del pignone, perché per la formula di Lewis:
»B99
J
ü
!!
I
|
JJ
E E
E I
‚
,
I ,
I .
L9BF
,
»B99 ∙ ü ∙ |E,
Per questa ragione si farà più resistente il pignone, poiché va prima in avaria. Si
corregge il pignone in senso positivo e la ruota in senso negativo, affinché non ci sia
una più resistente ed una meno.
Rendimento delle ruote dentate:
Ipotesi)
1. C’è una sola coppia di denti in presa ⟹ tutte le forze si trasmettono attraverso
questa coppia:
,
J
.
2. SI trascura l’attrito di rotolamento.
3. Non vi sono altre perdite ⟹ l’unico effetto di perdita è l’attrito di strisciamento.
Quando i denti ingrano c’è un piccolo urto, laddove le ruote sono realizzate per
bene, l’effetto dell’urto è ∼ 0, ma se non c’è precisione vi sarà urto (fanno rumore).
Equilibrio delle ruote: fase di recesso (i denti si allontanano)
C
C3
,
®+
®9
Elimino ï:
®9
sssss
ï¦ + !ï ∙ ¿p
è
I
I }
K
C
ï¦ + !ï ∙ õ sin '
I I
J
¿
.
ï¦B + !ï ∙ sssss
¿p + C
cos ' + !
cos ' + !
Condizioni ideali: !
⟹ ®9
ï¦ + !ï ∙ õ sin ' + C3 sin 'ö
1 + ! Dtan ' +
sin ' + C3 cos '
∙ ®+
sin ' C3 cos '
0 ⟹ ®9A
®+∙ ∙
1 + ! Dtan ' +
1 + ! Dtan '
sssss
}¿,
p ⟹C
C3 cos 'ö
+0
+/
C3
G
1 + ! Dtan '
⟹
C3 ∙ ®9A ,
G
C3
G
C3 ∙
G
∙ ®+
ã
(®9A non è costante, anche se ®+ è costante, ma varia in funzione della posizione
del punto di contatto).
sssss (arco di
L’espressione sopra scritta vale quando P si trova nel segmento ¿p
sssss (arco di accesso) la forza di attrito
recesso); quando si trova nel segmento ¿p
cambia di verso e C di segno. Si ottiene quindi:
®9
1
1
! Dtan '
C3
G
C3 ∙ ®9A
! Dtan ' + G
I rendimenti variano durante l’accoppiamento ⟶ ‡
ĪA
Ī
+
I
I .
Voglio un = medio per poter fare valutazioni energetiche sul motore da applicare
⟹ faccio riferimento al valore di un rendimento medio:
‚9
‚+
‚9
‡
®9
C3 ⟶ ‚9
1 + ! Dtan ' +
®9
®9A
1
1
C3
G 1
! Dtan '
J
,
- ®9 C3
3
! Dtan '
C3
G
C3
1
G
‚+
®+
F
- ®9 C3 +
(
≃ 1 + !C3 ª
1
1
+
F—
- ®9 C3
(
1
«
C3 > 0
Espressione valida sia in accesso che in recesso:
‚9
®9A
®+
®9A
F
- N1 + !C3 ª
(
CB + C+ + ! ª
°1 + !& ª
1
+
1
1
+
1
F—
«O C3 + - N1 + !C3 ª
CB C+
«N + O
2
2
1
1
+ « ¼B + ¼+ ±
J
J
(
®9A
‚+ °1 + &! ª
!
1+ ª
2
1
1
+ «
J
J
1
+
+
1
«O C3
CB C+
«N + O
¼B , ¼+ ±
Quindi:
‡
‚+
‚9
1
≃1
!& ª
1
1
+ «
J
J
¼B , ¼+
1
1
1 + !& D + G ¼B , ¼+
J
J
¼B , ¼+ è una funzione che tiene conto delle geometrie nell’arco di accesso e
recesso. (Il segno meno nell’equazione del rendimento vale se la dentatura è
interna, mentre se la dentatura è esterna vale il segno più).
Ruote dentate cilindriche a denti elicoidali:
La geometria dei denti è inclinata rispetto all’asse in modo da formare creste
elicoidali.
La superficie di un dente di una ruota ordinaria a denti diritti può essere considerata
ssss parallelo agli assi quando il piano d rotola sui cilindri di raggio ¦
da un segmento ãæ
ssss con un piano normale agli assi è un punto
(cilindri di base). Infatti ogni sezione di ãæ
della retta dei contatti che nel moto anzidetto genera un profilo. Se il segmento
ssssss la
anziché essere parallelo agli assi è inclinato di un angolo fz ( segmento ®}
superficie del dente non è più cilindrica, ma elicoidale, pur rimanendo costante il
profilo nella sezione normale agli assi. Le ruote cilindriche a denti elicoidali hanno le
seguenti caratteristiche:
1. L’ingranamento è più dolce (inizia in un punto e termina in un punto) ⟹ minori
urti e rumore e maggiore ‡,
2. L’arco di ingranamento risulta incrementato di tan fz e ⟹ l’arco di azione è
¯ !"j £#
incrementato di:
.
úûh ¡
3. Prescindendo dagli attriti, l’azione ¾ trasmessa fra due denti è normale al
sssss; essa può essere decomposta in una componente normale (ï agli
segmento ®}
assi ed in una componente (p ad essi paralleli.
LŽ
®
,
2
L•
LŽ tan ' ,
LB
LŽ tan fz
Vediamo vari tipi di ruote dentate; introduco la trasmissione del moto tra assi
incidenti ⟹ si avranno Ruote dentate coniche: le primitive saranno su una sfera
(siamo in tre dimensioni), ed analogamente alle ruote a denti dritti costruisco i
profili dentati sferici con tecniche simili (un po’ diverse da quelle viste
precedentemente, saranno curve differenti).
Anche esse sono di varie tipologie, che variano a seconda del tipo di direttrice del
dente: Rettilinee, Circolari, Spirale di Archimede, Evolvente di cerchio. Tali ruote
danno anche sforzi assiali; abbiamo bisogno di cuscinetti che sopportino tali sforzi (e
che tengano conto anche dell’errore di montaggio). Per questo sono più onerose dal
punto di vista di costruzione e dal punto di vista di manutenzione.
Ruote iperboloidiche:
La trasmissione del moto avviene tra assi sghembi ⟶ le primitive saranno degli
iperboloidi, accoppiate tra loro in modo puntiforme (non più attraverso le direttrici).
Ruote cilindriche a denti elicoidali:
Il contatto è sempre puntiforme, si utilizzano sempre per trasmissioni tra assi
sghembi (molto utilizzate nella trasmissione a vite senza fine tra assi ortogonali) ⟶
riduttore: tra ruota dentata e pignone (vite senza fine), in cui i profili dentati sono
modificati in modo tale da permettere un migliore moto:
‚.
+$=•B
+ ‚€
3<%Ž=Ž:
&
2
EE
K
!
90=
Ciò permette rapporti di trasmissione molto piccoli (considerato che la ruota senza
fine permette la continuità del moto con pochi denti); ciò conduce ad una regola
(pratica), dettata dalla logica:
1
,I
I
,
||
I
° ≤ ≤ 6±
6
Qual è lo svantaggio di tale accoppiamento? Il basso rendimento, che scende tanto
più scende il rapporto di trasmissione. Con questi riduttori possiamo arrivare a
rendimenti più bassi dello 0,5, ciò comporta l’irreversibilità, se proviamo a compiere
il moto retrogrado (molto importante); per permettere la reversibilità dovranno
cambiare il verso del momento rotore.
Ruote ipoidi:
Trasmissione tra assi sghembi, con ruote simili a quelle coniche; un esempio di
applicazione è il differenziale automobilistico (poiché il pignone può essere messo
sopra o sotto rispetto al centro dell’asse di trasmissione, questo comporta un
montaggio di tale asse migliore, cioè meno sottoposto ad urti con il terreno). Tutto
quello che concerne le ruote dentate si lega ai ruotismi.
Ruotismo:
Sono meccanismi formati da un ruote dentate e coppie rotoidali, sono di due tipi:
1. Ordinari: Gli assi delle ruote sono fissi (es: riduttori).
2. Epicicloidali: Uno o più assi sono mobili; l’organo su cui sono montati tali assi sono
detti porta-treno (es: differenziale).
Ruotismi ordinari:
Il rapporto di trasmissione di un rotismo ordinario è il rapporto tra la velocità
angolare del cedente e la velocità della ruota movente: se il ruotismo è composto da
ruote in serie:
°
v
µŽ
±
v
µ
v
µ v
µ• v
µt
v
µŽ
∙
∙
∙ …∙
v
µ v
µ v
µ•
v
µŽ5
J J
JŽ5
∙ ∙…∙
J J•
JŽ
Sappiamo che un ingranamento tra due ruote avrà assi con rotazione opposta
(inversione del senso di rotazione); per mantenerlo in evidenza poniamo un segno
meno, in modo tale da metterlo in evidenza:
J
J
v
µ
→ &v
µ
v
µ
v
µ '
.
II
I
J J•
∙
J Jt
v
µt
→ &v
µt
v
µ
v
µ '
.
II
•
II
I
Se negli assi intermedi ci sono due ruote, le loro velocità angolari sono uguali, allora:
v
µ v
µt v
µ(
∙
∙
… è
v
µ v
µ• v
µ)
I
I
E
I
Negli induttori ordinari ci sono delle regole sulla disposizione:
v
µ
v
µ
J
,
J
•
v
µ•
v
µ
J
,
J•
v
µ•
v
µ
v
µ• v
µ•
∙
v
µ v
µ
∙
•
J
J•
La ruota q è detta oziosa; non ha impatto sul rapporto di trasmissione, ma solo
senso della rotazione (cioè è sia condotta che motrice).
Ruotismi epicicloidali:
Hanno alcuni assi delle ruote mobili rispetto al telaio, sono meccanismi a due gradi
di libertà. Si determina una relazione che lega le velocità angolari delle ruote esterne
e la velocità angolare del membro al quale sono vincolati gli assi mobili (portatreno).
Si determina la relazione imponendo a tutto il sistema una velocità uguale e
contraria a quella del portatreno; il rotismo è ridotto ad un ruotismo ordinario ed il
rapporto fra le velocità risultanti delle ruote esterne è esprimibile mediante le
caratteristiche delle ruote componenti il ruotismo.
v
µ ,v
µŽ
Ω
+
Ià
Ià
v
µŽ
v
µ
µ
Ω
µ
Ω
E
I
I
(
!
I
E
•
*
II
•
E I
(
2
I
I
E
I E
|
.
Tre categorie di rotismi epicicloidali:
1B Ruotismi riduttori:
Una delle ruote esterne (v
µ v
µŽ è fissa ed il movente ed il cedente sono costituiti
dall’altra ruota e dal portatreno. Ha di nuovo senso parlare del rapporto di
trasmissione. Dalla formula di Wills, si ottiene:
Hp) v
µŽ 0 ruota fissa:
Movente portatreno:
v
µ
µ
Ω
µ
Ω
v
µ
Movente ruota uno:
Hp) v
µ
(
0 ruota fissa:
v
µ
µ
Ω
Movente portatreno:
µ
Ω
v
µ
Movente ruota uno:
(
(
(
1
1
1
1
(
1
(
Esempio:
v
µ
0, E
(
v
µ
µ
Ω
µ
Ω
I v ,
→
µ
( Ω,
Esempi di applicazione:
Riduttore a ruote coniche:
I
µ
Ω
I I
→
µ∙ 1
v
µ → Ω
(
µ
Ω
,
v
µ
*
v
µ →
v
µ
µ
Ω
II
1
:
(
J
J•
µ
Ω
v
µ
1
J
,
J + J•
J J•
,
J Jt
v
µt
µ
Ω
J
J•
(
J
J•
Riduttore a ruote cilindriche:
}
v
µt
µ
Ω
J
1
Jt
50,
49 ∙ 51
50
J•
1
(
49,
50
J
51:
1 50 + 1
50
1
1
J J•
J Jt
50
1
50
1
50
Ruotismi di questo tipo, che permetto forte riduzioni con molte ruote, hanno
rendimenti molto bassi.
2B Ruotismi combinatori:
Hanno due gradi di libertà ed hanno un movente ed un cedente.
3B Ruotismi compensatori:
Hanno due gradi di libertà, due cedenti ed un movente. Il più noto è il differenziale
automobilistico, che è un ruotismo a ruote coniche, dove il movente è il portatreno
ed i cedenti sono i due semiassi.
Le ruote 1 e 3 ruotano con lo stesso verso di rotazione; la ruota 2 è detta oziosa,
allora: (
1 (dalla formula di Wills).
In rettilineo v
µ
In curva v
µ
µ
°Ω
µ
v
µ• sono uguali ⟹ Ω
v
µ• sono diverse poiché:
v
µ +v
µ•
±
2
v
µ
v
µ• .
La ruota interna ha velocità più bassa
La ruota esterna ha velocità più alte
8. Organi flessibili:
I meccanismi ad organi flessibili sono caratterizzati da coppie cinematiche costituite
da un elemento flessibile (come ad esempio: cinghia, nastro metallico, catena) che si
avvolge sopra ad un elemento rigido (come ad esempio: puleggia, carrucola,
tamburo cilindrico).
Nota bene: Nessun elemento è perfettamente flessibile, per deformarlo è
necessario compiere lavoro, che non viene mai integramente restituito. Viene
recuperato il lavoro accumulato come energia elastica, non restituito quello
dissipato per attriti.
Problema ‡: La dissipazione pesa sul ‡
Caso ideale:
}
”,
‡
1
Effetto elastico prevalente:
m3 mš verso l’esterno ⟹ aumentano la forza motrice e la forza resistente
(“poggia e buca”):
}(
2 + m€
‡
}
,
m€ < mš ⟹ ‡ < 1
,‡
2 + mš
” ∙ õ2 + mš ö } ∙ 2 + m€
Effetto d’attrito prevalente:
m3 verso l’interno mš verso l’esterno:
}(
‡
}
,‡
” ∙ õ2 + mš ö } ∙ 2 + m€
2 m€
,
2 + mš
m€ > mš ⟹ ‡ < 1
Valutazione di m per:
1. Cinghie:
Equilibrio alla rotazione della puleggia:
} ∙ õ2 + m3 ö
Casi:
Ideale → }(
”
Reale → } ∙ õ2 + m3 ö
‚3:+;$•=
‚9
2 + m”2Θ ∙ N
2 + m3
‚.
1O
” ∙ 2 + m-
” ∙ õ2 + m- ö ⟹ }
}∙2∙Θ
”2Θ
”∙2∙Θ
m- m3
2 + m3
š∙õ.8g. ö
m- > m3
.8g/
” ∙ õ2 + m- ö
∙2∙Θ
2 + m3
”Θ m-
m3
Dunque:
‚3
2. Catene:
”Θõm-
m3 ö,
m3
m-
m
⟹
1
”∙2∙Θ
2¬
É∙3∙4
Nel caso di una catena può essere fatta una valutazione di m una volta noto il
coefficiente di attrito della coppia rotoidale costituita dai perni della catena:
‚3
”¦ Θ + }¦ Θ
ove: ¦
}+”
2
E I
!Θ≃”
K
II I ,
!Θ
I
!
.
⟹ 1
!!
2¬
É34
I
ÕË -Ë
É
K
II I ,
Macchine per rallentamento carichi:
1) Carrucola fissa:
La fune si avvolge sulla carrucola che ha un asse fisso collegato al telaio con una
staffa con accoppiamento rotoidale
Dall’equilibrio alla traslazione: ¾
Equilibrio dei momenti: } 2
m: L
! J
J E I
I I
,
à
!
}+”
m
I I
¦
I
à
” 2+m+¦ ⟹
, +m: ‚ !
•
I Ià
I
2+m+¦
”
2 m ¦
⟹}
}(
}(
}
”⟹‡
”
”
x”
1+
1
1
x
m+¦
2 ≃ ” ª1 + 2 m + ¦«
m+¦
2
2
x”
2) Carrucola mobile:
La fune è in parte vincolata ed in parte fissa sul telaio. Sulla puleggia è applicata la
forza resistente (discorde forze motrice)
p+}
”,
p + xp
}(
”
,
2
p 2+m+¦
”⟹ p
‡
}(
”
1+x
” 1+x
∙
2 x”
} 2
m
¦ ⟹}
xp,
1+x
2x
Nel moto retrogrado:
p
x} ”
K
1 + x }K ⟹ } K
1
, }(
1+x
”
, ‡K
2
}K
}=
”
2
∙
1+x ”
2
1+x
Paranchi:
I paranchi sono macchine costituite da una serie di carrucole fisse ed una serie di
carrucole mobili, rispettivamente montate su di un unico asse, e da una fune che i
avvolge alternativamente su di esse. Una delle estremità della fune è libera ed ad
essa è applicata la forza motrice; l’altra estremità può essere fissata alla parte fissa
od a quella mobile. Sono possibili quattro casi:
1. Tiro invertito e fune collegata alla parte mobile:
p( + p + p + ⋯ + pŽ5
p
xp(
p
xp
x p(
pŽ5
x
Ž5
}
x p(
‡
}(
}
Ž
p( ⟹ ”
⟹ }
”
p( 1 + x + ⋯ + x
xŽ x 1
”,
xŽ 1
xŽ 1
, ‡K
Ž
x x 1
1 1
1
xŽ x
1
1
xŽ
Ž5
}(
xŽ 1
p ⟹ p(
x 1 (
”
x 1
x xŽ 1
”
x 1
xŽ 1
2. Tiro invertito e fune collegata alla parete fissa:
Ho lo stesso risultato del caso precedente salvo che il numero delle carrucole è pari
anziché dispari.
3. Tiro diretto e fune collegata alla parete fissa:
Q=p( + p + p + ⋯ + pŽ5 + }
p
xp(
p
xp
x p(
}
x p( ⟹ ”
}
x p(
‡
Ž
Ž
}(
}
p( 1 + x + ⋯ + x
⟹ }
xŽ x
x Ž8
x Ž8
1
, ‡K
+ 1 xŽ x 1
Ž
1
”,
1
x Ž8
1
p ⟹ p(
x 1 (
}(
+1 x 1
x x Ž8
1
”
+1
”
x
x Ž8
1
1
4. Tiro diretto e fune collegata alla parte mobile:
Ho lo stesso risultato del caso precedente salvo che il numero delle pulegge è pari
anziché dispari.
5. Paranco differenziale:
È costituito da due carrucole fisse di diametro diverso solidali fra loro e da una
carrucola mobile. L’elemento flessibile è una catena che ingrana con la carrucola
fissa di diametro minore munita di denti; ciò per evitare lo slittamento della catena
sulla puleggia stessa.
p + p(
⟹ p(
K
”, p
xp(
•
”
x
, p
”
1+x
1+x
p 2 +m+¦
}
}(
} 2
” x 2 +m+¦
6
1+x 2
m ¦
”
ª1
2
m
2
2
2
«
2
¦ + p( 2
m
m
|
I
m
¦ ⟹}
J
I E |
p 2 +m+¦
p( 2
2
m ¦
¦
”
m+¦
7≃
6ª1 + 2
«x
1+x
2
¦
2
ª1
2
}
2
«, ‡
2
2
Ho arresto spontaneo se:
22
2
1+x
∙
, ‡K
2
x
2
2
22
1
x
2
2
∙
1
2
1+
x
2
¦
m+¦ m+¦
+
«7
2
2
Se trascuro la differenza 2 e 2 nei termini di attrito e suppongo che 1 + 2
”
ªx
1+x
m
22
g8§
.0
≃ x:
2
x 2
∙
2 x x+1
1
x 2
>1
2
Trasmissione con cinghie:
Per trasmette il moto bisogna che p ≠ p (differenza di tensioni), dunque devo
studiare come fa la cinghia a passare da p p
Equilibrio alla rotazione:
®9 2
®9
p
p 2
ò
®+
p p 2
®+ 2
Durante il contatto della cinghia sulla puleggia, la tensione passa dal valore p p e
viceversa. Voglio determinare la legge di variazione ⟹ determino l’equilibrio di un
elemento infinitesimo di cinghia:
Studio l’equilibrio lungo le direzioni radiali e tangenziali.
ï
!
J
J
E
K
I
!
I
E
Equilibrio direzione tangenziale:
p + p cos ª
p + p cos ª
K
!
I
'
«
2
'
«
2
E
p cos ª
p cos ª
'
«,
2
E
K
è
K
'
«+! ï ⇒ p ! ï
2
! JJ ′ II I
II I :
J
I
Equilibrio direzione radiale:
L:
9
E
I
¦2 '
!
I E
I ⇒
K
è!
J
I !
L
%
Massa elementino, ¦ Massa per unità di lunghezza della cinghia D G,
9
2 ' Lunghezza elementino infinitesimo di cinghia.
9
L*
p sin ª
2v
'
«
2
!
ï+¦
Siccome p
p '
K
.
'
'
« + p + p sin ª «
2
2
p sin ª
p '
E2v
I
' ⟹ p
pK e p
pK
⟹ pK
!
I I
E
I
¦
I
I
I
ï + L,
'
! ï, ho che:
p
!p ' ⟹ K
p
J
K
¦2 v
⟹I
ï,
! ',
"˜
, ⟹ log D G
"
/̃
'
p
I
¦
|
¦
!' ⟹ p K
La tensione p K cresce, fino a raggiungere p K per '
'
sin ª
⟹ pK '
pK
pK
: log N O
pK
0 ⟹ pK
¡
'
'
«≃ª «
2
2
ï
!',
.
pK
Attenzione:
La tensione non può variare con la legge: p K p K ¡ lungo tutto l’arco di
abbracciamento della cinghia sulla puleggia; infatti tali angoli hanno valori diversi
sulle due pulegge. La tensione varia con tale legge esponenziale lungo un certo arco
8 (arco di scorrimento) e rimane costante lungo l’arco restante 9 (arco d’aderenza).
m
m
f
ã
||
I
Determino il valore di f:
®+
p
K
p
®+
∙
2
p 2
£
£
1
,
pK
E
J
pK 2
pK
I
I ,
m ≠m ,
p K2
®+
∙
2
1
£
£
m
,
f+d ,
m
f ≃ 90=
f+d
&
2
1
1
Queste due relazioni non sono sufficienti per determinare il valore di f, che dipende
dal valore di p( (tensione nella condizione di pulegge scariche). Ammesso che la
cinghia si comporti in modo perfettamente elastico e trascurando le variazioni di
lunghezza negli archi di abbracciamento, affinché la cinghia in lavoro abbia la stessa
lunghezza della cinghia a riposo deve essere:
p(
p( p
p
,
JJ
I II | ,
…
I Ià,
…∙
…∙
!
J
p(
p +p
⟹ p(
2
da cui assegnati p( e ®+ posso calcolare f.
Dato p( , se ®+ cresce deve diminuire
: :; 8
: :; 5
®+
∙
22
+1
+•
£
1
£
, questo comporta l’aumento di f:
Quando f ha raggiunto il valore massimo pari all’angolo di abbracciamento della
puleggia minore, le due tensioni non possono crescere ulteriormente e fare così
equilibrio a ®+ . La cinghia scorre globalmente sulla puleggia, riducendo di solito la
scorrevolezza.
Cinghie a sezione trapezoidale: permettono di raggiungere valori più elevati del
coefficiente di attrito.
pK
2! ¾
2!
;#
hij <
hij <
ï, il coefficiente d’attrito diventa:
hij <
Rendimenti delle trasmissioni a cinghie:
Le principali cause di perdita nelle trasmissioni a cinghie sono:
ËÌ Per elasticità della cinghia:
La massa che passa attraverso le due sezioni deve essere uguale ⟹ la somma è
uguale a zero. È dovuta al fatto che per effetto delle deformazioni elastiche le
velocità periferiche non uguali. Infatti sezionando i due rami liberi delle cinghie
dovrà essere nulla la massa totale di cinghia che attraversa le sezioni per unità di
tempo e quindi indicando con • la massa per unità di lunghezza della cinghia scarica
si ha:
•
1+
p
…∙
•
1+
Essendo:
p
…∙
p >p ⟹
Ià
Ià
ª•
…
⟹
>
p
…∙
p
1+
…∙
1+
JJ
JJ
E I
•>• >•
v 2 2
∙
∙
v 2 2
∙
2
2
p
°
2
∙=
2
2
•
•
Un’ulteriore dimostrazione del fatto che
® v >® v ⟹ 2 p
x
±«
E
1
=
Per le cinghie indeformabili risulterebbe =
vale dunque:
v
v
°
>2 p
1+
p
…∙
x
±, … ∙
E•
x
•
•
1+
p
…∙
1; il rapporto effettivo di trasmissione
>
si evince da:
p
2
:
>
Quindi la puleggia motrice deve aderire al tratto più teso, viceversa quella
resistente; l’aderenza si ha dunque sempre dalla parte del ramo entrante.
ÉÌ Perdita per rigidezza:
Equilibrio dei momenti:
®9
®+
‡
p 2 +m
p 2
m
®+ ∙ v
®9 ∙ v
m
2
m
1+
2
1
1
p 2
m
p 2 +m
®+ 2
®9 2
p +p
G
p
p
≃ °1
p +p
D
G
p
p
D
1
1
m∙ª + «∙
2
2
2 p
2 p
2 p
2 p
p +m p +p
p
m p +p
p
m p +p
p +m p +p
m p +p
± ∙ °1
∙
2 p
p
p
p
m
p +p
2
m
p +
p +p
2
p
m p +p
±≃1
∙
2 p
p
mª
1 1 p +p
+ «∙
2 p
2
p
+1
£
1
£
>Ì Perdite per effetto ventilante:
È la perdita dovuta alla resistenza dell’aria sulla cinghia e sulla puleggia. Non è
facilmente valutabile, ma comunque varia sensibilmente con la velocità.
?Ì Perdite per attrito nei perni:
Anche questa può essere sensibile perché in genere i perni sono fortemente caricati
dalle tensioni p e p . Sotto questo aspetto sono molto convenienti i galoppini
tenditori, che mantengono costane la tensione p da vuoto a carico ciò permette di
ƒ
ƒ
avere mediamente p
1,15 — e p
0,15 —.
.
.
Per altro la cinghia è più sollecitata perché le flessioni per giro sono in numero
superiore. Il rendimento globale è, in genere, abbastanza elevato e può raggiungere
lo 85%. Pe motivi pratici non conviene avere rapporti di trasmissione al di fuori del
campo D , 3G e velocità periferiche superiori a 40, 50
•
Freni a nastro:
1) Ordinario:
9
Œ
.
Sono costituiti da una puleggia solidale all’albero, che vogliamo frenare. Sulla
puleggia si avvolge un nastro d’acciaio, bloccato in parte fissa non necessariamente
sul fulcro della leva, la quale è montata sul fulcro fisso del telaio. Sulla leva è
applicata la forza. La differenza sostanziale con la trasmissione a cinghia è che qui ho
uno scarrucolamento su tutto l’arco di abbracciamento.
p
p ¡ ricavata da trasmissione a cinghia, in cui non ho scarrucolamento quindi
è applicabile ai freni a nastro, faccio un’approssimazione)
Equilibrio della rotazione della puleggia e della leva:
®
p
p 2⟹®
pB
põ
L
L ⟹p
1ö2
¡
Se il ramo del moto si inverte p > p :
®K
p
p
p 2
p
¡
⟹p
p 2õ1
p
5 ¡
ö
5 ¡
L
,®
2õ1
L
2õ
5 ¡
ö
¡
1ö
,®
L
K
2∙
¡
¡
1
®K < ® significa che il freno a nastro funziona meglio (ha un momento frenante
maggiore) se v è orario (come nella figura) rispetto ad un v antiorario.
2) Differenziale:
La differenza da quello ordinario è che il nastro anziché essere montato in parte
fissa, è collegato alla leva in modo tale che i bracci p e p siano tali per cui
applicando la forza L il nastro si serri sulla puleggia.
p
⇒p
p
, p|
L
¡|
|
Essendo:
Ho che:
¡
p | +L ⇒p |
p
®
p
5 ¡
p
p
⇒p
p 2
¡
|
2
|
| + L ⇒ p õ|
¡
|
¡
|
¡
1
'
¡
|ö
L ⇒
L
L
| ¡ < 0 la forza L cambia di direzione. Questo significa che il freno entra
Se |
in azione anche se L 0 (freno ad azione spontanea). Se il senso di rotazione si
inverte cambia segno all’angolo '. In ogni caso deve essere verificata la condizione
che per piccole rotazioni della leva il nastro si serri su di essa. Questo comporta | >
| quando il funzionamento è quello indicato nella figura.
Quando si vuole un momento frenante circa uguale nei due sensi di rotazione si può
ricorrere alla disposizione nella figura. Essendo |
|
|.
®
2
∙
|
1
∙L
¡+1
¡
Poiché questa volta i momenti di p e p hanno segno concorde rispetto ad q.
9. Dinamica:
A A…
ª «
AI A º
A… A…3
+
A•< A•<
L: ∙ •<
… Energia cinetica,
…3 Energia potenziale,
•< Coordinata lagrangiana i-esima, variabili alle quali faccio riferimento per
individuare i gradi di libertà,
Gradi di libertà, tanti sono questi tante saranno • , • , … , •Ž ,
L: ∙ •< Forze lagrangiane, sistema di forze applicate al nostro sistema ridotto
all’i-esima coordinata lagrangiana.
Equazioni di moto di una macchina:
Nel caso di un meccanismo o di una macchina, quale normalmente intesa, in cui vi
siano soltanto membri che si muovono i moto piano ed il complesso abbia un solo
grado di libertà, ho delle espressioni che hanno una forma particolarmente
C
=
dei membri in movimento, il vettore B* C D E D ha al
semplice. Sia E
'
E 0
massimo dimensione 3E e ∧ F è una matrice 3 C 1. La matrice ®+ G
Gè
0 Á
ancora uno scalare che ha le dimensioni fisiche di un momento d’inerzia o di una
massa a seconda che la variabile indipendente rappresenti una rotazione V od uno
spostamento C.
L’energia cinetica è espressa dunque da:
1
1
Á+ V Vº ≡ E C Cº
2
2
E I
I I
≡E I I
I
Le forze elastiche e dissipative esterne sono normalmente nulle. Se supponiamo di
poter trascurare anche le perdite interne dovute agli attriti delle coppie cinematiche
risulta che:
A…*
«
I AVº
ª
A…*
AV
I
õF+ V Vºö
Vº
2
F+ V
V
F+ V VH +
1 F+ V
Vº
2
V
”
I V, Vº , I
Nel caso in cui la variabile indipendente sia uno spostamento, l’equazione prende la
forma:
I+ C Cº +
1 E+ C
Cº
2
C
L+ C, Cº , I
Si osservi che il momento I+ (o la forza lagrangiana L+ ) sono calcolate imponendo
che il lavoro compiuto da essi per una variazione unitaria della variabile
indipendente sia uguale al lavoro compiuto da tutte le forze applicate al sistema per
spostamenti dei loro punti di applicazione congruenti a quello della variabile
indipendente.
Masse di sostituzione:
passo ad un sistema di 1
Da un sistema di
I
Due casi:
N
…3
…*
+
•
•
…*
O
º3
1= Se ho come coordinata lagrangiana C:
I
ª
…*
«
Cº
…3
…*
+
C
C
2= Se ho come coordinata lagrangiana V:
I
ª
…*
«
Vº
…3
…*
+
V
V
LF
®ô
:
L-
L
® E
J
I
Posso ricavare l’equazione di moto:
I sistemi meccanici hanno membri (non mi interessa che siano rigidi) che hanno una
distribuzione di massa ⟹ “rottura” ⟹ calcolare le distribuzioni di massa di un
sistema con la distribuzione continua è complicato ⟹ meglio approcciare
l’equazione di Lagrange e la dinamica usando semplificazioni. Cosa sono le masse di
sostituzione? Schematizzo i membri; invece che con una distribuzione continua di
massa, con delle masse concentrate. Devo imporre che i due sistemi abbiano la
stessa energia cinetica, che è espressa da:
dove:
1
E
2
%
1 "
+ v
µ Γv
µ,
2
v
µ"
Γ
velocità angolare,
tensore/matrice/omografia d’inerzia: Γ
FF
KFFý
FF
FFý
Fý
Fý
FF
Fý L
F
FF , Fý , F momenti d’inerzia rispetto agli assi del sistema di riferimento,
FFý , Fý , Fý momenti d’inerzia centrifughi.
Affinché le energie cinetiche (delle masse continue e delle masse concentrate) siano
uguali:
Le masse devono essere uguali: ∑ŽN E<
®
∑Ž<N E< C<
∑Ž<N E< ü<
∑Ž<N E< J<
0
0, Se prendo un sistema di riferimento baricentro = 0, 0, 0
0
∑Ž<N E< C<
∑Ž<N E< ü<
∑Ž<N E< ü<
®CE
®üE , Se prendo un sistema non baricentrico,
®JE
dove: CE
∑•O0 9 F
∑•O0 9
Verificare la matrice Γ:
∑Ž<N E< õü< + J< ö
∑Ž<N E< õC< + J< ö
∑Ž<N
∑Ž<N
∑Ž<N
∑Ž<N
∑•O0 9 ý
, üE
E< õC< + ü< ö
E< C< ü< FFý
E< C< ü< FFý
E< ü< J< Fý
∑•O0 9
FF
S
Fý Q
Q
F
FýF R
FýF Q
Q
F ýP
Ho un totale di 10 equazioni.
, JE
∑•O0 9
∑•O0 9
Pertanto se si assegnano in modo arbitrario 10 punti, le precedenti equazioni
costituiscono un sistema i 10 equazioni nelle 10 incognite E< , che ammette in
generale una sola soluzione.
Se il moto è piano, assumendo l’asse J normale al piano del moto coincidente con il
piano J 0.
Non ho più ∑Ž<N E< J< 0, FF , Fý , FFý , FF , FF , dimostrazione del perché i momenti
d’inerzia centrifughi sono nulli:
v"
vF , vý , v
0, 0, v
Mi rimangono 4 equazioni:
∑ŽN E<
®,
∑Ž<N E< C<
0,
⟹ 00v
FF
∙ KFFý
FF
∑Ž<N E< ü<
Infine se allineo le 4 masse (a titolo di esempio):
Perdo: ∑Ž<N E< ü<
0,
FFý
Fý
Fý
FF
0
Fý L ∙ T 0 U
v
F
∑Ž<N E< õC< + ü< ö
Fv
F
0 ⟹ ho solo 3 equazioni.
Concludendo un corpo rigido, che si muove di moto piano, può essere sostituito, per
quanto riguarda l’energia cinetica, da 3 masse puntiformi allineate su di una retta
baricentrica.
Studio dinamico di meccanismi:
Nello studio di un meccanismo ad un grado di libertà l’approccio matriciale non
offre un sostanziale aiuto ed in genere conviene scrivere direttamente l’energia
cinetica del sistema, eliminare le variabili in sovrannumero mediante un preventivo
studio cinematico e scrivere direttamente l’unica equazione di Lagrange.
Esempio:
1. Ruotismo:
Raggi albero ≪ ruota ⟹ i raggi dell’albero sono ∼ trascurabili.
Momenti d’inerzia dell’albero ≪ ruota.
Scelgo come variabile lagrangiana
…*
V
1
1
1
F Vº + F + F K Vº + F• Vº•
2
2
3
, V•
•
V
V
Quindi:
…*
1
Vº F + F + F K
2
+ F•
•
1
F Vº , F+<;=••= B ô0
2 +ô0
I
I
…*
Vº
F+ô0 Vº ⟹
…*
V
® +v
0,
õF+ô0 Vº ö
…3
V
0
V
®• V•
E
® v +® v
® V +®
F+ô0 VH
®• v• ⟹ ®
‚9
F+ô0 VH
|
+
J
K
E
® +®
®•
I
Lavoro del momento esterno applicato al nostro meccanismo)
+
‚9
F+ VH
V
V•
® +®
Se ® + ®
> ®•
Se ® + ®
< ®•
V ⟹ ® +®
•
®•
•
⟹ F+ VH
®
®•
‚í
®í
®í0
º
• V•
V
º
• V•
• •
V•
• •
Vº
Vº ∙
V
®
+
+
V
⟹ il sistema ruota in modo concorde a ® e ® .
•
⟹ il sistema ruota in modo concorde a ®• .
•
Se ho coppie elastiche e viscose?
®í•
•
I JJ
•
‚9
V
®
I
•
V ⟹ ®í
• •
Vº ∙
•
‚9
Tutto avviene come se sull’albero 1 agisse una coppia viscosa di coefficiente:
F+ VH
F+ VH +
®
+
• •
I
Vº
• •
®
+
Vº
F+ VH
I
J
K
,
• •
• •
Vº
Se ci mettessi una coppia elastica:
®+
‚
®
+
V
F+ VH +
x V
x V V ,
‚
• •
x
Vº + x
V
V
V
V
®
V
V ⟹®
+
I
+
x
V ⟹ ‚
x
V
V
x
V
I
V
I
2. Quadrilatero articolato:
ssss , ¿é
ssss rispetto ai propri assi, Ez
Siano F , F• i momenti d’inerzia delle manovelle (ãæ
ssss e Fz il suo momento d’inerzia baricentrico.
la massa della biella (æ¿
Energia cinetica del meccanismo:
…*
1
1
1
1
F v + F• v• + Ez E + Fz Ω
2
2
2
2
ssss
ssss
1
ã{
1
1
ãæ
1
ssss + Fz v N O
F v + F• v N O + Ez v ãr
ssss
ssss
2
2
2
2
¿é
qæ
.
v
F + F•
ssss
7V /
¯•/
ssss + Fz 0 /
+ Ez ãr
ssss
¯/
å
Fô0 V
Momento d’inerzia ridotto alla coordinata Lagrangiana V :
ssss
ã{
V
ssss
I I
ãr
V , ⟹ Fô0 V ≠
ssss
qæ
V
Ora voglio ridurre il momento delle forze esterne alla nostra lagrangiana: le potenze
devono essere uguali.
®• v•
®•+ v
T®•+
(Potenza manovella
®•
ssss
ã{
ssss
¿é
®•+ V
®ô0 V U
Momento ridotto alla coordinata lagrangiana V )
Equazione di moto:
Fô0 V VH
1 Fô0 V
Vº + ⋯
2
V
Al posto di … ci sarebbe
;W
;-
®ô0 V , I
, trascurabile, viene messo in conto al secondo membro.
Dinamica delle macchine alternative:
1. Masse ridotte della biella di un manovellismo:
sssss Manovella, corpo solido che ruota rispetto ad un punto fisso ⟹ non è
q®
difficile calcolare …* .
Pistone/cursore, massa che descrive un moto alterno, lo schematizzo
come un punto materiale.
sssss Biella, problema.
}®
Sostituisco la biella con tre masse allineate poste in P (piede della biella), M (testa di
biella), G (baricentro della biella).
1. E€ + Eƒ + EE
2. E€ ∙
Ez
Eƒ ∙ |
3. E€ ∙
0
+ Eƒ ∙ |
Fz
Ž
°X
<N
Ž
°X
E<
<N
Ž
°X
<N
E< C<
E< C<
Ez ±
0±
Fz ±
Risolvo:
E€
Eƒ
Eƒ |
Fz
|
⟹
Eƒ |
+ Eƒ |
Fz ⟹ Eƒ
E€
Fz
Fz
| +|
Fz
|
EE
Ez
I valori delle masse dipendono dalla geometria della biella; nel caso limite di
approssimare la biella con un parallelepipedo di lunghezza e larghezza risulta:
E€
EE
Eƒ
Ez
1
E
12 z
2Ez
6
Ez
N1 +
6
+
2
2
E
3 z
O≃
Ez
6
La risoluzione può essere fatta anche mediante due sole masse E€ e Eƒ ed un
momento d’inerzia fittizio (nel senso che ad esso non corrisponde alcuna
distribuzione di massa) che indico con F( .
Le equazioni di equilibrio sono:
E€ + E ƒ E z
E€ ∙
Eƒ ∙ | 0
Y
E€ ∙ + Eƒ ∙ | + F( Fz
F|
|
Risolvo:
E€
Eƒ
Eƒ |
⟹
Eƒ |
+ Eƒ
Ez
Ez
Solitamente F( < 0 poiché:
E€
Ez
|
F(
Fz
Ez ∙ |
Tutte le masse tra ® Z danno un contributo inerziale minore rispetto al caso in cui
tutta la massa sia concentrata in ® (ci sono masse anche dopo ® che avranno un
contributo inerziale maggiore, ma non sono in grado di soppesare). Affinché questo
non si verifichi bisognerebbe che la biella fosse molto più lunga, ma è impossibile. Lo
stesso discorso è applicabile alle masse tra Z }.
2. Energia cinetica del manovellismo:
È la somma dei seguenti termini:
Energia cinetica della manovella
F9 v
Energia cinetica delle masse dotate di moto alterno (masse alternative)
EB
€
Energia cinetica della biella pari all’energia cinetica delle sue masse di sostituzione:
1
1
f
1
E€ € + Eƒ v + F( ª «
2
2
I
2
È chiaro che la massa E€ si somma alle masse alterne e Eƒ a quelle della manovella
(masse alterne); per quanto riguarda il termine F( D G si ha:
;•
;£
sin f
¶ sin V ª¶
f
I
cos f
f
I
F( ª
F(
¶v
f
«
I
v
JJ
¶v cos V
I
cos V
≃ ¶v cos V
cos f
f≪V
F( ¶ v cos V
F(
E
E
II
F( ¶ v 1
F(
v sin V
ƒ
F(
«
I
F( ¶ v
sin V
€
F( ¶ v sin V
Ricordando che:
€
⟹
€
[
v Dsin V + sin 2V G ≃ v sin V,
v sin V
poiché
[
+
¯
è piccolino e sin 2V ≪ 1
Ne segue che l’energia cinetica spettante a F( può essere in parete imputata alla
\
\
massa A/ posta in ® (che si aggiunge alle masse rotanti) ed in parte alla massa A/
¯
¯
posta in } (che si aggiunge alle masse alterne). Nel caso di biella e parallelepipedo
risulta:
E€
Ez
2
⟹ E€
F(
Eƒ
Ez Ez
+
2
6
Ez
2
F(
2
E ⟹ Eƒ
3 z
Ez
Energia cinetica di tutto il manovellismo:
…*
FB V
1
v °ªEB + E€
2
DEB + E€
\A
¯/
F(
«∙D
í
G D á• G
€
v
6
Ez
3
G + F9 + ªEƒ +
DEB + E€
\A
¯/
F(
«
ssss
G q{
±
1
lF V + F+=• nv
2 B
FB è funzione solo di V è il momento d’inerzia delle masse alterne (compresa la
massa di sostituzione della biella) ridotto all’asse di rotazione della manovella.
ª
€
v
ssss
q{
¶
sin V + sin 2V «
2
Equazione di Lagrange:
…*
Vº
F+=• + FB V
∙ Vº ⟹
õF+=• + FB V ö ∙ VH +
…*
Vº
1 FB V
Vº
V
2
I
ª
FB V
∙ Vº
V
…*
«
Vº
õF+=• + FB V ö ∙ VH + Vº
FB V
I
Equazione di moto delle macchine alterne:
õF+=• + FB V ö ∙ VH +
1
F V Vº
2 V B
®B V, I
3. Bilanciamenti delle macchine alternative monocilindriche:
Considero una motrice alternativa costituita da un manovellismo di spinta centrato
come la manovella ruotante a velocità costante. I suoi membri in movimento sono
soggetti alle seguenti forze alterne:
1. La spinta – L del fluido agente sulla testa del pistone.
2. La reazione 2€ esercitata sul pistone dalle pareti del cilindro, che in assenza di
attrito è normale all’asse del manovellismo.
3. La reazione 2( esercitata sulla manovella attraverso la coppia rotoidale in q, che
decompongo in 2=F e 2=ý .
4. La coppia resistente ®+ applicata all’asse per q.
Per il principio di d’Alembert (per un sistema dinamico, le forze d’inerzia possono
essere circa considerabili come se fosse applicate stazionarie ⟹ considero un
problema dinamico ∼ statico) questo sistema di forze è equilibrato dalle forze
d’inerzia delle masse del meccanismo; che sono:
1. La forza d’inerzia delle masse rotanti: E9 + Eƒ v diretta da q verso ® ed
essendo la distanza dal baricentro Z9 della manovella da q.
2. La forza d’inerzia delle masse alterne: E€ + E€ s€ dirette secondo l’asse del
manovellismo.
3. La coppia d’inerzia della biella pari a: F( fH .
Condizioni di equilibrio:
a
Q
2=F + L
2=F + L+ sin V + LB L 0
2=ý
^ 2=ý + L+ sin V + 2€ 0 ⟹
®+ + 2€ ssss
}q F( fH 0
Q̀
_
L+ L J
I !
LB L J
I
L L J
®+ ® E I
I I
ssss æ
}q
F( fH ® E I
I
E
I
!! II
L+ sin V + LB
®+ F( fH
L+ sin V
+
ssss
ssss }q
}q
®+ F( fH
2€
ssss
ssss }q
}q
I
J
|
Se il complesso delle azioni che sollecitano il telaio è uguale a zero ⟹ il meccanismo
si dice equilibrato/bilanciato. Per ottenere un bilanciamento basta annullare i
termini alternativi di maggiore ampiezza, che generano effetti di vibrazione. La
variazione ®+ è molto lenta ⟹ non produce inconvenienti. LB (forza alterna) è
diretta secondo l’asse del manovellismo ed ha carattere periodico, poiché è
proporzionale all’accelerazione s€ del piede di biella. È di difficile equilibratura. La
\ £H
coppia d’inerzia della biella
L J sAsss
€
Possibilità tecniche per annullare tali forze:
q
\A £H
ssss
€
} ha un’intensità limitata.
Forza rotante (facile annullamento):
E9 + E ƒ
Momento statico rispetto all’asse di rotazione della massa della
manovella e della massa di sostituzione della biella in ®; è nullo se il baricentro
della manovella si trova dalla parte opposta del bottone di manovella rispetto ad q
9
ed ad una distanza dall’asse pari a Š . Per fare questo basta disporre dei
contrappesi sull’albero a gomiti.
9™
Forza alterna:
s€ ≃ v cos V + ¶ cos 2V ; chiamo forze alterne del primo ordine quella parte di
forze alterne indipendente da ¶ e forze alterne del secondo ordine quella dovuto al
termine proporzionale ¶.
Teoricamente anche la forza alterna è eliminabile:
z
La massa che moltiplica s€ è : EB + Ez ⟹ annullabile facendo | < 0, cioè
*
sssss dalla parte di ®.
portando il baricentro della biella esternamente al segmento }®
Soluzione mai realizzata ⟹ in un manovellismo semplice le forze alterne non
possono mai essere completamente bilanciate.
Compensazione parziale:
Forze alterne del primo ordine:
Bilanciabile, aumento il contrappeso della manovella.
Forze alterne del secondo ordine
4. Bilanciamento di macchine alternative pluricilindriche:
Considero il motore alternativo a ï cilindri in linea (gli assi di tutti i cilindri sono
paralleli).
Sul telaio della macchina agiscono:
La coppia di reazione
Una forza, somma di tutte le forze alterne e rotanti di componenti:
C
B
X
Ž
<N
Ž
X
<N
C<
X
Ž
<N
lE+=• + v cos V< + EB¯• v cos V< + ¶ cos 2V< n
E+=• v sin V<
Un momento (valuto rispetto all’origine degli assi) di componenti:
a ®F
Q
Q
®ý
Q̀
Q®
_
X
Ž
<N
Ž
X
<N
Ž
X
<N
ü< J<
C< J<
E|
F( fH< ≃ X
Ž
<N
|
I
¶ F( v sin V
Posso annullare le singole forze rotanti contrappesando ciascuna manovella, oppure
annullo la loro somma contrappesando due manovelle.
Alternativa:
Disporre i cilindri in modo che le singole forze d’inerzia si annullino reciprocamente,
studio questo metodo. Il contributo delle forze alterne vale:
C
Ž
EB¯• v ªX
<N
Ž
B
EB¯• v ªX
<N
cos V< + ¶ X
Ž
<N
J< cos V< + ¶ X
cos 2V< «
Ž
J< cos 2V< «
<N
Il complesso di queste forze è un sistema equilibrato se:
X
Ž
cos V<
<N
Ž
X
J< cos V<
<N
Ž
X
cos 2 V<
<N
Ž
X
0 S
0R
P
J< 2 cos V<
<N
•
0 S
0R
P
|
I
•
|
!
J
I
!
I
J
E
I
Se indichiamo con m< lo sfasamento della manovella -esima rispetto alla prima, così
che risulti V< V + m< , le condizioni precedenti si scrivono:
X
Ž
a
Q
Q
Q
X
Ž
<N
Ž
<N
cos V X
Ž
cos V + m<
J< cos V + m<
X cos 2 V + m<
Q̀
<N
Q Ž
Q
X J cos2 V + m<
_ <N <
cos V X
Ž
<N
<N
Ž
cos 2V X
cos2 V X
Ž
<N
<N
cos m<
J< cos m<
sin V X
Ž
<N
Ž
sin V X
sin m<
J< sin m<
<N
Ž
sin2 V X
cos 2m<
<N
Ž
sin2 V X
J< cos 2m<
0
sin2 m<
<N
J< sin 2m<
0
0
Poiché l’angolo V varia con il tempo queste equazioni sono soddisfatte solo se:
X
Ž
<N
Ž
X
cos m<
<N
Ž
X
<N
Ž
X
<N
sin m<
J< cos m<
J< sin m<
0 S
Q
Q
0 Q
0R
Q
Q
Q
0
P
…•
|
I
!
J
I
E
0
X
Ž
cos2 m<
<N
Ž
X
<N
Ž
X
sin2 m<
J< cos2 m<
<N
Ž
X
0 S
Q
Q
0 Q
0R
Q
Q
Q
0
P
J< sin2 m<
<N
…•
|
I
!
J
I
Se sono verificate queste 8 equazioni ⇒ anche il sistema delle forze rotanti è
equilibrato:
a X E+=• v cos V<
<N
Q
Ž
Q
Q X E+=• v sin V<
Ž
<N
Ž
X E+=• v J< cos V<
Q̀ <N
Q Ž
Q
v J< sin V<
X E
_ <N +=•
0
0
0
0
Infine essendo: ∑Ž<N F( fH< ≃ F( ¶v ∑Ž<N sin V< ⟹ è nullo anche .
Osservo che m< sono soggetti all’ulteriore condizione di mantenere nel motore la
massima uniformità possibile della coppia motrice, dunque sull’albero vi devono
essere manovelle spostate ciascuna rispetto alla precedente di un angolo ':
m
'
2&
ï
0, m
E I
', m•
I E
2', … , m#
ï
;'
1 '
4&
ï
E I
•
II
I E
Dunque solo per particolari valori di ï la somma delle forze d’inerzia sarà nulla.
Per quanto riguarda i momenti:
Conviene prendere l’origine q degli assi nel punto medio dell’albero a gomiti e
disporre le manovelle in modo simmetrico. Se questo è possibile ⇒ il momento delle
forze d’inerzia è uguale a zero. Esempi:
ËÍ b
É:
' 2I E
&
⟹
m
0, m
&
Albero simmetrico
' 4I E
2&
⟹
m
Albero simmetrico
ÉÍ b
>:
' 2I E
2&
3
∑Ž<N L<\ 0
c Ž
∑<N ®<\ ≠ 0
⟹
m
∑Ž<N L<\ 0
c Ž
∑<N ®<\ ≠ 0
∑Ž<N L<\\ ≠ 0
c Ž
∑<N ®<\\ 0
∑Ž<N L<\ ≠ 0
c Ž
∑<N ®<\ 0
∑Ž<N L<\\ ≠ 0
c Ž
∑<N ®<\\ 0
0, m
0, m
2&
2&
,m
3 •
4&
3
∑Ž<N L<\\ 0
c Ž
∑<N ®<\\ ≠ 0
t4
t4
d4
' 4I E
⟹ m
0, m
, m•
La decomposizione della
•
•
•
manovella è identica a quella del motore a due tempi ⟹ stessi risultati.
>Í b
?:
' 2I E
&
2
⟹
m
Albero antisimmetrico, ∑Ž<N L<\
∑Ž<N L<\ 0
c Ž
∑<N ®<\ ≠ 0
' 4I E
&
⟹
∑Ž<N L<\\
c Ž
∑<N ®<\\
m
e
/
&
,m
2 •
0, m
0, quindi:
0, m
0
0
Albero simmetrico con ∑< L<\ 0
∑Ž<N L<\ 0
∑Ž<N L<\\ ≠ 0
c Ž
c Ž
∑<N ®<\ 0
∑<N ®<\\ 0
?Í b
f:
3&
2
&, m•
2&, mt
3&
2&
3
' 4I E
⟹
e
/
m
Albero simmetrico con ∑< L<\
∑Ž<N L<\
c Ž
∑<N ®<\
gÍ b
' 4I E
h:
0
0
&
⟹m
2
0
∑Ž<N L<\\
c Ž
∑<N ®<\\
0, m
e
/
Albero simmetrico con ∑< L<\
2&
,m
3 •
0, m
&
,m
2 •
4&
,m
3 t
2&, m)
2&, m(
5&
,m
2 i
8&
,m
3 (
10&
3
0
0
&, mt
0, quindi:
3&
,m
2 )
3&, md
7&
2
∑Ž<N L<\
c Ž
∑<N ®<\
∑Ž<N L<\\
c Ž
∑<N ®<\\
0
0
0
0
5. Motore a due cilindri a V:
Indico con f l’angolo formato dagli assi dei due cilindri e mi riferisco al sistema di
assi di figura. Su ogni cilindro agiscono sui rispettivi assi le seguenti forze:
∙ CŒ
E+=• v cos VŒ + E+=• v cos VŒ + ¶ cos 2VŒ
∙ BŒ
E+=• v sin VŒ
∙ BŒ
E+=• v sin V;
C
CΠ+ C; cos
∙ CŒ
E+=• v cos V; + EB¯• v cos V; + ¶ cos 2V;
Sul complesso agisce la forza:
B
BŒ
B; sin
f
2
BŒ
B; sin
f
2
f
f
+ BΠ+ B; cos
2
2
Sostituendo a CΠ, C; , BΠ, B; i loro valori si ottiene:
C
l E+=• + EB¯• v cos VŒ
B
l E+=• + EB¯• v cos VŒ
E+=• v sin VŒ
cos V; + EB¯• v ¶ cos 2VŒ + cos 2V; n cos
sin V; sin
f
2
+ E+=• v sin VŒ + sin V; cos
Si noti che E+=•
Eƒ +
9™
*
f
2
+
cos ªV
f
f
« + cos ªV + «
2
2
f
2 cos cos V
2
cos ªV
f
«
2
f
cos ªV + «
2
f
2 sin sin V
2
sin ªV
f
f
« + sin ªV + «
2
2
f
2 cos sin V
2
cos 2V
sin ªV
f + cos 2V + f
f
f
«
2
cos 2V + f
f
sin ªV + «
2
Si ottiene sostituendo:
C
ü
2 ªE+=• + EB¯• cos
2 ªE+=• + EB¯• sin
f
2
∙ perché la massa della manovella va suddivisa fra i
due maccanismi. Adesso osservando che VŒ
cos 2V
cos 2V; n sin
cos V; + EB¯• v ¶ cos 2VŒ
f
2
V
£
, V;
£
V + e:
2 cos f cos 2V
2 sin f sin 2 V
f
2 sin cos V
2
f
f
« v cos V + EB¯• v ¶2 cos f cos cos 2 V
2
2
f
f
« v sin V + EB¯• v ¶2 sin f sin sin 2V
2
2
Le componenti del primo ordine sono nulle se:
f
E+=• + EB¯• cos
0
2
j
f
0
E+=• + EB¯• sin
2
Ossia sommando:
2E+=• + EB¯• E9 + 2Eƒ + EB + E€
j
f
f
cos
sin
0
2
2
0
La prima equazione può essere soddisfatta con un opportuno valore di c e la
seconda facendo f 90= . Per f 90= si annulla anche la componente secondo C
della forza alterna del secondo ordine. Rimane solo una componente secondo ü del
secondo ordine che vale: EB¯• v ¶√2 sin 2 V.
Bilanciamenti di meccanismi piani:
La parte del bilanciamento è ben sviluppata per il manovellismo di spinta; più
recenti sono gli studi generali sul bilanciamento dei meccanismi piani. In generale è
possibile equilibrare le forze d’inerzia con opportuni contrappesi (bilanciamento
passivo), ma di solito rimane non equilibrata una coppia d’inerzia. Sebbene un buon
bilanciamento sia auspicabile in molte circostanze l’aggiunta di contrappesi aumenta
la coppia d’inerzia non bilanciata, le reazioni dei cuscinetti e la coppia motrice
necessaria per azionare il meccanismo. Pertanto molte volte la migliore soluzione
tecnica consiste in un bilanciamento parziale, in altri termini il problema deve essere
visto in un quadro più ampio con il fine di ottimizzare un progetto tenendo conto di
esigenze diverse, spesso contrastanti. Studieremo questo problema nel caso di un
quadrilatero articolato.
1. Bilanciamento attivo:
Dato il quadrilatero ã, æ, ¿, é di figura, qualora sul telaio sia montato un secondo
ssss e
quadrilatero ã, æK , ¿ K , é immagine speculare del piano rispetto alla retta ãé
ruotante in senso inverso, per ovvie ragioni di simmetria l’azione complessiva sul
telaio è diretta secondo la congiungente ãé stessa. Questa componente può essere
eliminata introducendo la seconda coppia di quadrilateri indicati in tratteggio,
ruotanti alla stessa velocità (bilanciamento attivo). Questo metodo di bilanciamento
è teoricamente non facile a realizzare ed ha per tanto un interesse puramente
tecnico.
2. Bilanciamento passivo:
Considero il quadrilatero ã, æ, ¿, é della figura ed indico con Z e Z• i baricentri
delle manovelle e con Z il baricentro della biella.
La porzione di ciascun baricentro rispetto all’asse del relativo membro è individuata
dal numero complesso:
Ãô
=<
;
<
La porzione di ciascun baricentro rispetto al telaio dai numeri complessi:
^J
J•
J
+
t+
â0
=
̙0 ̢0
•
̙/ ̢/
Ãô• â•
La forza d’inerzia totale che si scarica sul telaio è:
Ls
E JH + E JH + E• JH•
Essa risulta nulla se:
E J + E J + E• J•
I
â0
t
â0
+=
+ =•
â•
â/
E J + E J + E• J•
E + E + E• JE
I
I
Ossia se il baricentro complessivo dei membri in movimento rimane fisso.
Sostituendo a J , J , J• i rispettivi valori si ha:
E = +E
â0
+E =
â/
+ E• =•
â•
+
â•
I
I
D’altra parte da considerazioni geometriche risulta:
â0
Eliminando
â/
E = +
+
â/
t
•
fra queste due equazioni si ottiene:
E
E =
â0
+
•E
= +
E =•
â•
I
I
SI noti che essendo = , = , =• costanti, gli unici termini variabili col tempo sono gli
esponenziali â0 e â• . Quindi la condizione imposta può essere verificata solo se:
Dalla figura risulta =
E = +
E
E
E• =• 0
•E = +
0
+ = K e le condizioni precedenti si possono riscrivere:
E =
•E = +
E =K
E• =•
0
0
Esse determinano i momenti statici e le posizioni angolari del baricentro di due
membri, assegnate le analoghe grandezze del terzo; infatti in termini reali esse si
scrivono:
E
E K
E
E• •
j •
K
V
V
V• V + &
Dinamica delle motrici alternative funzionanti a regime periodico:
L’equazione di moto di una motrice alternativa soggetta ad un momento motore
ridotto ®9 ed ad un momento resistente ®+ è:
Á V VH +
1 Á V
Vº
2 V
®9
®+
Da questa si vede che anche nell’ipotesi ®9 ®+
I I la velocità angolare
ºV non può essere costante a causa della variabilità di Á V . La variabilità di Vº è
ancora provocata dalla variabilità di ®9 V e talvolta anche di ®+ . Per tali motivi in
una macchina alternativa è possibile soltanto una condizione di regime periodico ma
non di regime assoluto Vº
I I . Si definisce grado di irregolarità di una
macchina alternativa funzionante a regime periodico il rapporto:
v9BF v9<Ž
v9:;<=
Essendo v9BF e v9<Ž il valore massimo e minimo di v nel periodo e v9:;<= il
valore di v. Tanto più è piccolo quanto più la macchina si approssima alla condizione
di regime assoluto. Essendo in generale piccolo (da a
a seconda delle
•( •((
applicazioni della motrice), l’espressione precedente può anche essere modificata
come segue:
v9BF + v9<Ž
⟹E I
v9BF + v9<Ž
2
v9BF v9<Ž v9BF + v9<Ž v9BF v9<Ž
∙
v9:;<=
2v9:;<=
2v9:;<=
v9:;<= ≃
L’equazione dei lavori:
‚9
‚+
Δ…
2v9:;<=
Essendo una motrice alternativa: …
Á V v + Á+ v
…B + …+ può essere
scritta: ‚9 ‚+ Δ…B + Δ…+ .
Essa costituisce un integrale primo dell’equazione di moto della macchina. Noto
®9 V e ®+ V è possibile ricavare Δ… e quindi v per ogni valore di V compreso
entro il periodo Θ della macchina e da questo risultato si può calcolare il grado di
irregolarità . Il calcolo può essere condotto per via numerica o per via analitica
grafica, seguendo il procedimento appresso esposto, noto sotto il nome di metodo
di Tretgold.
Nel metodo di Tretgold la variazione di energia cinetica delle masse alterne è messa
in conto come lavoro delle forze d’inerzia alterne supposte note e sommate alle
forze motrici. In realtà le forze d’inerzia alterne non sono note perché il loro valore
dipende dalla velocità angolare v che è incognita, ma, essendo piccolo, possono
essere valutate in prima approssimazione per v v9:;<=
I I . Così
facendo si ha:
‚9
‚+
Δ…B + Δ…+
‚9
Δ…B
‚+
‚9 + ‚B
‚+
1
Á v
2 +
Δ…+
v=
Poiché Á+ è costante il massimo ed il minimo di v si ottengo quando è massima e
minima la differenza:
‚9 + ‚B
‚+
‚∗9
‚+
‚∗9
‚+
Pertanto risulta:
Da cui:
1
Á õv
2 + 9BF
1
Á+ v9BF
2
j
1
Á õv
2 + 9<Ž
v9<Ž ö
v=
v= ö
‚∗9
‚+
v9BF v9<Ž
2v9:;<=
‚∗9
9BF
‚+
x
9BF
9<Ž
‚∗9
‚+
9<Ž
x
Á+ v9:;<=
A parità di altre condizioni per diminuire occorre aumentare Á+ ossia calettare un
volano sull’asse della motrice. In pratica il calcolo si svolge nel modo che segue:
- Si valuta per V ®9 V e ®9B V
Momento motore dovuto alle forze
d’inerzia alterne.
- Si integra il diagramma di ®9 V + ®9B V per via grafica o numerica per
ottenere il diagramma ‚∗ V
- Si traccia il diagramma ‚+ V in base alla legge nota di variazione di ®+ V
- Si valuta la differenza di x.
La relazione precedente permette di calcolare per una data macchina od il Á+
necessario per avere un dato grado di irregolarità.
Dinamica dei moti oscillatori:
Lo studio delle vibrazioni degli organi delle macchine riveste grande importanza per
gli effetti che tali moti possono avere sul funzionamento della macchina e sulla sua
stessa vita. In alcuni casi i moti vibratori sono utilizzati per conseguire alcuni effetti
utili (ad esempio convogliatori a vibrazione) ma di solito il loto studio è effettuato al
fine di individuarne le cause ed i eliminarne o limitarne gli effetti dannosi. Gli organi
delle machine sono sistemi continui on massa ed elasticità distribuita. Lo studio dei
moti di sistemi elastici continui è possibile in modo rigoroso soltanto in casi molto
semplici che hanno un interesse tecnico limitato. D’altra parte per i problemi tecnici
è sufficiente uno studio approssimato basato quasi sempre sulla sostituzione del
sistema continuo ad infiniti gradi di libertà con un sistema discreto avente un
numero finito di gradi di libertà. Questo modo di procedere è giustificato anche dal
fatto che i modi di vibrare di pratico interesse corrispondono alle configurazioni più
semplici della deformata dell’organo vibrante. Il problema delle più opportuna
discretizzazione del sistema continuo in studio non è semplice; in alcuni casi la
soluzione è ovvia, in altri rimane un notevole margine di direzionalità. La differenza
fra i vari schemi possibili tende a ridursi al crescere del numero dei gradi di libertà.
Da un punto di vista matematico la differenza consiste nel fatto che i sistemi
continui sono rappresentabili con equazioni differenziali alle derivate parziali ed i
sistemi discreti con equazioni differenziali ordinarie. Il numero dei gradi di libertà del
sistema è definito come il numero di coordinate indipendenti atto a rappresentarlo
e coincide con il numero di equazioni differenziali necessario per descrivere la sua
evoluzione nel tempo. Le equazioni differenziali del complesso (“Modello
matematico” de sistema) sono in genere accoppiate fra di loro a costituire un
sistema; esse possono essere disaccoppiate mediante opportuni cambiamenti di
coordinate. Le vibrazioni possono essere libere o forzate. Nel primo caso il sistema
meccanico vibra in assenza di forze esterne e soltanto sotto l’azione di deformazioni
inziali; in assenza di fenomeni dissipativi (“smorzamento”) la vibrazione si mantiene
indefinitamente nel tempo ed è costituita da una somma di moti periodici aventi
frequenza costante e dipendente soltanto dalle caratteristiche fisiche del sistema
stesso (“modi o frequenze naturali” del sistema). Le vibrazioni forzate si
manifestano quando il sistema è soggetto ad una o più forze eccitatrici di tipo
alternativo. La frequenza di oscillazione coincide con la frequenza della forza
eccitatrice. Se questa è uguale ad una delle frequenza naturali del sistema si
manifesta il fenomeno della “risonanza” e l’ampiezza di vibrazione diventa molto
grande limata soltanto dallo smorzamento. I sistemi meccanici sono di solito
debolmente smorzati e le frequenze naturali possono anche essere determinate
supponendo nullo lo smorzamento, senza commettere errori apprezzabili. Pertanto
lo studio del sistema libero non smorzato porta ad informazioni essenziali anche per
lo studio del sistema forzato. Le forze smorzanti si manifestano in vaie forme, non
sempre rappresentabili matematicamente in modo semplice. I tipi più comuni sono:
- Attrito viscoso, proporzionale alla velocità;
- Attrito coulombiano, approssimativamente indipendente dalla velocità;
- Attrito aerodinamico, proporzionale al quadrato della velocità;
- Attrito isteretico, forma assai complessa, descritta nel seguito.
Sistemi ad un grado di libertà:
Nel caso di un corpo rigido in moto traslatorio o rotatorio soggetto a forze elastiche
e viscose, le equazioni di moto sono:
ECH
ÁVH
C
V
Cº + ! I
Vº + E I
A parte il diverso significato dei simboli le equazioni sono identiche e quindi basta
riferirsi ad una di esse. Il problema da risolvere è quello di determinare la funzione
C I una volta assegnata la forza ! I . Il problema può agevolmente essere risolto
in modo generale utilizzando la trasformazione di Laplace (‚lC n C
:
El C
C
E
Cº 0 n + l C
C 0
L
+
+
+
C 0 n+ C
EC 0 + ECº 0 + C 0
+
E +
L
L
+
E
+
+
⟹
}(
E +
+
Se tutti i valori iniziali sono nulli }(
0; inoltre il secondo termini non è
significativo per quanto riguarda le proprietà intrinseche del sistema vibrante. Salvo
casi particolarissimi si può quindi porre:
C
l™
=
v9
E
L
+
+
1
x
,
9
9,
x
+ 2=
2=
Pulsazione naturale non smorzata.
9
+1
L
,
:
9
Fattore di smorzamento.
Assegnata la funzione ! I la precedente relazione determina C I . Esempi:
1. ! I
1 I ;L
C
9
x
+ 2=
9
+1
L’andamento della funzione C I dipende dai poli della C
ossia dalle radici
dell’equazione: + 2=v9 + v9 0.
Poiché nei sistemi meccanici normalmente = è piccolo e minore di (quando è
dovuto ai soli smorzamenti interni del materiale), tali radici sono:
=v9 ± Âv9 ¨1
=
e la C I è espressa da:
C I
x 1
=v9 ± Âv3
5ná™ •
¨1
=
sin v3 I +
v3
J
¨1
I T
=
=
U
Si ottiene come è noto un’oscillazione smorzata di pulsazione v3 ; l’ampiezza si
riduce del fattore nel tempo
2. ! I
:
lL
m I
l™
n
1n
.
La forza eccitatrice, costituita da una forza di intensità molto grande che agisce per
tempi molto piccoli, può essere rappresentata con una funzione di DIrac:
C
x
+ 2=
9
C I
5ná™ •
x
v9
=
¨1
9
+1
sin v3 I
Si ottiene ancora un’oscillazione smorzata dello stesso periodo della precedente e
con la stessa legge di smorzamento.
3. ! I
sin vI
L
á
Œ / 8á/
È noto che in generale la C I si compone di due termini. Il primo (integrale
particolare) è dovuto alla forza eccitatrice ed è dello stesso tipo di questa; il secondo
(integrale generale dell’equazione omogenea) è costituito da un’oscillazione
smorzata avente le stesse caratteristiche delle precedenti. Il primo termine
rappresenta l’oscillazione e la deformazione a regime. Nel nostro caso la situazione
di regime è rappresentata da un’oscillazione della stessa pulsazione della forza
eccitatrice. Se interessa questo termine si ha:
C I
+:%<9:
°
v
∙
+ Âv
1
∙
2Â 1
9
x
+ 2=
9
x
9 v + Â2=
+1
9v
∙
∙
Υ
±
ŒNÃá
Ãá•
+°
1
∙
2Â 1
v
∙
Âv
9
9v
Ponendo:
1
x
9 v + Â2=
9v
®
â
x
x
+ 2=
Â2=
9
+1
9v
∙
∙
Υ
Ãá•
±
ŒN5Ãá
Con:
®
¨ 1
9v
x
+ 4=
I ª
9v
1
2=
9v
9v
«
Si ha:
C I
dove ® e
/ Œ / 8 nl Œ8
l™
™
+:%<9:
®∙
à á•8¢
2Â
à á•8¢
® sin vI +
sono rispettivamente modulo ed argomento della funzione:
valutata per
Âv.
Questo risultato è generale e non limitato a sistemi oscillanti ad un grado di libertà.
Tutte le volte che si ha un’espressione del tipo C
Z L ,
Z
Ammettenza meccanica generalizzata o flessibilità dinamica
E la ! I è una forza che varia con legge sinusoidale, l’oscillazione a regime vale:
C I
+:%<9:
|Z v | ∙ sinlvI +
I
Z v n
essendo v la pulsazione della fase eccitatrice, supposta di ampiezza unitaria.
Ritornando al semplice sistema oscillante già considerato è noto che l’ampiezza
della vibrazione può avere un massimo per valori di = che variano in un certo
campo. Il massimo di ® si ha per quel valore di v che rende minimo il denominatore
1
+ 4= 9 v ossia per v che soddisfa alla condizione:
9v
;
;á
l 1
9v
+ 4= v
9n
v+
2 1
9v
v9 ¨1
9v
2=
+ 8ξ v
0 da cui:
9
Questa pulsazione si dice pulsazione di risonanza del sistema. La risonanza ossia il
massimo dell’ampiezza si manifesta solo se: 2= ≤ 1 ossia per = ≤ ≃ 0,7.
Il corrispondente massimo dell’ampiezza ®9BF
Ī p
n¨
5n /
√
n¨ 5n /
; al rapporto
si dà il nome di fattore di risonanza, per = piccolo
Ī p
≃
n
”
“fattore di qualità”.
I fenomeni di risonanza sono in genere molto pericolosi negli organi delle macchine
perché con forze di intensità anche modesta, si possono avere deformazioni (e
quindi sollecitazioni del materiale) molto grandi. Il valore di ® inteso come rapporto
fra ampiezza della deformazione ed ampiezza della forza eccitatrice si denomina
anche flessibilità dinamica del sistema. Esso vale per quanto già visto:
®
¨ 1
Nel caso statico v
9v
1
0e ®
+ 4=
:
9v
1
©°1
; alla risonanza ®
v
v
Dv G ± + 4= Dv G
9
9
0
n¨ 5n /
il rapporto fra
flessibilità dinamica e flessibilità statica è proprio pari al fattore di risonanza. Ad
infinito per = 0,1 (valore già grande per materiali ferrosi) la flessibilità dinamica
alla risonanza è circa 5 volte la flessibilità statica. Consideriamo una curva relativa d
un determinato valore di = (sufficientemente piccolo) e consideriamo punti } e }
situati a destra ed a sinistra del massimo per i quali l’ampiezza si riduce a volte il
√
valore del picco. Si può verificare che essi corrispondono rispettivamente alle
v+ ¨1 2=, ω
v+ ¨1 + 2=.
pulsazioni: v
Il rapporto
á/ 5á0
á—
àá
á—
¨1 + 2=
¨1
2= ≃ 1 + =
1
=
2=
š
‡
detto anche “fattore di perdita”, può servire per determinare sperimentalmente = e
quindi il coefficiente di attrito viscoso. Questa proprietà risulta utile per la
determinazione sperimentale del modello matematico di un sistema vibrante.
10. Lubrificazione:
Parallelismo:
Fisica meccanica
Conservazione della massa
Ls E ∙ s
Fisica meccanica:
-
∼
∼
Fluidodinamica
Equazione di continuità
Equazione di Navier-Stokes
”s
c s
Ӽ
E∙ ̅
Ls :
Considero un fluido:
Punto materiale si trasforma in un volumetto, che evolve nello spazio dalla
configurazione iniziale Ω= ad una generica configurazione Ω I nell’istante I.
La generica particella Cs finirà in C̅ ⟹ C̅
s Cs
Associo alla particella delle grandezze:
! C̅ , I
¦∙ ̅
•
I Ià
¦
E I
Ià
Ià
E
Sorgente delle forze agenti sulla particella:
Voglio “trovare” Ls
|s C, I → ¦ ∙ ! ̅ !
E ∙ s:
J
Ià
E
Come faccio a scrivere come evolvono le quantità associate alle sorgenti con le
forze?
Procedo in modo assiomatico:
Newton: ”sº
I
Ls
-
r •
Ipotesi fisiche:
:
dunque:
!̅ +
-
r •
|s +
u- ! ̅ + ¦ ∙ ̅ ”s ⟹ ¦ ∙ ̅
I
t r•
t
t
- |s + Ls :
s
r •
”sº x
w
w
w
v
1B Il fluido è un continuo di Cauchy (effetti molecolari sono trascurabili, il fluido
non è fatto da atomi:
2B La massa si conserva (non esistono forze che creano/distruggono la massa)
3B Il fluido è omogeneo ed incomprimibile ¦ ≃ costante, quand’è che questo
accade? Liquidi, tratto oli ≃ liquidi )
4B Fluido Newtoniano, le tensioni sono proporzionali solo ai gradienti di velocità:
∝
A+
Aü
Considero solo l’attrito:
Gli strati si muovono con velocità diverse e strisciano l’uno sull’altro:
Se >
⟹ il primo strato tracina il secondo strato
B
5 Non ci sono effetti termici: 6 costante
Equazione di base della fluidodinamica:
…•
J
ï
I
¾I x
Ià
z …•
J
!
E
Teorema del trasposto (dimostrazione fatta in seguito):
-
r •
! ̅ C̅ , I
+
!̅
+
I E
I E
I
-
r •
! ̅ C̅ , I
La variazione di ! ̅ è data da:
±¾
+
II
-
r •
•
A! ̅
++AI
r •
Ià
E
E
!
̅ ∙ s !̅ ã
- La variazione ! ̅ dentro
- La variazione AΩ (il fatto che AΩ si sposti fa si che ci sia un punto che mi entra
ed esca da Ω
Ω
Utilità del teorema del trasposto ⟶ trovo equazione fondamentale della
fluidodinamica:
I
-
r •
⟹-
r •
⟹ -
r •
+
! ̅ C̅ , I
A! ̅
++AI
r •
A! ̅
+
AI
-
r •
r •
õ! ̅ ∙ ̅ " ö +
õ! ̅ ∙ ̅ " ö
{-s
µ} ö
+ ÕÓØõ-s ∙ Ø
{|
⟹
|s + ⟹ -
µ
~
|s
+
A! ̅
++AI
r •
-
r •
̅ ∙ s !̅ ã
-
r •
|s + ⟹
|s + ⟹
I, Ω
Applicazioni:
1B ! ̅ → ¦
̅
|s → 0
̅"
Equazione di continuità:
2B ! ̅ → ¦ ̅
• §ís
••
+
•§
D •• +
•§
•ís
¦D
••
¦ ̅G
+ Áís ∙ ̅ G
••
+
|s → ¦!í̅
¦ ̅ ̅"
Vari passaggi: ̅ D
•§
••
+
¦!í̅
¦ ̅
¦ ̅G + ¦ D
E
•ís
••
0
!
+ Áís ∙ ̅ G
E
J
¦!í̅
0 dall’equazione di continuità, Áís (Jacobiano)
¦!í̅
•ís F̅ ,•
•F̅
Quali sono le forze agenti sul fluido?
Ogni particella interagisce con delle forze d’interazione, prodotte dalla particelle
adiacenti:
|s ¦!í̅ +
»
»
F•F• + p
|s
lp
»
»FF
T ýF
F
Fý
»ýý
ý
F
ý
»
U
matrice degli stress,
F•F• pressioni,
p matrice 3C3, termini tangenziali dovuti agli
effetti dell’attrito.
6 Áís + Áís" →
F + p → |s
¦!í̅ +
µ ̅
6Δ
p
6
µ +
Ià n
Equazione di Navier-Stokes:
•ís
¦D
•§
••
••
+
sss
+ Áís ∙ ̅ G
¾ ¦≃
¦ ̅
I
I
0
Condizioni iniziali:
̅ C̅ , I
¦ C̅ , I
̅( C̅
¦( C̅
sss
̅ + ¦!ís
equazione continuità
⟹
̅
0
∀ C̅ ∈ Ω
∀ C̅ ∈ Ω
Condizioni al bordo:
̅ C̅ , I
¦ C̅ , I
+6
̅z=+;= C̅
¦z=+;= C̅
∀ I̅ ≥ I( , ∀ C̅ ∈ Ωz
∀ I̅ ≥ I( , ∀ C̅ ∈ Ωz
Teorema del trasposto (dimostrazione):
p + ¦!í̅
L C, I
µ
•¢
•F̅
Á C, I
det L
det L
! ̅ s Cs , I , I
I
- ! ̅ C̅ , I
rA
-
rA
Lo Jacobiano di è una funzione che mi dice se le mie particelle si
stanno espandendo/contenendo.
I
⟹E
⟹E
I
! ̅ C̅ , I
-
r •
!ù Cs , I , Á Cs , I
+
!ù ̅ C̅ , I ∙ Á C̅ , I
°ª
I
+(
Á C̅ , I «
!ù ̅ C̅ , I
‚
I
- ! ̅ s Cs , I , I ∙ Á Cs , I
+
rA
+(
+
A! ̅
++AI
r •
I
det L
̅ ƒ Á C̅ , I
Á C̅ , I
õ! ̅" ̅ ö +
+(
I
̅ C̅ , I ±
̅ ƒ Á C̅ , I
̅
Á C̅ , I
+
+(
„! ̅" ̅ …
ƒ +(
Á C̅ , I ƒ +(
+(
A!ù ̅
+ Áís C̅ , I ̅
AI
Áís C̅ , I ̅ + ! ̅ C̅ , I
|
!ù ̅ C̅ , I ∙ Á C̅ , I
!ù ̅ C̅ , I
- ‚
Á C̅ , I + !ù ̅ C̅ , I
I
rA
A!ù ̅
- ‚ + Áís C̅ , I ̅ + ! ̅ C̅ , I
rA AI
r •
det L < 0 E
!ù C̅ , I + ΔI ∙ Á C̅ , I + ΔI
- lim ‚
ΔI
rA à•→(
!ù ̅ C̅ , I
- ‚
+ !ù ̅ C̅ , I
I
rA
-
J
+ƒ
-
A! ̅
++!̅ ∙ ̅ " ∙
AI
r •
-
A!
++AI
•r •
r •
r •
ã
„õ s|s " ö s
̅ ∙ s !̅ ã
|s ∙ s ∙ s…
Principali tipi di lubrificazione:
1= Lubrificazione asciutto (zero) → non c’è lubrificante, possibile grazie a materiali
polimerici. Applicazione: bronzine, materiali sintetici. Costa poco, ma hanno limiti in
termini di carichi applicabili.
2= Lubrificazione limite (grasso). Uso fluidi caratterizzati da molecole che hanno
dimensioni caratteristicamente comparabili con le dimensioni caratteristiche della
rugosità. Applicazioni: bronzine, cuscinetti volventi.
3= Lubrificazione mista, caso particolare tra 2 e 4.
4= Lubrificazione fluidodinamica. Effetto di portanza
p Forze resistenti dovute all’opposizione del moto. Il contatto è completamente
mediato dal meato/meandro (fluido). Sfrutto la portanza:
Il corpo, che si muove su un fluido, è soggetto a delle forze risultanti. La risultante
delle pressioni del fluido è diretta verso l’alto → produce forze che il fluido fa sul
corpo, riuscendo a sostenere il carico che il fluido fa sul corpo. Applicazione:
cuscinetti fluidodinamici.
5= Fluidostatica: Ovviare al problema di quando il moto si ferma. Porto il
lubrificante in pressione dentro il meato. Se ottengo una forte sovrappressione ⟹
risultante delle forze che il fluido fa sull’albero ⟹ sostentamento anche se l’albero
gira lento o si ferma. Applicazione: cuscinetti fluidostatici.
‚ | !
J
‚
I
II !
E
I
E I
I | E
E I
- La lubrificazione fluidodinamica è necessaria quando v, ï aumentano in
contemporanea.
- Pochi v, tanti ï ⟹ uso cuscinetti volventi.
- Crisi coppia cinematica: elevati v, ï.
Modello coppia cinematica: (come si fa?)
T
̅ C, J
Ls , Ls
A¾
ü
U
ü
C, J
̅ C, J
U
I ,
I
Ls :F• necessarie per mantenere in moto le pareti su ¾ ed ¾ del meato.
quattro facce laterali; A¾$
Inizio con Navier-Stoke
!̅
s
c
T
E
µ + 6Δ
µ ̅
̅
0
̅
Uscita lubrificante; A¾:
Entrata lubrificante.
N O Campo delle velocità di un qualsiasi punto del
fluido che si trova nel meato.
Ipotesi:
1B Effetti inerziali (parte di accelerazione) trascurabile:
s
•ís
D •• + Áís ̅ G ≃ 0
1.1
1.2
•ís
••
∼ 0 → moti stazionari ⟹ studio problema a regime.
Áís ̅ ∼ 0 → moto fluido laminare, suppongo che il fluido non sia
caratterizzato da moti vorticosi.
2B Noni ci sono Ls :F• (di volume) applicate al fluido
!̅ ≃ 0
0
⟹c
L’unica forza sarebbe il peso, ma il peso del fluido è ridicolo rispetto
ai carichi applicati sulla coppia cinematica.
µ + 6Δ
µ ̅
̅
0
Condizioni iniziali: considero non dipendenza dal tempo (problema stazionario)
Condizioni al bordo: condizioni di aderenza
¾
̅
̅
Perché faccio il modello?
̅
̅
¾
¦
A¾
Output da calcolare:
-
Campo delle velocità → come si muove il fluido nel meato;
Campo delle pressioni → come si distribuiscono le pressioni nel meato;
Effetto portante: che coppia e forza ottengo;
Le } calcolate sono sufficienti a bilanciare i carichi?;
Portata lubrificante ”: quanto lubrificante esce ed entra?.
≪ 2*$+íB•$+B
Schiaccio → il fluido esce da tutte le parti → il moto del fluido lungo CJ (tangente) è
preponderante rispetto a ü (normale):
Derivate spaziali di ̅ ∼ 0; Moto schiacciamento quindi:
L† õLý ö ≫ L•BŽ%:Ž•: LF
A
a
AC
Q
Q
A
Aü
Q̀
QA
_ AJ
6
A
Aü
0⟹
6
A
Aü
Ricorda: 0
A
a
Q AC
Q
A
Aü
Q̀A
Q
_ AJ
C, ü
⟹ le derivate spaziali , lungo C e J sono trascurabili
rispetto alle derivate spaziali di , lungo ü.
1
2
3
µ + 6Δ
µ ̅⟹ µ
µ ̅:
6Δ
A
A
A
A
6N
+
+
O
AC
Aü
AJ
Aü
A
A
A
6N
+
+
O 0
AC
Aü
AJ
A
A
A
A
6N
+
+
O
AC
Aü
AJ
Aü
õ
̅≃0
L† ≫ L•BŽ%:Ž•: ö
õ
Lý ≫ LFý ö
Integro 1 e 3 :
-
→
→
A
Aü
ü
A
ü
Aü
A
Aü
A
Aü
-
-
u
t
t
t
s
1A
ü ü+6 AC
1 A
ü +
26 AC
ü
-
ü
-
1A
ü ü+6 AJ
1 A
ü
26 AC
1 A
ü
26 AJ
,
ü
ü
C, J
C, J ü +
A 1
A
ü→
AJ 6
Aü
1 A
ü +
26 AJ
Voglio adesso
,
,
1A
ü+
6 AC
A 1
A
ü→
AC 6
Aü
,
•
,
,
•
C, J ü +
•, t
ü
ü
C, J
ü→
C, J
1A
ü+
6 AJ
C, J
t
•
C, J
ü→
C, J
sfrutto le condizioni al bordo:
¾
¾
ü
ü
+
+
ü
ü
ü
ü
ü
ü
ü
ü
+
+
Il primo pezzo è il contributo quadratico di scorrimento, campo di velocità se le
superfici stanno ferme.
Il secondo pezzo è il contributo lineare di trascinamento, le superfici traslano il
meato, che trascina il lubrificante.
Per determinare le tre incognite fondamentali del problema
l’equazione di continuità:
A
A
A
+
+
AC Aü AJ
0
̅
Integro rispetto a ü, da ü a ü :
ý/
A
A
ü +ü
ý0 AC
ý0 AJ
ý/
A £ F,
! C, ü, J
AC ¡ F,
A! C, ü, J
AC
! C, f C, J , J
! C, ' C, J , J
A ý/
AC ý0
ü
Idem per w:
A
ü
AJ
ý0
ý/
-
¡ F,
A
; f C, J
AC
C, ü , J
A
ü+
ý0 AC
A ý/
AJ ý0
Sostituisco in 1 : 2
C, J
ü C, J
A
ü
Aü
A
! C, ü, J
AC
ü + ! C, f C, J , J
ü ; ' C, J
1 A
ü
26 AC
C, ü , J
ý/
ý/
ý0
£ F,
ü
Aü
AC
1 A
ü
26 AC
ü
ü;
Aü
+
AJ
Af C, J
AC
ü
ü
ü
+
ü
ü
ü
+
ý/
Aü
A
→ü
AC
ý0 AC
3 , ricordando K
ü C, J h
considero
0
-
Formula di Leibniz:
, ,
Aü
AJ
ü
ü
ü
ü
A ý/
AC ý0
3
! C, ' C, J , J
ü
ü
ü
+
ü
ü
+
Aü
+
AC
1‡ …
26
L e chiamando
1‡ …
26
spessore del meato.
A' C, J
AC
Aü
AC
2
Equazione di Reynolds:
A
ª
AC
•
A
A
«+ ª
AC
AJ
•
A
«
AJ
126
+ 66
A
A ü +ü
AC
66
+
AC
+
+
A
+
AJ
A ü +ü
AC
=Meato.
Incognita.
- 126
Termini di schiacciamento ( ∼ 0, ma non è detto che la
differenza di sia ∼ 0).
• $ 8$
• ˆ 8ˆ
0
/
0
/
- 66
+
Termine di velocità, mi dice come il moto
•F
•
tangenziale delle superfici va ad agire sulle pressioni.
• ý 8ý
• ý 8ý
0
/
0
/
- 66
+
Termini delle superfici, mi
•F
•F
dicono come la forma del meate agisce sulle pressioni.
C, J
A¾
B9z<:Ž•:
Come trovo i carichi che gravano sulla superficie?
Da trovo la velocità e poi i carichi e la portata. La risultante delle azioni che un
fluido fa sulla superficie:
Ls
-
»s +
B
Ls
-
»s +
Bs
”Œ$
-
̅ ∙ s ¾$
‰0
‰/
•‰Š
s
E
E
¾ ª
¾
-
•‰
̅ ∙ s ¾:
̅
s
!
!
¾
«
¾
»s
E
A¾$ A¾: , ”
I I
| !
I
Cuscinetti fluidodinamici a pettini (elemento che viene ricavato o sull’albero (figura
a sinistra) o sulla sede (figura a destra), opzione più comune e meno costosa):
Obiettivo: Voglio capire quali forze si scambiano questi due elementi.
Superficie cilindrica ⟹ superficie generate da una retta (in questo caso
¾
ortogonale a Cü, cioè parallela a J e simmetrica rispetto al piano Cü).
| Larghezza slitta / piano lungo J.
¾
Una delle due superfici che delimitano il meato (fissa).
È solo in funzione di C.
Dunque:
0,
0,
0
costante,
0,
0
0, C
ü C
ü C
ü
ü C
Dall’equazione di Reynolds:
A
ª
AC
•
A
A
«+ ª
AC
AJ
•
Relazione di campo:
•3
‹ •F
ü ü
•3
‹•
A
«
AJ
+
ü ü
$/
@
ü
66
C
,
66
I
,
,¿ E
I E
C
I
Ià
E
!
Siano ï , ï e p , p le componenti verticali e longitudinali di Ls e Ls
u
tLs
t
t
t Ls
s
-
‰0
-
‰/
® E
»s +
»s +
:
B
s
¾
Bs
¾
ï
Ls ∧ ’̅
- õ
p
Ls ∧ ̅
- D »F +
ï
Ls ∧ ’̅
- õ
‰0
Fý
F
‰/
- 6
‰/
A
Aü
F
Ž
•
…
Œ…
…
+ õ»ý +
Bö
ý
+
ý
ö ¾
+
Fý
ý
+
F
G ¾
Bö
ý
+
ý
ö ¾
B
‰0
Fý
»
A
Aü
6
F
+ õ»ý +
F
¾
-
‰/
B
ý
¾
6ª
A
A
+ « x
AC AJ ‘w
A
•w
6
w
Aü
w
•v
-
B
‰0
- 6
‰0
¾
A
¾
Aü
I
Ls ∧ ̅
p
- D »F +
‰0
-
‰/
F
B
B
F
F
+
Fý
ý
¾ +- 6
‰/
+
A
Aü
G ¾
F
ý
¾
e ý : componenti del versore normale alla superficie.
Grandezze importanti:
: Su entrambi i carichi entra in gioco sovrappressione ⟹ quanto riesco ad
innalzare la pressione sul meato?
6
•$
•ý
B
(diretta lungo C) del fluido
: Gradiente delle velocità, come varia la velocità
lungo ü. Genera resistenza (negativa).
Contributi secondari, quelli moltiplicati per
F,
possono essere negativi.
Portata:
”
-
•‰Š
¾$
-
•‰
¾:
Ipotesi ulteriori:
Il pattino / slitta sia infinitamente largo: | → + ∞ cioè:
spessore del pattino | ≫ meato
Dunque: Con buona approssimazione posso studiare quello che accade nel meato in
una sezione qualunque del meato
} E
^
C, J
C, ü, J
C, ü, J
q
| → +∞
Y
Sostituisco (le equazioni che ho ora) nell’equazione di Reynolds:
C
C, ü
0
¿
C
ª
•
J
C
66
«
C
I
Integro rispetto a C:
66
C
+
,
ª
:
C
I I
C
B
,
0 C
è
è!
J
C«
•
Altra integrazione:
CK
F
66
-
(
+
F
-
(
CK
•
+
Impongo le condizioni al bordo:
66
∗
B
M(
B
M(
B
M(
B
M(
CK
CK
CK
•
CK
•
+
∗
66
C
B
,
∃ un certo valore C ∗ , dove la pressione inverte il suo trend:
Ottengo che:
:
66
C
B
Nota bene:
Se
;@
;F
;@
;F
∼
∗
ª1
66
I
«
F
N-
(
I
⟹
CK
∗
;
;/3
;F /
O→
C
ª
•
C
,
66
«
C
<0
> 0 ⟹ Meato deve essere divergente nel senso del moto.
è una retta:
(
E
≃
(
•
> 0, poiché deve essere uguale ad una quantità negativa ed è moltiplicata .
HP) Cosa succede se
(
CK
-
• ;3
G
;F
D
;F
F
+
Spessore minimo del meato,
Spessore massimo del meato,
Parametro di forma del meato
rispetto allo spessore minimo:
(
C
( D1
@0 5@A
@A
+
E
CG ,
:
. Mi dice di quanto è inclinato il pattino
EE I
E
I →I
I →
‚
( ^ï
! E
ò
||
I
I
I
,
I
E
|
, E I
,E
I
E I
I E I
I
I II I
I J
J |
I
I
||
!
E
E
(
I|
Variabili adimensionali:
66
x
x
∗
B
=
ã
L
2
Z
J
E
(
E
E I
I
1+E
2+E
66
| E ,
E
sono
E I
E
Dopo E ∼ 1 la situazione peggiora ⟹ E
ï
66
ª
(
«
E
=
C
x DE, G,
1: Δ
•
E
E
•
I
I
,
(
E
I .
≅
(
II
.
Ià
|p |
6
(
V E
Coefficiente d’attrito equivalente:
!
|p |
ï
J
I I
E
,E
•
I pesa |p |, !! II
I
,
ï , !! II
I
Maggiore
⟹ maggiore spinta e resistenza
Fluido ideale 6 0 ⟹ non sostengo carico, non ho perdite
( minore ⟹ ï cresce come inverso del quadrato, p cresce come inverso lineare
HP) | è finito:
B
variano lungo J in prossimità di ± (facce laterali)
z
≠ 0 in prossimità di ± (buono, poiché da qualche parte il fluido deve uscire
negativo, poiché possibili perdite di pressione)
! aumenta: pzN <Ž<•= > pzN–
Coefficienti correttivi:
z
A titolo di esempio di un coefficiente di bordo, ho trovato un carico grande su
cuscinetti ï <
¼#
ï +:B¯:
|ï <
ï < trovato dal progetto.
Trovo ¼# .
Trovo ï + (carico reale sostenibile dal cuscinetto).
Coppia rotoidale:
1. Coppia rotoidale con perno oscillante:
È costituita da:
Due cilindri: ¾ , raggio 2 , asse (detto cuscinetto) coincidente con J, ha come
traccia il punto q , ruota intorno ad q con velocità angolare v
µ ; ¾ , raggio 2 , asse
(detto perno) parallelo a J, ha come traccia il punto q , possiede un moto di
rototraslazione del punto q e dalla velocità angolare v
µ .
La coppia cinematica, simmetrica rispetto al piano Cü, ha larghezza pari a |.
Ci sono due aperture attraverso le quali il meato entra A¾: ed esce A¾$ .
Ls , ® , Ls , ® sono le azioni esterne necessarie per mantenere in moto le pareti ¾
ed ¾ del meato.
sssssss
Spessore del meato V
ã
ã ≪ 2 , 2 ⟹ posso ricondurre lo studio della
coppia rotoidale a quella della slitta piana, introducendo opportune coordinate
cilindriche. Indicate con CŒ3 , üŒ3 , JŒ3 le variabili spaziali impiegate nello studio della
slitta piana, ho che:
CŒ3
Y üŒ3
JŒ3
V2
0
—
J
Le derivate sono dunque:
&<V<&
≤ ≤
|
|
≤J≤
2
2
V
1 A
A
a
∙
2
AV
AC
Œ3
Q
Q
A
A
AüŒ3 A
A
A
Q̀
Q
_ AJŒ3 AJ
˜
Il primo membro dell’equazione di Reynolds diventa:
1 A
ª
2 AV
•
A
A
«+ ª
AV
AJ
Velocità del punto q :
̅ q
I
º ’ ̅ + 'º ̅ ,
Ià
•
A
«,
AJ
sssssss
q
q
V, J
:
cos V ̅ + sin V ’̅
sin V ̅ + cos V ’̅
̅
’̅
Poiché: ã
q
(ricorda che ’̅ ∙ ̅
Quindi ho che:
sssssss
sssssss
q
ã ’̅ + ’̅ ⟹ q
ã
0, ’̅ ∙ ’̅
cos V + ¨
sssssss
q
ã
Lo spessore del meato
2
Con: m
2
sssssss
q
ã
1
cos V + 2
2
2
sssssss
q
ã +
2
≃ cos V + 2
E
sssssss
ã ã può essere quindi ricavato notando che:
2
cos V
m 1
2 (gioco radiale della coppia), ™
̅ ã
+v
µ ∧ ã
̅ q
:
g
.
Poiché:
¾ →^
sssssss
q
ã ’̅ + ’̅
º sin V ̅ + cos V ’̅ + 'º cos V ̅ + sin V ’̅ +
sssssss
+v
µ ∧õ q
ã ’̅ +
sin V ̅ + cos V ’̅ ö
Siccome: v
µ ∧ ’̅
̅ ã
µ ∧
º ’ ̅ + 'º ̅ + v
q
≪2
™ cos V
Per la formula fondamentale dei corpi rigidi:
̅ ã
2 sssssss
q ã cos V
;@
;ô
v ̅ ,v
µ ∧ ’̅
v ̅
l º sin V + 'º cos V +v 2 n ̅ + l
v cos V ̅ + sin V ’̅
º cos V + 'º sin V
sin V, per quanto riguarda il cilindro:
º sin V + 'º cos V + v 2
º cos V
Supponendo che 2 ≃ 2
;@
'º + v
;ô
0
;@
;ô
¾ →Y
v 2
0
0
2, trovo l’equazione di Reynolds:
v
sin V n’̅
1 A
ª
2 AV
•
A
A
«+ ª
AV
AJ
•
A
«
AJ
126 ª
+
º cos V
66
N
2
66
2 V
'º
+v
«+
V
V
v 2 + º sin V + 'º cos V + v 2
O
V
º sin V + 'º cos V + v 2
v 2
Attraverso delle semplificazioni posso scrivere:
1 A
ª
2 AV
•
A
A
«+ ª
AV
AJ
•
A
«
AJ
Le componenti della velocità ,
a
`
_
1 A
262 AV
1 A
26 AJ
66
sono:
+
v +v
V
126 ª º cos V + 'º
V
«
+
Le azioni Ls , ® , Ls , ® necessarie per mantenere in moto le parati del meato hanno
la seguente espressione:
Ls
-
»s +
B
s
¾
®
-
C̅
qs
∧
»s +
Bs
¾ ∧ xs
Ls
-
»s +
Bs
¾
®
-
C̅
qs
∧
»s +
Bs
¾ ∧ xs
”
-
̅∙s ¾
‰0
‰/
‰0
‰/
Per quanto riguarda la portata volumetrica di lubrificazione ”:
•‰Š
-
•‰
̅∙s ¾
Se poi A¾$ e A¾: sono costituite dalle sole facce laterali dei cilindri ¾ e ¾ (le
eventuali altre aperture sono trascurabili) si ottiene:
”
-
•‰Š
¾
2. Coppia rotoidale con perno non oscillante:
-
•‰
¾
L’ipotesi di perno non oscillante comporta delle agevolazioni:
- La velocità ̅ q del punto q è nulla ⟹ º 0 'º 0.
µ
v
- La velocità angolare del cuscinetto v
µ è nulla. Ho solo v
L’equazione di Reynolds assume la forma:
1 A
ª
2 AV
•
A
A
«+ ª
AV
AJ
•
A
«
AJ
66
Le componenti della velocità sono:
a
`
_
1 A
262 AV
1 A
26 AJ
+
V
v
2v
Riguardo le azioni essenziali per mantenere in moto le parati del meato introduco le
grandezze ï , } ï , } , cioè le componenti di Ls Ls rispettivamente ortogonali e
q.
parallele alla direzione di accostamento del perno al cuscinetto q
ï
Ls ∧ ’̅
- õ
}
Ls ∧ ̅
- D »F +
®
‰0
- „Cõ
‰0
- °6
‰0
ï
Ls ∧ ’̅
}
Ls ∧ ̅
®
- „ C
‰0
‰0
A
A
Cü 1C
F
+ õ»ý +
Bö
ýö
¾
- °6
+
Fý
ýG
¾
- °
B
F
+ õ»ü +
ö
1C
- õ
‰/
‰0
q
q
F
Fý
õ
F
1ü ö
+ õ»ý +
F
Fý
ª6
A
A
‰0
ü õ»C +
üª õ
1ü
- D »F +
- ° C
‰0
Fý
Bö
+
B
F
F
+ õ»ý +
ý
+
Bö
F
ý«
B
+
A
A
- ª6
‰/
ü
q
q
ª
+6
… ¾
F
B
F
B
A
A
ý±
¾
ý±
¾
¾
B
ý«
¾
A
Aü
ý«
¾
F
B
»F +
F
1ü «±
A
Aü
‰/
ü
B
Cü 1ü
- ª
¾
ýö
1C
1C + 6
ö ¾
ý
ýG
Fý
ö
F
B
‰0
ö
A
A
+6
+
F
Fý
+6
A
A
ý
… ¾
ý «±
¾
Considero l’equilibrio alla traslazione ed alla rotazione del fluido all’interno del
meato:
a
Q
Q
Q̀
Q®
_
} +}
®
ï +ï
ï
-
•‰
-
-
•‰
•‰
C̅
Bs
Bs
qs
¾∧ ̅
¾ ∧ ’̅
∧
0
Bs
0
¾ ∧ xs
0
3. Coppia rotoidale infinitamente larga con perno non oscillante:
Suppongo che la larghezza della copia tenda all’’infinito in direzione J, cioè | → + ∞
Vantaggi:
V
,V
-
0
Dal punto di vista fisico significa ammette che il meato sia molto allungato in
direzione J e trascurare le cadute di pressione, che inevitabilmente avremmo nella
realtà in prossimità dei bordi laterali.
L’equazione di Reynolds diventa:
1 A
ª
2 AV
•
A
66
v ⟹
V
AV
A
«
AV
66v2
+
•
66v2 -
⟹
ô
(
VK
+
-
ô
(
VK
•
+
La costante può essere determinata imponendo la condizione al contorno
&
& :
66v2
VK
4
M54
66v2
VK
4
M54
•
∗
,
∗
4
M54
4
M54
VK
VK
•
2m
1 ™
2+™
Dunque:
A
AV
66v2
ª1
ô
66v2 N-
(
∗
V′
2
«
∗
ô
-
(
V′
3O+
66v2
m
™ 2 ™ cos V sin V
+
2 + ™ 1 ™ cos V
Come trovo ? Devo conoscere il valore della pressione in corrispondenza di un
valore di V; a tale scopo suppongo che sia V̅
B ovvero che il meato sia messo
in comunicazione con l’ambiente esterno nel punto V V̅.
Andamento di V
B:
Da questo grafico noto che solo per V̅ V ∗ la funzione V
B sia sempre
∗
positiva (e nulla per V V ; al contrario per qualunque altro valore di V̅ la funzione
V
B presenta una zona negativa. Questo risultato è fisicamente inaccettabile,
poiché nella realtà in tale zona si ha la rottura del film di lubrificante per cavitazione.
La zona in questione non produce carico e quindi non collabora al sostentamento
del perno; si avranno dunque sia una riduzione che un disassamento della risultante
q come nel caso ideale.
che non risulterà più ortogonale alla direzione q
1 A
262 AV
L’equazione:
+
2v
permette anche in questo caso di determinare la componente della velocità (la
è nulla per ipotesi). Volendo inoltre calcolare le azioni: ï , } , ® per unità di
lunghezza agenti sul cilindro ¾ le equazioni:
a ï
Q
Q
Q
Q}
Q̀ ®1
Q
Q
Q
_
Ls ∧ ’̅
Ls ∧ ̅
-
¾1
- õ
‰0
- D »F +
diventano:
‰0
Cõ
- °6
¾1
Fý
Fý
A
A
F
F
F + õ»ý +
B
+ õ»ý +
F
B
+
Bö
Bö
Fý
ýö
ý
ýö ¾
ýG
¾
- °6
- °
ü D »F +
üª
‰0
‰0
B
B
A
A
F
F
+
+6
F
B
Fý
A
A
F
ýG
+6
ý «±
B
A
A
¾1
¾1
ý±
ý±
¾
¾
4
A
G
A +N(
ï
- °6
}
- °
®
- C ª6
a
Q
1 A
2v
+
262 AV
66v2 ™ 2 ™ cos V sin V
+
m
2 + ™ 1 ™ cos V
54
4
F
B
54
4
54
B
F
A
G
A +N(
+6
A
G
A +N(
F
ý± 2
B
V
ý± 2
V
üª
ý«
dove: F cos V, ý sin V, C 2 cos V e ü
equazioni appena scritte le equazioni:
Q̀
_
si ottengo i valori desiderati di ï , } , ® .
Tuttavia, poiché gli sforzi tangenziali: 6
•$
D
•+ +N(
B
F
+6
A
G
A +N(
ý« 2
2 sin V. Sostituendo nelle
V
risultano trascurabili rispetto alle
pressioni
B , nelle applicazioni pratiche le grandezze ï , } , ® possono essere
valutate come segue:
4
ï
- õ
B
ýö 2
V
}
- õ
B
Fö 2
V
®
54
4
54
4
-
54
CD
B
ýG +
ü
B
F
2 V
Sostituendo l’equazione:
66v2
m
™ 2 ™ cos V sin V
+
2 + ™ 1 ™ cos V
nelle equazioni sopra scritte e ricordando la proprietà di disparità della funzione , si
ottiene che:
ï
2
66v2 ª «
m
}
0
!
|® |
2ï
®
!
6v2
2&™
2 + ™ ¨1
™
2 4& 1 + 2™
m 2 + ™ ¨1 ™
mš C
26 C
6v2 š C
©
ï ¨6 C
2
66v ª «
m
6v2
m 1 + 2™
2
3™
C
2
š C
m
6v2
©
x ™
ï
nelle quali ! è il coefficiente di attrito equivalente della coppia rotoidale lubrificata.
Può essere interessante notare che la funzione:
1 + 2™
3™
che compare nell’espressione del coefficiente di attrito !, si mantiene molto
prossima ad uno in tutto l’intervallo 0.5 ≤ ™ ≤ 1 ovvero l’intervallo dei valori di ™
più comunemente adottati nel proporzionamento dei cuscinetti. Pertanto si può
concludere che, per valori abituali di ™, il coefficiente di attrito ! della coppia
rotoidale di larghezza infinita e perfettamente lubrificata valga circa:
m
,
2
dall’equazione }
0 si deduce quindi che la risultante delle azioni agenti sulla
coppia è ortogonale alla direzione di accostamento q
q . Per quanto riguarda le
grandezze ï , } , ® , esse possono essere calcolate mediante le equazioni scritte
sopra il paragrafo coppia rotoidale infinitamente larga con perno non oscillante. La
situazione appena descritta può essere anche rappresenta graficamente riportando
sul cuscinetto, coerentemente con le equazioni:
ï
4
- õ
54
B
ýö 2
V
4
}
- õ
54
4
®
-
54
Fö 2
B
CD
V
ýG +
B
ü
B
il campo di pressioni normali –
che la componente della pressione
proposito tale figura:
B
F
2 V
s agenti su ¾ (dove si è posto V̅ 0 dato
B non influisce sull’equilibrio). Si veda in
Più in particolare, a causa della disparità della funzione , le risultanti ¾̅ < , ¾̅ Œ del
campo di pressioni normali –
B s agente rispettivamente sui semicuscinietti
inferiore e superiore ¾ < , ¾ Œ , cioè:
¾̅
Œ
-
‰0›
»s +
Bs
¾
Œ
≅
4
-
(
B
s
¾
Œ
4
-
(
B
s 2 V
¾̅
Œ
-
‰0
»s +
Bs
4
¾<≅
-
B
(
s
¾
(
-
<
54
B
s 2 V
q del
hanno somma diretta ortogonalmente alla direzione di accostamento q
pernio (le eventuali altre aperture su ¾ , ¾ sono supposte trascurabili).
Per quanto concerne la portata volumetrica di lubricante ” (per unità di larghezza),
essa può essere calcolata sempre mediante la:
”
Si noti che in questo caso la:
-
•‰Š
”
̅∙s ¾
-
•‰Š
-
•‰
¾
-
•‰
̅∙s ¾
¾
darebbe ” 0 essendo
0; di conseguenza è necessario comunque supporre
l’esistenza di altre aperture su ¾ , ¾ per il passaggio del lubrificante anche se queste
ultime possono essere trascurabili da un punto di vista dinamico.
Coppia rotoidale di larghezza finita con perno non oscillante:
I risultati appena trovati posso essere estesi al caso di coppia rotoidale di larghezza
finita |. Da un punto di vista quantitativo, passando dal primo caso al secondo, si
osservano le seguenti differenze:
- La sovrappressione
B varia in questo caso anche lungo l’asse J e
presenta necessariamente, al variare di V, una zona in cui si annulla od
assume valori negativi (in tale zona il lubrificante non è attivo e non collabora
al sostentamento del perno); come conseguenza, a parità di altre condizioni,
la risultante delle pressioni risulta nel secondo caso inferiore (e non più
ortogonale ala direzione q
q ) rispetto alla risultante agente su una
striscia di larghezza | nel primo caso.
- La componente della velocità è in questa circostanza diversa da zero; si ha
ciò necessariamente una fuga laterale del lubrificante in direzione J.
- La fuga di lubrificante dal meato in direzione assiale (lungo J) deve essere
continuamente bilanciata con l’introduzione di altro lubrificante; essa viene
solitamente effettuata in zone che non danno contributo alla sostentazione
del carico (ad esempio mediante aperture sulla facce laterali dei cilindri o
direttamente su ¾ ); questo influisce nuovamente sulla riduzione e sul
disassamento dell’azione risultante.
- Nel caso in esame inoltre il coefficiente d’attrito è più alto quindi è più elevata
la potenza dissipata.
L’alimentazione del lubrificante può avvenire con l’impiego di mezzi elementari
oppure facendo ricorso ad una circolazione forzata; in questo caso un impianto
idraulico costituito da un serbatoio, un filtro, una pompa, un refrigerante dell’olio
caldo, tubazioni di collegamento ed organi ausiliari permette un efficiente ricambio
del lubrificante ed un sicuro controllo della temperatura. Se la portata di
alimentazione del lubrificante supera un certo minimo dipendente dalle condizioni
di funzionamento il perno si dispone nella sua sede in questo modo:
La zona di meato tratteggiata corrisponde alla zona portante; essa ha inizio nel
punto V
& e termina in un punto prossimo a V 0 (solitamente dalla parte
delle V positive); tale valore è individuato dalla condizione di contemporaneo
;3
annullamento delle sovrappressioni
.
B e dalla loro derivata
;ô
La forza Ls è quella necessaria applicare al cuscinetto per bilanciare il carico
gravante al perno. Tale forza ha sia un componente ï normale alla direzione di
accostamento q
q ed una componente } parallela ad essa.
Andamento dei parametri adimensionali:
ï∗
ï
2
66v2 D G
m
,
!∗
2
! ,
m
”∗
”
,
|v2m
in funzione di ™, per |
22
(Le linee tratteggiate rappresentano i valori delle prime due grandezze per | → +∞)
Nella soluzione del problema diretto ⟹ sono note le dimensioni della coppia
|, m, 2, il carico per unità di lunghezza ï , la viscosità 6 e la velocità angolare v,
bisogna determinar l’eccentricità , la portata ” ed il coefficiente di attrito !; si fa
spesso uso del numero di Sommerfeld:
¾=
2
6v D G
m
&ï
(la sua utilità è legata al fatto che contiene tutte le variabili normalmente specificate
dal progettista).
Coppia rotoidale di larghezza infinitamente piccola con perno non oscillante:
In questo caso si suppone che la larghezza | della coppia rotoidale sia trascurabile
rispetto al raggio 2:
|≪2
Da un punto di vista grafico si può fare riferimento alla coppia rotoidale con perno
non oscillante. Da un punto di vista modellistico ne consegue che le derivate di
rispetto a V ⟹ D
•3
ž/ Ÿ
•3
•ô
e
ž/ Ÿ
žô /
G sono trascurabili rispetto alle analoghe derivate rispetto
a J D e / G; si noti che questo non implica che dipenda solamente da J. Sotto
•
ž
tale ipotesi l’equazione di Reynolds diventa:
A
A
v
ª • « 66
AJ
AJ
V
dal momento che
riduce a:
V ⟹ posso portar fuori
A
AJ
66v
•
Integrando due volte rispetto a J, si ottiene che:
V, J
36v
•
V
J +
dalla derivata rispetto a J, si
V
V J+
V
da cui, imponendo le condizioni al contorno:
ªV,
V, J
|
«
2
|
ªV, «
2
B
36v
•
B
|
N
V 4
si ha:
J O
sssssss
dove V è dato da:
2
q
ã
2
2
cos V m 1 ™ cos V . Le
altre grandezze di interesse per il sistema, ovvero , , ï , ï , } , } , ® , ® ,
e ”, possono essere calcolate mediante le due equazioni scritte prima del paragrafo
della coppia rotoidale con perno non oscillante e le successive undici (esclusa quella
sull’equazione di Reynolds).
Lubrificazione fluidostatica:
Il lubrificante è mantenuto in pressione mediante mezzi esterni e non grazie ad
azioni dinamiche tra il lubrificante e gli elementi della coppia. Questo tipo di
lubrificazione è applicabile sia a cuscinetti reggispinta che a cuscinetti portanti. I
benefici di questa lubrificazione sono:
- È impiegabile anche quando gli elementi cinematici della coppia non sono in
moto relativo tra loro;
- Ammette l’utilizzo di meati di altezza constante;
- Consente di realizzare film di lubrificante di grande rigidezza (e quindi di
sostenere grandi carichi) mediante un opportuno controllo delle condizioni di
alimentazione;
- Permette l’impiego di lubrificante a bassa velocità, cui corrisponde un basso
valore del coefficiente di attrito della coppia.
Cuscinetto reggispinta:
Un albero ã rotante attorno al proprio asse con velocità angolare v e caricato con
una forza assiale } , porta ad un’estremità una parete piana ortogonale all’asse
dell’albero limitata dai raggi 2 e 2 . La parete di estremità dell’albero ¾ si affaccia
sulla parete piana ¾ di un membro fisso æ. Attraverso un foro ricavato in æ,
coassiale con l’asse dell’albero, viene inviato lubrificante sotto pressione entro un
pozzetto di raggio 2 ricavato in corrispondenza dell’estremità dell’albero. Il
lubrificante viene alimentato con pressione = costante per mezzo di un circuito
idraulico (non rappresentato in figura). Attraverso il foro la pressione del lubrificante
passa dal valore = (all’ingresso) al valore dentro il pozzetto. Il lubrificante sotto
pressione tende a sfuggire dal pozzetto verso la periferia, dando origine ad un
meato tra l’albero e la sua sede. La pressione del lubrificante, che dentro al pozzetto
può ritenersi costante, decresce dentro il meato dal centro verso la periferia fino a
raggiungere sul raggio esterno dell’albero il valore della pressione ambiente B .
Il problema in questione è semplificabile utilizzando opportune coordinate
cilindriche (con CŒ3 , üŒ3 , JŒ3 sono indicate le vecchie coordinate spaziali):
CŒ3
^üŒ3
JŒ3
ü
sin V
cos V
dove:
& < V ≤ &;
2 ≤
≤2 ;
0
di conseguenza si avrà, per le derivate:
A
a
ACŒ3
Q
Q
A
AüŒ3
Q̀
Q A
_ AJŒ3
sin V
A
Aü
cos V
A cos V A
+
A
AV
A
A
e per le velocità:
^
sin V A
AV
sin V º + cos V Vº
ý
cos V º
sin V Vº
sin V
cos V
+
+
+ cos V
sin V
ô
ô
ü ≤ü≤ü
Poiché inoltre:
j
+
+
ü
ý
ô
0,
ý
0, ü
costante
ô
0
v
L’equazione di Reynolds generalizzata diventa:
1A
A
1A
ª
«+
A
A
AV
0
alla quale vanno associate le condizioni al contorno:
B
su A¾$
su A¾:
Per quanto riguarda invece le componenti
•3
^
‹ •F
•3
‹•
danno:
j
+
ô
ü
ü
ü
ü
ü
ü
ü
ü
+
+
$/ 5$0
ý/ 5ý0
ˆ/ 5ˆ0
ý/ 5ý0
ü
ü
+
e
ü
ü
ô
della velocità, le equazioni:
+
+
1 A
ü ü
26 A
v
ü
Dalla simmetria del problema si ha poi che:
+
+
,ü ;
ô
ô
,ü
Di conseguenza l’equazione di Reynolds assume la forma:
che integrata due volte fornisce:
1A
A
ª
«
A
A
0
⟹
ln
+
Le costanti di integrazione e possono essere determinate imponendo le
seguenti condizioni al contorno:
^
-
2
•‰
B
̅∗ s ¾
-
•‰Š
̅∗ s ¾+-
•‰
̅∗ s ¾
@
-
(
+ 2&2
ü
”
0
dove la seconda condizione impone la conservazione della massa sul volume del
meato +9:B•= ; se ne deduce che:
6 6”
2
ln
ª
«
& •
B
La seguente equazione:
B
6 6”
2
ln
«
ª
2
& •
permette di valutare il valore di ”. Poiché però nella pratica è nota solamente la
pressione di alimentazione = occorre una relazione che leghi = e B . A tale scopo è
sufficiente applicare la legge di Poiseuille al condotto di alimentazione:
128 6”
& t
=
Le equazioni:
j
+
ô
1 A
ü ü
26 A
v
ü
permettono a questo punto il calcolo delle componenti + e ô della velocità mentre
per quanto riguarda le azioni esterne si ha (ricordando la simmetria del problema):
}
Ls ∗ ’̅
&2
B
+- õ
‰0
Fý
F
+ õ»ý +
Bö
ý
+
ý
ö ¾
&2
p
®
+-
B
Ls ∗ ̅
A
- 6
Aü
‰0
-
Cõ
‰0
- ° C6
‰0
./
4
- .0
./
‰0
¾
F
4
54
&
2
B
./
F
.0
+
+
F
ý
+ » +
ý
V
N-
s ¾+-
Bs
p +p
N-
s ¾+-
Bs
•‰Š
+
•‰
C̅
•‰
qs ⋀
G ¾
ý
A +
A ô
+ cos V
G
G
Aü ýN(
Aü ýN(
ö
B
J D »F +
sin V
&6v t
2
2
V
2
¾O ∗ ’̅
¾O ∗ ̅
s ¾+-
•‰
C̅
2&
B
.0
2
ln D G
2
A +
A ô
+ cos V
G
G O
Aü ýN(
Aü ýN(
A ô
G
Aü ýN(
N-
ý
A +
G
Aü ýN(
} +}
® +®
Fý
+-
B
2
B
54
sin V 6 N
•‰Š
&2
4
A
A
+ J6 ± ¾
Aü
Aü
•‰Š
¾
- - 6 sin V
6 Nsin V
- - 6
.0
- D »F +
54
+ cos
B
‰0
./
B
F
+
Fý
V
ý
+
0
F
ýG
¾
A ô
G O +
Aü ýN(
V
2t
} +}
0
p +p
0
qs ⋀
Bs
¾O ∗ ’̅
® +®
0
dove si è supposto B costante su A¾: e costante su A¾$ ; si noti inoltre come
nell’equazione di } sia stato anche considerato il contributo &2
B delle
pressioni nel pozzetto.
Si può infine calcolare il coefficiente di attrito ! del cuscinetto definito come il
rapporto tra il momento |® | necessario per mantenere l’albero in rotazione
uniforme ed il prodotto della forza assiale } per il raggio medio del cuscinetto:
!
2|® |
} 2 +2
;
ricordando le equazioni:
B
6 6”
2
ln
ª
«,
& •
2
quella di } ,
quella di ®
si ha poi:
!
•
2
6 2
&v 2 + 2 ©
3”} 2 + 2
In generale si può dimostrare che, per assicurare una buona rigidezza al cuscinetto,
entro il condotto di
è consigliabile fare in modo che la caduta di pressione =
alimentazione sia paragonabile a
B . Per ottenere una buona rigidezza si
richiede anche che l’altezza del meato sia la più piccola possibile. L’altezza del
meato tuttavia non può scendere al di sotto di un certo valore minimo che dipende
dalla rugosità delle superfici e dalle tolleranze di lavorazione.
Cuscinetto portante:
Il perno (di raggio 2 ), a cui è applicato il carico verticale L , è alloggiato da un
cilindro cavo di raggio 2 dentro il quale sono ricavati dei pozzetti (1, 2, 3, 4 in figura)
comunicanti con l’esterno per mezzo di forellini in direzione radiale; attraverso tali
fori è inviato dall’esterno lubrificante in pressione (ovvero = ). La portata di
lubrificante che giunge a ciascun pozzetto uguaglia a regime quella che sfugge dal
pozzetto stesso (attraverso canalini di scarico sia in direzione assiale che in direzione
longitudinale) verso l’ambiente (a pressione B ).
Per semplicità si suppone che il perno non ruoti v 0 ; questa è una condizione
limite di particolare interesse perché mette in luce una delle più interessanti
caratteristiche dei cuscinetti a sostentazione fluidostatica ovvero la loro attitudine a
funzionare anche a bassissime velocità. Inoltre essa è anche una condizione
cautelativa ai fini del calcolo della capacità portante del cuscinetto poiché,
all’aumentare della velocità angolare del perno, si sovrappone all’effetto
fluidostatico un effetto portante fluidodinamico con un conseguente aumento della
capacità portante stessa. Si suppone inoltre che la linea di azione del carico L passi
per la mezzeria di un pozzetto. Questa ipotesi semplifica la trattazione ma, al tempo
stesso, conduce a risultati non sempre cautelativi.
Prima di cominciare la trattazione analitica, è opportuno fare alcune considerazioni
atte ad illustrare il funzionamento del cuscinetto. Essendo i pozzetti relativamente
profondi si può ammettere che la pressione si mantenga costante all’interno di essi
(e pari rispettivamente a < con
1, 2, 3, 4). Ciò permesso, facendo riferimento
alla figura in alto, si osserva che, affinché il cuscinetto possa sopportare il carico L ,
occorre che nel pozzetto 2 si sviluppi una pressione superiore a quella t del
pozzetto 4 (i pozzetti 1 e 3 intervengono soltanto per impedire spostamenti laterali
del perno). Si nota poi che sia la pressione di alimentazione = che la pressione
ambiente B sono uguali per tutti i pozzetti. Pertanto per tutti i pozzetti è costante
la caduta di pressione =
B tra monte e valle. Tale caduta ha luogo,
praticamente, soltanto in due resistenze fluidodinamiche poste in serie:
La resistenza offerta dai fori di alimentazione 2= e la resistenza offerta dalla zona
che va dal pozzetto all’ambiente esterno 2< (con
1, 2, 3, 4). Affinché nel pozzetto
2 si sviluppi una pressione maggiore di quella che si ha nel pozzetto 4, occorre che la
resistenza complessiva del circuito comprendente il pozzetto 2 sia maggiore di
quella comprendente il pozzetto 4; in tal caso infatti la portata ” affluente al
pozzetto 2 è minore della portata ”t che affluisce al pozzetto 4 e di conseguenza la
è minore di =
caduta di pressione =
t . Ma questo è proprio quanto
accade quando, sotto l’azione del carico L , il perno si accosta al pozzetto 2
aumentando la resistenza fluidodinamica 2 . Riassumendo si ha quindi:
- Sotto il carico L il perno si accosta al pozzetto 2 aumentando la resistenza
fluidodinamica 2 .
- Aumenta la resistenza complessiva del circuito comprendente il pozzetto 2
(mentre diminuisce la resistenza del circuito che comprende il pozzetto 4).
- Aumenta la pressione nel pozzetto 2 e diminuisce la pressione t nel
pozzetto 4; si stabilisce così l’equilibrio del perno all’interno della sede
(l’entità dell’accostamento del perno dipende ovviamente dal valore di L ).
Questo permesso, si può impostare lo studio del cuscinetto ovvero, per una data
geometria e per un dato valore della pressione di alimentazione = , è possibile
determinare il valore del carico L e della portata di lubrificante ”. Nel seguito si
adotterà la seguente notazione:
Altezza del meato.
V
q .
Angolo che un raggio generico uscente da q , forma con il raggio che passa da
2d Angolo compreso fra due raggi uscenti da q e passanti per gli spigoli del
pozzetto.
2Γ Angolo compreso fra due raggi uscenti da q e passanti per gli spigoli dei
canalini di scarico.
|
æ
Dimensione assiale del pozzetto.
Dimensione assiale del pozzetto.
La figura sopra riportata, sviluppata in un piano, rappresenta la pianta di un
pozzetto. Si è posto:
'
ã
2d2
2Γ2
Come fatto in precedenza (coppia rotoidale con perno oscillante) si ha che:
m 1
™ cos V
nella quale m
2
2 è il gioco radiale della coppia e ™
:
g
.
Si è già osservato che la pressione si mantiene costante (pari < ) dentro ciascun
pozzetto. Essa poi raggiunge il valore B sul contorno esterno del pozzetto in
comunicazione con i canalini di scarico e quindi con l’ambiente (come si può vedere
dalla figura sopra riportata, è il contorno più spesso). In corrispondenza della fascia
compresa tra il contorno interno del pozzetto ed il suo contorno esterno a pressione
ambiente il perno è molto ravvicinato alla sua sede. Su tale fascia pertanto la
pressione non può essere considerata costatane ma deve variare dal valore
< dentro il pozzetto al valore B .
All’interno dell’intercapedine in questione nei due ratti circonferenziali la pressione
varia con una che può desumersi dall’equazione di Reynolds (scritta prima a
proposito della coppia rotoidale con perno non oscillante):
1 A
ª
2 AV
•
A
A
«+ ª
AV
AJ
•
ª
«
A
«
AJ
66
V
v
Poiché il perno è fermo v 0, supponendo in questo caso che, data la geometria
del problema,
J si ha:
J
•
J
0;
poiché poi
V se ne deduce che
J è lineare. Anche per quanto
riguarda i due tratti paralleli all’asse del cuscinetto, l’andamento della pressione può
essere stimato mediante l’equazione:
1 A
ª
2 AV
•
A
A
«+ ª
AV
AJ
•
A
«
AJ
66
V
v
Poiché v 0, supponendo, data la geometria del problema, che adesso si abbia
V si ottiene:
V
ª
•
V
«
0
75B
Dato che il tratto sul quale avviene la caduta di pressione Dlungo
G è piccolo
rispetto al raggio 2 , si può ammettere che nel tratto stesso
V assuma un
valore costante, pari ad esempio a quello corrispondente alla mezzeria del tratto
considerato (ovvero <K
V K e <KK
V<KK ); ossia si può ammettere che la
pressione
V vari anche in questo caso linearmente.
In definitiva sulla superficie piana rappresentata in proiezione (nella figura
rappresentante la pianta del pozzetto, comprensiva dell’intercapedine esterna) la
pressione < esercita un’azione risultante pari approssimativamente a:
ã+ æ+|
<
B
2
2
L’azione radiale risultante delle pressioni sul perno tuttavia non può essere calcolata
usando l’equazione:
V
ª
•
V
«
0
ma deve essere valutata ricordando che la pressione
superficie cilindrica:
L +<
ô ˜˜
≅-
ô˜
<
B
æ+|
cos V
2
2
<
ovvero anche:
L +< ≅
<
B
å8z
B
V
<
B
<
£8B
t.0
G
agisce su una
ô
æ+|
2 - cos V V
2
ô˜
æ+|
Γ+d
2 ªsin ªV<K +
«
2
2
2 Dsin DV<K +
B
˜˜
sin V<K «
sin V<K G.
Per quanto riguarda il carico esterno L agente sul perno si ha infine:
L
L+
L +t
æ + | 2 sin ª
t
ã+
«
42
Per il calcolo delle < occorre determinare la portata di lubrificante affluente a
ciascun pozzetto ”< . Se indichiamo rispettivamente con < e < il diametro e la
lunghezza dei fori di alimentazione, per la legge di Poiseuille si ha:
(
<
128 < 6”<
& <t
Per valutare le ”< è necessario invece determinare una relazione che leghi la portata
geometrica della coppia. Tale relazione si ottiene imponendo la conservazione della
portata attraverso il generico pozzetto:
”<
K
KK
K
KK
”B<
+ ”B<
+ ”*<
+ ”*<
K
KK
dove ”B<
, ”B<
sono le portata che sfuggono dal pozzetto in direzione assiale mentre
K
KK
”*< , ”*< sono le portata che sfuggono in direzione circonferenziale sui due lati del
K
KK
”B<
).
pozzetto (per simmetria si avrà ”B< ”B<
Ricordando:
1 A
262 AV
1 A
26 AJ
a
`
_
2v
+
Si ha che:
ô ˜˜
@
”B< ≅ - -
ô˜
(
@
ô ˜˜
- -
ô˜
(
1 <
66 æ
2
V
1 <
26 æ
B
|
@
2
ô ˜˜
2 -
ô˜
ô ˜˜
- (
ô˜
2
B
|
•
V≅
1 A
26 AJ
2
1 <
26 æ
V
1 <
66 æ
B
|
•
9<
ã+
2
2
V
ô
2
ª
«|
6 ô˜
B
˜˜
•
V
dove:
ô
2
2
ã + ô˜˜
˜˜
9<
V
K
KK
, ”*<
si ha invece, essendo v
Per quanto riguarda ”*<
@˜
K
”*<
≅- (
å8z
å8z
5
å8z
t
|ôNô˜
1
<
- å8z 262 ã
(
5
@˜
t
2
J
B
KK
:
ed analogamente per ”*<
@
0,
1 A
å8z 262 AV
5
å8z
- (
K
<
1
<
ã
262
J
1 <
126 ã
K
<
2
B
æ+|
2
K•
<
2
B
J
æ+| @
2
(
˜
K
<
1 <
126 ã
KK
”*<
2
A partire dalle equazioni:
a (
Q
Q”
Q <
”B<
Q̀
Q”K
Q *<
_
e:
<
B
nella quale:
®
'
ã+
,
æ |
Dall’equazione:
è possibile ricavare
f
<
K
Q̀
Q”*<
_
<
1+®
•
2
f
9<
x ' • +
3 m
3
B
B<
æ+|
2
KK•
<
128 < 6”<
<
& <t
K
KK
K
KK
”B<
+ ”B<
+ ”*<
+ ”*<
1 <
B • ã+
66 æ | 9< 2
1 <
B æ + | K•
<
2
126 ã
2
si arriva alla relazione:
a”<
Q
Q”
B
=
B
æ+|
,
ã
1+®
=
B
+®
K•
<
+
m•
x
KK•
<
32 < m •
&m<t
+®
mentre le equazioni:
K
KK
K
KK
”B<
+ ”B<
+ ”*<
+ ”*<
1 <
B • ã+
66 æ | 9< 2
1 <
B æ + | K•
<
2
126 ã
2
permettono di calcolare il valore della portata ”< e quindi quello della portata
complessiva:
” ” + ” + ”• + ”t ;
infine le:
aL
Q
Q̀
_
(
L+
<
L +t
128 < 6”<
& <t
t
æ + | 2 sin ª
ã+
«
42
consentono di valutare il carico esterno L .
Nella figura sottostante è riportata la capacità di carico del cuscinetto:
|L |
2 æ B
in funzione del fattore di forma:
t
m•
per diversi valori del rapporto:
=
B
Si osserva infine che il coefficiente di attrito della coppia è di norma molto piccolo,
specie alle basse velocità. Esso dipende ovviamente dalle azioni tangenziali che
nascono nelle fasce di contorno dei pozzetti dove il meato è sottile. Alle basse
velocità sulle azioni tangenziali non influisce sensibilmente la velocità di
trascinamento (secondo termina dell’equazione sottostante), ma solamente la
componente parabolica della velocità stessa (primo termine dell’equazione
sottostante):
1 A
2v
+
262 AV
Tale componente sviluppa inoltre sui bordi del pozzetto azioni tangenziali che
almeno in parte si compensano.