Lucidi 3a - Chimici Bicocca

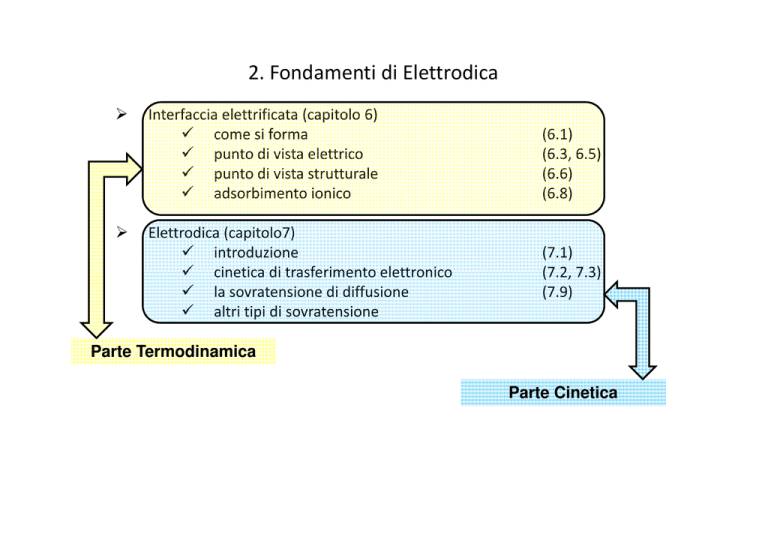
2. Fondamenti di Elettrodica
Interfaccia elettrificata (capitolo 6)
come si forma
punto di vista elettrico
punto di vista strutturale
adsorbimento ionico
Elettrodica (capitolo7)
introduzione
cinetica di trasferimento elettronico
la sovratensione di diffusione
altri tipi di sovratensione
(6.1)
(6.3, 6.5)
(6.6)
(6.8)
(7.1)
(7.2, 7.3)
(7.9)
Parte Termodinamica
Parte Cinetica
3. Fondamenti di Elettrodica (C:6 p:6.1)
L’elettrificazione di un interfaccia
Anisotropia dell’interfaccia,
l’equilibrio all’interfase = compromesso interfaccia/bulk;
Ridistribuzione delle cariche (elettrificazione)
Il doppio strato elettrico e la sua relazione con varie interfacce
caratteristiche fondamentali e importanza del doppio strato
3. Fondamenti di Elettrodica (C:6 p:6.1.2)
Anisotropia dell’interfaccia
Spostiamo la nostra attenzione dal BULK dell’elettrolita all’interfaccia Elettrodica
(interfaccia tra il conduttore IONICO e il CONDUTTORE ELETTRONICO).
In che modo la situazione è diversa?
Ogni particella (molecola o ione) nel BULK della soluzione sperimenta mediamente, in
condizioni di equilibrio, forze che sono indipendenti dalla direzione e dalla posizione
nell’elettrolita. Quindi (in condizioni di equilibrio) nel bulk della soluzione c’è omogeneità
e isotropia delle forze agenti.
Ogni elettrolita, tuttavia, ha dimensioni finite ed è a contatto con pareti (elettrodi
metallici, contenitori). COSA SUCCEDE nella zona immediatamente vicina alle pareti?
Uno ione sufficientemente
ANISOTROPICHE
vicino
alle
pareti dell’elettrodo sperimenta
forze
3. Fondamenti di Elettrodica (C:6 p:6.1.3)
Caratteristiche dell’interfase
Poiché al confine di fase esistono nuove forze (anisotropiche), le particelle si organizzano a
seconda delle forze che agiscono su di esse.
Il riarrangiamento delle particelle è un COMPROMESSO:
il conduttore elettronico (che agisce con le sue forze anisotropiche) richiede che sia gli ioni
sia le molecole di solvente adottino particolari conformazioni,
il conduttore ionico (bulk della soluzione elettrolitica) richiede che sia gli ioni sia le
molecole di solvente adottino particolari conformazioni in conseguenza alle forze
isotropiche che governano le soluzioni stesse.
Ioni e molecole adottano configurazioni di compromesso che sono caratteristiche della
regione di INTERFASE
3. Fondamenti di Elettrodica (C:6 p:6.1.5)
L’interfase elettrolitica si elettrifica
In una lamina microscopica di elettrolita in prossimità dell’elettrodo , parallela
all’elettrodo stesso, si osserverà:
1) un’orientazione dei dipoli di carica (struttura);
2) una carica netta in eccesso sulla lamina (carica).
L’elettroneutralità è rotta dalla parte dell’elettrolita e la regione elettrolitica di interfase
è carica ed elettrificata.
Quali sono le conseguenze sulla superficie del conduttore elettronico?
3. Fondamenti di Elettrodica (C:6 p:6.1.6)
Il doppio strato elettrico
La risposta dell’altra fase dipende dalla sua natura (isolante, semiconduttore, metallo…)
Consideriamo un conduttore metallico, cioè un impaccamento tridimensionale di ioni
positivi immersi in mare di elettroni mobili.
Gli ioni positivi sono poco sensibili all’interfaccia, ma gli elettroni sono molto veloci nel
rispondere ai campi elettrici.
Gli elettroni si muovono da o verso l’interfaccia (dipende dal campo). Quindi una carica
elettrica è indotta sul metallo, opposta a quella nell’elettrolita.
Supponiamo che la differenza di potenziale sia
1 V e che l’interfaccia abbia estensione di 100
nm, otteniamo un campo di 105
V/cm!
All’interfaccia esiste un gradiente di potenziale
ENORME che è l’ESSENZA dell’elettrochimica.
3. Fondamenti di Elettrodica (C:6 p:6.1.7)
Il doppio strato elettrico è una proprietà di molte interfacce
Esistenza della regione di separazione tra conduttore elettronico/conduttore ionico →
anisotropia delle forze all’interfaccia →
ridistribuzione delle particelle →
Formazione del doppio strato
Il doppio strato è comunque una caratteristica di TUTTE le interfacce che coinvolgono
almeno una fase costituita da particelle cariche o polari:
3. Fondamenti di Elettrodica (C:6 p:6.1.8)
Conoscere il doppio strato: carica e struttura
Le caratteristiche del doppio strato posso essere riassunte nei suoi due aspetti strutturali e
di carica:
carica: grandezza, estensione e distribuzione della carica in eccesso
all’interfase;
struttura: come le particelle che compongono le due fasi (elettroni, ioni,
dipoli, molecole neutre) si riorganizzano nella regione dell’interfase.
Questi due aspetti sono intimamente correlati. La carica è una caratteristica della struttura
assunta e viceversa.
Ridistribuzione
delle particelle
dell’elettrolita
caricamento
dell’interfase
elettrolitica
induzione di
carica interfase
metallica
differenza di
potenziale
all’interfaccia
Nel caso applicassimo un flusso di carica dall’esterno (sorgente) avremmo:
Flusso di
carica dalla
sorgente
caricamento
dell’interfase
metallica
induzione di
carica interfase
elettrolitica
differenza di
potenziale
all’interfaccia
Questa sequenza di eventi ci aiuta a capire come si formi il doppio strato, ma
questi processi avvengono SIMULTANEAMENTE!
3. Fondamenti di Elettrodica (C:6 p:6.1.9 & 6.1.10)
L’importanza del doppio strato
Il nostro problema si riduce a capire quali sono le proprietà dell’interfaccia. Per esempio si
può misurare delle variazione di energia libera associata con la formazione del doppio
strato. Oppure possiamo provare a modellizzare l’interfaccia attraverso la conoscenza del
tipo e della quantità di particelle, di come interagiscono (forze) e di come si comportano
nei campi di forza forza in gioco.
Dalle proprietà di bulk dobbiamo determinare la struttura del doppio strato e la
differenza di potenziale all’interfaccia.
Ubiquità del doppio strato:
particelle colloidali (interazione particella mezzo),
attrito tra metalli (lubrificazione con film di liquidi),
elettrodeposizione
corrosione
meccanismi molecolari in biologia
…
3. Fondamenti di Elettrodica (C:6 p:6.3)
La carica del doppio strato:
differenza di potenziale all’interfaccia
Misura della differenza di potenziale di un interfaccia,
interfacce idealmente polarizzabili
interfacce idealmente non polarizzabili
Il potenziale d’elettrodo
Il potenziale esterno o Volta
Il potenziale di superficie
Il potenziale interno o Galvani
Il potenziale elettrochimico e l’equilibrio
Le legge di Nernst
Semielementi galvanici
3. Fondamenti di Elettrodica (C:6 p:6.3.1)
Misura della differenza di potenziale: un’interfaccia indesiderata!
Per la misura si utilizzano strumenti (potenziometri, elettrometri, voltmetri) tutti con due
terminali (= fili metallici) che devono essere connessi al sistema in studio: un terminale è
connesso al conduttore elettronico e l’altro al conduttore ionico (= immerso
nell’elettrolita). Cosa sto realmente misurando?
Il terminale immerso nell’elettrolita ha tutte le
caratteristiche di una seconda interfaccia
elettrificata, che avrà una sua interfase
perturbata e un proprio doppio strato.
L’operazione di misura non può non coinvolgere
una seconda differenza di potenziale che
origina dalla nuova interfaccia
3. Fondamenti di Elettrodica (C:6 p:6.3.1)
La misura della differenza di potenziale
Il sistema di misura creato di fatto è un sistema elettrochimico (due conduttori elettronici
separati da un conduttore ionico) e quello che si può misurare in pratica è SOLO la
differenza di potenziale tra una serie di interfacce (almeno due) e non la singola
interfaccia conduttore elettronico/conduttore ionico (l’elettrodo).
Inoltre stiamo trascurando che differenze di potenziale si producono anche a altre
interfacce, ed esempio metallo/metallo.
3. Fondamenti di Elettrodica (C:6 p:6.3.1)
La differenza di potenziale in un sistema elettrochimico
Sistema elettrochimico: due metalli (Pt e Zn) uno immerso in una soluzione contenente
cationi del metallo di transizione (Zn2+) l’altra H2SO4. Le due soluzioni sono separate da una
membrana porosa.
L’operazione di misura può essere
schematizzata come:
V = PDM1 / S + ∑ PD
i
3. Fondamenti di Elettrodica (C:6 p:6.3.2)
La variazione della differenza di potenziale ai capi della cella
Supponiamo che il nostro strumento sia in grado di fornire una extra differenza di
potenziale (oltre a quella che sta leggendo):
V = PDM1 / S + PDS / M2 + PDM 2 / M1
Incrementando il potenziale V di un δV avremo:
δV = δPDM1 / S − δPDM2 / S + δPDM2 / M1
La variazione di potenziale si distribuisce su tutte le interfacce, ma i valori dipendono dalle
caratteristiche dell’interfaccia.
La variazione all’interfaccia metallo/metallo dipende solo dalla composizione dei due
metalli e non varia con il potenziale, se l’interfaccia M2/S è idealmente non polarizzabile
allora:
δV ≈ δPDM1 / S
Vale solo se l’interfaccia M1/S è idealmente polarizzabile.
3. Fondamenti di Elettrodica (C:6 p:6.3.3)
Polarizzabilità dell’interfaccia
Interfaccia idealmente non polarizzabile
Capacità del doppio strato
Resistenza al trasferimento di carica
Interfaccia idealmente polarizzabile
Capacità del doppio strato
Resistenza al trasferimento di carica
3. Fondamenti di Elettrodica (C:6 p:6.3.4)
La scala relativa dei potenziali d’elettrodo
Dal momento che un’interfaccia idealmente NON polarizzabile ha un valore di differenza di
potenziale INDIPENDENTE da variazioni del potenziale applicato, può essere utilizzata per
stabilire una scala RELATIVA dei potenziali con cui confrontare gli altri valori.
La convenzione è quella di porre uguale a 0 il valore di differenza di potenziale in soluzione
acquosa a un interfaccia non polarizzabile (Pt) in presenza di H+ (a=1) e H2 (f=1).
In queste condizioni il potenziale all’elettrodo è controllato dalla reazione di trasferimento
elettronico:
+
2Haq
+ 2e = H2,gas
Costruita un’interfaccia di questo genere,
qualsiasi altro potenziale può essere misurato
rispetto all’interfaccia; si ottiene una scala di
potenziali RELATIVA
3. Fondamenti di Elettrodica (C:6 p:6.3.5)
Il potenziale d’elettrodo
La misura della differenza di potenziale tra un’interfaccia elettrodica è impossibile,
qualsiasi esperimento disegni avrò sempre ALMENO due interfacce coinvolte.
Ha senso allora parlare di POTENZIALE d’ELETTRODO?
Si, possiamo immaginare di strutturare una SCALA RELATIVA dei potenziali riferiti a una
interfaccia di riferimento e MISURARE gli altri potenziali rispetto a questa.
Esiste comunque una scala ASSOLUTA, cioè riferita alla situazione dove le singole particelle
che compongono l’interfaccia sono a distanza sufficientemente grande da non interagire
(stato di riferimento). L’energia di un’interfaccia può allora essere CALCOLATA.
Come si può separare (o scomporre) il potenziale d’elettrodo?
Potenziale da ∞ in prossimità alla superficie
Potenziale attraverso la superficie
Potenziale totale
3. Fondamenti di Elettrodica (C:6 p:6.3.6/7)
La differenza di potenziale Volta
Prendiamo le due fasi (cariche), disassembiamole (cariche) portiamole nel vuoto e usiamo
una carica sonda per capire come varia il potenziale a una certa distanza dalla superficie.
Partiamo da una distanza infinita (potenziale nullo); le fasi sono cariche (potenziale
Coulombiano) e ci arrestiamo ad una distanza dalla superficie tale per cui le interazioni a
corto raggio sono ancora trascurabili.
Lavoro per portare la carica da ∞ a vicino alla
superficie (conduttore elettronico)
Lavoro per portare la carica da ∞ a vicino alla
superficie (conduttore ionico)
La differenza tra i due potenziali è chiamata POTENZIALE ESTERNO O VOLTA:
∆ Ψ = ΨM − ΨS
M S
Significato fisico: a ridosso dell’interfaccia esiste una differenza di potenziale, una parte di
questa differenza di potenziale è dovuta al fatto che le interfacce sono cariche, questa
parte è il potenziale Volta.
3. Fondamenti di Elettrodica (C:6 p:6.3.8/9)
La differenza di potenziale superficiale
Oltre alle carica l’interfaccia è caratterizzata dalla sua struttura (orientazione dei dipoli)
nell’interfase che la carica sonda deve attraversare. Immaginiamo di disassemblare le
interfacce (SCARICHE) ma con la loro struttura, portiamole all’infinito e utilizziamo ancora
la carica sonda.
Lavoro per portare la carica da ∞ a oltre la
superficie (conduttore elettronico)
Lavoro per portare la carica da ∞ a oltre la
superficie (conduttore ionico)
La differenza tra i due potenziali è chiamata POTENZIALE SUPERFICIALE:
∆ χ = χM − χS
M S
Significato fisico: a ridosso dell’interfaccia esiste una differenza di potenziale, una parte di
questa differenza di potenziale è dovuta al fatto che sulla superficie esistono dipoli che la
carica deve attraversare.
3. Fondamenti di Elettrodica (C:6 p:6.3.10)
La differenza di potenziale Galvani
Abbiamo scomposto il potenziale elettrostatico di una carica che va dall’infinito a DENTRO
la fase (sia essa conduttore elettronico sia conduttore ionico) in due termini, uno
Coulombiano e uno di superficie. I due termini hanno COMUNQUE una natura elettrica e
possono essere sommati a dare il potenziale totale all’interfaccia elettrodica:
∆ φ=M∆S Ψ +M∆S χ
M S
Questa differenza di potenziale è chiamata POTENZIALE INTERNO O GALVANI ed è di
natura elettrica.
φs = Ψs + χ s
Né χs né φs sono sperimentalmente accessibili
3. Fondamenti di Elettrodica (C:6 p:6.3.11/6.3.12)
Considerazioni sul potenziale Galvani
Il potenziale interno o Galvani sembrerebbe comprendere tutti i contributi necessari per
costruire il potenziale d’elettrodo. Tuttavia ci sono alcune considerazioni da fare sul suo
utilizzo pratico:
non può essere misurato sperimentalmente;
il suo stato di riferimento è un elettrone a riposo a distanza ∞;
comprende il potenziale elettrostatico dall’interno della fase all’infinito ma non
contiene NESSUN termine di interazione con il bulk della fase.
La separazione in due diversi contributi, uno dovuto alla carica e uno dovuto al
superamento della superficie ha aiutato a comprenderne la natura, ma non ha semplificato
il suo utilizzo, per esempio nel predire il verso di una reazione elettrochimica.
3. Fondamenti di Elettrodica (C:6 p:6.3.10)
Il contributo chimico
Cosa succede se portiamo la carica di sonda dall’infinito al bulk del sistema di un sistema
SENZA carica (senza interazioni elettriche)? Il lavoro corrisponde al POTENZIALE CHIMICO:
Lavoro per portare la carica da ∞ al bulk
(conduttore ionico)
∆φ = ∆Ψ + ∆χ = 0
Nel bulk della fase la particella
sperimenterà:
interazioni con gli ioni
interazioni con il solvente
interazioni con ioni e solvente
riorganizzati
Anche se di natura elettrostatica
queste forze possono essere
definite CHIMICHE perché il lavoro
per portare la carica all’infinito è - il
potenziale chimico
3. Fondamenti di Elettrodica (C:6 p:6.3.10)
Il potenziale elettrochimico: il lavoro TOTALE dall’infinito al bulk
Per calcolare il lavoro totale dall’infinito al bulk della fase tenendo conto di TUTTE le
interazioni, devo allora aggiungere un contributo CHIMICO (bulk della fase) ai termni che
derivano dalla presenza della superficie:
lavoro totale = lavoro chimico + lavoro elettrico
µ = µ + zFφ
che è la definizione di POTENZIALE ELETTROCHIMICO per una determinata specie.
Il potenziale elettrochimico contiene tutte le informazioni necessarie riguardo il lavoro
necessario per portare una mole di particelle i-esime cariche (se z=0 µ=µ) in una fase α
elettrificata avente potenziale galvani φ.
µiα = µiα + zFφα
Dalla legge di Fick avevamo visto che il gradiente di potenziale chimico è la driving force
per la diffusione, mentre il gradiente di potenziale elettrostatico era alla base dei moti di
deriva che sottendono alla conduzione. In questa ottica il gradiente di potenziale
elettrochimico può essere visto come LA DRIVING FORCE TOTALE per il movimento delle
cariche.
3. Fondamenti di Elettrodica (C:6 p:6.3.10.3)
L’equilibrio termodinamico tra due fasi
La driving force locale responsabile del moto delle cariche (o del flusso della specie jesima) è il gradiente di potenziale elettrochimico dµj/dx. Se siamo in presenza di un flusso
netto NON siamo in equilibrio, al contrario per avere equilibrio termodinamico deve valere
la condizione:
dµ j
=0
dx
se inoltre considerassimo un confine di fase (dx è sufficiente per attraversare l’interfaccia)
conduttore elettronico (M) conduttore ionico (S) integrando la precedente:
(µ j )M = (µ j )S
∆µ j = 0
che è il criterio per stabilire se un’interfaccia elettrodica è in equilibrio o no.
Se una reazione coinvolge specie cariche all’interfaccia allora la relazione di equilibrio alla
base della termodinamica chimica:
∑ νiµi = 0
i
diviene:
∑ νiµi = 0
i
3. Fondamenti di Elettrodica (C:6 p:6.3.15)
Il potenziale d’elettrodo
Dobbiamo fare un passo fondamentale: capire come le quantità che abbiamo costruito
“smembrando” le interfacce sono in relazione con le quantità che misuriamo.
Consideriamo il sistema elettrochimico più semplice possibile: un conduttore ionico
interposto tra due conduttori elettronici.
M1│S│M2
CuL
CuR
CuL│M1│S│M2│CuR
In fase di misura introduco delle interfacce addizionali(termini di contatto): la catena si definisce
“REGOLARMENTE APERTA”.
µeCuL − µeCuR
V=−
Gli elettroni sono le particelle che fisicamente si muovono
F
nel circuito esterno (= da cui dipende la misura): usiamole
per descrivere l’equilibrio (1 mole di elettroni sonda = -1F)
V=−
L
R
µCu
− FφCuL − µCu
− FφCuR
e
e
F
X
µeCu X = µCu
− FφCu X
e
L
R
µ Cu
− µCu
e
e
=−
+ φCuL − φCuR
F
(
)
Il primo termine è nullo (siamo in equilibrio e il metallo è lo stesso), il secondo NO perché
le interfacce SONO diverse: CuL│M1│S da una parte e S│M2│CuR dall’altra.
3. Fondamenti di Elettrodica (C:6 p:6.3.15)
Che cosa è VERAMENTE il potenziale d’elettrodo?
Quello che rimane è dunque:
V = φCuL − φCuR ≅
(
M1 S
) (
∆φ −
M2 S
∆φ
)
Il potenziale misurato ai capi di una catena regolarmente aperta è la differenza di potenziale
GALVANI delle due interfacce elettrodiche (conduttore elettronico/conduttore metallico) a
meno di (ALMENO un) termine di contatto.
3. Fondamenti di Elettrodica (C:7 p:7.2.7)
Le legge di Nernst
Consideriamo la generica reazione di scambio
elettronico ad un’interfaccia metallo soluzione:
Mz + + ze = M
Usiamo la relazione di equilibrio termodinamica:
∑ νiµi = −µM
∑ νiµi = 0
i
(
) (
)
− zµe + µM = − µMz+ − zFφS + − µ e + zFφM + µM = 0
z+
i
∑ νiµi = −µM
z+
i
(
)
(
)
− µ e + µM − zF φS − φM = ∆GMz+ / M − zF S ∆Mφ = 0
∆G
∆
GMz+ / M
=S ∆Mφ = −M ∆S φ
zF
Questa quantità si riferisce ad UN’INTERFACCIA quindi è una quantità
NON misurabile (∆
∆G è riferito ad una SEMIREAZIONE).
Se l’interfaccia è accoppiata con un’altra in cui è presente
una specie in grado di bilanciare gli elettroni in gioco
A z − = A + ze
∑ νiµi = −µA
i
z−
(
)
(
)
+ µA + zµe = − µ A z− − zFφS + µ A + µ e − zFφM = 0
∆GA z− / A
zF
= −S ∆M2 φ =M2 ∆Sφ
3. Fondamenti di Elettrodica (C:7 p:7.2.7)
Le legge di Nernst
La reazione globale di cella è:
Mz + + ze = M
A z − = A + ze
Mz + + A z − = M + A
∆GMz+ / M
zF
+
∆GA z− / A
zF
=
∆Greaz
= − M ∆Sφ +M2 ∆SφM = − V
zF
(
)
Che costituisce la quantità che misuriamo ai capi della cella.
Questa quantità si riferisce alla cella all’EQUILIBRIO (= condizioni reversibili) in cui:
∆Greaz = w e
∆Greaz = − zFV
Per cui il lavoro massimo che posso fare elettricamente è la carica x il potenziale.
In condizioni di equilibrio (e solo in condizioni di equilibrio) il corrispondente valore di V è
chiamato POTENZIALE REVERSIBILE (E) o FORZA ELETTROMOTRICE della CELLA (fem)
∆Greaz = − zFV
3. Fondamenti di Elettrodica
Dipendenza del potenziale reversibile dalla concentrazione
La reazione globale di cella è:
Mz + + A z − = M + A
0
∆Greaz
∆Greaz
RT
RT
aMa A
RT
1
0
E=−
=−
−
ln K eq = E −
ln Mz+ A z− = E01 −
ln Mz+ A z−
zF a a
zF
zF
zF
zF a a
Uguagliando le concentrazioni all’attività:
E = E01 −
1
RT
ln Mz+ A z−
zF a a
Convenzioni:
Le serie elettrochimiche sono scritte nel senso della riduzione.
Le serie elettrochimiche (E0) sono riportate VERSO l’elettrodo reversibile ad idrogeno
(SHE), il cui valore è indipendente dal pH per costruzione.
Nello scrivere una catena galvanica, si mette a sinistra la semireazione che tende a
decorrerre in senso ossidativo (anodico) a destra quella riduttiva (catodica) e la
fem = Edestra – E sinistra
Esempio:
Cu2+/Cu ha E0=-0.34 V a 25°C
Vuol dire:
3. Fondamenti di Elettrodica
Semielementi galvanici
1a Specie: Sono quelli costituita da un elemento o composto in
presenza dei corrispondenti cationi:
RT
0
E
E
=
+
ln a Zn2+
2+
2+
Zn /Zn
Zn / Zn
Zn(aq)2+ + 2e ⇔ Zn
2F
1/ 2
o anioni:
p
R
T
Cl
ECl / Cl- = E0Cl / Cl- +
ln 2
½ Cl2(g) + e ⇔ Cl-(aq)
2
2
F aClI potenziali sono definiti dalle rispettive equazioni di Nernst
2a Specie: Sono costituiti da un metallo ricoperto da un suo sale
immerso in una soluzione contenente anioni del sale:
AgCl(s) + e ⇔ Ag(s) + Cl(aq)-
E AgCl/Ag = E0AgCl/Ag +
RT
1
ln
F aCl-
Semielementi galvanici di ossidoriduzione: Sono costituiti da un metallo inerte
immerso in una soluzione contenente uno stesso ione
in due differenti stati di ossidazione:
Ce(aq)4+ + e ⇔ Ce(aq)3+
ECe4+ /Ce3+ = E
0
Ce 4+ / Ce3+
RT aCe 4+
+
ln
F aCe3+
3. Fondamenti di Elettrodica
Considerazioni su SHE
La scala relativa dei potenziali d’elettrodo si basa sull’interfaccia SHE, ma
non è spesso conveniente girare per il laboreatorio con una bombola di
H2 (puro…) per misurare i potenziali elettrochimici.
Nella pratica di laboratorio si utilizzano ALMENO altri due sistemi, molto
più semplici da implementare in cella (…).
Ag/AgCl reference electrode
AgCl(s) + e ⇔ Ag(s) + Cl(aq)-
E AgCl/Ag = E0AgCl/Ag −
E0AgCl/Ag ( V) = EH0
+
2 /H
RT
ln aClF
( V ) + 0.199( V )
Calomelano reference electrode
1/2 Hg2Cl2(s) + e ⇔ Hg(l) + Cl(aq)0
EHg2Cl2 /Hg = EHg
−
2 Cl2 /Hg
E0Cal ( V) = EH0
2
/ H+
RT
ln aClF
( V ) + 0.244( V )
3. Fondamenti di Elettrodica (C:6 p:6.3.14)
La funzione lavoro dell’elettrone.
Consideriamo il processo di estrazione di un elettrone da un metallo:
L’elettrone è estratto da un punto interno al
metallo dove esistono differenti tipologie di
interazioni chimiche ed elettrostatiche.
Quindi l’elettrone raggiunge la superficie e
deve attraversare la barriera dipolare.
Analogamente al caso generale, abbiamo un termine chimico (µeM) e un potenziale superficiale
(contributo zFχeM), non siamo interessati al potenziale esterno. La nuova bgrandezza che
abbiamo costruito è la FUNZIONE LAVORO DELL’ELETTRONE IN UN METALLO M:
ΦMe = −µMe − zFχMe
Questo lavoro è MISURABILE (anche se non scomponibile nei suoi termini fondamentali) e
costituisce una proprietà (impronta digitale) dei metalli