Carlo Dariol
FISICA DELLE PARTICELLE
ELEMENTARI
appunti tratti dalle lezioni del prof. Giovanni Organtini
Dipartimento di Fisica – Università “La Sapienza”
Descrizione generale
Nel corso delle lezioni verrà introdotto il Modello Standard attraverso l’analisi dei dati
sperimentali accumulati nel corso degli anni. L’attuale modello della Fisica delle Particelle
è costruito a partire da questi attraverso richiami di argomenti dei moduli di Meccanica
Quantistica e Relatività. In diverse occasioni i temi sono affrontati in modo formale,
anche se poco rigoroso, allo scopo di dare un’idea relativamente precisa di come si
costruiscono le moderne teorie della Fisica delle Particelle, senza entrare troppo nei
dettagli tecnici.
Obiettivo del corso è quello di fornire una panoramica delle attuali conoscenze in
questo campo che permetta al lettore di farsi un’idea del processo che ha portato alla
formulazione del Modello Standard.
Il modulo è composto da 7 lezioni:
LEZIONE 1 - INTRODUZIONE ALLA FISICA DELLE PARTICELLE
LEZIONE 2 - LO STUDIO SPERIMENTALE DELLE PARTICELLE
LEZIONE 3 - I QUARK
LEZIONE 4 - LE INTERAZIONI FONDAMENTALI
LEZIONE 5 - IL MODELLO STANDARD
LEZIONE 6 - IL BOSONE DI HIGGS
LEZIONE 7 - I RIVELATORI DI PARTICELLE
Sommario
Cap. 1
I raggi cosmici
p. 3
1. La scoperta dei raggi cosmici; la perdita di energia per ionizzazione;
identificare le particelle; decadimenti beta; ipotesi del neutrino.
2. Chi li ha ordinati? Scoperta del positrone, dei pioni e dei muoni.
3. Nuove grandezze fisiche. Conservazione del numero leptonico e barionico.
4. Ma quante sono? Scoperta della K e della Λ.
1
5. Facciamo ordine: classificazione delle particelle.
6. Test ed esercizi
Cap. 2
Identificare le particelle (imitare la natura)
1. Produzione artificiale di particelle.
2. Acceleratori
3. Sezione d’urto
4. Vita media.
5. Massa invariante e risonanze.
6. Particelle “strane”.
p. 32
Ottetto dei mesoni
Ottetto dei barioni a spin ½
Barioni a spin 3/2
7. Test ed esercizi
Cap. 3
Modello a quark
1. Composizione dei multipletti
2. I barioni a spin ½
3. I mesoni
4. I barioni a spin 3/2
5. Teoria del colore.
6. I nuovi quark
7. Test e quesiti
p. 52
Cap. 4
Le interazioni fondamentali
p. 73
1. Teoria delle interazioni fondamentali.
2. Diagrammi di Feynman.
3. Fotoni virtuali
4. L’equazione di Dirac.
5. I positroni
6. Riassunto
7. Elettrodinamica Quantistica. Effetto Compton. Effetto fotoelettrico.
8. Fabbriche di particelle. Annichilazione.
9. QED e fotoni liberi
10. Approccio informale
11. Test ed esercizi
Cap. 5
Il modello standard
1. Le interazioni forti
2. Il modello standard
3. La scoperta del TOP
4. L’interazione debole. I bosoni W e Z
5. Violazione della parità
6. Test ed esercizi
2
p. 108
Cap. 6
Il bosone di Higgs
1. Il campo di Higgs
2. La massa dei bosoni
3. Un po’ meno formale
4. La scoperta del bosone di Higgs
5. Test ed esercizi
p. 135
Cap. 7
Rivelatori moderni per la fisica delle particelle
1. Rivelatori in generale
2. Rivelatori interni
3. Rivelatori esterni
4. Test ed esercizi
p. 157
In tutto il corso si useranno le seguenti
CONVENZIONI
c 1
questo comporta che le velocità saranno misurate in frazioni della velocità della luce e
che tempi e lunghezze hanno l’unità di misura del reciproco di una energia e che massa e
quantità di moto hanno l’unità di misura di una energia
1
T L E
M p E
3
Cap. 1
I raggi cosmici
1.1. La scoperta dei raggi cosmici; la perdita di energia per
ionizzazione; decadimenti beta; ipotesi del neutrino.
La scoperta dei raggi cosmici (1912) segna la nascita della fisica delle particelle. Qual era
la situazione prima della scoperta dei raggi cosmici? Si sapeva dell’esistenza di poche
particelle:
- fotoni;
- protoni;
- elettroni, dapprima noti come raggi beta e poi identificati come particelle
costituenti la materia attorno ai nuclei atomici, all’epoca pensati come costituiti dai
soli (i neutroni non erano noti).
- particelle alfa, nuclei di elio.
Questo era tutto ciò che era noto.
Le particelle in questione interagiscono in modi diversi. Erano note le
- interazioni gravitazionali (la gravità è la più ovvia e naturale delle forze, e
tuttavia, per la fisica moderna, è la più sconosciuta, in quanto la più debole delle
interazioni).
- interazioni elettromagnetiche (interazioni tra cariche e tra correnti)
Non erano ancora note le
- interazioni forti, che rendono stabili i nuclei e impediscono ai protoni del nucleo
di respingersi e di far esplodere il nucleo; l’interazione forte è interazione più
intensa di quelle elettromagnetica, appunto molto più forte.
- interazioni deboli, responsabili dei decadimenti radioattivi dei nuclei atomici (o
meglio: si conoscevano già anche se la loro interpretazione non era ancora stata
acquisita).
Una storia esemplare
Il 1912 è la data di nascita della fisica delle particelle: in quell’anno si fanno delle
scoperte fondamentali; in particolare vengono scoperti i raggi cosmici. La scoperta dei
raggi cosmici avviene nel tentativo di spiegare la scarica degli elettroscopi, un
fenomeno che non sembrava così rilevante da attrarre l’attenzione dei fisici (un po’ è
l’analogo di quello che successe con la meccanica quantistica, nata dallo studio di un
argomento considerato non così rilevante o non così interessante quale lo spettro di
radiazione del corpo nero)
In che cosa consiste il problema dei raggi cosmici?
4
Cerchiamo di capirlo caricando dapprima un elettroscopio: strofiniamo una bacchetta e
con la bacchetta elettrizzata tocchiamo lo strumento. Lo strumento dovrebbe rimanere
carico finché non tocchiamo di nuovo lo strumento, scaricandolo. Invece, anche senza
toccarlo, lo strumento piano piano ritorna a indicare lo zero (posizione di equilibrio).
Qual è il problema?
Se c’è una carica elettrica sull’elettroscopio, questa carica dev’essere rimossa per
poterlo scaricare ed è necessario interagire con una interazione di tipo elettrico che
rimuova le cariche elettriche; questa carica può essere rimossa da qualche particella
elettricamente carica che passa nelle vicinanze dell’elettroscopio e che produce
l’interazione necessaria per poter rimuovere la carica dell’elettroscopio.
Capire la natura di queste
particelle era per certi fisici
oggetto di interesse (anche se
non per tutti era una cosa
particolarmente interessante da
studiare). All’epoca si riteneva
che i responsabili della scarica
dell’elettroscopio fossero i
nuclei radioattivi che si
sapevano emettere particelle
elettricamente cariche: elettroni,
particelle alfa, protoni…
Uno degli scienziati che più fornì informazioni rilevanti allo scopo di scoprire la natura
di queste particelle fu Domenico Pacini (1878-1934) il quale cominciò a fare delle
misure inizialmente a terra per cercare di individuare la natura di questi elementi
radioattivi, dopodiché…
5
…dopo alcuni infruttuosi tentativi di individuare la natura di queste particelle cominciò a
fare delle misurazioni in mare grazie al fatto che gli fu messo a disposizione dalla Marina
Militare il cacciatorpedieniere “Fulmine” (foto nella pagina precedente in basso a destra)
sul quale si mise a lavorare al largo di Livorno.
Cosa ci si aspettava dalla teoria? Se la scarica degli elettroscopi era effettivamente
dovuta alla presenza di nuclei radioattivi che emettono particelle cariche, poiché questi
nuclei radioattivi provengono dalla crosta terrestre, vicino alla costa la ionizzazione,
ovvero la velocità con cui si scaricano gli elettroscopi, dev’essere abbastanza alta; ma
allontanandosi dalla costa questa ionizzazione dovrebbe diminuire.
Quando si fece l’esperimento si scoprì qualcosa di sorprendente: vicino alla costa
si osservava sì una radiazione abbastanza grande, simile a quella che si osservava
nell’entroterra; tuttavia allontanandosi dalla costa non si osservavano significative
differenze rispetto a quello che si osservava sulla terraferma: non era possibile dunque
che l’agente ionizzante provenisse dalla crosta terrestre… a meno che non provenisse da
qualcosa che poteva essere presente (cioè sciolto) anche nel mare. L’idea di Pacini fu di
fare delle misure anche sotto il livello del mare per vedere quello che succedeva alle
divere profondità; secondo la teoria, alla superficie si sarebbe dovuto osservare una
intensità di ionizzazione del tutto simile a quella che si osservava sulla terra; scendendo
in profondità e avvicinandosi sempre più alla crosta del fondo del mare, dove gli
elementi radioattivi sono presenti in abbondanza, la ionizzazione avrebbe dovuto
aumentare; invece quello che si osservò fu il contrario: sulla superficie si osservava la
stessa ionizzazione che si osservava sulla terra, mentre scendendo in profondità si
osservava una sensibile diminuzione della ionizzazione. L’esperimento fu ripetuto nel
lago di Bracciano per evitare eventuali errori sistematici dovuti alla salinità dell’acqua… e
fornirono lo stesso risultato.
Col che Pacini pubblicò (sempre nel 1912) sulla rivista “il NUOVO CIMENTO”
un articolo che descriveva gli esperimenti fatti e i risultati concludendo con la frase
sottolineata in rosso:
6
Pacini cioè suppose che la “causa ionizzante” e che produceva la scarica degli
elettroscopi non provenisse dal terreno ma fosse presente nell’atmosfera. Purtroppo per
lui la radiazione non veniva dall’atmosfera ed egli non poteva accorgersene perché non
aveva la tecnologia necessaria per fare le misure.
Chi invece disponeva della tecnologia necessaria era
l’austriaco Viktor Hess (1883-1964), che aveva la
possibilità di fare le misure su un pallone aerostatico.
Quale fu la tipologia di misure che fece Hess,
probabilmente dopo aver letto l’articolo di Pacini? A terra
si doveva osservare una certa rapidità di scarica degli
elettroscopi, cioè si doveva osservare una ionizzazione del
tutto comparabile con quella descritta dagli studi di Pacini.
E salendo? Salendo di quota Hess osservò che l’intensità
di ionizzazione cresceva, aumentava sempre di più… e
cresceva in maniera esponenziale.
Nel diagramma si vede come la scarica degli elettroscopi cresce con l’altitudine in
maniera esponenziale; il grafico riporta le misure fatte da Hess e quelle ripetute negli anni
successivi da altri scienziati che confermarono quello che si osservava facendo quel
genere di misure; la conclusione era inequivocabile: la radiazione che provocava la
scarica degli elettroscopi non era (non è) presente nell’atmosfera ma deve venire da fuori
dell’atmosfera e man mano che ci si avvicina alla terra questa radiazione viene assorbita
dall’atmosfera stessa e diminuisce di intensità; è quindi di natura extraterrestre. Alcuni
anni dopo Robert Millikan (22 marzo 1868 – 19 dicembre 1943) la chiamò “raggi
cosmici”.
7
I raggi cosmici sono dunque i responsabili della scarica degli elettroscopi e oggi
sappiamo che sono costituiti per più del 90% da protoni che arrivano dallo spazio, dalle
regioni più profonde del cosmo, e urtano contro gli atomi dell’atmosfera provocando
una cascata di reazioni che alla fin fine sono quelle responsabili della scarica degli
elettroscopi.
Per quanto ne sappiamo oggi i raggi cosmici hanno uno spettro di energia
estremamente ampio: andiamo da pochi GeV fino a energie elevatissime 10 11 GeV,
ben sette ordini di grandezza più alte di quelle che si riescono a produrre negli
acceleratori di particelle.
Naturalmente la frequenza con la quale questi raggi cosmici arrivano sulla terra dipende
dall’energia: sono più abbondanti quelli a bassa energia: nella parte più bassa dello
spettro si osservano alcune decine di protoni per cm2 al secondo; ma possiamo arrivare
anche ad energie di 10 11 GeV con una frequenza molto più bassa ma tutto sommato
considerevole, circa 5 eventi l’anno per metro quadro.
8
Identificare le particelle
Scoperta la natura extraterrestre di questi raggi cosmici, quello che dobbiamo fare e di
individuarne la natura: si pensava che fossero costituiti da protoni, elettroni e particelle
alfa, le particelle allora conosciute; anche se non venivano dalla Terra e venivano dallo
spazio le particelle dovevano esser quelle e si cercò di identificarle, utilizzando strumenti
come la camera a nebbia, uno strumento di rivelazione di particelle elementari ideato
da Charles Thomson Rees Wilson nel 1899 e successivamente perfezionata nel 1912:
nella camera si trova del vapore molto vicino al punto di condensazione: quando una
particella carica la attraversa crea una traccia ionizzata la quale attrae per effetto
elettrostatico le particelle di vapore che si trovano vicino ad essa; questa concentrazione
di particelle provoca attorno alla traccia ionizzata la formazione di una piccola nube che
opportunamente illuminata appare come una nuvoletta bianca che si dissipa in pochi
secondi.
In questo modo è possibile osservare la traccia lasciata dai tracci cosmici, fotografarne le
tracce, misurarne la curvatura dovuta alla presenza di un campo magnetico cercando di
identificare in questo modo le particelle.
Come si fa a identificare le particelle osservandone le tracce?
Quello che possiamo misurare è il GRADO DI IONIZZAZIONE che le particelle
riescono a produrre nell’attraversare la camera a nebbia; e, come abbiamo anticipato
poco sopra, possiamo anche misurare la loro QUANTITÀ DI MOTO sfruttando la
misura della curvatura delle tracce che esse lasciano nella camera a nebbia.
9
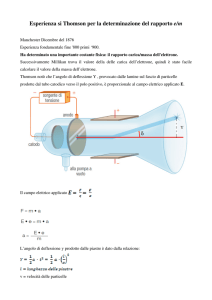
Perdita di energia
Per cercare di capire qual è il grado di ionizzazione che le particelle sono capaci di dare al
vapore dobbiamo studiare la perdita di energia della particella carica che attraversa il
materiale. Per farlo utilizziamo uno schema come quello della figura sotto.
Abbiamo una particella di carica q che si muove con velocità v nella direzione
rappresentata dall’asse del cilindro. La superficie del cilindro è quella sulla quale si trova
l’elettrone che subisce il campo elettrico prodotto dalla carica che si sta avvicinando
Dal momento in cui la carica si avvicina all’elettrone con parametro di impatto b
(ovvero la velocità v della carica ha una distanza b dall’elettrone), e poi se ne riallontana
passando dall’altra parte del cilindro, producendo un campo elettrico radiale rispetto alla
sua posizione, si osserva che la componente del campo elettrico lungo la direzione
parallela alla velocità della particella ionizzante cambia semplicemente di segno
(confronta le figure di sinistra e di destra), per cui possiamo limitarci a studiare la solo
componente del campo che dal punto di vista pratico agisce, ovvero la componente
perpendicolare alla velocità.
Dovendo studiare qual è l’effetto della componente perpendicolare al campo
elettrico sulle particelle del mezzo, possiamo calcolare la variazione della quantità di
moto delle particelle (gli elettroni) del mezzo attraversato dalla particella quando
subiscono gli effetti del campo elettrico prodotto dalla particella in movimento
e
E dx
v
dove si è usata la relazione vdt dx . Quanto vale l’integrale? Applichiamo il teorema di
p Fdt e E dt
Gauss sulla superficie indicata sopra:
2b E dx
q
0
da cui
E
dx
Sostituiamo sopra e ricaviamo:
p
e
eq 1
E
dx
v
2 0 vb
10
q
0 2b
p 2
e2q 2
1
da cui K
2 2
2 2 è la perdita di energia di una particella che ha
2m 8m 0 v b
incontrato un elettrone lungo il suo cammino e al quale ha ceduto una certa quantità di
moto.
Quindi la perdita di energia di una particella che attraversa un materiale con dn elettroni
è l’energia cinetica guadagnata dall’elettrone per il numero totale di elettroni dato dalla
densità volumetrica di elettroni Ne per il volume dV
p 2
e 2 q 2 N e dV
dE
dn
2m
8m 2 02 v 2b 2
Il dV sarebbe qui zero, ma la particella interagisce con tutte le particelle presenti in un
guscio cilindrico infinitesimo con parametro di impatto b.
dV 2b db dx
e 2 q 2 N e 2b db dx
dE
8m 2 02
v 2b 2
Dividendo a destra e sinistra per dx trovo la PERDITA DI ENERGIA SPECIFICA,
ovvero la perdita di energia per unità di percorso, ovvero la quantità di energia persa
dalla particella che attraversa un materiale di spessore dx con Ne elettroni per unità di
volume
dE
e 2 q 2 N e db
dx 4m 02 v 2 b
La particella interagirà con tutti gli atomi, con tutti gli elettroni del materiale, per cui
dobbiamo integrare sui possibili parametri d’impatto.
Se integriamo tra un valore minimo e un valore massimo del parametro d’impatto
dE
e2q 2 N e
dx 4m 02 v 2
bM
bm
db
b
l’integrale è facile
dE
e2q 2 Ne
bM
log
dx 4m02 v 2
bm
Perché vi è questa necessità di integrare tra un parametro minimo e un parametro
massimo di impatto? In linea di principio la particella q potrebbe interagire con una
11
particella a distanza nulla da sé stessa o a distanza infinita, e quindi dovrei integrare tra 0
e +infinito, ma così otterrei un integrale divergente. Il fatto che esista un minimo e un
massimo per il parametro di impatto è giustificato da alcune considerazioni cinematiche;
in particolare per quanto riguarda il valore minimo del parametro di impatto questo
deriva dal fatto che la massima energia cinetica trasferibile nell’urto tra la particella di
carica q e l’elettrone si ha quando la massa della particella incidente è molto più alta di
quella dell’elettrone. Se si studia l’urto tra due oggetti, uno di massa me e uno di massa M
molto più grande si osserva che la velocità massima che può acquisire l’elettrone
urtato da una particella di massa molto più alta che si muove con velocità v è 2v:
questo lo si può capire mettendosi nel sistema di riferimento dell’elettrone che vede
arrivare la particella di massa molto grande M con velocità v prima dell’urto e la vede
dopo l’urto allontanarsi alla stessa velocità.
Ricordiamo che la formula che dà la velocità di una particella in funzione delle due
masse e delle due velocità prima dell’urto (ricavata applicando conservazione di quantità
di moto e la conservazione dell’energia cinetica) è:
v1 '
m1 M 2 v1 2M 2 v2
m1 M 2
Applicata al nostro caso (avendo supposto che l’elettrone – particella 1 – fosse
inizialmente fermo), essa dà come velocità finale dell’elettrone
ve
2M
v 2v
me M
Esistendo un massimo della velocità dopo l’urto esiste anche un massimo dell’energia
trasferibile alla particella:
p 2
e2q 2
1
1
K
m2v 2
2 2
2 2
2m 8m 0 v b
2
il fattore gamma è presente per considerare possibili effetti relativistici quando sono in
gioco velocità relativistiche ma nel nostro caso non è molto rilevante
Questa disequazione è fatta di costanti e di termini che dipendono dal parametro
d’impatto e dalla velocità della particella, è cioè della forma:
A
Bv 4 che si traduce in una relazione sul parametro d’impatto efficace:
2
b
il parametro di impatto per il quale si ha il massimo trasferimento di energia
cinetica è quello per cui b
A 1
.
B v2
Il parametro di impatto deve essere superiore a una certa soglia, ecco perché c’è
un minimo tra i valori possibili del parametro d’impatto che dobbiamo considerare per
valutare la perdita specifica di energia.
Esiste poi un parametro d’impatto massimo semplicemente perché per valori
troppo grandi del parametro d’impatto il campo elettrico diventa così piccolo che non
12
produce più alcun effetto significativo. D’altra parte il campo E è schermato dalla
presenza di tutte le altre cariche. Ci deve dunque essere un parametro d’impatto massimo
che sostanzialmente dipende dal fatto che l’energia di ionizzazione di un elettrone
dall’atomo è limitata all’ordine di qualche eV.
dE
e2q 2 Ne
b
log M al valore di bm quello della
Sostituendo quindi nella
2
2
dx 4m0 v
bm
formula appena trovata e a bM una costante che dipende dall’energia di ionizzazione
dell’atomo la PERDITA SPECIFICA DI ENERGIA diventa
dE
e2q 2 Ne
log Cv 2
2
2
dx 4m0 v
La perdita specifica (per unità di percorso) di energia dipende dunque dal quadrato della
carica della particella, dalla densità specifica di elettroni, dal reciproco della velocità della
particella al quadrato e dal logaritmo del quadrato della velocità della particella.
La massima capacità di ionizzazione si ha quindi per velocità “piccole”:
una particella che penetra in un materiale perde velocità e la sua capacità di ionizzazione
aumenta.
La ionizzazione
Cerchiamo di studiare con un certo dettaglio l’espressione che abbiamo trovato. In realtà
dovremmo studiare un’espressione leggermente diversa da questa, quella che tiene conto
degli effetti quantistici e relativistici che bisogna considerare quando l’urto avviene alle
scale considerate. Tuttavia anche se si usa la formula (quantistica e relativistica) di Bethe
e Bloch, i risultati sono del tutto confrontabili con la formula che abbiamo derivato
sopra in maniera puramente classica. E quindi possiamo limitarci ad analizzare quella.
Il seguente grafico è ricavato con la formula di Bethe e Bloch, che tiene conto di
tali effetti, e dà la perdita specifica di energia in funzione del fattore beta-gamma della
particella, che di fatto è la sua velocità.
13
La perdita di energia specifica viene data in questi grafici in MeV g–1cm2 ossia in
MeV
g cm 2 :
2
Il denominatore g cm è (strano a dirsi) una UNITÀ DI MISURA DI DISTANZA
Essa è il risultato del un prodotto di una distanza per una densità:
d [ g cm 2 ] d [cm][ g cm 3 ]
essa non è altro che la distanza percorsa dalla particella nel materiale moltiplicata per la
densità del materiale attraversato. Essendo la densità dell’acqua pari a 1g/cm3, l’unità di
misura 1g/cm2 corrisponde sostanzialmente al percorso che farebbe la particella in
acqua:
d [ g cm 2 ]
d [cm ]
[ g cm 3 ]
è dunque una distanza normalizzata alla distanza che percorrerebbe una particella di quel
tipo nell’acqua.
Veniamo adesso ad analizzare la formula derivata per via puramente classica:
Per velocità molto basse (figura a sinistra) la ionizzazione cresce moltissimo (leggere il
grafico da destra a sinistra). Il termine logaritmico non conta tanto.
Aumentando la velocità l’energia raggiunge un minimo (per valori di βγ vicini a 3)
e poi comincia a salire con la velocità: ciò è dovuto al termine logaritmico che comincia a
dominare per velocità grandi (figura a destra): la velocità cresce ma cresce in maniera
debole, appunto come un logaritmo.
L’altra cosa interessante da notare è che questa espressione dipende dal numero di
elettroni, anzi dalla densità di elettroni Ne, ossia il numero di elettroni diviso per il
14
volume; e il volume lo possiamo pensare come la massa divisa per la densità del mezzo.
Il numero di elettroni e la massa dipendono dal numero di atomi NA.
Semplificando, si osserva che la densità di elettroni dipende dal rapporto Z/A. Il
fatto che l’idrogeno abbia una perdita specifica di energia molto più alta rispetto agli altri
elementi è dovuto al fatto per l’idrogeno il rapporto Z/A = 1 mentre per tutti gli altri
elementi chimici il rapporto Z/A è circa uguale a ½ (giù di lì) in quanto il numero di
nucleoni è il doppio o poco più del numero di protoni (o elettroni).
Per le diverse specie atomiche segnate nel grafico il rapporto Z/A tende a calare.
Per il carbonio è 0.5, per l’alluminio è 0.48, per il ferro è 0.46…
Dunque una particella perde, come minimo, 1-2 MeV per cm di acqua
attraversato. L’atmosfera terrestre “pesa” 760 mm di Hg, la cui densità è 15 volte quella
dell’acqua e questo significa che per attraversare tutta l’atmosfera una particella deve
avere l’energia sufficiente qualcosa dell’ordine dei 10-11 metri di acqua. Deve quindi
trattarsi di particelle molto ma molto più energetiche di quelle che si riusciva a produrre in
laboratorio da nuclei radioattivi utilizzando gli strumenti dell’epoca che erano in grado di
attraversare sì e no qualche decina di cm di acqua prima di essere del tutto assorbiti.
Quindi si cominciò a cercare nelle foto su eventi nelle camere a nebbia tracce di
energie molto alte.
Quesito: indica quale delle seguenti frasi descrive meglio quel che succede a un protone di
energia molto alta che penetra in un materiale
a. La perdita di energia è costante lungo tutto il percorso (a parte le fluttuazioni statistiche)
15
b. Il protone perde gran parte della sua energia nella fase iniziale di penetrazione, dopo di che ne perde
sempre meno, fino a quando, giunto a una certa velocità, comincia a perdere un po’ di più, ma
comunque meno che all’inizio.
c. Il protone rilascia quasi tutta la sua energia cinetica quando sta per fermarsi, a fine corsa.
[La risposta corretta è la c. Le curve del grafico
vanno lette da destra a sinistra.]
Le prime evidenze
Appena ci si rese conto che le energie dei raggi cosmici erano molto alte si cominciò a
cercare tracce di particelle molto energetiche nelle fotografie fatte su eventi che si
svolgevano in camera a nebbia.
Una delle prime evidenze sperimentali è visibile nella seguente fotografia:
fu fatta dal fisico russo Piotr Kapitsa (1894 – 1984) intorno al 1930. Kapitsa, emigrato
in Inghilterra dopo la Rivoluzione russa, divenne vice-direttore della ricerca sul
magnetismo al Cavendish Laboratory, nel 1924. Lì effettuò il primo esperimento con
una camera a nebbia posta in un campo magnetico, osservando le tracce curve di
particelle alfa (e progettò un apparato che raggiunse un campo magnetico di 32 T,
insuperato fino al 1956).
Nella foto sopra si vedono un certo numero di tracce di forma circolare, dovuta al
fatto che la camera a nebbia si trova in un campo magnetico; il raggio di curvatura della
traiettoria della carica immersa in B è dato dalla formula scritta sopra.
Misurando il raggio di curvatura delle tracce, conoscendo il campo B e
supponendo che la carica sia quella di un elettrone o qualche unità di questo, possiamo
misurare la quantità di moto.
Tra le molte tracce di forma circolare se ne vede una (parallela alla freccia gialla)
che appare completamente dritta: il fatto che quella traccia appaia dritta non vuol dire
che la traccia non è curva e che la particella non è elettricamente carica perché se la
particella non fosse elettricamente carica non potrebbe ionizzare il gas della camera a
nebbia e dunque non potrebbe produrre quella traccia: se appare dritta vuol dire che il
16
suo raggio di curvatura è sostanzialmente infinito, sicuramente più grande di quello che
si può misurare dati gli errori di misura in questo caso specifico. Quindi deve trattarsi di
una particella la cui quantità di moto è estremamente grande, molto più grande di quella
che si può ottenere in laboratorio.
Ci volle un po’ prima di capire la natura di queste particelle.
Prima di affrontare la determinazione della natura di queste particelle illustreremo
quello che nel frattempo si andava chiarendo sui decadimenti beta.
I decadimenti beta
In natura si osserva un certo numero di elementi trasformarsi in elementi dello stesso
peso atomico ma con un numero atomico diverso. Questo processo avviene con
l’emissione di un elettrone, spesso accompagnato da successive emissioni di altre
particelle; perlopiù la cosa veniva interpretata come il fatto che un elemento chimico si
trasforma in un altro con l’emissione di una carica elettrica dovuta all’estrazione di un
elettrone dal nucleo atomico.
Se si misura l’energia degli elettroni
provenienti da uno di questi elementi
(qui a sinistra è rappresentato lo spettro
in energia degli elettroni emessi dal
bismuto-210 che si trasforma in
polonio-210) si osserva che lo spettro è
continuo e presenta energie che vanno
da 0 fino a un massimo dell’ordine del
MeV.
Tutti i decadimenti radioattivi
degli elementi naturali hanno energie di
questo ordine di grandezza.
Il decadimento del bismuto veniva interpretato in questo modo: se il bismuto si
trasforma in polonio vuol dire che uno dei suoi neutroni si trasforma in un protone; per
fare questo deve emettere un elettrone affinché si conservi la carica elettrica:
n p e
Ma se questo fosse effettivamente il decadimento che avviene a livello
microscopico nel nucleo avremmo un problema di conservazione dell’energia.
Facciamo prima il conto relativistico e poi vedremo che la cosa si chiarisce da sé.
Scriviamo il quadrimpulso della particella iniziale, il neutrone: per la parte spaziale è 0
perché il neutrone è fermo; per quanto riguarda la sua parte temporale, ovvero la sua
17
energia, dobbiamo tener conto solo della sua energia a riposo, ovvero la massa del
neutrone. Il quadrimpulso si conserva: in seguito al decadimento deve pertanto essere
uguale alla somma dei quadrimpulsi dell’elettrone e del protone:
0, mn p, Ee p, E p
ora se facciamo il quadrato di entrambi i membri [bisogna farlo usando le regole della
cinematica relativistica, per cui si moltiplicano fra loro le componenti temporali (le due
energie) mentre le componenti spaziali si devono moltiplicare col segno cambiato]
otteniamo:
mn2 Ee2 pe2 E p2 p 2p 2 pe , Ee p p , E p
mn2 me2 m2p 2Ee E p 2 p p dove si è tenuto conto che pe p p
Sostituiamo alla quantità di moto al quadrato la differenza tra l’energia totale al
quadrato e l’energia a riposo (ossia la massa a risposo) al quadrato (dell’elettrone)
mn2 me2 m2p 2Ee E p 2 Ee2 me2
mn2 me2 m2p 2 Ee Ee E p
mn2 me2 m2p 2 Ee mn
Ee
mn2 me2 m 2p
2mn
Dunque, riassumendo, quando avviene un decadimento
l’energia dell’elettrone è la seguente:
Ee
n p e
mn2 me2 m 2p
2mn
, espressione fatta tutta di
costanti e dunque l’energia dell’elettrone emesso da un decadimento deve esser costante.
Per la precisione, tenendo conto che i neutroni pesano, in unità naturali, 940 MeV, i
protoni 938 MeV e un elettrone 511 keV, essa varrebbe
9402 0,5112 9382
Ee
MeV 1,998MeV 2MeV
2 940
D’altra parte questa cosa è del tutto ovvia: se nella meccanica relativistica energia e massa
sono due forme diverse di energia, la massa del neutrone può essere ceduta
integralmente al protone e all’elettrone in gran parte sotto forma di energia cinetica e in
parte per produrre la massa di queste due particelle; siccome inizialmente il protone è
fermo, classicamente le due quantità di moto dell’elettrone e del protone devono essere
l’una opposta all’altra e dunque non c’è possibilità per l’elettrone di assumere un’energia
variabile, ossia compresa tra 0 e 1MeV: l’energia dell’elettrone rimane fissata dalla
formula scritta sopra; se le particelle figlie fossero uguali la loro massa dovrebbe
semplicemente essere la metà di quella del neutrone; il fatto che le particelle figlie non
18
siano uguali fa sì che l’espressione delle loro masse ed energie sia appena un po’ più
complicata ma fissata.
Inizialmente si ipotizzò che nei processi microscopici l’energia potesse non essere
conservata; naturalmente questa è sempre una possibilità, perché la conservazione
dell’energia non è un dogma sacro ma è una conseguenza delle osservazioni sperimentali:
se osservo che il principio di conservazione dell’energia non è valido dovrò assumere che
non è valido. Tuttavia i fisici erano restii ad abbandonare dei principi che sembravano
funzionare perfettamente in altri contesti e dunque cercavano una soluzione a questo
problema.
La soluzione fu l’ipotesi dell’esistenza del neutrino.
L’ipotesi del neutrino
L’ipotesi dell’esistenza del neutrino è del 1930 e si deve a Wolfgang Pauli (1900 – 1958)
… che rifiutava (come molti) l’idea che
l’energia non si conservasse e ipotizzò
che il decadimento beta non fosse un
decadimento a due corpi come si
riteneva allora, ma un decadimento a
tre corpi, come mostra la figura a destra:
il neutrone doveva decadere in tre corpi
in modo che la somma delle quantità di
moto delle particelle che venivano fuori
dal decadimento del neutrone fosse p
1 p2 p3 0
comunque nulla…
…ma in modo anche che ciascuna delle tre particelle potesse portarsi via una porzione
qualunque della quantità di moto disponibile (compresa tra 0 e la massima disponibile
consentita dal principio di conservazione dell’energia). Poiché la terza particella non si
vede mai, essa doveva essere una particella neutra. Allora si conoscevano come uniche
particelle neutre il neutrone (…e un neutrone non poteva essere!) e il fotone, che però si
era in grado di rivelare. Inoltre la particella in questione, neutra, doveva essere molto
poco interagente perché non si riusciva a osservarla con nessun tipo di strumento. Era
quindi una particella molto penetrante, poco interagente con la materia e neutra.
La particella è quella che oggi chiamiamo neutrino.
n p e
Il decadimento beta si deve pertanto interpretare non come il decadimento di un
neutrone in un protone + un elettrone ma in un protone + un elettrone + un neutrino
Va detto che il nome di “neutrino” dato alla particella non fu quello inizialmente
previsto per la particella. In effetti quando si studiava questo processo il neutrone non
era ancora stato scoperto e il neutrino venne inizialmente chiamato “neutrone”. Quando
agli inizi del 1932 James Chadwick (1891 – 1974) “scoprì” il neutrone nei nuclei
atomici, Enrico Fermi (1901 – 1954) su suggerimento scherzoso di Edoardo Amaldi
(1908 – 1989) propose di chiamare “neutrino” la particella neutra del decadimento beta,
19
per distinguerla dal ben più grosso neutrone… e da allora invalse l’uso di chiamarlo così,
con questo suffisso all’italiana, che si impose in tutto il mondo.
I ragazzi di via Panisperna
(Oscar D’Agostino, Emilio Segre, Edoardo Amaldi, Franco Rasetti ed Enrico Fermi.)
Quesito: perché il decadimento beta non può essere un decadimento a due corpi?
a. Perché in questo caso il protone figlio del decadimento non potrebbe rimanere nel nucleo ospite, ma
dovrebbe esserne espulso.
b. Perché non esistono decadimenti a due corpi.
c. Perché in questo caso gli elettroni emessi dovrebbero essere monocromatici.
[La risposta esatta è la c.]
1.2. Chi li ha ordinati? Scoperta del positrone, del pione e del
muone.
“E questo? Chi lo ha ordinato?” La celebre
frase fu pronunciata nel 1936 dal fisico
Isidor Isaac Rabi (1898 – 1988) in una
conferenza nella quale venivano presentate
le nuove particelle che via via venivano
scoperte ed egli venne in quell’occasione a
conoscenza dell’esistenza del muone.
In effetti le nuove particelle cominciavano
a proliferare.
;
20
La prima nuova particella che si scoprì fu scoperta dal fisico statunitense di origini
svedesi Carl Anderson (1905 – 1991) nel 1932 grazie a una foto scattata in una camera a
nebbia: vi si vede una particella che nella parte superiore della foto ha una certa
curvatura dovuta al fatto che tutto il sistema è immerso in un campo magnetico; dalla
curvatura si può evincere la quantità di moto della particella;
la particella passa attraverso una striscia nera che è
un assorbitore di 6 mm di piombo e ne esce con una
curvatura maggiore, segno che ha perso una certa
quantità di energia e quindi una certa quantità di
moto; l’energia persa da questa particella è
esattamente quella che avrebbe perso un elettrone
attraversando i 6 mm di piombo, e perciò fu
identificata come un elettrone; peccato però che, per
come era orientato il campo B nell’esperimento,
l’elettrone avrebbe dovuto assumere una curvatura
contraria; doveva essere sì un elettrone… ma di
carica positiva!
Fu quello che venne chiamato il POSITRONE, ovvero l’antiparticella dell’elettrone, in
tutto e per tutto uguale all’elettrone ma con tutti i numeri quantici cambiati, in
particolare con la carica elettrica opposta a quella dell’elettrone.
La scoperta, abbastanza sorprendente (ma non del tutto sorprendente, perché in
fondo l’ipotesi del positrone era prevista dalle equazioni di Dirac di qualche anno prima),
fu seguita da altre.
Una delle foto che portò alla scoperta di nuove particelle è la seguente, fatta
sempre in una camera a nebbia:
vi si vede la particella arrivare da destra (o da sinistra a seconda di come si guardi la
foto), decadere in un’altra particella che lascia una traccia più lunga, che a sua volta
decade in una terza particella che lascia la terza traccia. Foto simili se ne trovano tante:
21
Qui sotto altre due:
Come si interpretano queste foto? La lunghezza della traccia centrale è sempre la
stessa; la particella che decade producendo la particella che lascia la traccia lunga deve
essere dunque una particella che decade sempre in due corpi, per le stesse ragioni per le
quali abbiamo fatto l’ipotesi del neutrino; solo se una particella decade in due corpi le
due particelle “figlie” hanno sempre la stessa energia (e la lunghezza della traccia più
lunga è proporzionale all’energia cinetica della particella). L’altra particella dev’essere
neutra, dato che non lascia nessun segnale nel rivelatore; presumibilmente si tratta di un
neutrino, come nel caso di un decadimento beta. La traccia lunga a sua volta “decade”
lasciando un’altra traccia più corta; questa terza traccia però non ha sempre la stessa
lunghezza: questa cambia nelle varie foto: ciò significa che la particella che ha lasciato la
traccia lunga decade con un decadimento a tre corpi (in modo che la particella carica, che
è l’unica che lascia la traccia, possa assumere un’energia variabile tra zero e il suo valore
massimo). Le altre due particelle devono essere due particelle neutre (non lasciano
traccia) e non possono essere dei fotoni altrimenti si sarebbe potuto vederli; quindi
devono essere due neutrini
Le foto sopra si interpretano dunque come la combinazione di due decadimenti:
la traccia lunga è quella lasciata da un MUONE (indicato con la lettera μ), che si
trova nell’uno o nell’altro dei due stati di carica; esso decade in tre corpi, uno dei quali
22
venne identificato con un elettrone con la stessa carica mentre gli altri due devono essere
due neutrini:
e
La particella “madre” del muone (cioè quella che decadendo ha prodotto il
muone) è una particella che venne chiamata PIONE (indicata con la lettera π), che si
trova in due stati di carica (in seguito si scoprirà che esiste anche un pione neutro); essa
decade in un muone e un neutrino:
Per spiegare questi decadimenti è necessario però introdurre nuove grandezze fisiche.
Quesito: come si capisce che la particella scoperta da Anderson è un positrone?
a. Dal fatto che la sua traccia è curva.
b. Dal fatto che la sua curvatura in campo magnetico è quella di una particella di carica positiva, mentre
la perdita di energia nel piombo è quella tipica di un elettrone.
c. Dal fatto che l’energia persa nell’attraversare il piombo è compatibile con quella di un elettrone.
[La risposta esatta è ovviamente la b.]
1.3. Nuove grandezze fisiche. Conservazione del numero
leptonico e barionico.
Perché fu necessario introdurre nuove grandezze fisiche? Perché alcuni decadimenti non
si osservavano mai. Ad esempio, il decadimento e era perfettamente
legittimo dal punto di vista cinematico in base alle leggi di conservazione note fino a quel
momento: si conserva l’energia e si conserva la carica elettrica; non c’è nessun motivo
per pensare che debba essere proibito; tuttavia questo decadimento (un muone che
decadere in un elettrone con energia fissa) non si osserva mai.
Per spiegare l’assenza di questo decadimento occorre ipotizzare l’esistenza di una nuova
“carica” posseduta dal muone e che si dovrebbe conservare dopo il decadimento: il
decadimento sarebbe cioè proibito perché non si conserverebbe questa nuova “carica” o
numero quantico. Questo numero è chiamato il NUMERO LEPTONICO. Viene
attribuirlo in maniera arbitraria: il muone negativo ha numero leptonico L pari a + 1 e il
muone positivo ha L pari a – 1:
L 1
L 1
Fatta questa ipotesi si può pensare che per un muone negativo il decadimento avvenga in
questo modo:
23
L
+1
e ...
+1
e che il numero leptonico + 1 venga conservato dall’elettrone negativo. Tuttavia questo
non spiegherebbe l’assenza del decadimento di cui sopra. L’unica spiegazione è che le
altre due particelle “figlie” del decadimento (due dunque!) debbano avere numero
leptonici di segno opposto, in modo da non alterare il numero leptonico di partenza:
L
e
+1
+1 +1 – 1
Se però i due neutrini hanno numero leptonico opposto non sono due neutrini identici,
ma un neutrino e un “ANTINEUTRINO”; conveniamo allora di soprassegnarlo e di
dargli numero leptonico pari a – 1
L
e
+1
+1 +1 – l
L’antineutrino ha tutti i numeri quantici di segno opposto di quelli del neutrino e dunque
anche il numero leptonico.
Anche l’assegnazione del numero leptonico a muoni, elettroni e neutrini
non spiega però la mancata osservazione di un altro decadimento, teoricamente
possibile secondo tutte le leggi di conservazione, compresa quella del numero leptonico:
quello di un muone in un elettrone e un fotone: e .
Dovrebbe essere possibile perché il numero leptonico si conserva.
L 1
oppure
L 1 … e dopo è lo stesso. E invece
Se non accade è perché il numero leptonico che sta a sinistra è diverso dal numero
leptonico che sta a destra. Dobbiamo cioè ipotizzare che il numero leptonico del muone
non è lo stesso del numero leptonico dell’elettrone. Dobbiamo allora distinguerli e
e un NUMERO LEPTONICO ELETTRONICO che vale L e 1 .
L 1
introdurre un NUMERO LEPTONICO MUONICO che vale
e
Assunto che questi numeri quantici non siano gli stessi, il decadimento sarebbe dunque
vietato perché non si conserva né il numero leptonico muonico (che da +1 passa a 0) né
il numero leptonico elettronico (che da 0 passa a +1):
L
Le
e
+1
+1
24
Se tuttavia, riprendendo il decadimento a tre corpi visto in precedenza
( e ), ipotizziamo che il neutrino e l’antineutrino siano anche di specie
diversa (uno muonico e l’altro elettronico),
e e
L
+1
+1
+1
Le
–1
con queste ipotesi si conservano i numeri leptonici muonico ed elettronico e si
spiegherebbe perché si osserva e e non si osserva e .
L’introduzione di questi due numeri quantici spiega anche perché il decadimento
beta non è un decadimento a due corpi: se fosse semplicemente
n p e
n pe
L
+1
Le
il numero leptonico elettronico passerebbe da 0 a +1.
Viceversa il decadimento a tre corpi n p e e (dove la terza particella è un
antineutrino della specie elettronica) permetterebbe la conservazione del numero
leptonico elettronico (pari a 0 in questo caso):
n p e e
L
+1 – 1
Le
Anticipando scoperte future diciamo che esiste un terzo leptone, il τ (leggi: tau),
con il suo neutrino ed entrambi con il loro numero leptonico tauonico.
TABELLA DEI NUMERI LEPTONICI
e , e
e , e
,
,
,
,
Le
1
–1
0
0
0
0
L
0
0
1
–1
0
0
L
0
0
0
0
1
–1
25
NON SI SONO MAI OSSERVATI DECADIMENTI DEL PROTONE
…del resto, se i protoni decadessero non ci sarebbero i nuclei atomici! Come si giustifica
l’impossibilità, ad esempio, del decadimento p e e , che pure conserverebbe sia
la carica elettronica sia il numero leptonico elettronico?
p
e e
L
–1 +1
Le
Si può “spiegare” l’assenza di decadimenti del protone introducendo un nuovo
numero quantico, IL NUMERO BARIONICO.
p
e e
L
Le
B
–1 +1
+1
Si attribuisce al protone (massa = 938 MeV) il numero barionico B = +1 (varrà +1
anche per il neutrone): in tal modo se non si conserva il numero barionico si “giustifica”
la mancata osservazione del decadimento in questione.
Viceversa, il decadimento del neutrone (massa = 940 MeV), dove il protone
finale ha lo stesso numero barionico del neutrone iniziale, è possibile.
n p e e
L
Le
B
+1 – 1
+1
+1
Ma quante sono le particelle? Sono solo quelle che abbiamo visto finora? No,
sono molte di più.
26
1.4. Ma quante sono? Scoperta della K e della Λ.
Si sono continuate a scoprire particelle su particelle, principalmente nei raggi cosmici.
Due sono in particolare le particelle che furono scoperte in quegli anni: la K e la Λ..
La K0
Era il 1946 quando Rochester e Butler scoprirono questa caratteristica traccia a “V” in
una camera a nebbia. Nella foto qui sopra si vedono le due tracce indicate con a e b
(evidenziate in verde a destra) uscire da un punto del detector che non è investito da
un’altra particella, segno che si tratta del decadimento di una particella neutra in
due particelle di carica opposta. La particella neutra prese il nome di K (kaone)
perché disegnava sul piano dello strumento una specie di K (vedi immagine a destra) se
si tiene conto del segmento ortogonale alla direzione della particella. Per la precisione il
kaone dà origine a due pioni di carica opposta.
La Λ0
Un’altra particella del tutto simile – ma diversa perché ha una massa evidentemente
diversa, come si può dedurre misurando le quantità di moto delle due particelle “figlie” –
fu scoperta nel 1947 durante uno studio delle interazioni dei raggi cosmici ed è quella che
si vede nell’immagine a pagina seguente. Vi si vedono ancora due tracce indicate con a e
b (evidenziate in verde nell’immagine a destra) che provengono da un punto del
rivelatore in cui non ci sono altre particelle, segno evidente che si tratta del decadimento
di una particella neutra (che quindi non lascia tracce nel rivelatore), presumibilmente
proveniente dall’evento che si riconosce al centro dell’immagine.
Le due tracce formano una specie di V rovesciata (vedi foto a destra) che ricorda
la lettera greca Λ; e così come le particelle della foto precedente vennero chiamate K per
la forma dell’evento cui davano origine queste vennero chiamate Λ.
27
Le due particelle in cui decade la particella Λ vennero poi identificate con un protone e
un pione.
Nonostante si prevedesse che la particella avesse una vita media dell’ordine di ~10−23 secondi, essa in realtà
mostrò una vita media dell’ordine di 10−10 secondi. La proprietà per la quale la particella mostrava una vita media
così lunga fu nominata stranezza (strangeness, in inglese) e portò alla scoperta del quark strange. Inoltre queste
scoperte portarono alla formulazione del principio di conservazione della stranezza, secondo il quale particelle
leggere decadono più lentamente se hanno stranezza (dovuto al fatto che i canali di decadimento non deboli
devono preservare la stranezza, che invece può essere violata da decadimenti deboli). Ma di tutto ciò parleremo
con maggior dettaglio più avanti.
1.5. Facciamo ordine: classificazione delle particelle.
Dato che le particelle aumentavano di numero fu necessario procedere a una
classificazione, inizialmente in base alla massa, oggi in base alle loro proprietà.
Innanzitutto le particelle si possono classificare in base allo SPIN. Abbiamo
quindi la prima grande suddivisione in FERMIONI, che hanno spin semintero, e
BOSONI, che hanno spin intero.
28
Inoltre le particelle si possono distinguere sulla base delle INTERAZIONI A
CUI DANNO LUOGO e quindi possiamo distinguerle in LEPTONI e
ADRONI.
Alla classe dei leptoni appartengono l’elettrone, il muone e tutti i neutrini visti fino
adesso e naturalmente le loro antiparticelle. Queste particelle non interagiscono per
interazione forte. Possono dare luogo a interazioni di tipo elettromagnetico se sono
cariche oppure di tipo debole se sono neutre, come i neutrini.
Tutte le altre particelle che interagiscono anche per interazione forte vengono
chiamate adroni: fra gli adroni ci sono i protoni e i neutroni che evidentemente
subiscono l’interazione forte ma ci sono anche le Λ che vengono prodotte per
interazioni forti. Anche i pioni carichi e neutri e i K sono adroni: la differenza è che il
protone, il neutrone e il Λ hanno spin semintero mentre i pioni e i K hanno spin intero,
per cui gli adroni possono essere a loro volta distinti in quelli che si chiamano barioni
(adroni di spin semintero) e mesoni (adroni di spin intero).
Fra i bosoni possiamo includere anche le particelle che compongono la luce, cioè i
fotoni.
Abbiamo quindi un quadro più o meno ordinato delle particelle scoperte nei raggi
cosmici.
29
1.6. Test ed esercizi
I neutroni pesano, in unità naturali, 940 MeV. I protoni 938 MeV. Se il decadimento beta
consistesse nella trasformazione di un neutrone in un protone e un elettrone, quale sarebbe la
quantità di moto di quest’ultimo nel sistema di riferimento del neutrone? [La massa di un
elettrone è pari a 511 keV in unità naturali]
a.
b.
c.
d.
e.
Trascurabile (l’elettrone resta praticamente fermo)
2 MeV
1 GeV
0.5 MeV
1 MeV
[Abbiamo visto che l’energia in quel caso sarebbe fissa,
pari a
Ee
mn2 me2 m 2p
2mn
ossia pari 1,998 MeV.
Ora è p2=E2– m2. La risposta è corretta è la b.]
Fino a qualche valore del prodotto βγ domina il termine 1/v2 nella formula che descrive la
perdita d’energia per ionizzazione?
a. quando βγ è molto grande
b. fino circa a 3
c. quando βγ tende a zero
d. per βγ circa uguale a 1
e. per valori molto minori di 3
[La risposta corretta è la b.]
Una particella carica attraversa un mezzo cedendo energia agli elettroni di questo. Se la
particella ha velocità v, qual è la velocità massima che può imprimere a un elettrone per urto?
a.
b.
c.
d.
e.
2v
v
infinito
0
4v
[La risposta corretta è la a.]
Le misure fatte da Hess indicano che a la ionizzazione media a circa 1 km dalla superficie
terrestre è di 10 ioni/cm3 s−1. Alla quota di 6 km la ionizzazione aumenta di un fattore 3 circa.
Le stesse misure indicano che la ionizzazione cresce esponenzialmente secondo la legge
I∝exp(x/λ). Stima il valore di λ.
a.
b.
c.
d.
e.
7 km
1 km
6 km
600 m
5 km
[I=I0 exp(x/λ), da cui I2/I1=exp(x2/λ – x1/λ) da cui 3=exp(5km/ λ ).
La risposta corretta è la e.]
30
Quale tra questi decadimenti è l’unico permesso?
a.
e e
b.
e e
c.
e e
d.
e e
e.
e e
[L’unico in cui si conservano numeri leptonici elettroni e muonici è quello della e.]
Quale tra questi decadimenti è permesso?
b. e
c.
d. e
e.
a.
[Il tauone può decadere in un leptone più leggero, creando un neutrino tauonico:
da escludere dunque le risposte a. e d. La risposta corretta sembra dunque la b… ma non si conserva il
numero elettronico. La lambda non ha mai carica negativa, e dunque nella e. non si conserva la carica.
Per esclusione rimane la c.]
31
Capitolo 2
Imitare la natura
Vorremmo studiare queste particelle con un certo grado di dettaglio. Per studiarle
dettagliatamente abbiamo bisogno di molte di queste particelle e non possiamo aspettare
che la natura le produca per caso; dobbiamo produrcele in laboratorio imitando i
processi che la natura mette in atto per produrre queste particelle nei raggi cosmici. Qual
è la ricetta per produrle? È semplice: E = mc2.
Se voglio produrre particelle la cui massa complessiva sia m devo disporre di una
quantità di energia almeno pari alla massa della particella che voglio produrre
moltiplicata per c2. Devo cioè imitare quello che avviene in natura, dove ciò che avviene
è che le particelle dei raggi cosmici primari, per lo più protoni urtano urtare le particelle
del gas che sta nell’atmosfera, nell’urto si sviluppa una certa quantità di energia che poi
può materializzare in altre particelle.
Questi gli argomenti del capitolo:
1. Produzione artificiale di particelle.
2. Acceleratori
3. Sezione d’urto
4. Vita media.
5. Massa invariante e risonanze.
6. Particelle “strane”.
7. Test ed esercizi
2.1. Produzione artificiale di particelle
Dal punto di vista della meccanica quantistica possiamo descrivere il processo di
produzione di particelle nel seguente modo: abbiamo uno stato iniziale composto da un
nucleo, per esempio di azoto, che sta nell’atmosfera, e un protone di una certa energia:
N, p
Quello che deve succedere in seguito all’urto del protone col nucleo di azoto è che il
protone e il nucleo di azoto devono scomparire e al loro posto devono apparire nuove
particelle. Abbiamo cioè bisogno di un operatore O che agisce sullo stato iniziale e che
sia composto dal prodotto di un operatore di creazione C seguito da un operatore di
distruzione D: si deve intendere che prima si applica l’operatore di distruzione e poi si
applica l’operatore di creazione (“C composto D”).
O N , p CD N , p
Quando si applica l’operatore di distruzione allo stato
vuoto al quale si applica poi l’operatore di creazione C:
CD N , p C 0
32
N, p
si ottiene uno stato di
il quale operatore produce le particelle dello stato finale.
C 0 X , ,
L’ampiezza di probabilità di produrre questo stato finale con le particelle segnate
sopra provenendo dallo stato iniziale N, p si può descrivere nella meccanica quantistica
come un elemento di matrice O composizione dell’operatore di distruzione D e di
creazione C tra gli stati iniziali e finali del processo che vogliamo produrre
X , , O N , p
Per poter realizzare eventi di questo tipo in laboratorio abbiamo bisogno di un fascio di
protoni accelerati da una differenza di potenziale di 340 milioni di Volt. Dobbiamo
quindi costruire degli acceleratori di particelle che permettano di dare alle particelle del
fascio l’energia necessaria per produrre le nuove particelle che vogliamo studiare.
2.2. Acceleratori di particelle
Come si costruisce un acceleratore di particelle? Si collegano due tubi di rame ai due poli
di una pila.
Tra i due tubi c’è una differenza di potenziale (ad esempio da 1,5 eV); se una particella
passa tra i due tubi di rame essa guadagna una certa energia, in particolare guadagna 1,5
eV se la particella ha carica unitaria. 1,5 eV è un po’ poco, bisogna dare alla particella
un’energia più alta: basterà mettere più pile in serie…
Con un milione di pile possiamo arrivare a 1MeV di energia per la particella? No, perché
con una differenza di potenziale di un milione di Volt sarà facile produrre indesiderate
scariche elettriche essendo il potenziale di rottura del materiale circostante molto più
basso di questo valore… e quindi questo sistema non funziona. Non possiamo dunque
produrre acceleratori di particelle con energia troppo alta mettendo le sezioni del mio
acceleratore in serie. Quello che possiamo fare però è usare un trucco molto semplice:
mettere le pile in serie ma invertite in modo alternato:
33
a sinistra abbiamo un campo verso destra, nella parte centrale un campo rivolto verso
sinistra, a destra un campo di nuovo rivolto verso destra. Una particella che si trovi nel
campo a sinistra viene accelerata e si sposta nel secondo tubo di rame.
Giunta dentro il secondo tubo di rame non sente alcun campo perché il tubo di rame fa
da gabbia di Faraday. In quel momento invertiamo il campo della sezione centrale (in
realtà invertiamo tutti i campi)
che diventa di nuovo un campo accelerante per la particella.
La particella entra quindi nel terzo cilindro di rame: di nuovo non sente alcun campo ma
continua a muoversi in quella direzione.
Di nuovo invertiamo i campi:
34
e quando esce dalla terza sezione di nuovo la particella si trova in un campo accelerante
In questo modo possiamo produrre una serie di campi acceleranti successivi che tuttavia
non richiedono differenze di potenziale enormi tra una sezione e l’altra. Se poi
riuscissimo a chiudere tutte le sezioni in fila in modo che la particella percorra una
traiettoria circolare avremmo realizzato uno strumento relativamente compatto come un
CICLOTRONE.
Un ciclotrone è un acceleratore di particelle piuttosto
piccolo. Com’è fatto?
È costituito da due contenitori metallici fatti a forma
di D, cavi all’interno, uno di fronte all’altro; sopra e
sotto ci sono due bobine di cavi elettrici in cui si fa
scorrere una corrente che produce un campo
magnetico (blu) che costringe le particelle a
percorrere traiettorie circolari all’interno delle due D.
Se applichiamo una differenza di potenziale tra la D (rovescia) di sinistra e la D di destra
si produce un campo elettrico (rosso) tra le due D; all’interno delle due D non c’è nessun
campo elettrico perché le D formano gabbia di Faraday ma tra l’una e l’altra c’è un
campo elettrico che può accelerare le particelle; quando una particella (accelerata)
attraversa la gap tra le due D finisce dentro una D e percorre a causa del campo B una
traiettoria semicircolare; quando la particella è arrivata al limite della gap invertiamo il
campo elettrico che accelera di nuovo la particella che percorre di nuovo una traiettoria
semicircolare di raggio più ampio (perché ha guadagnato energia e ha una quantità di
moto maggiore). La particella percorre dunque una traiettoria spiraleggiante di raggio
sempre maggio e quando raggiunge un raggio di curvatura tale da farla uscire dal canale
35
che si vede nello schema in alto a destra spegniamo il campo magnetico e la particella
esce in quella direzione avendo acquisito una energia pari alla differenza di potenziale tra
le due D moltiplicata per il numero di volte che la particella è passata da una D all’altra.
Negli acceleratori più moderni si usa un’altra tecnica: si inietta un’onda
elettromagnetica all’interno di una guida tonda, cioè di un tubo. Quest’onda
elettromagnetica è fatta di campi elettrici che sono diretti sempre in direzione dell’onda,
in senso negativo o positivo.
Le particelle si sincronizzano con l’onda elettromagnetica in maniera tale che le particelle
che seguono la traiettoria nominale si trovino nella parte discendente dell’onda
elettromagnetica; questo accade perché quelle che dovessero trovarsi per qualche motivo
in anticipo, cioè dovessero trovarsi più avanti (disegno a sinistra) “vedono” un campo
elettrico più basso e quindi vengono accelerate di meno rispetto alle altre e tendono
dunque ad addensarsi vicino alle particelle che seguono la traiettoria nominale .
Quelle che invece sono in ritardo (disegno a destra) vedono un campo elettrico più forte
e quindi sono accelerate e vengono spinte in aventi raggiungendo quelle che seguono la
traiettoria nominale. In questo modo le particelle si compattano e oscillano attorno a un
punto di equilibrio nel quale ricevono continuamente una spinta (come un surfista che si
muove “sull’onda” (sulla parete dell’onda!) e vengono così accelerate.
Disponendo di uno strumento di questo genere si può prendere un bersaglio,
36
mettere da una parte del bersaglio un rivelatore che funziona con un contatore, inviare
sul bersaglio un fascio di particelle con una quantità nota di particelle e misurare quante
di esse riescono ad attraversarlo. Quelle che non attraversano il bersaglio evidentemente
hanno interagito col bersaglio, quindi posso misurare la capacità di interazione delle
particelle con gli atomi del bersaglio.
Si cominciarono così a fare i primi esperimenti in laboratorio nei quali particelle
elettricamente cariche, tipicamente protoni che si ottengono ionizzando dell’idrogeno,
venivano accelerati e sparati contro bersagli fissi, misurando quello che succedeva a valle
del bersaglio.
2.3. Sezione d’urto
Che cosa posso misurare con gli esperimenti descritti nel capitolo precedente? Posso
misurare diverse quantità; in particolare posso misurare il numero di particelle che hanno
interagito. Da questo numero si ricava un parametro importante che è la sezione d’urto:
che cosa rappresenta questo valore?
Supponiamo di avere un fascio di N particelle che va sul bersaglio; il numero di
particelle che interagiscono col bersaglio fa sì che il numero di particelle a valle del
bersaglio sia inferiore: ci sarà quindi una variazione negativa nel numero di particelle dN
proporzionale al numero di particelle che ho inviato sul bersaglio
dN N
Il numero di particelle che interagiscono col bersaglio sarà poi proporzionale allo
spessore del bersaglio:
dN Ndx
Il numero di particelle che interagiscono sarà proporzionale anche alla densità del
bersaglio (ρ = numero di particelle per unità di volume, si misura in m– 3):
dN Ndx
La costante di proporzionalità è detta σ:
dN Ndx
σ è chiamata sezione d’urto perché ha le dimensioni di un’area.
37
La σ rappresenta la capacità di una particella di interagire con altre particelle, e il fatto
che abbia le dimensioni di un’area lo si capisce da una semplice analogia: nel gioco delle
freccette più è ampio il bersaglio più è facile colpirlo.
perciò la sezione d’urto può essere vista come una sorta di area efficace che viene “vista”
dalla particella sparata contro il bersaglio.
Ripartiamo dunque dalla nostra
dN Ndx
Per risalire a σ devo dunque calcolare quante erano le particelle N sparate contro il
bersaglio, quante sono quelle che lo hanno attraversato (e per differenza risalire a dN),
calcolare lo spessore e la densità del bersaglio.
Divido tutto per N:
dN
dx
N
Faccio l’integrale a sinistra e a destra:
dN
N dx
Il numero di particelle che si vedono a valle del bersaglio di spessore x è uguale a:
x
N x N 0 exp x N 0 exp
σρ ha le dimensioni di m–1 e perciò lo posso chiamare 1/λ. λ (che si misura in m)
rappresenta il cammino medio di una particella. Così si può misurare la sezione
d’urto semplicemente misurando N(x) e N(0).
Il barn
Il barn (simbolo b o bn, dal termine inglese “barn”, fienile) è un’unità di misura per
l’area, utilizzata in fisica nucleare e subnucleare per misurare sezioni d’urto tra
particelle elementari.
38
1 barn = 100 fm2 = 10 –28 m2 = 10 –24 cm2
Tale unità di misura nasce dal fatto che il raggio del nucleo atomico è dell’ordine di
10–12 cm, quindi la sua sezione d’urto geometrica sarà di 10 –24 cm2.
Se un nucleo viene disintegrato ogni volta che viene colpito si dice che la sua sezione
d’urto è di 1 barn, ovvero che tutta la sua area è efficace. Se per una qualsiasi ragione
avviene invece una disintegrazione ogni cento urti subiti diciamo che la sezione d’urto
efficace per quel nucleo è di 0,01 barn. Il barn non fa parte del Sistema Internazionale di
unità di misura ma è accettato come unità per l’uso corrente.
Quesito: Cos’è la sezione d’urto?
a. È una grandezza che permette di definire la probabilità d’interazione di una particella con la materia.
b. È la sezione delle particelle bersaglio.
c. Rappresenta la probabilità d’interazione di una particella con la materia.
[La risposta corretta è la a.]
2.4. Vita media
Un’altra grandezza fisica che possiamo determinare per le particelle instabili è la vita
media. Le particelle instabili non decadono a intervalli prefissati ma decadono in maniera
statistica: se ne produce un certo numero e poi queste cominciano a decadere a tempi
più o meno casuali, un po’ come fanno le bolle di sapone: quando abbiamo una ciotola
piena di bolle di sapone queste esplodono casualmente una dopo l’altra.
Questo processo, per quanto statistico e imprevedibile, presenta però delle
regolarità interessanti: la prima cosa che si può osservare è che il numero di particelle che
decadranno sarà proporzionale al numero di particelle preparate in laboratorio (così
come il numero di bolle di sapone che scoppiano sarà tanto più alto quanto più alto è il
numero di bolle di sapone presenti nella ciotola:
dN N
Anche il tempo di attesa è rilevante: più aspetto e più vedrò decadimenti:
dN Ndt
Il fattore di proporzionalità tra queste due grandezze deve essere un t – 1: chiamo questo
fattore 1/τ:
dN N
dt
τ è dunque il tempo di vita medio della particella:
Come prima, dividiamo per N:
dN
dt
N
dN
dt
Integriamo:
N
39
t
N t N 0 exp
Sarà dunque sufficiente contare le particelle dopo un tempo t, N(t), e quelle preparate
per il mio esperimento, N(0), per conoscere il tempo di vita medio delle mie particelle.
Quesito: cos’è la vita media di una particella?
a. Il tempo dopo il quale una particella decade
b. Il tempo trascorso il quale è sopravvissuto circa 1/3 delle particelle inizialmente presenti in un
campione.
c. Il tempo dopo il quale resta circa la metà delle particelle inizialmente presenti in un campione.
[La risposta esatta è la b.]
2.5. Massa invariante e risonanze
“Vedere” le particelle
A questo punto vorremmo “vedere” le particelle prodotte. Il problema è che la maggior
parte delle particelle prodotte hanno un tempo di vita medio così breve che è
praticamente impossibile osservarne la traccia: percorrono distanze troppo brevi per
essere osservate.
Come si riesce dunque a vedere la produzione di queste particelle?
Supponiamo di avere, per esempio, un fascio di pioni negativi (che possiamo
produrre accelerando dei protoni e mandandoli a sbattere sul bersaglio): acceleriamo
questi pioni e mandiamoli a sbattere su di un secondo bersaglio, producendo, ad
esempio in interazione coi protoni del bersaglio, una particella Λ. La Λ decade a sua
volta in un protone e in un π– (leggi: pai meno)… ma decade troppo presto per essere
osservata.
Come facciamo a stabilire che quel protone p e quel π – sono figli di una Λ e non venuti
fuori casualmente dal bersaglio per effetto di un altro tipo di processo?
Ciò che possiamo fare è la cosa seguente.
Supponiamo che le particelle che osserviamo nel rivelatore siano effettivamente figlie di
una particella di massa M. La particella M, nel sistema di riferimento in cui essa è ferma
40
ha nulla la parte spaziale del quadrimpulso e la parte temporale (l’energia) uguale alla
massa della particella, dato che è ferma.
Nel sistema di riferimento del laboratorio le particelle figlie avranno invece quantità di
moto p1 e p2 ed energie E1 ed E2.
Poiché il modulo-quadro del quadrimpulso è un invariante relativistico, possiamo
scrivere la seguente uguaglianza:
0, M 2 p1, E1 p2 , E2 2
Quadrando, a destra si ottiene il quadrato dei due quadrimoduli più il doppio prodotto
E12 p12 E22 p22 2( E1 E2 p1 p2 cos12 ) ; si
2
2
2
ottiene quindi M m1 m2 2 E1 E2 2 p1 p2 cos12
dei due quadrimoduli: M
2
Se misuro p1 e p2 delle due particelle nello stato finale e l’angolo che esse formano, e le
so identificare da come interagiscono nel rivelatore, cioè dal tipo di energia che perdono,
si può calcolare quella che viene detta la MASSA INVARIANTE delle due particelle,
che deve essere uguale alla massa della particella madre di cui le due particelle sono figlie.
Se non sono figlie di quella particella la loro “massa invariante” sarà un numero a caso
tra 0 e il valore massimo reso possibile dall’energia cinetica.
A questo punto possiamo fare un grafico nel quale riportiamo la sezione d’urto in
ordinata e in ascissa l’energia del centro di massa, cioè la massa invariante che abbiamo
ricostruito a partire dalle due particelle osservate nello stato finale.
Quello che ci aspettiamo di vedere è una distribuzione sostanzialmente piatta,
perché non c’è nessuna ragione per cui la massa invariante debba assumere un valore
particolare: ed è infatti quello che si vede sulla destra di questa distribuzione.
Ma quello che si vede sulla sinistra è un insieme di picchi, alcuni nello stato π+p, altri
nello stato π –p. Cosa significano questi picchi?
41
Per quel preciso valore di energia la probabilità di ottenere una coppia π+p (o una coppia
π – p) avente una massa invariante corrispondente al picco è più alta di quella di ottenere
una massa invariante di altro tipo.
Qual è la conseguenza di tutto ciò? Per comprenderlo facciamo un esempio con
un altro processo statistico, diverso ma in fondo simile: il lancio di due dadi.
Se si lanciano due dadi, quello che ci aspettiamo di vedere dopo qualche centinaio
(a sinistra) o dopo qualche migliaio (a destra) di lanci è qualcosa di questo tipo:
Si vede che il valore 7 esce più facilmente dei valori 2 e 12.
Se giocassi con due dadi truccati che danno sempre la stessa somma otterrei invece una
distribuzione del tipo dell’immagine a sinistra:
Se fossi un baro non giocherei sempre con i miei dadi truccati perché gli altri se ne
accorgerebbero subito; li userei di tanto in tanto… per vincere. Quello che otterrei in
questo secondo caso sarebbe una distribuzione del tipo a destra, ovvero la somma delle
due distribuzioni. Il picco significa che il valore uguale alla somma dei due dadi truccati
si presenta più frequentemente di quel che ci si aspetta.
Come si traduce tutto questo nelle osservazioni sulle particelle?
Se le particelle di cui calcolo la massa invariante sono prodotte per caso, la loro
distribuzione è una distribuzione piatta; se invece sono figlie di una particella decaduta la
loro massa invariante non può che essere quella della particella decaduta. E perciò si
42
osservano dei picchi. Identificando la posizione del picco si determina la massa della
particella decaduta.
Tutte le volte che si osserva un picco di questo genere – che si chiama
RISONANZA – significa che si è osservata una particella la cui massa invariante
corrisponde alla posizione del picco dell’energia del centro di massa.
Dallo studio di questi picchi si può anche stimare la vita media delle particelle
utilizzando il principio di indeterminazione: l’indeterminazione sull’energia, ovvero la
larghezza di questi picchi, moltiplicata per il tempo nel quale posso fare le misure,
ovvero la vita media delle particelle, dev’essere dell’ordine di ħ. Invertendo la relazione
posso trovare il tempo; e si calcola che il tempo di vita medio delle risonanze è
dell’ordine di 10 – 23 s.
Le risonanze non si possono osservare in un detector come tracce lasciate dalle particelle
sui rivelatori ma solo sotto forma di picchi nella sezione d’urto.
2.6. Particelle strane
Tra le particelle che si osservano essere prodotte dagli esperimenti si vede un certo
numero di particelle cosiddette “strane”.
Le particelle “strane” erano già state scoperte nei raggi cosmici: una di queste è la
Λ, scoperta nel 1947. Perché la Λ viene definita una particella strana? Perché la Λ viene
43
prodotta negli acceleratori a seguito di un urto tra un pione negativo e un protone. E
subito essa decade di nuovo in un pione negativo e un protone:
p p
Cosa c’è di “strano” in tutto questo? Se si misura la sezione d’urto di produzione delle Λ
si trova che essa è dell’ordine di qualche decina di millibarn (1mb = 10 – 27 cm2): essa è
una sezione d’urto tipica delle interazioni forti cioè della produzione di quelle risonanze
che abbiamo visto nel capitolo precedente.
Se si misura il tempo di decadimento della Λ questo non è dell’ordine di grandezza della
risonanza, cioè dell’ordine di 10 – 23s, ma molto più lento, dell’ordine di 10 – 10 s, segno
che l’interazione che fa decadere la Λ dev’essere di natura diversa di quella che ne
consente la produzione. La sezione d’urto è proporzionale al modulo quadro
dell’elemento di matrice dell’operatore che fa passare dallo stato iniziale in cui c’è un p e
un π – a quello finale in cui c’è una Λ.
f Hi
2
p H p
2
Nell’altro caso, quando si misura il tempo di vita medio della Λ, questo dovrebbe essere
proporzionale al modulo quadro dell’elemento di matrice dell’operatore che fa passare
dallo stato iniziale in cui c’è la Λ allo stato finale in cui c’è un p e un π–.
f H' i
2
p H ' p
2
Se i due operatori fossero operatori della stessa interazione, H e H’ dovrebbero essere
uguali, cambiano solo gli assi temporali; invece questo non avviene: la sezione d’urto e il
tempo di vita medio non sono tra loro compatibili: un operatore è tipico delle interazioni
forti, l’altro delle interazioni deboli.
Produzione associata
Quello che si scopre facendo esperimenti nei laboratori è che le particelle strane –
come la Λ – non vengono mai prodotte da sole ma vengono sempre prodotte
associate ad altre particelle, come la K0,
p K0
Poi la Λ decade in un pione negativo e un protone:
44
p
K
e anche la K0 decade in due o tre pioni:
anche in questo caso con tempi caratteristici delle interazioni deboli.
Sia la Λ che la K0 sono prodotte per interazione forte ma decadono per interazione
debole.
0
Queste particelle sono strane perché ci deve essere un qualche meccanismo che
impedisce all’interazione forte di far decadere la Λ nel canale di decadimento che
coincide con quello di produzione. In altre parole se siamo nella situazione di produrre la
Λ attraverso l’urto di un p e un π –
p p
invertendo l’asse temporale si dovrebbe osservare la stessa catena di produzione
p p
La prima riga dice che possiamo produrre una Λ con un’alta probabilità avendo a che
fare con una interazione forte, mentre il decadimento avviene con bassa probabilità
perché si tratta di una interazione debole.
La seconda riga, ottenuta girando l’asse del tempo, dice che abbiamo prodotto una
Λ da una interazione debole, e che questa è poi decaduta per interazione forte: ma
questo non si osserva mai.
Quindi dobbiamo inventarci un qualche meccanismo che impedisce all’interazione
forte di far decadere la Λ.
Ci deve essere una qualche forma di conservazione che deve essere violata da
un’interazione ma non dall’altra. Come possiamo operare? Che cosa dobbiamo
immaginare? Facciamo un esperimento: prendiamo un pendolo e facciamolo oscillare:
non si osservano differenze tra l’andata e il ritorno; anche mandando il filmato
all’indietro non ci si accorge di alcuna stranezza: le leggi fisiche sono invarianti per
inversioni temporali. Per riconoscere un’andata e un ritorno occorre introdurre un
qualche meccanismo che impedisca alla gravità di fare il suo lavoro.
È necessario dunque pensare a una nuova grandezza fisica che si conservi
nelle interazioni forti e non nelle interazioni deboli. Per evidenti motivi, questa
grandezza fisica è chiama “stranezza”.
È conservata nelle interazioni forti
Non è conservata nelle interazioni deboli
Viene dunque assegnata alle particelle strane una carica di stranezza che si conserva nelle
interazioni forti e non nelle deboli.
STRANEZZA
La produzione associata viene dunque spiegata in questo modo: prendendo un pione e
un protone (che non sono strane) la loro carica di stranezza è 0. Nello stato finale la Λ e
la K0 sono sì due particelle strane, ma che devono portare una carica di stranezza
opposta perché la stranezza si conservi: ad esempio alla Λ associo stranezza –1 e alla K0
associo stranezza + 1
45
L’interazione forte conserva la stranezza e dunque questo processo può avvenire. Ma
quando la Λ prova a decadere per interazione forte…
ci sarebbe una variazione di stranezza pari a +1… e questo l’interazione forte non lo può
fare perché conserva la stranezza.
La stranezza non ha invece alcun significato per l’interazione debole (per fare un
esempio analogo: l’interazione gravitazionale non “vede” la carica elettrica).
Questo fa sì che per interazione debole ci possa essere quel decadimento.
Analogamente la K0, che ha stranezza pari a +1, può decadere per interazione debole in
due (o tre) pioni, con stranezza finale dunque pari a 0.
A questo punto possiamo mettere in ordine tutte queste particelle costruendo delle
tavole periodiche, sia perché le particelle sono cresciute di numero sia perché sono
diverse le grandezze fisiche che possiamo associare a una particella.
Possiamo classificarle non solo in base allo spin e alle interazioni cui sono soggette ma
anche in base alla loro carica elettrica e alla loro carica di stranezza.
46
TAVOLE PERIODICHE
L’ottetto dei mesoni
Ricordiamo che i mesoni sono particelle a spin = 0 che interagiscono per interazione
forte e cioè sono adroni
Come si legge?
In diagonale la carica.
In orizzontale la stranezza.
47
Una tavola analoga si può costruire con i barioni di spin ½
L’ottetto dei barioni di spin ½
Come si legge? Come prima.
In diagonale la carica.
In orizzontale la stranezza.
48
Altra tabella si può fare per i barioni di spin 3/2 (che si scoprono negli acceleratori):
sono le quattro Δ, le tre Σ* (leggi: “sigma star”, simili alle Σ ma più pesanti) e le due Ξ*
(leggi “csi star”, simili alla Ξ)
Barioni di spin 3/2
Come si legge la tabella?
Come al solito. In diagonale la carica.
In orizzontale la stranezza.
Il fatto che queste particelle si dispongano su queste tavole fa pensare che possano non
essere elementari ma a loro volta costituite da altre particelle più piccole in virtù delle
quali si producono queste regolarità.
49
2.6. Test e quesiti
Perché le Λ e i K sono definite particelle strane?
a. Perché sono prodotte per interazione forte e decadono per interazione debole.
b. Perché non sembravano avere alcun ruolo nella costituzione della materia.
c. Perché sono prodotte per interazione forte a partire da uno stato identico allo stato finale del
decadimento che però avviene per interazione debole.
[La risposta esatta è la c.]
Nei raggi cosmici si osservano molti muoni provenienti dal decadimento π→μ+ν dei pioni, a
loro volta prodotti dall’interazione di protoni con i nuclei N dell’atmosfera: p+N→π+X dove X
rappresenta un generico stato che conserva i numeri quantici. Quale tra le seguenti
rappresenta l’ampiezza di probabilità del processo?
a.
b.
c.
d.
e.
⟨μν|O|π⟩
⟨μν|O|π⟩+⟨πX|O′|pN⟩
⟨μν|O|π⟩⟨πX|O′|pN⟩
⟨πXμν|O′|pN⟩
|⟨μν|O|π⟩⟨πX|O′|pN⟩|2
[La risposta corretta è la c.]
Quanti sono i mesoni strani?
a. 8
b. 1
c. 3
d. 5
e. 4
[Due mesoni hanno stranezza +1 e due hanno stranezza – 1.
Stranezza pari a 0 non è stranezza. La risposta corretta è la e.]
Come cambia la sezione d’urto di un processo con lo spessore del bersaglio?
a.
b.
c.
d.
e.
Non cambia. La sezione d’urto è indipendente dallo spessore del bersaglio
Diminuisce come un esponenziale
Dipende dal processo: in certi casi cresce e in altri no
Va come il logaritmo dello spessore del bersaglio
Cresce linearmente con lo spessore del bersaglio
[La risposta corretta è la a.
Con lo spessore diminuisce esponenzialmente la quantità di particelle che attraversano il bersaglio.]
In un esperimento in cui pioni positivi si inviano su un bersaglio si osserva che la sezione
d’urto di produzione di una coppia π+ + p presenta un intenso picco quando l’energia del
centro di massa raggiunge 1.232 MeV. Come s’interpreta quest’osservazione?
a. La distribuzione dei prodotti di decadimento è tale per cui casualmente si producono alcuni picchi
qua e là
b. Nell’urto si produce una risonanza di carica +1 e di massa pari a 1.232 MeV/c2
c. L’interazione tra i pioni e il bersaglio è più intensa per pioni di energia tale per cui l’energia nel centro
di massa vale proprio 1.232 MeV
d. Nell’urto si produce una risonanza di carica +2 e di massa pari a 1.232 MeV/c2
e. Ci troviamo di fronte a una nuova interazione
[La risposta corretta è la d.]
50
In un piccolo ciclotrone si accelerano protoni usando un campo magnetico B=10G. Il raggio
del ciclotrone è di 15 cm. Qual è la velocità massima che i protoni possono avere in uscita da
questo strumento?
a. 14000 kms−1
b. 14 ms−1
c. 14000 ms−1
d. non si può calcolare: occorre conoscere il materiale di cui è fatto il ciclotrone
e. 14×10 8 ms−1
[La formula è r=mv/qB da cui v=rqB/m. 1G=10−4 T.
Date le basse velocità in gioco si può trascurare il fattore relativistico.
La risposta corretta è la c.]
Quale particella si può trovare nel decadimento di una Ξ – ?
a. Un protone o un neutrone
b. Una Σ di qualunque carica
c. Soltanto una Σ –
d. Una Ξ* –
e. Una qualunque delle particelle dell’ottetto di barioni. (sbagliata)
Il barione Ξ – ha massa m = 1321 MeV, q = – 1. Una Σ – ha massa di 1197 MeV, stessa carica, stesso
spin e massa inferiore.
Se fosse corretta la a. servirebbe poi o una particella di carica – 1 (nel caso una delle due fosse un
neutrone) o addirittura ne servirebbero due (nel caso la particella trovata fosse il protone).
Una Ξ* – ha spin 3/2 e ha massa m = 1387 MeV, più pesante della Ξ –
In generale nel verificare se un decadimento è possibile si devono controllare i principi di
conservazione. La conservazione della carica è banale, la conservazione dell’energia impedisce che una
particella decada in particelle più pesanti, quella del momento angolare impedisce che una particella con
un dato spin decada in particelle con spin tali da non costituire uno stato con momento angolare totale
uguale a quello della particella madre; la conservazione del numero leptonico impone che i figli di un
leptone portino, complessivamente, lo stesso numero. Infine è necessario tenere in conto che alcune
grandezze non sono conservate, ma possono cambiare soltanto di una quantità ben determinata. Ad
esempio nei decadimenti deboli il numero quantico di stranezza non è conservato e si può avere
ΔS=±1.
La particella Ξ – decade in una Λ e un π – ed è prodotta in associazione con i K0. Il decadimento
fu osservato nel 1955 in un evento registrato in emulsioni nucleari esposte ai raggi cosmici.
Quante tracce a forma di V osservarono nell’emulsione i ricercatori che analizzarono l’evento?
N.B. tutte le particelle coinvolte nell’evento hanno vita media sufficientemente breve a decadere
nell’emulsione. Si trascuri la possibile conversione di fotoni in coppie elettrone-positrone.
a. 1
b. 4
c. 2
d. nessuna
e. 3
[Quante sono le K0 prodotte? Sono due (e ciascuna, decadendo, mostrerà una “V”), in quanto la
stranezza totale deve valere 0, la Ξ – ha S= –2 e le K0 hanno S=+1; si può escludere che tali particelle
siano i prodotti di decadimento di una particella con stranezza diversa da zero perché non ci sono
particelle con stranezza la cui massa sia tale da produrre Ξ – in associazione con più K0. Ricordando
che la Λ a sua volta decade in una coppia di pioni (un’altra V) le tracce a V dovevano essere in tutto 3.]
51
Cap. 3
Modello a Quark
La regolarità con cui le particelle studiate nel capitolo precedente si dispongano su queste
tavole fa pensare che possano non essere elementari ma a loro volta costituite da
particelle più piccole in virtù delle quali si producono le regolarità. Un modello fu
proposto indipendentemente da Gell-Mann e da Zweig nel 1964. Sempre a Gell-Mann
si deve il termine “quark” con cui furono chiamate tali costituenti, termine mutuato da
una frase non-sense presente in “Finnegan’s wake” di Joyce: “three quarks for Mr
Mark”. Il modello che andremo a costruire è detto pertanto “modello a quark”.
Vedremo:
- la composizione dei multipletti (di barioni e di mesoni)
- i quark
- la costruzione del decupletto di barioni a spin 3/2 a partire dai quark
- la costruzione dell’ottetto di mesoni (introdurremo la possibilità che esistano degli
“antiquark” con cariche di tutti i generi opposte a quelle dei quark)
- la costruzione dell’ottetto di barioni a spin ½)
L’esistenza del decupletto di barioni porterà a ipotizzare l’esistenza di un nuovo
tipo di carica (il “colore”), la cui esistenza è resa necessaria dal fatto che i quark sono
fermioni e quindi soggetti al principio di Pauli. L’introduzione della carica di “colore”
consentirà di spiegare perché possiamo avere particelle che in linea di principio,
ammettendo la sola esistenza dei tre quark senza la carica di colore, non potrebbero
esistere.
L’introduzione (o la “scoperta”) di nuovi quark si rivelerà necessaria per spiegare
la scoperta di nuove particelle. I nuovi quark furono scoperti esattamente nella stessa
maniera in cui furono scoperti gli altri, osservando nuove particelle negli urti fra adroni.
Il numero di particelle, che sembrava essersi ridotto grazie all’introduzione dei quark,
ricominciò così a crescere: da tre divennero quattro… e dopo qualche anno furono
cinque.
3.1. La composizione dei multipletti
Analizziamo la composizione dei multipletti per cercare di capire come si possono
interpretare assumendo che le particelle che li compongono siano composte di particelle
più piccole. Nei multipletti ci sono degli adroni, che sono dei fermioni che subiscono
l’interazione forte. I loro eventuali costituenti devono essere a loro volta degli adroni. E
poiché gli adroni a spin più alto sono i barioni a spin 3/2 quello che possiamo pensare è
che le particelle che compongono questi multipletti siano particelle a spin 1/2 e di
doverne combinare almeno tre per ottenere una particella di spin totale uguale a 3/2. Le
particelle costituenti gli adroni devono anche essere elettricamente cariche perché le
52
particelle che andranno a costituire avranno carica elettrica negativa, positiva o nulla e in
un caso addirittura positiva con modulo pari a 2. Questi componenti devono avere carica
elettrica positiva o negativa per poter dare origine a particelle di carica nulla e, almeno in
certi casi, devo anche avere una carica di stranezza perché devono dare origine a
particelle composte che complessivamente mostrano una carica di stranezza.
Abbiamo dunque bisogno di tre oggetti, tre fermioni, di spin ½ e dotati di carica
elettrica; questi tre fermioni li chiamiamo “quark” e devono essere di tre specie diverse
(dette anche “sapori” dei quark),
Il QUARK UP ha una carica pari a 2/3 di quella del protone e stranezza S = 0.
Lo rappresentiamo come una torre quadrata di mattoncini LEGO alta 2 unità di una
qualche unità di misura. Ogni unità rappresenterà una carica pari a + 1/3
Un altro sapore di quark di cui possiamo aver bisogno è quello che chiamiamo
QUARK DOWN: ha una carica elettrica pari a – 1/3 di quella del protone ed è privo
di stranezza. Utilizzando sempre i mattoncini LEGO ci conviene rappresentarlo con un
buco quadrato al centro (una carica negativa!) e un’altezza pari a una unità.
Infine abbiamo bisogno di un quark che porti una carica di stranezza che dovrà
servire per costruire particelle con una qualche carica di stranezza. Il QUARK
STRANO avrà una carica pari a – 1/3; con i LEGO avrà un buco quadrato in mezzo,
di altezza un’unità, e gli mancherà un lato… per essere “strano”: S = – 1.
Quesito: a quale categoria appartengono i quark?
a. bosoni
b. adroni
c. leptoni
[La risposta esatta è la b.]
3.2. Barioni a spin 3/2
Con i tre quark che abbiamo appena definito cerchiamo di dare vita a delle combinazioni
che corrispondano alle caratteristiche delle particelle osservate sperimentalmente.
Cominciamo col cercare le combinazioni che danno luogo ai barioni di spin 3/2. Poiché
i quark hanno ciascuno spin 1/2 per costruire una particella di spin 3/2 sarà
sufficiente metterne insieme tre con i tre spin allineati.
53
Per capire quali particelle possiamo ottenere, prendiamo tutte le combinazioni di tre
quark diversi o meno tra loro e vedere quali caratteristiche complessive hanno le
particelle “composte”.
Cominciamo a costruire la particella che
si ottiene con 3 QUARK DOWN: si
ottiene una particella che ha spin = 3/2,
carica elettrica
q = (–1/3)+(–1/3)+(–1/3)= – 1
e stranezza S=0.
La costruzione è evidente col modellino
a mattoncini: un buco alto tre unità…
con tutti i bordi completi.
Questa particelle effettivamente esiste tra quelle scoperte nei raggi cosmici o negli
acceleratori: ed è particella Δ– che nel nonetto dei barioni occupa la prima posizione in
alto a sinistra.
Altra combinazione possibile di tre quark è
quella che si ottiene con 2 QUARK
DOWN + 1 QUARK UP: la carica totale
è (–1/3)+(–1/3)+(+2/3)= 0 (particella
neutra, la costruzione con i LEGO è
piatta, non presenta né buchi né
protuberanze), la stranezza è S=0 (non vi è
nessun quark strano)
Questa particelle effettivamente esiste tra quelle scoperte nei raggi cosmici o negli
acceleratori: ed è particella Δ0 che nel nonetto dei barioni occupa la seconda posizione
in alto a sinistra.
Terza possibile combinazione: 2 QUARK
UP + 1 QUARK DOWN: la carica totale
è (+2/3)+(+ 2/3)+(–1/3)= +1 (particella
con carica unitaria, la costruzione con i
LEGO presenta una protuberanza di
altezza tre unità = 1), la stranezza è S=0
(non vi è nessun quark strano)
e spin = 3/2
Tale particella esiste ed è la particella Δ+.
54
Con TRE QUARK UP si ottiene la
particella di
carica q = (+2/3)+(+ 2/3)+(+1/3)= +2
stranezza S = 0
e spin = 3/2.
È la particella Δ++.
Cominciamo a utilizzare i quark strani.
Con UN QUARK STRANO + DUE
DOWN si ottiene una particella di
carica q = (–1/3)+(–1/3)+(–1/3)= – 1
stranezza S = –1
e spin 3/2.
Tali particella esiste nel nonetto di barioni,
ed è la Σ*–.
Con un quark per sorte,
ossia con UN QUARK UP, UN
QUARK DOWN e UN QUARK
STRANO si ottiene una particella (priva)
di carica q = (+2/3)+(–1/3)+(–1/3)= 0
stranezza S = –1
e spin 3/2 (un barione).
Tali particella esiste nel nonetto di barioni,
ed è la Σ*0.
Ultima combinazione con un quark strano:
con DUE QUARK UP e UN QUARK
STRANO si ottiene una particella con
carica q = (+2/3)+(+2/3)+(–1/3)= +1
stranezza S = –1
e spin 3/2 (un barione).
Tali particella esiste nel nonetto di barioni,
ed è la Σ*+.
Costruiamo le combinazioni con due quark strani
55
Con DUE QUARK STRANI + UN
QUARK DOWN si ottiene la particella di
carica q = (–1/3)+(–1/3)+(–1/3)= – 1
stranezza S = – 2
e spin 3/2 (un barione).
Tali particella esiste nel nonetto di barioni,
ed è la Ξ*–.
Infine, ultima combinazione
Con DUE QUARK STRANI + UN
QUARK UP si ottiene la particella (priva)
di carica q = (–1/3)+(–1/3)+(+2/3)= 0
stranezza S = – 2
e spin 3/2.
Tali particella esiste nel nonetto di barioni,
ed è la Ξ*0.
Di combinazioni con tre quark ce ne sarebbe un’altra:
quella che si ottiene con TRE QUARK STRANI.
Essa dovrebbe avere stranezza S = – 3
carica q = (–1/3)+(–1/3)+(–1/3) = – 1
Questa particella non esisteva tra quelle conosciute, o meglio,
non era ancora stata scoperta quando fu proposto il “modello
a quark”…
Ma vuoi vedere che questa particella non è ancora stata scoperta perché non si avevano
ancora energie sufficienti a produrla? Era possibile in effetti che questa particella avesse
una massa più alta di quelle all’epoca raggiungibili. I ricercatori si misero dunque a
cercare negli acceleratori più potenti disponibili all’epoca una particella che avesse queste
caratteristiche. Quello che si trovò al Brookhaven National Laboratory in un
esperimento fatto con camera a bolle1 in quel 1964, ovvero poco dopo che Gell-Mann e
Zweig ebbero proposto il loro modello, fu quello che si vede nelle foto a pagina
seguente:
1
La CAMERA A BOLLE è uno strumento di rivelazione di particelle elementari ideato e
realizzato per la prima volta da Donald Arthur Glaser nel 1952. È simile per concezione alla camera a
nebbia (o di Wilson) del 1899. Lo strumento (facente parte dei rivelatori a ionizzazione) usa una
quantità di liquido surriscaldato oltre il punto di ebollizione, quindi molto instabile, e tale da provocare
nuclei di ionizzazione con anche piccole perturbazioni dovute a particelle cariche. Quando viene
irraggiato con un fascio di particelle, quelle cariche lo ionizzano e provocano l’ebollizione del liquido in
prossimità della traccia ionizzata: in questo modo facendo una fotografia nel momento in cui si invia un
fascio di particelle si vede una fila di bollicine che corrisponde alla traccia delle particelle cariche.
56
La camera a bolle era ovviamente tenuta in un campo magnetico, in modo da far
assumere alle particelle cariche una traiettoria curva dalla cui curvatura risalire alla
quantità di moto di ciascuna particella. L’evento, riportato sopra a destra “ripulito” e qui
sotto ingrandito mostra quanto segue:
vi si vede una particella di carica elettrica negativa
(dal disegno non si vede bene, ma se ne può
misurare la curvatura) che emette una particella
neutra (non la si vede ma… la si evince) e un
pione negativo (traccia 4 verso destra). La
particella neutra che non si vede poco dopo
decade in una Λ0 e una π0, particelle entrambe
elettricamente neutre ma il π0 dopo un po’ decade
in due fotoni (che è il decadimento tipico del π0, e
si può dunque identificare il π0 dai fotoni (7) e (8))
e la Λ decade come al solito in un pione (5) e un
protone (6).
Ricostruendo la catena di decadimenti si osserva
che a ogni decadimento c’è una variazione della
stranezza di una unità: dalla Ξ0 che ha stranezza S
= – 2 e decade in una Λ0 che ha stranezza S = – 1,
che a sua volta decade in particelle senza
stranezze.
La particella che ha dato origine a questa catena dovrebbe avere stranezza S = – 3…
proprio quella che mancava dalla tabella di barioni costruita fino a quel momento. A
questa particella fu dato il nome di Ω – ed è l’unica con stranezza pari a – 3.
Ecco dunque tutte le combinazioni cui possiamo dare origine coni tre quark fissati
all’inizio (escludendo le combinazioni con cariche opposte che vengono identificate con
le antiparticelle del nonetto, ormai promosso a decupletto.
57
3.3. I mesoni
I mesoni – in quanto adroni, cioè particelle che subiscono l’interazione forte –
dovrebbero essere costituiti delle stesse particelle di cui sono costituiti i barioni. Se i
barioni subiscono l’interazione forte è perché i quark di cui sono composti subiscono
l’interazione forte; e quindi i mesoni, essendo adroni, devono essere costituiti da quark
pure loro. I mesoni però, al contrario dei barioni, hanno spin intero. In particolare,
nell’ottetto dei mesoni, le particelle hanno tutte spin pari a 0.
Un modo per costruire particelle di spin 0 è quello di usare due particelle di spin ½
che possano avere SPIN UP e SPIN DOWN in modo da poter avere una particella
che abbia momento angolare totale nullo. Il problema è che mettendo assieme due quark
– le particelle necessarie per averne una di spin 0 – non si riesce a costruire una particella
di carica +1 oppure –1 oppure 0. Le cariche che si costruiscono sono tutte frazionarie,
mentre in natura non si osservano mai cariche che siano una frazione della carica
elettrica del protone.
Quali sono i mesoni?
58
Abbiamo quattro K, tre π e una η. I due K0 si distinguono l’uno dall’altro perché uno ha
stranezza +1 e l’altro ha stranezza – 1: quindi devono essere l’uno l’antiparticella
dell’altro. Gli altri due K, quelli carichi, uno positivo e l’altro negativo, si possono
considerare l’uno l’antiparticella dell’altro. E così i π– rispetto ai π+: sono particelle
perfettamente uguali salvo per la carica elettrica; quindi si possono considerare l’uno
l’antiparticella dell’altro. Il π0 e l’η non hanno né carica elettrica né carica di stranezza,
quindi devono essere considerati ciascuno l’antiparticella di sé stesso.
Dobbiamo quindi riuscire a costruire, con i mattoni che abbiamo ipotizzato essere
quelli giusti – i tre quark – le particelle dell’ottetto dei mesoni.
Se delle particelle esistono le antiparticelle, è possibile/probabile che dei quark
esistano gli antiquark. Un ANTIQUARK sarà una particella la cui carica sarà opposta di
quella del quark corrispondente.
Nel caso del QUARK ANTI-UP la carica elettrica sarà –2/3 anziché +2/3, il
QUARK ANTI-DOWN avrà carica +1/3, come pure il QUARK ANTISTRANO. I
quark anti-up e anti-down non avranno nessuna carica di stranezza, mentre il quark antistrano avrà stranezza +1. Possiamo rappresentare queste particelle con la stessa tecnica
vista per il decupletto dei barioni, ossia con le LEGO, e con le stesse analogie:
il quark ANTI-UP avrà un buco al centro profondo 2 unità, mentre il quark ANTIDOWN sarà una piccola torre quadrata alta 1 unità, così come l’ANTI-STRANO cui
sarà anche aggiunto un bordo di stranezza.
Cerchiamo quindi di comporre quark (di spin ½) con anti-quark (di spin –½) in modo
da avere particelle di spin nullo… e costruire l’ottetto di mesoni!
Cominciamo con il K0: esso ha q = 0 e S = +1: dobbiamo utilizzare un anti-quark
strano; per far sì che la carica totale sia nulla dobbiamo mettergli vicino un quark di
carica – 1/3, cioè un anti-down.
Quello che otterremo sarà
il K0.
59
Se invece mettiamo assieme un ANTI-STRANO + UP si ottiene una particella di carica
q = + 1 e stranezza S = +1
Questa è il K+.
La particella STRANO + ANTISTRANO corrisponderà a
una particella di stranezza S = 0 e carica q = 0.
Abbiamo così costruito … una π o una η?
Sulla base della composizione degli altri pioni (che vedremo tra un attimo), possiamo
dedurne che si tratta di una particella η, particella priva di stranezza ma i cui
componenti portano una carica di stranezza.
0
Il π0 si può invece considerare la combinazione di un u u , oppure di un d d .
Sarebbe anche possibile che π0 fosse un s s , ma questa è una combinazione molto
speciale che non ha partner carichi, come invece li ha il π0, come vedremo tra poco.
Delle due combinazioni che danno origine al π0 qual è quella corretta? Se queste due
combinazioni sono diverse… esiste una terza particella priva di stranezza e priva di
carica elettrica? No, non si trova nessuna particella che abbia q = 0 e S = 0 diversa dal π 0
e diversa dall’η. Sappiamo che in meccanica quantistica uno stato può essere la
sovrapposizione di stati diversi: lo stato u u si mescola allo stato d d per dare lo
stato π0, che quindi è considerato una sovrapposizione dei due stati: non c’è modo
di distinguerli dal punto fisico, i due stati sono indistinguibili fra loro. Nel caso invece
dell’ s s qualcosa cambia perché i costituenti hanno una carica di stranezza.
Il π0 è una combinazione lineare degli stati u u e d d .
Le altre combinazioni possibili di due quark sono la UP+ANTI-DOWN ( u d ) e la
sua antiparticella costituita da DOWN+ANTI-UP ( d u ), rappresentate qui sotto.
60
La prima ha carica q = +1, la seconda ha carica q = – 1
ed entrambe hanno carica di stranezza nulla, S = 0, poiché non vi è nessun quark strano
in esse. Queste particelle si possono dunque interpretare come il π+ e il π –.
Poiché entrambe non contengono quark strani riteniamo che anche il π0 non contenga
quark strani.
Le ultime due combinazioni possibili di quark e antiquark sono la s d e la s u
Esse danne luogo entrambe a particelle con stranezza S = – 1 perché contengono un
quark s. La prima ha carica q = 0 mentre la seconda ha carica q = – 1. La prima dunque
è l’antiparticella di K0. La seconda è la K – .
Ricapitolando dunque: i mesoni sono costituiti da un quark e un antiquark. Devono
essere costituita da quark perché i quark sono i costituenti dei barioni a spin 3/2 che
sentono l’interazione forte; questo vuol dire che sono i quark a subire l’interazione forte;
e poiché i mesoni, particelle di spin ½, subiscono anch’essi l’interazione forte (cioè sono
adroni), devono anch’essi essere costituiti da quark. Con tre quark però non si possono
fare particelle di spin 0. Si potrebbero fare con due particelle, ma con due non si
riescono a fare le particelle di carica +1, 0 o –1; l’unica possibilità è quella di usare
particelle e antiparticelle in modo che le cariche dell’una possano annullare le cariche
dell’altra. Nell’ottetto di mesoni non facciamo dunque che combinare quark e antiquark,
e le possibili combinazioni sono nove ma due di esse danno origine allo stesso mesone
in quanto indistinguibili tra loro.
Tra le otto combinazioni ci sono quelle che danno luogo ai quattro K, due neutri e due
carichi; i due neutri hanno stranezza opposta, uno +1 e l’altro – 1 perché contengono
rispettivamente un quark antistrano e un quark strano. Invece le particelle senza
stranezza sono le π0, le π+, le π– e le η. Le π+ e le π– sono uno l’antiparticella dell’altro
perché sono la combinazione di un quark e un antiquark di specie diversa: questo
permette di costruire particelle con carica elettrica diversa da 0. Le tre combinazioni
possibili che danno una particella neutra sono u u , d d e s s ; poiché il π+ e il
π– non hanno stranezza, sembra ragionevole ipotizzare che il π0 non contenga alcun
61
quark strano, e quindi dovrebbe essere o u u o d d : queste due combinazioni
sono però del tutto equivalenti al fine di ogni misura che si possa eseguire, quindi sono
di fatto indistinguibili l’una dall’altra sperimentalmente; d’altra parte in meccanica
quantistica esiste il principio di sovrapposizione, cioè uno stato può essere la
sovrapposizione di più stati: lo stato π0 si può interpretare come la sovrapposizione
ovvero come la combinazione lineare di due stati, uno composto da u u e l’altro da
d d : a seconda della misura che si esegue si può vedere l’uno o si può vedere l’altro;
in effetti noi vediamo sempre una combinazione dei due stati e non possiamo
distinguerli tra di loro.
Appare altrettanto ragionevole assegnare la combinazione s s alla particella η, della
quale non esistono versioni cariche (in generale costituite da quark di specie diversa);
d’altra parte la η non ha nemmeno lei alcuna carica di stranezza, ma il motivo in questo è
perché è composta di quark di stranezza opposta.
Quesito: di cosa sono composti i mesoni?
a. di due quark
b. di un quark e un antiquark
c. di un quark e un antiquark dello stesso sapore
[La risposta corretta è la b.]
Ricapitolando (in orizzontale la stranezza, in diagonale la carica). questa è la
composizione dei mesoni.
us K
d s K0
u u 0
d d 0
s s
d u
su K
ud S= 0
sd K0
62
S = +1
S = –1
3.4. I barioni a spin ½
Abbiamo visto nel 3.2. che il decupletto di barioni a spin 3/2 si spiega semplicemente
con la combinazione di tre quark: UP, DOWN e STRANGE.
L’ottetto di mesoni si spiega con le stesse particelle ma combinate in maniera diversa con
gli ANTIQUARK.
Sperimentalmente si è osservata però anche l’esistenza di un ottetto di barioni a spin ½.
Si possono ottenere particelle di spin ½ combinando tre quark di spin ½? Certo, è
sufficiente che due dei tre abbiano spin di somma pari a 0
Quindi possiamo spiegare l’ottetto di barioni a spin ½ con la stessa tecnica del modello a
quark. Ma a differenza del decupletto di barioni a spin 3/2 qui ne abbiamo solo otto.
Come si legge l’ottetto?
In diagonale la carica, in orizzontale la stranezza (prima riga S = 0, seconda riga S = – 1,
terza riga S = – 2)
Poiché lo spin è ½ due quark devono avere spin SU e uno deve avere spin GIÙ.
Come nel caso del decupletto dei barioni a spin 3/2, ci aspetteremmo di trovare dei
barioni a spin ½ che si distribuiscono su una tavola triangolare simile: ovvero quella del
disegno a sinistra:
63
Invece quello che si trova è la tavola a destra, che ha la forma di un esagono. Perché i
barioni a spin 3/2 sono dieci e quelli a spin ½ sono solo otto? Per capirlo possiamo
sovrapporre le due tavole: notiamo che c’è una certa somiglianza: nel decupletto dei
primi ci sono quattro particelle prive di stranezza e con carica che va da –1 a + 2, mentre
nell’ottetto dei secondi se ne trovano solo due, con gli stati di carica 0 e +1.
Le particelle con stranezza S = – 1 compaiono nella stessa disposizione, se non nello
stesso numero. Non ci interessa tanto il numero quanto le combinazioni cui si dà luogo
in questo caso. Anche le Ξ della terza riga si corrispondono (nel decupletto abbiamo le
“star”). Manca invece la combinazione che nel decupletto era stata attribuita alla Ω–.
Osservando attentamente la sovrapposizione dei due diagrammi si nota che nell’ottetto
mancano i vertici del triangolo del decupletto. Le combinazioni Δ–, Δ++ e Ω– non sono
64
combinazioni casuali: sono in effetti combinazioni molto speciali: sono le tre
combinazioni costituite da tre quark uguali:
d d d
u u u
s s s
Quindi nell’ottetto di barioni a spin ½ si hanno esattamente le stesse combinazioni che si
avevano nel decupletto dei barioni a spin 3/2 ma mancano quelle di tre quark tutti
uguali. Non è così strano che manchino proprio quelle; piuttosto non è normale che
esistano nel decupletto: i quark infatti sono particelle a spin ½, sono cioè fermioni, e
obbediscono al principio di Pauli: “Non ci possono essere due o più particelle di spin
semintero che si trovino nello stesso stato”. Quindi non sono “normali” le combinazioni
d d d , u u u , s s s , vietate dal principio di
Pauli. Com’è che allora le abbiamo trovate nel decupletto dei barioni a spin 3/2? La
soluzione al problema della loro esistenza verrà dall’ipotesi dei cosiddetti “quark
colorati”.
3.5. Teoria del colore.
Riscriviamo la combinazione
u u u nel seguente modo:
65
I tre quark hanno la massa del quark UP e dunque hanno la stessa energia (immaginiamo
che i quark siano fermi all’interno della particella), hanno la stessa carica elettrica pari a
+2/3, la stessa stranezza S = 0, lo stesso momento angolare pari a ½ e, a differenza
dell’ottetto di barioni a spin ½, hanno anche uguale la terza componente del momento
angolare.
Ma per il principio di esclusione di Pauli due fermioni non possono occupare lo stesso
stato:
non è possibile; invece
è possibile perché
le due particelle uguali hanno spin opposto. Quindi non è che manchino delle
combinazioni nell’ottetto dei barioni a spin ½, ma ce ne sono di troppe nel decupletto
dei barioni a spin 3/2. Ma se vengono osservate significa che deve essere possibile
costruirle.
Se la combinazione
esiste, e se vogliamo salvare il principio di Pauli,
dobbiamo assumere che le tre particelle siano tra loro distinguibili per qualche altra
caratteristica: se sono distinguibili per una caratteristica che non sia la carica, la stranezza
o lo spin ma un “nuovo tipo di carica” allora non si trovano nello stesso stato. Questa
“nuova carica” però non è mai stata osservata. Occorre pensare a una “nuova carica”
che non sia osservabile attraverso gli esperimenti, e che perciò sia “interna” al quark. E
dovendo occupare i tre quark lo stesso stato per quel che riguarda gli altri parametri,
abbiamo bisogno di tre stati di questo “nuovo tipo di carica”. Non essendo la fantasia
dei fisici così straordinaria, a questo nuovo tipo di carica si attribuì il nome di colore:
esistono dunque quark in tre diversi stati di colore: ROSSO, VERDE e BLU.
è dunque una combinazione possibile.
Questa carica di colore non riusciamo mai a vederla negli esperimenti, non è “esposta”
agli esperimenti, non vi è cioè nessuna interazione che sia proporzionale a questa carica
di colore. Dobbiamo allora ipotizzare che le uniche combinazioni possibili siano quella la
cui somma di colore sia sempre pari a 0.
Ad esempio, la particella Σ0, che ha stranezza pari a – 1, e nessuna carica elettrica, dovrà
essere immaginata come composta da tre quark di colore diverso, ad esempio
0 d rosso uverde sblu
Non sappiamo ancora perché succede questo ma sappiamo che deve essere così perché è
l’unico modo di spiegare l’esistenza di queste combinazioni e il fatto che questa carica di
colore non si riesce a misurare in nessun modo. È anche abbastanza evidente – o
66
perlomeno c’è il sospetto – che questa carica di colore sia effettivamente la carica che
permette l’interazione forte tra particelle: in fondo, tutte le particelle formate da quark
sono adroni, che sentono l’interazione forte; e come l’interazione gravitazionale ha come
sorgente la massa, e l’interazione elettrica ha come sorgente la carica elettrica, così anche
l’interazione forte avrà una sorgente che molto probabilmente è la carica di
colore. L’interazione forte tra due protoni deve dipendere dunque dall’interazione forte
dei loro quark che interagiscono per la loro carica di colore. Possiamo cioè pensare alla
forza attrattiva tra due protoni come a una sorta di forza di Van der Waals non di tipo
elettromagnetico ma di tipo forte. La forza forte che lega i protoni è quello che si
“vede” all’esterno del singolo protone: sarà un’interazione un po’ più debole di quella
che esiste tra quark all’interno di uno stesso protone ma abbastanza grande da tenere
insieme i protoni nel nucleo.
Perché gli effetti di questa interazione di colore non si sono mai visti? Facendo degli
esperimenti dovrei riuscire a vedere delle particelle di carica frazionaria e persino
colorate… ma qualunque esperimento si faccia non consente di trovare una particella di
questo tipo. Si immagina allora che esista un qualche meccanismo di confinamento che
fa sì che i quark delle particelle fisiche che si osservano non possano uscire dalle
particelle medesime, per cui non si possono osservare liberi. Questo fatto inizialmente
fece pensare che questi quark non fossero delle particelle fisiche realmente esistenti ma
fossero solo un artificio matematico. Vedremo però più avanti che i quark esistono in
quanto tali e si può spiegare il loro meccanismo di confinamento per cui quello che
possiamo vedere nei rivelatori non sono mai quark liberi ma soltanto particelle
(combinazioni di questi quark) prive di qualunque carica di colore.
Naturalmente questo sarà vero anche per i mesoni, dove le due particelle di cui sono
costituiti, un quark e un antiquark, dovranno anch’esse essere colorate con colori a
somma nulla (=bianco), ad esempio un quark rosso e l’altro anti-rosso, oppure uno blu e
l’altro anti-blu.
Quesito: cosa distingue i barioni dell’ottetto da quelli del decupletto?
a. La composizione in termini di quark
b. Il numero di quark di cui sono composti
c. Lo spin delle particelle
[La risposta corretta è la c.]
3.6. Nuovi quark
Col passar del tempo si fecero nuovi esperimenti che condussero alla scoperta di nuovi
quark. Non è così utile andare a vedere come furono scoperti i singoli nuovi quark: il
meccanismo è lo stesso che ha condotto alla scoperta dei quark appena conosciuti, cioè
attraverso esperimenti nei quali si facevano collidere degli adroni con dei nuclei atomici,
producendo nuove particelle che poi decadono. Osservando i prodotti di decadimento e
67
calcolando la loro massa invariante si osservano dei picchi, che corrispondono alla
particella di cui sono figlie i prodotti del decadimento.
La particella
J /
Samuel C. C. Ting e il suo gruppo (1974) con il manifesto che mostra il picco di massa invariante
osservato nell’acceleratore presso cui si teneva l’esperimento
Facendo esperimenti con acceleratori più potenti nel 1974 il gruppo di Samuel Ting vide
comparire un nuovo picco a energie più alte di quelle che si erano osservate in
precedenza: la nuova particella fu chiamata J / (gei-psai). Non se ne poteva spiegare
l’esistenza alla luce del modello a quark messo a punto fino a quel momento, avendo già
esaurito tutte le possibili combinazioni; la nuova particella doveva essere costituita di
nuovi quark: J / è una particella neutra a spin 0 e non ha carica di stranezza: doveva
quindi essere costituita da un quark e un antiquark privi di quella che in gergo è chiamata
carica di sapore, cioè i due quark non dovevano essere né un UP, né un DOWN né uno
STRANGE; la J / venne pertanto interpretata come combinazione di un quark
chiamato CHARM e del suo antiquark, l’ANTICHARM:
J / cc
La CHARM ha
q = + 2/3
S=0
C = 1.
Questa particella non fu trovata per caso ma venne cercata perché era stata predetta da
tre fisici, di cui uno italiano:
Sheldon Lee Glashow
John Iliopoulos
68
Luciano Maiani
i quali, analizzando i decadimenti delle particelle fino ad allora conosciuti, avevano
concluso – per spiegare i rapporti relativi dei tempi di decadimenti di queste particelle –
che doveva esistere un quarto quark oltre ai tre conosciuti fino allora; questo quarto
quark venne attivamente cercato. La sua scoperta venne in realtà fatta
indipendentemente da due gruppi di ricerca, uno allo Stanford Linear Accelerator
Center, capeggiato da Burton Richter, e uno al Brookhaven National Laboratory,
condotto da Samuel Ting al MIT, un gruppo la chiamò J e l’altro la chiamò
Effettivamente notarono di aver scoperto la stessa particella e entrambi i gruppi
annunciarono le loro scoperte l’11 novembre 1974. L’importanza di questa scoperta è
evidenziata dal fatto che la successiva serie di rapidi cambiamenti nella fisica delle
particelle del tempo divenne nota come la “rivoluzione di novembre”. Richter e Ting
vennero premiati per la loro scoperta condivisa con il Premio Nobel per la fisica nel
1976.
La particella
Υ
Alcuni anni più tardi si scoprirono altre particelle di massa ancora più pesante.
Nel 1977 al Fermi National Accelerator
Laboratory, noto anche come Fermilab, un gruppo
di ricercatori guidato da Leon Lederman, scoprì –
attraverso l’osservazione nei decadimenti di coppie
di muoni – uno stato risonante a una massa pari a
9,5 GeV non compatibile con nessun oggetto
precedentemente noto (vedi disegno a destra). Di
nuovo non si poteva costruire utilizzando i quark
scoperti fino a quel momento: non aveva
stranezza, aveva carica nulla, era un mesone (che
fu chiamato upsilon)… aveva tutta una serie di
caratteristiche che già erano appannaggio di altre
combinazioni: doveva essere la combinazione di
un quark e di un antiquark di nuova
generazione che fu chiamata BOTTOM o
BEAUTY. Tale quark era stato teorizzato nel
1973 dai fisici Makoto Kobayashi e Toshihide Nello schema si vedono i diversi picchi
ascissa la massa invariante e in
Maskawa per spiegare la violazione della simmetria (in
ordinata la sezione d’urto) della nuova
CP.
particella che venne chiama ypsilon
bb
69
Il BOTTOM ha
q = – 1/3
S=0
C=0
B= – 1
Oltre all’UP, al DOWN e al STRANGE, esistono dunque anche il quark CHARM e il
quark BOTTOM o BEAUTY.
La particella
Oltre alle particelle appena citate, che sono adroni perché formate dall’urto di altri
adroni, in una serie di esperimenti condotti tra il 1974 e il 1977 da Martin Lewis Perl e
dai suoi colleghi allo SLAC fu scoperta la particella TAU. (Lewis Perl ricevette per essi il
premio Nobel nel 1995, che condivise con Frederick Reines. Quest’ultimo vinse il
premio per la scoperta del neutrino.)
A differenza di quelle sopra, il TAU non interagisce per interazione forte ma solo
elettromagneticamente o debolmente: è dunque un LEPTONE. Il TAU può trovarsi in
soli due stati di carica (come l’elettrone e il muone) e dato che in tutto e per tutto
assomiglia all’elettrone e al muone si assume che anche per la TAU esista un neutrino
specifico, di sapore “tau”, il quale deve esistere nei due stati di neutrino e di antineutrino
ciascuno con numero leptonico opposto all’altro.
m 2 m p
e e
70
3.7. Test ed esercizi
Quante diverse specie di neutrini esistono?
a. una sola
b. tre
c. sei
d. otto
e. due
[La risposta corretta è la b.
Non confondere le specie (o sapori) con i possibili stati, due per ciascun neutrino.]
Dall’analisi dei decadimenti delle particelle strane Glashow, Iliopoulos e Maiani predissero
l’esistenza di una particella. Quale?
a. Il positrone
b. Il leptone τ
c. Il barione Ω−
d. Il quark c
e. Il quark b
[La risposta corretta è la d.
Essi previdero l’esistenza della particella J/Ψ che fu pensata composta di c e anti-c]
Se rappresentiamo un quark s con mattoncini per le costruzioni dei bambini in modo che
assuma la forma di una U con 4 unità di lato, come si rappresenta un quark s¯?
a. Con un rettangolo 2×1
b. Con un quadrato di due unità
c. Con un rettangolo 3×2
d. Esattamente come il quark s
e. Con un quadrato di 4 unità di lato
[La risposta corretta è la c.]
Quanto valgono i numeri quantici di stranezza, charm e bellezza della particella J/Ψ?
a. S=0; C=0; B=-1
b. S=1; C=0; B=-1
c. S=-1; C=0; B=1
d. S=0; C=0; B=0
e. S=0; C=0; B=1
[Il quark bottom ha bottomness = – 1, il quark antibottom ha bottomness = 1.
La risposta corretta è la d.]
Per quale motivo non esistono adroni a spin 1/2 che occupano i vertici del triangolo nel
diagramma qS?
a. Per il principio di Pauli
b. Non ci sono quark che abbiano i giusti numeri quantici
c. Per la conservazione del momento angolare
d. Perché non c'è modo di combinare quark in modo da costruire adroni di spin 1/2 che abbiano le
caratteristiche richieste
e. Perché si tratta di particelle molto instabili
[La risposta esatta è la a.]
Quale tra questi decadimenti è permesso?
71
a.
b s
b.
b c e e
b d e e
d. b c e
e. b s c
c.
[Il bottom ha q= – 1/3, come lo strange e il down. Il quark charm ha q= +2/3.
Muoni ed elettroni negativi hanno q = – 1. In a. c. d. e. non si conserva la carica.]
72
Cap. 4
Teoria delle interazioni fondamentali
Questa è dunque la situazione
fino a questo momento (anno 1976)
In questo capitolo affronteremo i seguenti
argomenti:
1. Teoria delle interazioni fondamentali.
2. Diagrammi di Feynman.
3. Fotoni virtuali
4. L’equazione di Dirac.
5. I positroni
6. Riassunto
7. Elettrodinamica quantistica
8. Fabbrica di particelle
9. La QED dei fotoni liberi
10. Analogie
Se vogliamo capire il panorama delle particelle elementari che abbiamo scoperto fino
adesso dobbiamo comprendere di più come avvengono le interazioni a livello
microscopico, dobbiamo cioè elaborare una teoria delle interazioni fondamentali.
Lo scopo di questo corso esula dalla possibilità di spiegare in maniera esaustiva e
rigorosa tutta la teoria delle interazioni tra le particelle elementari: occorrerebbe un corso
di livello universitario. Ci limiteremo a dare delle informazioni abbastanza precise e
circostanziate ma non completamente rigorose che però dovrebbero essere sufficienti a
comprendere quello che si trova scritto sui siti web, su wikipedia… a scopo più o meno
divulgativo e a fornire qualche spunto per trovare una maniera di veicolare questi
contenuti agli studenti.
Per introdurre una teoria delle interazioni fondamentali quello che dobbiamo fare
è, dal punto di vista quantistico, trovare la descrizione di un processo in cui abbiamo uno
stato iniziale che in seguito a una interazione si trasforma in uno stato finale diverso:
Ad esempio, nello stato iniziale potremmo avere un pione negativo e un protone e nello
stato finale potremmo avere la produzione di una Λ e di una K nella produzione
associata. Questa trasformazione da uno stato iniziale a uno stato finale in meccanica
quantistica è rappresentabile come l’azione di un operatore S che esegue la
trasformazione:
f S i
73
Nel caso in cui lo stato finale sia uguale allo stato iniziale, cioè nel caso in cui non ci sia
stata alcuna interazione l’operatore è semplicemente l’operatore-identità, cosa non
particolarmente interessante. Ciò che interessa invece è riuscire a scrivere S in modo da
rappresentare l’operazione che trasforma lo stato iniziale in uno stato finale diverso.
Cosa si fa di solito negli esperimenti? Ad esempio si misura la sezione d’urto della
produzione di una Λ e di una K dall’urto di un pione e di un protone.
Il modulo-quadro del prodotto matriciale (una probabilità) andrà correlato con ciò che si
osserva
f Si
2
Partiamo da un processo più semplice per capire come è fatta S: la diffusione di due
elettroni. Supponiamo di avere due elettroni nello stato iniziale con quantità di moto
diverse, indicate rispettivamente con p e con q.
i e p eq
Supponiamo che questi elettroni stiano andando l’uno contro l’altro: a un certo istante la
loro distanza sarà così piccola da rendere abbastanza forti le forse di tipo elettrostatico
repulsive per cui questi due elettroni tenderanno a respingersi e cambieranno direzione e
dunque anche quantità di moto.
La prima cosa da far sparire (dal punto di vista formale) è far sparire i due elettroni
iniziali, cioè applicare uno dopo l’altro due operatori-distruzione (indicati con l’apice
negativo),
p q i 0
uno, quello a destra, che distrugge l’elettrone con quantità di moto q, l’altro, quello a
sinistra, che distrugge l’elettrone con quantità di moto p. Rimaniamo con uno stato di
“vuoto” rispetto alle particelle dello stato iniziale; queste particelle non possono però
sparire: nello stato finale osserviamo ancora due particelle, che però hanno quantità di
moto diverse. Per produrre lo stato finale dobbiamo quindi introdurre due nuovi
operatori, di creazione (indicati con l’apice +) di elettroni con quantità di moto q’ e p’:
p' q' p q i e p 'eq '
Applicando in sequenza i quattro operatori, ritroviamo nello stato finale i due elettroni
con quantità di moto q’ e p’.
S però non può contenere soltanto operatori di distruzione e creazione di particelle,
perché se ci fossero solo le particelle queste non potrebbero interagire: la distruzione e la
successiva creazione di particelle non è quello che si osserva nell’universo: le particelle
hanno bisogno di un campo per interagire, un campo che cambi la quantità di moto di
74
queste particelle. La presenza del campo è indicata dalla Π che è funzione della posizione
delle particelle che interagiscono, x e x’.
Π in realtà non è funzione della posizione delle particelle ma della loro distanza relativa:
x x'p' q' p q i f
quando le particelle sono abbastanza vicine, cioè quando x – x’ è abbastanza piccola,
l’interazione diventa abbastanza intensa da produrre il cambiamento della loro quantità
di moto.
Dunque, l’operatore S che descrive tutto il processo deve essere rappresentato dalla
combinazione di due operatori di distruzione di elettroni, seguiti da due di creazione di
elettroni e da un operatore che rappresenta l’interazione tra gli elettroni.
Cerchiamo di dare una veste grafica a questa sequenza di operazioni, anche per
schematizzare e rendere più semplice l’interpretazione del tutto: due linee orientate l’una
verso l’altra rappresenteranno lo stato iniziale: indicheranno in qualche modo la quantità
di moto dei due elettroni, ovvero la direzione verso cui si stanno muovendo; le linee
vanno l’una verso l’altra. Dobbiamo immaginare che il tempo scorra verso destra. Man
mano che passa il tempo la distanza tra i due elettroni diventa via via più piccola,
dopodiché le due particelle vanno distrutte: quando agiscono gli operatori di distruzione
le linee spariscono
Quando si applica l’operatore di creazione dei due nuovi elettroni dobbiamo di nuovo
disegnare due linee, che devono però avere direzioni diverse, quelle della quantità di
moto q’ e p’ risultanti dall’interazione: gli elettroni che prima si stavano avvicinando ora
si allontanano:
75
Per rappresentare l’interazione tra i due elettroni possiamo mettere una linea ondulata
(indicata con γ) che colleghi le due parti del grafico e che rappresenti l’operatore Π, il
quale dipenderà dalla distanza (x – x’) tra le due particelle che stanno interagendo:
Come si può interpretare l’operatore Π? Visto che gli operatori che danno luogo alle
linee che rappresentano i fermioni che stanno interagendo sono delle linee di fatto
rappresentabili dal punto di vista formale come degli operatori di creazione e di
distruzione di qualcosa (in questo un elettrone), in questo caso possiamo immaginare di
aver creato un oggetto con un opportuno operatore A+ nel punto x (quello in alto) e di
averlo poi distrutto con l’operatore A– nel punto x’ (che è quello in basso)
Dal punto di vista classico non c’è un punto in cui avviene l’interazione, l’interazione
avviene lungo tutta la traiettoria. Ma dal punto di vista quantistico posso immaginare,
dato che la posizione, per esempio, è qualcosa che non posso misurare, che l’interazione
avvenga nel momento in cui un elettrone si trova in x e l’altro in x’.
La linea ondulata potrebbe rappresentare una qualche particella che viene creata da un
opportuno operatore nel punto x in alto dove il primo elettrone cambia la sua quantità di
moto e viene poi distrutta da un altro opportuno operatore nel punto x’, in basso, dove
è l’altro elettrone che cambia la sua quantità di moto.
Π deve quindi contenere due operatori, uno di creazione e uno di distruzione, che
devono agire tra due stati di vuoto, in quanto la linea ondulata deve essere creata e
distrutta prima di poter essere osservata sperimentalmente.
L’espressione prodotto di due operatori di creazione e distruzione tra due stati di vuoto
A+(x)A–(x) si chiama “PROPAGATORE DEL CAMPO”.
Quesito: come si rappresenta un’interazione in fisica delle particelle?
a. Come un operatore, o un prodotto di operatori, che agendo sullo stato iniziale lo
trasformano nello stato finale
b. Con un vettore che rappresenta una forza
76
c. Come la produzione, da parte di ciascuna particella di materia, di un campo che
modifica le proprietà dello spazio circostante la particella
[La risposta esatta è la a.]
4.2. Diagrammi di Feynman
Richard Feynman (1918 – 1988)
Un disegno come quello a destra è un “diagramma di Feynman”: è una serie di linee in
cui ogni linea dritta rappresenta una particella di materia, ogni linea ondulata rappresenta
il campo, il punto in cui il campo si connette alla particella di materia è il punto dove
avviene l’interazione. Nella figura sopra è rappresentata l’interazione elettrostatica tra
due elettroni: quando sono giunti a una distanza sufficientemente breve interagiscono
per mezzo del campo (linea ondulata), quindi si allontanano l’uno dall’altro.
Tali diagrammi prendono il nome dal fisico che li ha inventati e la loro importanza è
fondamentale nella fisica delle particelle: non sono semplicemente dei disegnini che
illustrano in maniera schematica quello che succede a livello di interazione di tipo
quantistico tra le particelle ma sono un vero e proprio strumento matematico: a ciascuna
linea di un diagramma di Feynman si può associare una operazione matematica che i
fisici teorici sanno combinare opportunamente per ricavare informazioni preziose sulla
probabilità che un determinato processo avvenga; sono quindi espressioni matematiche
il cui modulo quadro fornisce la probabilità che avvenga la transizione dallo stato iniziale
(rappresentato alla sinistra del diagramma) allo stato finale (rappresentato nella parte
destra).
77
Le linee dritte rappresentano gli elettroni che stanno interagendo; la linea ondulata
rappresenta l’interazione. Che tipo di interazione è? Di fatto potremmo immaginare
gli operatori di creazione e distruzione che producono quella linea ondulata come un
operatore di creazione e distruzione di una qualche particella che rappresenta la
propagazione del campo. Che particella deve essere quella che dà luogo all’interazione
che stiamo analizzando?
L’interazione che stiamo analizzando è una interazione di repulsione elettrostatica tra
elettroni. Noi sappiamo, dagli esperimenti fatti con l’elettroscopio, che particelle
elettricamente cariche come gli elettroni interagiscono attraverso il campo elettrico; e se
si prende una particella carica e la si fa muovere (una corrente) si produce un campo
magnetico; particelle cariche in movimento sono sensibili agli effetti di un campo
magnetico che si trova in una certa regione di spazio; quindi sappiamo dalla fisica
classica che gli elettroni interagiscono tra loro attraverso quello che oggi chiamiamo
campo elettromagnetico: la linea ondulata nel diagramma di Feynman deve quindi (in
qualche modo) rappresentare il campo elettromagnetico.
Sappiamo – dagli esperimenti di diffrazione della luce – che la luce è un’onda; di che
tipo? Ce lo dicono le equazioni di Maxwell (1831 – 1879), che teorizzano che campi E e
B possono propagarsi attraverso un’onda elettromagnetica
E 0
B 0
B
E 0
t
E
B 0 0
t
NEL VUOTO
B
2 2
c B 0
2
t
2E
2 2
c E 0
2
t
2
La velocità dell’onda elettromagnetica è proprio la velocità della luce, c. È immediato
associare a un’onda luminosa un’onda elettromagnetica: quindi il campo magnetico deve
essere presente all’interno della luce. D’altra parte, dalla meccanica quantistica, sappiamo
che, se prendiamo un elettroscopio carico e lo illuminiamo con una luce di frequenza
sufficientemente elevata, esso si scarica (per effetto fotoelettrico). Nel corso di
meccanica quantistica abbiamo visto che questo fenomeno portò Einstein a ipotizzare
l’esistenza dei quanti di luce, o fotoni. Riassumendo: la luce “contiene” il campo
elettromagnetico, il quale è responsabile dell’interazione fra elettroni; la luce è un flusso
di fotoni: la conclusione è che l’oggetto scambiato tra i due elettroni interagenti deve
essere un fotone.
Come si legge allora il diagramma di Feynman: i due elettroni che si stanno avvicinando
l’un l’altro si scambiano a un certo punto un fotone: uno dei due elettroni “cede” un
78
fotone e, per la conservazione della quantità di moto la sua quantità di moto cambierà, e
cambierà quindi direzione; l’altro elettrone assorbe il fotone “lanciato” dall’altro, assorbe
la sua energia e quantità di moto e potrà a sua volta cambiare direzione… per cui da uno
stato in cui ci sono due elettroni con quantità di moto p e q giungiamo a uno stato in cui
ci sono due elettroni con quantità di moto p’ e q’.
L’oggetto A(x) che dobbiamo mettere nel propagatore dei diagrammi di Feynman –
pezzo che costituisce parte integrante dell’operatore S che consente di trasformare lo
p ' , q ' S p, q
stato iniziale nello stato finale secondo la
rappresentare il campo elettromagnetico.
– deve in qualche modo
A(x) = campo (di bosoni)
Tutte le particelle che rappresentano un campo devono essere dei bosoni (con spin
intero)… perché per i bosoni non vale il principio di Pauli. Se valesse per loro il
principio di Pauli non potrebbero stare nello stesso stato; noi sappiamo invece che se ci
sono più sorgenti di campo, in un punto preciso dello spazio devono agire i campi
prodotti dalle varie sorgenti (principio di sovrapposizione), campi nello stesso stato dal
punto di vista classico; dal punto di vista quantistico dobbiamo immaginare che vi siano
bosoni prodotti da sorgenti diverse che arrivano nello stesso punto dello spazio con
identiche caratteristiche e dunque con lo stesso stato di energia, quantità di moto… I
campi dunque che rappresentano delle interazioni devono essere associati a
bosoni.
Le particelle che interagiscono sono invece dei fermioni. Nella rappresentazione dei
diagrammi di Feynman e anche dal punto di vista matematico i fermioni (ogni elemento
del diagramma di Feynman può essere tradotto in un preciso operatore matematico che
poi permette di calcolare l’ampiezza di probabilità di una transizione) sono rappresentati
da operatori del tutto simili (a parte dettagli irrilevanti) a quelli che traducono le linee
ondulate del campo. E come le onde possono diventare particelle in meccanica
quantistica, così le particelle possono diventare onde secondo la relazione di De Broglie:
p
mv
Dunque le particelle rappresentate nei diagrammi di Feynman come linee dritte sono
pensabili in meccanica quantistica come onde che si propagano esattamente come fanno
i campi:
Ψ(x) = campo (di fermioni)
Non vi è dunque nessuna differenza – nel formalismo che andremo ad adottare – tra il
campo di un fotone e il campo di un elettrone, cambiano solo i dettagli di come vengono
scritti gli operatori corrispondenti.
79
4.3. Fotoni virtuali
Ruotiamo leggermente il diagramma di prima per dare maggiormente il senso del tempo
che trascorre verso destra
Lo scorrere del tempo è in realtà del tutto irrilevante in un diagramma di Feynman che è,
per i fisici teorici, soprattutto uno strumento di calcolo che associa a ciascuna linea
l’operatore giusto.
L’elettrone in alto a sinistra a un certo punto cambia direzione perché emette un fotone,
il quale porta via una parte della quantità di moto iniziale dell’elettrone, il quel dunque,
per effetto della conservazione della quantità di moto, deve cambiare direzione.
Nel frattempo si sta avvicinando a questo elettrone un altro elettrone, proveniente dalla
sinistra in basso, che intercetta il fotone emesso dal primo elettrone, lo assorbe e ne
assorbe la quantità di moto, deviando così anch’esso la sua velocità
Siamo sicuri che l’oggetto che sta lì in mezzo è un fotone identico a quelli che
stanno in un’onda elettromagnetica (quelli che abbiamo ritenuto responsabili
dell’effetto fotoelettrico)?
No… non è identico!
I fotoni sono particelle a massa nulla e i fotoni che vengono scambiati tra elettroni
nei diagrammi di Feynman non possono avere massa nulla.
Vediamo perché.
pi , Ei p f , E f p , E
è la conservazione del quadrimpulso; se si
conserva il quadrimpulso si conserva anche il quadrimodulo: a sinistra esso è pari a E2 –
80
p2 (cioè la massa dell’elettrone) mentre a destra avrò il quadrato del primo quadrimpulso
(di nuovo la massa dell’elettrone) più il quadrato del secondo (il quadrimpulso del
fotone è nullo se ipotizziamo che la massa di questi fotoni sia nulla) più il doppio
prodotto dei due quadrimpulsi calcolato col prodotto scalare della cinematica
relativistica.
m m 2 E f E 2 p f p
2
2
da cui otteniamo:
E f E p f p cos
E f E E 2f m 2 E cos
eliminiamo il fattore in comune e quadriamo:
E 2f E 2f m2 cos2
E 2f 1 cos2 m2 cos2
m 2 cos2
E
1 cos2
2
f
Questa espressione è priva di senso perché l’energia finale (al quadrato) dell’elettrone
dovrebbe essere negativa…
Questo ci dice che il fotone scambiato non è un fotone perfettamente identico a quelli
che compongono l’onda elettromagnetica; il fotone scambiato deve essere un
FOTONE MASSIVO. Come tale, esso non può esistere per un tempo indefinito: noi
non osserviamo mai fotoni dotati di massa. Questi elettroni, una volta emessi, devono
necessariamente essere “raccolti” da qualcuno, da qualche elettrone nelle vicinanze; se
non vi è nessun elettrone nelle vicinanze deve essere “rimangiato” dallo stesso elettrone
che lo ha emesso. Dunque i fotoni che costituisco il campo elettromagnetico e ai quali si
imputa l’interazione tra particelle cariche non possono di fatto essere osservati. Vengono
quindi definiti FOTONI VIRTUALI.
I fotoni virtuali non possono essere osservati come tali, ma si può assumere che esistano
e calcolare l’ampiezza di probabilità della transizione dallo stato iniziale a quello finale
usando le regole di Feynman e questa ampiezza di probabilità, una volta calcolata,
coincide quasi esattamente, entro gli errori sperimentali, con quella che viene misurata
sperimentalmente. La teoria quindi è consistente. Quella che ci stiamo facendo è l’idea
classica di un processo quantistico: può essere utile a suggerire una qualche
rappresentazione mentale ma non deve condizionare la nostra visione: ciò che davvero
conta sono le equazioni che scriviamo su un pezzo di carta.
Di questi fotoni virtuali osservo gli effetti… e quindi li misuro.
Quesito: è possibile che un elettrone emetta un fotone cambiando direzione?
81
a. Sì. Gli elettroni interagiscono per interazione elettromagnetica e quindi emettono
fotoni
b. Solo in presenza di almeno un’altra particella di materia
c. No, mai. Non si conserva il quadrimpulso
[La risposta corretta è la b.]
4.4. L’equazione di Dirac
Come sono fatti gli operatori che rappresentano le linee dei diagrammi di Feynman?
Cerchiamo di intuire come sono costruiti nei vari casi.
IL FOTONE LIBERO
1
Ax , t
V
ik x
ik x
Ak t e A k t e
k
vi si riconosce l’espansione in serie di Fourier di un segnale periodico: una somma di
termini oscillanti con frequenze diverse preceduta da un fattore di
normalizzazione. Il fotone libero si propaga come un’onda nello spazio. L’unica
differenza rispetto al fotone classico è che i vettori Ak e A– k non saranno semplicemente
degli scalari ma degli oggetti più complicati, opportuni operatori di creazione e di
distruzione di fotoni, appunto. Poiché il fotone libero classicamente rappresenta un’onda
e le onde sinusoidali che sono le componenti di queste somme sono soluzioni
dell’equazione dell’oscillatore armonico è chiaro che la propagazione di un fotone libero
sarà rappresentabile in termini di operatori di distruzione e creazione di oggetti soluzioni
dell’equazione d’onda dell’oscillatore armonico. L’unica differenza rispetto agli oscillatori
visti in meccanica quantistica è che qui bisogna considerare oscillatori relativistici. Il
fotone libero dunque non è altro che un oggetto che ha l’aspetto matematico di un’onda
che si propaga più o meno liberamente.
Se il fotone libero è una sovrapposizione di onde sinusoidali, il fotone virtuale è la
sovrapposizione di tutte le possibili onde che conservano il quadrimpulso scambiato
nell’interazione.
L’ELETTRONE LIBERO
L’elettrone soddisfa l’equazione
E 2 p 2 m2
che posso riscrivere come p E m 0
In meccanica quantistica quella p, quella E e quella m non sono semplici numeri ma sono
degli operatori
2
a p
x
2
2
x a y p y a z p z at E bm 0
2
Se questa quantità vale sempre zero significa che l’operatore associato vale sempre zero.
82
In meccanica quantistica la quantità di moto è i moltiplicato per il gradiente (stiamo
parlando in unità di ħ, c = 1) e l’energia è la derivata rispetto al tempo:
i
i
i
i
ax
ay
az
at bm 0
y
z
t
x
Devo trovare i valori dei coefficienti ax, ay, az e at (che sono matrici) e di b che
rendono vera l’equazione qualunque siano i valori che risultano dall’applicazione
dell’operatore a uno stato dell’elettrone. Cosa non facilissima da fare… Tali coefficienti
non possono essere le matrici 2x2 di Pauli, ma devono essere almeno matrici 4x4. Dirac
le costruì a partire dalle matrici di Pauli e da esse ricavò le combinazioni che fanno sì che
sia b= –1. Tali combinazioni sono le famose QUATTRO MATRICI γμ DI DIRAC,
con le quali l’equazione sopra acquista la seguente, celebre veste:
Equazione di Dirac
i
m 0
x
Si osserva anche che la soluzione di questa equazione non esiste se Ψ non è un oggetto
complesso: è un oggetto a quattro componenti chiamato SPINORE che rappresenta la
propagazione libera di un elettrone.
L’equazione deve valere in realtà per qualunque fermione in propagazione libera.
Paul Dirac scrisse la sua equazione (per descrivere come un elettrone si doveva
propagare liberamente) nel 1928, cioè ancor prima che venissero analizzare le interazioni
tra particelle con i meccanismi sopra.
La matrice di Dirac si trova scritta in forme diverse nei vari libri: ad esempio, utilizzando
la convenzione di Einstein per cui
x
i m 0
essa diventa
in maniera manifesta covariante relativisticamente perché la sommatoria di prodotti di
quantità con indice in alto per oggetti con lo stesso indice in basso in cinematica
relativistica equivale a uno scalare e quindi tutta l’equazione è fatta di uno scalare meno
un altro scalare (la massa del fermione) moltiplicato per uno spinore e quindi è
relativisticamente invariante.
83
Se poi a questa convenzione si aggiunge la convenzione secondo la quale non serve il
simbolo di sommatoria sugli indici ripetuti, l’equazione di Dirac diventa
i
Infine, talvolta il prodotto
l’equazione diventa allora:
m 0
viene scritto con delta barrato (leggi: de slash);
Comunque la si scriva, la descrizione di un fermione libero avviene attraverso uno
spinore che rispetta le prescrizioni dell’equazione suddetta.
Alla fine, l’elettrone libero apparirà come una funzione del tipo:
ip x iEt
x u p e
p
qualcosa che ha quattro componenti e dipende dalla quantità di moto.
Questa è una soluzione dell’equazione di Dirac e rappresenta il campo dell’elettrone
libero. Questo oggetto assomiglia moltissimo a quello che abbiamo scritto per il campo
dei fotoni: in entrambi i casi abbiamo degli oggetti oscillanti che si propagano come
onde. L’unica differenza tra un fotone e un elettrone è che il fotone è un oggetto con
spin=1 (lo si capirà da un’altra serie di considerazioni che vedremo più avanti) mentre
l’elettrone è un oggetto di spin ½ e dunque quella u p davanti è un operatore a quattro
componenti, che assomiglia a un quadrivettore relativistico con tre componenti spaziali e
una componente temporale, pur essendo una cosa del tutto diversa… che viene
moltiplicata per un fattore oscillante.
Il positrone
La cosa scoperta da Dirac analizzando la propagazione di un elettrone libero è la
E 0 …e fin qui non c’è
nulla di strano… ma se assegniamo all’energia un valore negativo, E 0 , ugualmente
seguente: possiamo avere elettroni con energia positiva
troviamo una soluzione per l’equazione di Dirac; la sostituzione di un’energia positiva
con un’energia negativa iEt iEt equivale a invertire la direzione del tempo:
t t . Che significato ha tutto ciò?
Un elettrone di energia negativa si comporta dunque come un elettrone che si
muove a ritroso nel tempo. Se si filma un elettrone che si muove in un campo magnetico
si osserva che, a causa della forza di Lorentz, percorre una traiettoria circolare con un
certo verso; guardando il filmato all’indietro si vede l’elettrone percorrere la medesima
traiettoria nel verso opposto, come se avesse una carica opposta. Non si è in grado di
stabilire se il filmato va in avanti o all’indietro senza conoscere la carica della particella.
84
Un elettrone che va indietro nel tempo equivale a tutti gli effetti a un elettrone di carica
positiva. Dirac dunque anticipò l’esistenza dell’antimateria, in particolare l’esistenza degli
elettroni positivi, cioè i positroni.
L’equazione di Dirac fu scritta prima della scoperta di Anderson. Si sapeva già
perciò che doveva esistere l’antiparticella dell’elettrone… perché la soluzione di
positrone è una soluzione possibile per l’equazione di Dirac. Il fatto che la soluzione sia
possibile non vuol dire che la particella necessariamente ci deve essere… ma in qualche
modo la si attendeva, o meglio, non risultò così sorprendente trovarla.
4.5. I positroni
Se il positrone è del tutto equivalente a un elettrone che si muove all’indietro nel
tempo… cosa possiamo dire a riguardo?
Nel diagramma sotto il tempo scorre da sinistra verso destra: due elettroni viaggiano uno
verso l’altro, uno emette un fotone che viene raccolto dall’altro e i due elettroni quindi si
allontanano; il diagramma rappresenta dunque la diffusione di un elettrone su un altro
elettrone.
I diagrammi di Feynman non vanno però interpretati alla lettera: sono degli strumenti
matematici che consentono di sostituire a ogni elemento grafico un operatore tale che si
possa calcolare alla fine l’ampiezza di probabilità di transizione tra lo stato iniziale e lo
stato finale. Possiamo ridisegnare il diagramma ruotato verso destra. Se immaginiamo
che il tempo scorra sempre verso destra
vediamo un elettrone in basso a sinistra che viene avanti nel tempo e, dopo aver emesso
un fotone, torna indietro nel tempo; quello a destra viene indietro nel tempo e dopo aver
assorbito l’elettrone torna in avanti nel tempo. Come si deve interpretare? Alla luce della
teoria di Dirac si può interpretare in questo modo: la particella che sembra andare
indietro nel tempo non è un elettrone ma in realtà un positrone, l’antiparticella
dell’elettrone., che si muove verso destra, nella direzione positiva del tempo e si avvicina
all’elettrone. Quando positrone ed elettrone vengono in contatto spariscono entrambi
(processo di annichilazione): questo non viola alcuna regola o principio di conservazione
85
(a parte quello dell’energia, ma è problema che “risolveremo” a breve): la carica elettrica
totale iniziale è nulla (quella dell’elettrone è negativa, quella del positrone è positiva ma in
valore assoluto la loro somma è nulla); le due particelle si toccano, svaniscono, e al loro
posto compare un fotone… che però deve essere virtuale (abbiamo visto che nel
diagramma in cui c’è una linea fermionica con una linea bosonica il diagramma
medesimo non può dare risultati fisici sensati). Questo bosone è costretto dal fatto di
possedere una massa a “materializzare in una coppia particella-antiparticella (lo si evince
dal fatto che le due frecce sono orientate una nella direzione positiva del tempo e l’altra
nella direzione negativa del tempo).
Abbiamo dunque un diagramma nel quale è previsto un nuovo fenomeno, quello
dell’ANNICHILAZIONE: una particella e un’antiparticella (un fermione e un
antifermione) annìchilano dando vita a un campo bosonico, ovvero formando un
fotone che dopo un po’ produce una nuova coppia fermione-antifermione. Qui non c’è
nulla che ci dice che la coppia fermione-antifermione dello stato finale sia identica alla
coppia iniziale, potrebbe essere una coppia fermione-antifermione qualunque, e dunque
dovremmo poter osservare questo fenomeno.
Ritorniamo un attimo a considerare i
POSITRONI come ELETTRONI A ENERGIA NEGATIVA
Perché in molti testi si dice che gli elettroni a energia negativa (prima che si trovasse la
soluzione del positrone) costituivano un problema?
In linea di principio il fatto di avere delle energie negative è un problema fino a un certo
punto: nella fisica classica si affrontano problemi in cui le energie possono anche
assumere valori negativi. Tuttavia il punto è che questi valori negativi delle energie sono
sempre limitati: in realtà l’energia di una particella è sempre positiva, non fosse altro che
perché è la radice quadrata di p2 + m2; se a volte otteniamo un numero negativo, ad
esempio quando scriviamo l’energia gravitazionale tra due corpi, è perché, potendo
scegliere in modo arbitrario dove fissare l’energia nulla (le energie sono misurabili a
meno di una costante: quello che conta sono le differenze di energia, non il valore
dell’energia in assoluto), abbiamo fissato lo zero all’infinito; ma quando troviamo un
valore negativo dell’energia possiamo in realtà sempre trovare un valore costante da
sommare a questa energia per farla tornare positiva e rendere così felice Einstein che
può scrivere che l’energia di un oggetto è uguale alla radice quadrata di p2 + m2; il punto
di difficoltà dell’equazione di Dirac (prima che si trovasse la soluzione del positrone)
non era dunque tanto nelle energie negative quanto nel fatto che le energie
negative permesse non erano limitate dal basso;
86
in altre parole un elettrone libero può avere una energia minima pari alla sua massa e una
energia massima che può andare fino a più infinito, mentre se consideriamo tutte le
possibili soluzione dell’equazione di Dirac dobbiamo ammettere che ci siano elettroni
che hanno una energia massima pari alla massa dell’elettrone e una energia minima che
può andare fino a meno infinito: l’energia di questi elettroni non è limitata dal basso… e
questo che non va bene perché vorremmo poter avere sempre la facoltà, aggiungendo
una costante arbitraria, di riportare i valori dell’energia a valori positivi…
… a meno che (appunto) non si assuma che gli elettroni a energia negativa sono
delle particelle fermioniche in tutto e per tutto uguali agli elettroni ma con un
comportamento tale da far sembrare che rispetto agli elettroni abbiano i segni cambiati
delle cariche, dato che tutto va come se il tempo scorresse all’indietro: la soluzione è
dunque il positrone.
4.6. Riassunto
PER I FERMIONI
I fermioni sono particelle di materia, quindi devono obbedire alla legge della cinematica
relativistica
E 2 p 2 m2
Dal punto di vista quantistico però energia e quantità di moto non sono degli scalari
banali ma sono la prima la derivata rispetto al tempo e la seconda il gradiente di una
funzione particolare; quindi bisogna scrivere un’equazione che contenga questi operatori
applicati alla funzione d’onda di un fermione che si sta muovendo liberamente nello
spazio e che abbia la proprietà che elevando al quadrato quella che secondo l’equazione
di Schrödinger è considerata l’energia ci faccia ottenere il quadrato dell’operatore
quantità di moto più il quadrato della massa. Facendo queste operazioni di giunge
all’equazione di Dirac
i
m 0
87
nella quale ci sono le quattro componenti spazio-temporali del quadrimpulso (le tre
derivate spaziali dell’impulso e quella temporale dell’energia) moltiplicate per qualcosa
che però, per poter dare una soluzione, non può essere uno scalare ma un insieme di
matrici 4x4, le gamma di Dirac. L’operatore che rappresenta un fermione che si propaga
nello spazio dev’essere qualcosa che ha quattro componenti sulle quali agiscono questi
operatori 4x4 che mescolano le varie componenti della funzione d’onda del fermione
man mano che questa si propaga.
Per la meccanica quantistica l’elettrone non è qualcosa di localizzato in un punto ma è
qualcosa che si propaga in tutto lo spazio come un’onda; quindi ci sarà un termine a
moltiplicare questo oggetto di quattro componenti a rappresentare la propagazione di
un’onda libera e che quindi avrà la forma di un esponenziale complesso oppure la
somma di un seno e un coseno con tutte le possibili frequenze che può assumere un
fermione.
uk expip x iEt
k
PER I BOSONI
I fotoni sono quelli che nella meccanica quantistica rappresentano le onde
elettromagnetiche e in qualche modo devono essi stessi rappresentare il campo
elettromagnetico. Dal momento che la luce, che è fatta di fotoni, si propaga sotto forma
di onde, questi fotoni devono essere rappresentabili da operatori che hanno la forma di
qualcosa di ondulatorio, e quindi come una somma infinita di termini nei quali ci sono
tutte le possibili frequenze che i fotoni possono assumere nella regione di spazio in cui si
sta considerando la presenza del campo
A Ak expip x iEt
k
Poiché sia fotoni si possono interpretare in termini di onde sia i fermioni si possono
interpretare in termini di onde (esattamente come i campi) non c’è sostanziale differenza
fra onde di campo e onde di materia.
Ora, se vogliamo interpretare
l’interazione tra due particelle di materia
in una regione di spazio dobbiamo
considerare l’interazione come il prodotto degli operatori delle particelle di
materia e gli operatori delle particelle di
campo:
In particolare avremo una somma infinita di termini che rappresentano tutte le possibili
onde di particelle di materia che si possono avere in linea di principio nel volume; una
somma infinita di termini che sono tutti i possibili fotoni che si possono avere nel
88
volume e una somma infinita di termini che rappresentano tutte le possibili onde di
particelle di materia che possono interagire con le prime.
f
... ...... A A ...... ... i
Quando si prende questo operatore e lo si “racchiude” tra uno stato iniziale e uno stato
finale di un certo tipo, tutti gli infiniti prodotti che non agiscono sullo stato iniziale o
sullo stato finale danno come risultato zero e dunque gli unici termini che sopravvivono
sono gli operatori che distruggono lo stato iniziale, consentono la propagazione del
campo da uno dei due fermioni incidenti all’altro dei due fermioni incidenti, e
consentono la creazione dello stato finale. Alla fine sopravvivono pochi degli infiniti
operatori possibili nella matrice di interazione S.
Questa matrice calcolata tra lo stato iniziale e lo stato finale ci dà l’ampiezza di
probabilità per la transizione che porta lo stato iniziale ad assumere lo stato finale; il
modulo quadro di questa quantità ci dà la probabilità di transizione… e tale probabilità è
legata alla sezione d’urto se sto rappresentando un evento in cui ho nello stato iniziale
due particelle che collidono e nello stato finale i prodotti della collisione,
f Si
2
oppure un tempo di decadimento se nello stato iniziale ho una particella e nello stato
finale ho due o più particelle che sono i prodotti del decadimento della particella.
Questi elementi che hanno carattere puramente matematico si possono rappresentare
graficamente come linee dritte nel caso di fermioni e ondulate nel caso dei bosoni che
rappresentano i campi:
Questi diagrammi sono utili per riuscire a calcolare “in modo semplice” questi elementi
di matrice (nel senso che è più facile farlo usando i diagrammi di Feynman piuttosto che
calcolando tutti i possibili prodotti tra operatori che potrebbero essere presenti nella
transizione).
Di fatto quindi il diagramma di Feynman è uno strumento matematico che mi consente
il calcolo della sezione d’urto o dei tempi di decadimento ma dal punto di vista
concettuale possiamo interpretare quello che si vede nel diagramma di Feynman come
un processo nel quale un fermione emette un bosone di campo che viene raccolto da un
altro fermione e quindi l’interazione viene rappresentata come lo scambio di un
qualche “mediatore” del campo; in pratica con la meccanica quantistica si torna a una
visione delle forze non più come di azioni a distanza ma di forza che agiscono in un
punto preciso, laddove le particelle si toccano (quasi).
89
Quesito: quanti tipi di operatori devono esserci nell’elemento di matrice che descrive
un’interazione tra particelle?
a. Due: i campi fermionici che descrivono le particelle interagenti
b. Almeno due campi fermioni e uno bosonico
c. Uno: il campo bosonico che rappresenta l'interazione
[La risposta esatta è la b.]
4.7. Elettrodinamica quantistica
Abbiamo così tutti gli ingredienti per cominciare ad analizzare i processi, ad esempio, di
natura elettromagnetica. La teoria che include tutti questi processi prende il nome di
elettrodinamica quantistica (QED) e il suo sviluppo si deve a Richard Feynman che
introdusse i diagrammi che portano il suo nome.
Possiamo studiare tutti i processi che hanno a che fare con l’interazione elettromagnetica
tra fermioni elettricamente carichi disegnando tutti i possibili diagrammi che portano da
uno stato iniziale designato allo stato finale che ci interessa
Cominciamo da un processo piuttosto semplice, in parte già illustrato, sulla base del
quale abbiamo costruito questa teoria. Il processo in questione è quello della diffusione
elastica tra particelle elettricamente cariche
Due elettroni, avvicinandosi l’uno all’altro, si respingono per effetto della repulsione
elettrostatica: abbiamo visto che questo processo si può interpretare come la cessione di
un fotone da parte di una particella e la raccolta del medesimo da parte dell’altra. Se un
elettrone emette un fotone l’elettrone perde una parte della sua quantità di moto che
viene raccolta dall’altro elettrone quando assorbe completamente il fotone emesso dal
primo: quindi è naturale che due particelle cambino direzione e quantità di moto; lo
scambio di fotone lo si può interpretare come lo scambio di un palla da bowling tra due
ragazzi che stanno sullo skateboard; quello che ha lanciato la palla, per effetto della terza
legge di Newton va indietro, chi raccoglie la palla, per effetto della quantità di moto
trasportata dalla palla da bowling va indietro anche lui…
90
Un processo analogo è responsabile dell’attrazione coulombiana: dal punto di vista
formale non c’è differenza tra la repulsione e l’attrazione, il diagramma è lo stesso;
l’unica cosa che cambia è il segno delle cariche attribuite ai fermioni e quindi ciò che
succede è che le particelle invece di allontanarsi si avvicinano. Uno si potrebbe chiedere
come sia possibile che due particelle si avvicinino scambiandosi un fotone visto che
quello che ci si aspetterebbe è ciò che abbiamo visto prima. Lo si può comprendere
guardando una partita di tennis: i giocatori si scambiano la palla tra di loro e finché si
scambiano la palla “sono costretti” a rimanere nel campo a giocare. Se uno dei due
giocatori vuole andare a bere un goccio d’acqua lo può fare solo nel momento in cui non
c’è la palla che va avanti e indietro; nel momento in cui cessa lo scambio del mediatorepalla-da-tennis cessa l’interazione tra i due tennisti, finalmente liberi di andare a fare ciò
che vogliono. Possiamo quindi spiegare anche l’attrazione coulombiana attraverso lo
scambio di un mediatore: questo scambio costringe le due particelle elettricamente
cariche di cariche opposta a stare l’una vicino all’altra perché sono costrette per qualche
motivo a scambiarsi questa particella di campo e quindi a rimanere legate una nel campo
dell’altra.
Effetto Compton
Un processo del tutto analogo che si può rappresentare con un diagramma di Feynman è
l’effetto Compton, che consiste nella diffusine di un fotone da parte di un elettrone.
Abbiamo un fotone nello stato iniziale con una certa
quantità di moto e una certa energia che incide su un
elettrone che nello stato iniziale si trova in un certo
livello energetico all’interno dell’atomo al quale
appartiene, ma che per la trattazione dell’effetto
Compton si può trattare come libero.
Nel momento in cui il fotone interagisce con l’elettrone, il fotone scompare
completamente e nel diagramma di Feynman si disegna il propagatore (non di un
fotone ma) di un elettrone che ha acquisito tutta l’energia del fotone incidente, quindi ha
aumentato la propria energia, si propaga per un po’ di tempo e un po’ di spazio ma in
modo inosservabile e subito dopo “si divide” in un elettrone che si trova nello stato
finale di un elettrone diffuso dall’urto con il fotone iniziale e in un altro fotone di energia
diversa da quella del fotone che lo aveva colpito.
Non c’è niente in questo diagramma che imponga che l’energia del fotone dello stato
finale sia uguale a quella del fotone dello stato iniziale; l’unica cosa che conta – per il
principio di conservazione dell’energia – è che siano uguali le somme delle energie dello
stato iniziale e dello stato finale. Nel diagramma si vede che i due stati iniziale e finale
sono connessi attraverso il propagatore di un fermione.
91
Che cos’è un “PROPAGATORE DI FERMIONE”? Qualcosa del tutto analogo al
“propagatore di un fotone”; è il prodotto di un operatore di creazione di un fermione
per l’operatore di distruzione di un fermione preso tra due stati di vuoto; infatti quello
che si vede è che nel momento in cui il primo fotone viene assorbito dall’elettrone dello
stato iniziale si crea un nuovo elettrone diverso da quello incidente e subito dopo questo
elettrone viene distrutto; quindi da uno stato iniziale di vuoto creiamo un elettrone e poi
lo distruggiamo subito dopo riproducendo uno stato di vuoto; da questo stato di vuoto
può emergere un elettrone e un fotone.
Che questo processo rappresenti effettivamente l’effetto Compton ovvero che
descriva bene quello che accade a livello microscopico lo si capisce da questo: se
associamo a ciascuna di quelle linee, a quelle ondulate, a quelle dritte, al propagatore,
tutti gli operatori matematici che le regole di Feynman impongono di utilizzare quando si
ha un diagramma di questo genere e si calcola il valor medio di questo operatore tra due
stati iniziale e finale che sono quelli che effettivamente osservo e se ne calcolo il modulo
quadro, quello che si ottiene dovrebbe essere la probabilità di osservare un fotone in un
determinato stato finale avendo un certo fotone in un determinato stato iniziale e di
osservare un elettrone in un certo stato finale avendo a disposizione un elettrone in un
certo stato iniziale. Ebbene: se si confronta questa probabilità con quello che si misura
sperimentalmente si trova una coincidenza perfetta. Quindi dobbiamo desumerne che
questo diagramma rappresenta molto bene quello che avviene a livello microscopico. A
noi non interessa cosa davvero avvenga a livello microscopico, ma che a livello
microscopico si possano descrivere le cose anche se non si vedono in modo tale da
riprodurre tutte le misure sperimentali che possiamo fare.
Effetto fotoelettrico
Un altro effetto che consideriamo è l’effetto
fotoelettrico, che consiste nel fatto che un fotone,
interagendo con un elettrone all’interno di un
materiale, viene completamente assorbito – il fotone
non esiste più – e dal materiale viene emesso un
elettrone che se ne va via libero dal materiale; è il
fenomeno che poi effettivamente ha dato origine alla
meccanica quantistica, insieme allo studio dello
spettro di corpo nero.
Nella QED l’effetto fotoelettrico consiste in questo: nello stato iniziale abbiamo un
elettrone che sta in un atomo e un fotone: il fotone viene assorbito, quindi viene
distrutto in un punto assieme all’elettrone dello stato iniziale; leghiamo lo stato iniziale
attraverso il propagatore elettronico ad uno stato finale nel quale abbiamo l’elettrone
dello stato finale, libero e fuori dall’atomo, mentre non si osserva alcun fotone nello
stato finale. Ora questa cosa dal punto di vista cinematico non è possibile: non possiamo
avere un propagatore che diventa un elettrone senza emettere un’altra particella per
92
conservare il suo quadrimpulso; deve succedere quindi che il fotone superstite deve
essere in qualche maniera assorbito dall’intero atomo o dagli altri elettroni o dal nucleo, e
quindi non si vede più: a livello microscopico quello che si vede è un elettrone in un
atomo che raccoglie un fotone che proviene dall’esterno e nello stato finale troviamo un
atomo privo di un elettrone che se ne va libero. Il secondo fotone – che nell’effetto
Compton se ne andava via – nell’effetto fotoelettrico viene semplicemente rimangiato
dall’intero atomo e quindi non si vede nello stato finale. Tuttavia il diagramma di
Feynman è sostanzialmente lo stesso: l’unica cosa che cambia è che nello stato finale non
ci sarà la funzione d’onda di un fotone libero ma ci sarà la funzione d’onda dell’atomo,
che sarà un oggetto fermo perché troppo pesante per potersi muovere in seguito all’urto
col fotone.
L’effetto fotoelettrico è anche sfruttato tecnologicamente in molti modi: tutte le
fotocamere moderne funzionano con questo principio: un fotone arriva su una fetta di
silicio, viene assorbito, la fetta di silicio emette degli elettroni che forniscono una certa
quantità di corrente a un dispositivo, questa corrente si misura e l’intensità della corrente
è proporzionale all’intensità luminosa che ha colpito il pixel di silicio.
In tutti gli smartphone c’è un dispositivo che funziona sulla base di un processo
puramente quantistico.
Di nuovo si può fare il calcolo della probabilità di transizione tra uno stato iniziale
in cui c’è un fotone e un elettrone all’interno di un atomo e uno stato finale in cui c’è un
elettrone libero e l’atomo che in qualche modo ha rinculato a seguito dell’urto;
calcolando con le regole di Feynman l’ampiezza di transizione e facendo il modulo
quadro dell’ampiezza si ottiene la probabilità di osservare questo fenomeno, che coincide
perfettamente con quella che si misura sperimentalmente. Ancora una volta le regole di
Feynman ci permettono di “descrivere” quello che avviene nei volumi piccolissimi della
meccanica quantistica, ovvero questo effetto di scambio, di assorbimento e di emissione,
di particelle bosoniche da parte dei fermioni.
Quesito: in un diagramma di Feynman che rappresenta la repulsione tra elettroni l’interazione
si rappresenta con lo scambio di un fotone virtuale. Come si rappresenta invece l’attrazione tra
due particelle di carica opposta?
a. esattamente nello stesso modo. Il fotone rappresenta l’interazione e non va inteso come un oggetto
puntiforme che è effettivamente scambiato tra le particelle.
b. non abbiamo ancora una teoria coerente che consenta di rappresentare questo tipo d'interazioni.
c. con un “anti-fotone”: un fotone, cioè che si comporta in modo opposto con le cariche elettriche
rispetto a quanto fa il fotone
[La risposta esatta è la a.]
93
4.8. Fabbriche di particelle
Annichilazione
Veniamo ora a quel processo cui abbiamo accennato quando abbiamo detto che nei
diagrammi di Feynman l’orientazione dell’asse del tempo non ha particolare importanza.
Se disegniamo il diagramma di Feynman come nella figura sotto, se immaginiamo la linea
del tempo orientata verso destra quello che si vede è un elettrone in basso a sinistra e un
positrone in alto a sinistra (che a tutti gli effetti è un elettrone che si muove indietro nel
tempo). Ora se questi due oggetti si incontrano in un punto, il processo che si deve
verificare secondo il diagramma di Feynman è quello già citato di “annichilazione” di
particelle
cioè le due particelle vengono distrutte dall’operatore di distruzione nella matrice S e al
loro posto compare un fotone virtuale γ che ha un’energia pari alla somma delle energie
degli elettroni incidenti nel centro di massa e una quantità di moto pari alla somma delle
loro quantità di moto. Questo fotone si può propagare per un po’ ma non può farlo
all’infinito perché è un fotone virtuale, ha una massa diversa da zero, e come tale non
può esistere; quindi a un certo punto deve trasformarsi in una coppia fermioneantifermione; perché in una coppia fermione-antifermione? Perché non avendo numeri
quantici particolari il fotone deve trasformarsi in una coppia di particelle che stanno in
uno stato in cui tutti i numeri quantici sono conservati; se abbiamo un elettrone nello
stato finale, la particella che lo accompagna non può che essere un positrone in modo
che la carica netta del sistema elettrone-antielettrone sia uguale a quella del fotone, cioè
zero, e la carica netta leptonica sia zero (elettrone e positrone hanno carica leptonica
opposta) come quella del fotone…
In questo diagramma però non c’è nulla che impedisca al fotone di trasformarsi in una
qualunque coppia fermione-antifermione. È chiaro che avendo avuto il fotone origine da
una coppia elettrone-positrone è possibile che di nuovo si trasformi in una coppia
elettrone-positrone… ma potrebbe anche trasformarsi in una coppia μ+ μ– … oppure
ancora in un quark e un antiquark.
Facendo dunque scontrare elettroni e positroni ci aspettiamo di veder formarsi
coppie anche di natura diversa da quella di partenza. Questo esperimento si può fare:
si prendono fasci di elettroni e fasci di positroni, si fanno accelerare in un anello di
accelerazione e si fanno scontrare l’uno con l’altro; esperimenti di questo tipo sono stati
94
fatti per numerosi anni in diversi laboratori di ricerca e quello che si vede nell’immagine
sotto è un evento raccolto all’acceleratore LEP con il rivelatore L3
Al LEP si acceleravano elettroni e positroni fino a far assumere loro esattamente la
stessa energia in maniera tale che quando si scontravano al centro di un detector il centro
di massa rimanesse fermo; nel centro di massa si produce quindi un fotone virtuale che
subito dopo materializza in una coppia fermione-antifermione che a quel punto non ha
più memoria della direzione di provenienza dei leptoni iniziali e dunque i due fermioni
prodotti possono essere prodotti ad un angolo qualunque: nel disegno sopra si vedono
due leptoni che viaggiano secondo l’asse orizzontale e che al centro del detector
formano una coppia μ+ μ– (le due linee diagonali rosse); questo è dunque un evento in
cui da una coppia di elettroni produco una coppia di muoni, abbiamo cioè cambiato la
natura di due particelle secondo un processo che è benissimo descritto da un diagramma
di Feynman.
Di nuovo facendo il conto della probabilità di produrre una coppia di muoni a partire
dallo scontro tra un elettrone e un positrone dalle regole di Feynman si trova
esattamente il valore della sezione d’urto (che si può misurare) di questi processi.
Abbiamo dunque la confidenza che i diagrammi di Feynman funzioni perfettamente.
Questo potrebbe essere anche un ottimo sistema per produrre i famosi quark che
abbiamo ipotizzato essere i costituenti delle particelle adroniche. Questi costituenti sono
degli adroni che hanno carica frazionaria rispetto al protone (+2/3 oppure – 1/3)
Quindi in un processo di annichilazione elettrone-positrone in teoria si potrebbero
produrre anche coppie quark-antiquark: quindi dovremmo vedere nel rivelatore tracce di
particelle di carica +2/3 e – 2/3 oppure +1/3 e – 1/3 a seconda dei quark prodotti. Ma
cercando i quark in questo modo non li si trova mai…
Però quello che si trova è qualcosa che assomiglia molto a dei quark.
95
Nel disegno a sinistra e nella rappresentazione a destra si ha una vista di quel che accade
quando i due fasci si scontrano: la vista è trasversale rispetto alla direzione di elettroni e
positroni, che hanno direzione entrante o uscente rispetto al foglio. Le particelle nate
dallo scontro tra elettroni e positroni al centro del detector si diffondono in tutte le
direzioni e hanno almeno una componente della quantità di moto trasversale rispetto alla
direzione perpendicolare al foglio.
Vi si vedono numerose tracce cariche e alcuni eventi neutri che si possono identificare
come diversi adroni: la loro carica totale è sempre nulla, tutti i numeri quantici sono
nulli, la stranezza totale è nulla… ma non si vedono mai quark e antiquark, per cui se
anche il fotone nato dallo scontro elettrone-positrone materializza in una coppia quarkantiquark, per una qualche ragioni questi due si ricompongono immediatamente negli
adroni che formano i multipletti studiati in precedenza.
Quesito: quali particelle si possono produrre nel processo di annichilazione elettronepositrone?
a. L’annichilazione tra elettroni e positroni può dar luogo alla produzione di qualunque coppia
fermione-antifermione purché l’energia nel centro di massa sia sufficiente.
b. L’annichilazione tra elettroni e positroni può dar luogo solamente alla produzione di un’altra coppia
elettrone-positrone
c. L’annichilazione tra elettroni e positroni può dar luogo alla produzione di qualunque coppia di
particelle purché lo spin totale dello stato finale sia nullo
[La risposta esatta è la a.]
96
4.9. La QED dei fotoni liberi
Un fenomeno ben descritto dai diagrammi di Feynman è la cosiddetta
produzione di coppie
Quello che si osserva in certi eventi è il fenomeno seguente: supponiamo di avere un
fotone altamente energetico, con una energia almeno pari al doppio della massa
dell’elettrone. Quando il fotone gamma interagisce con del materiale quello che si
osserva sperimentalmente è che il fotone “converte” in una coppia e+ e – .
Nella camera a bolle immersa nel campo magnetico (foto a destra) si vede cioè
comparire “dal nulla” una coppia elettrone-positrone in un punto del rivelatore dove
“non arrivano” altre particelle (il fotone è neutro e non lascia traccia).
Il fatto che le due particelle assumano traiettoria spiraleggiante e che il raggio di
curvatura diminuisca sempre di più è dovuto al fatto che elettrone e positrone si
muovono nel liquido della camera a bolle, ionizzando il liquido e perdendo così energia.
Com’è possibile la produzione di coppie? Abbiamo già visto come il diagramma di
Feynman riportato sopra a sinistra non può dare risultati sensati. In effetti, se si
calcola l’ampiezza di transizione tra lo stato finale in cui ho un fotone e lo stato finale in
cui ho due elettroni, tale ampiezza è zero, in quanto non si conserva il quadrimpulso, che
nello stato iniziale per il fotone è zero (la massa del fotone è nulla) mentre nello stato
finale dobbiamo avere almeno le masse dei due elettroni. Tale processo non è
realizzabile e appare dunque corretto che i diagrammi di Feynman ci diano un’ampiezza
di transizione pari a zero.
Perché questo processo si verifichi è necessaria la presenza di almeno un altro fermione
che rinculi e assorba una parte dell’impulso che viene perso dal fotone. In effetti non si
osserva mai un fotone “convertire” nel vuoto. I fotoni “convertono” soltanto
quando interagiscono con la materia. Per rappresentare dunque un processo di
questo genere abbiamo bisogno di aggiungere una linea fermionica (disegnata in basso
nel diagramma sotto, che rappresenta una qualche particella della materia all’interno della
quale penetra il fotone che deve convertire, che scambia un fotone con uno dei due
fermioni che vengono prodotti dalla conversione del gamma.
97
Vediamo dunque nel diagramma di Feynman che uno dei due
fermioni della coppia “convertita” (quello in basso) scambia
una parte della sua quantità di moto (attraverso un fotone)
con il fermione presente nella materia. Questo consente la
produzione di coppie perché in questo caso il quadrimpulso si
conserva. E in effetti se si calcola l’ampiezza di probabilità che
questo processo avvenga utilizzando le regole di Feynman si
trova un numero diverso da zero… e non solo diverso da
zero ma il suo modulo quadro è uguale a quello che si misura
sperimentalmente.
Altro fenomeno ben descritto dai diagrammi di Feynman è quello di
Bremsstrahlung (radiazione di frenamento… o Raggi X)
Abbiamo un processo che dal punto di vista dei diagrammi di Feynman è molto
simile alla produzione di coppie. Nello stato iniziale abbiamo un elettrone libero che si
avvicina (quello evidenziato in azzurro), interagisce attraverso lo scambio di un fotone
con un elettrone del mezzo (evidenziato in verde)
Attraverso l’interazione con la materia quello che accade è che l’elettrone libero dello
stato iniziale sparisce completamente, si produce in un propagatore fermionico il quale a
un certo punto emette un fotone libero, reale, con massa nulla. Nello stato finale,
l’elettrone evidenziale in azzurro che prosegue la sua corsa avendo perso una parte della
sua energia che è stata ceduta attraverso il fotone che è stato emesso. Questo è il
fenomeno dell’irraggiamento. Quindi, quando un elettrone penetra in un materiale, per il
fatto di venire frenato dal materiale fa sì che esso irraggi dei fotoni.
Questo non è un processo misterioso: è un processo noto da molto tempo: è il processo,
ad esempio, attraverso il quale si producono i raggi X con i quali si fanno le radiografie:
si usa una grossa differenza di potenziale per accelerare notevolmente degli elettroni e si
mandano a sbattere contro un bersaglio di tungsteno. L’interazione col bersaglio fa sì
che questi elettroni, in un processo di Bremsstarhlung, emettano una certa quantità di
radiazione, che a seconda dell’energia dell’elettrone incidente e della natura del materiale
possono dar luogo nello stato finale a fotoni di energia diversa; nel caso della radiografia
questi fotoni emessi sono proprio nella banda X.
Questo processo è del tutto simile a quelli che stanno alla base del funzionamento di
tutti i dispositivi che funzionano a onde elettromagnetiche: i telefoni cellulari, i wi-fi, la
98
televisione, la radio. In tutti questi casi ci vuole un’antenna (un pezzo di filo metallico)
nella quale si fanno muovere gli elettroni in su e in giù con moto accelerato: a causa di
questo moto accelerato si produce un campo elettromagnetico che si propaga
tutt’attorno sotto forma di onde elettromagnetiche; e non è altro che questo processo
qui: l’elettrone interagisce attraverso lo scambio di un fotone con un’altra particella del
materiale che sta attraversando, e se interagisce vuol dire che sta subendo una forza da
parte di quella particella; questa forza lo accelera (in positivo o in negativo) e quello che
accade è che l’elettrone emette dei fotoni che non sono altro che la rappresentazione
quantistica delle onde elettromagnetiche.
Anche in questo caso, utilizzando le regole di Feynman, è possibile calcolare la
probabilità che un elettrone penetrando in un certo materiale emetta un fotone di una
certa lunghezza d’onda. Questo numero coincide con la probabilità calcolata
sperimentalmente.
I vari esempi riportati mostrano che la teoria appare una teoria di grande successo:
l’interazione tra due fermioni “avviene” dunque attraverso lo scambio di un bosone.
Quesito: come si producono i positroni in laboratorio?
a. Si estraggono da antiatomi di idrogeno
b. Grazie al processo che consente di produrre coppie dalla materializzazione di fotoni nel vuoto
c. Attraverso il processo di produzione di coppie nel quale un fotone materializza in una coppia e+ e –
grazie all’interazione con la materia
[La risposta esatta è la c.]
4.10. Approccio informale
Ecco infine qualche suggerimento su come introdurre in maniera un po’ meno informale
gli argomenti delle pagine precedenti che non sono certo semplici.
Sfrutteremo alcuni aspetti degli argomenti degli anni precedenti.
Dobbiamo rappresentare l’interazione tra particelle. Dobbiamo cioè scrivere l’equazione
del moto di una qualche particella all’interno dell’universo. Qual è una possibile
equazione del moto? U = cost
Questa equazione è facile da scrivere; qualsiasi legge della fisica, portando a
sinistra ciò che è a destra diventa del tipo A = 0. Poiché 0 è costante, la legge avrà la
forma scritta sopra. Un’equazione del moto di questo tipo non ha però grande interesse.
Ci sono dei casi però in cui la medesima equazione riserva degli aspetti interessanti:
prendiamo ad esempio un oggetto di massa m nel campo gravitazionale terrestre: la sua
energia totale è la somma di energia potenziale e di energia cinetica.
1
U mgh mv 2
2
99
Questa quantità deve rimanere costante in un processo in cui non si hanno perdite di
energia. Questa legge equivale a quella sopra, solo che abbiamo esplicitato il valore di
quella costante.
Questo è ciò che si insegna agli studenti di un liceo… solo che questa espressione
non è del tutto corretta: questa somma non è proprio quella di una particella nel campo
gravitazionale terrestre, ma è “circa” uguale ad essa:
1
U mgh mv 2
2
Sappiamo infatti che quell’mgh è solo una approssimazione dell’energia potenziale
gravitazionale della particella; tuttavia è una approssimazione molto buona in quanto
quell’h è molto piccolo del raggio terrestre.
Tuttavia, dal punto di vista formale la formula corretta dell’energia è la seguente:
U G
mM 1 2
mv
r0
2
l’energia potenziale gravitazionale corretta è uguale al potenziale gravitazionale calcolato
alla distanza r0 dal centro della Terra moltiplicato per la massa m della particella.
Per calcolare tale energia a una distanza r r dal centro della terra possiamo
espandere il potenziale gravitazione in serie di Taylor e trovare la seguente espressione:
mM
U G
r0
r r 2
1 2 ...
r0 r0
la parentesi è una somma infinità che però dà luogo a un valore finito.
Quello che noi facciamo quando utilizziamo l’mgh non è altro che considerare che l’1
(primo termine della sommatoria) è una costante, e poiché l’energia potenziale è definita
a meno di una costante possiamo sommare all’energia potenziale proprio il termine
corrispondente a quell’1. Dunque h non è altro che quel r . L’mgh è dunque il secondo
termine dello sviluppo in serie di Taylor dell’energia potenziale gravitazionale.
Quindi, nell’esprimere l’energia gravitazionale di un corpo possiamo tener conto
solo di questo secondo termine, l’unico che abbia rilevanza.
Nel caso dell’interazione tra particelle possiamo fare qualcosa di analogo: la
grandezza che “rappresenta” l’interazione deve contenere i due oggetti che
rappresentano le particelle che stanno interagendo:
U A
La psi-barra e la psi rappresentano in qualche maniera le due particelle, esattamente
come nell’energia potenziale gravitazionale sono presenti le due masse; poi nel caso
dell’energia gravitazionale abbiamo il G che rappresenta l’andamento del campo, mentre
nel caso dell’interazione tra particelle abbiamo un α che rappresenta la costante di
100
accoppiamento che esprime quanto è intensa l’interazione tra le particelle; infine il
termine A rappresenta semplicemente come varia il campo con la distanza
Quindi, anche se non sappiamo esplicitare compiutamente la psi-barra e la psi
possiamo comunque assumere che l’energia di interazione tra le due particelle per mezzo
del campo creato dalle particelle medesime è qualcosa che, almeno al primo ordine dello
sviluppo, si può scrivere come U A , dove sono registrate le caratteriste
dell’una e dell’altra particella (caratteristiche riguardanti il fatto che quelle particelle sono
sorgenti di un determinato campo) moltiplicate per il campo attraverso il quale le due
particelle interagiscono; il tutto moltiplicato per una costante che serve a dare le
dimensioni giuste al prodotto e per utilizzare la scala di unità di misura che preferiamo.
La U potrà quindi essere molto complicata ma nel primo termine dello sviluppo
dovrà contenere i tre termini sopra; anche se non so come sono psi-barra, psi e A,
posso però rappresentare l’interazione in questo modo:
Sappiamo però che il processo per cui un elettrone si trasforma in un elettrone
con energia diversa emettendo un fotone non è possibile perché non conserva il
quadrimpulso; questo fenomeno non produce alcun fenomeno fisico osservabile quindi
questo fenomeno non può esistere: questo significa che il primo termine dello sviluppo
in serie dell’energia di interazione tra le due particelle deve risultare un valore zero per la
probabilità che questo processo avvenga. Devo allora scrivere almeno il secondo termine
dello sviluppo perturbativo:
U 2 A A
[al secondo termine avremo infatti l’energia all’ordine più basso moltiplicata per se stessa
per la costante di accoppiamento al quadrato che starà fuori]
Siccome ciascuna delle due parentesi si possono rappresentare esattamente con il
diagramma usati prima,
101
il prodotto delle due parentesi si potrà ottenere unendo i due diagrammi per la linea
ondulato ottenendo uno dei diagrammi di Feynman che abbiamo ottenuto in maniera
più formale nelle precedenti lezioni
Quindi possiamo rappresentare lo scattering tra due elettroni (cioè la repulsione tra di
essi) pensando che l’energia di interazione sia il prodotto di due oggetti che a loro volta
non sono altro che il prodotto di rappresentazioni matematiche degli oggetti che
interagiscono e del campo aggiustati in modo tale che al primo ordine dello sviluppo
diano zero e al secondo ordine dello sviluppo perturbativo diano qualcosa di sensato.
Un altro processo che possiamo analizzare è il processo di annichilazione: abbiamo la
stessa forma dell’energia: una parentesi che rappresenta il primo ordine dello sviluppo,
una seconda parentesi che rappresenta sempre il primo ordine dello sviluppo… e
quando moltiplichiamo tra loro le due parentesi otteniamo qualcosa che è proporzionale
al secondo ordine dello sviluppo perturbativo dell’espressione (complicata a piacere)
dell’energia di interazione tra i due “oggetti” che interagiscono:
U 2 A A
Moltiplicare le due parentesi significa attaccare tra di loro i due oggetti “in qualche
maniera”. Quello che si può ottenere è qualcosa del genere:
102
dove i due diagrammi sono attaccati per la linea ondulata ma sono orientati in maniera
diversa; abbiamo ottenuto quello che altrove abbiamo descritto più formalmente come
“processo di annichilazione”;
se invece, partendo dalle stesse formula dell’energia potenziale tra due particelle, ovvero
dagli stessi due diagrammi, e uniamo questi ultimi per una linea dritta otteniamo il
seguente diagramma
che corrisponde all’effetto Compton… e se aggiungiamo un atomo che assorbe il fotone
dello stato finale (in alto a destra) possiamo anche rappresentare il processo di effetto
fotoelettrico.
Dunque, partendo dall’analogia con l’espressione dell’energia gravitazionale, possiamo
concludere che non importa quanto complicata sia l’espressione dell’energia di
interazione tra le particelle a livello quantistico ma quel che possiamo dire è che
all’ordine più basso dello sviluppo in serie l’energia dipenderà dalla funzione d’onda delle
due particelle e dalla funzione d’onda del campo e posso rappresentare questo prodotto
con una linea dritta che entra, una linea dritta che esce e in mezzo una linea ondulata che
rappresenta il campo; siccome questo processo è vietato per la conservazione del
quadrimpulso è evidente che il primo termine dello sviluppo perturbativo deve dare zero
come probabilità di transizione; bisogna andare almeno al secondo ordine dello sviluppo,
cioè prendere i termini del primo ordine e moltiplicarli per se stessi; e possiamo
rappresentare graficamente questa moltiplicazione come l’attaccatura di due diagrammi
elementari (“del primo ordine”) per una qualunque delle loro linee, con l’avvertenza di
attaccare linee dritte con linee dritte e linee ondulate con linee ondulate (non si possono
trasformare i bosoni in fermioni, e viceversa), ma tutti i possibili modi in cui si possono
combinare i due diagrammi elementari sono leciti e ognuno di essi rappresenta un
processo possibile e previsto dalla dinamica quantistica.
Quesito: l’energia potenziale gravitazionale di un oggetto di massa m alla quota h si scrive
come mgh. Quella di un pianeta di massa m a distanza r dal Sole di massa M si scrive come
GmM/r. Dire quale delle seguenti affermazioni è corretta:
103
a. Le due espressioni sono diverse perché l'interazione che fa cadere gli oggetti sulla Terra è diversa da
quella che tiene i pianeti in orbita. I pianeti non cadono sul Sole.
b. Tra le due espressioni non c’è alcuna differenza perché l’interazione è la stessa: il fatto è che la prima
è un’approssimazione della seconda quando h << r.
c. Tra le due espressioni non c’è alcuna differenza perché l’interazione è la stessa: il fatto è che la prima
è un’approssimazione della seconda quando h è grande.
[La risposta corretta è la b.]
4.11. Test ed esercizi
Come si rappresenta formalmente un campo di bosoni?
a. come un operatore di creazione seguito da uno di distruzione
b. dipende dallo spin del campo
c. come una serie di oscillatori armonici
d. come il prodotto di esponenziali
e. come un vettore
[La risposta corretta è la c.]
Qual è la corretta espressione della sezione d’urto del processo che porta dallo stato |i⟩ allo stato |f⟩ ?
a. C⟨f|S|i⟩ dove C è un’opportuna combinazione delle quantità cinematiche delle particelle che ha le
dimensioni di una superficie
b. C|⟨f|S|i⟩|2 dove C è una costante universale
c. C|⟨f|S|i⟩|2 dove C è un’opportuna combinazione delle quantità cinematiche delle particelle che ha
le dimensioni di una superficie
d. ⟨f|S|i⟩
e. |⟨f|S|i⟩|2
[La risposta corretta è la c.]
Quale, tra le seguenti relazioni, può rappresentare un processo di decadimento beta di un
neutrone? Nelle alternative gli operatori di creazione di una particella sono rappresentati dal
simbolo della particella scritto in maiuscolo con un + come apice, quelli di distruzione con un
− come apice e il campo che provoca l’interazione con Π. Per i neutrini gli operatori sono
rappresentati come Nν±.
a. |peν⟩=ΠNν+E+P+N−|n⟩
b. |peν⟩=ΠNν−E−P−N+|n⟩
c. |peν⟩=Π|n⟩
d. |peν⟩=Nν+E+P+N−|n⟩
e. |peν⟩=(Π+Nν+E+P+N−)|n⟩
[La risposta corretta è la a.]
Di quale particella l’equazione di Dirac (iγμ∂μ−m)Ψ=0 rappresenta la propagazione libera?
a. Dei positroni
b. Dei fotoni
c. Dei soli elettroni
d. Di tutti i fermioni
e. Di tutte le particelle subatomiche
[La risposta corretta è la d.]
104
Quale diagramma rappresenta l’effetto Compton?
a.
b.
c.
d.
e.
[La b. è quella corretta]
Quando si traduce un diagramma di Feynman nella probabilità di un processo, ogni vertice
contribuisce con un fattore 1/137. Qual è il rapporto tra la probabilità del processo
rappresentato nel diagramma a destra rispetto al processo all’ordine più basso, rappresentato
nel diagramma a sinistra?
a. 1/4
b. (1/137)4 ≃ 3×10−9
c. questo processo non esiste
d. 1/3
e. (1/137)6 ≃ 15×10−14
[Sei sono i vertici del secondo diagramma, due quelli del primo.
105
(1/137)6 /(1/137)2 = (1/137)4 . La risposta corretta è la b.
Dato un operatore O che descrive l’interazione, un tale operatore si può espandere in serie di Taylor e
si può scrivere coma la somma di operatori del tipo A+A2+A3+A4+....
Come si è visto nelle lezioni questi operatori hanno un corrispondente “grafico” nel diagramma di
Feynman. Quindi un processo qualsiasi si può scrivere troncando la serie all’ordine più basso e
disegnando il diagramma di Feynman corrispondente (che è quello con il minimo numero di vertici). Lo
stesso processo si può rappresentare con diagrammi a più vertici che rappresentano i contributi allo
sviluppo in serie di ordine più alto.
Nel caso dell’interazione tra elettroni, questa si può rappresentare all’ordine più basso con un
diagramma nel quale è scambiato un fotone, ma anche con un diagramma nel quale se ne scambiano
due (o un qualunque altro diagramma con due vertici in più). Se la probabilità del primo processo (con
un fotone) è proporzionale ad α, quella con due fotoni ha una probabilità proporzionale ad α2.]
Cosa rappresenta questo diagramma?
a.
b.
c.
d.
e.
Niente: si tratta di un diagramma che non può esistere
Il decadimento di un π0
Un processo nel quale un quark u emette due fotoni e torna indietro
La collisione di due quark con due fotoni
La produzione di un campo elettrico da parte di una particella carica
[La risposta corretta è la b.]
Come si può definire il propagatore di un campo A?
a. Come il valor medio del prodotto di un operatore di distruzione e uno di creazione del campo in due
punti diversi dello spazio-tempo, calcolato tra due stati di vuoto
b. Come l’ampiezza di probabilità di un processo nel quale una particella mediatrice del campo viene
creata
c. Come la probabilità di osservare una particella virtuale che si sposta tra due punti dello spazio-tempo
d. Come il valor medio del prodotto di un operatore di distruzione e uno di creazione del campo in due
punti diversi dello spazio-tempo tra gli stati iniziale e finale di una reazione
e. Come il valor medio della somma di un operatore di distruzione e uno di creazione del campo in due
punti diversi dello spazio-tempo, calcolato tra due stati di vuoto
[La risposta corretta è la a.]
Con quale probabilità si può verificare il processo e→e+γ?
a. Nulla. Il processo è vietato dalla conservazione del quadrimpulso
b. P=1: il processo avviene certamente prima o poi e non avendo specificato dopo quanto tempo
dobbiamo assumere che t→∞.
c. P
m 2 cos2
con m pari alla massa dell’elettrone e θ uguale all’angolo formato tra la direzione
1 cos2
dell'elettrone e quella del fotone nello stato finale
106
d. La probabilità vale m 2 Ee E 2 pe p dove m è la massa dell’elettrone, Ei l’energia delle
2
particelle dello stato finale e pi la loro quantità di moto.
e. Dipende dall’energia dell’elettrone. Si calcola come il modulo quadro di ⟨eγ|O|e⟩
[La risposta corretta è la a.]
Cosa rappresenta un diagramma di Feynman con due vertici?
a. Niente, perché un diagramma con due vertici ha probabilità nulla di verificarsi
b. La probabilità che avvenga un processo
c. La probabilità di un processo all’ordine più basso della teoria perturbativa
d. L’ampiezza di probabilità di un processo all’ordine più basso della teoria perturbativa
e. L’esatta descrizione di ciò che avviene a livello microscopico quando due elettroni interagiscono
[La risposta corretta è la d.]
107
Cap. 5
Il modello standard
5.1. Le interazioni forti
Diversamente dal fotone, mediatore della forza elettromagnetica, la cui carica elettrica è
nulla e non trasporta carica elettrica (la carica elettrica delle singole particelle viene
conservata nell’interazione tra le particelle che vi partecipano), il GLUONE, mediatore
dell’interazione forte, non può essere un oggetto privo della carica attraverso la
quale viene prodotto.
Il gluone (rappresentato da una molla) deve poter assicurare
l’interazione tra quark che hanno colori diversi: la sorgente delle
interazioni forti è la carica di colore e due quark di qualunque
colore interagiscono nello stesso modo; quindi è necessario che il
mediatore di questa interazione trasporti la carica di colore
perché non è necessario assicurare la conservazione della carica di
colore su ciascuna delle particelle partecipanti.
Vediamo un esempio concreto.
Vediamo l’interazione tra due quark attraverso la mediazione di
un gluone. I due quark che provengono dal lato sinistro
dell’immagine possono essere di qualunque colore: interagiscono
comunque nello stesso modo
Supponiamo che quello in basso a sinistra sia un quark rosso.
Se il quark che proviene dall’altro lato è
un quark blu quello che deve accadere è
che il gluone che viene scambiato in
questo processo (disegno a destra) deve
possedere una carica di colore rosso e
una carica di colore blu in modo tale da
assicurare la possibilità di trasferire
l’interazione tra un quark rosso e un
quark blu e viceversa. Non ha
importanza se la carica viene trasferita
da su a giù o da giù a su… e dal
diagramma di Feynman non possiamo
dire in quale verso proceda il gluone. In
un certo senso il gluone si muove in
tutte e due direzioni…
…oppure non si muove affatto: il gluone è qualcosa che traduce una sequenza di
operatori matematici e quindi noi lo immaginiamo come qualcosa che viene scambiato e
108
si muove solo perché stiamo traducendo in immagini qualcosa che dal punto di vista
formale (matematico!) è però qualcosa di completamente diverso. Tuttavia (per
visualizzare il processo) possiamo immaginare che ci sia una carica rossa e una carica blu
che fluiscono in due direzioni diverse in maniera tale da consentire l’interazione tra i due
quark. Non c’è nessuna ragione particolare per cui la carica debba conservarsi nel punto
in cui viene emesso o assorbito il gluone.
In effetti, quello che potrebbe succedere conservando tutte le
cariche di colore complessive è la cosa seguente: il quark
rosso che stava in basso, assorbendo la carica blu trasportata
dal gluone rosso-blu, diventa un quark blu mentre quello blu
che stava in alto, assorbendo il quark blu-rosso che trasporta
anche la carica rossa, diventa rosso. Si può cioè dire che la
carica rossa è stata trasportata verso l’alto e la carica blu è fluita
verso il basso grazie al gluone che ha trasportato entrambi i
colori. Con queste posizioni si garantisce che tutte i quark
possano interagire tra di loro indipendentemente dalla loro
carica di colore ma con un mediatore diverso da quello delle
interazioni elettromagnetiche.
Dovendo il gluone trasportare le cariche di colore, non ci può essere solo quello rossoblu (in realtà è un anti-blu) ma ci devono essere tutte le combinazioni possibili con due
componenti di carica di colore: un colore e un anti-colore. Chiamando r, g, b le
componenti rosse, verdi e blu (red, green e blue), i gluoni base possibili sono nove:
rr rg rb gr gg gb br bg bb
ma solo otto di essi sono indipendenti. Una possibile base è:
2 , rr gg 2bb
6
, rr gg
Se esiste il diagramma di Feynman riportato sopra, deve esistere anche il sottodiagramma
riportato sotto:
Tuttavia, se ammettiamo che il gluone non abbia massa
(come non ce l’ha il fotone), il diagramma a sinistra
(esattamente come nel caso del fotone) darà ampiezza di
transizione nulla ed è dunque privo di interesse in quanto
tale: è impossibile che un oggetto privo di massa
decada in una coppia di particelle con massa perché
questo violerebbe i principi di conservazione della
quantità di moto e dell’energia, ovvero del quadrimpulso
(come nel caso dell’interazione elettromagnetica).
Tuttavia questo diagramma è parte del diagramma più complesso che si può costruire
“agganciando” questo diagramma ad altri diagrammi in modo da avere lo scambio di un
gluone virtuale, non un gluone reale come in questo caso.
Quindi possiamo pensare a processi che avvengono nel seguente modo:
rg , rb , gb , gr , br , bg
109
Supponiamo di avere un’interazione e+ e– del tipo di quelle che si sono viste negli
acceleratori negli anni passati, e come quelle che abbiamo visto in una delle lezioni
precedenti nella quale si parlava della possibilità di produrre coppie di fermioneantifermione a partire dallo scontro elettrone-positrone agli anelli di accumulazione dove
si fanno scontrare queste particelle.
Se faccio interagire un elettrone con un positrone l’interazione sarà di tipo
elettromagnetico e quello che si otterrà è che queste particelle annichilano in un fotone
che si propaga e subito produce una coppia fermione-antifermione. Supponiamo che la
coppia fermione-antifermione prodotta sia una coppia di quark, in particolare una coppia
di quark up, ovviamente un u e un anti-u.
Abbiamo già anticipato che negli esperimenti non si osservano mai quark liberi prodotti
on queste reazioni ma si osservano sempre e soltanto degli adroni che appartengono ai
multipletti scoperti negli anni precedenti.
Perché accade ciò? Evidentemente sia il quark u sia il quark anti-u prodotti per effetto
dell’interazione elettromagnetica emettono ciascuno un gluone. Il quark u emette un
gluone virtuale che deve materializzare in una coppia quark-antiquark: nel disegno sopra
si ipotizza che sia una coppia strano-antistrano (s – s barra) e il quark anti-u fa la stessa
cosa: emette un gluone virtuale che può sopravvivere solo un tempo molto breve e dopo
materializza in una coppia quark-antiquark: nel disegno sopra si mostra una coppia
down-antidown (d – d barra). Nello stato finale non ci sono dunque due quark ma sei tra
quark e antiquark; questi sei tra quark e antiquark si possono combinare insieme grazie
all’interazione forte in maniera tale da costituire delle particelle incolori (cioè prive di
carica di colore). A seconda dei modi in cui i sei si riorganizzano a tre a tre (dando vita a
ee 0
dei barioni) potremmo avere l’evento
la lambda conterrà uno dei quark della coppia u e sarà formata da un d e un s
l’antisigma-zero sarà composta dagli altri tre quark. La differenza tra una sigma-zero e
un’antisigma-zero sta nel segno della stranezza trasportata dal quark strano.
Un’altra possibilità è però la seguente (nel caso che i quark si combinino a due a due,
dando origine a tre mesoni):
ee K 0 K
110
Come si vede, è rispettata la conservazione della carica elettrica (nulla nello stato iniziale
e nulla nello stato finale), è rispettata la conservazione di tutto ciò che si deve conservare
e nello stato finale si osservano particelle che “non espongono” la loro carica di colore.
I quark liberi non si possono vedere … ma si possono misurare
Se i quark non si possono vedere come possiamo affermare che esistono? La fisica è una
scienza sperimentale: non posso dire all’universo come funzionare, ma è l’universo che
dice a me come funziona e io devo adattare le mie leggi in base a quello che osservo;
dunque, se immagino che esista un qualche meccanismo che spiega certi fenomeni che
osservo poi devo essere in grado di verificare che questo meccanismo avvenga
effettivamente in natura.
Quello che posso fare è misurare la sezione d’urto di produzione di un certo tipo di
particella in un certo tipo di eventi, fare i conti con i diagrammi di Feynman di quanto
dovrebbe essere quella sezione d’urto, confrontare i due numeri e se i numeri “tornano”
posso dedurne che la mia interpretazione è corretta. Tuttavia il fatto di utilizzare i
diagrammi di Feynman sui quark non garantisce che i quark esistano (potrei utilizzare dei
diagrammi di Feynman con degli adroni alla fine): è solo la misura che mi garantisce
l’esistenza dei quark.
Se non posso vedere un quark libero (cioè una particella di carica frazionaria) posso però
misurare gli effetti della sua presenza dentro gli adroni. Come si fa?
Posso utilizzare il fatto che le interazioni forti e le interazioni elettromagnetiche dal
punto di vista formale sono descritte dallo stesso tipo di diagramma e posso combinare
queste informazioni con il fatto nel caso delle interazioni elettromagnetiche attraverso il
diagramma di annichilazione, quello nel quale e+ e – possono produrre una coppia
fermione-antifermione il risultato dello stato finale può essere sia una coppia di leptoni
che nulla hanno a che fare con l’interazione forte, sia una coppia di adroni che io
presumo essere il risultato della combinazione di diversi quark.
Vediamo come si fa questa misura.
La perdita di energia specifica per unità di lunghezza di una particella elettricamente
carica che attraversa un certo materiale è data dalla formula di Bethe e Block che in
questo corso abbiamo dato nella sua formulazione classica:
quello che importa in questo caso è il fatto che la perdita di energia specifica dipende dal
quadrato della carica elettrica dell’elettrone e dal quadrato della carica elettrica della
particella incidente nel materiale. La carica dell’elettrone c’è perché l’elettrone è una delle
particelle che partecipano a questa interazione, la carica della particella incidente c’è
perché quella è l’altra particella che interagisce nel materiale. Ora, se avessimo un
elettrone che interagisce con un altro elettrone il risultato sarebbe che la perdita di
energia specifica sarebbe e2e2, quindi e4. Allora le interazioni che danno luogo alla
111
perdita di energia per ionizzazione (formula di Bethe e Block) sono evidentemente di
natura elettromagnetica, e quindi da questa espressione vediamo che le interazioni di tipo
e.m. producono una probabilità di transizione che è proporzionale alla potenza 4 della
carica elettrica; quindi quello che dobbiamo pensare è che, se calcoliamo la sezione
d’urto di un processo e+ e– che produce e+ e– , il risultato che ci si deve aspettare è che
la sezione d’urto (proporzionale al modulo quadro del diagramma di Feynman sotto
riportato) sia proporzionale a e4.
In effetti, pendendo le regole di Feynman e mettendole in un calcolatore e calcolando il
modulo quadro dell’elemento di matrice in cui nello stato finale c’è la coppia e+ e– e
nello stato finale c’è ancora una coppia e+ e–, il valore che si trova è effettivamente
proporzionale a e4.
Il fatto che ci sia la quarta potenza è che perché ci sono due elettroni (elettrone e
positrone) a sinistra e due elettroni (elettrone e positrone) a destra.
E quindi ci aspettiamo che quell’ e4 derivi dal prodotto dell’e2 che riguarda le particelle a
sinistra per l’e2 che riguarda le particelle a destra.
Usando le stesse regole di Feynman posso calcolare la sezione d’urto nel caso in cui la
coppia la coppia elettrone-positrone iniziale conduca non a una coppia dello stesso tipo
ma a una coppia di tipo diverso. Per esempio, supponiamo che da e+ e– si produca per
annichilazione una coppia quark-antiquark. Allora quello che ci si deve aspettare è che le
regole di Feynman conducano a una sezione d’urto che è proporzionale a e2 q2, dove q è
la carica delle particelle che si trovano a destra, che in questo caso è una carica
frazionaria (stiamo parlando di quark)
La sezione d’urto è qualcosa di più complicato della semplice probabilità di transizione
dallo stato iniziale allo stato finale che si può ottenere attraverso le regole di Feynman;
c’è tutta un’altra serie di fattori che deve tenere conto del flusso delle particelle incidenti,
della maniera in cui si distribuiscono le particelle nello stato finale… ci sono varie
complicazioni per giungere al calcolo effettivo della sezione d’urto. Se però misuriamo la
112
sezione d’urto per un tipo di evento e la sezione d’urto per un altro tipo di evento, e
faccio il rapporto, quello che si vede è qualcosa del genere: supponiamo ad esempio di
misurare il rapporto tra la sezione d’urto di elettrone-positrone che va in quark-antiquark
e la sezione d’urto di elettrone-positrone che va in muone positivo – muone negativo:
La sezione d’urto al numeratore sarà proporzionale al modulo quadro dell’elemento di
matrice generato dalla trasformazione in operatori (trascrizione in termini di operatori)
del diagramma di Feynman (vedi sopra); e così la sezione d’urto che si trova al
denominatore: tutti gli altri fattori (il flusso di particelle incidenti, le modalità con cui si
distribuiscono le particelle nello stato finale, eccetera) saranno circa uguali nelle due
sezioni d’urto; l’unica cosa che cambia, in effetti, in queste due sezioni d’urto è
semplicemente la natura delle particelle dello stato finale; quindi, nel rapporto, tutti
questi fattori aggiuntivi che servono per passare da una probabilità di transizione a una
sezione d’urto si devono cancellare; il rapporto tra queste sezioni d’urto, che è qualcosa
che posso misurare, deve essere uguale al rapporto tra le probabilità di transizione
ottenute dai diagrammi di Feynman, e queste due probabilità sono identiche perché
identici sono i diagrammi, cambia solo il fattore delle cariche dello stato finale: tale
rapporto (vedi sopra) sarà dunque uguale a q2/e2… se è vera la teoria dei quark!
Ora però in questo tipo di eventi non si osservano dei quark specifici ma un getto di
adroni e devo allora poter sommare su tutti i tipi di adroni che si possono produrre in
questo tipo di eventi, cioè devo fare la somma su tutti i possibili sapori di quark che
posso produrre al mio acceleratore in base all’energia che ho a disposizione. Se quindi ho
una energia sufficientemente alta da permettermi di produrre coppie di tutte le specie di
quark di cui abbiamo parlato nel modello a quark ci aspettiamo un risultato come il
seguente:
2
1 2 2 2 11
qi
R 3 3 3 2
3
3 3
i e
- down, strange e botton hanno carica –1/3
- il quark up e il quark charm hanno carica +2/3
- per ognuno di questi cinque quark ci sono tre colori diversi (e dunque ecco il 3
davanti)
113
Ci si aspetta quinti che il rapporto tra la sezione d’urto in adroni di e+ e– e la sezione
d’urto di e+ e– in e+ e– sia 11/3.
Si può dunque fare questa misura (andando in un acceleratore!) cambiando l’energia degli
elettroni, cambiando quindi l’energia nel centro di massa in cui si verifica l’urto e
misurando la sezione d’urto in adroni e la sezione d’urto in muoni; facciamo il rapporto;
riportiamo in un grafico tale rapporto in funzione dell’energia nel centro di massa;
otterremo un grafico come quello che segue: la sua complicatezza nasce dal fatto che vi
sono diversi picchi (indicati dalle varie particelle) che corrispondono al fatto che, per
certi valori della energia nel centro di massa, la probabilità di produrre una particella la
cui massa è proprio uguale a quella dell’energia nel centro di massa è molto più alta del
normale. Quindi dobbiamo guardare il rapporto R non dove ci sono questi picchi ma
laddove non si forma nessuna particella particolare: tra un picco e l’altro si può osservare
quanto vale questo rapporto.
Oltre la soglia di produzione del π (lì dove si forma la Y), il rapporto R è proprio 11/3 (è
poco sotto 4): la previsione è perfettamente rispettata.
Conclusione: una volta che si ha la possibilità di produrre cinque quark il rapporto tra le
sezioni d’urto è proprio quello previsto dal modello.
Man mano che si scende con l’energia nel centro di massa si osservano degli
scalini nel valor medio di questa R: sono dovuti al fatto che al di sotto di una certa soglia
di energia non è possibile produrre coppie quark-antiquark con una massa superiore a
quella dell’energia nel centro di massa, si produce un quark in meno e quel rapporto
diventa più piccolo di 11/3.
114
5.2. Il modello standard
Tentiamo un riepilogo generale di quello che è considerato il modello standard della
fisica delle particelle elementari che include sia i “campi di materia”, cioè quei campi
fermionici che rappresentano quelle che ordinariamente chiamiamo “particelle”, sia i
“campi di radiazione” ossia i mediatori delle interazioni. Non abbiamo ancora parlato
delle interazioni gravitazioni e delle interazioni deboli, ma è il caso di fare un riassunto,
anticipando qualche risultato.
Il modello standard si compone di un certo numero di campi di materia e di un certo
numero di mediatori: vediamo i cinque QUARK trovati finora (in viola) (sappiamo oggi
che esiste un sesto quark chiamato “top” o “true”).
Ci sono poi i sei LEPTONI (in verde): elettrone, muone e tauone, ciascuno in due
possibili stati di carica, e i rispettivi neutrini, privi di carica elettrica.
Di queste 12 particelle, le 9 che sono cariche (esclusi i neutrini, neutri, appunto)
partecipano alle INTERAZIONI ELETTROMAGNETICHE.
Quelle in viola sono adroni, e dunque sentono anche l’INTERAZIONE FORTE; quelle
colorate in verde invece l’interazione forte non la “vedono” e non sono in grado di
assorbire/emettere un gluone.
115
QUARK e LEPTONI sentono tutti gli effetti della INTERAZIONE DEBOLE.
Dato che possiedono massa (fino a qualche tempo fa si pensava che i neutrini non
avessero massa, oggi si ritiene che una massa, seppur piccolissima, ce l’abbiano) quark e
leptoni sentono anche l’INTERAZIONE GRAVITAZIONALE, la quale tuttavia oggi
non trova posto nel modello standard perché di essa non conosciamo quasi nulla di
come agisca a livello quantistico: l’interazione gravitazionale è la più debole di tutte ed è
molto difficile fare esperimenti nei quali si possano osservare i fenomeni gravitazionali a
livello quantistico.
Accanto ai campi di materia ci sono i CAMPI BOSONICI (a destra, in rosso) cioè i
campi che fungono da mediatori delle interazioni.
Sotto i già noti fotoni e gluoni vi sono la Z0, neutra, e le W+ e W –, con carica
rispettivamente uguale a quella del protone e dell’elettrone, che sono i mediatori
dell’INTERAZIONE DEBOLE.
Oltre a queste particelle vi sono le antiparticelle.
Adroni e leptoni (particelle di materia) hanno tutti spin ½
5.3. La scoperta del TOP
Il quark TOP è stato scoperto al TEVATRON2, negli U.S.A., nel 1995, grazie agli
esperimenti CDF e DØ, in eventi in cui si facevano collidere protoni e antiprotoni in
un acceleratore circolare.
In questi eventi quello che può accadere – attraverso i soliti diagrammi di annichilazione
di Feynman – è la produzione di un top e di un antitop con un certo numero di altre
particelle che servono per conservare tutti i numeri quantici della reazione.
Ricordiamo che in questi processi ciò che collide non sono il protone e l’antiprotone in
quanto tali ma i quark di cui sono formati: si ha quella che viene chiamata “la
frammentazione del protone”: quelli che collidono sono un quark del protone e un
antiquark dell’antiprotone che annichilano in un gluone il quale materializza in una
coppia top-antitop; il resto dei frammenti del protone continua a muoversi in avanti,
“adronizza” per il solito processo per il quale non possono esistere quark liberi nello
stato finale, si vengono a produrre altre particelle che poi si legano a produrre adroni
privi di carica forte, quindi incolori.
Le due particelle della coppia top-antitop, a differenza di tutte le coppie che si potevano
produrre agli acceleratori a energia più bassa, come nel caso del charm-anticharm e del
strange-antistrange o del bottom-antibottom, che producono i mesoni neutri che poi
decadono in altre particelle, hanno la proprietà di decadere troppo rapidamente per
2
Il Tevatron è un acceleratore di particelle (o sincrotrone) del Fermi National Accelerator
Laboratory a Batavia (IL), a una trentina di miglia da Chicago, negli USA. Il Tevatron accelera protoni e
antiprotoni in un anello di 6,3 km sviluppando un’energia che arriva fino a 1 TeV.
116
consentire la produzione di un mesone neutro: uno si potrebbe aspettare che dalla
coppia top-antitop si produca una particella neutra del tutto analoga alla η (eta) o alla Υ
(iupsilon) o alla J-Ψ (gei-psai): invece top e antitop non producono una particella stabile
e il motivo è che decadono prima di interagire e legarsi a formare un bosone neutro: top
e antitop vengono quindi identificati attraverso i loro decadimenti dai quali si ricostruisce
la massa invariante e si osserva un picco in questi eventi.
In questo caso il top decade in un botton e un W+ (un mediatore della forza debole) che
subito decade in una coppia quark-antiquark di specie diversa, naturalmente, per far sì
che la coppia quark-antiquark abbia complessivamente carica pari a +1:
t bW bqq ' .
L’evento si osserva come una serie di jet adronici che provengono dal centro del
rivelatore.
L’antitop invece decade in un antibottom e un W –, in cui l’antibottom produce poi un
jet e invece l’evento viene identificato grazie al fatto che il W – può decadere anche in un
muone negativo e il suo neutrino
t b W b .
Ciò che si può cercare è dunque un evento di questo tipo tra le migliaia, milioni di eventi
che vengono prodotti in questi acceleratori: se ne trovano, si vedono delle risonanze e
quindi si dice che è stata identificata una nuova particella che in questo caso è il top.
Oggi dunque sappiamo che esiste questo sesto quark di carica elettrica +2/3 con il
numero quantico di top pari a 1 e gli altri numeri quantici nulli.
Nome
Symbol Carica Strange Charm
ness
(e)
up
u
2/3
0
0
down
d
– 1/3
0
0
strange
s
– 1/3
–1
0
charmed
c
2/3
0
1
bottom
b
– 1/3
0
0
top
t
2/3
0
0
Bottom
ness
0
0
0
0
–1
0
Top
ness
0
0
0
0
0
1
Energia a
riposo MeV)
360
360
540
1500
5000
170 000
Lo spin è ½ per tutti e il numero barionico è 1/3 per tutti. Per gli antiquark il numero barionico è –
1/3, tutti i valori sopra sono cambiati di segno… mentre lo spin è sempre ½ .
117
I mediatori dell’interazione debole (il Z0, il W+ e il W –) sono tre, uno neutro e due
carichi. Questi mediatori sono stati scoperti al collisore Super Proton Synchroton (SPS)
del CERN di Ginevra nel 1984 grazie a due esperimenti, l’UA1 e l’UA2 (i cui nomi
derivano da Underground Area: data l’enorme estensione dell’acceleratore SPS, la
collisione avveniva in un punto di interazione nel sottosuolo collocato al di fuori dei due
siti principali del CERN, a Meyrin e a Prevessin). La scoperta di queste particelle valse il
premio Nobel a Carlo Rubbia e a Simon Van der Meer. In questi esperimenti si facevano
di nuovo collidere protoni e antiprotoni e nella collisione si potevano produrre dei
bosoni Z che poi decadevano in una coppia fermione-antifermione, oppure nei bosoni
W+ e W – che decadono o in una coppia quark e antiquark di specie diversa oppure in un
leptone più un neutrino.
I mediatori dell’interazione debole, a differenza degli altri mediatori (fotoni e
gluoni), non hanno massa nulla ma anzi sono molto pesanti, pesano circa 90 volte il
peso di un protone. Questo comporta che le interazioni deboli siano interazioni a
corto range.
Se un elettrone, attraverso un qualunque diagramma
di Feynman, emette un fotone questo fotone si può
propagare a distanze infinite dall’elettrone perché,
avendo massa nulla, riesce a mantenere validi tutti i
principi di conservazione. La forza di interazione
elettromagnetica ha raggio infinito.
Nel caso di un mediatore debole questo invece non è
possibile.
Gli elettroni, che certamente interagiscono per interazione elettromagnetica attraverso lo
scambio di un fotone, devono tuttavia avere anche la possibilità di interagire con i
mediatori dell’interazione debole dato che possono anche essere parte di uno stato finale
mediato dall’interazione debole (pensiamo per esempio al decadimento-beta del cobalto60, nel quale, nello stato finale, si trovano un elettrone e il neutrino). Quindi deve essere
possibile anche il diagramma sotto: gli elettroni cioè devono poter emettere un bosone,
per esempio lo Z0, che viene raccolto da un altro
elettrone.
Questo meccanismo dovrebbe competere (anche se,
ci si perdoni il gioco di parole, più debolmente, visto
che l’interazione debole ha una costante di accoppiamento più bassa rispetto a quella dell’interazione
elettromagnetica) con l’interazione elettromagnetica;
invece questo genere di competizione non si osserva:
a grandi distanze dal nucleo atomico non si osserva
nessuna interazione di tipo debole.
Lo Z deve avere un corto range (come il W+ e il W –, del resto il decadimento beta
avviene entro le dimensioni del nucleo), ovvero deve potersi propagare per distanze
118
molto molto brevi. Se deve propagarsi per distanze molto brevi significa che deve anche
avere una vita media corta (e viceversa). E questo è compatibile col fatto che abbia
massa, dato che deve sempre valere sempre il principio di indeterminazione Et .
Quando un elettrone emette uno Z0, se lo Z0 è una particella massiva l’elettrone deve
perdere una parte della sua energia per consentire la sua produzione, ma questa perdita
di energia è vietata dal principio di conservazione dell’energia… a meno che questa
perdita non possa avvenire all’interno di un tempo talmente breve da non essere
misurabile. In altre parole quello che pensano i fisici è che l’elettrone può sì produrre una
particella Z dotata di massa, dunque violando il principio di conservazione dell’energia,
purché questa violazione avvenga in un tempo talmente breve da non essere misurabile
sperimentalmente, in maniera tale cioè che quando lo Z viene assorbito da un altro
elettrone il principio nella sua globalità rimane salvo.
Quindi dobbiamo assumere che la Z che viene prodotta in questi processi debba essere
L
. Poiché t
se ne deduce che la Z, una volta
E
v
v
L
prodotta, può percorrere una distanza
. Questa spiega dunque perché un
E
libera per un tempo t
bosone massivo deve essere il mediatore di una interazione a corte range.
Quesito: quante sono le particelle di materia che compongono il modello standard?
a. 3
b. 9
c. 12
[La risposta corretta è la c.]
5.4. L’interazione debole
Che cos’è l’interazione debole? Chiamata anche per ragioni storiche “forza debole” o
“forza nucleare debole” è una delle quattro interazioni fondamentali della natura. La
forza debole è responsabile del decadimento beta dei nuclei atomici, associato alla
radioattività, per il quale un neutrone si trasforma in un protone con l’emissione di
elettroni (radiazione beta) e neutrini.
L’interazione debole può avvenire tra leptoni e quark (interazioni semileptoniche), tra
soli leptoni (interazioni leptoniche) o tra soli quark (interazioni non leptoniche), grazie
allo scambio di bosoni vettori molto massivi detti W± e Z0. Poiché tutti i leptoni sono
interessati dagli effetti dell’interazione debole, essa è la sola forza che negli esperimenti di
laboratorio interviene sui neutrini, per i quali la gravità è trascurabile.
L'interazione debole è unificata a quella elettromagnetica nella teoria elettrodebole,
secondo la quale esse sono due diverse manifestazioni di un’unica interazione, detta
appunto elettrodebole, è quella che provoca il decadimento del neutrone.
119
Come dobbiamo immaginarcela? Certamente non come qualcosa che, classicamente,
“attrae” o “respinge”. In generale, è più corretto pensare alle interazioni come capaci di
provocare una variazione di stato. Anche in fisica classica si possono trovare degli
esempi utili: una forza applicata a un gas, per esempio, non ne provoca l’accelerazione,
questa grandezza fisica non ha senso per un gas; quello che succede è che cambia lo
stato del gas: la sua pressione, il suo volume e/o la sua temperatura.
Lo stato è costituito dall’insieme di grandezze fisiche indipendenti che si possono
misurare di un sistema e che ne determinano l’evoluzione temporale. Nel caso di un
punto materiale lo stato è definito quando sia definita la sua velocità (tradizionalmente lo
stato è costituito da posizione e velocità, ma si può sempre trovare un sistema di
riferimento in cui la posizione coincide con l’origine del sistema); una forza che provoca
un’accelerazione si manifesta, nel caso di oggetti fermi, con una variazione della
posizione. Per questa ragione le forze gravitazionali, elettriche e magnetiche, quando
agiscono su punti materiali, si manifestano come un’attrazione o una repulsione.
Nel caso dei punti materiali la massa non è tipicamente inclusa nello stato perché
solitamente è costante. Se però può cambiare, lo stato di un punto materiale è
determinato dall’insieme delle grandezze fisiche posizione, velocità e massa. Una forza che
agisce su questo sistema ne può modificare lo stato cambiandone la massa. È quel che fa
una forza debole.
Con questa visione dello stato si capisce molto meglio il significato della meccanica
quantistica: un’interazione è qualcosa che determina il cambiamento da uno stato iniziale
a uno finale, esattamente come nel caso classico.
I bosoni W + e W –
Come si spiegano le interazioni deboli con i diagrammi di Feynman e la presenza di
questo tipo di mediatori? Ci è sufficiente ricordare che il neutrone e il protone sono
particelle composte di quark.
Qui a destra è rappresentato un tipico
decadimento beta (che potrebbe anche
essere il decadimento di un neutrone in volo,
che decade in un protone, un elettrone e un
antineutrino). Il tempo scorre verso l’alto.
All’inizio abbiamo un neutrone (segnato in
verde). Trascorso un certo tempo, uno dei
due quark d del neutrone emette un bosone
W – e nel fare questo perde una carica
negativa, e quindi, per la conservazione della
carica [– 1/3 – (– 1) = 2/3] deve trasformarsi
in un quark u. Nello stato finale abbiamo
dunque un protone formato da un quark d e
due quark u.
120
Nel frattempo il W – si propaga e giunto al termine della vita consentitagli dal principio
di indeterminazione materializza in due particelle di materia, un neutrone e un
antineutrino (si osservi che la linea che rappresenta l’antineutrino è diretta in senso
contrario rispetto a quella che rappresenta l’elettrone e dunque è come se andasse al
contrario nel corso del tempo).
Gli altri due quark del neutrone continuano a viaggiare indisturbati vicini a quello che ha
subito l’interazione e abbiamo adesso un protone anziché un neutrone.
L’esistenza dei bosoni W+ e W – permette dunque di spiegare i decadimenti beta, o il
decadimento del neutrone, e i decadimenti beta di tutte le particelle strane che
procedono più o meno nello stesso modo: si tratta di prendere un quark, far emettere a
questo quark un bosone W+ e W – , il quark si trasforma in un altro quark di specie
diversa e il W+ e il W – danno vita a un leptone e a un neutrino oppure, se hanno massa
sufficiente, possono dare origine a una coppia di quark.
Questo tipo di interazione può avvenire solo tra particelle cariche visto che il W+ e il W –
trasportano la carica elettrica e la carica elettrica va conservata.
Il bosone Z 0
Ci sono altre particelle però, come per esempio i
neutrini, che per poter interagire con altre
particelle, per esempio con gli elettroni, hanno
bisogno di un mediatore privo di carica
elettrica: questo mediatore è lo Z0, che può
condurre a diagrammi come quello a sinistra, in
cui un neutrino interagisce appunto con un
elettrone facendolo deviare: il neutrino
coinvolto nell’urto non si vede nel rivelatore
perché difficilmente lascia una traccia essendo
neutro mentre si dovrebbe vedere l’elettrone che
vien fuori da un punto in cui non c’era nulla.
121
Lo Z0 può essere prodotto anche in eventi di tipo annichilazione, per esempio nel caso
che segue:
un elettrone e un positrone si scontrano e annichilano, e
nell’annichilazione, invece di produrre un fotone gamma,
producono un bosone Z0. Lo Z0 poi si accoppia alle
particelle di materia e può dare nello stato finale di
nuovo una coppia e+ e– (come nel disegno a fianco)
oppure una coppia μ+ μ– o τ+ τ– oppure adroneantiadrone o quark-antiquark (tutte le combinazioni
sono ammesse)
Come si fa a osservare questo evento? Possiamo prendere degli elettroni e dei positroni,
farli scontrare a energia sufficiente alta da produrre un mediatore Z0 reale e non virtuale
(in questo tipo di interazioni il mediatore è sempre virtuale, ha una massa che non è
quella nominale della particella: è il caso del fotone che ha una massa nominale pari a
zero, ma il propagatore ha una massa diversa da zero, per la conservazione del
quadrimpulso). Nel caso dello Z0 la massa nominale non è zero ma circa 90 volte la
massa del protone per cui può succedere che se l’energia nel centro di massa è proprio
uguale alla massa dello Z0 il propagatore che si viene a produrre non è virtuale ma è una
particella Z0 reale che sopravvive per un certo tempo e poi decade in una coppia di
fermioni… Ed ecco perché nel grafico in cui avevamo riportato il rapporto tra le sezioni
d’urto in adroni diviso quello in muoni compare il picco sulla destra corrispondente alla
massa della Z.
Andando con l’energia nel centro di massa dei leptoni interagenti proprio alla massa
dello Z la probabilità di produrre uno Z è molto alta, molto più alta di produrre un
fotone virtuale che si troverebbe ad avere una massa molto lontana da quella nominale.
122
Ora, poiché una Z decade molto più facilmente in una coppia di adroni e meno in una
coppia di muoni si vede quel picco in quella posizione: il picco indica la presenza di una
particella bosonica che è proprio il mediatore delle forze deboli ed è in quel caso il
mediatore reale e non la particella virtuale che viene scambiata solo nel tempo inferiore a
quello consentito dal principio di indeterminazione. Potrebbe essere una particella
stabile, ma stabile non è perché le interazioni deboli sono a corto range e la particella
decade immediatamente in una coppia di fermioni.
Quesito: come si deve interpretare, alla luce del Modello Standard, il decadimento beta?
a. Come la trasformazione di un quark d in un quark u con emissione di un W che a sua volta produce
un elettrone e il suo neutrino.
b. Come l’emissione di un fotone virtuale che materializza in una coppia elettrone-positrone con
successiva trasformazione del positrone in un quark e un neutrino.
c. Come la trasformazione di un neutrone in un protone con emissione di un bosone Z che decade in
elettrone e neutrino.
[la risposta esatta è la a.]
5.5. La violazione della parità
La legge di parità, detta anche di “inversione spaziale” afferma: “Se A è un fenomeno
reso possibile dalle leggi della fisica, il fenomeno C che sia l’immagina di A in
uno specchio è ugualmente permesso dalle leggi della fisica”. La riflessione
operata dallo specchio si chiama operazione P.
La scoperta della violazione della parità si ebbe in
un esperimento condotto nel 1956 che aveva lo
scopo di comprendere perché i K decadessero in
modi così distinti l’uno dall’altro
Le K0 decadono in due o tre pioni e questo
risultava poco spiegabile alla luce della teoria allora
vigente: i due pioni avrebbero dovuto essere
favoriti rispetto ai tre pioni, perché sembra più
facile produrre due pioni che tre; ma non era così.
Per cercare di capire tali fenomeni la professoressa
Chieng Shiung Wu mise in atto degli esperimenti,
piuttosto complicati per la verità, per cercare di
capire il comportamento delle interazioni deboli in
Chieng Shiung Wu (1912 – 1997) particolari circostanze.
Non entreremo nei dettagli dell’apparato sperimentale ma ci concentreremo sui principi
su cui si basa tale esperimento.
123
Si prendono degli atomi di cobalto-60 e poiché il loro spin (in unità di ħ) è 5 si fa in
modo che questi spin, con l’ausilio di un campo magnetico esterno, risultino allineati
tutti nella stessa direzione.
Il Cobalto-60 è radiattivo: produce decadimenti beta: si trasforma in nichel emettendo
un elettrone e un antineutrino.
Il decadimento può essere schematizzato come nella figura sopra: il nichel rimane
sostanzialmente fermo e quindi l’elettrone e il neutrino devono avere delle quantità di
moto (rappresentate con le frecce lunghe e strette) opposte l’una all’altra.
Poiché lo spin del cobalto è 5 e quello del nichel è 4 per la conservazione del momento
angolare i due spin dell’elettrone e del neutrino (entrambi pari a ½) devono essere
allineati come mostrato in figura, in modo tale da sommarsi con lo spin del nichel e dare
lo spin del cobalto.
All’epoca si credeva che la parità dovesse conservarsi: ovvero non c’era nessun motivo
per pensare che un esperimento fisico dovesse preferire gli assi orientati in un modo
piuttosto che in un altro. Ossia: se faccio oscillare le mie chiavi davanti allo specchio e
guardo la ripresa cinematografica del me reale e del me riflesso non ho modo di capire
quale dei due è quello reale.
Quelle che fu fatto nell’esperimento di Madame Wu fu analizzare il comportamento
delle quantità di moto e dei momenti angolari in un sistema di riferimento in cui i versi
degli assi cartesiani erano stati cambiati, come se fossero visti allo specchio.
Immaginiamo di guardare allo specchio una quantità di moto: essa cambia di segno
(cambia il verso).
Se però immagino di guardare allo specchio qualche cosa che ruota (per cui il momento
angolare è rivolto, per la regola della mano destra, ad esempio, verso destra), visto allo
specchio il suo momento angolare continua a puntare verso destra.
124
Dunque le quantità di moto cambiano verso per inversione di parità mentre i momenti
angolari non cambiano verso. Di conseguenza, se questo è un possibile decadimento del
cobalto-60 nel quale l’elettrone viene emesso in direzione opposta rispetto allo spin
iniziale del cobalto, dovrebbe essere possibile osservare anche il decadimento visto allo
specchio (con le quantità di moto delle due particelle invertite e i due spin rimasti uguali).
Invece si scopre che il decadimento visto allo specchio non si osserva mai.
Vi è quindi una palese violazione dell’invarianza per parità.
Questa osservazione fu inizialmente abbastanza choccante: nessuno credeva che in
natura si potesse non conservare la parità, ovvero che ci fosse una differenza tra destra e
sinistra. Ma questo è quello che si osserva in natura.
Una volta che ci si abitua all’idea conviene cercare di capire perché avviene questo.
Lo spin di un elettrone può essere orientato secondo la sua quantità di moto o essere
antiparallelo ad essa; ma siccome la quantità di moto di un elettrone dipende dal sistema
in cui lo osservo (se lo osservo da un sistema di riferimento che si muove più
velocemente dell’elettrone la sua quantità di moto cambia segno), anche lo spin
dell’elettrone dipende dal sistema di riferimento.
Nel caso del neutrino o dell’antineutrino (particelle di massa praticamente nulla che si
muovono quasi alla velocità della luce) lo spin è una grandezza intrinseca del neutrino e
una volta prodotto un neutrino con un certo tipo di spin, quello spin non cambia
qualunque sia il sistema di riferimento in cui lo si osserva.
Se dunque il decadimento di cui sopra non si osserva mai, significa che non esistono
antineutrini elettronici in cui lo spin è antiparallelo alla quantità di moto, e
125
dunque non esistono neutrini elettronici per cui lo spin è parallelo alla quantità di
moto: è come se un neutrino, visto allo specchio, non riflettesse la propria immagine
Tutto questo implica che esistano particelle con particolare ELICITÀ (proiezione del
sp
vettore di spin nella direzione del suo impulso: e
p se misurato in unità di ħ,
sp
): lo spin di queste particelle è sempre orientato in un determinato
oppure H s p
modo e mai nell’altro (o sempre parallelo o sempre antiparallelo al momento. L’elicità di
una particella non è in generale un invariante di Lorentz. Infatti mediante una
trasformazione di Lorentz che manda p → – p si può cambiare il segno dell’elicità della
particella. Questa operazione non è possibile per particelle di massa nulla poiché esse si
propagano con la velocità della luce e dunque non è possibile fare una trasformazione di
Lorentz che mandi p → – p, segue di conseguenza che per queste particelle l’elicità è
una grandezza Lorentz-invariante.
Lo spin del neutrino è un buon numero quantico perché non dipende dal sistema di
riferimento nel quale lo misuro.
La bontà di questa interpretazione fu confermata da un altro esperimento, fatto da
Maurice Goldhaber nel 1958 (“l’elicità del neutrino elettronico è negativa”), che
confermò che le particelle fanno differenza tra destra e sinistra.
Il fatto che esistano particelle destrorse e sinistrorse anche se dello stesso tipo ha
implicazioni importanti sulle quali faremo alcune elaborazioni un po’ formali ma poco
rigorose, essendo l’argomento molto complesso…. e per fare un po’ di esercizio di
meccanica quantistica.
La matematica è un’opinione
Quello che si può fare in meccanica quantistica è misurare il valore di una grandezza
fisica e tale valore, ad esempio quello dell’energia, può essere descritto in due modi
diversi:
126
Schrödinger
Emis
Heisenberg
x E x dV
Emis E
può essere descritto secondo la meccanica ondulatoria di Schrödinger o secondo la
meccanica operatoriale di Heisenberg, in ogni caso è il valor medio (o atteso) di un
operatore tra due stati di particella, siano essi descritti in termini di funzione d’onda o di
bra- e -ket.
Il motivo per cui esistono due diverse descrizioni dello stesso fenomeno (due
meccaniche quantistiche!) è perché, al contrario di quello che pensa la maggior parte
delle persone, la matematica È un’opinione; è la fisica a non esserlo. La fisica
pretende che i risultati di una certa teoria aderiscano ai risultati che si possono
sperimentare in laboratorio; in matematica no: si parte da degli assiomi e se ne traggono
le conseguenze, e gli assiomi sono completamente arbitrari.
GALILEO GALILEI: “Egli [l’universo] è scritto in lingua matematica, e i suoi
caratteri son triangoli, ed altre figure geometriche, senza i quali mezi è impossibile a
intenderne umanamente parola”.
Perché la matematica è la lingua con la quale è scritto l’universo? Perché con la
matematica possiamo inventare un alfabeto e un dizionario coi quali costruire delle
regole sintattiche che ci portano alla descrizione dell’universo che osserviamo. Così
come lo stesso concetto si può esprimere in lingue diverse (italiano, inglese, francese…)
così lo stesso fenomeno fisico si può descrivere in lingue diverse (con la meccanica
ondulatoria di Schrödinger o con la meccanica operatoriale di Heisenberg).
Scegliamo dunque una di queste due rappresentazioni.
Pensiamo alla misura dell’energia di una particella nella meccanica di Heisenberg: tale
energia è il valor medio dell’operatore energia tra due stati di particella:
Emis E
Prendendo lo stato di questa particella e moltiplicandolo per un fattore di fase qualunque
127
ei
quando vado a calcolare il valor medio dell’energia, tale fattore di fase entra nel calcolo
come tale a destra e come coniugato a sinistra: i due fattori di fase si cancellano e il
risultato dell’operatore di energia è lo stesso:
Emis ei Eei Emis
Possiamo dunque sempre moltiplicare per qualunque fattore di fase lo stato di particella
senza che cambi il risultato della misura, ossia senza che cambi la fisica che gli operatori
descrivono in questo contesto.
Se stessi misurando non l’energia di una particella che si muove a bassa velocità ma
l’energia di una particella relativistica e quantistica, allora non basta usare
l’operatore costituito dallo scalare-energia E ma devo usare la rappresentazione
dell’energia corretta: per un elettrone la rappresentazione corretta è quella che si
deduce dall’equazione di Dirac; dobbiamo cioè sostituire all’operatore E quello che
descrive il moto libero di un elettrone e che traduce la relazione relativistica secondo la
quale E2 – p2 = m2 .
Di nuovo, moltiplicando per un fattore di fase arbitrario gli stati della particella
Emis ei i( m)ei i( m)
i m
non cambia nulla: dunque i fattori di fase sono sostanzialmente inosservabili: non c’è
modo di misurarli: ogni volta che cerco di misurali questi si cancellano nei loro valori
medi e non posso accedere al loro valore. Pertanto posso scrivere lo stato con un fattore
di fase del tutto arbitrario. Non c’è nessun motivo perché questo fattore di fase debba
essere lo stesso per tutti i punti dell’universo; un elettrone può essere distribuito con la
sua funzione d’onda in una regione più o meno ampia dello spazio e in ciascuno di
questi punti dello spazio potrebbe esserci un fattore di fase arbitrario; del resto vale
anche la relatività speciale: se io misuro un fattore di fase in un certo punto x, in un
punto che misura una certa distanza da questo il fattore di fase può essere diverso perché
il segnale non si è potuto propagare abbastanza rapidamente da un punto all’altro per
segnalare che nel primo punto è cambiato il fattore di fase. Potremmo anche far
dipendere dalle coordinate x il fattore di fase arbitrario che usiamo per alterare lo stato di
una particella singola:
ei ( x )
Se vado a calcolare il valor medio dell’energia in questo caso specifico,
Emis ei ( x )i( m)ei ( x )
, quello che succede è che intanto
ho due addendi, uno che contiene l’operatore quantità di moto (che in meccanica
quantistica è un operatore di derivazione) e l’altro che contiene l’operatore scalare m:
128
Emis ei ( x )i ei ( x ) i ei ( x ) mei ( x )
Nel secondo addendo i fattori di fase si annullano e continuano ad essere inosservabili (e
l’operatore del secondo addendo si riduce all’operatore scalare m).
Nel primo addendo invece succede qualcosa di particolare: è presente la derivata del
prodotto del fattore di fase per lo stato di cui si sta misurando l’energia:
ei ( x ) i ( x)ei ( x ) ei ( x )
Dunque, sostituiti i due termini nell’operatore, otteniamo
Emis ei ( x ) ( x)ei ( x ) e i ( x )i ei ( x )
i m
In entrambi i primi due addendi i fattori di fase continuano a elidersi e rimane
Emis ( x) i i m
Rispetto a quello che avevamo all’inizio (il secondo e il terzo termine dell’espressione
sopra), l’utilizzo del fattore di fase arbitrario ha fatto comparire il primo termine
(x)
contenente la derivata della fase (nella parentesi quadra), che però dovrebbe essere
arbitraria; questo termine aggiuntivo nuovo rispetto all’inizio dovrebbe permetterci di
misurare la fase. E tuttavia il risultato della misura dell’energia non dovrebbe dipendere
dalla scelta arbitraria della fase. Cosa significa questo? Significa che nell’operatore che
misura l’energia ci deve stare un termine che, oltre a lasciare invariati i termini
che avevamo all’inizio, fa sparire il termine aggiuntivo che all’inizio non c’era, la
cui media dipende dal fattore di fase.
Notiamo che il termine aggiuntivo ha proprio la forma di quello che nei diagrammi di
Feynman descrive l’interazione tra particelle: A , termine che è costituito
da un coefficiente arbitrario α (che dipende dall’intensità dell’interazione) moltiplicato
per uno stato complesso coniugato che moltiplica un operatore che moltiplica un altro
stato.
Quello che possiamo dire, dunque, è che l’interazione fra due particelle è una
conseguenza del fatto che l’energia di interazione tra queste due particelle deve
essere invariante per trasformazioni locali di fase dello stato.
In altre parole: io ho un operatore che descrive l’energia dei vari elettroni che si trovano
in una certa regione di spazio; ebbene questo operatore deve essere fatto in modo tale
che il suo valore medio non possa cambiare per una scelta arbitraria della fase utilizzata
per descrivere lo stato; se questa energia non può cambiare è necessario che le particelle
(gli elettroni) che stanno in questa regione di spazio interagiscano tra loro (l’interazione è
cioè una conseguenza dell’invarianza dell’operatore energia per trasformazioni locali
della fase dello stato della particella libera).
129
Questo modo di far nascere le interazioni va sotto il nome di TEORIA DI GAUGE
(leggi: gheig) secondo la quale le interazioni tra particelle nascono imponendo
l’invarianza dell’operatore che restituisce l’energia delle particelle per trasformazioni di
qualche tipo (in questo caso per trasformazioni locali di fase).
Sapendo che le interazioni sono il risultato di una invarianza per trasformazioni di fase e
che le particelle destrorse e sinistrorse non sono uguali dal punto di vista delle
interazioni, dovremmo poter cambiare la fase delle particelle sinistrorse in maniera del
tutto indipendente da quello che facciamo con le particelle destrorse; ci dovrebbero
dunque essere delle interazioni che valgono per le particelle destrorse e delle interazioni
che valgono per le particelle sinistrorse. Dovremmo dunque cambiare il modo in cui si
scrive l’interazione tra particelle in modo da includere questa differenza tra particelle
destrorse e sinistrorse e cambiare la fase delle une indipendentemente da quello che si fa
con la fase delle altre.
Questo però non si può fare per le particelle dotate di massa perché la massa delle
particelle destrorse è uguale alla massa delle particelle sinistrorse; in altre parole se le
interazioni si possono assimilare alle mani (la destra è diversa dalla sinistra), le masse
sono come gli occhi (il destro è uguale al sinistro). Abbiamo dunque un problema:
nell’operatore che descrive l’energia abbiamo termini che descrivono l’interazione tra
particelle che dipendono dalla destrorsità o sinistrorsità della particelle e termini che
restituiscono la massa della particella che devono essere uguali per particelle destrorse e
sinistrorse; cambiando la fase delle particelle la massa delle particelle cambia in maniera
diversa a seconda che siano destrorse o sinistrorse: un modo per far sì che la massa non
cambi è imporre che questa massa sia zero: allora il termine legato alla massa sparirebbe
completamente e non ci sarebbe questo problema. Dal punto di vista sperimentale però
sappiamo benissimo che le masse delle particelle non sono nulle; quindi dobbiamo
trovare un modo per includere la massa delle particelle nell’operatore che ci restituisce
l’energia senza violare l’invarianza di gauge: questo è ciò che motiva il meccanismo di
Higgs che darà origine all’ipotesi che esiste una particella (il bosone di Higgs)
responsabile della presenza delle masse delle particelle dell’universo.
Quesito: quali tra queste particelle non esiste?
a. Un antineutrino elettronico con spin parallelo alla propria quantità di moto
b. Un antineutrino elettronico con spin opposto alla propria quantità di moto
c. Un neutrino elettronico con spin opposto alla propria quantità di moto
[La risposta corretta è la b.]
5.6. Test ed esercizi
Gli esercizi di questa lezione richiedono sovente di calcolare energia e/o quantità di moto dei prodotti
di decadimento. Non vi è una regola pratica universalmente valida per calcolarli, al di là di utilizzare il
principio di conservazione del quadrimpulso. Possono esserci eventuali semplificazioni, ma vanno
valutate caso per caso.
130
Si può utilizzare la conservazione del quadrimpulso per componenti, ovvero risolvere le due equazioni
derivanti dalla conservazione dell’energia (componente temporale) e della quantità di moto
(componente spaziale del quadrivettore impulso). Nel sistema della particella madre, di quadrimpulso
P=(M,0), significa imporre M=E1+E2…, 0=p1+p2+…
Oppure si può richiedere la conservazione del modulo quadro del quadrimpulso:
2
P =(p1+p2+…)2 calcolato con le regole del modulo quadro del quadrimpulso (E2 – p2 = cost), insieme
alla conservazione della quantità di moto: p1+p2+…=0
Solitamente questa seconda opzione è più immediata, almeno nel caso di decadimento a due corpi.
Una semplificazione si ha quando i prodotti della reazione sono due particelle identiche, come
ad esempio il decadimento di un pione neutro in due fotoni. Nel sistema di riferimento del centro di
massa, in cui la particella iniziale è a riposo, le energie delle particelle prodotte sono uguali e pari alla
metà della massa della particella madre. Una seconda possibilità è che la particella iniziale decada in
particelle molto più leggere, come ad esempio nel decadimento τ→e+νe+ντ. In questo caso le particelle
finali acquisiscono una quantità di moto elevata, tanto da poterne trascurare la massa e utilizzare
l’approssimazione E≈|p|
Un pione carico decade in un muone + un neutrino (ricordiamo che, dovendosi conservare la
carica elettrica e il numero leptonico deve essere π+→ anti-μ + νμ e π−→ μ + anti-νμ ): determinare il
momento finale del muone.
Massa del pione = 139,6 MeV
Massa del muone = 105,7 Mev
Massa del neutrino ≈ nulla
Assumendo a riposo il pione, i due quadrimpulsi iniziale e finale sono pi=(mπ,0) e pf=(Eμ+pν, 0) (il
neutrino ha massa… nulla, per cui Eν=pν). Uguagliando la norma dei due quadrimpulsi: |p i|2=|pf|2
otteniamo mπ2= Eμ2+pν2+2 Eμpν .
Usando il fatto che pμ= – pν, ovvero che pμ= pν, ed esplicitando Eμ2 = pμ2+ mμ2, otteniamo
un’equazione nell’unica incognita richiesta dal problema, appunto pμ:
m2 p 2 m2 p 2 2 p 2 m2 p
eleviamo al quadrato e semplificando:
p 29,8MeV
E
p
m
2
m2 2 p 2 2 p 4 m2 p 2
m2 m2
2m
che è pure la quantità di moto (e l’energia del neutrino)
p2 m2 110MeV
In generale, se vogliamo ricavare le energie delle due particelle figlie, possiamo riscrivere la
conservazione del quadrimpulso
quadrato si ottiene:
pM p1 f p2 f
come
pM p1 f p2 f .
pM2 2 pM p1 f p12f p22 f
e utilizzando la formula della norma al quadrato del quadrimpulso si ottiene
M 2 2EM E1 f pM p1 f m12 m22
131
Elevando al
Se supponiamo la particella madre M inizialmente ferma allora
diventa
pM 0
ed
EM M
e l’equazione
M 2 m12 2ME1 f m22
Da cui si ricava
E1 f
M 2 m12 m22
2M
. Ovviamente
E2 f
M 2 m22 m12
2M
Quindi, con i dati dell’esercizio precedente sarebbe
E 110MeV E 30MeV
La particella J/Psi ha una massa di poco più di 3 GeV. Quanto deve valere più o meno la
massa del quark c?
a. 0.511 MeV
b. 1.5 GeV
c. 170 GeV
d. 1 GeV
e. 3 GeV
[Un quark c e un quark anti-c danno vita alla J/Psi, quindi
ciascuno deve avere una massa pari alla metà della J/Psi. La risposta corretta è la b.]
La sezione d’urto d’interazione tra due elettroni è proporzionale...
a. alla carica elementare
b. alla massa dell’elettrone
c. al quadrato della carica elementare
d. alla quarta potenza della carica elementare
e. alla somma delle cariche elementari
[La risposta corretta è la d.]
Quanti sono i leptoni nel Modello Standard?
a. 6
b. 12
c. 16
d. 3
e. 4
[La risposta corretta è la a.]
Quanto vale il rapporto R tra la sezione d’urto di elettroni in adroni e quella in muoni per
energie nel centro di massa inferiori a quella della soglia di produzione di due quark strani?
a. 1/9
b. 5/9
c. 5/3
d. 11/3
e. 1
[Si osservi, nel diagramma relativo, il primo pianerottolo: è un numero vicino a 2.
2
qi
Si usi la formula R 3 con i soli quark up e down. La risposta corretta è la c.
i e
Ricordiamo che nella somma si conteggiano le cariche elettriche dei vati tipi quark al quadrato che si
possono produrre a (al di sotto di) una certa energia; il 3 davanti è il numero di colori in cui ciascun
quark si può produrre.]
132
Di quanto aumenta il rapporto R tra la sezione d’urto di produzione di adroni e di muoni da
parte di elettroni per ciascun quark di tipo down?
a.
b.
c.
d.
e.
di 1/3
di 2/3
di 1/9
di 1 (errata)
di 3
[La carica di – 1/3 elevata al quadrato da un contributo pari a 1/9.
Ogni tipo di quark esiste in 3 stati di colore, indistinguibili. Nella sezione d'urto totale è quindi
necessario considerare sempre questi 3 contributi. La risposta corretta è la a.]
Un quark top decade in un quark b, un muone e il suo neutrino. Quale ci aspettiamo che sia
l’ordine di grandezza dell’energia del muone nel sistema di riferimento del top?
a. 60 GeV
b. 170 GeV
c. 104 MeV
d. Dipende dall’energia del top
e. 85 GeV
Massa del quark top
Massa del bottom
Massa del bosone W
Massa del muone
= 173 GeV
= 4,2 GeV
= 80 GeV
= 0,106 GeV = 106 MeV
Assumendo a riposo il quark top, come chiede il testo, possiamo calcolare le energie delle “figlie” con le
formule esplicitate a inizio di capitolo
M t mb2 mW2
Eb
68GeV
2M t
M t mW2 mb2
EW
105GeV
2M t
pb Eb2 mb2 67.8GeV
pW EW2 mW2 68GeV
2
2
Si osservi che nella formula che dà la quantità di moto, il numeratore equivale (formula di Erone)
all’“area” di un triangolo avente per “lati” le tre masse di madre e figlie.
2
p1 f
M 2 m12 m22
m12
2M
M
2
m12 m22
2M
2
4m12 M 2
m12 m22 2m1M M 2 m12 m22 2m1M
m m M m m1 m m2
2M
2M
Significa qualcosa? Boh.
Noti impulso ed energia della particella W, che a sua volta decade in muone e neutrino, ci apprestiamo
a calcolare l’energia del muone. Come?
Se il bosone W fosse fermo (nel riferimento del bosone) le energie di muone e neutrino
sarebbero
M
2
M W m2
2
E
2M W
M W m2
2
40GeV
E
2M W
40GeV
ovvero ognuna delle
due “nipoti” si porterebbe via la medesima energia… e quantità di moto. Possiamo ipotizzare che
questo accada anche con il bosone in movimento… il muone, avendo massa, si porterà via qualcosa in
133
più del neutrino, qualcosa che deve superare di poco la metà di 105 GeV. In ogni caso il neutrino si
porterà via almeno 40GeV per cui al muone non possono restare più di (105 – 40) GeV. La risposta
corretta è la a.
Esiste un procedimento rigoroso ed è il seguente: riprendendo la formula ricavata dalla
conservazione del quadrimpulso:
M 2 2EM E1 f pM p1 f m12 m22
La quantità che non è univocamente determinata è l’angolo formato tra il vettore
p2 f
) e il vettore
p1 f (o
il vettore
p M , ovvero gli angoli che i vettori formano con la direzione di volo della particella
che decade. Energie e quantità di moto finali sono infatti funzione di una variabile angolare.
In alternativa) Si possono utilizzare le trasformazioni di Lorentz per cambiare sistema di riferimento
e utilizzare il sistema del centro di massa della particella secondaria che decade. A questo punto si può
procedere esattamente come nel primo decadimento. Una volta determinati i quadrimpulsi delle
particelle finali, con la trasformazione inversa si può esprimere tutto nel sistema di riferimento del
centro di massa della particella madre, introducendo in questo passaggio una variabile angolare.
134
Cap. 6
Il bosone di Higgs
6.1. Il campo di Higgs
C’è un ulteriore ingrediente nel Modello Standard: il bosone di Higgs.
La necessità del bosone di Higgs dipende dal fatto che la teoria fin qui delineata poggia
sulla considerazione che le interazioni affrontate richiedono alcuni principi di
simmetria… che però in certe occasioni vengono violati.
Il fatto che queste principi di simmetria vengano violati impone che nel modello delle
interazioni che poi conduce alla possibilità di calcolare i diagrammi di Feynman non si
possano considerare le masse delle particelle; questo significa che le masse delle particelle
che partecipano alle interazioni in un diagramma di Feynman debbano essere tutte nulle,
il che è contrario all’esperienza: sappiamo di avere massa e se siamo fatti di “campi di
materia” evidentemente la massa deve venire dalla massa delle particelle di cui siamo
formati; del resto la massa la misuriamo nei nostri esperimenti; quindi – di sicuro – c’è
qualcosa di sbagliato nella teoria: ci deve essere qualcosa che riesce a dare massa alle
particelle senza violare la simmetria che le equazioni che determinano le interazioni
devono soddisfare. O c’è qualcosa di sbagliato… o c’è qualcosa che manca al modello
fin qui costruito: dobbiamo trovare il modo di introdurre le masse senza violare i
principi di simmetria di cui sopra.
Per fare questo in maniera coerente dovremmo introdurre la teoria quantistica dei campi,
che è qualcosa di complicato; tenteremo allora di dare solamente un’idea di quale sia il
meccanismo che fornisce massa alle particelle utilizzando argomenti puramente classici.
Noi sappiamo trattare bene l’interazione gravitazionale e sappiamo scrivere l’energia di
~
U
m
G
una particella di massa m in un campo gravitazionale: G
~
G
dove
è il
potenziale gravitazionale.
Nel caso che il campo sia generato da una M più grande il potenziale vale:
~
M
M
G G
G 2 rˆ dr
r
r
Tale potenziale dipende dal lavoro fatto dalle forze del campo; esso risulta uno scalare,
funzione del campo gravitazionale e delle coordinate.
Una cosa del tutto analoga avviene con le interazioni elettriche: l’energia di una
particella carica in un campo elettrico è data da
135
U E qV
dove, anche qui, il potenziale (la differenza di potenziale) dipende dal lavoro fatto dalle
forze del campo:
1 Q
Q rˆ dr
V
40 r 40 r 2
e quindi è funzione scalare del campo elettrico e delle coordinate.
Per quanto riguarda i campi magnetici, quando la sorgente del campo magnetico è una
corrente elettrica, possiamo scrivere qualcosa di simile: l’energia di una spira percorsa da
~
U
I
B
una corrente I è pari a
, ancora una volta il prodotto tra ciò (in questo caso
B
la corrente) che determina l’interazione e qualcosa che può essere indicato come sotto
~
B dSzˆ B (tecnicamente è un flusso)
~
B non è quello che classicamente viene indicato come un potenziale ma è pur sempre
uno scalare funzione del campo e delle coordinate dell’elemento di superficie dS.
Abusando delle notazioni, chiamiamo questo
~
B
“potenziale del campo magnetico”.
In altre parole, l’energia di una particella (di massa, di carica, di corrente) che si trova
immersa in un campo è sempre scritta nella forma di una costante di accoppiamento
che determina l’intensità del campo generato da una sorgente dello stesso tipo di quella
che “sente” il campo moltiplicata per un potenziale (che non è necessariamente quello
che conosciamo dalla fisica classica ma è più genericamente una) funzione scalare delle
coordinate e del campo.
~
U G mG
U E qV
~
U B IB
Ci sono alcuni campi tra loro autointeragenti. Per esempio, il campo B interagisce col
campo E a formare le onde elettromagnetiche. Il campo magnetico B interagisce con sé
stesso producendo la possibilità di immagazzinare energia magnetica all’interno di un
solenoide la cui densità di energia è data da
u BB
1 2
B
20
Nel caso dei condensatori, possiamo immagazzinare energia di tipo elettrostatico, e la
densità di energia di autointerazione del campo elettrico con sé stesso è pari a
u EE
1
0E2
2
136
L’energia di ogni oggetto dell’universo si può dunque scrivere come somma di due
“modi”:
~ i
U ci Fi Fi Fi Volume
2
Il primo addendo è funzione dei campi e di quantità a loro volta responsabili di
generare il campo con il quale l’oggetto sta interagendo: per esempio,
~ ~
F
nel caso che i sia Gi (potenziale gravitazionale) il coefficiente ci è la massa che sta
all’interno del campo gravitazionale, massa a sua volta sorgente di campo gravitazionale.
~
F
che i sia Vi (potenziale
nel caso
elettrico) il coefficiente ci è la carica che sta
all’interno del campo elettrico, carica a sua volta sorgente di campo elettrico.
~ ~
F
nel caso che i sia Bi (con abuso di notazione: potenziale magnetico) il coefficiente
ci è la corrente che sta all’interno del campo magnetico, corrente a sua volta sorgente di
campo magnetico.
Il secondo termine della formula dell’energia ci dice che una porzione dell’energia
deriva dal fatto che i campi possono interagire con sé stessi. La costante
per motivi dimensionali.
i sta lì solo
2
Nel caso del campo elettrico Fi Fi E
2
nel caso del campo magnetico Fi Fi B
rispettivamente densità di energia del campo elettrico e del campo magnetico, che vanno
ovviamente moltiplicate per un volume, se stiamo calcolando l’energia all’interno di un
volume.
Per capire meglio dove stiamo andando a parare, faremo un esempio specifico dove
fisseremo il tipo di interazione che andiamo a considerare.
Consideriamo un condensatore a facce piane e parallele (distanti d e di superficie A),
all’interno del quale vi è un campo elettrico uniforme. Inseriamo nel condensatore una
carica elettrica a una certa distanza da una delle due armature, per cui tra la carica
elettrica e l’armatura più in basso ci sarà una differenza di potenziale
137
V .
L’energia totale nel volume dentro il
condensatore è dunque
U qV
0
2
E 2 Ad
che rientra nella forma più generale
vista prima.
Questa è dunque l’energia in quel
volume… se ci si limita alla fisica
classica!
Con Einstein però le cose cambiano: dobbiamo considerare anche l’energia a riposo
della particella:
U qV
0
2
E 2 Ad mc 2
Ora la forma mc2 non rientra nella forma di energia vista prima; è un termine che non
proviene da un effetto di tipo dinamico, cioè non dipende dall’interazione di qualcosa
con qualcos’altro (o con se stesso)…
Proviamo a trovare una spiegazione assumendo che, anziché l’mc2, ci sia un’altra forza
sconosciuta: dovremmo allora scrivere l’energia nella maniera seguente:
U qV
0
~ b
E 2 Ad aW W 2 Ad
2
2
Si deve intendere che la particella a è a sua volta in grado di produrre un campo W il cui
~
potenziale è espresso da W , mentre W2 rappresenta l’autointerazione del campo con sé
stesso. Nella formula sopra, dunque, il primo e il terzo temine rappresentano
l’interazione della particella con il campo, mentre il secondo e il quarto termine
rappresentano le energie delle autointerazioni dei campi con sé stessi.
~
Facciamo un’altra ipotesi: che sia il campo W che il relativo potenziale W abbiano
~
ciascuno un valore minimo, che indicheremo con W0 e con W0 , come sotto:
W W0
~ ~
W W0
L’energia si può allo scrivere come:
b
~
2
U U class a W0 W0 Ad
2
138
Espandiamo i prodotti:
b 2
b
~
U U class aW0 a W0 Ad 2 Ad bW0Ad
2
2
Cominciamo ad analizzare il terzo di questi cinque “nuovi” termini aggiuntivi:
b 2
W0 Ad
2
è un termine fatto tutti di costanti: b è la costante di accoppiamento, W0 è
il livello minimo di energia consentito per il potenziale di questo “nuovo” campo, Ad è il
volume del condensatore; e poiché l’energia di un sistema è definita a meno di una
costante, tale termine può essere eliminato; dal punto di vista dinamico non produce
alcun effetto: che ci sia o non ci sia, quando si va a derivare, cioè a calcolare variazioni,
sparisce.
Rimaniamo con 4 termini:
b
~
U U class aW0 a 2 Ad bW0Ad
2
~
a
W
Il primo dei quattro termini rimasti,
0 , è anch’esso costante; è una costante che
dipende però dalla particella (dal tipo di particella!) che abbiamo messo nel volume:
potrebbe essere che per qualche accidente tale termine valga proprio mc2: la formula
allora diventa
U U class
b 2
mc a Ad bW0Ad
2
2
Il motivo per cui (come ci obbliga a fare la relatività) dobbiamo aggiungere il termine
mc2 sarebbe dunque perché la particella interagisce con questo campo che nell’universo
ha un valore minimo diverso da zero; il termine da aggiungere dipenderebbe da quanto
quella particella si accoppia (cioè quanto intensamente interagisce) con questo campo;
quell’ a dipende esclusivamente dalla natura della particella e potrebbe quindi spiegare la
presenza dell’ mc2, che a questo punto sarebbe determinato dalla dinamica del sistema e
non piovuto lì a caso.
Il secondo termine, a , è il prodotto della costante di accoppiamento della particella
con il campo (sempre a) moltiplicata per il potenziale di questo “nuovo” campo qualora
fosse presente con valori maggiori rispetto al valore minimo di tutto l’universo. In altre
parole, se in una regione dell’universo questo campo fosse presente a un livello un po’
più alto di quanto lo sia in tutto il resto dell’universo, in questa regione dell’universo si
dovrebbero vedere degli effetti di tipo dinamico sulle particelle perché tali particelle
si accoppierebbero oltre che col campo al livello minimo anche con quello a livello più
alto.
139
Chiamiamo questo campo “CAMPO DI HIGGS”, e al termine
diagramma di Feynman come quello che segue
.
a associamo un
dicendo che il termine a (costante di accoppiamento per il potenziale in eccesso)
rappresenta l’interazione della particella con il campo di Higgs residuo (quello in
eccesso rispetto al valore minimo)
Il terzo dei quattro termini rimasti,
b 2
Ad , come tutti i termini che dipendono dal
2
campo al quadrato, deve rappresentare l’autointerazione del campo con sé stesso
(ovvero l’energia immagazzinata in un volume e dovuta al campo presente in quel
volume); ovviamente riguarda il campo “in eccesso” rispetto al valore minimo, e quindi
dobbiamo immaginare di stare in una regione di universo dove questo “nuovo” campo
di Higgs è un po’ più alto di quello che sta altrove: in questa regione dovrebbe essere
possibile vedere il campo che interagisce con sé stesso.
Dal punto di vista del diagramma di Feynman di questa interazione dobbiamo poter
vedere un campo di Higgs che emette o assorbe un campo di Higgs cambiando
direzione, o addirittura un campo di Higgs che si trasforma in due campi (o bosoni) di
Higgs.
L’ultimo termine, bW0Ad , dipende dal campo “in eccesso” presente nella regione
considerata moltiplicato per il suo stesso campo al valore minimo. In una regione in cui
il campo di Higgs non è al minimo, il campo interagisce con sé stesso ma interagisce
anche col suo minimo… e l’ultimo termine traduce appunto questo fatto.
Questo fenomeno è lo stesso che dà origine alla massa delle particelle fermioniche: in
quel caso la particella che si trova in una regione dell’universo si trova sempre a
140
interagire col campo di Higgs al suo valore minimo. L’interazione con questo livello
minimo produce un termine costante che dipende dalla particella in esame ed è il termine
che rappresenta la massa della particella. Analogamente, se in una regione dell’universo
c’è un campo di Higgs più grande del valore minimo possibile, l’interazione di questo
campo con il campo al valore minimo possibile produrrà un termine aggiuntivo
all’energia del tutto simile a quello che la particella ha generato interagendo col campo al
livello minimo.
Quindi possiamo interpretare quest’ultimo termine bW0Ad dicendo che il campo di
Higgs deve mostrare una massa, quest’ultimo termine è la massa del campo di Higgs.
Come si fa a fare in modo che un campo possieda un valore minimo diverso da zero?
Torniamo al caso classico, dove la densità di energia (del campo elettrico, ad esempio),
va secondo il quadrato del campo, quindi il suo grafico è una parabola con vertice
nell’origine (nel grafico sotto le due grandezze sono state espresse in unità arbitrarie per
semplificare i valori):
Se invece il potenziale di un qualche tipo di campo fosse espresso da una legge diversa
(come la polinomiale di quarto grado riportata nell’immagine sotto, ad esempio),
l’andamento della densità di energia sarebbe espresso da una curva (si veda il disegno
sotto) in cui il minimo non è nello zero.
141
(Possiamo pensare tale funzione come il prodotto di una ulteriore autointerazione del
campo con sé stesso.)
Se il campo di Higgs seguisse una legge di tale tipo allora, qualora in una regione di
spazio non fosse presente il campo di Higgs (e il valore del potenziale fosse zero), dal
momento che un campo di Higgs farebbe diminuire tale potenziale, il campo di Higgs si
genererebbe spontaneamente… dato che, con un campo di Higgs, il sistema
confluirebbe verso una situazione più favorevole.
In altre parole, possiamo pensare che un Universo completamente vuoto sia
estremamente instabile e che tenda ad evolvere spontaneamente verso una condizione
nella quale è presente una certa quantità di campo di Higgs. Quando un sistema evolve
spontaneamente verso una condizione lo fa perché la nuova condizione è
energeticamente favorevole rispetto a quella iniziale: un Universo vuoto (pieno di nulla)
ha quindi un’energia maggiore rispetto a quella posseduta da un Universo riempito di
campo di Higgs.
Il problema consiste nel fatto che, in linea di principio, di questi minimi ce ne
potrebbero essere più d’uno. In particolare non si può escludere, nota ormai la massa del
bosone, che esista un minimo più favorevole rispetto a quello in cui ci troviamo oggi. Se
esistesse quest’altro minimo l’Universo potrebbe transire spontaneamente verso questa
condizione, nella quale le leggi fisiche sarebbero del tutto diverse e dunque non
potremmo esistere.
Per adesso limitiamoci a ipotizzare che tale campo interagisca con sé stesso non solo
come ma come (e che quindi il grafico sia quello rappresentato sopra).
Aggiungere all’energia di interazione un termine che varia col campo alla quarta è del
tutto coerente con l’ipotesi che l’energia di una regione dell’universo contribuiscano tutte
le interazioni delle particelle con i campi e tutte le interazioni dei campi con sé stessi… e
2
4
142
questa sarebbe semplicemente una interazione un po’ diversa da quella del campo
elettrico o del campo magnetico.
Ritorniamo dunque all’espressione dell’energia
b
~
U U class aW0 a 2 Ad bW0Ad
2
e consideriamo i primi due termini, entrambi contenenti il fattore a: l’intensità con cui
una particella si accoppia al campo di Higgs deve essere proporzionale ad a; il secondo
termine ci dice che l’energia dovuta all’interazione della particella col campo di Higgs è
proporzionale a questo fattore a che dipende dalla particella. Tale fattore a è dunque
quello che determina la massa della particella.
Quesito: in cosa il termine di energia a riposo differisce dagli altri nell’espressione dell’energia
complessiva in una regione di spazio?
a. nel fatto che questo termine non appare come un'interazione tra una particella e un campo o tra
campi
b. nel fatto che questo termine ha dimensioni fisiche diverse dagli altri termini
c. nel fatto che questo termine è costante
[La risposta corretta è la a.]
6.2. La massa dei bosoni
Il bosone di Higgs, per dare massa alle particelle, deve interagire con esse. E deve agire
tanto più intensamente quanto maggiore è la massa delle particelle.
Se il bosone di Higgs può interagire con le particelle, il diagramma di Feynman che
rappresenta questa interazione potrebbe essere quello riportato sotto: il bosone di Higgs
si accoppia, per esempio, ai bosoni W e Z che sono i mediatori della forza debole; questi
bosoni, a differenza dei bosoni fotone e gluone che sono privi di massa, sono molto
pesanti (circa 90 volte un protone); e dunque si accoppiano volentieri col bosone di
Higgs, ovvero l’interazione tra il bosone di Higgs e i bosoni vettori dell’interazione
debole dev’essere piuttosto intensa.
143
Anche i fermioni, cioè le particelle dotate di massa, escludendo i neutrini (anche se
recentemente si è stabilito che i neutrini hanno massa a causa di fenomeni che vedono
un neutrino trasformarsi in un altro… Ma la loro massa è così piccole che si possono
considerare privi di massa) devono poter interagire col bosone di Higgs, e quindi per tali
particelle immaginiamo un diagramma di Feynman come quello che segue:
Questo diagramma rappresenta anche il decadimento di una particella, ovvero il bosone
di Higgs, in una coppia fermione-antifermione, e quindi è possibile che un bosone di
Higgs, una volta prodotto, decada in una coppia fermione-antifermione (possono essere
sia leptoni che quark e antiquark), oppure decadere in una coppia di bosoni vettori, ad
esempio W+ e W –. Non è consentito a un bosone di Higgs decadere in due fotoni
perché i fotoni non si accoppiano al bosone di Higgs dato che i fotoni sono privi di
massa. Non c’è un’interazione diretta tra bosone di Higgs e fotoni ma indiretta ci
può essere, nel senso che il decadimento del bosone di Higgs in due fotoni si può
osservare attraverso il decadimento mostrato nell’immagine sotto: il bosone di Higgs si
accoppia più intensamente con le particelle la cui massa è molto grande; la particella con
la quale il bosone di Higgs si accoppia più volentieri è il quark top (che pesa 170 volte un
protone); il bosone di Higgs potrebbe pertanto decadere in una coppia top-antitop; il top
potrebbe emettere un fotone e quindi annichilare con l’antitop emettendo un secondo
fotone:
Quindi è consentito dalla teoria il decadimento di un bosone di Higgs in due fotoni
purché mediato da un loop (cioè una curva chiusa) di leptoni e in particolare da una
coppia top-antitop.
144
Attraverso la teoria si può anche prevedere qual è la probabilità che un bosone di Higgs
decada in uno o in un altro canale. Possiamo disegnare un grafico con in ascissa la massa
del bosone di Higgs (che possiamo far finta di non conoscere) e calcolare in funzione di
essa il Branching Ratio, ovvero il rapporto fra un canale di decadimento e il totale dei
decadimenti.
Nel grafico sotto si vede, ad esempio, che un bosone di massa intorno ai 120-130 GeV
(cioè 120-130 volte la massa del protone) decadrebbe perlopiù in una coppia b-bbarra con
probabilità del 70%; non può decadere in una coppia t-tbarra perché non ha abbastanza
massa (dovrebbe avere una massa di almeno 170+170 GeV). Giù in fondo alla striscia si
vende che c’è anche una probabilità che il bosone decada in una coppia di fotoni, ma
essendo la scala logaritmica tale probabilità è circa di 2 x 10 – 3.
145
Le masse dei bosoni vettori
I bosoni di Higgs, oltre che delle masse dei fermioni, sono responsabili anche delle
masse dei bosoni vettori dell’interazione debole. Abbiamo già detto che
mZ mW 90mp
e abbiamo detto anche che, per il fatto di avere questi bosoni vettori massa così elevata,
il raggio d’azione delle interazione debole deve essere molto breve (altrimenti non si
spiegherebbe come mai le particelle prodotte da un decadimento beta vengano tutte
fuori sostanzialmente dallo stesso punto; se l’interazione debole potesse essere a lungo
range un atomo di cobalto potrebbe influenzare un altro atomo di cobalto distante da lui
e far uscire un elettrone da quello o un protone da un altro atomo ancora. E questo non
avviene.
Se un elettrone interagisse per forza debole con un altro elettrone, dovrebbe emettere un
bosone di 90 GeV, più di 10.000 volte se stesso.
L’unica possibilità è che l’emissione di questa particella avvenga in tempi così brevi da
rendere questa particella del tutto inosservabile.
Poiché il principio di indeterminazione dice che
Et
il tempo di esistenza di questo bosone deve allora essere inferiore
t
E
prima che trascorra questo tempo la particella deve essere riassorbita dal medesimo
elettrone o da un altro elettrone.
L
t
v E
da cui si deduce il range della forza debole:
v
L
E .
Maggiore è la massa (o energia), minore il raggio d’azione.
Per rendere possibile l’interazione elettrodebole bisogna violare il principio di
indeterminazione per un tempo inferiore a quello previsto per la loro osservabilità.
146
Il bosone di Higgs, oltre a spiegare le masse dei fermioni, spiega perché le masse dei
bosoni vettori della forza debole hanno massa grande. E per rendere tutto comprensibile
useremo lo stesso procedimento che è servito per spiegare il meccanismo di Higgs, con
un procedimento abbastanza formale ma per nulla rigoroso.
Nel caso dunque che in una regione di spazio ci sia interazione elettromagnetica sia
interazione debole l’energia sarà data da una somma di densità di energia, la prima
riconducibile al campo elettrico, la seconda al campo debole.
U
0
2
E2
w0 2
Z
2
Ora l’energia è funzione scalare dei campi: possiamo pensare che sia
U F F
0
E
0
w0 2
E,
Z
2
2 w0
Z
2
Se, giunti a questo punto, aggiungiamo la presenza del campo di Higgs, questo campo
si deve accoppiare con F che adesso ha due componenti, quindi anche deve avere
due componenti
e posso pensarlo come un campo in cui le due componenti abbiano ciascuna un valore
minimale i cui si somma un campo residuo i
L’interazione tra il campo elettrodebole e il campo di Higgs ci dà dunque la seguente
energia:
0
U int
0
0
w0 1 1
F
E,
Z 0
2 2 2
2
U int
0
2
E 10 1
w0
Z 20 2
2
Ricordiamo che l’energia del campo di Higgs (quando aveva una sola componente)
aveva la forma seguente
147
Se ora il campo di Higgs ha due componenti (che possiamo immaginare della stessa
forma) possiamo immaginare che la sua rappresentazione tridimensionale sia la seguente:
Il valore minimo di questa energia del campo di Higgs sta nella valle del “sombrero”:
sono infiniti i punti (un’intera circonferenza) in cui il campo di Higgs sta al suo minimo:
uno di quei punti è rappresentativo del nostro universo,
148
Il fatto che il campo elettrico non interagisce col campo di Higgs dipende dal fatto che
0
quel punto sta sull’asse 2 , per cui in quel punto 1 0 ,
L’energia vale allora
U int
0
2
E1
w0
Z 20 2
2
Il campo E allora interagisce solo col “residuo” campo di Higgs, in condizioni normali
quel campo vale zero e dunque il campo E non interagisce col campo di Higgs; il campo
E, dunque, può interagire con il campo di Higgs ma non ha una massa perché non è
moltiplicato per la costante del campo; mentre il bosone Z, quando si accoppia con la
seconda componente del campo di Higgs fornisce un termine all’energia che è quello
segnato in verde sotto:
e che rappresenta la MASSA DEL BOSONE.
Il fatto che i fotoni abbiano massa nulla e che i bosoni vettori dell’interazione debole
abbiano una massa notevole risulta così ancora conseguenza di un principio di
simmetria: l’universo, quando nasce, nasce simmetrico, ha un certo grado di simmetria
che gli permette di finire in uno stato che è equivalente a infiniti altri stati (la valle del
sombrero) che corrispondono al valore minimo del potenziale di Higgs. Dopo esser nato
l’universo è finito in un particolare punto di quella valle, l’orientazione di uno degli assi
lungo i quali si hanno le interazioni è risultata fissata… e uno dei bosoni che
rappresentano le interazioni e che interagiscono col bosone di Higgs (tocca ai fotoni)
non prende massa; gli altri invece sì.
Quesito: il decadimento di un bosone di Higgs in due fotoni...
a. è vietato perché il bosone di Higgs si accoppia soltanto alle particelle con massa
b. è permesso all'ordine superiore dello sviluppo attraverso un loop.
149
c. è favorito perché le particelle dello stato finale non hanno massa e non occorre spendere energia per
produrle.
[La risposta esatta è la b.]
6.3. Un po’ meno formale
Dopo le complicatezze del capitolo precedente, ecco ora un’esposizione meno formale
più adatta per gli studenti di scuola superiore.
Quello che è difficile da capire è come faccia un’interazione a fornire massa a qualche
cosa. La caratteristica principale del bosone di Higgs che gli consente di dare massa alle
particelle è il fatto che si tratta di un campo autointeragente. Questa non è una novità nel
campo della fisica: anche il campo elettromagnetico interagisce con sé stesso.
Una regione di spazio con un campo di Higgs presente è assimilabile a una distribuzione
(ordinata) di magnetini; se a un certo punto facciamo entrare una biglia d’acciaio in
questa regione di spazio, la biglia risente del campo magnetico prodotto dai magnetini e
un certo numero di magneti si attacca alla biglia e ne riduce la capacità di movimento.
La biglia d’acciaio rappresenta la particella priva di massa che interagisce col campo di
Higgs, che si attacca ad essa e le impedisce di muoversi liberamente alla velocità della
luce, quindi la particella acquista una certa massa.
Cosa fa di un muone una particella diversa dall’elettrone? La massa… ovvero il muone
interagisce col campo di Higgs più fortemente di un elettrone. Cosa significa questo,
facendo riferimento all’esempio dei magnetini? La “biglia” muone interagisce più
fortemente col campo di Higgs, cioè più magnetini le si attaccano e la sua capacità di
movimento viene ostacolata in misura maggiore di quanto non succeda alla “biglia”
elettrone.
Una distribuzione regolare di magnetini abbastanza larga (poco densa) rappresenta il
campo di Higgs al suo valore minimo. Se ci fosse un campo residuo (un campo di Higgs
con un valore un po’ più alto del valore minimo, cioè qualche magnetino in più, cioè
qualche particella uguale a quella che produce il campo), questo campo residuo potrebbe
interagire con sé stesso e avere lui stesso un comportamento del tutto simile a quello di
una particella, invece di propagarsi all’infinito viene trattenuto da sé stesso (o da bosoni
della stessa natura) e in questo modo acquista massa. Il bosone di Higgs rivelato negli
esperimenti al Cern di Ginevra non è altro che il campo di Higgs che interagisce con sé
stesso e quindi forma una specie di “grumo” di campo di Higgs che si muove come se
fosse una particella: se si fanno delle misure di massa si trova una massa diversa da zero,
quindi è come se fosse una particella. Il campo di Higgs diventa quindi una particella dal
punto di vista classico, rivelabile attraverso un opportuno esperimento… come appunto
è avvenuto nel 2012 al CERN di Ginevra, negli esperimenti ATLAS e CMS condotti con
l’acceleratore LHC.
150
6.4. La scoperta del bosone di Higgs
La scoperta del bosone di Higgs nel 2012 è stata resa possibili dall’uso di uno strumento
molto avanzato, l’LHC (Large Hadron Collider), un acceleratore che produce interazioni
tra fasci di protoni a energia molto elevata
Attualmente l’LHC sta lavorando con energia nel centro di massa pari a 13-14 TeV;
quando è stato scoperto il bosone di Higgs lavorava con energia nel centro di massa pari
a 7 TeV.
Come è stata possibile la scoperta?
Quello che si fa in un laboratorio al CERN in cui c’è questo strumento è far circolare
fasci di protoni in un tubo a vuoto, tubo che si trova in un tunnel scavato sotto terra e
lungo complessivamente 27 km.
In questo tunnel le particelle circolano in due versi opposti e in certi punto prestabiliti
dell’anello vengono fatte scontrare tra di loro; nell’urto si producono migliaia di nuove
particelle (l’energia del centro di massa è davvero molto alta, milioni di volte l’energia di
un protone), particelle anche di massa molto elevata: ad esser precisi, nell’LHC non si
scontrano i protoni ma i loro costituenti, i quark, quindi l’energia del centro di massa
non è quella dell’urto fra due protoni ma un po’ più bassa perché ciascun quark trasporta
un’energia e una quantità di moto inferiore a quelle di un protone; si tratta comunque di
energie molto alte che permettono di produrre nuove particelle, in particolare
consentono la produzione di un bosone di Higgs.
Che cosa può succedere in una collisione tra protoni? Nella collisione tra un quark e un
antiquark si può materializzare un bosone di Higgs, il quale però non è visibile nel
rivelatore, che vedrà soltanto i prodotti di decadimento di questo bosone. Ci sono due
canali particolarmente importanti per la scoperta del bosone di Higgs: il decadimento in
due fotoni, per cui nello stato finale si osservano due fotoni di altissima energia a
grande angolo rispetto al punto in cui i due fasci si sono scontrati (li vediamo nel
disegno a sinistra, a pagina seguente)
151
oppure si può osservare uno stato finale in cui ci sono quattro leptoni: quattro elettroni
o quattro muoni o (come nel disegno sopra a destra) due elettroni e due muoni).
Il decadimento in due fotoni è sfavorito nel decadimento di un bosone di Higgs; tuttavia
il decadimento più favorito, quello in una coppia bb (leggi: b-b barra), in uno scontro
protone-protone sarebbe praticamente invisibile perché è molto difficile distinguere i
prodotti di decadimento dell’Higgs dai prodotti di frammentazione del protone, mentre
il decadimento in due fotoni è un segnale molto chiaro, facilmente identificabile, per cui
quello è uno dei canali preferiti.
Il canale in quattro leptoni è quello in cui il bosone di Higgs decade in una coppia di
bosoni Z, ciascuno dei quali può decadere o in una coppia di elettroni o in una coppia di
muoni, e quindi si hanno tutte le combinazioni possibili: 4 elettroni, 4 muoni, 2 e 2.
Come si osserva dunque un bosone di Higgs?
Si osserva facendo una distribuzione della massa invariante dei due fotoni dello stato
finale osservati nel detector.
Se questi due fotoni fossero emessi in processi del tutto casuali, ci si aspetterebbe una
distribuzione come quella rappresentata dalla linea continua verde, dove si vede che la
probabilità di vedere nello stato finale due fotoni che assumono una massa invariante
bassa è maggiore di trovare due fotoni che abbiano una massa invariante alta. Questo è
ragionevole ed è quello che ci si aspetta di ottenere in uno scontro tra protoni.
152
Ma nella distribuzione sopra si osserva un picco, poco sopra i 120 GeV: la probabilità di
osservare due fotoni intorno ai 125 GeV è un po’ più alta di quella che ci si aspetterebbe
se le coppie di fotoni provenissero da eventi casuali: quel picco indica che in quella
regione di massa invariante ci sono certamente coppie di fotoni provenienti da eventi
casuali ma anche da eventi in cui i due fotoni non sono casuali, eventi in cui i due fotoni
hanno una massa invariante è esattamente di 125 GeV e sono il frutto del decadimento
di una particella di 125 GeV in due fotoni.
Osservando una distribuzione di questo genere si può solo dire di aver “osservato” una
particella di 125 GeV che decade in due fotoni, non si può dire di avere “scoperto” il
bosone di Higgs; per dire di “aver scoperto il bosone di Higgs” dovrei cercare di trovare
un altro picco in un altro canale di decadimento previsto dalla teoria per il bosone di
Higgs che si trovi sempre a 125 GeV; l’altezza di questo picco dovrà essere tale per cui il
rapporto tra il numero di eventi che corrispondono al decadimento in due fotoni e il
numero di eventi che corrispondono al decadimento in 4 leptoni sia compatibile con
quello previsto dalla teoria per il bosone di Higgs. Posso allora cercare nello scontro
protone-protone gli eventi in cui nello stato finale ci sono quattro leptoni. Questi quattro
leptoni potranno ancora una volta a) essere il frutto di eventi casuali; b) essere i leptoni
di decadimento di due bosoni Z prodotti nella collisione tra due protoni (i due bosoni Z
decadono ciascuno in due leptoni per cui nello stato finale si hanno quattro leptoni); c)
essere i prodotti di decadimento di un bosone di Higgs.
Cerchiamo gli eventi dunque che a partire da una collisione di protone si concludono
con quattro leptoni (eventi piuttosto rari, in verità) e quello che si vede è una
distribuzione come nell’immagine che segue:
153
In azzurro c’è la distribuzione degli eventi in funzione della massa invariante che mi
aspetto per fenomeni del tutto casuali; la presenza dei picchi è semplicemente dovuta al
fatto che vi è una probabilità non nulla di produrre due Z, senza che questi due Z siano
figli di un bosone di Higgs. Ma tra i due picchi ce n’è uno, evidenziato in rosso, non
previsto da una teoria che escludesse il bosone di Higgs, e in corrispondenza di una
massa invariante di 125 GeV: la conclusione è che stiamo osservando la stessa particella
che ha prodotto il picco nel grafico precedente a questo in cui si rappresentava la massa
invariante dei due fotoni; se poi contiamo il numero di eventi trovati nell’uno (due
fotoni) e nell’altro canale (quattro leptoni) e facciamo il rapporto tra i due numeri
troviamo lo stesso numero previsto dalla teoria per il bosone di Higgs (naturalmente
entro gli errori sperimentali). La conclusione è che ho osservato sperimentalmente la
produzione di un bosone di Higgs che ha una massa pari a 125 GeV.
6.5. Test ed esercizi
Il bosone di Higgs è stato cercato a lungo, senza successo, a LEP: un collisore e+e− che ha
operato fino a energie nel centro di massa di quasi 200 GeV. Il canale per la produzione di
Higgs più promettente è quello rappresentato dal diagramma di Feynman riportato sotto.
154
Come mai non è stato trovato?
a. Perché l’energia nel centro di massa non era sufficiente
b. Perché i rivelatori non erano abbastanza efficienti
c. Perché il bosone di Higgs è neutro e nel rivelatore non si poteva vedere
d. Perché non si era capito che un bosone Z non poteva decadere in sé stesso più un’altra particella
e. Perché a quell’energia la sezione d’urto del processo è bassissima
[Il bosone Z di energia 200 GeV non può produrre
un bosone Z (massa = 90 GeV) più un bosone di Higgs (massa = 125 GeV).
La risposta corretta è la a.]
Osserva il seguente diagramma di Feynman.
Il diagramma rappresenta uno dei possibili modi
attraverso il quale si può produrre un bosone di
Higgs all’acceleratore LHC, che è un collisore di
protoni. Nel diagramma sono presenti quark top,
la cui massa è di circa 170 GeV. Poiché il bosone
di Higgs si accoppia a tutti i quark, come i
gluoni, al posto del quark top potrebbe esserci un
quark u, la cui massa è di poco superiore ai 2
MeV.
Qual è il rapporto tra l’ampiezza di probabilità del diagramma in figura e quello nel quale sono
presenti quark u al posto dei quark t?
a. ∞ perché il diagramma con il quark u dà contributo nullo
b. 1
c. 85
d. 85000
e. 340
[L'accoppiamento gluone-quark non dipende dal tipo di quark, mentre l’accoppiamento bosone di
Higgs-quark è proporzionale alla massa del quark. La differenza tra i due diagrammi in questione è
dovuta soltanto al vertice che coinvolge il bosone di Higgs. Poiché la massa del bosone di Higgs è
85000 volte quella del quark up la risposta esatta è la d.]
Se il potenziale del campo di Higgs nel suo valore minimo valesse 1 GeV, quale sarebbe, in
unità naturali, la costante di accoppiamento tra il campo di Higgs e un elettrone di massa 0.5
MeV?
a. 1
b. 2×10 3
155
c. 0.5
d. 0.75×10 8
e. 0.5×10−3
[La costante di accoppiamento per il potenziale di Higgs al suo valore minimo
deve dare la massa della particella. La risposta corretta è la e.]
Qual è la probabilità di osservare un decadimento di un bosone di Higgs in quattro fermioni
carichi? Il decadimento è H→ℓ+ℓ−ℓ+ℓ− con ℓ=μ oppure e.
a. <2×10−2
b. circa 0.1
c. quasi 1
d. si tratta di un decadimento non previsto
e. dipende dalla natura dei leptoni
[la risposta si ricava dai due diagrammi che danno la frequenza degli eventi.
La risposta corretta è la a.]
Quanto vale la massa del bosone di Higgs?
a. 2×10−25 kg
b. 1.7×10−27 kg
c. 1 μg circa
d. 0.2×10−35 kg
e. 6.7×10−17 kg
[La risposta corretta è la a.]
Se, in opportune unità, il campo di Higgs nel vuoto vale 2, quale fra le seguenti espressioni ne
rappresenta la densità di energia nel vuoto?
a.
u 2 2 4
b.
u 2 4
c.
u 8 2 4
d.
u 2 2 2 4
e.
u 4 2 4
[Il valor medio del campo di Higgs tra due stati di vuoto è quello per il quale il potenziale di Higgs
assume il suo valore minimo. Occorre quindi cercare quale, tra le densità d’energia proposte, ha un
minimo dove richiesto. I minimanti delle cinque possibilità sono a. φ=1; b. φ=1/√2; c. φ=2;
d. φ=1/√2; e. φ=√2. La risposta corretta è la c.]
Quale relazione sussiste tra le costanti di accoppiamento di un elettrone con un campo di
Higgs ae e quella di un muone con un campo di Higgs aμ?
a. ae = aμ
b. ae < aμ
c. ae > aμ
d. le costanti di accoppiamento non sono ancora state misurate
e. ae ≈ aμ
156
[La massa delle particelle dipende da quanto è forte l’accoppiamento col campo di Higgs,
cioè dal valore della costante di accoppiamento con questo campo.
La massa del muone è 200 volte quella dell'elettrone. La risposta corretta è la b.]
157
Cap. 7
Rivelatori
Dall’analisi dei dati sperimentali è stato possibile costruire un modello di funzionamento
dell’universo nel quale ci sono un certo numero di leptoni e di quark che interagiscono
attraverso lo scambio di mediatori che hanno la caratteristica di essere bosoni (particelle
a spin intero) e nel quale le masse delle particelle sono il prodotto dell’interazione delle
stesse con il campo di Higgs. Ma come si osservano le particelle? E come abbiamo fatto
a scoprire il bosone di Higgs?
7.1. I rivelatori in generale
Abbia già visto come funziona un certo numero di rivelatori (camera a nebbia, camera a
bolle, ciclotrone); non abbiamo visto come funziona una emulsione nucleare (?)
possiamo immaginare che i rivelatori moderni funzionino con frequenze di eventi
estremamente elevate: ad esempio, a LHC si hanno 40 milioni di collisioni al secondo e
quindi è necessaria una serie di rivelatori che sia in grado di fornire risultati in tempi
brevissimi.
Non rimane che illustrare i principi di funzionamento di questi rivelatori più moderni
che si usano negli acceleratori di particelle.
Nella figura sopra si vede l’esplosione (il disegno esploso) di un tipico rivelatore per
anelli di collisione dell’ultima generazione. Ha una simmetria cilindrica; l’asse del cilindro
coincide con la traiettoria dei fasci; le particelle si scontrano al centro di questo cilindro,
che appare uno strumento fatto come una cipolla di strati di rivelatori diversi a seconda
della distanza dal punto di interazione chiamato “vertice”.
Il cilindro ha lungo tutta la superficie laterale e lungo le basi una serie di rivelatori,
ciascuno dedicato a una particolare categoria di particelle.
158
La macchiolina nera che si vede a destra, sulla piattaforma azzurra (così come quella che
si vede nella figura in basso al centro) è la sagoma di un uomo disegnato in scala; se ne
deduce che si tratta di rivelatori estremamente grandi e la loro grandezza è dovuta al
fatto che devono essere in grado sostanzialmente di assorbire l’energia di particelle
estremamente veloci, di diverse centinaia di GeV, talvolta anche di TeV.
Vediamo un po’ più in dettaglio com’è fatto un rivelatore di questo genere.
Vicino al vertice di interazione, vicino cioè alla parte più interna, c’è un
tracciatore, un dispositivo che serve per visualizzare le tracce lasciate dalle
particelle cariche che emergono dal “vertice”. Questo strumento deve stare molto
vicino al vertice perché deve essere in grado di osservare, per quanto possibile, i vertici
secondari di decadimento di particelle a vita media sì relativamente lunga che però
decadono comunque nei primi centimetri o millimetri dopo essere nate.
Attorno a questo strumento se ne trova un altro, un calorimetro
elettromagnetico, indicato in azzurro), dedicato alla misura dell’energia di particelle che
interagiscono elettromagneticamente (elettroni, positroni, fotoni).
Successivamente, un altro strato di rivelatori, detto calorimetro adronico (giallo ocra),
ha lo scopo di assorbire tutte le particelle che interagiscono per interazione forte (gli
159
adroni, appunto) e che non vengono tipicamente assorbite dal calorimetro
elettromagnetico in quanto troppo pesanti per poter essere assorbite.
Qualche volta tutti questi strumenti (come nel caso del detector rappresentato in figura,
il rivelatore CMS-Compact Muon Solenoid dell’esperimento a LHC), altre volte solo i
tracciatori del vertice, si trovano immersi in un campo magnetico quasi sempre
uniforme: tale campo serve a fare in modo che le particelle cariche prodotte nell’evento
assumano una curvatura (inversamente proporzionale alla loro quantità di moto in virtù
della forza di Lorentz) dalla quale risalire alla carica elettrica e alla quantità di moto delle
particelle. Quindi, all’esterno del calorimetro adronico è presente una bobina di filo
elettrico (che nel caso specifico del CMS è una bobina superconduttrice (superconductin
solenoid, segnato in bianco) perché deve produrre un campo magnetico piuttosto intenso,
dell’ordine dei 4 Tesla; e per produrre un campo magnetico così intenso occorre una
corrente molto elevata, che farebbe fondere qualunque conduttore convenzionale: per
questo si usa un superconduttore, nel quale la resistenza opposta al passaggio della
corrente è nulla e l’effetto Joule si riduce praticamente a zero).
All’esterno della bobina superconduttrice sono presenti degli strati di rivelatori
per muoni (in grigio) intervallati da degli assorbitori in ferro (le strutture rappresentate
in rosso nella figura). Gli assorbitori in ferro hanno il duplice scopo di assorbire
parzialmente l’energia delle particelle ma soprattutto quello di “chiudere” il campo
magnetico su se stesso: il campo magnetico prodotto dalla bobina all’esterno della stessa
si chiuderebbe infatti abbastanza lontano e sarebbe piuttosto debole; con il ferro le linee
di forza del campo magnetico si concentrano nel ferro, e risulta più intenso (non come
all’interno della bobina superconduttrice ma comunque di 2 Testa, sufficiente a far
curvare i muoni che giungono al di là della bobina e che dunque possono essere rivelati
segnati in chiaro tra le parti rosse e che permettono di ricostruire la traccia del muone
arrivato sin lì.
Vediamo (a pagina seguente) una sezione traversale del detector (sezione
ingrandita dello spicchio segnato nell’angolo della figura). A sinistra c’è il “vertice”, il
punto in cui i protoni si scontrano al centro del rivelatore in LHC; dalla collisione
mergono diverse particelle. Attorno al punto di collisione ci sono gli strati di rivelatore di
silicio (Silicon Tracker) che fungono da tracciatori, servono cioè per misurare la traccia
delle particelle cariche che lo hanno attraversato; poiché tutto lo strumento si trova
immerso in un campo magnetico generato dalla bobina (l’arco in grigio e nero che si
trova dopo il giallo ocra e prima del rosso) le particelle cariche subiscono una curvatura,
in un senso se cariche negativamente, nell’altro se cariche positivamente. Dalla misura
della curvatura delle particelle si evince la loro quantità di moto. Nel tracciatore lasciano
un segnale soltanto le particelle cariche, le uniche in grado di ionizzare il materiale di cui
è fatto il tracciatore, nella fattispecie il silicio. Le particelle neutre come gli adroni neutri,
i neutroni e i fotoni non lasciano tracce. I fotoni vengono assorbiti dal calorimetro
elettromagnetico (l’arco segnato in verde); al di là di esso non giunge più alcun fotone.
Lo stesso destino tocca agli elettroni e ai positroni, i quali sono distinguibili dai fotoni
per il fatto di avere nel tracciatore di silicio una traccia carica associata… che termina
160
appunto nel calorimetro elettromagnetico dove si osserva un deposito di energia
consistente, compatibile con quella che deve provenire da una particella con una quantità
di moto tale per cui p2 + m2 è uguale all’energia (al quadrato!) misurata nel rivelatore.
Quesito: quale rivelatore s’impiega per misurare l’energia dei fotoni?
a. Il calorimetro elettromagnetico
b. Il calorimetro adronico
c. Il tracciatore in silicio
[La risposta corretta è la a.]
Al di là del calorimetro elettromagnetico passano tutte le particelle che non sono né
fotoni, né elettroni, né positroni.
Gli adroni (i protoni, i neutroni e tutte le altre che si possono immaginare, in particolare
le K che decadono in tre pioni) vengono assorbiti dal calorimetro adronico (segnato in
giallo ocra), che ha il compito di assorbire tutte le particelle che abbiano attraversato il
campo elettromagnetico. Le uniche particelle che riescono a sfuggire al calorimetro
adronico sono i muoni, perché non sono adroni, non interagiscono per interazione forte,
hanno interazioni più deboli, di tipo elettromagnetico e debole, in particolare di tipo
elettromagnetico (le interazioni deboli sono molto più deboli di quelle
elettromagnetiche); interagiscono quindi con le stesse interazioni con cui interagiscono
161
gli elettroni, ma essendo molto più pesanti (un muone pesa circa duecento volte un
elettrone) non vengono assorbiti né dal calorimetro elettromagnetico né dal calorimetro
adronico, che riescono ad attraversare completamente; riescono ad attraversare anche la
bobina superconduttrice (in grigio e nero) per arrivare all’esterno del rivelatore, dove si
trova il ferro del giogo di ritorno del magnete (nel disegno le linee di forza del campo
magnetico prodotto dalla bobina sono “entranti” nel foglio nella regione all’interno della
bobina e quindi sono “uscenti” all’esterno, e si richiudono per lo più all’interno del ferro
del rivelatore); il muone che arriva con una certa curvatura all’esterno del rivelatore,
trovando un campo magnetico diretto in direzione opposta cambia curvatura; attraversa
dunque questi strati di ferro tra i quali si trovano dei tubi rivelatori riempiti di gas (i
rettangolini della figura); il gas viene ionizzato dal muone che vi passa attraverso;
all’interno del tubo si misura un segnale elettrico che denuncia il passaggio di una
particella carica; vedendo quali sono i tubi che si sono accesi al passaggio della particella
si riesce a ricostruire la traiettoria della particella.
Vediamo ora come funzionano in dettaglio singoli rivelatori fin qui descritti.
7.2. I rivelatori interni
Cominciamo dai TRACCIATORI IN SILICIO, di cui vediamo una foto sotto.
162
I tracciatori in silicio sono quella sorta di mattonelle (piastre in silicio) che si vedono
nella foto, disposte a formare dei cilindri concentrici e parzialmente sovrapposte in
modo da non lasciare spazi attraverso i quali le particelle potrebbero passare senza essere
evidenziate. Le piastre sono incise con le stesse tecniche litografiche che si usano per la
produzione di chip presenti nei circuiti elettronici, in modo tale da costituire una rete
molto fitta di microscopici condensatori. In pratica si prende un materiale di supporto
(sostanzialmente lastre di silicio) sulle cui facce si depositano degli ossidi di metalli che
facciano contatto elettrico (il silicio funge cioè da dielettrico);
questi condensatori vengono polarizzati in modo che esista una certa differenza di
potenziale tra un’armatura e l’altra. In condizioni standard, essendo la differenza di
potenziale tra le due armature costante, in questi rivelatori non passa alcuna corrente; se
però il rivelatore viene attraversato da una particella carica, questa può ionizzare il silicio,
liberando quindi ioni di silicio ed elettroni di silicio che migrano nelle due direzioni
opposte che corrispondono alle armature del condensatore producendo una debolissima
corrente, che viene amplificata, misurata e registrata. Sapendo dove si trova il singolo
condensatore/rivelatore attraversato dalla particella si può quindi ricostruirne la
traiettoria.
Naturalmente si deve ricostruire la traiettoria di migliaia di particelle che vengono
prodotte nel vertice di interazione a distanze molto piccole e quindi serve una densità di
condensatori piuttosto elevata: un rivelatore come quello che stiamo descrivendo è fatto
con qualcosa dell’ordine dei dieci milioni di singoli condensatori che devono essere
“letti” uno per uno per poter ricostruire completamente tutto l’evento.
Le particelle neutre invece non lasciano traccia.
Le particelle cariche che hanno attraversato il rivelatore di silicio perdono un po’ di
energia… ma poca, perché il silicio è assai poco denso, la maggior parte dello spazio è
vuoto, e dunque, subìta una certa curvatura per via del campo magnetico (curvatura che
viene misurata), finiscono quasi tutte nel CALORIMETRO ELETTROMAGNETICO, strumento che ha la funzione di assorbire tutta l’energia delle particelle incidenti,
almeno quelle di tipo elettromagnetico (elettroni, positroni e fotoni). Il nome di
163
“calorimetro” deriva dal fatto che un calorimetro ha la funzione di assorbire tutta
l’energia dissipata sotto forma di calore da un oggetto che vi viene posto in mezzo. In
questo caso il calorimetro elettromagnetico ha la funzione di contenere tutta l’energia
delle particelle che entrano al suo interno.
Nel caso del rivelatore al CMS, il calorimetro
elettromagnetico è fatto con dei cristalli
trasparenti come quello che si vede nella
figura a destra, cristalli di un materiale
molto pesante (tungstato di piombo, e il
nome ci dice che è fatto di tungsteno e
piombo) che deve produrre molte interazioni
con le particelle che arrivano.
Questi cristalli sono “scintillanti”: una volta assorbita l’energia delle particelle, dopo
un tempo molto breve (decine di nanosecondi) emettono un debolissimo lampo di luce
la cui intensità è proporzionale all’energia delle particelle che si sono fermate al suo
interno. Per questo su un lato del cristallo viene incollato un fotorivelatore, un fotodiodo
a valanga con il suo collettore che deve essere polarizzato opportunamente con una
differenza di potenziale e letto; quindi si legge un impulso di corrente che è
proporzionale alla luce vista dal fotorivelatore, la quale è a sua volta proporzionale
all’energia rilasciata nel calorimetro.
Cosa succede a un elettrone o a un positrone che penetra in un calorimetro
elettromagnetico? Si verifica una serie di eventi che produce quello che viene indicata
col nome di “SCIAME ELETTROMAGNETICO”: l’elettrone entra nel calorimetro
e grazie all’interazione con i nuclei del materiale che lo costituisce (non riportati nello
schema sotto) può “fare emissione”, cioè emettere uno o più fotoni: il fotone emesso
può essere così energetico da produrre una coppia elettrone-positrone in presenza di un
nucleo del materiale; gli e+ e – prodotti possono a loro volta irraggiare fotoni che
possono a loro volta produrre coppie e+ e – …
164
Questo processo di moltiplicazione a cascata delle particelle fa sì che man mano che
aumenta il numero di particelle presenti nello sciame l’energia delle particelle diminuisce
sempre di più, fino a quando l’energia dei costituenti lo sciame è così bassa che i fotoni
non riescono più a produrre coppie elettrone-positrone, i positroni annichilano nel
materiale e gli elettroni ionizzano il materiale. Questo processo a cascata fa sì che si
sviluppi all’interno del cristallo (come si vede nella simulazione rappresentata nel disegno
qui sotto) un vero e proprio sciame di particelle, composto alla fine da migliaia di
particelle tra le quali ci sono elettroni e positroni che causano la ionizzazione del
materiale scintillante
In che cosa consiste la ionizzazione del materiale scintillante? Consiste nel fatto che, per
interazione elettromagnetica, l’elettrone che passa vicino a un nucleo del materiale
emette un fotone (fig. 1) che viene assorbito da un elettrone delle molecole del materiale;
questo elettrone, assorbito il fotone, acquista energia e si porta in uno stato di energia
più alta (fig. 2) dando luogo a una molecola eccitata, la quale, dopo un tempo più o
meno lungo a seconda del materiale impiegato nei rivelatori, si diseccita parzialmente
(attraverso meccanismi di vario tipo ma che sostanzialmente non producono radiazione
elettromagnetica: si tratta di passaggi attraverso stati rotovibrazionali oppure attraverso
stati metastabili, anche attraverso l’emissione di fotoni, però di lunghezza d’onda molto
bassa) ed emette un fotone (fig. 3), che ha energia inferiore a quello assorbito.
Per cui, se il materiale ha la proprietà di assorbire fotoni di una certa energia ma è
trasparente a fotoni di energia più bassa, come ne caso del tungstato di piombo, l’energia
che viene immessa nel tungstato di piombo dopo un po’ viene trasformata tutta in luce
che si propaga attraverso il cristallo trasparente del cristallo di tungstato di piombo, e
può essere misurata dal fotorivelatore incollato su una delle facce.
Il calorimetro elettromagnetico è dunque costituito da una serie di cristalli di tungstato
di piombo disposti a formare un cilindro di raggio poco più di un metro, sorretto da
strutture di alluminio. Al CMS ci sono circa 75000 di questi cristalli, ciascuno col suo
fotorivelatore. Ce ne sono sulla superficie laterale del cilindro ma anche sulle basi.
165
All’esterno del calorimetro elettromagnetico arrivano solo particelle che non sono né
positroni, né elettroni, né fotoni. Queste particelle devono essere assorbite e se ne deve
misurare l’energia nella maniera più completa possibile.
Il principio sul quale si basa il funzionamento del CALORIMETRO ADRONICO è
sostanzialmente lo stesso sul quale si basa il funzionamento del calorimetro
elettromagnetico: è cioè costituito di un materiale sufficientemente pesante da produrre
molte interazioni con gli adroni che lo attraversano. Gli adroni, urtando contro i nuclei
del materiale del calorimetro adronico, esattamente come fa un fascio di adroni che va a
sbattere su un bersaglio, producono altre particelle, la cui energia è necessariamente più
bassa di quella degli adroni incidenti; queste nuove particelle urtano altri elettroni e altri
nuclei del materiale, producendo a loro volta altre particelle, che avranno energia ancora
più bassa, e così via, fino a quando le particelle prodotte hanno energia così bassa che
non riescono più a produrre nuove particelle. Le particelle che si sono generate in questi
urti possono essere elettricamente cariche e dunque possono produrre ionizzazione del
materiale; a questo punto si può misurare almeno la componente elettricamente carica di
questo sciame adronico (non quindi neutroni, π0, Λ…)
Quesito: quali particelle riescono ad attraversare entrambi i calorimetri?
a. Tutte le particelle neutre
b. I fotoni
c. I muoni
[La risposta corretta è la c.]
Per fare in modo che i calorimetri siano abbastanza compatti si usano materiali
abbastanza pesanti che fungono da assorbitori senza la possibilità di misurare l’energia, la
quale è misurata a campione, cioè non si misura tutta l’energia depositata dallo sciame
adronico nel calorimetro ma la si misura solo a intervalli predefiniti, e quindi si misura
solo una frazione dell’energia persa ma questa è sufficiente per ricostruire l’integrale di
tutta l’energia depositata nel calorimetro.
Qui sotto a sinistra si vede una foto di un settore del calorimetro adronico che è fatto
con degli strati di ottone tra i quali sono inserite delle lastre di un scintillatore in
questo caso plastico, cioè non di cristallo ma di una plastica scintillante, che funziona
con lo stesso principio del cristallo, ma essendo molto meno densa ha la sola funzione di
rivelare la componente ionizzante degli sciami adronici. La componente ionizzante degli
sciami adronici produce quindi in definitiva luce in questi fotoscintillatori che viene
rivelata da fotorivelatori e trasformata in segnali elettrici che vengono misurati.
166
Ancora una volta, questi settori a forma di trapezio vengono messi uno di fianco all’altro
in modo da formare una corona cilindrica le cui basi vengono chiuse da delle strutture
che permettono di chiudere tutte l’angolo solido e misurare quindi l’energia delle
particelle sparate ad ogni angolo e in tutte le direzioni
Sotto si vede il calorimetro adronico completato che sta per essere inserito della bobina
superconduttrice.
167
Qui sotto si vede invece la simulazione di uno sciame adronico misurato dalla
collaborazione ICARUS che è stata in grado di rivelare le singole particelle prodotte in
uno sciame adronico e quindi di visualizzare lo sciame.
In questo caso la particella entra da destra, comincia a interagire con il materiale di cui è
fatto lo strumento producendo altre particelle che man mano producono altre particelle
che quando interagiscono col materiale lasciano un segnale elettrico che può essere
memorizzato e utilizzato per ricostruire graficamente l’evento
Questi sciami hanno una lunghezza che dipende dall’energia della particella incidente;
noi misuriamo l’energia a profondità diverse e in questo modo riusciamo a ricostruire
l’energia complessiva che doveva avere la particella prima di entrare nel calorimetro
adronico.
Calorimetro elettromagnetico e calorimetro adronico sono segmentati su tutta la
superficie in maniera da sapere dove è entrata o passata la particella.
7.3. I rivelatori esterni
Al di fuori del calorimetro adronico non riesce ad arrivare alcuna particella se non i
muoni. Per la verità anche i neutrini attraversano tracciatore, calorimetro
elettromagnetico e calorimetro adronico, ma non hanno carica elettrica e interagiscono
solo debolmente e quindi è praticamente impossibile rivelarli. Su un evento di questo
genere la presenza di neutrini si evince dalla cosiddetta “energia mancante”. Infatti la
quantità di moto, inizialmente nulla sul piano trasverso, deve conservarsi. Se su quel
piano (il piano della figura ripetuta sotto) non è nulla significa che la componente
vettoriale che serve per rendere nulla la quantità di moto su quel piano deve essere stata
portata via dal rivelatore attraverso invisibili nel rivelatore, come i neutrini.
La componente della quantità di moto è nulla solo sul piano trasverso perché le
particelle che si scontrano sono protoni che non sono particelle puntiformi; se si
trattasse di elettroni e positroni, particelle puntiformi, la quantità di moto sarebbe nulla
in tutte le direzioni longitudinale e trasversale. Nel caso dei protoni ciò che si scontra è
una coppia di quark-antiquark o due muoni e quindi non possiamo sapere nulla lungo
168
l’asse dei fasci che si scontrano. Quindi possiamo solo affidarci alla conservazione della
quantità di moto sul piano trasverso.
I muoni non vengono catturati all’interno della bobina perché interagiscono per
interazione elettromagnetica ma sono troppo pesanti per essere assorbiti dagli strumenti
del rivelatore interni alla bobina; riescono a sfuggire e si possono osservare grazie alla
ionizzazione che lasciano nella parte esterna dello strumento. Lasciano anche delle tracce
all’interno, ma dall’interno è difficile dire se si tratti di muoni o elettroni; mentre, se
osservo delle tracce anche all’esterno posso dire con ragionevole certezza che si tratta di
muoni. I muoni vengono rivelati dai rivelatori disegnati sotto come rettangoli chiari che
si trovano tra gli assorbitori di ferro.
Questi rettangoli sono dei tubi a sezione rettangolare (di cui qui sotto a destra si vede
una foto), riempiti di un gas; dentro vi è un filo elettrico tenuto ad alto potenziale:
quando il muone attraversa il tubo
ionizza il gas e si ha quindi un
passaggio di corrente tra la parete
del tubo e il filo all’interno; si
amplifica e si misura questa corrente,
si determina quale dei tubi è stato
attraversato dal muone e in questo
modo si riesce a ricostruire
completamente la traiettoria del
muone.
169
Qui sotto si vede lo strumento quasi completo, manca solo la base del cilindro. Si vede al
centro il tracciatore in silicio che sta per essere inserito al centro del rivelatore. Il
calorimetro elettromagnetico non si vede, avvolto com’è da quello adronico. Si vede la
bobina all’interno di un recipiente, perché per diventare superconduttrice deve essere
raffreddata con dell’elio liquido
Con questo aggeggio possiamo allora misurare la quantità di moto della particella, la
carica e il grado di interazione col materiale.
Diremo che
- la particella è un fotone se ha lasciato un segnale piuttosto intenso nel calorimetro
elettromagnetico che non sia associato a una traccia lasciata nel tracciatore;
- la particella è un elettrone o un positrone se ha lasciato un segnale piuttosto
intenso nel calorimetro elettromagnetico che sia correlato a una traccia carica
(positiva o negativa) lasciata nel tracciatore;
- la particella è un adrone se lascia una traccia nel tracciatore di vertice associabile a
un segnale piuttosto intenso nel calorimetro adronico;
- la particella è un adrone neutro se lascia un segnale intenso nel calorimetro
adronico non correlato ad alcuna traccia nel tracciatore di vertice;
- le particelle che riescono a raggiungere la parte esterna (i tubi di gas) sono muoni.
Le migliaia di tracce di ogni evento vengono acquisite dal computer, che fa una prima
rapida analisi dell’evento e misura la quantità di energia depositata in certe parti del
detector.
Quando i protoni si scontrano accade spesso che i protoni frammentino e i frammenti
vanno in avanti o all’indietro rispetto alla direzione dei fasci.
170
Gli eventi interessanti sono invece quelli in cui vengono prodotte particelle a grande
angolo rispetto alla direzione dei fasci. Quando ciò accade, il sistema di computing
veloce del rivelatore (il trigger) lo rivela e acquisisce tutte le informazioni relative
all’evento; queste informazioni vengono poi utilizzate dai fisici per ricostruire, anche
sotto forma di immagini, l’evento.
7.4. Quesiti ed esercizi
In un calorimetro i processi di sviluppo di uno sciame continuano fino a quando l'energia delle
particelle è superiore a un’energia detta energia critica Ec. Un modello molto semplice di
sviluppo di uno sciame prodotto da un fotone è il seguente:
1. il fotone, inizialmente di energia E materializza in una coppia elettrone-positrone in cui ciascuno dei
figli ha energia pari a E/2
2. ciascuna delle particelle prodotte irraggia un fotone di energia pari alla metà di quella della particella
madre, che quindi ne conserva la metà di quella che aveva inizialmente.
3. Ogni fotone materializza nuovamente in una coppia come al punto 1
4. Ogni elettrone o positrone emette un fotone perdendo metà della sua energia
Il processo va avanti in modo tale che dopo N passi ci sono 2N particelle tra fotoni, elettroni e
positroni. Lo sviluppo dello sciame si arresta quando l’energia delle particelle presenti scende sotto
l’energia critica.
Quale tra le seguenti formule fornisce un’indicazione del numero di passi complessivi dello
sciame?
a. N=αE con α costante
b. N=exp(−E/Ec)
c. N=log(E/Ec)/log2
d. N=E/Ec
e. N=(E/Ec)−2
[Il processo continua finché (1/2)N E<Ec. La risposta corretta è la c.]
Due bande di energia di uno scintillatore sono separate di 3 eV. Tra di esse si trova uno stato
metastabile a 2.70 eV dallo stato di energia più basso. Qual è la lunghezza d’onda tipica dei
fotoni di scintillazione?
a. 270 nm
b. 540 nm
c. 460 nm
d. 1250 nm
e. 320 nm
[La risposta corretta è la c.]
171
Osserva l’immagine che rappresenta un evento registrato a LHC
Di che tipo di evento si tratta?
a. Z→e+e−
b. È un muone dei raggi cosmici che ha attraversato il rivelatore
c. H→γγ
d. Z→μμ
e. È una particella che decade in adroni
[La risposta corretta sembra la b.]
Si tratta di un elemento di un rivelatore. Di che tipo di rivelatore potrebbe trattarsi?
a. di un calorimetro
b. di una camera a bolle
c. di un rivelatore di muoni
172
d. di un tracciatore di silicio
e. di un tracciatore a gas
[La risposta corretta è la a. Si tratta di un elemento di un calorimetro elettromagnetico]
Guarda lo schema di questo rivelatore.
A tuo avviso si potrebbe trattare di...
a. di un rivelatore per neutrini
b. non può essere un rivelatore
c. un rivelatore per un esperimento a un collider
d. un rivelatore per un esperimento a bersaglio fisso
e. di un rivelatore da mandare nello spazio
[La risposta corretta sembra la d.]
In un rivelatore a un collider si osserva un intenso deposito isolato di energia nel calorimetro
adronico. Che tipo di particella può averlo prodotto?
a. un muone
b. un protone (errata)
c. un fotone
d. un neutrone
e. un elettrone
[Tutte le particelle cariche, quindi anche i protoni, descrivono tracce curve nel tracciatore interno e
rilasciano energia nel calorimetro elettromagnetico. Se si vede un deposito isolato di energia nel
calorimetro adronico deve trattarsi di un adrone che non ha lasciato traccia nel tracciatore; la risposta
esatta è quindi la d.]
173
Osserva l’immagine
a destra: si tratta di
un evento registrato
dall’esperimento
ALEPH a LEP (un
collider e+e− in cui
si producono bosoni
Z). Di che tipo di
evento si tratta?
a. Z→μμγ
b. Z→e+e−
c. Z→γ
d. Z→q-antiquark
e. Z→ννγ
[La parte in rosso rappresenta il calorimetro adronico, la parte in verde il calorimetro elettromagnetico,
lo strato blu la bobina che genere il campo magnetico. La risposta esatta è la…?]
Osserva l’immagine
a destra: si tratta di
un evento registrato
dall’esperimento
OPAL a LEP (un
collider e+e− in cui
si producono bosoni
Z). La torre gialla
rappresenta un
deposito nel
calorimetro
elettromagnetico. Di
che tipo di evento si
tratta?
a. Z→qq¯
b. Z→ννγ
c. Z→μμγ
d. Z→e+e−
e. Z→γ
[La risposta esatta è la e.]
174
Nell’immagine a destra si osserva
una traccia carica che raggiunge i
rivelatori più esterni (in rosso) e
altre tracce disposte in modo
asimmetrico, che appartengono a
particelle assorbite dai rivelatori più
interni, oltre a pochi depositi isolati
nei calorimetri. Come si può
interpretare quest’evento? Quale
particella potrebbe essere stata
prodotta?
a. un W decaduto in un muone e un
neutrino
b. un adrone neutro
c. una J/Ψ che decade in due muoni
d. una Z che decade in particella e
antiparticella
e. un bosone di Higgs che decade in
due fotoni
[La risposta corretta è la a.]
Osserva la ricostruzione di un evento a LHC.
175
Nell’immagine le linee rosse connettono segnali rivelati nelle camere esterne al magnete e nel
tracciatore centrale. Come si può classificare questo evento?
a.
b.
c.
d.
e.
Z→qq¯
W→eν
H→ZZ
Z→μ+μ− (errata)
H→γγ
[La risposta esatta è la c.
Ciascuno dei due Z decade in una coppia di muoni, per cui si osservano quattro tracce.]
176
Carlo Dariol
particelle
:
Ebbene sì… è stata una straordinaria rottura di
EDIZIONI DEL CUBO
Ultima revisione: gennaio 2017
www.elevamentealcubo.it
177