anno scolastico 2009 / 2010
ELETTRONICA per Elettrotecnica ed Automazione
3° anno
CIRCUITI COMBINATORI
Un circuito combinatorio (o rete combinatoria) è un insieme interconnesso di porte
logiche il cui output, istante per istante dipende unicamente dallo stato che gli ingressi
della rete hanno nell’istante medesimo e non dai valori che questi hanno assunto negli
istanti precedenti.
Una rete logica altro non è che una realizzazione fisica di una funzione binaria di variabili
binarie. I circuiti combinatori implementano, pertanto, le funzioni logiche esprimibili
nell’algebra di Boole.
I circuiti logici sono componenti hardware che manipolano informazione binaria. I circuiti di
base sono detti PORTE LOGICHE (logical gate). Per descrivere i comportamenti dei
circuiti digitali si può usare un’algebra (notazione matematica) che specifica l’operazione di
ogni gate e permette di analizzare e sintetizzare (disegnare) il circuito.
PORTE LOGICHE
Le porte logiche sono dei semplici circuiti elettronici che possono essere considerate dei
blocchi attraverso i quali poter svolgere delle operazioni logiche. Tali operazioni devono
sottostare alla cosiddetta algebra binaria o Booleana: essa si basa sugli stati “VERO” o
“FALSO” (TRUE or FALSE, in inglese) che, in elettronica, corrispondono al "passaggio" o
"non passaggio" di corrente elettrica e quindi ai cosiddetti "LIVELLI LOGICI" "0" e "1".
Le operazioni logiche fondamentali sono AND, OR, XOR, NOT. A queste si aggiungono le
versioni con l'uscita invertita delle prime tre che sono NAND, NOR, XNOR. Queste non
sono altro che, rispettivamente: AND+NOT, OR+NOT, XOR+NOT.
A parte la funzione NOT che ha un solo ingresso e le XOR e XNOR che dispongono al
massimo di due ingressi, le altre porte logiche possono disporre, teoricamente, di un
qualunque numero di ingressi, tutte invece dispongono di una sola uscita (o al massimo
anche dall'uscita complementare ovvero invertita).
Funzione logica AND
La funzione logica AND fornisce un'uscita "vera" solo quando tutti gli ingressi sono "veri".
Analogamente, una porta logica AND fornisce un livello logico "1" solo quando tutti gli
ingressi presentano un livello logico "1".
Da un punto di vista algebrico la funzione AND è rappresentata dal prodotto degli ingressi:
OUT = A * B
1
anno scolastico 2009 / 2010
ELETTRONICA per Elettrotecnica ed Automazione
3° anno
A
B
OUT = A*B
0
0
0
0
1
0
1
0
0
1
1
1
Un esempio pratico è il seguente:
La funzione logica OR
La funzione logica OR fornisce un'uscita "vera" quando almeno un ingresso è "vero".
Analogamente, una porta logica OR fornisce un livello logico "1" quando almeno un
ingresso presenta un livello logico "1".
Da un punto di vista algebrico la funzione OR è rappresentata dalla somma degli ingressi:
OUT = A + B.
A
B
OUT = A+B
0
0
0
0
1
1
1
0
1
1
1
1
Un esempio pratico di questa funzione è il seguente:
2
anno scolastico 2009 / 2010
ELETTRONICA per Elettrotecnica ed Automazione
3° anno
La funzione logica NOT
La funzione logica NOT fornisce un'uscita "vera" quando il suo ingresso presenta una
condizione "falsa" e viceversa. Analogamente, una porta logica NOT fornisce un livello
logico "1" quando il suo ingresso presenta un livello logico "0" e viceversa.
Da un punto di vista algebrico la funzione NOT è rappresentata dal complemento
dell’ingresso.
A
OUT = A
0
1
1
0
Un esempio pratico è dato dallo schema seguente: la lampada si accende quando
l’interruttore è aperto, si spegne quando è chiuso.
3
anno scolastico 2009 / 2010
ELETTRONICA per Elettrotecnica ed Automazione
3° anno
La funzione logica XOR
La funzione logica XOR fornisce un'uscita "vera" solo quando i due ingressi presentano le
condizioni logiche opposte. Analogamente, una porta logica XOR fornisce un livello logico
"1" solo quando i due ingressi presentano livelli logici opposti.
Dal punto di vista algebrico questa funzione è rappresentata da una somma particolare,
espressa con il simbolo ⊕ che ci indica che 1+1 = 0, al contrario di quanto avviene per la
funzione OR, ma che rende questa funzione più simile all’aritmetica binaria in cui 1 + 1 = 0
con riporto di 1.
A
B
OUT = A ⊕ B
0
0
0
0
1
1
1
0
1
1
1
0
Le Funzioni logiche NAND e NOR
Le funzioni logiche che abbiamo esaminato finora sono fondamentali. Tutte le altre
funzioni logiche possono essere ricavate da una combinazione di queste fondamentali. Un
esempio è dato dalle funzioni NAND e NOR che si ottengono negando l’uscita
rispettivamente dalla AND e della OR.
A
B
OUT = A * B
A
B
OUT = A + B
0
0
1
0
0
0
0
1
1
0
1
1
1
0
1
1
0
1
1
1
0
1
1
1
4
anno scolastico 2009 / 2010
ELETTRONICA per Elettrotecnica ed Automazione
3° anno
La negazione dell’uscita è rappresentata dal pallino posto su di essa.
In realtà anche la funzione XOR può essere ricavata da una combinazione delle prime tre.
Abbiamo che:
Si ricava dal circuito combinatorio:
Che è la realizzazione con porte logiche della funzione OUT = ( A * B) + (A * B ).
RICHIAMI DELL’ALGEBRA DI BOOLE
Come abbiamo detto in precedenza l’algebra di Boole è uno strumento che ci permette di
analizzare e sintetizzare un circuito logico.
I componenti dell’algebra booleana sono i seguenti:
Ø OPERATORI: sono le funzioni logiche AND, OR, NOT;
Ø Regole di trasformazione ed equivalenza tra operatori booleani;
Ø OPERANDI booleani: possono assumere sono due valori (vero / falso oppure 1 / 0).
Le regole fondamentali dell’algebra booleana sono le seguenti:
Idempotenza:
A + A = A;
A*A=A
Proprietà commutativa:
A + B = B + A;
A*B=B*A
Proprietà associativa:
(A+B)+C = A+(B+C);
(A*B)*C = A*(B*C)
5
anno scolastico 2009 / 2010
ELETTRONICA per Elettrotecnica ed Automazione
3° anno
Complementazione:
A + Ā = 1,
A*Ā=0
Proprietà distributiva:
A*(B+C) = A*B+A*C;
A+(B*C) = (A+B)*(A+C)
Ricorsività della negazione:
A =A
Proprietà di assorbimento:
A + 0 = A;
A*1=A
A + 1 = 1;
A*0=0
A + A *·B = A;
A *·(A + B) = A
A+Ā*B=A+B
A * (Ā + B) = A * B
Teoremi di De Morgan
Combinando opportunamente queste proprietà si giunge ai teoremi di De Morgan,
espressi dalle equazioni:
A+B = A+ B
A* B = A + B
6
anno scolastico 2009 / 2010
ELETTRONICA per Elettrotecnica ed Automazione
3° anno
ALCUNI ESEMPI PRATICI
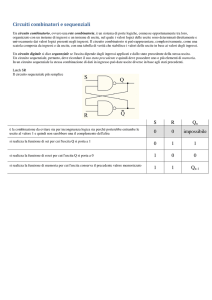
Il circuito addizionatore (half adder)
Un esempio pratico di logica combinatoria è dato dal circuito addizionatore che esegue la
somma binaria di due ingressi e ci fornisce il risultato con il riporto:
Le funzioni logiche, rispettivamente per l’uscita somma e l’uscita riporto sono:
S = X ⊕Y
C = XY
Nel complesso dunque questo circuito implementa una funzione logica avente due
ingressi e due uscite la cui tavola della verità è:
0
somma
A ⊕ B
0
riporto
A*B
0
0
1
1
0
1
0
1
0
1
1
0
1
A
B
0
7
anno scolastico 2009 / 2010
ELETTRONICA per Elettrotecnica ed Automazione
3° anno
Il circuito addizionatore completo (full adder)
Il circuito addizionatore visto sopra ha il limite di addizionare solo due ingressi. Nel caso in
cui si sommino numeri con un numero di bit maggiore uguale di 2 è necessario tenere in
conto anche i riporti provenienti dai bit di peso più basso come nell’esempio seguente:
c3
c2
c1
c0
A
a3
a2
a1
a0
B
b3
b2
b1
b0
c2 +b3 +a3
c1 +b2 +a2
c0+ b1+ a1
b0+ a0
riporto
A+B
c3
dove ax e bx indicano i singoli bit del numero cx il bit di riporto.
La figura sopra è lo schema di un addizionatore completo. Si tratta in pratica di due
addizionatori in cascata i cui riporti sono sommati in una porta OR. L’uscita della porta OR
è il riporto complessivo. La tavola della verità di questo circuito è:
Cin
0
0
0
0
1
1
1
1
B
0
0
1
1
0
0
1
1
A
0
1
0
1
0
1
0
1
somma
0
1
1
0
1
0
0
1
Cout
0
0
0
1
0
1
1
1
8
anno scolastico 2009 / 2010
ELETTRONICA per Elettrotecnica ed Automazione
3° anno
Come visibile nella figura sopra, è possibile collegare più circuiti di questo tipo per ottenere
un addizionatore di numeri binari di lunghezza qualunque.
Il circuito multiplexer
Il circuito multiplexer è costituito da N ingressi ix , M ingressi di controllo cx ed un’uscita u.
Tramite gli ingressi di controllo si seleziona uno ed uno solo degli ingressi e viene portato
all’uscita.
La rappresentazione del multiplexer è la seguente:
La funzione logica del multiplexer è la seguente:
u = (i0 * c 0 * c1 ) + (i1 * c 0 * c1 ) + (i2 * c 0 * c1 ) + (i3 * c 0 * c1 )
La realizzazione del multiplexer e la tavola della verità sono le seguenti:
9
anno scolastico 2009 / 2010
ELETTRONICA per Elettrotecnica ed Automazione
3° anno
c1
c0
u
0
0
i0
0
1
I1
1
0
I2
1
1
I3
Il demultiplexer
Un circuito demultiplexer viene definito come l'inverso di un circuito multiplexer, ossia
come un elemento funzionale capace di commutare un solo ingresso su due o più uscite.
Per
convenzione,
le
uscite
"non
attivate"
assumono
il
valore
costante
0,
indipendentemente dal valore assunto dall'ingresso "dati". Notare che questa convenzione
pone un vincolo sui codici che possono essere utilizzati per trattare le informazioni in
uscita da un demultiplexer: il valore 0 deve poter essere interpretato come un valore non
significativo, una condizione di riposo, ecc., in quanto questo valore viene assegnato a
tutte le uscite non connesse con l'ingresso.
In figura é riportato un esempio di realizzazione di un demultiplexer a 2 uscite (comandato
da un segnale di controllo c) in grado di commutare informazioni codificate su due bit.
c1
c0
u0
u1
u2
u3
0
0
c0
0
0
0
0
1
0
c0
0
0
1
0
0
0
c0
0
1
1
0
0
0
c0
10
anno scolastico 2009 / 2010
ELETTRONICA per Elettrotecnica ed Automazione
3° anno
Il decoder
Il decoder (decodificatore) è un circuito ha n ingressi di controllo e 2n uscite. La funzione
espletata è di portare a valore logico 1 solo l’uscita corrispondente al codice di controllo
fornito. Il decoder può avere un ingresso di enable che ha il compito di disabilitare tutte le
uscite, indipendentemente dallo stato degli ingressi Cx.
C2
C1
C0
U0
U1
U2
U3
U4
U5
U6
U7
0
0
0
1
0
0
0
0
0
0
0
0
0
1
0
1
0
0
0
0
0
0
0
1
0
0
0
1
0
0
0
0
0
0
1
1
0
0
0
1
0
0
0
0
1
0
0
0
0
0
0
1
0
0
0
1
0
1
0
0
0
0
0
1
0
0
1
1
0
0
0
0
0
0
0
1
0
1
1
1
0
0
0
0
0
0
0
1
Per questo circuito, che ha più uscite, è necessario scrivere una funzione logica per ogni
uscita. Per l’uscita U0 vale: U0 = C0 * C1 * C 2
L’ encoder
Il codificatore o encoder fa la funzione inversa del decodificatore. Il codificatore ha 2n
ingressi ed n uscite. Quando un ingresso è attivo alle uscite è presente il numero binario
che identifica l’ingresso. Questi circuiti dispongono anche di un’uscita GS (group signal)
che segnala quando almeno un ingresso è attivo. Questo segnale è importante perché ci
permette di distinguere lo stato di almeno un ingresso attivo dallo stato di nessun ingresso
attivo in cui il valore che assumono le uscite non ha significato.
Supponendo di avere un codificatore con 8 ingressi e 3 uscite la tavola della verità sarà:
11
anno scolastico 2009 / 2010
ELETTRONICA per Elettrotecnica ed Automazione
3° anno
I0
I1
I2
I3
I4
I5
I6
I7
U2
U1
U0 GS
0
0
0
0
0
0
0
0
x
x
x
1
1
0
0
0
0
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
1
0
0
0
1
0
0
0
0
0
0
1
0
0
0
0
0
1
0
0
0
0
0
1
1
0
0
0
0
0
1
0
0
0
1
0
0
0
0
0
0
0
0
1
0
0
1
0
1
0
0
0
0
0
0
0
1
0
1
1
0
0
0
0
0
0
0
0
0
1
1
1
1
0
Si suppone che gli ingressi siano attivi a livello logico alto.
Comparatori
Scopo di un circuito comparatore é il confronto tra due numeri binari. Il confronto può
essere effettuato per verificare l'uguaglianza oppure una relazione d'ordine del tipo
"maggiore", "minore", ecc.
Comparatori di uguaglianza
Questi possono essere realizzati a partire dalla funzione elementare XNOR a due ingressi.
Dalla tavola di verità di questa funzione vediamo che, interpretando l'uscita 0 come "falso"
e l'uscita 1 come "vero", possiamo ottenere immediatamente in uscita il risultato del
confronto per rilevare l'uguaglianza tra le due variabili di ingresso.
Possiamo estendere il circuito in modo da operare il confronto tra due numeri con più bit,
utilizzando una funzione del tipo XNOR per ogni coppia di bit corrispondenti da
confrontare, calcolando poi l'AND tra i confronti di ogni cifra. Per esempio, in figura é
illustrata la realizzazione di un circuito comparatore per rilevare l'uguaglianza tra due
ingressi codificati ciascuno su 3 bit (usando ovviamente lo stesso codice per i due
ingressi).
12
anno scolastico 2009 / 2010
ELETTRONICA per Elettrotecnica ed Automazione
3° anno
La funzione booleana del circuito in figura è:
u = (a0 ⊕ b0 ) * (a1 ⊕ b1 ) * (a2 ⊕ b2 )
Comparatori a > b per numeri in codice binario
Il circuito diventa più complesso se dobbiamo confrontare due numeri per stabilire se uno
è maggiore dell’altro. Il confronto deve partire dalla cifra più significativa: se le due
rappresentazioni differiscono nella cifra più significativa, allora possiamo subito concludere
se la relazione a > b é vera o falsa, senza bisogno di considerare le cifre successive. Solo
se le cifre più significative delle due rappresentazioni a confronto sono uguali, allora
dobbiamo passare all'esame delle cifre successive per arrivare a concludere il valore di
verità della relazione di confronto. La soluzione consiste nell'individuare un modulo base di
confronto tra una coppia di cifre, e nel replicare tale modulo tante volte quante sono le
cifre delle rappresentazioni binarie da confrontare.
Il circuito di confronto può essere realizzato con un modulo circuitale con 4 ingressi e due
uscite, che realizza le operazioni di confronto su una singola cifra. Indichiamo con A e B le
due variabili di ingresso al modulo corrispondenti alla cifra "corrente" da esaminare per le
due rappresentazioni binarie; indichiamo con C e D due variabili di ingresso ausiliarie che
ci riportano la codifica del risultato del confronto sulle cifre più significative. In particolare,
stabiliamo di indicare con C=1 la condizione "i confronti precedenti non hanno portato
nessun risultato definitivo", e con C=0 la condizione "l'esito del confronto é già noto a
seguito del confronto delle cifre precedenti". Nel caso C=0, interpretiamo poi D=0 come
risposta "no, a non é maggiore di b" ed invece D=1 come risposta "si, a > b". Indichiamo
infine con E e R le due uscite che codificano l'esito del confronto. In particolare
13
anno scolastico 2009 / 2010
ELETTRONICA per Elettrotecnica ed Automazione
3° anno
indicheremo con E=1 la condizione "neanche l'esame di questa cifra ci permette di dare
una risposta definitiva", e con E=0 la condizione "la risposta é stata determinata"; in
quest'ultimo caso R=0 significa "no", mentre R=1 significa "si, a > b".
Per esempio un circuito comparatore a 3 bit può essere realizzato connettendo tre repliche
di tale modulo come illustrato in figura:
14