Il prezzo di picco

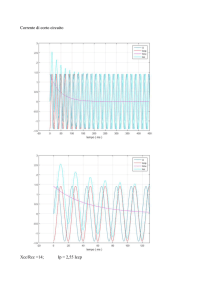
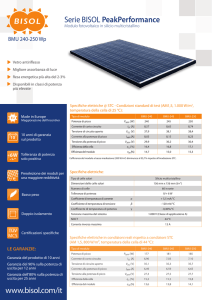
La regolazione del livello e
della struttura dei prezzi
Prezzi di picco
• Per i beni o servizi (come l’energia elettrica, le
telecomunicazioni) caratterizzati da periodicità della
domanda, la teoria propone una particolare strategia di
discriminazione di prezzo nota come prezzi multiorari (peak
load pricing)
Prezzi di picco
• I prezzi di picco riguardano servizi infrastrutturali come
elettricità, gas, telecomunicazioni, che:
1. hanno domande caratterizzate da fluttuazioni periodiche
2. non possono essere immagazzinati
3. devono essere comunque forniti a tutti i consumatori
l’impresa predispone una capacità degli impianti adeguata a
soddisfare la domanda nei periodi di picco
dunque, negli altri periodi (off peak) ha capacità produttiva
inutilizzata
Quali prezzi consentono di allocare in modo ottimale la domanda
tra il periodo di picco e fuori picco? Come ripartire i costi?
Prezzi di picco con un solo impianto
• Consideriamo due periodi di tempo di identica lunghezza con
funzioni di domanda indipendenti tra loro e constanti nel
tempo => il picco di domanda è stabile nel periodo
considerato
• Questo metodo:
1. riflette le condizioni tecnologiche della produzione
2. impone il più efficiente criterio di allocazione delle risorse
Prezzi di picco con un solo impianto
• Hp: il bene o servizio non può essere immagazzinato
• Hp: un’unica struttura produttiva che soddisfa la domanda
durante tutto il giorno (diviso in intervalli di tempo); i
consumatori hanno domande diverse per vari intervalli
temporali
• Due periodi temporali: le funzioni di domanda sono p1(y1) e
p2(y2), con y1 ≥ y2
p1(y1) è la domanda di picco
p2(y2) è la domanda fuori picco
Prezzi di picco
•
Domanda di picco
•
Domanda fuori picco
•
Capacità di breve periodo
•
Costo variabile
•
Costo fisso
•
Costo marginale di breve periodo
•
Costo marginale di lungo periodo
Prezzi di picco con un solo impianto
Il prezzo
di picco
è uguale
a SRMC e
LRMC
Il prezzo
fuori
picco è
pari al
costo
marginale
di breve
periodo
Prezzi di picco con un solo impianto
• La funzione di costo dell’impresa è caratterizzata da:
β = costo unitario costante per unità di capacità produttiva
b = costo marginale di breve periodo => costo unitario
variabile
• Il costo variabile b è costante fino a un livello di quantità pari
a y, che è la quantità MASSIMA domandata durante il picco,
è la capacità massima di produzione dell’impianto
• Il costo marginale di breve periodo è parallelo all’asse delle
ascisse fino a y, dopodiché è verticale
• LRMC (costo marginale di lungo periodo) è parallelo all’asse
delle ascisse e pari a (b + β)
Prezzi di picco con un solo impianto
• La strategia di picco consente di fissare due prezzi:
1. Il prezzo fuori picco che è uguale al SRMC: p2 = b
=> Il prezzo fuori picco è pari al costo marginale di breve
periodo
2. Il prezzo di picco p1 = b + β
il prezzo di picco è uguale al LRMC
l’uguaglianza del prezzo di picco al LRMC consente di usare
l’impianto in maniera efficiente
dimostrazione
Prezzi di picco con un solo impianto
• Perché non è efficiente fissare un prezzo pu che non è
differenziato per periodi temporali?
1. Perché i consumatori, nel momento fuori picco, si trovano a
pagare un prezzo più alto (e quindi a ricevere una quantità
inferiore) rispetto a p2 che consente una utilizzazione ottima
dell’impianto
2. Nel picco, c’è un eccesso di domanda rispetto alla situazione
ottimale p1, e questo incremento di produzione non copre i
costi che sostiene l’impresa per incrementare l’output oltre
il livello ottimale y
graficamente..
Prezzi di picco con un solo impianto
Riduzione
della domanda
fuori picco
Sovraccapacità
produttiva con
prezzo unico
Prezzi di picco con più impianti
• Ipotizziamo di avere un parco di generazione dell’energia
elettrica => più impianti con diverse tecnologie
Problema dei prezzi di picco con più impianti:
• Quando ci sono più impianti, occorre determinare come si
devono attribuire i costi di capacità se non tutti i
consumatori sono serviti dallo stesso impianto
Prezzi di picco con più impianti
Ci sono impianti:
• con alti costi fissi e bassi costi variabili (base load) come gli
impianti nucleari
• con basti costi fissi e alti costi variabili (quando il
combustibile è costoso) e che quindi vengono fatti funzionare
per brevi periodi di tempo
• In particolare gli impianti sono caratterizzati da costi fissi Bi
e costi variabili bi tali che:
Bi > Bi-1
bi < bi-1
Bi-1 + bi-1 > Bi + bi
Funzione di costo per impianti diversi
Prezzi di picco con più impianti
• L’impresa deve configurare la capacità ottimale di
produzione
deve considerare la funzione di domanda dei consumatori
(curva di carico)
identificare il numero di kW impegnati in ogni intervallo di
tempo
• Gli impianti sono impiegati in ordine di merito economico:
l’impresa regolata impiega prima gli impianti che nel lungo
periodo sono più efficienti (quindi quelli più economici se
vengono utilizzati nel l/p, come il nucleare), e poi comincia
ad impiegare gli impianti meno efficienti, fino a raggiungere
il livello di quantità richiesto
• La scelta degli impianti avviene a partire da quelli che sono
più economici se vengono usati per un maggior periodo di
tempo, e continua fino a individuare l’impianto marginale
cioè l’ultimo impianto che copre il livello di produzione
richiesto
Curva di carico e allocazione efficiente dei costi tra i tre tipi
di impianti
A ciascun
incremento di
potenza viene
assegnato il
costo marginale
del tipo di
impianto che
viene scelto
per espandere
la capacità
complessiva
• Il prezzo per kWh è pari al costo variabile dell’ultimo
impianto che viene fatto funzionare (quindi il CV più alto) e
l’impresa copre i costi variabili di tutti gli impianti in funzione
Prezzi di picco nel caso di più impianti
• Nel caso di più impianti, si stabiliscono tariffe binomie con
una quota fissa che copre i costi di capacità dell’impianto
marginale, e una quota variabile legata all’uso dell’energia
Sussidi incrociati
• Il regolatore può consentire all’impresa di ricorrere ai sussidi
incrociati per finalità redistributive
1. Valutiamo l’efficienza dei sussidi incrociati
2. Illustriamo un test che verifica l’esistenza di sussidi incrociati
• Dire che ci sono sussidi incrociati per la fornitura di un
servizio significa dire che alcuni utenti pagano p < MC e
questa differenza viene applicata ad altri utenti che pagano
un prezzo p > MC
• Esempio: tariffe dell’energia elettrica applicate a utenti
urbani e rurali
Sussidi incrociati
• L’applicazione di una tariffa:
Ca = MC medio ponderato
porta a una domanda OR di kWh/annuo per gli utenti rurale e
OU per gli utenti urbani
Sussidi incrociati e perdita di benessere
Problemi dei sussidi incrociati:
1. I sussidi comportano delle perdite alla società NEL SUO
COMPLESSO
2. L’impresa regolata può applicare sussidi incrociati per
evitare l’entrata nel mercato di altre imprese (=>
p<MC non per scopi sociali ma per finalità strategiche)
Sussidi incrociati e perdite di benessere
B è il surplus dei
consumatori
rurali che
pagano
p < MC rurale
CaCuFE è l’area che
rappresenta la perdita
di benessere per i
consumatori urbani
che pagano p > MC
urbano
Test che verifica l’esistenza di sussidi
• È possibile inoltre che l’impresa applichi sussidi incrociati per
evitare l’entrata nel mercato di altre imprese (=> p<MC non
per scopi sociali ma per finalità strategiche)
Cosa può fare il regolatore per controllare i prezzi praticati
dall’impresa regolata?
•
Può limitare la discrezionalità dell’impresa nel definire i
prezzi dei servizi, vincolando i prezzi, cioè fissando una
soglia min e max entro cui l’impresa regolata può fissare il
prezzo
Esempio:
• due servizi, 1 e 2, con prezzi di vendita p1 e p2
Soglia minima di prezzo
• Consideriamo il costo incrementale per il bene 1 (cioè il costo aggiuntivo per
produrre 1, quando già produco 2) che è:
• Se i ricavi che derivano dalla vendita del bene 1 sono maggiori del costo
incrementale sostenuto per produrlo, allora i prezzi sono liberi da sussidi
(stessa cosa per il bene 2):
• (se c'e' un ricarico rispetto ai costi minimi, probabilmente non c'e' sussidio)
=> Soglia minima: si tiene conto del costo incrementale
Soglia massima di prezzo
• Se i ricavi derivanti dalla vendita di un bene o servizio (y2)
sono minori o uguali dello stand alone cost (che è il costo che
l’impresa sostiene per produrre solo quel servizio)
p2* y2 ≤ C(0, y2)
allora vuol dire che l’impresa non sta sussidiando il prezzo di
vendita di altri servizi. Se fosse il contrario, altre imprese
potrebbero entrare. E il fatto che così non e' implicherebbe
che ci sono sussidi
i compratori di quel servizio non stanno sussidiando i
compratori di altri servizi
=> Soglia massima: si tiene conto dello stand alone cost