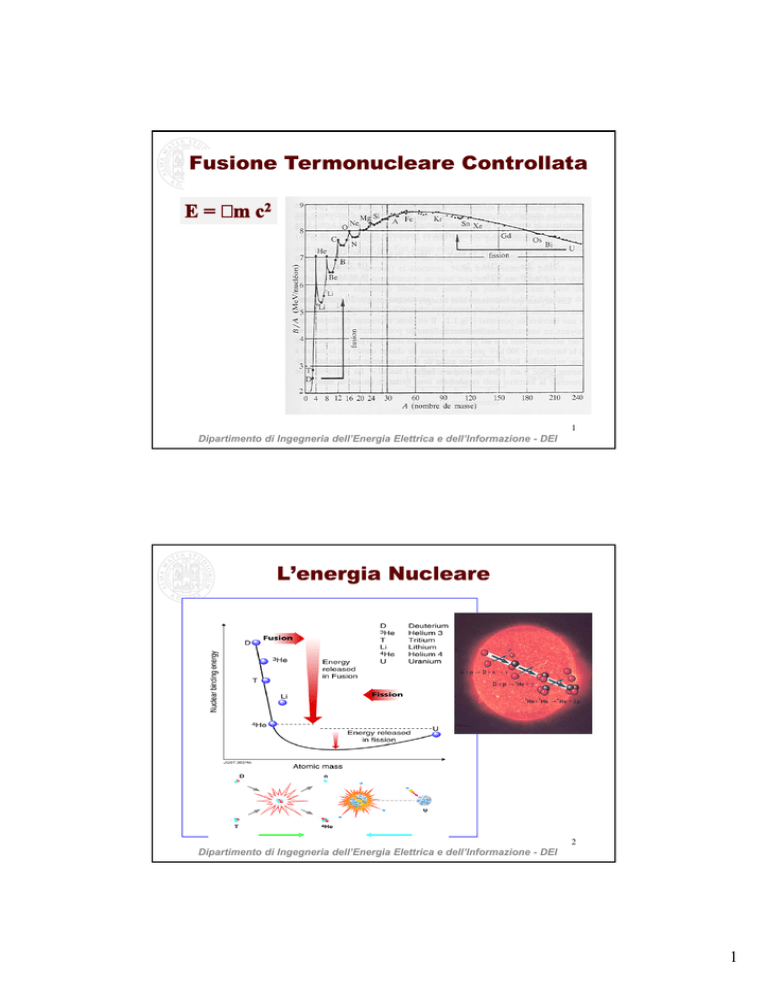
Fusione Termonucleare Controllata
1
Dipartimento di Ingegneria dell’Energia Elettrica e dell’Informazione - DEI
L’energia Nucleare
2
Dipartimento di Ingegneria dell’Energia Elettrica e dell’Informazione - DEI
1
Reazioni Nucleari della FTC
Reazioni
D+D
D+T
D + He3
DD, DT, DHe3
T (1 MeV) + p (3 MeV)
50 %
He3 (0.8 MeV) + n (2.45 MeV) 50 %
He4 (3.5 MeV) + n (14.1 MeV)
He4 (3.7 MeV) + p (14.7 MeV)
- D (deuterio) isotopo stabile dell’idrogeno, allo 0.015 % nell’acqua.
- T (trizio) elemento instabile derivante da:
Li6 + n He(2 MeV) + T(2.7 MeV)
Li7 + n He + T + n - 2.5 MeV
Li (litio) elemento naturale con Li6 al 7.4 % ed il Li7 al 92.6 %.
3
Dipartimento di Ingegneria dell’Energia Elettrica e dell’Informazione - DEI
Confinamento
Magnetico di
Plasmi
Fusionistici:
Le particelle
cariche, gli ioni e
gli elettroni, sono
confinate dai
campi magnetici, i
neutroni fuggono.
I(Btr)
I(Bz)
Dipartimento di Ingegneria dell’Energia Elettrica e dell’Informazione - DEI
2
Altre Reazioni della FTC
Reazioni secondarie presenti con la reazione
primaria DT:
T+T
He3 + He3
T + He3
He4 + 2n + 11.3 MeV
He4 + 2p + 12.9 MeV
He4 + n + p + 12.1 MeV [51 %]
He4 + D + 14.3 MeV
[43 %]
He5 + p + 14.3 MeV
[6 %]
4
He + n
5
Dipartimento di Ingegneria dell’Energia Elettrica e dell’Informazione - DEI
Reazioni della FTC senza Neutroni
p + B11
3He4 (8.66 MeV)
p + Li6
He3 (2.3 MeV) + He4 (1.72 MeV)
6
Dipartimento di Ingegneria dell’Energia Elettrica e dell’Informazione - DEI
3
Sezioni d’Urto per le Reazioni della FTC
7
Dipartimento di Ingegneria dell’Energia Elettrica e dell’Informazione - DEI
Barriera Coulombiana
W=
Z1Z 2 e 2
4 0 r
W0 =
Z1 Z 2 e 2
4 0 R 0
Z1Z 2 e 2
4 e0 R 0
R0
r
8
Dipartimento di Ingegneria dell’Energia Elettrica e dell’Informazione - DEI
4
Integrali di Reazione per la FTC
f v =
Rf
=
n1 n 2
+
f1 ( v 1 ) f2 ( v 2 ) v 1 - v 2 f ( v 1 - v 2 ) dv 1 dv 2
-
m3
s
9
Dipartimento di Ingegneria dell’Energia Elettrica e dell’Informazione - DEI
Bilancio Energetico della FTC
Guadagno energetico dovuto alle reazioni di fusione:
Pf = n1 n2 <fv> Q
Pf, = n1 n2 <fv> Q
dove Q e Q sono l’energia totale e l’energia delle sole particelle
(He4) rilasciate durante un evento di fusione (per reazioni DT
Q = 3.5 MeV e Q = 17.6 MeV)
10
Dipartimento di Ingegneria dell’Energia Elettrica e dell’Informazione - DEI
5
Bilancio Energetico della FTC
Perdite radiative:
Se sono presenti solo isotopi dell’idrogeno non si hanno
radiazioni di linea, ma solo di bremstralung:
Pb = 1.43 10 -40 Z n i n e T
W / m
3
Se vi sono impurezze con particelle ad elevato numero atomico
si hanno elevati contributi di perdita dovuti a radiazioni di linea.
Perdite di confinamento:
L’energia del plasma per unità di volume è data da:
Ec =
3
k n e Te + n i Ti
2
Al finire del confinamento dopo c secondi, la perdita di energia è
Pc =
Ec
c
11
Dipartimento di Ingegneria dell’Energia Elettrica e dell’Informazione - DEI
Bilancio Energetico della FTC
Criteri per la FTC:
- Ignizione:
- Pareggio:
Pf, Pb + PC
Pf Pb + PC
Reazioni DD con n = ne = ni, T = Te = Ti, per l’ignizione:
¼ n 2 v f Q
n c
3knT
+ 1.43 10 -40 n 2 T
c
3knT
¼ v f Q - 1.43 10 - 40 T
12
Dipartimento di Ingegneria dell’Energia Elettrica e dell’Informazione - DEI
6
Bilancio Energetico della FTC
13
Dipartimento di Ingegneria dell’Energia Elettrica e dell’Informazione - DEI
Bilancio Energetico della FTC
Criterio di Lawson
- Potenza rilasciata dopo un ciclo: Pout Pf + Pb + PC
- Potenza da fornire per la fusione: Pin Pb + PC
Detto il rendimento di conversione, per l’autosostentamento deve essere:
Pout ≥ Pin
Reazioni DD con n = ne = ni, T = Te = Ti, per l’ignizione:
n c
3knT
¼ v f Q
- 1.43 10 - 40 T
1-
14
Dipartimento di Ingegneria dell’Energia Elettrica e dell’Informazione - DEI
7
Bilancio Energetico della FTC
15
Dipartimento di Ingegneria dell’Energia Elettrica e dell’Informazione - DEI
Confinamento Magnetico
Il confinamento del plasma da fusione (T ≥ 10 keV) nella FTC a confinamento magnetico viene realizzato con bottiglie magnetiche che sfruttano la proprietà delle particelle cariche che si muovono ad elica lungo pareti di tubi di flusso magnetici.
16
Dipartimento di Ingegneria dell’Energia Elettrica e dell’Informazione - DEI
8
Confinamento Magnetico
+
Una scarica in un gas induce
un campo di induzione
azimutale che si compone con
la corrente e produce una forza J
centripeta che agisce sulle
particelle cariche del plasma.
Tale fenomeno prende il nome
di effetto pinch.
J
B
17
Dipartimento di Ingegneria dell’Energia Elettrica e dell’Informazione - DEI
Superfici Magnetiche
Dall'equazione di conservazione della quantità
di moto e dall'equazione di Ampere:
u uu p + J B
t
B 0J
L'equazione di conservazione della quantità
di moto all'equilibrio diviene:
p = J B
moltiplicando scalarmente tale equazione
per J e per B:
J p = 0
B p = 0
J e B giacciono su
superfici isobare.
18
Dipartimento di Ingegneria dell’Energia Elettrica e dell’Informazione - DEI
9
Configurazioni Lineari
Per le scariche nelle configurazioni lineari (z - pinch)
dalla continuità della quantità di moto:
dp
=-J z B
dp=-J z B dr
dr
Dall'equazione di Ampere:
1
2
l Bdl =0I z 2 rB = r 0J z B = 2 0 rJ z
Z-Pinch
+
r 2 dp = -½ 0 J 2z r 3dr
Detto R il raggio esterno della scarica, p = 0 per r = R:
R
R
Iz
R
2
d pr =0
2
2
r dp=-2 rpdr R p
0
0
B
0
R
R 2 p r 2 dp =
0
0
R
J r dr
2 3
z
2
0
R2 p
0 2
I
8 z
0
8
J 2z R 4
Jz costante
19
Configurazioni Lineari - Relazione di Bennet
R2 p
0 2
Iz
8
p
B2
2 0
+
R2n
Si definisce con N =
il numero di particelle per
unità di lunghezza della scarica. Poiché p = nk(Ti+Te)
si ottiene la relazione di Bennet per le configurazioni
lineari (z-pinch):
Nk Ti + Te
0 2
I
8 z
Per un plasma in ETL con temperatura de gas
uguale alla temperatura degli elettroni la relazione
di Bennet diviene:
0 2
Nk T
I
16 z
Iz
B
20
Dipartimento di Ingegneria dell’Energia Elettrica e dell’Informazione - DEI
10
Configurazioni Lineari - Relazione di Bennet
Si definisce il parametro beta (da non confondere
con il parametro di Hall) come rapporto fra
pressione termodinamica e pressione magnetica: :
=
+
p
B / 2 0
2
(Il parametro beta βθ , tipico dell’effetto pinch, non va
confuso con il parametro di Hall.)
=
R. Bennet
p
B2 / 20
p
Nk Ti + Te
Iz
B2
20 2 Iz2
20
8 R
B
0 2
Iz
8
21
Dipartimento di Ingegneria dell’Energia Elettrica e dell’Informazione - DEI
Configurazioni Lineari - Z-Pinch stabilizzato
Un spostamento della scarica Z-pinch provoca un aumento di B all’interno della colonna ed una diminuzione di B all’esterno.
J
Si ha perciò una forza di Lorentz più intensa all’interno che all’esterno provocando una
instabilità con amplificazione dello scostamento
Dalla geometria lineare.
Per bilanciare lo Z-pinch si sovrappone un
campo di induzione magnetica B parallelo
all’asse, le cui linee di forza rimangono all’interno della scarica poiché B è parallelo a
J. B costringe le particelle cariche a muoversi
lungo le proprie line di forza e la scarica a non
scostarsi dalla geometria lineare. Per lo Z-pinch
stabilizzato la relazione di Bennet è anche in
questo caso:
0
2
Nk Ti + Te
8
I z
J
+
B
B
22
Dipartimento di Ingegneria dell’Energia Elettrica e dell’Informazione - DEI
11
Configurazioni Toroidali
Per eliminare le perdite di particelle nelle regioni elettrodiche parallelamente all’asse della scarica e di energia a causa dei contatti con gli elettrodi, si sono utilizzate le configurazioni toroidali.
23
Dipartimento di Ingegneria dell’Energia Elettrica e dell’Informazione - DEI
Configurazioni Toroidali
All’interno del toro B, e quindi la forza di Lorentz, è più intenso che all’esterno. Il toro di plasma tende ad espandersi. Si sovrappone quindi
un campo magnetico parallelo all’asse maggiore del toro Bz che si somma alla componente B all’esterno del toro e si sottrae all’interno. Si ottiene perciò un effetto di equilibrio che bilancia il toro e previene la sua
espansione.
B campo poloidale
confinante
B campo toroidale
stabilizzante
Bz: campo equilibrante
24
Dipartimento di Ingegneria dell’Energia Elettrica e dell’Informazione - DEI
12
Configurazioni Toroidali
Calcolo di Bz:
Forze che agiscono lungo la componente radiale:
- Fp: di pressione termodinamica;
- Fm: di pressione magnetica che corrisponde a Wm =½LI 2 (energia magnetica);
- Fz: di campo verticale dovute a Bz.
z
a
R
Dal principio dei lavori virtuali:
dL p = p dV = p 2 R 0 + dR - 2 R 0 a 2 =
= 2 2 a 2 p dR
R0
r
0
I f2
4
Coordinate toroidali:
r,
8R
Coordinate cilindriche: R, z,
d 0 R ln
2
dW m
dL
a
Fm =
= ½I 2
= ½I 2
=
dR
dR
dR
8R
0
L coefficien te di autoinduzi one del plasma. Per toro sottile (R a)
= ½I 2 0 ln
1
a
8R
Fp =
dL p
dR
= 2 2 a 2 p = 2 Nk Te T =
e distribuzi one di corrente uniforme :
L 0 R ln
2
a
25
Configurazioni Toroidali
Fp ed Fm tendono a far espandere il
toro, Fz è diretta verso l’interno del
toro:
Fz = 2 R 0 I Bz
Dall’equilibrio delle forze si ottiene:
Fp + Fm = Fz
Bz = I
0 8R 0
ln
1
4 R 0 a 2
26
Dipartimento di Ingegneria dell’Energia Elettrica e dell’Informazione - DEI
13
Configurazioni Toroidali
Fattore di sicurezza: q
Il passo della linea di forza del campo
magnetico è:
p r = 2 r
B
B
B
B
B
Il fattore di sicurezza, funzione di r, è:
p
p r
r B
q r =
=
2R 0 R 0 B
Comportamento ergodico delle linnee di campo: q è un numero irrazionale, le linee di campo si avvolgono sulle superfici isobariche ricoprendole
completamente.
Comportamento non ergodico delle linnee di campo: q è razionale, le linee di campo dopo q giri si chiudono su sestesse.
27
Dipartimento di Ingegneria dell’Energia Elettrica e dell’Informazione - DEI
Configurazioni Toroidali
Configurazioni Magnetiche
B
B
p
B
Tokamak - Stellarator
p
B
Reversed Field Pnch
28
Dipartimento di Ingegneria dell’Energia Elettrica e dell’Informazione - DEI
14
Configurazioni Toroidali
Toro con B
In uno stellarator la corrente di plasma è
nulla e tutti i campi sono prodotti dall’esterno.
Poiché, per la solenoidalità di B B 1/R,
se fosse presente solo B , si indurrebbe una
velocità di deriva di curvatura che genera
una separazione di carica e un campo elettrico conseguente. Si determina quindi una
velocità di deriva dovuta ad E dello stesso
verso per particelle negative e positive, che
tende a far espandere il toro di plasma.
vC
R
vE
+
E
B
vC
B
Toro con
B e B
E’ necessario un campo B che fa ruotare
le particelle positive dal basso verso l’alto
e le particelle negative dall’alto verso il basso limitando l’effetto di E.
29
Dipartimento di Ingegneria dell’Energia Elettrica e dell’Informazione - DEI
Instabilità nel Plasma Fusionistico
Instabilità MHD (macroscopiche): riguardano la posizione
di equilibrio del plasma e causano la disruzione della scarica
a seguito di spostamenti dalla posizione di equilibrio;
Instabilità microscopiche: riguardano le grandezze del trasporto e causano perdite sia di particelle che di energia.
30
Dipartimento di Ingegneria dell’Energia Elettrica e dell’Informazione - DEI
15
Instabilità nel Plasma Fusionistico
Analisi dell’equilibrio
• Principio dell’energia: Per mezzo delle equazioni di continuità e delle equazioni di Maxwell si può esprimere l’energia potenziale del sistema U( in
funzione dello spostamento . La posizione di equilibrio è data da = 0.
Equilibrio stabile: U( ) > U(0)
Equilibrio instabile: U( ) < U(0)
• Analisi modale: Si studia per mezzo del modello MHD il comportamento
della configurazione per uno spostamento rispetto la posizione di equilibrio:
= ’(r) expi[(m n ) ]
In corrispondenza delle condizioni al contorno si hanno le instabilità dei modi
poloidali m = 0, 1, 2,... che si dicono instabilità a flauto (o a salsiccia), kink (a
treccia), del secondo ordine, ecc., e le instabilità dei modi toroidali n = 0,1,2,3...
31
Dipartimento di Ingegneria dell’Energia Elettrica e dell’Informazione - DEI
Instabilità nel Plasma Fusionistico
m=0
m=1
m =2
a. instabilità a salsiccia;
b. instabilità a treccia;
c. instabilità del secondo
ordine.
32
Dipartimento di Ingegneria dell’Energia Elettrica e dell’Informazione - DEI
16
Instabilità nel Plasma Fusionistico
Controllo delle instabilità in un Tokamak:
q a =
a B
m
R 0 B
dall’espressione di q(a) e poiché dalla legge di Ampere (legge di
Biot-Savart per geometria rettilinea) I = 2 aB / 0, si ottiene:
2
2 a B
I <
m 0R 0
33
Dipartimento di Ingegneria dell’Energia Elettrica e dell’Informazione - DEI
Riscaldamento del Plasma Fusionistico
PJ = EJ = J2/: poiché T3/2, aumenta con T e ciò limita
l’effetto Joule. Inoltre I e quindi J sono limitati poiché q(a) > m.
Per elevare la temperatura sono necessari metodi di riscaldamento addizionali:
- riscaldamento adiabatico [T/n = cost.]
- iniezione di neutri
- radiofrequenze (f = 10 MHz-100 GHz)
34
Dipartimento di Ingegneria dell’Energia Elettrica e dell’Informazione - DEI
17
Riscaldamento del Plasma Fusionistico
Riscaldamento adiabatico
T/n = cost.
35
Dipartimento di Ingegneria dell’Energia Elettrica e dell’Informazione - DEI
Riscaldamento del Plasma Fusionistico
Riscaldamento a radiofrequenze
eB
me
eB
i =
mi
e =
L = pi 1+
(f 100 GHz)
(f 10 MHz)
pe2
pi2
U = pe2 + e2
(f 1 GHz)
(f 100 GHz)
36
Dipartimento di Ingegneria dell’Energia Elettrica e dell’Informazione - DEI
18
Riscaldamento del Plasma Fusionistico
Iniezione di neutri
Af particelle del fascio
Af + A+ Af+ + A (scambio di carica)
Af + e Af+ + 2e (ionizz. elettronica)
Af + A+ Af+ + A+ + e (ionizz. ionica)
I(x) = I0 exp[-x/ ]
=1/(Qionizz n) a/4
(a raggio min. toro)
37
Dipartimento di Ingegneria dell’Energia Elettrica e dell’Informazione - DEI
Macchine Toroidali
Macchina Tokamak - Effetto Trasformatorico
Nucleo magnetico in aria
Nucleo magnetico in ferro
Dipartimento di Ingegneria dell’Energia Elettrica e dell’Informazione - DEI
19
Macchina Tokamak
Il tokamak richiede una
configurazione compatta
(a
R 0, B θ
BΦ affichè IΦ )
q a =
a B
m
R 0 B
Dipartimento di Ingegneria dell’Energia Elettrica e dell’Informazione - DEI
Macchina Tokamak
Avvolgimenti Principali
Dipartimento di Ingegneria dell’Energia Elettrica e dell’Informazione - DEI
20
Macchina
Tokamak
I(Btr)
I(Bz)
Dipartimento di Ingegneria dell’Energia Elettrica e dell’Informazione - DEI
Macchina Tokamak
Andamento delle Correnti durante un Impulso
Corrente degli avvolgimenti
di campo toroidale
Corrente degli avvolgimenti
di campo trasformatorico
Corrente di plasma
Dipartimento di Ingegneria dell’Energia Elettrica e dell’Informazione - DEI
21
Macchina Tokamak
Pl.Maj. rad.
0.935
Pl. Min. Rad. 0.31
Pl. Current
1.6
Tor. Field
m
m
MA
8
T
Tor. Field En.
160
MJ
Pol. Field En.
200
MJ
Pulse Rep. Rate: 1 pulse every 20 min.
Dipartimento di Ingegneria dell’Energia Elettrica e dell’Informazione - DEI
Macchina Tokamak
Principali Machine
Tokamak
R0 [m]
a [m]
B [T]
IP [MA]
T15
Russia
2.43
0.70
5.5
2.3
JT60
Giappone
3.00
0.95
4.5
2.7
TFTR
USA
2.55
0.90
5.2
3.0
JET
UE
2.96
1.25 (2.1)
3.45
5.1
Dipartimento di Ingegneria dell’Energia Elettrica e dell’Informazione - DEI
22
Macchina Tokamak
JET - Joint European Torus (Culham GB)
Dimensioni: R0 = 2.96 m, a = 1.25 (2.1) m, B = 3.45 T, Iφ = 5.1 MA
Dipartimento di Ingegneria dell’Energia Elettrica e dell’Informazione - DEI
JET - Joint European Torus (Culham GB)
Manutenzione remota
Dipartimento di Ingegneria dell’Energia Elettrica e dell’Informazione - DEI
23
Tokamak Fusion Test Reactor - TFTR
Princeton Plasma Physics Laboratory
Design
Achieved
R0
2.1 - 3.1 m
2.1 - 3.1 m
Pl.Maj. Rad.
a0
0.4 - 0.85 m
0.4 - 0.96 m
Pl. Min. Rad.
Bϕ
5.2 T
6.0 T
Tor. Field
Iϕ
3.0 MA
3.0 MA
Pl.Current
PNBI
33 MW
39.5 MW
N. Beam Pow.
PICRF
12.5 MW
11.4 MW
ICRF Power
Dipartimento di Ingegneria dell’Energia Elettrica e dell’Informazione - DEI
Prestazioni
Q=
Q =
Pf
PIN
Pf,
PIN
(dove: PIN = PC+Pb)
Dipartimento di Ingegneria dell’Energia Elettrica e dell’Informazione - DEI
24
Reversed
Field Pinch
Dipartimento di Ingegneria dell’Energia Elettrica e dell’Informazione - DEI
Reversed
Field Pinch
RFX Padova
Dipartimento di Ingegneria dell’Energia Elettrica e dell’Informazione - DEI
25
Stellarator
Macchina in
regime continuo
Stellarator
Wendelstein 7-X
Max Plank Inst. für Plasmaphysik, Greifswald, Germany
Major radius: Minor radius: Plasma volume
Non‐planar coils:
Planar coils: 20
Number of ports:
Rot. transform:
Induction on axis:
Stored energy:
Heating power
Pulse length: 5.5 m
0.53 m
30 m3
50
299
5/6 ‐ 5/4
max. 3T
620 MJ 15 ‐ 30 MW
30 min
Machine height:
4.5 m
Maximal diameter: 16 m
Machine mass:
725 t
Cold mass: 392 t
W7‐X symmetry: 5 identical modules
Module symmetry: 2 flip‐symmetrical halfs
52
Dipartimento di Ingegneria dell’Energia Elettrica e dell’Informazione - DEI
26
53
ITER
International Thermonuclear Experimental Reactor
Cadarache (Proveza), France
Solenoide Centrale
Nb3Sn, 6 moduli
Bobine Toroidali
ITER entrerà in funzione nel 2019. Nel 2027
produrrà una potenza elettrica di 500 MW per
circa 15 minuti.
Nb3Sn, 18 moduli,
5,3 T sull’asse del
plasma
Avvolgiment:Poloidali
Criostato
24 m alto x 28 m dia.
Nb-Ti, 6
Caratteristiche del plasma
Raggio maggiore: 6.2 m
Raggio minore medio: 2 m
Volume: 840 m3
Corrente: 15 MA
Densitá: 1020 m-3
Temperatura: 15-20 keV
Potenza Fusione: 500-700 MW
Durata impulso > 300 s
Port Plug
Pompe
Criogeniche 8
54
Dipartimento di Ingegneria dell’Energia Elettrica e dell’Informazione - DEI
27
ITER
Camera da vuoto e sistema
per il remote handeling
55
Dipartimento di Ingegneria dell’Energia Elettrica e dell’Informazione - DEI
ITER
Riscaldamento Addizionale
q
56
Dipartimento di Ingegneria Elettrica
28
ITER
Sistema Magnetico
57
Dipartimento di Ingegneria dell’Energia Elettrica e dell’Informazione - DEI
ITER
Costo Stimato
• Il costo stimato per la costruzione è di 4 260 M EURO
(valore 2005).
• Circa 5 000 M EURO sono stati stimati per 20 anni di
operazione.
• Il contributo dei Partners per la costruzione è:
EU:
JA – RF – CN – KO – US – IN:
50%
10% ciascuno
• 10% del totale è tenuto come riserva.
58
Dipartimento di Ingegneria dell’Energia Elettrica e dell’Informazione - DEI
29
EU Strategia
DEMO :
Dimostrare
produzione energia
elettrica a scala FPP
DEMO
ITER: fattibilita’
Scientifica e technologica
Fusion Power Plant(FPP):
Sicuro ed accettabile per
Impatto Ambientale e Costo
59
Dipartimento di Ingegneria dell’Energia Elettrica e dell’Informazione - DEI
Centrale FTC
Breeding Blanket
Poloidal Field Coil
Toroidal Field Coil
Power Conversion
System
Heating &
Current drive
Supply Electric
Power to the Grid
D+T+ashes
Pumping
Isotope
Separation
60
Dipartimento di Ingegneria dell’Energia Elettrica e dell’Informazione - DEI
30
Centrale FTC
Sicurezza ed impatto ambientale
61
Dipartimento di Ingegneria dell’Energia Elettrica e dell’Informazione - DEI
31











