Descrivere il diagramma termodinamico (p-v) dell’acqua e disegnarvi l’andamento di una
isoterma con T<Tc
Calcolare il livello di pressione sonora Lp con p=6,3 x 10-3 Pa; (p0 = 2 x 10-5 Pa)
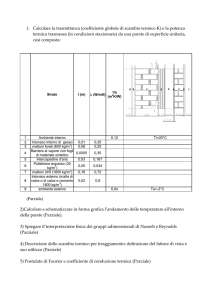
Calcolare la quantità di energia termica trasmessa da una parete così composta:
(dall’esterno verso l’interno)
intonaco esterno; s = 2 cm; , λ = 0,8 W/mK,
mattoni pieni; s = 30 cm; , λ = 0,6W/mK,
isolante termico; s = 6 cm; , λ = 0,04 W/mK,
mattoni forati; s = 8 cm; , λ = 0,5 W/mK,
intonaco interno; s = 2 cm; , λ = 0,8 W/mK,
αi = 8 W/m2K; αe = 23 W/m2K;
∆T = 20 °C
Descrivere il diagramma psicrometrico
Calcolare il livello di pressione sonora Lp con p=6,3 x 10-2 Pa; (p0 = 2 x 10-5 Pa)
Calcolare la quantità di energia termica trasmessa da una parete così composta:
(dall’esterno verso l’interno)
intonaco esterno; s = 2 cm; , λ = 0,8 W/mK,
mattoni pieni; s = 24 cm; , λ = 0,7 W/mK,
isolante termico; s = 4 cm; , λ = 0,03 W/mK,
mattoni forati; s = 8 cm; , λ = 0,5 W/mK,
intonaco interno; s = 1,5 cm; , λ = 0,7W/mK,
αi = 8 W/m2K; αe = 23 W/m2K;
∆T = 25 °C
Calcolare il rendimento massimo di un motore termico operante fra due sorgenti aventi le seguenti
temperature: t1 = 500 °C e t2 = 20°C
Scambio termico per convezione: numero di Nusselt
I principi della Dinamica
Enunciati del Secondo principio della Termodinamica;
Principali grandezze fotometriche;
Scambio termico per irraggiamento fra due superfici piane parallele di lunghezza infinita;
Il ciclo di Carnot;
Disegnare il diagramma termodinamico (p-v) per l’acqua;
Calcolare il titolo di una miscela aria e vapor d’acqua avente le seguenti caratteristiche: ps = 0,030
bar, ϕ = 60%, patm = 1 bar
Disegnare e descrivere il diagramma psicrometrico
Trasmissione del calore in regime variabile (inerzia e diffusività termica)
Calcolare il Livello Sonoro risultante dalla somma dei seguenti livelli: L1 = 70 dB, L2= 50 dB (in assenza
di calcolatrice è sufficiente impostare il calcolo)
Equazione di stato dei Gas Perfetti;
Trasmissione del calore: espressione della Trasmittanza;
Descrivere il diagramma (p-v) per l’acqua;
Il principio di Archimede;
Equazione di stato dei Gas Perfetti
Calcolare la Trasmittanza di una parete così composta (procedendo dall’interno):
intonaco interno : s= 2 cm; λ = 0,70 W/mK
laterizio : s= 24 cm; λ = 0,50 W/mK
isolante termico : s= 4 cm; λ = 0,050 W/mK
laterizio : s= 8 cm; λ = 0,40 W/mK
intonaco interno : s= 2 cm; λ = 0,70 W/mK
intonaco esterno : s= 2 cm; λ = 0,70 W/mK
αi = 8 W/mαi = 8 W/m2K K
αe = 23 W/m2K
Enunciati del secondo principio della termodinamica
Legge di Fourier
Definizione di potere fonoisolante
Scala Internazionale della temperatura
Descrizione del ciclo di Carnot
Convezione naturale e forzata
Il problema della condensa interstiziale nelle murature
Calcolare il titolo di una miscela aria e vapor d’acqua che si trova nelle seguenti condizioni: U.R.
= 50%, ps = 0,030 bar
Rendimento (o coeff.economico) del Ciclo di Carnot
Potenza termica scambiata per irraggiamento fra due superfici piane e parallele, di estensione
pari ad “S”, assimilabili a corpi neri
Descrivere e schematizzare il diagramma psicrometrico
Definizione di decibel
L’entropia;
Principali sostanze inquinanti dell’aria indoor;
Calcolare l’entalpia di una miscela d’aria e vapor d’acqua che si trova nelle seguenti condizioni: t
= 20°C, x = 7 gv/kga
Equazione di Bernoulli.
Un motore avente rendimento pari a ε = 22% sviluppa un lavoro L = 930J. Calcolare l’energia termica
scambiata con la sorgente a temperatura maggiore (Q1) e quella scambiata con la sorgente a temperatura
inferiore (Q2).
Evidenziare sul diagramma psicrometrico le principali trasformazioni delle miscele di aria e vapore d’acqua
Scambio termico per convezione naturale e forzata
Una miscela aria e vapore d’acqua si trova alla temperatura di 20°C (cui corrisponde una pressione di
saturazione ps = 0,023 bar). Calcolare il titolo della miscela.
Scambio termico per irraggiamento tra superfici piane affacciate nell’ipotesi di corpi neri e grigi
Primo principio della termodinamica per sistemi chiusi ed aperti
Calcolare il coefficiente globale di scambio termico di una parete così composta:
- intonaco interno
(s = 2 cm ; λ = 0,80 W/mK)
- pietra
(s = 40 cm; λ = 0,60 W/mK)
- isolante termico
(s = 6 cm; λ = 0,040 W/mK)
- laterizio forato
(s =8 cm; λ = 0,40 W/mK)
- intonaco esterno
(s = 2 cm; λ = 0,70 W/mK)
Equazione di Bernoulli (ipotesi di validità e formulazione)
Gas perfetti. Rappresentare su un diagramma (p v) una trasformazione isoterma. Calcolare la quantità di
calore e lavoro scambiati lungo la trasformazione.
Un motore avente rendimento pari a ε = 22% sviluppa un lavoro L = 930W. Calcolare la potenza termica
scambiata con la sorgente a temperatura maggiore (Q1) e quella scambiata con la sorgente a temperatura
inferiore (Q2).
Evidenziare sul diagramma psicrometrico le principali trasformazioni delle miscele di aria e vapore d’acqua
Scambio termico per convezione naturale e forzata: Numero di Nusselt
Calcolare la potenza termica trasmessa da una parete, in condizioni stazionarie, di superficie pari a 22 m2
, così composta
tipo di materiale
coeff. di conducibilità termica,
spessore dello strato
(cm)
λ (W/mK)
intonaco esterno
mattoni pieni
isolante termico
mattoni forati
intonaco interno
2
αi = 8 W/m K
0,80
0,6
0,040
0,5
0,75
2
30
6
8
1,5
2
αe = 23 W/m K
ti = 21°C
te = 2 °C
Un Ciclo di Carnot opera fra due temperature t1 e t2, rispettivamente: t1 = 600°C, t2 = 100 °C. Calcolare il
rendimento del Ciclo.
Calcolare l’entalpia di una miscela aria-vapor d’acqua aventi le seguenti caratteristiche: t= 26°C, x = 8
gv/kga.
Trasmissione del calore per convezione e analisi mediante numeri puri.
Calcolare la potenza termica scambiata per irraggiamento fra due superfici piane e parallele
2
(intercapedine) assimilabili a corpi neri, aventi una superficie di 20 m , che rispettivamente si trovano alle
temperature di 24°C e 60°C.
Definire le varie forme di energia.
Disegnare e descrivere il diagramma termodinamico p-v dell’acqua. In particolare descrivere le proprietà
dei vapori della zona compresa fra la curva limite inferiore e superiore.
Una slitta viene trattenuta da un bambino su una collina coperta di neve (da considerarsi priva di attrito) per
mezzo di una corda. La slitta pesa 77 N. Calcolare la forza che il bambino deve esercitare sulla corda e la
forza che la collina esercita sulla slitta.
Una parete perimetrale è composta da mattoni semipieni di densità pari a 700 kg/m3. Una seconda parete
3
è invece composta da blocchi in pietra di densità pari a 1200 kg/m . Supponendo che le due pareti abbiano
lo stesso comportamento per quanto attiene la trasmissione di energia termica in regime stazionario, come si
differenziano in regime dinamico?
Disegnare e descrive il digramma psicrometrico. Su di esso riportare una tipica trasformazione a titolo
costante (riscaldamento e raffreddamento).
Calcolare la potenza termica trasmessa da una parete, in condizioni stazionarie, di superficie pari a 22 m2
, così composta
tipo di materiale
intonaco esterno
mattoni pieni
isolante termico
mattoni forati
intonaco interno
coeff. di conducibilità termica λ
spessore dello strato
(cm)
2
30
6
8
1,5
0,80
0,6
0,040
0,5
0,75
2
αi = 8 W/m K
2
αe = 23 W/m K
ti = 21°C
te = 2 °C
nota: i valori di λ riportati in tabella sono espressi in Unità del Sistema Internazionale
Inoltre, calcolare e schematizzare in forma grafica l’andamento delle temperature all’interno della parete.
Calcolare il livello di intensità sonora LI sapendo che l’intensità sonora in esame è pari a 10–3 W/m2 e che
–12
2
W/m .
l’intensità sonora di riferimento è pari a 10
Calcolare l’entalpia di una miscela aria-vapor d’acqua aventi le seguenti caratteristiche:
t= 26°C
x = 8 gv/kga.
Sul diagramma psicrometrico data una temperatura di bulbo umido (tbu = 13°C) ed una temperatura di bulbo
secco pari a quella della miscela in oggetto (tbs= 26°C) schematizzare la costruzione grafica che serve per
determinare l’Umidità Relativa della miscela.
Calcolare il livello di pressione sonora Lp sapendo che la pressione sonora in esame è pari a 2 x 10 –2 Pa e
–5
che l’intensità sonora di riferimento è pari a 2 x 10 Pa.
Calcolare la potenza termica scambiata per irraggiamento fra due superfici piane e parallele (intercapedine)
2
assimilabili a corpi neri, aventi una superficie di 20 m , che rispettivamente si trovano alle temperature di
24°C e 60°C.
Un Ciclo di Carnot opera fra due temperature t1 e t2, rispettivamente:
t1 = 500°C
t2 = 30 °C
Calcolare il rendimento del Ciclo.
Disegnare e descrivere il diagramma termodinamico p-v dell’acqua. In particolare descrivere le proprietà dei
vapori della zona compresa fra la curva limite inferiore e superiore.
Calcolare il titolo di una miscela aria-vapor d’acqua che si trova nelle seguenti condizioni: ps (ta = 30°C) = 0,034
bar; U.R. = 50%.
Tre resistori sono collegati in parallelo. Calcolare la resistenza totale sapendo che R1 = 3Ω; R2 = 6Ω ; R3 =
9Ω.
Una parete perimetrale è composta da mattoni semipieni di densità pari a 700 kg/m3. Una seconda parete è
3
invece composta da blocchi in pietra di densità pari a 1200 kg/m . Supponendo che le due pareti abbiano lo
stesso comportamento per quanto attiene la trasmissione di energia termica in regime stazionario, come si
differenziano in regime dinamico?
Descrivere il diagramma termodinamico (p-v) dell’acqua e disegnarvi l’andamento di una isoterma con T<Tc
Calcolare il titolo ed entalpia di una miscela aria-vapor d’acqua aventi le seguenti caratteristiche: t= 26°C,
ps=0.033 bar, U.R.=70%
Calcolare la quantità di energia termica trasmessa da una parete così composta:
intonaco esterno; s = 2 cm; ,λ = 0,8 W/mK,
mattoni pieni; s = 30 cm; , λ = 0,6W/mK,
isolante termico; s = 6 cm; , λ= 0,04 W/mK,
mattoni forati; s = 8 cm; , λ = 0,5 W/mK,
intonaco esterno; s = 2 cm; , λ = 0,8 W/mK,
2
2
αi = 8 W/m K; αe = 23 W/m K;
Equazione di Bernoulli: campo di validità, formula, applicazioni;
Ciclo di Carnot;
Scambio termico per convezione: tipologie, analisi mediante numeri puri.
Descrivere il diagramma termodinamico (p-v) dell’acqua e disegnarvi l’andamento di una isoterma con T<Tc
calcolare il livello di pressione sonora Lp con p=4 x 10-3 Pa; (p0 = 2 x 10-5 Pa)
Descrivere il funzionamento di uno psicrometro; note che siano le temperature di bulbo bagnato e di bulbo
secco, pari a 15°C e 26°C, schematizzare su un diagramma psicrometrico la procedura per determinare
l’umidità relativa della miscela
Disegnare schematicamente sul diagramma termodinamico (p-v) un ciclo frigorifero
Principali leggi dell’irraggiamento termico
1° e 2° Principio delle Termodinamica per sistemi chiusi
Calcolare il titolo ed entalpia di una miscela aria-vapor d’acqua aventi le seguenti caratteristiche: t= 26°C,
ps=0.033 bar, U.R.=70%
Disegnare schematicamente sul diagramma termodinamico (p-v) un ciclo diretto
Determinare l’altezza massima raggiunta da un corpo che viene lanciato verso l’alto ad una velocità iniziale
di 15 km/h, trascurando l’azione degli attriti.
Calcolare la potenza termica trasmessa da una parete di 7 m2 così composta:
intonaco esterno; s = 1,5 cm; λ = 0,8 W/mK,
mattoni pieni; s = 12 cm; λ = 0,6 W/mK,
isolante termico; s = 4 cm; λ = 0,03 W/mK,
mattoni forati; s = 8 cm; λ = 0,6 W/mK,
intonaco interno; s = 1,5 cm; λ = 0,8 W/mK,
2
2
αi = 8 W/m K; αe = 23 W/m K.
Temperatura interna di progetto: 20°C
Temperatura esterna di progetto: -5 ° C
Rappresentare il diagramma termodinamico pressione – volume specifico dell’acqua e individuare le diverse
fasi. Disegnare sul diagramma una curva isoterma con t inferiore alla temperatura critica.
Determinare la velocità raggiunta da un corpo di massa M = 500 g che scivola su un piano privo di attriti
inclinato di 45° dopo un tempo di 2 s. Il corpo parte da una velocità iniziale di 30 km/h.
Definizione di calore specifico a volume costante ed a pressione costante.
Descrivere il diagramma psicrometrico e schematizzare le seguenti trasformazioni:
a titolo costante;
a entalpia costante;
a temperatura costante.
Significato di decibel A.
Calcolare il livello di pressione sonora risultante dalla somma dei seguenti livelli:
L1 = 65 dBA
L2 = 67 dBA.
Significato dei coefficienti di scambio termico superficiale (o coefficienti di adduzione) α.
Significato e determinazione grafica della temperatura di rugiada. Descrizione del metodo grafico di Glaser
per la verifica della formazione di condensa interstiziale.
Determinare il tempo necessario a raggiungere la massima quota da un corpo che viene lanciato verso l’alto
ad una velocità iniziale di 25 km/h.
Si trascuri l’azione degli attriti.
Rendimenti della macchina termica, della macchina frigorifera e della pompa di calore
Trasmissione del calore per convezione naturale e forzata: analisi mediante numeri puri
Determinare la velocità raggiunta da un corpo di massa M = 300 kg che scivola su un piano privo di attriti
inclinato di 45° percorrendo uno spostamento di 3 m. Il corpo parte da una velocità iniziale di 30 km/h.
Primo principio della termodinamica per sistemi chiusi.
Calcolare la potenza termica trasmessa da una parete di 7 m2 così composta:
intonaco esterno; s = 1 cm; λ = 0,7 W/mK,
mattoni semipieni; s = 10 cm; λ = 0,55 W/mK,
isolante termico; s = 6 cm; λ = 0,04 W/mK,
mattoni forati; s = 8 cm; λ = 0,5 W/mK,
intonaco interno; s = 1,5 cm; λ = 0,7 W/mK,
2
2
αi = 8 W/m K; αe = 23 W/m K.
Temperatura interna di progetto: 20°C
Temperatura esterna di progetto: 0 ° C
Definizione di suono e di livelli sonori.
Grandezze caratteristiche delle miscele di aria secca e vapore acqueo
Descrizione del metodo grafico di Glaser per la verifica della formazione di condensa interstiziale.
Esemplificare l’andamento delle pressioni parziali del vapore in alcuni casi tipici.
Descrivere il diagramma psicrometrico schematizzare la procedura per la determinazione della temperatura
di rugiada.
Significato di inerzia termica.
Differenza tra moto laminare e moto turbolento
Il principio di Archimede ed il principio di Pascal
Caratteristiche prestazionali dei materiali termoisolanti: coefficiente di conducibilità termica.
Diagramma pressione – volume specifico dell’acqua pura.
La legge di Stevino e la pressione idrostatica
Equazione di stato dei gas perfetti.
Legge di Stefan – Boltzmann, legge di Wien.
l Sistema Internazionale e le sue sette unità di misura fondamentali
ciclo di Carnot e suo coefficiente economico
definizione e significato della temperatura di rugiada: esempio di calcolo sul diagramma psicrometrico
Sapendo che αi = 8 W/m2K e αe = 23 W/m2K, scegliendo tra i materiali sotto elencati comporre un elemento
di tamponamento esterno (composto da almeno tre strati) e calcolarne la trasmittanza:
intonaco λ = 0,070 W/mK
mattoni pieni
λ = 0,060 W/mK
mattoni semipieni λ = 0,050 W/mK
blocchi di pietra λ = 0,070 W/mK
poroton
λ = 0,055 W/mK
lana di vetro
λ = 0,050 W/mK
polistirene espanso
λ = 0,040 W/mK
sughero cellulare λ = 0,055 W/mK
la legge di Stevino e la pressione idrostatica
ciclo frigorifero ed effetto utile
temperatura di bulbo secco e bagnato: lo psicrometro di Assman: esempio di calcolo sul diagramma
psicrometrico
determinare la percentuale di volume emerso di un cubetto di ghiaccio che galleggia sull’acqua, nota la
3
3
densità del ghiaccio (917 kg/m ) e dell’acqua (1000 kg/m ).
secondo principio della termodinamica: enunciati
principali proprietà delle miscele aria e vapore
condensa interstiziale e diagramma di Glaser
il principio di Archimede per corpi completamente immersi o galleggianti. La legge di Pascal
pompa di calore e coefficiente di prestazione COP
principali trasformazioni delle miscele di aria umida
Resistenze al moto dei fluidi nei condotti: perdite di carico distribuite e concentrate
Equazione di stato dei gas perfetti e principali leggi dei gas perfetti
Calcolare titolo ed entalpia di una miscela caratterizzata da: t = 20°C, UR = 0,5, ps = 0,023 bar
Legge di Fourier e coefficiente di conduzione termica
determinare lo spazio percorso da un corpo che si muove con moto uniformemente accelerato al tempo
2
t=2s, sapendo che v0 = 30 km/h, x0 = 0 e a=3 m/s
Campana dei vapori saturi: titolo di un vapore saturo umido e calore latente di vaporizzazione
Schematizzare e descrivere il diagramma psicrometrico
Scambio termico per irraggiamento tra due corpi grigi e principali leggi dell’irraggiamento termico
Fluidodinamica: definizioni di moto laminare e turbolento; numero di Reynolds;
Miscele di aria e vapore acqueo: calcolo di titolo ed entalpia in funzione di altre coordinate; definizione di
grado igrometrico;
Determinare l’andamento delle temperature in una parete così composta:
intonaco
s = 1,5 cm; λ = 0.8 W/mK
mattoni pieni s = 14 cm; λ = 0.75 W/mK
lana minerale s = 4 cm; λ = 0.04 W/mK
mattoni forati s = 8 cm; λ = 0.6 W/mK
intonaco
s = 1 cm; λ = 0.8 W/mK
2
coefficiente di adduzione interna: 8 W/m K
2
coefficiente di adduzione esterna: 23 W/m K
temperatura interna: 20°C
temperatura esterna: 0°C
Determinare l’inclinazione massima di piano affinché un corpo di massa 100 kg scivoli in presenza di fattore
di attrito statico pari a 0,4;
Determinare su un diagramma psicrometrico le seguenti trasformazioni di miscele di aria e vapore acqueo:
trasformazione adiabatica di umidificazione;
deumidificazione in condizioni di saturazione;
riscaldamento a titolo costante.
Determinare la potenza termica trasmessa attraverso una parete così composta:
intonaco
s = 1 cm; λ = 0.8 W/mK
calcestruzzo s = 10 cm; λ = 0.8 W/mK
polistirolo s = 5 cm; λ = 0.04 W/mK
mattoni forati
s = 8 cm; λ = 0.6 W/mK
intonaco
s = 1 cm; λ = 0.8 W/mK
Quale delle seguenti due strutture è caratterizzata da maggiore inerzia termica?
- parete in calcestruzzo spessa 50 cm;
- parete sandwich in lastre di legno spesse 1 cm con interposta lana minerale spessa 4
cm.
Equazioni del moto uniforme e del moto uniformemente accelerato;
Definizione di:
capacità termica
calore specifico a volume costante
calore specifico a pressione costante.
Determinare la potenza termica scambiata tra due lastre di estensione infinita, parallele, di cui una nera ed
una grigia (α = 0,8).
La temperatura della prima superficie è 20 °C; quella della seconda è 80 °C
Scrivere le principali leggi dell’irraggiamento.
Equazioni del bilancio delle masse e del bilancio energetico (equazione di Bernoulli) nella meccanica;
Primo principio della termodinamica per sistemi chiusi ed aperti;
Scambio termico per convezione:
metodologia per la determinazione del coefficiente di scambio termico convettivo.
Fluidodinamica: perdite di carico distribuite e concentrate.
Diagramma bidimensionale pressione volume specifico dell’acqua:
individuare la zona dei vapori saturi e quella dei vapori saturi secchi.
Determinare quale spessore deve avere una parete omogenea in calcestruzzo (λ = 0,8) al fine di offrire la
stessa resistenza termica di una parete così composta:
intonaco
s = 1 cm; λ = 0.8 W/mK
polistirolo
s = 2 cm; λ = 0.04 W/mK
mattoni forati s = 8 cm; λ = 0.6 W/mK
intonaco
s = 1 cm; λ = 0.8 W/mK
Definizione di suono e di livello di pressione sonora. Somma di livelli sonori in dB.
Schematizzare su un diagramma termodinamico pressione – volume specifico un ciclo di Carnot;
determinarne quindi il rendimento.
Definire l’inerzia e farne esempi applicativi.
Definizione di diffusività termica.
Perdite di carico in fluidodinamica
Schematizzare i seguenti processi su un diagramma psicrometrico:
Calcolo dell’umidità relativa note temperatura di bulbo umido e asciutto
Calcolo della temperatura di rugiada
Modalità di calcolo della trasmissione per calore in convezione naturale
Definizione di suono e di livello di pressione sonora; effettuare la somma di 60 + 50 dB
Diagramma pressione – volume specifico dell’acqua
Determinare la trasmittanza e l’andamento delle temp. in una parete di superficie unitaria così composta:
Intonaco (s= 2 cm; λ = 0,8 W/m K)
Mattoni forati (s= 8 cm; λ = 0,6 W/m K)
Isolante (s= 6 cm; λ = 0,035 W/m K)
Mattoni pieni (s= 12 cm; λ = 0,7 W/m K)
Intonaco (s= 1 cm; λ = 0,8 W/m K)
2
Coeff. di adduzione interno ed esterno: 8 e 23 W/m K
Temperature interna ed esterna: 20 e 5 °C
Primo principio della termodinamica per sistemi chiusi ed aperti
Definire i gas perfetti e esprimerne l’equazione di stato
Determinare la potenza termica trasmessa tra due superfici piane ed affacciate di Superficie pari a 5 m2, di
cui una nera ed una grigia avente a = 0,6, poste alle temperature di 30°C e 5 °C.
Scrivere le formule delle diverse forme di energia meccanica
Perdite di carico distribuite ed accidentali; il diagramma di Moody
Determinare l’andamento delle temperature interne in una parete di superficie unitaria così composta:
Intonaco di gesso (s= 1 cm; λ = 0,6 W/m K)
Mattoni pieni (s= 12 cm; λ = 0,8 W/m K)
Isolante (s= 6 cm; λ = 0,035 W/m K)
Mattoni forati (s= 8 cm; λ = 0,7 W/m K)
Intonaco (s= 2 cm; λ = 0,8 W/m K)
2
Coeff. di adduzione interno ed esterno: 9 e 23 W/m K
Temperature interna ed esterna: 20 e 0 °C
Significato di decibel A.
Enunciati del secondo principio della termodinamica; significato di entropia.
Determinare la trasmittanza e l’andamento delle temp. in una parete di superficie unitaria così composta:
Intonaco (s= 2 cm; λ = 0,8 W/m K)
Mattoni pieni (s= 25 cm; λ = 0,7 W/m K)
Isolante (s= 8 cm; λ = 0,04 W/m K)
Intonaco (s= 1 cm; λ = 0,8 W/m K)
2
Coeff. di adduzione interno ed esterno: 8 e 23 W/m K
Temperature interna ed esterna: 20 e 0 °C
Equazioni della cinematica.
Rendimento di un motore termico; coefficiente di prestazione di una pompa di calore e di un ciclo frigorifero.
Modalità per determinare, su un diagramma psicrometrico, la quantità di acqua di condensa in un processo
di deumidificazione conoscendo lo stato iniziale e finale della miscela a e la portata in massa.
Le leggi di Newton nella meccanica
Il ciclo di Carnot.
Scambio termico per irraggiamento tra superfici affacciate e non affacciate (fattore di vista diverso da 1).
Caso di corpi neri e grigi.