La luce dalle stelle
Come trovare la stella polare
Riconoscere le costellazioni presenti scrivendone il nome
Disegnare lo schema
Riconoscere le stelle più brillanti
Disegnare l’eclittica e/o la fascia zodiacale
Disegnare l’equatore galattico
Riconoscere eventuali pianeti presenti
Riconoscere principali oggetti di Messier (galassie, ammassi stellari)
Dove e quando è stata scattata la foto?
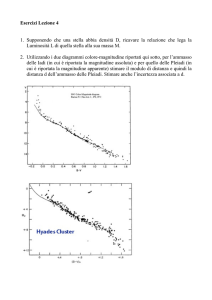
E’ stato recentemente osservato un nuovo sciame meteorico.
Osservate la mappa sottostante:
Dalla mappa calcolate il radiante di questo sciame meteorico, e riconoscete,
disegnandole, le costellazioni presenti nella mappa (utilizzare il nome
latino). Come si potrebbe chiamare questo nuovo sciame meteorico secondo
le convenzioni utilizzate?
Ophs! Manca un’importante stella nella cartina: sapreste dire in quale
costellazione e come si chiama la stella?
Mare Moscoviense
3
6
1
7
8
4
2
5
Mare Moscoviense D=277Km
1 Pasteur:
2 Hilbert:
3 Mendeleiev:
4 Gagarin:
5 Leibniz:
6 Korolev:
7 Hertzsprung:
8 Valentini:
La scala delle magnitudini
La definizione originale per osservazioni ad occhio nudo era
dovuta a Ipparco (160-127 a.C.):
• le stelle più brillanti erano di 1a magnitudine;
• le stelle più deboli erano di 6a magnitudine.
La definizione quantitativa “moderna” (schema di Pogson) è:
1a magnitudine è 100 volte più brillante della 6a → una
differenza di 5 magnitudini corrisponde ad un rapporto tra le
intensità pari a 100.
1 magnitudine → un rapporto di intensità pari a 2.512
La magnitudine apparente
La magnitudine apparente è una
misura di come un oggetto appare
brillante in cielo.
Magnitudine apparente e flusso
Se le stelle 1 e 2 hanno magnitudini visuali
apparenti m1 e m2 il rapporto tra flussi è
F1/F2=10 -(m1-m2)/2.5
Betelgeuse
m= 0.41
ovvero:
m1- m2 = -2.5 log(F1/F2)
Esempio: Betelgeuse e Rigel
Con una differenza in magnitudini di:
0.41-0.14 = 0.27
il rapporto tra i loro flussi è
FBet/FRig = 10-(0.41-0.14)/2.5 = 0.78
Rigel
m= 0.14
Colore = Temperatura !
La maggior parte delle stelle emette
circa come un corpo nero.
Il colore di una stella è collegato alla
sua temperatura superficiale.
La radiazione di corpo nero
Lo spettro continuo di una stella è
approssimativamente uno spettro di corpo nero.
La lunghezza d’onda alla quale un corpo nero ha
il picco è data dalla legge di Wien:
λmax = (2.898 × 10-3 m K) / T
Il flusso di energia irraggiato è dato dalla legge di
Stefan:
F = σ T4 W m-2
dove σ = 5.67 × 10-8 W m-2 K-4
Dal punto di vista astronomico il colore di una stella si
misura a partire dalle magnitudini un due bande (filtri)
diverse, per esempio:
filtro B (Blu)
lunghezza d’onda centrale λ0 = 440 nm
banda passante Δλ = 100 nm
filtro V (Visibile)
lunghezza d’onda centrale λ0 = 550 nm
banda passante Δλ = 90 nm
L’indice di colore è la differenza tra le magnitudini
apparenti misurate nei due filtri:
C = mB-mV = B-V
La classificazione delle stelle
Le stelle sono classificabili in base
a due proprietà osservate:
• Luminosità;
• Righe di assorbimento;
La classificazione spettrale: è basata
sulle righe di assorbimento numero e
intensità delle righe di ass. dipendono
della temperatura.
Le stelle irraggiano come corpi neri.
La luminosità dipende dalla temperatura superficiale e dal raggio:
La Luna piena, nelle migliori condizioni
osservative,
ha
una
magnitudine
visuale apparente totale m = -12.74.
Nelle stesse condizioni osservative,
quanto vale la sua magnitudine
apparente totale quando è a primo
quarto?
m = -2.5 log10 (funit * S / F0)
mfull = -12.74
S’ = S/2
m’ = -2.5 log10(funit * S’/ F0) = -2.5 log10(funit * (S/2) /
F0) = -2.5 log10(funit * S / F0) + 2.5 log10(2)
ovvero
m’ = m + 2.5 log10(2) = -12.74 + 0.75 = -11.99
Nel corso di una guerra stellare, una civiltà impazzita taglia in
due metà una stella (!), senza variarne densità e temperatura.
Come cambia la magnitudine della stella ?
𝒓=
𝑹
𝟑
𝟐
𝒓𝟐
𝒓
𝒎 − 𝒎𝒐𝒓𝒊𝒈 = −𝟐. 𝟓 𝒍𝒐𝒈 𝟐 = −𝟓 𝒍𝒐𝒈
𝑹
𝑹
𝟏
𝟓
= −𝟓 𝒍𝒐𝒈 𝟑 = + 𝒍𝒐𝒈 𝟐 = 𝟎. 𝟓𝟎𝟐
𝟑
𝟐
Le distanze delle stelle
La parallasse trigonometrica (eliocentrica):
Misura dello spostamento angolare apparente di una
stella in cielo dovuto al moto orbitale della Terra.
Definisce l’angolo parallattico p, ovvero l’angolo sotteso
dal raggio dell’orbita terrestre come visto dalla stella.
p diminuisce all’aumentare della distanza della stella (d).
Questo è l’unico metodo diretto per misurare la distanza
delle stelle.
Formula dei piccoli angoli per legare d e p:
p (radianti) = 1 AU/d
Parallasse e parsec
1 parsec è la distanza alla quale l’angolo parallattico è
1 arcsec.
Il metodo parallattico è limitato principalmente dal
potere risolutivo.
Formula per la parallasse
trigonometrica:
Il limite di distanza è
~50 pc da terra;
~1000 pc dallo spazio (satellite Ipparco)
p(҆҆″) = 1/ d
p in arcsec
Ma serve per calibrare metodi più indiretti e forma la d in parsec (pc)
base della scala delle distanze.
Nota: 1 pc = 3.086 ×1016 m = 3.26 ly
Esempio: la stella più vicina Proxima Centauri
ha una parallasse di 0.76′′
→ d = 1/p = 1.3 pc (4.3 ly)
Distanza e brillanza intrinseca
La brillanza apparente di una stella dipende dalla sua distanza secondo la legge
dell’inverso del quadrato:
F = L/(4πD2)
poco fa abbiamo trovato che Rigel è 1.28 volte più brillante di Betelgeuse;
ma è anche 1.6 volte più distante
→ Rigel è intrinsecamente più brillante di Betelgeuse di un fattore 1.28×1.62=3.3.
La Magnitudine Assoluta è una misura della brillanza intrinseca.
Definizione di Magnitudine Assoluta
La magnitudine assoluta è la magnitudine che una stella avrebbe se fosse posta ad
una distanza di 10 pc dal Sole.
(F/F′) = (d/D)-2= (D/d)2
m-M = -2.5 log(F/F′)
m −M = 2.5 log(d/D)2 = 5 log(d/10)
Esempio:
Betelgeuse m= 0.41 d= 152 pc
Rigel m= 0.14 d=244pc
Betelgeuse m= 0.41 d= 152 pc
Rigel m= 0.14 d=244pc
m −M = 5 log(d/10)
Betelgeuse M= -5.5
Rigel M= -6.8
La magnitudine apparente del Sole, vista dalla Terra, è
-26,8. Si calcoli la magnitudine apparente del Sole
vista dai seguenti pianeti: Mercurio, Venere, Marte,
Giove e Saturno.
Mercurio
0,4
Venere
0,7
Marte
1,6
Giove
5,2
Saturno
9,5
Pianeta
D (u.a.)
mSole(D)
Mercurio
Venere
Marte
Giove
Saturno
0,4
0,7
1,6
5,2
9,5
mSole(Mercurio) = -26,8-2,0 = -28,8
mSole(Venere) = -26,8-0,8 = -27,6
mSole(Marte) = -26,8+1,0 = -25,8
mSole(Giove) = -26,8+3,6 = -23,2
mSole(Saturno) = -26,8+4,9 = -21,9
Il modulo di distanza
Se possiamo determinare la magnitudine assoluta
di una stella indipendentemente possiamo
conoscere la sua distanza.
La differenza tra la magnitudine apparente e la
magnitudine assoluta è nota come modulo di
distanza.
L’espressione del modulo di distanza
assumere diverse forme equivalenti:
può
I moti propri
Al passare del tempo le posizioni delle stelle in
cielo cambiano a seguito del loro moto orbitale
attorno al centro della galassia.
Questi spostamenti sono noti col nome di Moti
Propri:
misurati in arcsec/anno;
tipicamente < 1 arcsec/anno;
il più grande vale 10.3′′/anno
(stella di Barnard).
La velocità spaziale (vettore) di una stella può
essere determinata combinando il moto
proprio (componente sul piano del cielo; è
necessario conoscere la distanza della stella)
con la velocità radiale misurata dall’effetto
Doppler.
Stella
Alpha(J2000)
Delta(J2000)
Moto proprio arcsec/anno
Alkaid
13h 47.5m
49d 18.8’
RA -0.12 DEC -0.02
Mizar
13h 23.9m
54d 55.5’
RA 0.12 DEC -0.02
Alioth
12h 54.0m
55d 57.6’
RA 0.11 DEC -0.01
Megrez
12h 15.4m
57d 02.0’
RA 0.10 DEC 0.01
Phecda
11h 53.8m
53d 41.7’
RA 0.11 DEC 0.01
Merak
11h 01.8m
56d 22.9’
RA 0.08 DEC 0.03
Dubhe
11h 03.7m
61d 45.1’
RA -0.14 DEC -0.04
Disegnate la costellazione alla posizione del 2000 e a quella
del 18000.
Telescopi rifrattori
Telescopi riflettori - Newtoniano
Formato da uno specchio parabolico (primario) che riceve la luce e la
invia ad uno specchietto inclinato (secondario), situato nel fuoco, che
a sua volta la riflette lateralmente verso l'oculare.
Ottimo per le osservazioni di oggetti deboli grazie alla focale generalmente
corta f/4-f/8. Bassa aberrazione.
La presenza del secondario intercetta una percentuale della luce entrante
e produce una sensibile diminuzione del potere risolutivo.
Telescopi riflettori - Cassegrain
Si differenzia dal precedente per lo specchio secondario, di forma
iperbolica, che a sua volta convoglia l'immagine verso l'oculare passando
per una feritoia situata al centro dello specchio principale.
In questa maniera l'osservatore viene a trovarsi come per i rifrattori
dietro allo strumento.
Il Cassegrain è corretto da aberrazione sferica e presenta un coma
abbastanza debole.
Telescopi riflettori – Ritchey-Chretien
È un telescopio uguale al Cassegrain, solo che gli specchi sono entrambi
iperbolici.
Grazie a ciò risulta privo di aberrazione sferica e di coma, quindi
perfettamente aplanatico.
Telescopio Ritchey-Chretien 1910 (sviluppo del Cassegrain)
Primario iperbolico
Secondario iperbolico
Telescopio Schmidt-Cassegrain 1920 (sviluppo dello Schmidt e del Cassegrain)
Primario sferico
Secondario sferico
Lastra corretrice
Telescopio Maksutov 1944 (sviluppo del Cassegrain)
Primario sferico
Secondario sferico
Menisco correttore
Potere risolutivo dei telescopi
Il potere risolutivo di un buon sistema ottico viene limitato dalla diffrazione
della luce all’apertura di ingresso del telescopio.
Criterio di Rayleigh
Due frangie possono considerarsi risolte al limite quando
il massimo centrale di una delle figure di diffrazione
coincide con il primo minimo dell’altra (caso c)
= 1.22 /D
(radianti)
= 2.52 * 105 /D (arcsec)
Ingrandimento e campo di vista
L’ingrandimento si calcola della semplice relazione:
γ=D/A
dove D è il diametro della pupilla d’ingresso e A è il diametro della pupilla
di uscita.
La scala dell’immagine viene determinata solamente dalla lunghezza focale
f del telescopio.
La scala sul piano focale in “/mm si calcola con la formula:
=206264/(D/F)
=206264/f
dove D è sempre il diametro del telescopio, F è la focale, ed f la lunghezza
focale.
Prestazioni di un telescopio
Luminosità: la luminosità di una immagine del telescopio dipende dalla dimensione della superficie
che raccoglie la luce, ovvero dall’apertura del telescopio.
Maglim ≈ m0 + 5 log D
Θ ≈ A = πr2
Un fattore importante sulla luminosità del telescopio è l’ingrandimento introdotto da un eventuale
oculare. Maggiore è l’ingrandimento, maggiore risulta la perdita di luce.
In generale per un telescopio si considera la scala sul piano focale:
l = 206265 / (D*F) “/mm