Conoscenze necessarie II
Una questione di capitale importanza (molto da secchioni)
A pagina 117 del libro consiglio un articolo di Antonia Campus e Giancarlo De Vivo circa la
relazione fra funzione di domanda di capitale e funzione di domanda di investimento.
Approfondiamo qui meglio quel punto. Questo post è soprattutto indirizzato agli studenti e ai
dilettanti avanzati.
Perché è importante?
Le critiche in tema di teoria del capitale (lezione 2: 11-115) si rivolgono alla funzione di domanda
di capitale - anche se sono troppo complicate da esporre. Si può per lo meno dimostrare che la
curva di domanda di investimento, centrale nella macroeconomia neoclassica e ahinoi in Keynes
(lezione 3: 142-151), si deriva dalla curva di domanda di capitale, per cui se è errata la seconda,
sarà errata la prima.
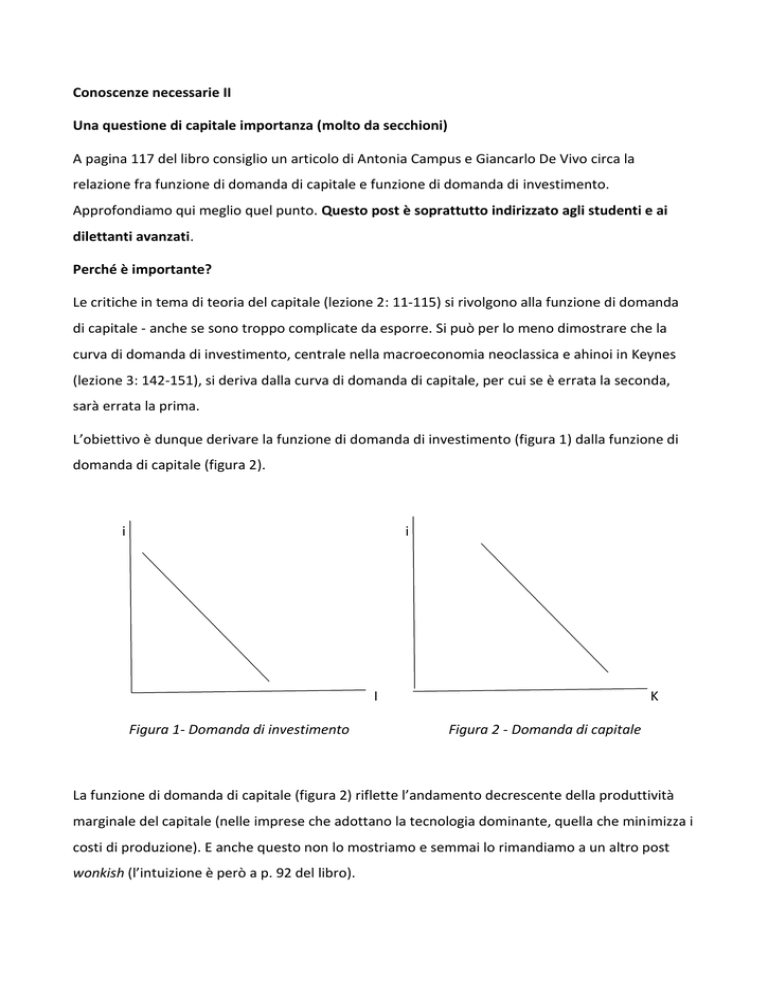
L’obiettivo è dunque derivare la funzione di domanda di investimento (figura 1) dalla funzione di
domanda di capitale (figura 2).
i
i
I
Figura 1- Domanda di investimento
K
Figura 2 - Domanda di capitale
La funzione di domanda di capitale (figura 2) riflette l’andamento decrescente della produttività
marginale del capitale (nelle imprese che adottano la tecnologia dominante, quella che minimizza i
costi di produzione). E anche questo non lo mostriamo e semmai lo rimandiamo a un altro post
wonkish (l’intuizione è però a p. 92 del libro).
Questa non ve la risparmio, ma è proprio wonkish! Le due funzioni esprimono, rispettivamente
come flusso e come stock, un medesimo fenomeno (la domanda di capitale) e, associate a curve di
offerta di risparmio, determinano il tasso di interesse. La domanda di investimento è associata alla
funzione di offerta di risparmio, un flusso che dipende dalla propensione marginale al risparmio, la
quota del reddito corrente che i soggetti intendono risparmiare. La domanda di capitale è
associata alla funzione di offerta dello stock di risparmio (in inglese il risparmio come flusso è
definito saving e quello come stock, savings). Lo stock di risparmio è il cumulo dei risparmi offerti
di anno in anno e detenuti, ad esempio, in titoli rappresentativi del capitale reale delle imprese.
Parte dei titoli ogni anno scade, per cui i soggetti possono rinnovare o meno i prestiti. Non
indaghiamo qui oltre l’argomento, tranne per sottolineare che il tasso di interesse determinato da
domanda e offerta di capitale come flusso (investimento) o come stock, è ovviamente il medesimo
(figure 3 e 4). E’ questo il tasso di interesse naturale di cui si parla spesso nel libro (p. 92 e passim).
i
i
saving
savings
in
I
Figura 3- Domanda e offerta di capitale (flusso)
K
Figura 4 – Domanda e offerta di capitale (stock)
Perché la questione è importante? La relazione causativa fra risparmi e investimenti (chi dei due
spiega l’altro) è lo snodo centrale della macroeconomia: se gli investimenti si adeguano (in media
sul ciclo economico) ai risparmi di capacità (quelli che scaturiscono dal pieno impiego degli
impianti) attraverso la flessibilità del tasso di interesse (pp. 92-96 del libro), hanno ragione i
marginalisti a dire che non vi sono problemi di domanda effettiva, almeno nel lungo periodo.
Dal trattore alla vanga. In economie avanzate gli impianti saranno in generale sufficienti ad
impiegare tutte le forze di lavoro; in economie più arretrate essi saranno in generale insufficienti e
pur con impianti che marciano a pieno regime resterà un residuo di disoccupazione detta
strutturale. A rigore, secondo la teoria marginalista, la flessibilità del salario nel mercato del lavoro
(l’altro mercato chiave della macroeconomia marginalista accanto a quello risparmi-investimenti)
dovrebbe condurre alla piena occupazione di tutto il lavoro. La caduta del salario reale dovuta alla
concorrenza dei disoccupati nei confronti degli occupati spingerebbe infatti gli imprenditori a
passare a tecniche a maggiore intensità di lavoro, per esempio dismettere i trattori man mano che
vanno fuori uso e ad adottare vanghe. Non molto plausibile? Beh, a guardare ciò che accade in
Italia lo è: l’occupazione aumenta, la produttività cala, vale a dire la disponibilità di braccia a buon
mercato (di cui non è politically correct spiegare l’origine) porta a un degrado tecnologico. Non c’è
bisogno, naturalmente, della teoria marginalista per arrivarci. Basta Marx.
Apriscatole
Per semplificare supponiamo che la produzione di svolga su cicli annuali (comincia il primo
gennaio e termina con la consegna del prodotto il 31 dicembre), e che i beni capitali K durino due
cicli produttivi (al termine del secondo anno di vita vanno fuori uso).
Rammentiamo che per definizione gli investimenti lordi (IL ) sono la somma degli investimenti netti
(IN), dunque dell’incremento netto dello stock di capitale; e dei rimpiazzi (R), dunque della
sostituzione dei beni capitali andati fuori uso per obsolescenza (noi abbiamo appena assunto che
lo facciano dopo due anni di attività). In formule
IL = IN + R
(relazione 1)
Faremo due casi.
Solo rimpiazzi
Supponiamo nel primo caso che gli investimenti netti siano zero, per cui
IL = R
Nella figura 5 viene tracciata sia la funzione di domanda di capitale che quella degli investimenti
lordi (qui coincidente con i rimpiazzi). Per ricavare la seconda dalla prima si faccia questo esercizio
ipotetico: si supponga un tasso di interesse i1; a quel tasso lo stock di capitale desiderato dagli
imprenditori è K1. In queste ipotesi, quanto è la domanda annuale di investimenti lordi? Dato che
questi consistono solo di rimpiazzi, e ogni anno si deve rimpiazzare metà dello stock, tale domanda
sarà ½ K1. Supponiamo poi che il tasso di interesse sia i2; a questo tasso lo stock di capitale
desiderato dagli imprenditori sarà K2, e la conseguente domanda di rimpiazzi ½ K2. Si può ripetere
l’esercizio per altri ipotetici tassi (ovviamente quando i = imax, il K desiderato sarà zero; e viceversa
quando i = 0, la domanda di capitale sarà massima, pari a K0, casi estremi questi di puro interesse
grafico). Pochi punti, al limite ne bastano due (A e B), sono sufficienti per tracciare la funzione di
domanda di investimento lordo. Essa sarà decrescente come la “madre”, la funzione di domanda
di capitale. Le due funzioni esprimono infatti uno stesso fenomeno, la domanda di capitale, l‘una
in termini di flusso (IL) e l’altra in termini di stock (K).
i
imax
i2
B
domanda di capitale
i1
A
domanda di investimento lordo
½K2
K2
½K1
½K0
K1
K0
K
Figura 5 – Domanda di investimento lordo con investimento netto pari a zero
In formule, la relazione 1 si riduce a: IL = R = ½ K*, dove K* è il capitale desiderato e installato al
tasso di interesse prevalente in quel momento del tempo.
Circolare, circolare! Nel caso il capitale sia solo “circolante”, duri cioè solo un ciclo produttivo, la
funzione di domanda di capitale coinciderà con quella di investimento lordo (rimpiazzi). Per
esempio, se in una economia agricola il capitale consistesse di solo grano per la semina, al
principio dell’anno tutto il capitale dovrebbe essere ripristinato in quanto esso è stato tutto
consumato durante l’anno. In questo caso si ha IL = R = K*, la domanda di capitale coincide con la
domanda di rimpiazzi. (Per memoria, il “capitale fisso” è quello che dura più cicli produttivi, per
esempio un aratro).
Solo investimenti netti
Col secondo caso isoliamo la domanda di investimento netto trascurando la domanda di
investimenti per rimpiazzi (o alternativamente si può supporre che i beni-capitali non vadano mai
fuori uso, siano eterni). Nella figura 6 tracciamo di nuovo per prima la funzione di domanda di
capitale. Supponiamo dapprima che al tasso i0 l’economia sia in equilibrio nel senso che lo stock di
capitale desiderato è uguale a quello effettivo K0. In questa situazione non vi sono investimenti
netti, gli imprenditori sono contenti con lo stock di capitale che già posseggono.
Supponiamo poi che il tasso di interesse scenda a i1. Al nuovo tasso gli imprenditori desidereranno
uno stock di capitale K1 maggiore di quello effettivo K0, per cui desidereranno effettuare un
investimento netto pari a K1 – K0 = K1 = IN1. Riportiamo la distanza K1 a partire dall’origine sì da
individuare il punto A. Continuate l’esercizio per altri ipotetici tassi di interesse: per esempio, se il
tasso di interesse fosse invece sceso a i2, gli imprenditori avrebbero desiderato uno stock di
capitale K2 e un investimento netto pari a K2 – K0 = K2 = IN2. Riportate la distanza K2 a partire
dall’origine sì da individuare un punto B. Potremmo ripetere l’esercizio per altri ipotetici tassi di
interesse, ma i due punti A e B sono sufficienti per tracciare la funzione di investimento netto.
i
imax
i3
i0
domanda di investimento netto
i2
B
i1
A
domanda di capitale
0
IN2
IN1
K0
K2
K1
Legenda: tratto 0-IN1 = K1 – K0 = K1; tratto 0-IN2 = K2 – K0 = K1
Figura 6 – Domanda di investimento netto
K
In formule si ha IN = K* – K0, dove K* è il capitale desiderato al tasso di interesse prevalente in quel
momento del tempo e K0 è il capitale esistente (installato al tasso prevalente in un momento
precedente). Mettendo assieme i due casi e ricordano la relazione 1, la domanda complessiva di
capitale sarà, nelle ipotesi fatte: IL = IN + R = (K* – K0) + ½ K*. Lascio alla vostra matita, sicuramente
più abile di me al computer, di tracciare il grafico relativo.
“Le discese ardite, e le risalite…”. Scusi professore, ma se il tasso di interesse invece di scendere da
i0 fosse salito per esempio a i3 nella figura 6? Lei deve essere quello che faceva le domande nel
libro e cercava il pelo dell’uovo. Uno sraffiano in erba, insomma!
In questo caso gli imprenditori desidereranno un capitale K3 minore di K0 (quadrante destro della
figura 7) ovvero vorranno effettuare un investimento lordo negativo o disinvestimento:
K3 – K0 = -K3 = -IN3.
Graficamente (quadrante sinistro della figura 7) la funzione di domanda di investimento netto
giace in territorio negativo. Essa parte da i0, in quanto in corrispondenza a quel punto lo stock di
capitale esistente è pari a quello desiderato e non vi sono né investimenti, né disinvestimenti.
Quando il tasso è i1, il disinvestimento desiderato è, appunto, K3 – K0 = -IN3.
Tuttavia vi è un limite all’irreversibilità degli investimenti, vale a dire se un imprenditore si vuole
disfare di un investimento ha due opzioni. Prima di vederle facciamo due osservazioni:
(a) quando il tasso di interesse muta (come da i0 e i1 nell’esempio) i prezzi dei beni mutano. In
concorrenza, quello che abbiamo nel libro (pp. 36-37) denominato “prezzo normale” (o “naturale”,
o di “lungo periodo”) è quello che praticano le imprese che adottano i beni-capitali (ovvero la
tecnica) più adatti al nuovo tasso i1. Queste imprese riceveranno anche un tasso di profitto
normale (o naturale o di lungo periodo).
(b) Le altre imprese (quelle che ancora utilizzano la tecnica relativa al tasso i0), sono obbligate ad
accettare il prezzo normale e rimangono nel mercato se riescono a praticare un prezzo che copra
almeno i costi di produzione al netto degli ammortamenti e del tasso di interesse normale. Se
riescono a effettuare i rimpiazzi, e magari avere un rendimento netto sul capitale (sebbene
inferiore al tasso normale), questo è definito “quasi-rendita”. La “quasi-rendita” è il rendimento di
un bene-capitale non tecnologicamente adeguato al dato tasso di interesse prevalente (o
eventualmente surclassato da una tecnologia che consente di produrre a costi inferiori).
Ed ecco dunque le due opzioni per gli imprenditori che si vogliono disfare di un bene capitale
inadeguato al nuovo tasso di interesse:
(c) se non è proprio più conveniente produrre con quel bene capitale perché i costi di produzione
(persino al netto dei profitti e dell’ammortamento) risulterebbero al di sotto del prezzo normale di
vendita del prodotto, allora il bene capitale va dismesso e vale come rottame (l’imprenditore fa il
renziano, insomma).
(d) se è ancora conveniente produrre con quel bene capitale perché i costi di produzione (al netto
dei profitti e dell’ammortamento) sono al di sotto del prezzo normale di vendita, il produttore
potrà recuperare qualcosa del valore del bene-capitale. Se è fortunato, il prezzo di vendita del
bene consentirà sia l’ammortamento del valore iniziale del bene-capitale e magari una quasirendita. In questo caso, lentamente, con l’accumulazione degli ammortamenti, l’imprenditore
recupererà il costo iniziale dell’investimento. Una volta recuperato tale valore esso verrà investito
in un bene-capitale più adeguato al nuovo tasso di interesse. Non è però detto che il prezzo di
vendita prevalente sia tale da consentire il recupero pieno dell’investimento iniziale; se ciò non
accade, l’imprenditore farà perdite in conto capitale (capital losses).
(Le considerazioni da (a) a (d) sono del tutto generali e si applicano anche se la teoria dei prezzi
adottata fosse quella dei prezzi di produzione di Sraffa).
Un’ultima considerazione molto wonkish e specifica alla teoria del capitale marginalista, riguarda i
fatto che quando muta il tasso di interesse vi possono essere delle “capital losses”. Nella teoria
marginalista il “capitale” è un “fattore originario” il cui valore è noto prima e indipendentemente
dalla distribuzione - un nonsense, come sappiamo. Secondo i marginalisti, inoltre, quando muta il
tasso di interesse, il capitale deve mutare “forma” adattandosi alle nuove tecniche (il che lo
concediamo, come processo di lungo periodo), rimanendo immutato di valore. Non solo però il
suo valore muta, e nelle direzioni più svariate, come dimostrato da Sraffa (per cui la funzione di
domanda di capitale non è decrescente, come nei grafici visti sopra), ma può inoltre diminuire per
le perdite in conto capitale appena notate. Se nel disequilibrio, nella transizione da un equilibrio
all’altro, uno dei “dati” della teoria muta, la teoria è incapace di dirci dove ci porta il cuore: se una
teoria non sa prevedere (almeno in via di principio e all’interno di mille semplificazioni) dove va la
realtà, si vede che non l’ha capita. A lezione, a fine anni settanta, Garegnani ci disse che il
problema del capitale nella teoria dominante non è uno, ma è un “coacervo” di problemi.
i
i3
i0
domanda di capitale
-IN3
0
K3
K0
K
Legenda: tratto -IN – 0 = K3 – K0
Figura 7 – “Disinvestimento”
Un professore tutto matto. Un’altra domanda professore. Tornando alla Figura 6, ma
discostamenti del tasso di interesse (in su o in giù) rispetto a un ipotetico tasso iniziale in cui lo
stock era aggiustato sono le uniche cause dell’investimento netto? Così sembra che, per i
marginalisti, quando l’economia è in equilibrio è anche statica (non cresce né declina).
Questo quesito ci porta su terreni complicati! Possiamo dire questo: una volta che l’economia è in
equilibrio, cioè gli imprenditori posseggono uno stock di capitale adeguato al tasso di interesse
prevalente (che è poi quello “naturale” di cui si è parlato nel libro), subentra un’altra ragione per
cui vi possono essere investimenti netti: l’aumento (o declino) della domanda aggregata.
Ma professore “Ma sa l'e`, matt?” Nel libro ci ha convinto che per i marginalisti la domanda è
irrilevante, e ora ci dice che spiega addirittura gli investimenti!
No, tranquilli. In un qualche modo la domanda aggregata ci deve essere da qualche parte anche
per i marginalisti; in fondo nel libro lo dico: tutti gli economisti parlano di domanda e offerta,
anche se solo i marginalisti hanno curve di domanda e offerta. Ma vediamo al dunque. In equilibrio
per i marginalisti la domanda aggregata cresce al tasso di crescita delle forze di lavoro – più
precisamente della popolazione in età lavorativa che intende lavorare al salario reale di equilibrio.
A tale salario, infatti, tutti i “new entrants” nelle forze di lavoro trovano impiego. Di conseguenza
la produzione cresce e come, conseguenza dell’aumento della produzione, ecco che anche la
domanda aggregata cresce al ritmo di ingresso delle nuove leve lavorative - vale la Legge di Say
vista nella prima lezione del libro, pp. 52-55, che possiamo così qui riformulare: la crescita della
produzione determina la crescita della sua domanda. Insomma, in questa economia gli stock di
lavoro e di capitale (quest’ultimo via investimenti netti), la produzione e la domanda aggregata
crescono tutti allo stesso tasso, quello delle forze di lavoro. E’ la Legge di Say, bellezza!
Relazioni pericolose
Nel libro (p. 156) abbiamo citato autori come Krugman che nei blog, ma non nei libri di testo,
ammettono che nella realtà gli investimenti non dipendano dal tasso dell’interesse - al riguardo si
veda, ad esempio, lo studio della Federal Reserve citato in bibliografia, che sulla base di una
indagine empirica sostiene questa conclusione. E’ l’andamento della domanda aggregata che,
guidando le aspettative degli imprenditori, determina le decisioni di investimento. Si potrebbe a
questo punto invertire il processo, e dire che se la figlia è malata (la funzione di investimento), lo è
anche la madre (la domanda di capitale). E se la curva decrescente di domanda di capitale è
malata (o meglio, non esiste), ciao teoria marginalista della distribuzione. Bye-bye, orevuar, auf
wiedersehen.
Il bello poi, è che a questo punto rimane vera l’intuizione di Keynes che il tasso di interesse è un
fenomeno monetario – non è cioè determinato da domanda e offerta di risparmio. Ma il tasso di
interesse è una variabile distributiva, può fare ad esempio da benchmark a quello che gli
imprenditori considerano come tasso normale di profitto (la banca centrale influenza i tassi a
breve orientano e questi influenzano i tassi a lunga a cui possono riferirsi gli imprenditori). E allora
la banca centrale è una istituzione che può entrare a gamba tesa nel conflitto distributivo. Sraffa
avanzò questo suggerimento in Produzione di merci a mezzo di merci (Einaudi, 1960); soprattutto
Massimo Pivetti l’ha ripresa e sviluppata (ma si veda anche il saggio di Stirati)
Riferimenti
Antonia Campus e Giancarlo De Vivo (1980) Preferenza per la liquidità e moltiplicatore nella Teoria
Generale: una recente interpretazione di Keynes, «Ricerche Economiche», 24/3-4.
Massimo Pivetti (1991) An Essay on Money and Distribution , Macmillan, London.
Steve A. Sharpe and Gustavo A.Suarez (2014) The insensitivity of investment to interest rates:
Evidence from a survey of CFOs. Federal Reserve Board, Washington, D.C., FEDS 2014-02
Antonella Stirati (2001) Inflation, Unemployment and Hysteresis: an Alternative View, Review of
Political Economy, ottobre 2001.
“Ma sa l'e`, matt?” è un omaggio a Dario Fo (e Jannacci) di “Ho visto un re”.
Appendice: su una presunta incoerenza
In una discussione pubblica (Roma-Corviale, 29 ottobre 2016) mi è stato obiettato: come fai Sergio
a dire che il tasso di interesse (i) non influenza gli investimenti (I) per poi sostenere che influenza la
spesa per costruzioni che è classificata fra gli investimenti.
Il fatto che la spesa nel settore delle costruzioni (in particolare quella in edilizia privata, ma quello
che sto per dire vale in larga misura anche per le opere pubbliche) sia classificata fra gli
investimenti andrà bene all'Istat, ma non all'economista.
Quando l'economista mainstream scrive I = I(i) lo fa avendo in mente (se non lo ha in mente è
perché viene dato per ovvio ciò che ovvio non è) che quando il tasso di interesse diminuisce,
scattino i meccanismi di sostituzione fra capitale e lavoro, per cui si passa a tecniche a maggiore
intensità di capitale, e questo implica investimenti netti. Ciò è vero per gli investimenti industriali e
solo per quelli.
Naturalmente solo per la mente dei mainstream gli investimenti industriali dipendono dal tasso di
interesse: sia la teoria, leggi Sraffa-Garegnani-Pasinetti, che la pratica, vedi Federal Reserve Board,
Washington, D.C.. The insensitivity of investment to interest rates: Evidence from a survey of CFOs.
Steve A. Sharpe and Gustavo A. Suarez (e relativa bibliografia), ci dicono che gli investimenti
dipendono dall'acceleratore, in nessun senso o modo dal tasso di interesse.
Quindi quando io contesto in teoria e in pratica che scrivere I = I(i) è sbagliato, mi riferisco agli
investimenti industriali (quelli che sono oggetto dei meccanismi di sostituzione neoclassici).
Ciò detto, può andar bene per gli statistici classificare le abitazioni private accanto agli
investimenti industriali, ma per l'economista keynesiano sono un bene di consumo a lunga durata,
e in questo senso argomento che il tasso di interesse influenza positivamente l'acquisto di nuove
abitazioni nell'ambito della sua influenza sui consumi autonomi (quelli finanziati dal credito al
consumo).
Circa gli investimenti in opere pubbliche, solo in senso molto lato sono incremento di capacità
produttiva, il grande Ackley nel suo modello econometrico dell'economia italiana la classificava
infatti come spesa pubblica autonoma. E la loro dipendenza dal tasso di interesse passa solo
attraverso il minor costo dell'indebitamento pubblico eventuale.
Riassumendo, il tasso di interesse:
- non influenza gli investimenti industriali, spiegati dall'acceleratore;
- influenza spesa per nuove abitazioni (o ristrutturazioni) nell'ambito della sua influenza sui
consumi autonomi;
- influenza le opere pubbliche decise autonomamente dal governo via minor costo
dell'indebitamento.
Nessuna incoerenza dunque, basta non essere schiavi di via Cesare Balbo. Una buona analisi
economica conta (specie poi se la rilevazione empirica le dà ragione).










