BvqEqF о о о о ∧ ∙ + ∙ = BvqF о о о ∧ ∙ = ) sin(α ∙ ∙ ∙ = BvqF о о о Bv

** ITN - Caboto - Gaeta ** Fisica - prof. Vindice Luigi **IISS-Caboto- Gaeta**Fisica-prof. Vindice Luigi-
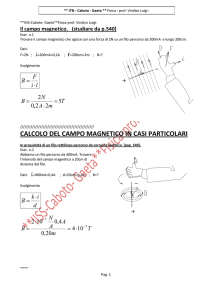
Il campo magnetico: introduzione.
Facciamo l'ipotesi di avere un elettrone che viaggia a velocità
v
ed è immerso in un campo elettrico e in un
campo magnetico stazionari (che non cambiano nel tempo). La sua energia cinetica non può variare ma la
sua traiettoria sicuramente varia. (per le rappresentazioni grafiche vedi di seguito). Nasce una forza in base
alla :


 
F  q E  qv  B
equazione o forza di Lorentz
dove:
 =rappresenta il prodotto vettoriale (vedi in seguito)
F= forza applicata dal campo elettrico e magnetico sulla carica elettrica [N]
q=carica elettrica [C]
E=intensità del campo elettrico [N/C]
v=velocità carica elettrica [m/s]
1N
1N
B= intensità del campo magnetico [T] Tesla
1T 

A m
C
m
s
Quindi dimensionalmente i due addendi sono in N come deve essere.
**
Se è presente solo il campo magnetico che agisce sulla carica elettrica l'espressione di cui sopra diventa:

 
F  qv  B
equazione o forza di Lorentz
e il prodotto vettoriale va risolto

 
F  q  v  B  sin( )
(lasciamo il simbolo dei vettori perché l'orientamento è importante)
dove
sin()= è il seno dell'angolo  tra v e B
Se v e B sono perpendicolari
 
vB
accade che sin()=1
quindi

 
F  qv  B
equazione o forza di Lorentz
**
A questo punto notiamo che
q
==> q  i  t
t
l
v
t
i
dove:
t= intervallo di tempo [s]
l = lunghezza del conduttore elettrico (filo) che viene percorso dalla carica elettrica (elettrone).
pertanto:
Pag. 1
**IISS-Caboto- Gaeta**Fisica-prof. Vindice Luigi-


 
l 
F  q  v  B  i  t   B ==>
t
 

F  i  l  B 2a legge di Laplace
/////////////////////////////////////////////////////////////////////////////////
Il campo magnetico influenza la carica elettrica che percorre un
conduttore.
*
Se consideriamo un conduttore lineare immerso in un campo magnetico, sperimentalmente si osserva che
su tale conduttore agisce una forza che è direttamente proporzionale all’intensità della corrente elettrica i
e alla lunghezza del filo l. La costante di proporzionalità che lega F con i e l è B.
Teniamo presente che il verso convenzionale della corrente è dal + al - (quello reale è dal polo negativo– al
polo positivo +).
La relazione matematica che lega tali grandezze
viene espressa dalla 2a legge di Laplace che
vettorialmente si scrive:

 
F  l i  B
In tale espressione preferiamo indicare i come
vettore e non l perché è importante vedere il
verso (convenzionale) della corrente elettrica
per poter applicare la regola della mano destra
di cui parleremo in seguito. Teniamo inoltre
presente che
i
e
l
hanno la stessa
direzione e lo stesso verso.
Ovvero con B perpendicolare ad i :
F  l  i  B
Quindi è
B
F
i l
Se conosciamo il verso della corrente e quello del campo
magnetico possiamo individuare il verso della forza con
cui il filo viene spinto.
Dove:
l = lunghezza filo [m]
i = intensità di corrente [A]
 = prodotto vettoriale
1a REGOLA DELLA MANO DESTRA (serve ad individuare il
B è il vettore Campo Magnetico
verso di F conoscendo il verso di i e di B)
perpendicolare ad i
Viene aperta la mano destra in modo che il pollice è rivolto
[T] Tesla.
L’unità di misura di B è il Tesla [T]
N
T
A m
nel verso di i e le restanti dita nel verso di B . Dal palmo
della mano quindi esce la forza F.
/////////////////////////////////////////////////////////////////////////////////
Pag. 2
**IISS-Caboto- Gaeta**Fisica-prof. Vindice Luigi-
Calcolo e geometria del campo magnetico in casi particolari
**
In prossimità di un filo rettilineo percorso da corrente elettrica.
B
0 i

2  d
Legge di Biot-Savart
Con:
B= campo magnetico [T] Tesla
T  m permeabilità magnetica nel
0  4   107
A
vuoto.
i=
intensità di corrente [A]
d= distanza dal filo del punto nel quale si vuole
valutare B [m]
Si applica la 2a regola della mano destra (che
serve ad individuare il verso di B conoscendo il
verso di i in un conduttore lineare):
si dispone il pollice secondo i e si chiude la
mano destra sul palmo. Il verso di chiusura della
mano fornisce il verso di B.
****
In una spira circolare percorsa da corrente elettrica.
B
0 i

2 r
Con:
B= campo magnetico [T] Tesla
T  m permeabilità magnetica nel
0  4   107
A
vuoto.
i=
intensità di corrente [A]
r= raggio della spira [m]
Si applica la 3a regola della mano destra (che
serve ad individuare il verso di B conoscendo il
verso di i in una spira):
si chiude il palmo della mano destra secondo
i
Essendo F  l  iB  l  i  B  B  F
i l
e
il pollice ci fornisce il verso di B.
[ B]  T 
****
Pag. 3
N
Am
**IISS-Caboto- Gaeta**Fisica-prof. Vindice LuigiIn un solenoide percorso da corrente elettrica.
B  0  N 
i
l
Con:
B= campo magnetico [T] Tesla
T  m permeabilità
0  4   107
A
magnetica nel vuoto.
i=
intensità di corrente [A]
N= numero di spire
l = lunghezza del solenoide [m]
Da notare come si dispone i polo
Nord e quello Sud.
****
Spira rettangolare in un campo magnetico. Principio di funzionamento di un motore elettrico in corrente
continua.
La spira rettangolare è
immersa nel campo
magnetico generato da un
magnete che va dal polo
Nord al polo Sud.
Se nella spira circola
corrente, con la regola della
mano destra, si può
determinare il verso della
forza a cui ognuno dei due
lati della spira, paralleli al
magnete, sono sottoposti.
Questo è lo schema di
funzionamento di un
motore elettrico.
/////////////////////////////////////////////////////////////////////////////////////////////
Pag. 4
**IISS-Caboto- Gaeta**Fisica-prof. Vindice LuigiESPERIENZA DI OERSTED (1777-1851)
Interazione fra correnti. Verso della corrente opposta.
Prendiamo due fili percorsi
da correnti di verso opposto
(il verso della corrente è dal
+ al -). La corrente i1
produce un campo
magnetico B1 sul filo 2.
Infatti con la regola della
mano destra (1° regola) si
dispone il pollice secondo i1
sul filo1 e si chiudono le dita
della mano destra sul palmo.
Tale verso di chiusura è
quello di B1 .
Quindi B1 agisce su i2 e
induce una forza F2.
Quest’ultima ha pedice 2 in
quanto agisce sul filo2.
La 2° regola della mano
destra dice che dobbiamo
disporre il pollice secondo il
verso della corrente i2, e le
altre dita secondo B. Il verso
uscente dal palmo della
mano destra è quello di F2.
In tale caso F1 e F2 sono
opposte e quindi i fili si
respingono.
****
Pag. 5
**IISS-Caboto- Gaeta**Fisica-prof. Vindice LuigiInterazione fra correnti. Verso della corrente concorde.
Prendiamo due fili percorsi
da correnti di verso opposto
(il verso della corrente è dal
+ al -). La corrente i1
produce un campo
magnetico B1 sul filo 2.
Infatti con la regola della
mano destra (1° regola) si
dispone il pollice secondo i1
sul filo1 e si chiudono le dita
della mano destra sul palmo.
Tale verso di chiusura è
quello di B1 .
Quindi B1 agisce su i2 e
induce una forza F2.
Quest’ultima ha pedice 2 in
quanto agisce sul filo2.
La 2° regola della mano
destra dice che dobbiamo
disporre il pollice secondo il
verso della corrente i2, e le
altre dita secondo B. Il verso
uscente dal palmo della
mano destra è quello di F2.
In tale caso F1 e F2 sono
concorrenti e quindi i fili si
attraggono.
****
Calcolo interazione fra correnti.
Teniamo presente che B è perpendicolare ad
i.
Osserviamo che il filo 2 è percorso dalla corrente i2 e su quest’ultima agisce il campo B1 provocato da i1 .
In tale situazione agisce sul filo 2 una la forza F2 .
La lunghezza l dei due fili è la stessa. Inoltre con d indichiamo la distanza tra i fili.
F2  l  i2  B1
Ovvero essendo F1=F2
k i i l
F 1 2
d
ma
Bl 
k  il
d
Quindi
F2 
k  i1  i2  l
d
Con:
k= 2x10-7N/A (nel vuoto)
i1 = intensità di corrente nel filo 1
i2 = intensità di corrente nel filo 2
l = lunghezza del filo [m]
[A]
[A]
d= distanza tra i fili [m]
/////////////////////////////////////////////////////////////////////////////////////////////////
Pag. 6