CAPITOLO 12 – AZIONAMENTO CON MOTORE SINCRONO A RILUTTANZA
12.1 – Azionamento con motore sincrono a riluttanza
Come già discusso nel par.9.3, e ripreso nel par.11.1, il motore sincrono a riluttanza può essere
considerato come un motore sincrono a poli salienti con avvolgimento trifase di statore e privo di
eccitazione di rotore.
Nelle prime realizzazioni, le salienze di rotore erano ottenute rimuovendo alcuni denti da rotori
convenzionali, e queste macchine con potenza d’uscita modesta sono state utilizzate per parecchio
tempo, anche se le loro non eccellenti prestazioni, unite ad un prezzo abbastanza elevato, ne hanno
frenato l’espansione. (La gabbia serviva per l’avviamento)
Attualmente, i motori a riluttanza usano rotori con barriere di flusso, o laminati assialmente, per
produrre elevati rapporti di salienza, con una potenza d’uscita comparabile con quella di
corrispondenti motori asincroni.
Vi sono importanti applicazioni industriali (p.e. pompe per lavatrici) ove è molto apprezzato avere
un rotore in cui non circoli alcuna corrente. Inoltre il fatto che si tratti di un motore sincrono ne rende
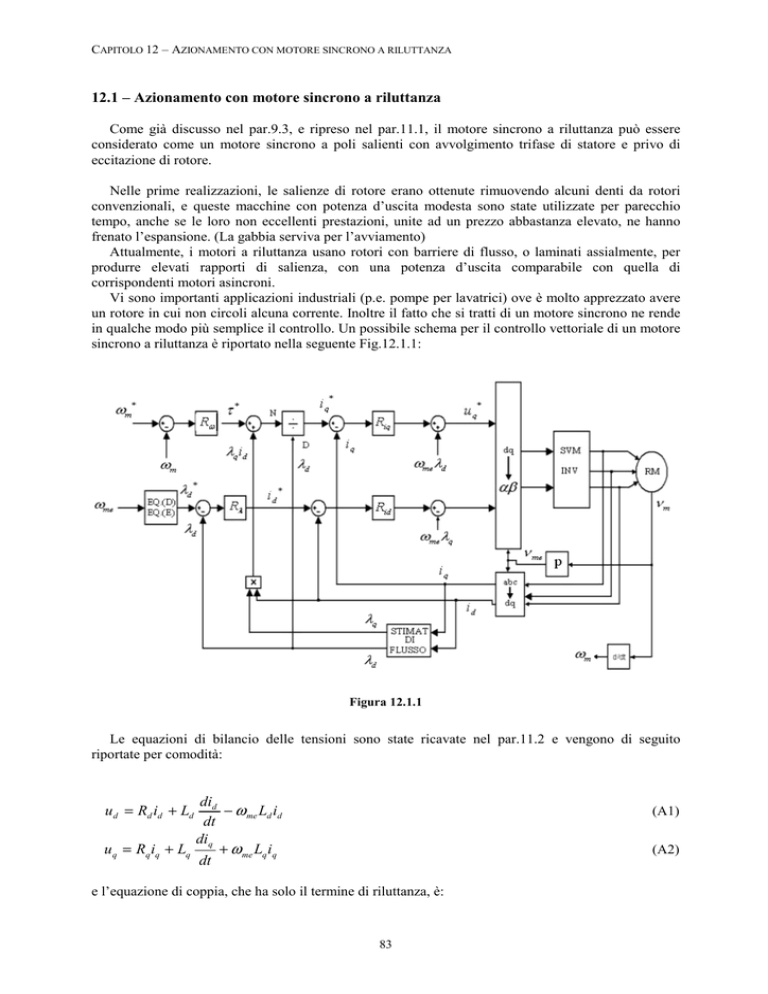
in qualche modo più semplice il controllo. Un possibile schema per il controllo vettoriale di un motore
sincrono a riluttanza è riportato nella seguente Fig.12.1.1:
Figura 12.1.1
Le equazioni di bilancio delle tensioni sono state ricavate nel par.11.2 e vengono di seguito
riportate per comodità:
did
− ω me Ld id
dt
di
u q = Rq iq + Lq q + ω me Lq iq
dt
ud = Rd id + Ld
(A1)
(A2)
e l’equazione di coppia, che ha solo il termine di riluttanza, è:
83
CAPITOLO 12 – AZIONAMENTO CON MOTORE SINCRONO A RILUTTANZA
τ=
3
3
p ( Ld − Lq )id iq = p (λd iq − λq id )
2
2
(B)
Nel caso del motore IPM si era visto come pur essendo possibile un controllo ad orientamento di
campo con id*=0, questa non fosse la soluzione che massimizza il rapporto coppia/corrente. Nel caso di
motore sincrono a riluttanza un controllo con id*=0 non sarebbe neppure possibile, dato che non vi è
flusso prodotto dal rotore. Scrivendo:
iq =
2
i S − id
2
(C)
e sostituendola nella (B), derivando poi rispetto ad iq si trova la traiettoria ottimale per la corrente id (e
dunque iq) nel piano delle correnti nel funzionamento a coppia costante.
Si ha subito:
*
id = −
iS
2
= − iS cos
π
(D)
4
e le curve di coppia sono iperboli aventi gli assi Id e Iq come asintoti orizzontali e verticali. In
deflussaggio si può fare lo stesso ragionamento che è stato presentato per i motori IPM; i risultati
ricavati nel par.() sono ancora validi se in essi si sostituisce Λmg=0.
L’equazione relativa alla corrente Id* in deflussaggio risulta la seguente:
2
2
2
2
2
− ( Lq − Ld )( Ld I S ) − ( Lq − Ld )
*
Id =
2
2
Uf
Ω me
2
2
( Lq − Ld )
=−
1
2
Lq − Ld
dove si è posto:
U f = U S − RS I S = (U d − RS I d ) + j (U q − RS I q ) .
Anche in questo caso, infine, la velocità base si può definire come:
84
2
( Ld I S −
Uf
Ω me
)
(E)
CAPITOLO 12 – AZIONAMENTO CON MOTORE SINCRONO A RILUTTANZA
2
Ωb =
− b ± b 2 − 4ac
2a
2
2
a = Lq I q + Ld I d
dove
2
b = 2 RS I d I q ( Ld − Lq )
2
2
2
(F)
2
2
c = −U d − U q + RS ( I d + I q )
Il flusso λd* viene calcolato come λd*=Ldid* e id* viene calcolata con la (D) o con la (E) a seconda che la
velocità Ωme sia rispettivamente inferiore o superiore alla velocità base indicata dalla (F).
Il regolatore di velocità Rω produce un riferimento di coppia τ*; avendo presente l’espressione (B)
si intuisce immediatamente come si possa ricavare il riferimento di corrente iq*:
*
iq = (
2
τ + λq i d ) / λd
3p
Nello schema, dunque, si intende ancora mantenere per iq il significato di corrente produttrice di
coppia,e per id quello di componente che genera il flusso.
Il regolatore di flusso Rλ produce infatti quello che viene considerato un riferimento di corrente id*.
Dalle equazioni di tensione (A) si evince poi la necessità di disaccoppiare i due anelli di
regolazione di corrente tramite opportuni termini di disaccoppiamento ωmeλd e -ωmeλq , per bilanciare
ed annullare gli effetti degli stessi termini presenti con segno opposto nel modello del motore.
Com’è evidente, lo schema di Fig.12.1.1 richiede in più punti la stima del flusso del motore, che è
ottenuta tramite il blocco definito ‘STIMATORE DI FLUSSO’ tramite le equazioni:
λd = Ld id
λq = Lq iq
(G)
a partire dalle correnti id e iq iniziali.
Questa soluzione presenta due punti deboli, riconducibili entrambi alla possibilità di variazione
delle induttanze del motore (specialmente Lq) al variare delle condizioni di carico.
Una imprecisione su Lq porta ad una errata stima del flusso. Vengono quindi forniti riferimenti non
corretti id* e iq* e pertanto ci si allontana dal punto di funzionamento “a massima efficienza”. Si ha poi
un errore nella valutazione della velocità base, e si può entrare in deflussaggio troppo presto o troppo
tardi; nel primo caso si perde la possibilità di produrre coppia:
Se si pensa di dover andare in deflussaggio dal punto A si scende verso B e quindi si perde coppia; si
poteva riuscire ancora in A, e la dinamica ne avrebbe guadagnato.
85
CAPITOLO 12 – AZIONAMENTO CON MOTORE SINCRONO A RILUTTANZA
Nel secondo caso si cerca inutilmente di rimanere in A, finchè intervengono i limiti di tensione dei
regolatori di corrente, che saturano togliendo loro l’abilità di controllare la corrente, che comunque
vede il suo punto di funzionamento spostarsi verso B. Infine, per le imprecisioni sui parametri possono
anche esservi disaccoppiamenti difettosi negli anelli di corrente.
Una soluzione ai problemi precedenti è offerta dalla disponibilità di accurati stimatori di flusso; un
esempio è di seguito descritto.
Le equazioni del bilancio di tensione per il motore sincrono a riluttanza, scritte in un sistema di
riferimento stazionario (α,β) si derivano direttamente da quelle scritte in (a,b,c) ( ) applicando loro
la trasformazione indotta dalla matrice Tabc/αβ, ricavata nel par.6.1 e qui riportata per praticità:
Tabc / αβ
− 1/ 2 − 1/ 2
1
2
=
0
3 / 2 − 3 / 2
3
1 / 2 1 / 2 − 1 / 2
Tralasciando la componente omopolare si scrive*:
S
S
u S = RS i S +
dλ S
dt
S
(H)
dλa
dt
dλ
ub = Rib + b
dt
u a = Ria +
*
vale sempre scrivere:
...
s
s
s
dove us , is e λs sono i vettori spaziali di tensioni, correnti e flussi concatenati in un sistema “s”
solidale allo statore.
La (H) indica una prima strada per il calcolo del flusso, ottenuto come integrale della fcem:
t
λS = ∫ (u S S − RS iS S )dt
S
(I)
0
Come sarà provato nello studio degli azionamenti per motore asincrono (cfr. par.15.4) una stima
tramite la (I) risulta imprecisa a basse velocità, per gli errori dovuti alla resistenza di statore e ai
disturbi di misura.
Lo schema proposto è un osservatore di flusso che si basa sull’utilizzo simultaneo di H e della stima
basata sul modello matematico del flusso, descritto dalle (G), come descritto dall’equazione seguente:
∧
λSS =
~
λS S
~
sτ g
1 + sτ g
~r
= λS e jϑme
S
(
λS r = λd + jλq
S
v S − RS i S
1
~
λS S
)+
s
1 + sτ g
(L)
e dove g=1/τg rappresenta il guadagno dell’osservatore.
86
CAPITOLO 12 – AZIONAMENTO CON MOTORE SINCRONO A RILUTTANZA
Lo schema a blocchi relativo all’equazione (L) e seguenti è riportato in Fig. 12.1.2:
Figura 12.1.2
Figura 12.1.2
Dimostrazione dello schema:
~S
1 S
1 ~ S ~ S v S − Ri S
1 ~ S λS
S
−
λ S = ( v − Ri ) − (λ S − λ S ) =
λS +
s
sτ g
sτ g
S
τg
~S
v S − Ri S λ S
1
~
λS S (1 +
)=
+
sτ g
s
sτ g
~S
~S
λS
sτ g
S
λ
v S − Ri S
=(
)(
)+ S
1 + sτ g
s
1 + sτ g
Dalla (L) si noti come il contributo dovuto all’integratore sia pesato con un filtro passa alto, per
attenuare gli effetti della sua scarsa precisione a basse velocità (ovvero a basse pulsazioni ωme). Il
modello del flusso invece funziona meglio lontano dai transitori e alle basse velocità, ovvero
frequenze, e per questo è stato pensato con un filtro passa-basso. La somma dei due pesi è unitaria a
tutte le frequenze.
Spesso, nella pratica si adottano per [L] dei modelli molto accurati e complessi, che tengono conto dei
dettagli costruttivi della macchina, la cui trattazione esula dai compiti del presente testo. Si può solo
accennare che in ogni caso, gli eventuali errori di modello a bassa velocità non riguardano la zona di
deflussaggio e dunque vengono facilmente compensati dall’anello di regolazione di velocità. Un
modello accurato del flusso serve quando sia richiesto un controllo di coppia.
Se invece basta un buon controllo di velocità, si può anche ricorrere allo scherma con anello esterno di
tensione del tutto analogo a quello studiato per i motori IPM, ove al posto dell’equanzione (A) si usi
l’equazione (D).
12.2 – Modelli applicabili al controllo reale
Un primo problema che appare evidente guardando i grafici che mostrano le caratteristiche
magnetiche dei motori è l’elevata quantità di informazioni che contengono e la loro difficile
rappresentazione analitica in quanto andamenti sufficientemente non lineari.
87
CAPITOLO 12 – AZIONAMENTO CON MOTORE SINCRONO A RILUTTANZA
La valutazione teorica e sperimentale che l’effetto di accoppiamento magnetico tra gli assi
comporta, sia in termini di coppia massima sia di controllo, sono stati descritti in letteratura [?]. Le
conclusioni sono che per ottenere un miglior controllo della macchina, sarebbe vantaggioso poter
inserire nel controllo anche il comportamento magnetico reale della macchina stessa.
Quello che si vuole mostrare in questo paragrafo è come la relazione λdq(idq) possa essere
rappresentata tramite modelli semplificati contenenti in un numero limitato di parametri tutta
l’informazione.
Per questo motivo sono stati tentati diversi metodi per la rappresentazione del modello magnetico
della macchina. Onde evitare un eccessivo numero di casi proposti ci si è concentrati per questa analisi
su una sola macchina (la M1) mostrando questa i diversi modelli e risultati una volta applicato il
controllo.
Modello a variabili separabili
Se si trascura l’effetto delle perdite nel ferro si può provare che le aree comprese tra le due curve di
λd e le due di λq , indicate in Figura 2.5 con ∆Wd e ∆Wq , devono essere uguali fra loro. Infatti,
l’energia (coenergia) accumulata deve essere funzione dello stato (id,iq) solamente. Con riferimento
alla figura 2.5, si può assumere che la coenergia W(id,iq) può essere calcolata applicando la (2.2) o la
(2.3). Il punto di lavoro considerato è (id,iq), mentre id’ e iq’ sono variabili ausiliarie, introdotte per il
calcolo degli integrali.
id
'
iq
W = ∫ λd (id ,0)did + ∫ λq (id , i )diq = Wd + Wq − ∆Wq
'
'
'
o
0
iq
id
(2.2)
q
W = ∫ λq (0, iq )diq + ∫ λd (id , iq )did = Wq + Wd − ∆Wd
'
0
'
'
'
(2.3)
o
Segue immediatamente che :
id
iq
∆Wd = ∆Wq = ∆W (id , iq ) = ∫ [λd (id ,0) − λd (id , iq )]did = ∫ [λq (0, iq ) − λq (id , iq )]diq
'
'
0
Applicando l’operatore differenziale
'
'
'
'
(2.4)
0
∂ ∂
ad ambo i membri della (2.4), si trova la nota
∂id ∂iq
condizione (2.5), che, nelle scienze elettriche, è nota con il nome di condizione di reciprocità.
88
CAPITOLO 12 – AZIONAMENTO CON MOTORE SINCRONO A RILUTTANZA
∂λ d ∂λq
∂ 2 ( ∆W )
=
=−
∂iq
∂id
∂id ∂iq
(2.5)
Questa condizione deve essere comunque soddisfatta in un contesto conservativo (ipotesi fatta).
Il modello proposto parte dall’assunzione che la differenza di coenergia ∆W(id,iq) possa essere
espressa dalla (2.6), ovvero come prodotto di due funzioni F e G dipendenti dalla sola id e iq
rispettivamente.
∆W(id,iq)≅F(id)G(iq)
(2.6)
A partire dalla (2.4), la quale implica che la reciprocità sia verificata, e prendendo le derivate
parziali
∂
∂
e
, si ottengono le equazioni (2.7) e (2.8), che rappresentano le variazioni dei flussi
∂iq
∂id
dovute all’interagenza magnetica.
∂ ( ∆W )
= λdo (id ) − λd (id , iq ) = ∆λd
∂id
(2.7)
∂ ( ∆W )
= λdo (iq ) − λq (id , iq ) = ∆λq
∂iq
(2.8)
Sostituendo nella (2.7) e (2.8) la (2.6) si possono ottenere le equazioni (2.9) e (2.10), dove (F’) e
(G’) sono le derivate prime di (F) e (G) rispettivamente.
λd (id , iq ) ≅ λdo (id ) − F ' (id )G (iq )
λq (id , iq ) ≅ λdo (iq ) − F (id )G ' (iq )
(2.9)
(2.10)
Le espressioni (2.9) e (2.10) mostrano come possa essere sufficiente conoscere (λdo) e (λqo) e le
funzioni (F) e (G) per descrivere completamente il comportamento magnetico della macchina. Queste
2 funzioni sono ottenute nel seguente modo.
Fissato l’intervallo di variazione di entrambe le correnti non deve superare due valori massimi (Ido)
e (Iqo) cui corrispondono rispettivamente i valori F0=F(Ido) e G0=G(Iqo), si introducono questi valori in
(2.9) e (2.10) e si ottengono le equazioni (2.11) e (2.12), che permettono di valutare le derivate F’(id) e
G’(iq), a meno dei fattori F0 e G0.
Go F ' (id ) = λdo (id ) − λd (id , I qo )
(2.11)
Fo G ' (iq ) = λdo (iq ) − λq ( I do , iq )
(2.12)
L’integrazione delle espressioni (2.11) e (2.12) permette di ottenere GoF(id) e FoG(iq). Per id=Ido e
iq=Iqo queste funzioni assumono il valore (FoGo) che così risulta essere noto. In questo modo il
problema è completamente risolto, infatti è sufficiente trasformare le equazioni (2.9) e (2.10) nelle
(2.13) e (2.14) per avere un modello completo:
λd (id , iq ) = λdo (id ) −
Go F ' (id ) • Fo G (iq )
(2.13)
Go Fo
89
CAPITOLO 12 – AZIONAMENTO CON MOTORE SINCRONO A RILUTTANZA
λq (id , iq ) = λqo (iq ) −
Go F (id ) • Fo G ' (iq )
(2.14)
Go Fo
Nelle figure 2.6 e 2.7 è riportato l’andamento delle funzioni (F) e (G), ricavate per il motore M1.
Le funzioni mostrate sono normalizzate, in modo da essere misurate in V⋅s⋅A=Joule. Si può notare che
i valori FoG(Iqo) e GoF(Ido) non sono esattamente uguali, come richiesto dalla (2.5), questo può essere
associabile ad errori di misura. Si potrà quindi adottare un valore medio nelle espressioni (2.13) e
(2.14).
90