Elementi di Statistica Sociale
CdL in Servizio Sociale
Prova scritta
20 settembre 2007
1. Descrivere brevemente le caratteristiche delle differenti scale di misura, riportando anche
una variabile di esempio per ogni scala
SOLUZIONE:
La misurazione dei fenomeni può essere ricondotta alle scale di misura le
quali colgono le differenti proprietà delle variabili oggetto di studio. In base alle proprietà possiamo
elencare le differenti scale secondo un ordine crescente di proprietà: la scala nominale è relativa alle
variabili le cui modalità consentono unicamente il confronto in termini di uguaglianza: sesso, colore
degli occhi, ecc; per le variabili misurate su scala ordinale è lecito operare non solo una distinzione
in termini di uguaglianza ma anche in termini di ordinamento (prima-dopo, maggiore-minore):
altezza (misurata in alto, medio, basso); se le prime due scale sono riferite alle variabili dette
qualitative, le seguenti si riferiscono alle variabili quantitative: la scala ad intervalli è usata per
misurare le variabili metriche per le quali è lecito, oltre che il confronto in termini di uguaglianza e
di ordinamento, considerare costante la distanza tra due posizioni (ad. Es. la temperatura misurata
su scala Celsius); infine la scala di rapporti che, insieme alle caratteristiche delle scale precedenti,
prevede l’esistenza di uno zero assoluto che indica l’assenza della proprietà (ad es. il conteggio, la
lunghezza, la temperatura in gradi kelvin) e prevede la possibilità di effettuare i rapporti.
2. La tabella seguente riporta la distribuzione dei voti ottenuti dagli studenti di una facoltà di
Palermo alla prova di inglese, distinta per genere.
Voto
18
20
22
23
24
25
26
28
30
Genere
Maschio Femmina
3
2
6
4
7
1
9
6
3
10
12
9
5
6
8
8
11
8
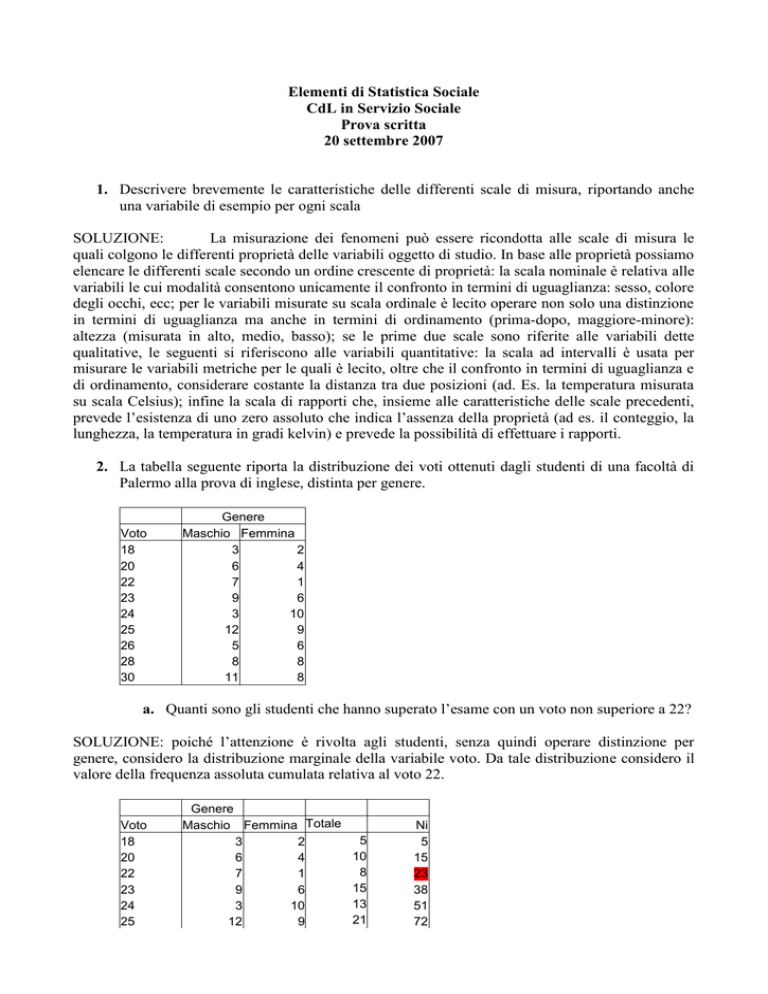
a. Quanti sono gli studenti che hanno superato l’esame con un voto non superiore a 22?
SOLUZIONE: poiché l’attenzione è rivolta agli studenti, senza quindi operare distinzione per
genere, considero la distribuzione marginale della variabile voto. Da tale distribuzione considero il
valore della frequenza assoluta cumulata relativa al voto 22.
Voto
18
20
22
23
24
25
Genere
Maschio Femmina Totale
3
2
6
4
7
1
9
6
3
10
12
9
5
10
8
15
13
21
Ni
5
15
23
38
51
72
26
28
30
5
8
11
11
16
19
6
8
8
83
99
118
Il numero di studenti che supera l’esame con un voto non superiore a 22 è 23.
b. Qual è il voto medio degli studenti maschi, femmine e senza distinzione per genere?
SOLUZIONE:
Voto (xi)
18
20
22
23
24
25
26
28
30
Totale
media
ni
Maschio
xi*ni
3
6
7
9
3
12
5
8
11
64
54
120
154
207
72
300
130
224
330
1591
=1591/64
=24,84
ni
Femmina
xi*ni
2
4
1
6
10
9
6
8
8
54
36
80
22
138
240
225
156
224
240
1361
=1361/54
=25,20
ni
Totale studenti
xi*ni
5
90
10
200
8
176
15
345
13
312
21
525
11
286
16
448
19
570
118
2952
=2952/118
=25,02
Il voto medio dei maschi è 24,84, per le femmine è 25,20 e per gli studenti in generale è 25,02
c. Qual è la probabilità per uno studente di ottenere un voto superiore a 25?
SOLUZIONE: facendo riferimento alla distribuzione dei voti senza distinzione per genere,
determinata nell’esercizio 2a, la probabilità è data dal rapporto tra num. di casi favorevoli (ovvero il
totale di studenti che conseguono il voto di 26, 28 e 30: 11+16+19=46) e il numero di casi possibili
(118). Tale probabilità è pari a 0,39
d. Rappresentare tramite Box-Plot le due distribuzioni
SOLUZIONE: Maschi
n=64
Minimo=18
Massimo=30
(n+1)/4=65/4=16,25 la cui parte intera è 16 e quella decimale è 0,25
Q1=x(16)+0,25*(x(17)-x(16))=22+0,25*(23-22)=22,25
(n+1)*3/4=65*3/4=48,75 la cui parte intera è 48 e quella decimale è 0,75
Q3=x(48)+0,75*(x(49)-x(48))=28+0,75*(28-28)=28
n/2= 32
Mediana=(x(32)+x(33))/2=(25+25)/2=25
Voto
Mediana = 25
25%-75%
= (22,5, 28)
Min-Max
= (18, 30)
16
18
20
22
24
26
28
30
32
Femmine
n=54
Minimo=18
Massimo=30
(n+1)/4=55/4=13,75 la cui parte intera è 13 e quella decimale è 0,75
Q1=x(13)+0,75*(x(14)-x(13))=23+0,75*(24-23)=23,75
(n+1)*3/4=55*3/4=41,25 la cui parte intera è 41 e quella decimale è 0,25
Q3=x(41)+0,25*(x(42)-x(41))=28+0,25*(28-28)=28
n/2= 27
Mediana=(x(27)+x(28))/2=(25+25)/2=25
Voto
Mediana = 25
25%-75%
= (24, 28)
Min-Max
= (18, 30)
16
18
20
22
24
26
28
30
32
e. E' più variabile la distribuzione dei voti dei maschi o delle femmine?
SOLUZIONE: per confrontare la variabilità della distribuzione dei voti dei maschi con quella delle
femmine, determino il coefficiente di variabilità: questo è dato dal rapporto tra la radice quadrata
della varianza e il valore assoluto della media
Voto (xi)
18
20
22
23
24
25
26
28
30
Totale
media
varianza
Il CV=0,137
ni
Maschio
xi*ni
3
6
7
9
3
12
5
8
11
64
xi-media (xi-media)^2 (xi-media)^2*media
54 -6,85938
47,05103
141,1531
120 -4,85938
23,61353
141,6812
154 -2,85938
8,176025
57,23218
207 -1,85938
3,457275
31,11548
72 -0,85938
0,738525
2,215576
300 0,140625
0,019775
0,237305
130 1,140625
1,301025
6,505127
224 3,140625
9,863525
78,9082
330 5,140625
26,42603
290,6863
1591
749,73
24,84
=749,73/64
=11,71
Voto (xi)
18
20
22
23
24
25
26
28
30
Totale
media
ni
varianza
Femmine
xi*ni
2
4
1
6
10
9
6
8
8
54
xi-media (xi-media)^2 (xi-media)^2*media
36 -7,2037
51,89335
103,7867
80 -5,2037
27,07853
108,3141
22 -3,2037
10,26372
10,26372
138 -2,2037
4,85631
29,13786
240 -1,2037
1,448903
14,48903
225 -0,2037
0,041495
0,373457
156 0,796296
0,634088
3,804527
224 2,796296
7,819273
62,55418
240 4,796296
23,00446
184,0357
1361
516,7593
25,20
=516,7593/54
=9,57
Il CV=0,123
È più variabile la distribuzione dei voti dei maschi.
3. Un valore del coefficiente di correlazione pari a -0,82 indica:
a. Una forte relazione lineare
b. Una debole relazione lineare
c. L’assenza di relazione
d. Concordanza
e. Discordanza
SOLUZIONE: a. ed e.
4. Supponendo che il coefficiente di correlazione riportato nel punto 3. sia stato ottenuto per le
variabili età (espressa in anni) e velocità nella corsa a piedi (espressa in kilometri al minuto):
a. Individuare la variabile dipendente e la variabile indipendente
b. Indicare una plausibile stima del coefficiente di regressione e darne una
interpretazione
c. Rappresentare con il grafico opportuno la relazione stimata
d. Qual è il grado di bontà dell’adattamento che ci si attende?
SOLUZIONE:
a. L’età è la variabile indipendente e la velocità nella corsa è la variabile dipendente (è l’età
che influenza la velocità di correre, non il contrario!)
b. Sulla base del coefficiente di correlazione, -0,82, un plausibile valore del coefficiente di
regressione stimato non può che avere segno negativo, dato appunto che vi è discordanza tra
le variabili. Se ad esempio il valore di b* fosse pari a -0,001 questo indicherebbe che un
aumento di un anno di età comporterebbe la riduzione della velocità media di 0,001 km/m.
c. Supponendo una velocità media di 5km/h, ovvero 0,08 km/m circa (5/60) e considerando
tale valore come la stima dell’intercetta a*, la retta di regressione stimata passa per i punti A
(18 ; 0,08-0,001*18=0,062) e B (30 ; 0,08-0,001*30=0,05). (p.s. una velocità di 0,062km/m
significa una velocità di 3,73km/h…)
0,07
Velocità (Km/m)
0,06
0,05
0,04
0,03
0,02
0,01
0
17
19
21
23
25
27
29
31
Età (anni)
d. Considerato il coefficiente di regressione, il coefficiente di determinazione è pari a (0,82)^2=0,67. Questo indica una scarsa bontà di adattamento.