UNIVERSITÀ DEGLI STUDI DI NAPOLI
“FEDERICO II”
FACOLTÀ DI SCIENZE MATEMATICHE,
FISICHE E NATURALI
Corso di Laurea in Fisica
Tesi di Laurea Triennale
La Costante di Hubble
Relatore
Candidato
Prof. Paolo Scudellaro
Ilena De Rubertis
matr. 567/189
ANNO ACCADEMICO 2008/2009
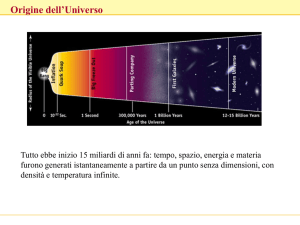
INTRODUZIONE Fino alla fine dell’Ottocento il problema cosmologico ha riguardato solo le stelle ed i pianeti. Rispetto alle cosmologie antiche è cruciale, oggi, il confronto con le osservazioni ed i loro dati. Attraverso la crescita tecnologica, questi hanno portato ad allargare l’ambito da considerare fino agli estremi oggi noti. Nel 1929, Hubble affermò l’esistenza di una relazione lineare tra il redshift (lo “spostamento verso il rosso”) della luce emessa dalle galassie (allora dette ‘nebulose’) e la loro distanza, relazione che coincide con la legge empirica qualora il redshift z sia direttamente proporzionale alla velocità V di recessione. Il legame tra V e z è lineare solamente per z molto più piccolo di 1, mentre per z maggiori dipende dal particolare modello di universo in espansione scelto. La legge empirica di Hubble è stata la prima importante conferma osservativa della soluzione cosmologica di Friedmann delle equazioni di Einstein. L’importanza storica della legge di Hubble sta nell’aver eliminato i modelli statici di universo (Einstein, de Sitter, Minkowski) che erano largamente favoriti prima della scoperta dell’espansione dell’Universo. (La conseguenza più famosa di questo pregiudizio fu, del resto, l’introduzione da parte di Einstein di una costante cosmologica nelle sue equazioni, proprio allo scopo di rendere statico l’universo che esse predicevano.) I modelli cosmologici moderni sono basati sulla teoria della Relatività Generale, utilizzata per descrivere l’universo su grandi scale I
Introduzione tramite la metrica spazio‐temporale di Robertson‐Walker, che soddisfa alle caratteristiche di omogeneità ed isotropia ottenute dai dati osservativi, rispettando, quindi, il Principio Cosmologico. Alla base di ogni considerazione sull’Universo, si trova oggi il Modello Cosmologico Standard, che si basa sulle equazioni di campo di Einstein e sul Principio Cosmologico. Nel Modello Cosmologico Standard, l’espansione dell’universo è descritta dalla variazione nel tempo di un parametro, il fattore di scala, che esprime appunto il modo in cui varia la distanza fisica tra due punti dell’Universo (e che è lo stesso per ogni coppia di galassie). Il modo in cui tale fattore di scala dipende dal tempo è scritto nelle equazioni di Friedmann per un Universo in espansione. Nei diversi modelli cosmologici la costante di Hubble è costante solo in un dato istante cosmologico. Questo valore, però, cambia nel tempo. La sua variazione nel tempo è indicata dal parametro di Hubble al tempo t , indicato con H (t ) ; intendiamo con costante di Hubble H 0 il valore attuale. L’evoluzione di H è dovuta agli effetti della forza gravitazionale della materia (visibile e oscura) presente nell’universo, che tende a rallentare l’espansione, e della cosiddetta energia oscura, che invece tende ad accelerarla; la costante cosmologica è la forma particolare più semplice di energia oscura. Misure condotte in anni recenti, a partire dal 1998, sembrano indicare che l’espansione dell’universo stia in questo momento accelerando. Per determinare in modo accurato la costante di Hubble è, comunque, essenziale considerare galassie distanti in modo che i dati non siano dominati dalle velocità peculiari. Questa tesi si propone di descrivere sommariamente, tra l’altro, alcune misure di distanza in modo da poter ricavare un valore accurato di H 0 , che sia legato ad una serie di parametri cosmologici che descrivono il nostro universo. La principale difficoltà nella misura della costante di Hubble è una determinazione accurata delle distanze da galassie, in quanto essa richiede l’uso di una scala delle distanze, affetta da errori dovuti ad inevitabili incertezze osservative. Il problema diventa più acuto per galassie distanti, in quanto la densità proiettata delle stelle diventa maggiore. Non esiste un metodo diretto per ottenere una stima sicura delle distanze. Ne vengono utilizzati due basilari: la parallasse e la candela standard. Bisogna, quindi, effettuare una calibratura senza la quale possiamo solo misurare distanze relative e non assolute. Di solito, II Introduzione si usa una serie di candele standard, la più vicina delle quali calibrata con il metodo della parallasse. Pertanto, ogni misura nella scala della distanze implica una calibratura e introduce errori. Studi di supernovae a redshift cosmologici hanno dimostrato che supernovae distanti sono più deboli di quelle attese assumendo il modello di Eistein‐de Sitter, per il quale Ω m = 1 e Ω Λ = 0 . Nella tesi vengono discussi, del resto, diversi metodi che consentono di determinare la costante di Hubble: metodi locali, metodi che usano lenti gravitazionali oppure l’effetto Sunyaev‐Zel’dovich, ma soprattutto le misure delle relazioni Periodo‐Luminosità e Periodo‐
Luminosità‐Colore di Cefeidi nelle Nubi di Magellano, nonché misure attraverso la relazione di Tully‐Fisher, oppure il Piano Fondamentale e le relazioni D ‐ σ . Ogni metodo contiene una propria percentuale di errore. La combinazione di tutti i metodi, dando un peso maggiore al metodo delle Supernovae di Tipo Ia, porta ad un valore H 0 ≈ 70kms −1 Mpc −1 . Nella tesi, dopo una breve introduzione storica, viene introdotto il Modello Cosmologico Standard e, poi, il problema della misura delle distanze, commentando ‐ senza alcun tentativo di essere esaustivi ‐ come i vari metodi conducano a valori di H 0 che in gran parte sono vicini tra loro, pur conservando errori ed incertezze specifici dell’ambito in cui sono stimati. III CAPITOLO 1 L’importanza delle distanze in cosmologia 1.1
Alle origini del discorso cosmologico Tutte le culture, da sempre, si sono interrogate sull’essenza dell’uomo e sulla sua posizione nell’Universo. Contemplando il cielo punteggiato di stelle, si sono preoccupate di costruirne una chiave di lettura che rendesse anche conto del futuro umano, di come siano distribuiti gli spazi destinati all’Essere e quelli destinati al Divenire. È in sostanza ciò che si è venuto a ripresentare, in forme più o meno evolute, in tutte le costruzioni cosmologiche sviluppate fino ai nostri giorni. In India si è sviluppata la cosmologia vedica, contenuta nelle più antiche scritture che ci siano note. Essa si concentra ampiamente sugli aspetti statici dell’Essere. L’Induismo, infatti, amplia il concetto di Essere nel Brahman, entità suprema primordiale personale che include sia l’Essere che il non‐Essere. Originariamente, del resto, è a partire dal Brahman che si stabilisce una relazione, ancora indistinta, tra luce, azione e gravità quali agenti del reale. Lo scopo della descrizione vedica delle articolazioni dell’Essere è proprio il confronto con lo spazio. Successivamente, e in tutt’altra cultura, tale spazio viene ancora riservato dal libro della Genesi all’articolazione dell’Essere. Qui, dopo la creazione del caos primordiale, è il verbo che agisce e crea la luce, fino a fare risaltare la centralità dell’uomo sulla scena cosmica, 1
L’importanza delle distanze in cosmologia insieme al dominio di una sequenza temporale segnata dai giorni. Tutto avviene ormai nel tempo, è “divenire”. Così, al tempo ciclico della cosmologia vedica si viene a contrapporre il tempo lineare della cosmologia giudaica. Poi nel corso dello sviluppo della cultura ellenica, la storia del pensiero cosmologico compie un primo significativo passo in avanti, essenziale a focalizzare il processo che porta alla cosmologia moderna. Il quinto secolo avanti Cristo, in effetti, è stato un periodo di rivoluzioni ideologiche su tutto il pianeta, con la venuta del Buddha in India, di Confucio e Lao‐Tse in Cina, di Zarathustra in Mesopotamia. Nel mondo ellenico è stato il secolo di Pitagora. A lui e alla sua scuola sono state accreditate molte acquisizioni di matematica, mostrando anche come le punte più avanzate del pensiero logico e scientifico potessero diventare strumento di elaborazione cosmologica. Ogni numero viene associato ad una divinità, capace di agire e costruire nel mondo. Ad esempio l’Uno, emblema dell’unità dell’essere, è assolutezza stessa dell’Essere, come Brahman, ed è destinato ad articolarsi nelle molteplicità senza tuttavia esserne corrotto; esso viene anche visto come il fuoco primordiale. Il Due è la madre Terra, la sostanza primordiale. Il Tre si riconduce alla divinità solare e al suo ruolo maschile. E così via, in una progressione che costituisce e costruisce l’esistente. Due secoli più tardi, Aristarco da Samo ha rinunciato all’Uno inconoscibile e introdotto per primo il sistema eliocentrico. 2 L’importanza delle distanze in cosmologia 1.2
Le galassie In sostanza, nell’avvicendarsi di essere e divenire, fino alla fine dell’Ottocento il problema cosmologico ha riguardato solo le stelle e i pianeti. La scoperta dell’esplosione di supernovae nelle nebulose (una supernova può raggiungere una luminosità di ≈ 10 9 LΘ , oltre un miliardo di volte la luminosità del Sole) e l’osservazione di un’anticorrelazione tra il piano della via Lattea e la distribuzione di queste nebulose introducono, quindi, nuovi ingredienti. Va riconosciuto ad Hubble il merito di aver sdoganato le galassie, riconosciute finalmente come elementi fondanti di un Universo su cui si può finalmente speculare a partire, questa volta, da misure ‘cosmologiche’. Negli anni Ottanta, tra l’altro, si è discusso molto del fatto che la distribuzione della materia cosmica potesse essere un frattale. Nessun dato, all’epoca di Hubble, poteva del resto escluderlo. Ma, se la distribuzione fosse sul serio tale, non esisterebbe alcuna scala di isotropia e omogeneità, e il lavoro dei relativisti per la soluzione di importanti e difficili problemi di fisica‐matematica non avrebbe mai trovato aderenza alla realtà fisica, cosa che invece poi si è verificata. Si può, così, porre negli anni Venti la data di partenza della cosmologia scientifica. È in quell’epoca che viene certificata la natura extra‐galattica delle galassie, i veri e propri mattoni su cui comincia ad edificarsi la cosmologia. Per questa scoperta, Edwin Hubble ha ben meritato tutti i riconoscimenti che gli furono allora tributati e che, oggi, sono testimoniati dal nome del primo telescopio spaziale. Rispetto alle cosmologie antiche, è diventato ormai cruciale il confronto con le osservazioni e i loro dati. Il procedimento della cosmologia è attualmente simile in gran parte a quello di tanti altri ambiti di indagine della fisica, giungendo forse a prospettare che è il divenire del mondo la base concreta del suo stesso essere, così riuscendo almeno in parte a risolvere i dubbi antichi. 1.3
La nascita della cosmologia scientifica moderna 3 L’importanza delle distanze in cosmologia Nel 1924 ebbe luogo la 33a Riunione della American Astronomical Society. Ad essa non partecipò Edwin P. Hubble, ma vi venne comunque letta la sua famosa comunicazione sul risultato di un programma di osservazioni con il nuovo telescopio da 100 pollici di Mount Wilson. Esse dimostravano che M31 nella costellazione di Andromeda era in realtà un sistema stellare esterno alla Via Lattea e ad essa simile. Hubble, infatti, aveva identificato in M31 delle stelle cefeidi che egli usava come indicatori di distanza. Le cefeidi sono delle stelle variabili sulla scala dei giorni e, grazie alla fotometria svolta in collaborazione con Humason, Hubble aveva ricavato i periodi P di quelle presenti in Andromeda, deducendone le luminosità L . Dal confronto tra L e la luminosità apparente l (ovvero quella rilevabile dal punto d’osservazione) di ciascuna cefeide, ossia tramite la legge l =
L
, è facile ricavare la distanza d . Hubble valutò, così, la distanza di M31 in 250 4πd 2
Kpc a fronte di un raggio della Via Lattea di 10 Kpc (il parsec, pc, è l’unità di distanza più comunemente usata in astronomia e vale 3.26 anni‐luce circa 3.09 ⋅ 1016 m ). Nonostante la distanza di M31 sia, in effetti, considerata oggi 3 volte maggiore, usando i dati corretti sulle cefeidi, già le distanze fornite da Hubble collocavano definitivamente M31 al di fuori della Via Lattea. Questa scoperta segna, dunque, la nascita dell’astronomia extragalattica. Il suo primo dato significativo riguarda proprio la nostra stessa galassia, la Via Lattea (Milky Way), per la quale si misura una luminosità totale e si stima una massa M mw tra 1011 e 1012 M Θ (un intervallo non dovuto a difficoltà sperimentali, ma alla progressiva scoperta di nuove componenti oscure). Le unità LΘ e M Θ sono la luminosità intrinseca e la massa del Sole, rispettivamente di 4 ⋅ 10 33 erg / sec e 2 ⋅ 10 33 grammi . Ma la vera astronomia extragalattica si interessa di ciò che è esterno alla Via Lattea, delle galassie simili (o non) alla Via Lattea che si osservano in ogni direzione e a profondità diverse. La distanza media galassia‐galassia, λ gg , è di 3 con un’incertezza sperimentale inevitabile e la necessità di operare una scelta sulla massa minima degli oggetti cui attribuire la qualifica di “galassia”. Si noti che la distanza di M31 dalla Via Lattea è inferiore al Mpc e le nubi di Magellano sono ancora più vicine. Invero, le galassie tendono a presentarsi in gruppi legati gravitazionalmente; alcuni sono semplici sistemi binari, mentre altri sono più 4 L’importanza delle distanze in cosmologia consistenti, come il Gruppo Locale in cui si trovano la Via Lattea e M31, fino a giungere ad ammassi di migliaia di galassie, come Abell 1689. Per aggregazione progressiva, il gas forma le stelle, le stelle formano le galassie, le galassie formano gruppi e ammassi. Si tratta sempre di sistemi gravitazionalmente legati, seppure in condizioni dinamiche assai difformi. Su scale di distanza maggiori; oltre i 10 Mpc, riscontriamo associazioni di oggetti come i superammassi e tutta una rete cosmica di filamenti e superfici. Tra i filamenti risaltano dei grandi vuoti, di raggio fino a 30 ‐ 40 Mpc. D’altra parte, al crescere della scala delle masse, cala sempre più il contrasto di densità tra i sistemi aggregati e gli spazi circostanti. Si va da un contrasto di densità di 20 ordini di grandezza per le stelle ad uno di 7 per le galassie e 2 per gli ammassi, fino ad 1/5 circa per i superammassi. Ciò rende legittimo pensare che, su scale di masse e distanze ancora maggiori, si approssimi l’omogeneità, in concordanza coi risultati forniti dai radiotelescopi, ad esempio, e coi dati sul fondo cosmico a microonde (CMB, cosmic microwave background), rilevato per la prima volta da Arnold A. Penzias & Robert W. Wilson nel 1965, che testimoniano di una isotropia superiore a 1:105. Ad Edwin Hubble si accredita anche la scoperta dell’espansione dell’Universo, il moto d’insieme delle galassie che va, appunto, sotto il nome di ‘flusso di Hubble’. Fu Hubble, infatti, a suggerire, nel 1929, che valesse la celebre “legge di Hubble”: v = H 0 d (1.1) Fig.1: relazione velocità‐distanza tra nebulose extragalattiche. 5 L’importanza delle distanze in cosmologia dove d è la distanza delle galassie osservate e v la loro velocità di allontanamento, fornendo per H 0 un valore di ~ 500 (km/s)/Mpc, tale dunque che la velocità di allontanamento crescesse linearmente con la distanza di 500 km/s per ogni Mpc in più. Anche se la legge v = H 0 d si è rivelata corretta, il valore di H 0 fornito da Hubble è oggi considerato errato, nonostante dimostrasse che i dati ne avevano permesso la stima. Essa si basava sulla misura dei redshift delle righe spettrali di una ventina di galassie, entro 5 – 6 Mpc, oltre i quali il telescopio di Mount Wilson e le tecniche spettroscopiche dell’epoca non permettevano di andare. Poiché, però, a queste distanze i dati sono dominati dalle velocità peculiari, in effetti il ‘flusso di Hubble’ non si può ancora veramente vedere. In ogni caso, nel suo articolo del 1929 [1] dopo aver affermato l’esistenza di una rozza relazione lineare tra velocità e distanza, Hubble riesce perfino a prevedere l’uso dei suoi dati numerici nelle discussioni riguardanti la curvatura dello spazio, riferendosi così nettamente alla Relatività Generale e al contributo che alle teorie cosmologiche relativistiche poteva venire dalle osservazioni. In ciò attestando la consapevolezza della nascita di una metodologia scientifica che, in seguito, è stata pienamente sviluppata e, ancor oggi, fornisce supporto alla ricerca extragalattica. 6 CAPITOLO 2 Elementi di cosmologia teorica 2.1
La cosmologia moderna La cosmologia descrive l’Universo come un unico sistema fisico, studiandone la struttura a larga scala e l’evoluzione. Alla base di ogni considerazione sull’Universo oggi si trova il Modello Cosmologico Standard, che si propone di descriverne l’evoluzione dalle sue fasi iniziali fino al tempo attuale. Esso si basa su due elementi fondamentali: le equazioni di campo di Einstein, che descrivono il comportamento di un qualsiasi sistema fisico sotto l’effetto della gravità, e il cosiddetto Principio Cosmologico in base al quale l’Universo è una singola entità dinamica e termodinamica, omogenea ovunque ed isotropa intorno ad ogni suo punto. L’Universo attuale, soprattutto se lo osserviamo su distanze “piccole”, è però tutt’altro che omogeneo ed isotropo: sono ben evidenti distribuzioni di materia dense, come ad esempio le galassie, circondate da un mezzo intergalattico molto meno denso. Così è anche per le stelle all’interno delle galassie. Se però osserviamo porzioni molto ampie, in media la distribuzione di materia ci appare uniformemente distribuita ovunque. Come già detto, il primo trentennio del Novecento segna l’inizio della cosmologia moderna e si assiste al passaggio dai modelli cosmologici mitico‐religiosi‐descrittivi a quelli fisico‐
7
Elementi di cosmologia teorica matematici‐osservativi grazie ai lavori di Einstein, Hubble, Friedmann e molti altri. Einstein applica per primo la Relatività Generale al problema cosmologico, mentre Hubble, come visto precedentemente, dimostra che le galassie sono sistemi esterni alla Via Lattea ed in recessione da noi; da parte sua, Friedmann trova una soluzione delle equazioni di Einstein confrontabili con il principio cosmologico, ma in espansione. In fisica, generalmente, vengono introdotti dei principi spesso basati su idee di simmetria che riducono il numero di gradi di libertà da considerare. I primi cosmologi hanno costruito modelli semplificati per descrivere alcuni aspetti dell’Universo. Prima della scoperta dell’espansione dell’Universo, ad esempio, è stato proposto un modello cosmologico statico. Nel Modello Cosmologico Standard, l’espansione dell’Universo è descritta dalla variazione nel tempo di un parametro, il fattore di scala, che esprime appunto come varia nel tempo la distanza fisica tra due punti dell’Universo ed è lo stesso per ogni coppia di galassie. Risolvere la dinamica cosmologica vuol dire, in effetti, ricavare l’evoluzione temporale di questo fattore di scala dalle equazioni di Einstein. Tali equazioni collegano la distribuzione di energia, e quindi di massa, alle proprietà geometriche (curvatura) dello spazio‐tempo. 2.2
L’Universo statico Lo stesso Einstein modificò le equazioni di campo con l’aggiunta di un termine cosmologico, al fine di rendere statiche le soluzioni. Si possono studiare tali modelli cosmologici statici utilizzando la metrica ds 2 = eν (r )c 2 dt 2 − e λ (r ) dr 2 − r 2 dΩ 2 , (2.1) dove il primo termine indica che la sfera può evolvere nel tempo, il secondo, che la sfera può avere un raggio. Einstein ipotizzò che l’Universo fosse una sfera stazionaria, usando gli esponenziali per evitare l’annullamento del tempo e dello spazio. Considerando la condizione di conservazione dell’energia, si ricava dp 1
dν
+ ρc 2 + p
= 0 . dr 2
dr
(
)
(2.2) Si suppone che non ci siano in media gradienti di pressione, per cui (ρc
2
+p
) ddrν
= 0 . (2.3) Risolvere questa equazione significa determinare il tipo di Universo: 8 Elementi di cosmologia teorica dν
= 0 , dr
(ρc
2
)
+ p = 0 , dν
= 0 e ρc 2 + p = 0 , dr
(
)
universo di Einstein; (2.4) universo di De Sitter; (2.5) universo di Minkowski. (2.6) Consideriamo, anzitutto, l’Universo di Einstein. La (2.4) implica ν = cos t . Assumendo ν = 0 , possiamo effettuare la sincronizzazione degli orologi cosmici. Il modello ottenuto è statico ma non stabile. Si ricava dall’equazione: 1 ⎛
8πG ⎞
= ⎜ Λ − 4 p ⎟ , 2
R
c
⎝
⎠
Λ ≡ ΛE =
(2.7) 4πG
ρc 2 + 3 p . 4
c
(
)
(2.8) Inserendo la (2.8) nella (2.7), si ottiene per il raggio caratteristico R la seguente espressione 1
4πG
= 4 ρc 2 + p > 0. 2
c
R
(
)
(2.9) La costante cosmologica ha, quindi, l’effetto di bilanciare la forza gravitazionale che, da sola, provocherebbe il collasso dell’Universo. Λ E può essere valutata assumendo che l’Universo sia un “gas di galassie”, in modo da poter trascurare la pressione rispetto alle altre grandezze, quindi, in questo caso: ΛE =
4πG
ρ 0 c 2 , 4
c
(2.10) dove con ρ 0 si è indicato il valore presente di ρ . Sostituendo i valori numerici si ottiene: Λ E ≈ 10 −57 cm −2 , (2.11) da cui in termini di lunghezze: 1
R≈
ΛE
≈ 3 ⋅ 10 28 cm ≈ 10 4 Mpc . (2.12) Consideriamo, ora, l’Universo di Minkowski. Esso si ottiene imponendo che, oltre la condizione (2.4) e conseguentemente eν (r ) = 1 , si abbia anche: (ρc
2
)
+ p = 0 , ρc 2 = 0 , p = 0 . (2.13) In questo modo la (2.9) diventa: 1
4πG
= 4 ρc 2 + p = 0 2
c
R
(
)
(2.14) 9 Elementi di cosmologia teorica e ciò implica che: R → ∞ . (2.15) Si vede che: ⎞
⎟⎟ , ⎠
⎛ r2
e −λ = 1 − ⎜⎜ 2
⎝R
(2.16) da cui: ν
e =e
−λ
r2
= 1 − 2 → 1 . R
(2.17) Otteniamo, quindi, un universo piatto e vuoto, del tipo di Minkowski. Consideriamo, infine, l’Universo di De Sitter, per il quale: ρc 2 = 0 , p = 0 (2.18) Esso risulta interessante in quanto dall’ipotesi di un universo vuoto ( ρc 2 = 0 e p = 0 ), senza assumere la staticità, con dν
= 0 , risulta l’espansione dell’universo. Dalla (2.17) ricaviamo: dt
ρc 2 = − p ⇒ ρc 2 = 0 , p = 0 . (2.19) Dalle equazioni di Einstein, si ha: eν = e −λ = 1 −
r2
, R2
(2.20) dove: 1
Λ
= . 2
3
R
(2.21) 3
. Λ
(2.22) Ne segue: R=
Anche in questo caso il raggio dell’universo va come (Λ )
−1
2
. Il ruolo della costante cosmologica è, dunque, quello di definire un raggio. Con questi risultati è possibile riscrivere la metrica di De Sitter come: ds 2 = c 2 dt 2 − e
2 ct
R
(dr
2
)
+ r 2 dΩ 2 , (2.23) e si avrà, dunque, un’espansione esponenziale con un fattore di scala che dipende dal tempo: a (t ) = e
Λ
ct
3
. (2.24) 10 Elementi di cosmologia teorica (Si tratta di una soluzione diventata, poi, di fondamentale importanza per i modelli inflazionari.) In sintesi, i tre tipi sono: −1
1. universo di Einstein, Λ ≡ Λ E , a E ≡ Λ E 2 ; curvatura positiva; 1
⎤
⎡
2
Λ
⎛
⎞
⎢
2. universo di De Sitter, ρc = 0, p = 0, a(t ) = exp ⎜ ⎟ ct ⎥ ; vuoto in espansione; ⎢⎝ 3 ⎠ ⎥
⎦
⎣
2
3. universo di Minkowski, ρc 2 = 0, p = 0, eν = e − λ = 1 ; piatto e vuoto. 2.3
La metrica di Robertson‐Walker (e il modello di Einstein‐de Sitter) La Teoria della Relatività Generale viene utilizzata per descrivere l’Universo su grandi scale costruendo una metrica spazio‐temporale che soddisfi alle caratteristiche di omogeneità ed isotropia ottenute dai dati osservativi. Per poter scrivere le equazioni di Einstein per un Universo in accordo con la legge di Hubble, vengono trascurati i moti locali delle galassie rispetto al moto complessivo di espansione. Pertanto si utilizzano coordinate comobili, le quali seguono il moto complessivo che anima la materia dell’universo, in modo tale che l’espansione risulti non come un cambiamento della posizione relativa delle galassie, ma come un cambiamento della parte spaziale della metrica. Consideriamo, inoltre, l’Universo come un fluido continuo. Assegniamo ad ogni elemento del fluido le tre coordinate spaziali x α (α = 1,2,3) , dette coordinate comobili. Ogni punto dello spazio‐tempo può pertanto essere definito dalle coordinate x α ,corrispondenti all’elemento del fluido che sta passando per il punto. In tal modo le coordinate degli elementi fluidi non cambiano nel tempo. L’universo appare diverso a diverse distanze dall’osservatore comovente, in quanto la visione locale dell’Universo alle varie distanze è influenzata dal ritardo temporale della ricezione dei fotoni che viaggiano alla velocità della luce finita. Occorre, del resto, definire un tempo cosmico o universale, cui tutti gli osservatori possano riferirsi. Assumiamo, a tal fine, che al tempo t = 0 tutte le componenti materiali dell’Universo, le galassie, si siano sincronizzate su un tempo che chiamiamo appunto tempo cosmico t . Successivamente le diverse componenti materiali si sono evolute in modo indipendente, ciascuna con un tempo proprio τ , misurato da un orologio a riposo con la materia circostante. In ciascun punto il tempo proprio τ coincide con il tempo cosmico t , ma non con il tempo di un osservatore 11 Elementi di cosmologia teorica lontano a causa dei ritardi nella trasmissione dei segnali. Tuttavia la sincronizzazione iniziale permette, sulla base della legge di evoluzione cosmologica data dal modello utilizzato, di ricavare i ritardi degli osservatori lontani e ricondurre gli eventi al tempo cosmologico. Si può pertanto descrivere l’evoluzione dell’Universo utilizzando un sistema di riferimento basato su coordinate comoventi con la materia rispetto alla quale gli osservatori siano a riposo e utilizzando il tempo proprio come tempo cosmico. Le proprietà geometriche dello spazio‐
tempo vengono descritte da una metrica e la metrica spazio‐temporale più generale che descrive un universo che rispetti il Principio Cosmologico è quella di Robertson‐Walker: 2
2
2 ⎡ dr
ds 2 = (cdt ) − a (t ) ⎢
+ r 2 dϑ 2 + sin 2 ϑdϕ 2
2
⎣1 − kr
(
)⎤⎥ , ⎦
(2.25) dove abbiamo usato le coordinate sferiche polari (r , ϑ , ϕ ) quali coordinate comoventi ( r è, per convenzione, adimensionale). L’elemento ds 2 separa due punti che hanno coordinate x = (t , r , ϑ , ϕ ) , dove t è il tempo proprio, mentre a (t ) è una funzione che ha le dimensioni di una lunghezza ed è chiamata fattore di scala cosmico o parametro di espansione. Il parametro di curvatura k è una costante che può assumere valori 1, 0, o ‐1. In particolare, per un fluido perfetto omogeneo ed isotropo con densità di energia ρc 2 e pressione p , le soluzioni delle equazioni di Einstein sono le equazioni di Friedman: . 2
a −
1
(8πGρ + Λ )a 2 = −kc 2 , 3
(2.26) ..
4 ⎛
3p ⎞ 1
a
= − πG⎜ ρ + 3 2 ⎟ + Λ , 3 ⎝
a
c ⎠ 3
(2.27) dove, in base alla (3.1), a = a (t ) è proprio il fattore di scala dell’Universo, k è la costante di curvatura uguale a ‐1, 0 o 1, rispettivamente per una geometria negativamente curva, spazialmente piatta o positivamente curva, ρc 2 è la densità di massa‐energia dell’Universo e p è la pressione, mentre con i punti rappresentiamo le derivate rispetto al tempo proprio cosmologico. Λ è la costante cosmologica, inizialmente introdotta da Einstein per rendere statiche le soluzioni cosmologiche e considerata da lui stesso “il più grande errore della sua vita” dopo la scoperta dell’espansione cosmologica da parte di Hubble. Negli ultimi anni, invece, (grazie alla proposta dei modelli inflazionari e l’introduzione dell’energia oscura) la 12 Elementi di cosmologia teorica costante cosmologica è diventata un ingrediente fondamentale per la cosmologia moderna, poiché è un termine che fornisce un’accelerazione. Inoltre, bisogna considerare l’equazione per la conservazione dell’energia (tensore energia‐
impulso della materia che, per un fluido perfetto, si riduce agli elementi della diagonale principale) ⎛.⎞
a
ρ c + 3⎜⎜ ⎟⎟(ρc 2 + p ) = 0 , ⎜a⎟
⎝ ⎠
.
2
(2.28) e la condizione (equazione di stato) di fluido perfetto: p = γρc 2 , (2.29) con 0 ≤ γ ≤ 1 , intervallo di Zeldovic, intervallo per il quale il nostro fluido è definibile come fluido perfetto standard. Le equazioni (2.26), (2.27), (2.28), (2.29) rappresentano le equazioni del modello cosmologico standard. Analizziamo alcune soluzioni delle equazioni cosmologiche. (Assumiamo c 2 = 1 .) Ottenere ⎧
⎩
⎫
⎭
informazioni su ⎨a, a, ρ 0 , p 0 ⎬ e, indipendentemente, su {Λ, k , γ } significa assegnare un .
modello cosmologico. Gli universi di Einstein‐de Sitter sono semplici modelli cosmologici in cui si assume che: 1. la metrica dello spazio‐tempo sia di Friedmann‐Robertson‐Walker; 2. la materia sia un fluido perfetto; 3. la costante cosmologica sia nulla (Λ = 0 ) ; 4. i modelli siano spazialmente piatti (k = 0 ) . ⎛
⎝
⎞
⎠
Risolvere le equazioni in tal caso significa trovare a (t ) = a⎜ t ; a 0 , a 0 , ρ 0 , Λ, k , γ ⎟ e .
ρ (t ) = ρ ⎛⎜ t ; a 0 , a , ρ 0 , Λ, k , γ ⎞⎟ . .
⎝
0
⎠
Dall’equazione per la conservazione dell’energia (2.28) e moltiplicando per il volume comobile a 3 , otteniamo: ρ ⎛ a0 ⎞
=⎜ ⎟
ρ0 ⎝ a ⎠
3(γ +1)
. (2.30) 13 Elementi di cosmologia teorica Sostituendo nella (2.26), con Λ = 0 , e k = 0 , si ricava: . 2
k 0 = a a (3γ +1) , (2.31) d ⎡ 2 (γ +1) ⎤
⎢a
⎥ = cos t . dt ⎣
⎦
(2.32) e, quindi, 3
Integrando questa equazione, si ha: 3
a2
(γ +1)
= ct + b . (2.33) Assumendo b = 0 , in modo che si abbia a = 0 per t = 0, si ricava infine: a ⎛t
=⎜
a 0 ⎜⎝ t 0
2
⎞ 3(γ +1)
⎟⎟
⎠
(2.34) che diventa: a(t ) ∝ t
⎛ 2 ⎞
⎜⎜
⎟⎟
⎝ 3(γ +1) ⎠
. (2.35) ρ (t ) ∝ a −3(γ +1) , (2.36) Si ha, così: e dalla seconda equazione di Friedmann possiamo, poi, ricavare la curvatura, definendo la densità critica: 2
⎛.⎞
3 ⎜a⎟
ρc ≡
. 8πG ⎜⎜ a ⎟⎟
⎝ ⎠
(2.37) Lo spazio è chiuso (k = 1) , aperto (k = −1) o piatto (k = 0 ) se il parametro di densità: Ω(t ) =
ρ
ρc
(2.38) è maggiore, minore od uguale ad uno. Definendo la densità adimensionale di energia relativa alla costante cosmologica al tempo Λ
kc 2
corrente come Ω Λ ≡
, così come quella della curvatura, Ω k ≡ 2 e della materia 3H 02
H0
ρ
ordinaria Ω m ≡
ρc
⎛
3H 02 ⎞
⎜
⎟ , si può (con la prima) considerare la presenza di ‘energia ⎜ ρc ≡
⎟
G
8
π
⎝
⎠
14 Elementi di cosmologia teorica oscura’ nell’Universo. Essa, nell’espansione, diventa prima o poi dominante sugli altri termini. La prima equazione di Friedmann può scriversi sinteticamente come: Ω m + Ω Λ + Ω k = 1 . (2.39) A seconda dei momenti nella storia evolutiva dell’Universo, uno dei tre termini viene a dominare sugli altri due. Ω k = 0 implica un Universo piatto, nel quale la densità di energia della materia insieme a quella relativa alla costante cosmologica è uguale alla densità critica. Il fatto che una maggiore o minore densità di materia‐energia incurvi di più o di meno lo spazio‐tempo, vuol dire che la possibilità di avere un Universo spazialmente aperto o chiuso dipende proprio dalla densità di materia‐energia. Se la densità è al di sopra di un certo valore critico, le forze attrattive delle varie parti dell’Universo tenderanno a fermare la recessione delle galassie, fino a generare un processo di contrazione cosmica contrario all’espansione. Se la densità è al di sotto o uguale ad un certo valore critico, la forza attrattiva è insufficiente e l’espansione continuerà per sempre. Tale valore critico della densità è stato già introdotto per definire Ω m ed è direttamente desumibile dalla prima equazione di Friedman per Λ = 0 e k = 0 , al tempo presente. Esso è dell’ordine di 10 −29 h 2 grcm −3 (dove h ≡
H0
km −1 sMpc ), 100
corrispondente a circa 3 atomi di idrogeno per un volume di mille litri di spazio. 2.4
La costante di Hubble Consideriamo la metrica di Robertson‐Walker. Ponendo dt = 0 introduciamo la distanza propria, d p , di un punto P da un altro punto P0 necessario per definire l’origine di un insieme di coordinate polari r , ϑ , ϕ , vale a dire la distanza (misurata da osservatori) che collega P a P0 al tempo t , ottenuta ponendo dϑ = dϕ = 0 r
dp = ∫
0
adr '
(1 − kr )
'2
1/ 2
= af (r ) , (2.40) 15 Elementi di cosmologia teorica dove la funzione f (r ) è, rispettivamente, f (r ) = sin −1 r (2.40a) f (r ) = r , (k = 0) (2.40b) f (r ) = sinh −1 r (2.40c) La distanza propria al tempo t si può relazionare a quella del tempo presente t 0 d p (t 0 ) = a 0 f (r ) =
a0
d p (t ) , a
(2.41) dove a 0 rappresenta il valore di a (t ) in t = t 0 . Possiamo definire, invece di una coordinata comobile r , una coordinata comobile radiale di P , definendo una distanza comovente d c ≡ a 0 f (r ) (2.42) In questo caso la relazione tra coordinate comobili e coordinate proprie diventa: dc =
a0
dp a
(2.43) La distanza propria d p di una sorgente può cambiare nel tempo a causa della dipendenza temporale del parametro di espansione a . In questo caso una sorgente in P ha una velocità radiale, velocità propria, rispetto all’origine data da: .
.
.
d
a
v p (t ) ≡ d p (t ) = d p (t ) = a(t ) f (r ) =
d p (t ) dt
a(t )
(2.44) L’equazione (2.44) è la legge di Hubble e la quantità: a(t )
H (t ) =
a(t )
.
(2.45) è il parametro di Hubble (in quanto non costante nel tempo). Il valore di questo parametro valutato al tempo presente H (t 0 ) ≡ H 0 , è la ‘costante di Hubble’ e non è conosciuto in modo accurato. Attualmente, si ritiene che abbia un valore intorno a: H 0 ≅ 65kms −1 Mpc −1 . (2.46) L’equazione (2.44) si può, infatti, anche ricavare in un altro modo. Consideriamo un triangolo definito da tre punti spaziali O, O’ e P. Assumiamo che questi punti siano abbastanza vicini gli uni agli altri, in modo da poter trascurare effetti di curvatura relativistici spazio‐temporali. Se l’Universo evolve in modo omogeneo ed isotropo, il triangolo OO’P deve essere sempre simile al triangolo originale. Questo significa che la 16 Elementi di cosmologia teorica a
. Di a0
lunghezza di tutti i lati deve essere moltiplicata per lo stesso fattore di scala conseguenza la distanza tra due punti deve essere moltiplicata per lo stesso fattore. Abbiamo quindi l=
a
l 0 , a0
(2.47) dove l 0 ed l sono le lunghezze del segmento di linea che congiunge due punti ai tempi t 0 e t , rispettivamente. Dalla (2.47) si ricava, così, la legge di Hubble (2.44). Una proprietà della legge di Hubble, implicita nel precedente ragionamento, consiste nel poter trattare ogni posizione spaziale come l’origine del sistema di coordinate. Riferendoci nuovamente al triangolo OO’P, abbiamo infatti v p = vo' + v p ' = Hr , (2.48)
così che: v p ' = H (r − d ) = Hr ' , (2.49) che rappresenta la legge di Hubble, espressa nel punto O’. Dalla definizione del parametro di Hubble (2.45) e considerando la (2.35), ricaviamo 1+ 3γ
−
2
a=
t 3(1+γ ) 3(1 + γ )
.
(2.50) Pertanto la (2.45) diventa: H=
2
. 3(1 + γ )t
(2.51) Il parametro di Hubble H (t ) misura la velocità di espansione in ogni istante di tempo t , per ogni modello che rispetti il Principio Cosmologico. Quindi la sua variazione nel tempo dipende dal contenuto energetico dell’Universo. La (2.51) consente di ricavare il valore attuale del parametro di Hubble, ossia la costante di Hubble H0 =
2
. 3(1 + γ )t 0
(2.52) Otteniamo, quindi, il “tempo di Hubble”: 17 Elementi di cosmologia teorica t0 =
2
−1
H 0 , 3(1 + γ )
(2.51) che dipende dal tipo di fluido considerato tramite γ . .
Poichè il rapporto tra a ed a è dato dall’equazione (2.51) per la densità ρ si ottiene l’espressione: ρ (t ) =
1
2
6πG (1 + γ ) t 2
(2.52) In breve, i modelli di Einstein‐de Sitter sono assegnati dalle soluzioni: a ⎛t
=⎜
a 0 ⎜⎝ t 0
2
⎞ 3(γ +1) ρ ⎛ a 0 ⎞
⎟⎟
, =⎜ ⎟
ρ
⎝ a ⎠
0
⎠
3(γ +1)
, 3(1+γ )
t
2
2
−
−1
= (1 + z ) 2 , H =
H 0 , , t 0 =
3(1 + γ )t
3(1 + γ )
t0
ρ (t ) =
1 + 3γ
1
, q =
. 2 2
2
6πG (1 + γ ) t
(2.53) Distinguiamo tre principali casi caratterizzati dal valore di γ : 1. γ = 0 (polvere); 2. γ =
1
(radiazione); 3
3. γ = 1 (stiff‐matter). Nel caso 1. l’universo è dominato da polvere con pressione nulla, vale a dire materia non relativistica (barioni). La soluzione è data da: 2
3
a ≈ t , ρ ≈ a −3 , t = t 0 (1 + z ) 2 , H =
−
3
2
2 −1
1
1
, t 0 = H 0 , ρ (t ) =
, q = (2.53) 2
3t
3
2
6πGt
Nel caso 2. l’universo è dominato da materia relativistica (fotoni o neutrini). La soluzione è data da: 1
a ≈ t 2 , ρ ≈ a −4 , t = t 0 (1 + z ) , H =
−2
3
1
1 −1
, t 0 = H 0 , ρ (t ) =
, q = 1 (2.54) 2
2t
32πGt 2
Nel caso 3. l’universo è dominato da un fluido rigidissimo come potrebbe essere accaduto in epoche primordiali. La soluzione è data da: 1
3
a ≈ t , ρ ≈ a −6 , t = t 0 (1 + z ) , H =
−3
1
1
1 −1
, t 0 = H 0 , ρ (t ) =
, q = 2 (2.55) 3t
3
24πGt 2
Utilizzando l’equazione (2.34) e le sue espressioni derivate ricaviamo un’espressione per il “parametro di decelerazione” definito come: 18 Elementi di cosmologia teorica ..
q≡−
aa
. 2
a
..
a
1 + 3γ
. =−
=
2
2
aH 0
(2.56) Il fattore di scala cosmico si può espandere in una serie di potenze per tempi t vicini a t 0 : 1
⎡
⎤
2
2
a(t ) = a 0 ⎢1 + H 0 (t − t 0 ) − q 0 H 0 (t − t 0 ) + ...⎥ , 2
⎣
⎦
(2.57) dove q 0 = q (t 0 ) . Il parametro di Hubble ha le dimensioni di un inverso di un tempo; q , invece, è adimensionale. Introduciamo il redshift, una nuova variabile collegata al parametro di espansione a e osservabile direttamente. Infatti, gli Universi statici sono contraddetti proprio dall’evidenza osservativa del redshift delle galassie. Definiamo il redshift di una sorgente luminosa, ad esempio di una galassia distante, nel seguente modo: z=
λ0 − λe
, λe
(2.58) dove λ0 è la lunghezza d’onda di radiazione dalla sorgente osservata ad O, preso come origine del sistema di coordinate, al tempo t 0 ed emesso dalla sorgente al tempo precedente t e . La sorgente si muove con l’espansione dell’universo e si trova ad una distanza comovente r . La lunghezza d’onda di radiazione emessa dalla sorgente è λe . La radiazione viaggia lungo una geodetica dalla sorgente all’osservatore in modo tale che ds 2 = 0 e, quindi: t0
r
cdt
∫t a(t ) = ∫0
e
= f (r ) . dr
(1 − kr )
1
2 2
(2.59) f (r ) non cambia in quanto r è una coordinata comobile e sia sorgente che osservatore si muovono con l’espansione cosmologica: t e → t 0 , t e + δt e → t 0 + δt 0 . Sottolineiamo che δt e potrebbe essere diverso da δt 0 ma, per δt piccoli, si trova: δt e
a(t e )
Se, in particolare, δt =
1
νe
e δt 0 =
1
ν0
=
δt 0
a(t 0 )
. (2.60) , avendo indicato con ν e e ν 0 le frequenze della luce emessa e osservata, rispettivamente, avremo: 19 Elementi di cosmologia teorica ν e a = ν 0 a 0 , (2.61) o, in modo equivalente, a
λe
=
a0
. (2.61) a0
. a
(2.62) λ0
Ricaviamo, dall’equazione (2.61): 1+ z =
Mettendo il redshift, così definito nell’equazione (2.57) otteniamo 1 ⎞
⎛
2
z = H 0 (t 0 − t ) + ⎜1 + q 0 ⎟ H 02 (t 0 − t ) + ... 2 ⎠
⎝
(2.63) da cui: t0 − t =
1
H0
⎡ ⎛ 1 ⎞ 2
⎤
⎢ z − ⎜1 + 2 q0 ⎟ z + ...⎥ . ⎠
⎣ ⎝
⎦
(2.63) Adesso, si può dare l’espressione di r in funzione di z . Ricordando che, per un raggio luminoso vale la (2.62), possiamo usare le equazioni (2.62) e (2.63), ed avere r=
c ⎡
(t 0 − t ) + 1 H 0 (t 0 − t )2 + ...⎤⎥ . ⎢
a0 ⎣
2
⎦
(2.65) Sostituendo l’equazione (2.63) nella equazione (2.65) otteniamo infine z=
c
a0 H 0
1
⎡
(1 + q0 )z 2 + ...⎤⎥ . z
−
⎢
2
⎦
⎣
(2.66)
20 CAPITOLO 3 Misure della costante di Hubble 3.1
La misura delle distanze in cosmologia Le distanze delle nebulose extragalattiche dipendono dall’applicazione dei criteri di luminosità assoluta a stelle i cui tipi possano essere riconosciuti. Queste includono, tra le altre, variabili Cefeidi, novae e stelle blu. I valori numerici dipendono dal punto zero della relazione periodo‐luminosità per le Cefeidi. Questo metodo è ristretto a poche nebulose la cui risoluzione risulta buona considerando gli strumenti esistenti. Le luminosità apparenti delle stelle più luminose in tali nebulose forniscono stime delle distanze di tutti i sistemi extragalattici nei quali anche poche stelle possano essere rivelate. Le luminosità apparenti principali delle nebulose stesse offrono stime ragionevoli delle distanze principali. I dati nell’articolo originale di Hubble [1] indicavano una correlazione lineare tra distanze e velocità. Sarebbero stati necessari nuovi dati su oggetti più distanti per ridurre, però, gli effetti del moto peculiare. Le velocità radiali di 46 nebulose extragalattiche erano utilizzabili, anche se le distanze individuali erano stimate solo per 24. Le 22 nebulose per le quali le distanze non risultavano utilizzabili furono trattate in due modi. La distanza principale del gruppo derivata dalle magnitudini apparenti è paragonata con la principale delle velocità 21
Misura della costante di Hubble corrette per il moto solare, mentre le distanze furono calcolate da queste ultime, ricavando così la magnitudine assoluta dalla magnitudine apparente. Nel dopoguerra, con l’utilizzo dei telescopi da 4 metri, l’analisi del flusso di Hubble fu spinta oltre i 10 Mpc, grazie al lavoro dei gruppi guidati da de Vaucouleurs e da Sandage & Tammann. Il valore di H 0 , al finire degli anni Cinquanta, era sceso sotto i 100 (km/s)/Mpc, con Sandage & Tammann che lo portavano fino a 50‐55 (km/s)/Mpc. Questa fu la vera scoperta del flusso di Hubble. Per parametrizzare la costante di proporzionalità della legge di Hubble, si pone H 0 = 100h(km s )Mpc , dove h è il parametro di Hubble adimensionale. I dati più recenti danno h ≈ 0.72 ± 0.03 , un valore cui si arriva convolvendo i risultati di diverse tecniche, per esempio usando i dati sullo spettro della anisotropie della CMB (la radiazione di fondo a 2.73 K). Ma il modo principale resta comunque l’utilizzo di dati sul moto delle galassie più lontane, perché le velocità di allontanamento effettivamente osservate v = H 0 d + v p cos ϑ siano poco inquinate dal rumore dovuto alle velocità peculiari v p di cui conta la proiezione nella direzione di vista, con ϑ l’angolo tra v p e tale direzione). La velocità peculiare della Via Lattea, per esempio, è circa un millesimo delle velocità della luce c, quindi ~300 km/s; si tratta di un valore abbastanza tipico e si può notare che H 0 d raggiunge un valore ~300 km /s a una distanza d h ≈ (3 h )Mpc . Per h ≈ 0.71 è d h ≈ 5Mpc , sicché un segnale significativo sul flusso di Hubble si ha oltre i 10 Mpc, mentre non vi è nessun segnale del genere sotto i 5 Mpc. A conferma dell’impossibilità di confrontare l’equazione v = H 0 d con i dati di Hubble, sta il valore allora fornito per H₀: sia pure rinormalizzandolo in modo da scontare l’errore sulla distanza delle stelle cefeidi, che Hubble e Humanson usarono come indicatori di distanza, si ottiene ~ 170 (km/s)/Mpc. Se quel valore fosse vero, l’età del cosmo sarebbe di 6 miliardi di anni; cosa assurda,visto che in esso vi sono sicuramente stelle più vecchie di 10 miliardi di anni. A distanza di ottant’anni, disponiamo oggi di campioni statisticamente ben selezionati, che includono galassie fino a distanze anche maggiori di 1 Gigaparsec, mille volte più lontane di quelle viste da Hubble allora. Oltre a confermare la coerenza del flusso di Hubble, l’analisi di questi campioni permette di confermare le ipotesi su cui si basano i modelli relativistici. (In 22 Misura della costante di Hubble primis, è confermato che, salendo di scala, ci si approssima sempre più a un regime di isotropia e omogeneità.) A questo proposito, va citato l’articolo di Hubble del 1931 [2], nel quale sono discussi i metodi per determinare le distanze di nebulose extragalattiche e la magnitudine assoluta media è riesaminata sulle basi sia della revisione di Shapley del punto zero della curva periodo‐luminosità per le Cefeidi che di osservazioni più ampie di stelle coinvolte nelle nebulose. 3.2
Definizioni di distanza Il sistema di coordinate comobili che abbiamo adottato precedentemente si riferisce alla distanza propria d p negli spazi descritti dalla metrica di Robertson‐Walker. Non possiamo misurare in modo diretto, però, tale distanza propria d p per gli oggetti astronomici in modo diretto. Oggetti distanti sono osservati solo attraverso la luce che emettono in un tempo finito e le misure vengono fatte solo lungo l’insieme di traiettorie luminose che ci giungono dal passato, il cono luce passato. Imtroduciamo, quindi, alcuni tipi di distanza che sono di solito direttamente misurabili. Consideriamo, anzitutto, la distanza di luminosità d L 1
⎛ L ⎞2
dL ≡ ⎜
⎟ , ⎝ 4πl ⎠
(3.1) dove L indica la potenza emessa da una sorgente da un punto P che si trova ad una distanza r , al tempo t ; l rappresenta la potenza ricevuta per unità di area (il flusso) al tempo t 0 da un osservatore posto in un altro punto P0 . L’area di una superficie sferica centrata in P e passante attraverso P0 al tempo t 0 è 4πa 02 r 2 e i fotoni emessi dalla sorgente arrivano su questa superficie redshifttati dall’espansione dell’Universo di un fattore a
. a0
Troviamo, quindi: L
l=
4πa 02 r 2
⎛ a
⎜⎜
⎝ a0
2
⎞
⎟⎟ , ⎠
(3.2)
23 Misura della costante di Hubble dalla quale ricaviamo: d L = a02
r
. a
(3.3) Da quest’ultima equazione si ottiene: dL =
c
H0
(
)
1
⎤
⎡
2
⎢ z + 2 1 − q 0 z + ...⎥ , ⎦
⎣
(3.4) in contrasto con la definizione di distanza propria data precedentemente, che ha la forma d p = a 0 r , con f (r ) data dalle equazioni (2.40) del cap. 2. Definiamo, ora, la distanza diametro angolare d A . Indicando con D P (t ) il diametro proprio di una sorgente posta nella coordinata r al tempo t , sia Δϑ l’angolo sotteso da D P D p = arΔϑ . (3.5) Definiamo la distanza d A : dA =
DP
= ar . Δϑ
(3.6) In accordo con il Principio Cosmologico, se i corpi celesti sono distribuiti in modo omogeneo ed isotropo su larga scala, è interessante considerare la relazione m‐z tra magnitudine apparente m di una sorgente ed il suo redshift z , relazione importante in quanto fornisce anche un modo per determinare il parametro di decelerazione q 0 . Dalla (3.4), infatti, otteniamo: l=
LH 02
L
=
[1 + (q0 − 1)z + ...] . 4πd L2 4πc 2 z 2
(3.7) Di solito gli astronomi utilizzano non tanto la luminosità assoluta L e il flusso apparente l ma quantità collegate a queste: la magnitudine assoluta M e la magnitudine apparente m . La scala delle magnitudini è definita in modo logaritmico, prendendo un fattore 100 nel flusso ricevuto per considerare una differenza di 5 magnitudini. Il punto zero può essere fissato in diversi modi; per ragioni storiche, viene considerata la Polare, al fine di ottenere una magnitudine di 2.12 nella luce visibile. Si intende, per magnitudine assoluta, la magnitudine apparente che avrebbe una sorgente se fosse posta ad una distanza di 10 parsec. La relazione tra distanza luminosa di una sorgente, la sua magnitudine apparente m e la sua magnitudine assoluta M è data, quindi, dal modulo di distanza m − M = −5 + 5 log d L ( pc ) . (3.8) 24 Misura della costante di Hubble Usando l’equazione (3.7) troviamo: m − M ≅ 25 − 5 log10 H 0 + 5 log cz + 1.086(1 − q 0 )z + ... (3.9) con H 0 in kms‐1Mpc‐1 e c in kms‐1. Ricordiamo che 1 Mpc = 106 pc e che i logaritmi sono, spesso, definiti in base 10. Il comportamento di m( z ) è sensibile al valore di q 0 solo per z > 0.1. In realtà, però, ci sono molti altri fattori che intervengono in questo tipo di analisi. L’equazione (3.9) nel regime in cui possa considerarsi accurata, vale per z > z max ~ 0.2 e fornisce una stima di H 0 insieme alla forte conferma della validità della legge di Hubble e, quindi, del Principio Cosmologico. 3.3
Fenomenologia e misura Le prime determinazioni di distanza includono quelle delle galassie NGC 6822, M33 e M31 e la stima della costante di Hubble negli ultimi 20 anni è risultata compresa in un intervallo tra 70 e 75 km s ‐1 Mpc‐1. Hubble, oltre a determinare le distanze, considerò anche i redshift delle linee spettrali nello spettro delle galassie (misurati precedentemente da Slipher). In effetti, egli determinò una relazione lineare tra distanza e velocità di recessione delle galassie, proprio tramite l’esistenza di una relazione tra distanza e redshift. Mentre le velocità di recessione si misurano osservando un oggetto con delle righe di emissione tramite uno spettrografo che evidenzi l’eventuale effetto Doppler, la misura delle distanze è, invece, più complicata, nel senso che occorre una candela standard, vale a dire un oggetto di luminosità conosciuta, oppure una riga standard, vale a dire un oggetto che emetta ad una lunghezza d’onda conosciuta, per potere usare la sua luminosità apparente o dimensione angolare per calcolarne la distanza. Originariamente, Hubble usò le Cefeidi, particolari stelle variabili, per determinare le distanze. Esse sono stelle giganti blu. Il nome di questa classe di stelle deriva da δ Cephei, la prima variabile di questo tipo osservata nella nostra galassia. Successive osservazioni hanno, poi, individuato stelle Cefeidi in altre galassie, in primis nelle due nubi di Magellano, le più prossime a noi. La proprietà importante che definisce le Cefeidi è il tipo di pulsazioni, con la loro forma caratteristica, con una ripida crescita seguita da una graduale caduta, e un periodo direttamente proporzionale alla luminosità. Tale relazione periodo‐luminosità è 25 Misura della costante di Hubble stata scoperta da Leavitt studiando un modello di variabili Cefeidi nella Grande Nube di Magellano (LMC). 3.4
Metodi locali e Cefeidi In linea di principio, una misura della costante di Hubble può essere fatta tramite un singolo oggetto il cui spettro riveli la sua velocità di recessione e la cui distanza o luminosità sia accuratamente conosciuta. In pratica, l’oggetto deve essere abbastanza lontano affinché il contributo dominante al moto sia la velocità associata all’espansione generale dell’Universo (il flusso di Hubble), che aumenta linearmente con la distanza, al contrario di altre velocità che derivano dall’ interazione gravitazionale con la materia vicina. Sfortunatamente, non ci sono oggetti la cui luminosità possa essere determinata in modo non ambiguo se osservata a distanze di decine di Mpc. Infatti, si utilizzano le misure di distanza di oggetti vicini per calibrare la luminosità degli oggetti più distanti. In questo modo, però, gli errori si propagano negli errori nella scala di distanza e, di conseguenza, nella costante di Hubble. L’intervallo di stime recenti per quest’ultima, così, va dai 60 ai 75 km s‐1 Mpc‐1. L’effetto di parallasse, d’altra parte, fornisce una misura attendibile di distanza solo per stelle vicine. Il moto della terra attorno al sole produce, infatti, un cambiamento apparente nella posizione di stelle vicine (rispetto a stelle che sono a distanze molto più grandi e appaiono fisse). Lo spostamento ha un periodo di un anno e un’ampiezza angolare nel cielo fornito dal rapporto tra la distanza Terra‐Sole e la distanza della stella. La definizione del parsec, in effetti, è la distanza che dà una parallasse di un arco secondo, ed è equivalente a 3.26 anni‐
luce, o a 3.09 · 1016 m. (Il campo delle misure di parallasse è stato recentemente rivoluzionato dal satellite Hipparco, che ha misurato migliaia di distanze di parallasse stellare, includendo le osservazioni di 223 Cefeidi Galattiche, 26 delle quali sono significative.) Poiché alcune stelle relativamente vicine si trovano in ammassi aperti, contenenti poche centinaia di stelle, esse possono essere riportate su un diagramma di Hertzsprung‐Russell, che fornisce la loro temperatura, dedotta dal colore tramite la legge di Wien in funzione della luminosità apparente. Questi diagrammi rivelano una sequenza caratteristica, la sequenza principale, che ordina dalle rosse deboli alle blu luminose. Questa sequenza corrisponde alla fase principale dell’evoluzione stellare e in essa le stelle si trovano per la maggior parte della 26 Misura della costante di Hubble loro vita, quando stanno bruciando costantemente idrogeno. Dato che, in alcuni ammassi vicini, abbiamo stelle considerabili sostanzialmente tutte alla stessa distanza e per le quali gli effetti di parallasse possono dare la distanza assoluta, la sequenza principale può essere calibrata in modo da predire la luminosità assoluta della stella della sequenza principale di un dato colore. Applicando questo anche ad altri ammassi, se ne può così ottenere la distanza assoluta. Inoltre, è possibile determinare la distanza di oggetti molto vicini, appena fuori della nostra stessa galassia, come le Nubi di Magellano Piccola (SMC) e Grande (LMC), usando vari calibratori, tra cui variabili Mira, stelle RR Lyrae e stelle variabili Cefeidi. Di queste, le Cefeidi sono le più intrinsecamente luminose ed, effettivamente, possono essere viste sia in LMC sia in galassie molto più distanti. Senza di loro, la connessione tra LMC e galassie esterne sarebbe difficile. Oggi, grazie ad Hubble Space Telescope (HST) le Cefeidi presenti in tali galassie possono essere identificate in modo molto attendibile. Quelle rivelate con il telescopio spaziale HST, in ogni caso, non permettono misure dell’espansione dell’Universo, in quanto non sono abbastanza distanti perché la velocità dominante sia quella del flusso di Hubble. Infine, le distanze misurate con le Cefeidi servono a calibrare altri indicatori. Il più importante tra questi in cosmologia è dato dalle supernovae di tipo Ia (SNe), che possono essere osservate a grandi distanze, permettendo un paragone tra redshift e distanza, da cui ricavare il valore della costante di Hubble. Le SNe di tipo Ia sono prodotte da sistemi binari nei quali una stella gigante perde massa verso una nana bianca. Sebbene la luminosità assoluta di un’esplosione che così viene a determinarsi non sia costante, le supernovae di tipo Ia hanno curve di luce simili tra loro. Indicatori alternativi che possono essere usati al posto delle SNe Ia per la determinazione di H 0 si basano sulla correlazione di alcune proprietà di galassie facilmente osservabili con la loro luminosità. Ad esempio, la velocità di rotazione v di taglio delle galassie a spirale va con la luminosità L come L α v4 , (3.10) relazione di Tully‐Fisher. In modo equivalente, per le galassie ellittiche esiste una relazione,nota come relazione di Faber‐Jackson, tra la dispersione di velocità centrale σ e la magnitudine totale L B , 27 Misura della costante di Hubble L B α σ 4 . (3.11) Altre proprietà misurabili di galassie ellittiche che si correlano bene con la luminosità possono essere poste, inoltre, sul cosiddetto “piano fondamentale”. Esso collega tre proprietà: la luminosità, il raggio effettivo re , vale a dire il raggio entro il quale è emessa metà della luce della galassia, e la dispersione di velocità stellare centrale. Se si rappresentano le galassie ellittiche in uno spazio a tre dimensioni in base alla loro luminosità L , alla dispersione di velocità centrale σ 0 e alla brillanza superficiale Σ e , si scopre che esse non si distribuiscono su tutto il volume ma definiscono un piano particolare, detto appunto piano fondamentale, la cui importanza deriva proprio dal fornire un collegamento diretto tra i parametri fisici fondamentali delle galassie: −1
⎛ c ⎞⎛ M ⎞
−1
2
⎟⎜ ⎟ σ 0 Σ e ⎝ 2π ⎠⎝ L ⎠
re = ⎜
(3.12) dove re e σ 0 sono misurabili. (Le stelle nelle galassie più vicine presentano maggiore irregolarità nella distribuzione della luminosità superficiale.) 3.5
Problemi di misura La distanza di LMC è probabilmente la meglio conosciuta e dà la parte meno controversa della scala della distanza. Calibrazioni indipendenti, che usano variabili RR Lyrae, Cefeidi e ammassi aperti, risultano consistenti con una distanza di ~ 50 kpc per LMC. Mentre tutti i singoli metodi hanno errori sistematici, il loro accordo entro gli errori fa comunque pensare ad una misura corretta. (Inoltre, è stata fatta una misura indipendente usando la supernova di tipo 2 1987A in LMC.) La distanza da LMC più adottata è tra 18.50 e 18.54 in unità di modulo di distanza e corrisponde, come già detto, ad una distanza di 50‐51 kpc. Il probabile errore in H 0 di ~ 2% è ben al di sotto del livello degli errori sistematici (in altre parti della scala di distanza). Se la relazione periodo‐luminosità fosse perfettamente lineare e universale, vale a dire se potessimo applicarla in tutte le galassie e in tutti gli ambienti, il problema di trasferire la distanza LMC verso galassie esterne sarebbe semplice. Problemi che coinvolgono la fisica e la 28 Misura della costante di Hubble fenomenologia delle Cefeidi, in effetti, costituiscono una parte cospicua di errore e rappresentano la prima sorgente di differenze nei valori derivati di H 0 . La differenza tra luminosità delle Cefeidi LMC e Galattiche può raggiungere 0.3 magnitudini, corrispondenti ad una differenza del 15% nelle distanze dedotte. Almeno una parte di questa differenza è quasi certamente dovuta ad effetti di metallicità. (Il termine “metalli” si riferisce ad ogni elemento più pesante dell’elio.) Uno dei metodi più promettenti per determinare direttamente le distanze è fornito dalle stelle binarie separate ad eclisse. Nelle stelle binarie vicine, dove le componenti possono essere risolte, una stima della distanza permette infatti la determinazione della separazione angolare, il periodo e l’ampiezza della velocità radiale; in stelle binarie ad eclisse più distanti, ossia in altre galassie, la separazione angolare non può essere misurata direttamente, ma se potessimo ottenere la luminosità superficiale stellare (ad esempio, dallo studio delle linee spettrali), insieme alla conoscenza del raggio stellare e del flusso osservato ricevuto da ogni stella, potremmo ottenere una determinazione di distanza. (Questo metodo è stato usato per ricavare la distanza da M33 di 964 ± kpc.) Un altro metodo che coinvolge le rotazioni di stelle attorno al centro di una galassia distante è il metodo della parallasse rotazionale, dove vengono osservati sia il moto proprio, corrispondente alla rotazione circolare, sia la velocità radiale di stelle nella galassia. Va sottolineato che analisi indipendenti degli stessi dati, ottenuti anche con lo stesso metodo, danno spesso valori differenti. Considerando la fotometria, si assume che la differenza tra LMC e le relazioni P‐L (periodo‐
luminosità) galattiche sia dovuta interamente alla metallicità. Sebbene la correzione di metalliticità dipendente dal periodo sia un effetto determinante, comunque, ci sono altre differenze che rendono H 0 diverso di pochi percento nelle varie misure. Si tenga, poi, conto che è più difficile vedere Cefeidi deboli. Sono state viste, infatti, solo cefeidi più luminose e di breve periodo; quindi dalla relazione P‐L nelle galassie distanti risulta una sottostima delle distanze. Trascurando i bias si ottengono differenze di diversi percento, ma è difficile quantificare questo fattore. In sintesi, misure di distanze locali convergono entro il 15%, una prova del fattore 2 di incertezza che ha prevalso fino agli ultimi anni Ottanta. (Sono possibili altre prove che 29 Misura della costante di Hubble coinvolgono, però, errori sistematici significativi e, in particolare, richiedono un accordo generale sulla fisica degli effetti di metallicità sulle relazioni P‐L delle Cefeidi.) Attualmente, l’assunzione di un Universo spazialmente piatto comporta H 0 = 73 ± 3Kms −1 Mpc −1 . Assumendo un Universo non esattamente piatto, otteniamo una degenerazione in H 0 , nel senso che ogni sua decrescita di 20 Kms −1 Mpc −1 aumenta la densità totale dell’Universo di 0.1 in unità di densità critica. Studi di supernovae a redshift cosmologici hanno dimostrato che esse sono più deboli di quanto atteso considerando corretto il modello spazialmente piatto di Einstein‐de Sitter, per il quale Ω m = 1 e Ω Λ = 0 . Se consideriamo l’Universo non esattamente piatto, viene raggiunta una misura (con un errore del 5%) di H 0 = 71.6 +−44..73 Kms −1 Mpc −1 . 3.6
Relazioni Periodo‐Luminosità e Periodo‐Luminosità‐Colore delle Cefeidi nelle Nubi di Magellano Nel 1912 Leavitt annunciò la scoperta della relazione P‐L ed essa è ancora dibattuta. Sebbene determinata facilmente attraverso i periodi delle Cefeidi, è difficile accertare la luminosità di Cefeidi Galattiche, a causa della loro distanza dalla Terra e del loro alto arrossamento. Inoltre, il punto zero della relazione P‐L dipende dalla metalliticità. L’HST ha scoperto molte Cefeidi che possono essere usate per completare la calibratura delle relazioni P‐L e P‐L‐C. Un uso più importante di queste consiste, come già detto, nel determinare la costante di Hubble H 0 , il cui valore deve essere ancora rifinito. Le Nubi di Magellano hanno vantaggi su altri oggetti per quanto riguarda la calibratura delle relazioni P‐L‐C e P‐L delle Cefeidi. Sono state rivelate Cefeidi adatte ad analizzare le calibrature delle Cefeidi anche nella nostra galassia ma, purtroppo, sono ancora poche. D’altro canto, le Nubi di Magellano sono vicine e contengono Cefeidi. Esse sono omogenee nella loro composizione chimica, permettendo errori piccoli dovuti alla metallicità. Un altro gruppo di calibratori è costituito dalle giganti rosse, che sono abbondanti vicino al Sole (la loro calibratura può essere verificata con misure di parallasse con il satellite Hipparco). Sono abbastanza luminose da essere viste più da lontano e sono presenti in grande quantità in LMC e SMC. La loro magnitudine di banda I è inoltre largamente 30 Misura della costante di Hubble indipendente dall’età. Nelle Nubi di Magellano possono avere distribuzioni spaziali diverse rispetto alle Cefeidi; possono esistere, quindi, errori sistematici. A loro volta questi ultimi implicano errori nelle distanze di galassie e, di conseguenza, un errore risultante in H 0 . Le Cefeidi nella nostra galassia non possono essere usate per calibrare le relazioni in quanto lontane dal Sole. Vengono allora usati altri metodi con stelle binarie che si eclissano, metodo che usa le stelle RR Lyr, metodo che usa gruppi di stelle rosse, comunque considerando le Nubi di Magellano le più adatte per la calibratura. È stata effettuata la media dei risultati ricavati da tutti questi metodi, ottenendo un valore del modulo di distanza da LMC pari a 18.22 ± 0.05 mag. 3.7
Metodo della lente gravitazionale Le lenti gravitazionali possono essere usate per determinare la costante di Hubble. Si sfrutta il fatto che la luce viene deviata dall’azione di un campo gravitazionale, così che l’osservatore nota effetti di distorsione o ingrandimento delle immagini che riceve. L’uso principale delle lenti gravitazionali consiste nel determinare le distribuzioni di massa nella galassia lente, dal momento che posizione e luminosità delle immagini portano informazioni sul potenziale gravitazionale della lente. Il lensing gravitazionale ha il vantaggio che questi effetti sono indipendenti dal tipo di materia, luminosa o oscura. In questo modo possono essere provati gli effetti di materia barionica o non barionica. Redsdal è stato il primo a notare che, se la sorgente è variabile, è possibile misurare una distanza assoluta nel sistema e, quindi, la costante di Hubble. Consideriamo le traiettorie luminose dalla sorgente all’osservatore corrispondenti a immagini individuali lensate; il tempo impiegato dalla radiazione sarà diverso per ognuna. La luminosità, quindi, raggiungerà l’osservatore a tempi diversi corrispondenti a traiettorie luminose diverse. Una misura del tempo di ritardo τ corrisponde a misurare la differenza tra tali tempi. Se i redshift di sorgente e lente sono noti, possiamo ricavare H 0 . Molti ritardi temporali sono stati misurati a lunghezze d’onda radio, dall’esame di quei sistemi nei quali un quasar fosse una sorgente ad immagini multiple. Di recente, hanno dominato ritardi otticamente misurati, dovuti all’utilizzo di un piccolo telescopio ottico in un luogo con un buon seeing per un monitoring fotometrico. Del resto, ritardi radio temporali richiedono grandi quantità di tempo su interferometri (long‐baseline) che non esistono in 31 Misura della costante di Hubble gran numero. Il problema con il ritardo temporale delle lenti sta nella forma del potenziale gravitazionale espresso dalle lenti. In aggiunta, tutta la materia lungo la linea di vista contribuisce al potenziale che determina il lensing in quanto, avendo ad esempio uno strato di distribuzione di massa uniforme in una regione, non interessano tanto le posizioni delle immagini e i flussi, che pure formano restrizioni sul potenziale del lensing, quanto i tempi di ritardo. Nonostante le difficoltà per ottenere modelli di massa dalle lenti, la misura di H 0 è migliorata in diversi modi. Alcune lenti hanno più costrizioni sul modello di massa di altre. Inoltre, è possibile usare le dispersioni di velocità stellare misurate nella galassia lente. Tali misure, però, non sono molto usate, sebbene i modelli di massa nelle galassie forniscano un valore di z di ~ 0.5, tipico delle galassie che fungono da lente. La combinazione di informazioni sul lensing e la dinamica stellare forniscono una misura che è in principio una costrizione diretta sulla massa. Il metodo ha grandi barre di errore dovute in parte alle dipendenze sulla forma delle orbite stellari ma anche perché queste misure sono difficili, visto che ogni galassia richiede circa una notte di buon seeing. Dobke e King hanno così ottenuto il valore H 0 = 72 ± 8kms −1 Mpc −1 , mentre analisi più recenti portano ad H 0 = 66 ± 3kms −1 Mpc −1 . In conclusione, il lensing ha cominciato a rendere un contributo utile ad H 0 , sebbene barre di errore siano probabilmente ancora simili a quelle dei metodi locali o CMB diversi anni fa. 3.8
Misura della costante di Hubble attraverso la relazione di Tully‐Fisher (TF) Molta cosmologia moderna si basa su una misura accurata delle distanze da sorgenti extragalattiche. Esse sono determinate usando una scala di distanza extragalattica EGL (extragalactic distance ladder), calibrata dalla distanza da stelle variabili Cefeidi in LMC. Questa stima della distanza è incerta e introduce, così, errori nelle determinazioni di distanze extragalattiche. Possiamo esaminare le Cefeidi in galassie a spirale distanti tramite la relazione di Tully‐Fisher, che mette in relazione la velocità rotazionale massima di una galassia a spirale con la sua luminosità. Questa relazione viene usata soprattutto 32 Misura della costante di Hubble nell’infrarosso, dove la relazione è indipendente dalla morfologia. Questo dà la possibilità di determinare la costante di Hubble in modo accurato. Uno scopo determinante dello Space Telescope Key Project è stato proprio quello di studiare più accuratamente suddetta relazione, con l’analisi di tre galassie per mezzo di telescopi terrestri, senza usare galassie con un angolo di inclinazione troppo alto o basso. Una parte del progetto riguarda i dati fotometrici. Le correzioni vanno riportate a tre sorgenti primarie: estinzione galattica, estinzione interna e correzione k . L’estinzione interna è ancora dibattuta a causa di incertezze nel sistema di classificazione morfologica. Per questo motivo sono state usate le correzioni derivate da Tully ed altri, in quanto non dipendenti dalla morfologia. Va comunque tenuto presente che la luce viaggia attraverso più polvere e gas in una grande galassia, nel qual caso è necessaria più correzione per l’estinzione. La più grande sorgente di errore nella relazione TF riguarda, invece, l’angolo di inclinazione della galassia, angolo determinato da un’analisi fotometrica. Le ampiezze delle linee devono essere corrette anche per il redshift. Una delle indagini più complete è stata fatta da Giovanelli (1997), basandosi sulla fotometria e sulle ampiezze delle linee radio. Questo esame riguarda 2000 galassie a spirale negli ammassi, lontane abbastanza da avere velocità di recessione di oltre 10.000kms‐1. Prendendo in media 15 ammassi di galassie si trova per H 0 un valore di 73 ± 2 (random) ± 9 (sistematico), attraverso l’esame della banda I, ottenendo un valore per la costante di Hubble abbastanza vicino a quello accettato. Un esame della banda H consente di ottenere un valore della costante di Hubble di 67 ± 3 (random) ± 10 (sistematico), valore molto diverso dal precedente. Al fine di spiegare queste differenze nel valore di H 0 è stata esaminata la relazione tra due misure di ampiezze di linea e la fotometria e poi la distribuzione di colore. Poiché H 0 non è sensibile alle diverse scale di distanza, si è analizzato il problema da un punto di vista fotometrico. La principale sorgente di errore è la differenza sistematica nella banda H dovuta ai diametri delle isofote, con una distribuzione di colore che gioca un ruolo importante. Sfortunatamente questi problemi non sono risolti se manca un insieme consistente di magnitudini nella banda H, difficile essendo il cielo più luminoso di 100 volte nella band H che in I. Questo va sottratto ai profili di luminosità superficiale nelle parti più esterne della galassia. Pertanto 33 Misura della costante di Hubble l’errore sistematico trovato è la causa di una sovrastima della distanza, ponendo così limiti alla precisione di misure di H 0 dallo studio di Tully‐Fisher. 3.9
L’uso del Piano Fondamentale e le relazioni Dn e σ La distanza delle galassie negli ammassi Leo I, Virgo e Fornax è calcolata usando il piano fondamentale (FP) e le relazioni Dn e σ . Queste ultime costituiscono indicatori di distanza secondari. Il piano fondamentale stabilisce una relazione tra raggio, luminosità ed energia cinetica media delle stelle nelle galassie ellittiche. La relazione tra luminosità L e distribuzione della velocità delle stelle in una galassia σ è stata scoperta da Faber e Jackson nel 1976. Questo ha permesso di usare galassie early‐type per misurare ammassi più distanti, calibrando la relazione FP usando galassie early‐type vicine che sono state studiate precedentemente, con distanze accurate ottenute da Cefeidi, ed estrapolando la relazione per galassie massive ad ammassi distanti. Il valore della costante di Hubble può essere derivato da queste distanze. Queste stime devono essere paragonate a quelle provenienti da altri metodi per trovare il valore più accurato di H 0 , aspettandosi che il flusso di Hubble domini le irregolarità della velocità locale. Al fine di stabilire una relazione tra misura angolare e distanza metrica per galassie in ammassi chiusi, sono state usate relazioni periodo‐luminosità di variabili Cefeidi. Usando la fotometria, il Piano Fondamentale e le relazioni Dn e σ sono calibrati usando galassie locali, calibrazione poi estesa agli ammassi Leo I, Virgo e Fornax per stabilire le distanze di galassie in questi ammassi e derivare un valorre di H 0 = 78 ± 5± 9 Kms‐1Mpc‐1. Nel 1987 Dressler introdusse la luminosità superficiale. Dn rappresenta il diametro di metà luminosità definito in modo tale che metà della luminosità totale di una galassia si trovi al suo interno. La relazione Dn ‐ σ usa la grandezza della galassia e la luminosità superficiale, insieme ad altri parametri usati per definire la relazione di Faber‐Jackson. Allo scopo di utilizzare le relazioni FP e Dn ‐ σ come indicatori di distanza, devono essere fatte due importanti assunzioni: i rapporti M L corrispondono a parametri di struttura nello stesso modo dappertutto e le galassie early‐type hanno una popolazione stellare simile per una galassia di massa data. I calcoli si basano su dati fotometrici e spettroscopici, tenendo conto 34 Misura della costante di Hubble che le misure spettroscopiche di σ dipendono sia dalla distribuzione delle orbite che dalla luce. La distanza può essere calcolata direttamente dal punto zero del Piano Fondamentale (log re) e dal piano fondamentale angolare ( log ϑe , dove ϑe è l’ampiezza angolare). Sono state effettuate correzioni sulla metalliticità nelle relazioni P‐L delle Cefeidi, per la campionatura dei bias che derivano dall’osservazione delle stelle più luminose nella galassie e per la coincidenza spaziale di galassie ellittiche e a spirale. Il valore finale adottato per la costante di Hubble è H 0 = 73 ± 4 ± 9kms −1 Mpc −1 . Errori sistematici derivano dall’incertezza nella distanza delle Nubi di Magellano e piccole incertezze nei calcoli del piano fondamentale, trovando un’incertezza totale di 11 %. 3.10 Una ricalibratura dalle Distanze delle Cefeidi alle Supernovae di Typo Ia Hubble Space Telescope Key Project, sulla scala delle distanze extragalattiche, ha inizialmente consentito di derivare distanze basate sulle Cefeidi da 7 supernovae di tipo Ia. Queste ultime sono caratterizzate da una luminosità significativa e da precisione di circa l’8% nelle misure di distanza sia nel vicino che nel lontano Universo. Si pensa che le supernovae di tipo Ia si formino da esplosioni termonucleari di una nana bianca che brucia nel suo nucleo elementi del gruppo del ferro (Ni, Co, Fe). Questa natura esplosiva è un risultato di materia instabile sottoposta ad una alta compressione gravitazionale i cui elettroni sono quasi relativistici. Le supernovae SNe Ia non sono più considerate candele standard di luminosità costante, ma con una evidente dispersione della luminosità del picco recentemente scoperto. Nel 1999 Philips e altri hanno scoperto una relazione tra magnitudine assoluta delle supernovae di tipo Ia e l’andamento della luminosità. Il valore di H 0 viene calcolato per le bande B, V ed I. Le supernovae di tipo Ia costituiscono lo strumento più attendibile per calcolare le distanze extragalattiche ed, infine, per determinare la costante di Hubble fornendo un valore pari a H 0 = 68 ± 2 (random) ± 5 (sistematico) kms‐1Mpc‐1, un risultato 35 Misura della costante di Hubble consistente con quelli basati sulla relazione di Tully‐Fisher e con le fluttuazioni di luminosità superficiale. Nel 1998, l’assunzione di un valore noto di H 0 ≈ 72 ha portato a scoprire, tramite le SNe Ia, un’accelerazione cosmica, spiegabile solo con l’introduzione di energia oscura (la cui forma più semplice è data dalla costante cosmologica Λ ) nell’Universo. 3.11 Costante di Hubble determinata con l’effetto Sunyaev‐Zel’dovich L’effetto Sunyaev‐Zel’dovich (SZE) fu scoperto analizzando gli effetti delle interazioni tra elettroni caldi in un mezzo intracluster (ICM) con fotoni appartenenti alla CMB (Sunyaev & Zel’dovich 1969, 1972). Gli ammassi di galassie, infatti, contengono gas caldi ( ≈ 6 ⋅ 10 7 K ) intrappolati nelle loro buche di potenziale, molto più calde della radiazione CMB ( ≈ 3K ). Una misura della costante di Hubble può essere ottenuta paragonando i dati riguardanti l’emissione di raggi x di un ammasso di galassie con l’effetto termico. Siccome i fotoni dalla CMB passano attraverso il caldo ICM, in un ammasso di galassie, alcuni di loro interagiscono con gli elettroni di alta energia e vengono diffusi in diverse direzioni. L’energia dal gas caldo IC viene trasferita alla radiazione CMB e una frazione dei fotoni sono spostati dal lato di Rayleigh‐Jeans (basse frequenze) al lato di Wien (alte frequenze) dello spettro di Planck. Questo processo è conosciuto come comptonizzazione. I fotoni, a causa dell’omogeneità e dell’isotropia generale di CMB, passano attraverso il gas dell’ammasso guadagnando energia. Di conseguenza lo spettro della CMB viene distorto ed essendo osservato come spettro di un corpo nero perfetto, si possono misurarne le variazioni, sebbene i rivelatori non possano percepire la piccola scala. Sunyaev e Zel’dovich interpretarono questa distorsione spettrale come un cambiamento relativo nella temperatura CMB. È necessaria la risoluzione della distanza diametro angolare d A in termini di quantità osservabili per determinare la distanza dall’ammasso e fare delle assunzioni su di esso al fine di determinare la distanza lungo la linea di vista dall’ammasso. Si assume infatti che il gas sia uniforme e, in equilibrio idrodinamico, distribuito in modo sferico per evitare complicazioni riguardanti l’anisotropia. 36 Misura della costante di Hubble Dal momento che gli ammassi di galassie utilizzati possono essere a redshift alti ( z ~ 0.55), la geometria dell’universo stesso può influenzare le osservazioni e, quindi, il valore dedotto dipende dal modello cosmologico. Osservazioni Chandra di tre ammassi hanno consentito di trovare un valore di H 0 pari a 69 ± 8 Kms‐1Mpc‐1 per Ω M =0.3 e Ω Λ =0.7, valori molto vicini a quello di Hubble Key Project. 3.12 Unione dei vincoli sulla costante di Hubble Uno dei traguardi principali di Hubble Space Telescope è stato quello di determinare la costante di Hubble con un’accuratezza inferiore al 10%. Osservando le Cefeidi in diverse galassie vicine devono essere considerati i moti su larga scala dovuti a fattori diversi dal flusso di Hubble. I vari moti che riguardano le velocità osservate di galassie includono la rotazione della nostra stessa galassia, il movimento della nostra galassia rispetto al centro del Gruppo Locale, la velocità del Gruppo Locale rispetto all’ambiente di microonde cosmico (CMB), l’inclusione del Gruppo Locale nel nucleo del superammasso locale e altri movimenti su larga scala. Per compensare queste velocità, devono essere fatte diverse modifiche alle velocità osservate, correggendole mediante un modello lineare multi attrattore, che corregge i movimenti dovuti alla nostra velocità verso ogni attrattore. Ne discende l’utilizzo della seguente equazione per determinare la velocità degli oggetti caratteristici dell’espansione dell’universo: Vcos mic = V H + Vc , LG + Vin ,Virgo + Vin ,GA + Vin , Shap + ... , (3.13)
dove V H è la velocità eliocentrica osservata, Vc , LG è la correzione per la velocità della Via Lattea attraverso il centro del Gruppo Locale e ognuna delle componenti Vin si riferisce alle velocità di caduta della galassia verso uno specifico attrattore. Ogni tecnica usata per determinare le distanze contiene, comunque, una percentuale di errore. Per calcolare la propagazione degli errori nelle stime delle distanze, è stato proposto un codice di simulazione per ricreare Key Project al computer. Alla fine, vengono combinati 37 Misura della costante di Hubble tutti i metodi, dando un peso maggiore al metodo delle supernovae di tipo Ia, determinando un valore finale per H 0 pari a 71 ± 6 Kms‐1Mpc‐1. Va notato, tra l’altro, che le distanze ottenute con variabili Cefeidi potrebbero essere intaccate da valori di metalllicità, fornendo un valore diverso per la costante di Hubble pari ad H 0 = 68 ± 6kms −1 Mpc −1 . La più importante incertezza nelle osservazioni rimane, in ogni caso, quella della distanza dalla Grande Nube di Magellano (LMC). La distanza adottata è normalmente di 50 Kpc (m‐M = 18.50 ± 0.13mag) e costituisce, da sola, il 6.5% di incertezza nelle misure. Un altro errore da notare riguarda, naturalmente gli strumenti usati.
38 CONCLUSIONE Molto succintamente, si può affermare che questo lavoro di tesi ha percorso alcuni dei punti salienti della cosmologia negli ultimi 80 anni. La nascita della astronomia extragalattica, con le misure di Hubble della distanza di M31 quale oggetto necessariamente al di fuori della Via Lattea, discende dall’amplificazione improvvisa di un campo d’indagine già allora ritenuto vastissimo. A questo, sempre con Hubble e la sua scoperta di una relazione tra le velocità di recessione delle galassie e le loro distanze, va aggiunta l’introduzione di un’espansione in cosmologia fino ad allora negata. Per comprendere l’importanza di ciò, basti ricordare che Hubble ha fatto gran parte delle sue più importanti scoperte dal 1929 al 1931, mentre Friedmann aveva scritto e risolto le sue equazioni per un Universo in espansione già nel 1921. Ma nessuno, e tanto meno Einstein, aveva badato a modelli allora puramente teorici, in un’epoca in cui l’Universo era ritenuto statico. Lo sviluppo tecnologico che da allora ad oggi continua ad accompagnare le ricerche astronomiche e cosmologiche non mancheranno, inevitabilmente, di sorprenderci ancora e richiederci nuovi modelli e mentalità aperta per interpretare dati non sempre prevedibili. 39
BIBLIOGRAFIA [1] E.Hubble, Proc.. Nat. Acad. Sci., 15, 168‐173 (1929) [2] E. Hubble and M. L. Humason, American Astronomical Society, 43‐80 (1931) [3] E. Damon, D. Eisler, D. Rasolt, A. Shawkyle Story, A. teymourian, and G. Vesper, Astronomy 233, 1‐61 (2004) [4] N. Jackson, Living Reviews in Relativity, 10, (2007), 1‐52 (2007) [5] J. S. Bagla, Physics.pop‐ph, 1‐10, (2009) [6] S. Bonometto, Cosmologia & Cosmologie, Zanichelli (2008) [7] P. J. E. Peebles, Principles of Physical Cosmology, University Press (1993) [8] J. Binney and Michael Merrifield, Galactic Astronomy [9] Capozziello e Funaro, Introduzione alla Relatività Generale,Liguori Editore (2005) [10] Coles & Lucchin, Cosmology (2002) [11] Springer, Chow (2008) [12] Weiberg, Gravitation and Cosmology, United States of America, (1972)
40
INDICE Introduzione………………………………………………………………………….I Capitolo 1: L’importanza della distanze in cosmologia…………………..……1 1.1: Alle origini del discorso cosmologico………………………..…..1 1.2: Le galassie………………………………………………………..….3 1.3: La nascita della cosmologia scientifica moderna……………..…3 Capitolo 2: Elementi di cosmologia teorica…………………………………......7 2.1: La cosmologia moderna…………………………………….……..7 2.2: L’Universo statico……………………………………………..……8 2.3: La metrica di Robertson‐Walker (e il modello di Einstein‐de Sitter)…………………………………………………………..……11 2.4: La costante di Hubble……………………………………..………15 Capitolo 3: Misure della costante di Hubble……………………………….....21 3.1: La misura delle distanze in cosmologia………………….…….21 3.2: Definizioni di distanza………………………………….……….23 3.3: Fenomenologia e misura………………………………………..25 3.4: Metodi locali e Cefeidi………………………………….………..26 3.5: Problemi di misura……………………………………………....28 41
Misura della costante di Hubble 3.6: Relazioni Periodo‐Luminosità e Periodo‐Luminosità‐Colore delle Cefeidi nelle Nubi di Magellano………………………….30 3.7: Metodo delle lenti gravitazionali………………………….…....31 3.8: Misura della costante di Hubble attraverso la relazione di Tully‐Fisher (TF)………………………………………………...32 3.9: L’uso del Piano Fondamentale e le rlazioni Dn e σ …………34 3.10: Una ricalibratura dalle distanze delle Cefeidi alle Supernovae di tipo Ia………………………………………………………….35 3.11: Costante di Hubble determinata con Sunyaev‐Zel’dovich…36 3.12: Unione dei vincoli sulla costante di Hubble…………………37 Conclusioni……………………………………………………………39 Bibliografia……………………………………………………………40 Indice…………………………………………………………………..41 42