OQ3-onde materia e spazio

Appunti preparati per il corso di Istituzioni di Fisica della Materia corso di laurea in Scienza e
Ingegneria dei Materiali
Titolo del manoscritto: “Onde e quanti”
Copyright 2002 - Lorenzo Marrucci
Ultimo aggiornamento: 4 aprile 2005
Capitolo 3 – Onde nella materia e nello spazio
La catena lineare di pendoli studiata nel capitolo precedente è un sistema discreto a una singola
dimensione spaziale (sistema “1D”). Essendo discreto, esso ci ha permesso di affrontare la
descrizione della sua dinamica con le semplici leggi fisiche dei sistemi di corpi e con i metodi di
analisi studiati nel primo capitolo a proposito dei sistemi di oscillatori. Essendo a una sola
dimensione, cioè per il quale una sola coordinata spaziale – ad esempio la x – basta per individuare
la posizione, ha reso più semplice il fenomeno della propagazione ondulatoria.
In questo capitolo abbandoniamo il modello della catena discreta di pendoli con cui abbiamo
appreso le basi della fisica delle onde e affrontiamo i primi sistemi “veramente continui”.
Tratteremo le onde elastiche longitudinali sulla sbarra solida, le onde trasversali sulla corda tesa e il
suono in un tubo pieno d’aria, tutti esempi di onde di spostamento in mezzi materiali. Passeremo
poi alle onde elettromagnetiche nello spazio vuoto. Questo studio ci fornirà anche una strada
naturale per arrivare all’equazione delle onde in tre dimensioni (3D) e alle sue soluzioni più
semplici, le onde piane e le onde sferiche. L’analisi della sovrapposizione di onde che si propagano
in tre dimensioni conduce infine ad introdurre i fenomeni di interferenza e diffrazione.
3.1 Onde elastiche longitudinali in una sbarra solida
La catena di pendoli studiata nel corso del precedente capitolo è un esempio di onde meccaniche
controllate dalla massa e dall’elasticità. Il limite continuo che abbiamo studiato è particolarmente
idoneo a descrivere il caso in cui le masse e le molle del sistema sono estremamente piccole e
ravvicinate. Se le masse e le molle vengono ridotte di dimensioni fino al punto da diventare
essenzialmente gli atomi che costituiscono un pezzo di materia solida e le forze di attrazione e
repulsione atomica tra questi, abbiamo ancora un comportamento simile a quello della catena di
pendoli, purché le deformazioni del solido rimangano piccole.
Consideriamo ad esempio una sbarra solida e sottile di composizione e di sezione S omogenea e di
lunghezza L, come in figura, e chiamiamo x l’asse longitudinale della sbarra.
F
S
x
L
δL
Se la sbarra viene tirata ad un estremo con una forza F parallela all’asse x, mantenendo fermo
l’estremo opposto, la sbarra subirà un allungamento (o un accorciamento se la forza ha il verso
opposto, cioè tende a comprimere la sbarra) come illustrato nella figura. Per forze non troppo
intense, la variazione di lunghezza δL è proporzionale alla forza applicata F come per una molla
1
(ovviamente una molla molto rigida, a meno che il materiale di cui è fatta la sbarra non sia
particolarmente soffice), ossia vale la legge di Hooke. La costante elastica di proporzionalità è a sua
volta inversamente proporzionale alla lunghezza della sbarra L e direttamente proporzionale alla sua
sezione S, per cui si ha
F = Y S δL / L
(1.1)
dove Y è una costante caratteristica del materiale di cui è composta la sbarra, detta modulo elastico
di Young. Confrontando la (1.1) con le costanti introdotte per caratterizzare l’elasticità delle molle e
della catena di pendoli, vediamo che il prodotto (YS) è quello che nella catena di pendoli era stato
chiamato modulo elastico K, e il fattore (YS)/L = K/L è quello che per una singola molla è chiamato
costante elastica, e che in precedenza abbiamo indicato con ke. Al contrario di ke e di K, il modulo Y
è però una caratteristica del materiale di cui è fatta la sbarra e quindi non dipende né dalla sua forma
né dalle sue dimensioni.
Il materiale di cui è composta la sbarra è anche caratterizzato da una densità di massa ρ, definita
come la massa per unità di volume. A partire da ρ è possibile definire la massa per unità di
lunghezza, o densità lineare di massa, ρl, tramite la relazione ρl = ρS. Quindi la sbarra può essere
caratterizzata da una massa e da una risposta elastica alle deformazioni entrambe distribuite lungo la
direzione x, proprio come il sistema di pendoli nel limite continuo. Questo suggerisce che la sbarra
si comporti in modo del tutto analogo alla catena di masse e molle studiata nel capitolo precedente
(ovvero alla catena di pendoli nel limite in cui il filo di sospensione è infinitamente lungo, e
comunque nel limite continuo). Ci dovremmo aspettare quindi che la sbarra possa essere percorsa
da onde in cui localmente ad ogni istante si ha uno spostamento ξ della materia rispetto alla
posizione di equilibrio parallelo all’asse x della sbarra, e descritto quindi da una funzione ξ(x,t) che
obbedisce all’equazione delle onde di D’Alembert.1 Onde di questo tipo vengono dette onde
elastiche longitudinali. La velocità di queste onde sarà data dalla stessa espressione (2.12) del
capitolo precedente, cioè
velocità delle onde elastiche longitudinali sulla sbarra:
v0 =
K
YS
Y
=
=
ρl
ρS
ρ
(1.2)
che quindi dipende solo dal materiale di cui è composta la sbarra, tramite il suo modulo di Young Y
e la sua densità di massa ρ. Più in generale, sono dette onde longitudinali tutte le onde in cui il
movimento oscillatorio della materia avviene lungo la direzione di propagazione dell’onda stessa.2
Le onde elastiche longitudinali sono le onde che trasportano il suono all’interno dei solidi. Perciò a
volte esse sono dette semplicemente onde sonore nei solidi. Inserendo nella (1.2) i valori del
modulo di Young e della densità di vari materiali, possiamo ottenere la velocità di propagazione
delle onde longitudinali. Valori tipici per metalli e rocce si aggirano intorno ai 6000 m/s.
1
Questo fatto, valido nel limite in cui gli spostamenti ξ(x,t) sono abbastanza piccoli, può essere dimostrato in modo
formale studiando la dinamica di elementi infinitesimi di sbarra con un metodo simile a quello che useremo nel
prossimo paragrafo per la corda tesa.
2
Per estensione sono dette onde longitudinali anche le onde per le quali non vi è movimento di materia, ma esiste un
campo vettoriale associato all’onda e diretto nella direzione di propagazione dell’onda stessa. Attenzione però a non
confondere questo campo vettoriale con il vettore d’onda k, che introdurremo più avanti, che è per definizione orientato
come la direzione di propagazione dell’onda.
2
3.2 Onde trasversali sulla corda tesa
Le onde studiate nel paragrafo precedente, così come quelle della catena di pendoli del capitolo
precedente (nel limite in cui il filo di sospensione è infinitamente lungo), sono entrambi esempi di
onde longitudinali, in cui cioè il movimento oscillatorio della materia avviene nella stessa direzione
in cui l’onda si propaga.
E’ però possibile considerare anche sistemi in cui il movimento oscillatorio della materia avviene in
direzione ortogonale a quella di propagazione dell’onda. In questo caso le onde sono dette onde
trasversali.3 Come esempio di un semplice sistema meccanico che esibisce tale comportamento,
consideriamo in questo paragrafo la dinamica di una corda flessibile, lunga e sottile, mantenuta
costantemente in tensione, come le corde di una chitarra o di un altro strumento musicale.
La tensione T della corda è definita come l’intensità della forza con cui due porzioni adiacenti
qualsiasi della corda, considerate come corpi indipendenti, si “tirano” reciprocamente (ricordiamo
che per il principio di azione e reazione la forza con cui una parte di corda tira l’altra è uguale e
opposta alla forza con cui la seconda parte tira la prima), come illustrato nella seguente figura.
T
−T
In ultima analisi la tensione è determinata dalla forza con cui la corda è tirata ai due estremi, come
avviene ad esempio nella figura seguente (la forza con cui la corda è tirata a un estremo deve essere
sempre uguale e opposta a quella con cui la corda è tirata all’altro estremo, perché altrimenti tutta la
corda comincerebbe ad accelerare nella direzione della forza più intensa).
mT g = T
mT
Assumiamo che la corda sia flessibile e omogenea, con una massa per unità di lunghezza o densità
lineare di massa ρl = m/L, dove m è la massa totale della corda e L la sua lunghezza. Se è posta in
vibrazione in qualche modo, la corda si discosta dalla sua forma rettilinea di equilibrio,
deformandosi. La figura seguente rappresenta una possibile “istantanea” della corda mentre vibra.
y
x=L
x
3
Come vedremo più avanti a proposito delle onde elettromagnetiche, questa denominazione può essere estesa al caso di
onde che non coinvolgono alcun movimento di materia ma che sono descritte comunque da un campo vettoriale che si
mantiene sempre perpendicolare alla direzione di propagazione dell’onda.
3
In questa figura abbiamo anche introdotto un sistema di riferimento cartesiano con l’asse x
coincidente con la retta di equilibrio della corda. Per il momento assumiamo per semplicità che tutti
i movimenti della corda avvengano nel piano xy. Ma come descriviamo matematicamente questi
movimenti? In altre parole, qual è il campo che descrive la dinamica della corda (l’equivalente del
campo ξ(x,t) usato in precedenza)?
Immaginiamo di suddividere mentalmente la corda in N elementi “infinitesimi”, ciascuno di
lunghezza ∆l =L/N così piccola da poter essere considerato come un punto materiale. Come per la
sbarra, un elemento di corda può essere individuato dalla sua coordinata x all’equilibrio. Il suo moto
è invece specificato dalle sue coordinate dinamiche xd(x,t) e yd(x,t). Questa rappresentazione del
moto della corda è illustrata nella figura seguente (dove l’elemento di corda seguito nel suo moto è
indicato in grassetto):
y
xd(x,t), yd(x,t)
x
x
Le due funzioni xd(x,t) e yd(x,t) sono quindi due campi che devono essere usati insieme per
descrivere la dinamica del sistema. Questo mostra che a volte è necessario considerare più di un
campo per descrivere un sistema fisico. Tuttavia, noi ora introduciamo nel nostro modello la
seguente notevole semplificazione: assumiamo che le vibrazioni della corda siano piccole. In
questo caso, è evidente che per tutti gli elementi della corda i movimenti longitudinali lungo x
saranno sempre molto più piccoli dei movimenti trasversali lungo y, cioè possiamo porre |xd − x| <<
|yd| (questo in realtà implica anche che stiamo ignorando le eventuali onde elastiche longitudinali
sulla corda). Quindi in prima approssimazione possiamo semplicemente trascurare i piccolissimi
spostamenti longitudinali e seguire solo i movimenti trasversali lungo y degli elementi di corda. In
altre parole, poniamo cioè xd(x,t) ≈ x, costante nel tempo, e ci resta così il solo campo yd(x,t) a
descrivere la dinamica del sistema. D’ora in avanti, per brevità, rimuoviamo il pedice d e
scriveremo semplicemente y(x,t) dato che la possibilità di confusione è scomparsa.4 Quindi, lo
spostamento trasversale y(x,t) di ciascun elemento di corda è il campo che descrive la dinamica
della corda, nella nostra approssimazione (cioè gioca lo stesso ruolo della ξ degli esempi
precedenti). Il nostro compito è ora di determinare l’equazione differenziale che governa questo
campo.
Come per i pendoli, il punto di partenza è l’equazione di Newton Ftot = ma, riferita in questo caso al
singolo elemento di corda. Per determinare la forza totale Ftot è utile fare un disegno dell’elemento
con tutte le forze applicate (salvo il peso della corda che supponiamo trascurabile):
4
Va comunque tenuto ben presente che nell’espressione y(x,t) che useremo, la y e la x hanno un ruolo ben diverso: la
prima è una variabile dinamica che descrive il moto, analoga alla ξ usata finora, mentre la seconda è una coordinata
spaziale, che individua il tratto di corda in esame.
4
T(x+∆x)
∆l
α
−T(x)
y(x+∆x) = y(x) + ∆y
y(x)
x
∆x
In questo disegno abbiamo introdotto la funzione T(x), definita come il vettore che descrive la forza
di tensione che il tratto di corda successivo al punto x esercita sul tratto di corda precedente al punto
x. Il modulo di T(x) è pari alla tensione T precedentemente definita, mentre la direzione è quella
della retta tangente alla corda nel punto x (questa proprietà corrisponde al fatto che la corda è
perfettamente flessibile). Inoltre nella figura abbiamo indicato con ∆x la proiezione dell’elemento di
corda sull’asse x e con α(x) l’angolo che la tangente alla corda forma con l’asse x in ciascun punto,
e che quindi definisce la direzione sia dell’elemento di corda (trascurandone la curvatura) che della
forza T(x). La forza totale è quindi Ftot = T(x+∆x)−T(x) ≈ (∂T/∂x)∆x. A noi interessa solo la
componente y di questa forza, che è data da:
Ftot , y =
∂Ty
∂x
∆x =
∂T sin α
∂α
∆x ≈ T
∆x
∂x
∂x
(2.1)
dove nell’ultimo passaggio abbiamo assunto che (i) il modulo T della tensione può essere
considerato costante e (ii) che gli angoli α(x) sono tutti piccoli per cui al primo ordine di
approssimazione il seno può essere sostituito con l’angolo stesso (espresso in radianti). Entrambe
queste assunzioni derivano dall’ipotesi che le deviazioni della corda dall’equilibrio sono piccole e
che gli spostamenti lungo x degli elementi di corda sono trascurabili in prima approssimazione. E’
ora necessario riesprimere α(x) in termini del campo y(x), cosa che può essere fatta con la seguente
relazione trigonometrica:
α( x) ≈ tan α( x) ≈
∆y ∂y
≈ ( x)
∆x ∂x
(2.2)
Per completare l’equazione dobbiamo calcolare la massa dell’elemento di corda, che è pari a ∆m =
ρl∆l = ρl∆x/cosα ≈ ρl∆x, e l’accelerazione componente y, che è pari a ay = ∂2y/∂t2. Combinando
queste espressioni nella Ftot,y = may e semplificando il fattore ∆x presente in ambo i membri
dell’equazione, otteniamo la seguente
equazione della corda tesa (piccole vibrazioni):
ρl
∂2 y
∂2 y
=
T
∂t 2
∂x 2
(2.3)
Questa equazione è identica alla (1.7) del capitolo precedente, salvo per la sostituzione in questo
caso del modulo elastico K con la tensione T. Si tratta quindi di un’equazione di D’Alembert come
la (1.8) del capitolo precedente, con la costante v0 che fissa la velocità delle onde (trasversali) sulla
corda tesa data da
5
velocità delle onde sulla corda tesa:
v0 =
T
ρl
(2.4)
Le soluzioni ondulatorie dell’equazione (2.3) sono evidentemente date dalle stesse espressioni
trovate nel capitolo precedente, salvo per la sostituzione del modulo elastico K con la tensione T.
C’è però una differenza sostanziale tra la corda tesa e la catena di masse e molle, che risulta
evidente dal modo con cui abbiamo determinato l’equazione differenziale che governa questi due
sistemi. Infatti, la catena di masse e molle nel limite continuo è un sistema governato esattamente
dall’equazione delle onde, mentre la corda tesa (sempre nel limite continuo, anche se in questo caso
questo limite è praticamente esatto) è governato in realtà da un’equazione nonlineare complicata
(anzi da un sistema di equazioni che coinvolge anche gli spostamenti lungo x), che si riducono solo
approssimativamente all’equazione lineare (1.3) nel limite di piccole deviazioni dall’equilibrio. La
situazione è del tutto analoga a quella riscontrata nel primo capitolo quando abbiamo considerato il
sistema massa-molla che è governato esattamente dall’equazione lineare dell’oscillatore armonico e
il pendolo che è governato da un’equazione non lineare che si riduce approssimativamente a quella
dell’oscillatore armonico nel limite di piccole oscillazioni. In pratica l’equazione (1.3) è
implicitamente il risultato di una procedura di linearizzazione per piccole deviazioni
dall’equilibrio. L’equazione esatta della corda tesa, che non abbiamo determinato, è invece una
complicata equazione differenziale alle derivate parziali non lineare. Lo stesso vale anche per le
onde sulla sbarra considerate nel paragrafo precedente (la linearizzazione qui era meno evidente
perché entra solo nell’espressione della forza elastica) e in generale praticamente per tutte le onde
meccaniche.
Vediamo ora quale sia l’energia trasportata dalle onde sulla corda tesa. L’energia cinetica non
pone particolari difficoltà concettuali. Il contributo di un elemento di corda è infatti pari a
2
1
1  ∂y 
energia cinetica di un elemento di corda: ∆Ek = ∆m v 2 = ρ l   ∆x
2
2  ∂t 
(2.5)
Il ragionamento da fare per l’energia potenziale è invece un po’ più sottile. L’energia potenziale
della corda tesa deriva dalla sua elasticità e dal fatto che per vibrare la corda deve necessariamente
subire un allungamento. Infatti, un elemento di corda che a riposo possiede una lunghezza ∆x, un
volta in movimento possiede una lunghezza data approssimativamente da
2
 1  ∂y  2 
 ∂y 
∆l = ∆x 2 + ∆y 2 = ∆x 1 +   ≈ ∆x 1 +   
 ∂x 
 2  ∂x  
(2.6)
(dove abbiamo trascurato i movimenti lungo x degli estremi dell’elemento di corda e per ottenere
l’ultima espressione abbiamo utilizzato lo sviluppo in serie di Taylor troncata, in funzione della
quantità piccola ∂y/∂x). Notate che la variazione di lunghezza δ∆l = ∆l − ∆x è descritta da termini
che sono quadratici nel campo y(x,t), cioè sono termini che finora avevamo trascurato rispetto a
quelli lineari. Ma nel calcolo dell’energia i termini lineari si annullano e i primi termini utili sono
quelli quadratici, che quindi non possono essere più trascurati. Una volta calcolato l’allungamento
dell’elemento di corda, dobbiamo determinare l’incremento di energia elastica che ne risulta. A
questo scopo non è necessario introdurre il modulo elastico della corda, che non conosciamo. Infatti
l’incremento di energia elastica ∆Ep di un elemento di corda sarà anche pari al lavoro δL fatto
contro la tensione T della corda per indurre l’allungamento dell’elemento, cioè
6
2
T  ∂y 
energia potenziale di un elemento di corda: ∆E p = T δ∆l = T ( ∆l − ∆x ) ≈   ∆x
2  ∂x 
(2.7)
La densità spaziale di energia dell’onda si ottiene sommando l’energia cinetica (2.5) e quella
elastica (2.7) e dividendo per ∆x. Il risultato è quindi il seguente:
2
densità di energia onde sulla corda vibrante:
dE 1  ∂y  1  ∂y 
= ρl   + T  
dx 2  ∂t  2  ∂x 
2
(2.8)
Notate che questo risultato è del tutto simile all’espressione (6.6) del capitolo precedente, relativo
alla densità di energia delle onde sulla catena di masse e molle. Di conseguenza tutte le altre
relazioni sull’energia ricavate nel paragrafo 6 del capitolo precedente sono valide anche per le onde
sulla corda vibrante, salvo per la sostituzione del modulo elastico K con la tensione T. Anche in
questo caso, però, va tenuto presente che l’espressione (2.8) è solo un’approssimazione quadratica
di una dipendenza nonlineare più complessa, mentre la (6.6) del capitolo precedente è esatta.
Per concludere questo paragrafo, notiamo che anche la sbarra solida del paragrafo precedente può
essere posta in vibrazione trasversale, e questo dà luogo a onde elastiche trasversali. Esse sono
ancora una volta governate dall’equazione di D’Alembert (nell’approssimazione linearizzata), ma in
cui il modulo elastico di Young è sostituito da un altro modulo elastico relativo alle deformazioni di
taglio. Perciò, le onde elastiche trasversali viaggiano ad una velocità diversa da quelle longitudinali
(quasi sempre minore), e si comportano come onde indipendenti (nell’approssimazione
linearizzata).
3.3 Polarizzazione e momento angolare delle onde trasversali
Nel paragrafo precedente abbiamo supposto che le vibrazioni della corda fossero limitate al piano
xy. Ora rimuoviamo questa restrizione, e consideriamo vibrazioni trasversali della corda sia in
direzione y che in direzione z. Per descriverne la dinamica dobbiamo introdurre i due campi y(x,t) e
z(x,t). Generalizzando i ragionamenti fatti nel paragrafo precedente, si può dimostrare che
nell’approssimazione linearizzata, questi due campi sono governati dal seguente sistema di due
equazioni differenziali:
∂2 y 1 ∂2 y
−
=0
∂x 2 v 02 ∂t 2
∂2z 1 ∂2z
−
=0
∂x 2 v 02 ∂t 2
(3.1)
con la costante v0 data sempre dalla (2.4). E’ anche possibile sintetizzare le due equazioni (3.1) in
una singola equazione vettoriale per il vettore spostamento trasverso r = (0, y, z) dell’elemento di
corda, come segue:
∂ 2r 1 ∂ 2r
equazione differenziale di onde trasversali:
−
=0
∂x 2 v02 ∂t 2
(3.2)
dove le operazioni di derivazione parziale su r(x,t) vanno eseguite separatamente, cioè componente
per componente. Quindi r(x,t) è un campo vettoriale che descrive la dinamica del sistema.
7
Le due equazioni nella (3.1) sono disaccoppiate, per cui le soluzioni di ciascuna equazione sono le
stesse trovate nel capitolo precedente. La soluzione del sistema si ottiene semplicemente mettendo
insieme le soluzioni di ciascuna equazione, facendo però attenzione a introdurre simboli diversi per
le costanti o le funzioni arbitrarie che compaiono in ciascuna di esse.
Ad esempio, la soluzione generale potrà essere scritta nel modo seguente (dove per chiarezza
abbiamo usato sia la notazione vettoriale che quella per le componenti y e z):
 f ( x − v 0t ) + g y ( x + v 0t ) 
 y ( x, t ) 
soluzione generale: r ( x, t ) = 
= f ( x − v 0t ) + g ( x + v 0t ) =  y
 (3.3)

 z ( x, t ) 
 f z ( x − v 0t ) + g z ( x + v 0t ) 
Le onde armoniche (modi normali) più generali che si propagano nella direzione positiva dell’asse x
vanno scritte nel modo seguente:
 y ( x, t )   Ay cos(kx − ωt + ϕ y ) 
onde armoniche (notazione reale): r ( x, t ) = 

=
 z ( x, t )   Az cos(kx − ωt + ϕ z ) 
(3.4)
Notate che un modo normale è per definizione una soluzione avente una unica frequenza ω di
oscillazione, per cui la ω da introdurre nelle due componenti della (3.4) deve essere la stessa
(altrimenti si avrebbe ancora una soluzione valida, ma non un modo normale). Di conseguenza
anche la costante k deve essere la stessa, perché è fissata dalla relazione di dispersione (2.13) del
capitolo precedente. Ampiezze e fasi possono essere invece diverse per le due componenti.
In notazione complessa, la (3.4) può essere scritta nella seguente forma più compatta:
A 
 y ( x, t ) 
onde armoniche (notazione complessa): r ( x, t ) = 
= A c eikx −iωt =  cy  eikx −iωt

 z ( x, t ) 
 Acz 
(3.5)
dove il vettore complesso Ac = [Ay exp(iϕy), Az exp(iϕz)] contiene tutte le informazioni sull’onda
armonica per una data frequenza e direzione di propagazione.
Quanta energia è trasportata da un’onda armonica data dalla (3.4) o (3.5)? Anche in questo caso,
generalizzando i ragionamenti fatti nel paragrafo precedente si troverà che l’energia dell’onda è
data semplicemente dalla somma delle energie associate separatamente alla componente y e alla
componente z. A partire dall’espressione (2.8), l’energia di ciascuna componente può essere riscritta
nella forma descritta dall’espressione (6.10) del secondo capitolo, salvo per la sostituzione k2K →
k2T = ω2ρl. La densità di energia totale dell’onda sarà quindi data da una delle seguenti espressioni
equivalenti:
densità di energia onda armonica:
dE
= k 2T ( Ay2 + Az2 ) = ω 2 ρl ( Ay2 + Az2 ) = ω 2 ρl A c
dx
2
(3.6)
dove nell’ultima espressione abbiamo introdotto il modulo-quadro del vettore complesso Ac,
definito come |Ac|2 = |Acy|2+|Acz|2.
E’ interessante analizzare ora quale moto compia un dato elemento di corda, ossia quale sia la
traiettoria descritta dal vettore r(t) per un punto x fissato, per un’onda armonica qualsiasi. E’
8
abbastanza agevole dimostrare a partire dalla (3.5) (provateci da soli: è un semplice esercizio di
geometria analitica) che l’orbita dell’elemento ha in generale una forma ellittica, come quella
descritta nella figura seguente:
z
r(t)
y
Per una data onda, l’ellisse è la stessa qualsiasi sia il punto x considerato, ossia è una caratteristica
dell’intera onda. I tre parametri che definiscono l’ellisse (ad esempio la lunghezza degli assi
maggiore e minore e l’inclinazione di uno di essi rispetto all’asse y) sono determinati dalle
ampiezze Ay e Az e dalla differenza delle due fasi ϕy−ϕz, con delle formule che omettiamo (notiamo
che l’onda armonica possiede anche un quarto parametro caratteristico indipendente, dato ad
esempio da una delle due fasi ϕy o ϕz, che fissa esclusivamente la fase temporale con cui l’orbita
ellittica viene descritta dall’elemento di corda). Dei tre parametri che definiscono l’ellisse, uno
corrisponde ad un parametro di ampiezza che fissa cioè la dimensione dell’ellissi, e può essere dato
ad esempio dal modulo |Ac| o all’energia ⟨dE/dx⟩ trasportata dall’onda. I due parametri restanti
specificano invece la forma e l’orientazione dell’ellissi (incluso il verso di percorrenza, orario o
antiorario), indipendentemente dalla sua dimensione, ed insieme definiscono la cosiddetta
polarizzazione dell’onda. Una possibile scelta di questi due parametri è costituita ad esempio dal
grado di ellitticità, specificato dal rapporto tra asse maggiore ed asse minore, e dall’angolo che
l’asse maggiore forma con l’asse y. Il caso generale fin qui discusso è detto polarizzazione ellittica,
per distinguerlo da alcuni casi limite di particolare importanza che adesso esamineremo.
Il caso in cui l’ellitticità è infinita, cioè l’ampiezza dell’asse minore si annulla e l’ellisse si riduce ad
un segmento come nella figura seguente, costituisce il caso di polarizzazione lineare di un’onda.
z
ψ
y
In un’onda polarizzata linearmente, quindi, il moto r(t) si riduce ad una semplice oscillazione lungo
una singola direzione. La polarizzazione è specificata completamente dall’angolo ψ tra questa
direzione di oscillazione e l’asse di riferimento y. In un’onda polarizzata linearmente la vibrazione
dell’intera corda avviene in un unico piano, che viene detto piano di polarizzazione. Notate che
questa definizione di polarizzazione lineare è applicabile anche al caso di onde non armoniche, per
le quali non è invece definibile la polarizzazione ellittica. Un esempio banale è quello di un’onda
della corda tesa in cui la componente z(x,t) = 0 (Az = 0 nel caso di onde armoniche), ossia la cui
vibrazione avviene solo nel piano xy, come quelle studiate nel paragrafo precedente. Analogamente
è polarizzata linearmente nel piano xz un’onda per la quale y(x,t) = 0 (Ay = 0 per le onde
armoniche). Un’onda polarizzata linearmente in una direzione qualsiasi ψ è in generale descritta da
due campi y(x,t) e z(x,t) proporzionali tra loro, ossia si ha z(x,t) = C y(x,t), dove C = tan ψ. Nel caso
9
di un’onda armonica, questa condizione si traduce nel fatto che le fasi delle due componenti devono
essere uguali, ossia ϕy = ϕz, e nel fatto che il rapporto tra le ampiezze fissa l’angolo ψ secondo la
relazione tan ψ = Az/Ay.
Un altro caso particolarmente importante è quello in cui l’ellissi di polarizzazione si riduce ad una
circonferenza, un caso limite detto di polarizzazione circolare. Un’onda armonica si dice
polarizzata circolarmente quando il campo r(x,t) al variare del tempo t descrive un moto circolare
uniforme. In altre parole, se seguiamo nel tempo il moto di un elemento di corda corrispondente ad
una x fissata, lo vedremo girare in cerchio attorno all’asse di equilibrio x, come nella figura
seguente:
z
r(t)
y
La “velocità angolare” della rotazione coincide con la frequenza angolare ω. E’ facile convincersi
che questo particolare tipo di onda armonica si realizza quando le ampiezze delle componenti y e z
dell’onda sono uguali, ossia Ay = Az , e le loro fasi soddisfano alla relazione ϕz = ϕy ± π/2, ossia le
due componenti sono “sfasate” di un quarto di periodo. Il segno del ± è pari a + se il campo gira in
senso orario nel piano yz (visto dalla direzione verso cui punta l’asse x, ossia verso cui viaggia
l’onda, come nella figura precedente) ed è pari a − se il campo gira in senso antiorario (come nella
figura). Queste due possibilità corrispondono a due onde diverse, la cui polarizzazione è detta
rispettivamente circolare destra e circolare sinistra. In notazione complessa, la polarizzazione
circolare è caratterizzata dalla seguente relazione tra le ampiezze complesse delle componenti: Acz =
±iAcy, o equivalentemente dal vettore Ac = (1, ±i) A, dove A è una qualsiasi ampiezza complessa
scalare.
Abbiamo visto come l’onda polarizzata circolarmente dipende dal tempo in un punto fissato. Ora
per completarne la descrizione dobbiamo fissare il tempo t e vedere come varia il campo con la
posizione x. In altre parole, ci chiediamo come sia fatta una “istantanea” del campo di un’onda
polarizzata circolarmente, ossia nel caso della corda tesa, quale sia la forma della corda a ogni dato
istante. La risposta, come è facile verificare a partire dall’espressione analitica del campo, è una
forma ad elica, come quella illustrata nella figura seguente.
z
y
x
Al crescere di x il campo r descrive una circonferenza nel senso opposto a quello temporale (cioè
antiorario se ± = + e orario se ± = −), se vista dal lato verso cui punta la x (ossia verso cui viaggia
l’onda).
10
Le onde polarizzate circolarmente hanno anche un’altra proprietà che le rende particolarmente
interessanti. Esse infatti, oltre all’energia, trasportano momento angolare. Per la precisione, si può
associare a queste onde una densità lineare di momento angolare diretto come l’asse x (ricordate che
il momento angolare è un vettore). Infatti il momento angolare associato a un elemento di corda che
ruota attorno all’asse x è dato da
momento angolare di un elemento di corda:
∂y 
 ∂z
∆Lx = ∆m  y − z  = ± ρlω A2 ∆x
∂t 
 ∂t
(3.7)
dove A = Ay = Az è l’ampiezza reale di ciascuna componente dell’onda. Dividendo ambedue i
membri della (3.7) per ∆x si ottiene la densità di momento angolare. E’ interessante confrontare
questo risultato con la densità di energia media trasportata dall’onda, data dalla (3.6). Otteniamo
così la seguente relazione, particolarmente semplice:
densità di momento angolare di un’onda polarizzata circolarmente:
dLx
1 dE
=±
dx
ω dx
(3.8)
Questa relazione tra momento angolare ed energia ha anche il notevole pregio di avere validità
generale. Essa resta valida, ad esempio, per le onde elettromagnetiche. Va detto infine che anche le
onde polarizzate ellitticamente trasportano momento angolare, anche se la relazione con l’energia
non è più così semplice.
E’ però importante a questo punto sottolineare un aspetto relativo alla polarizzazione delle onde
armoniche che potrebbe non essere immediatamente evidente. Un’onda armonica di frequenza
assegnata ω può avere infinite polarizzazioni diverse, descritte in notazione complessa
dall’equazione (3.5). Tuttavia, possono essere individuate solo due polarizzazioni che siano
linearmente indipendenti. In altre parole, un’onda armonica polarizzata in un modo qualsiasi in
notazione complessa può essere sempre scritta in forma di combinazione lineare di due sole onde
armoniche “di base”. Ad esempio, si possono utilizzare come base della combinazione lineare due
onde con polarizzazione lineare lungo direzioni diverse (ad esempio ortogonali tra loro, come lungo
y e lungo z), oppure si possono usare due onde polarizzate circolarmente, una “destra” e una
“sinistra”, o anche due onde polarizzate ellitticamente.
Da un punto di vista più matematico, notiamo che i vettori ampiezza complessa Ac che compaiono
nella (3.5) formano uno spazio vettoriale (complesso) a due dimensioni. Date due onde di “base”
caratterizzate da ampiezze Ac1 e Ac2 linearmente indipendenti (ossia non proporzionali tra loro,
dove la proporzionalità in questo caso include anche eventuali coefficienti complessi), qualsiasi
altra onda avrà un’ampiezza complessa Ac che può essere scritta nella forma Ac = a1 Ac1 + a2 Ac2.
In particolare, è spesso vantaggioso, ma non indispensabile, scegliere polarizzazioni ortogonali tra
loro come base, dove l’ortogonalità in campo complesso è definita dalla relazione Ac1⋅Ac2* = Ac1,y
Ac2,y* + Ac1,z Ac2,z* = 0.
Ricollegandoci ora alla possibilità discussa nel capitolo precedente di scrivere un’onda qualsiasi in
forma di combinazione lineare (o integrale di Fourier) di onde armoniche (cioè di modi normali), le
considerazioni appena fatte implicano che nel caso delle onde trasversali non è necessario includere
nella combinazione lineare tutte le possibili polarizzazioni: ne bastano solo due (purché
indipendenti, ad esempio ortogonali tra loro).
11
3.4 Onde di spostamento longitudinale in aria: il suono
Consideriamo ora un altro esempio di un sistema che esibisce onde longitudinali di spostamento
molto simili a quelle elastiche sulla sbarra solida considerate nel primo paragrafo: un tubo cilindrico
contenente aria. Assumiamo che l’aria all’interno del tubo si possa muovere solo avanti e indietro
parallelamente all’asse x del tubo, e che l’attrito con le pareti del tubo sia trascurabile. Il movimento
di un elemento di aria è illustrato dalla figura seguente.
ξ
x
La situazione può essere analizzata in modo del tutto analogo a quanto fatto per la sbarra solida. La
dinamica dell’aria può essere descritta dal campo degli spostamenti ξ(x,t). L’unica differenza in
ultima analisi è il modo con cui l’aria risponde alla compressione o alla dilatazione. Infatti l’aria
non è elastica per cui non possiede un modulo elastico Y. Ciò nonostante, l’aria nel tubo risponde ad
una forza applicata ad un estremo del tubo che provi ad “allungarla” o a comprimerla, ad esempio
mediante un pistone a tenuta stagna, come nella figura seguente.
F
Infatti, l’aria come tutti i gas produce una pressione p sulle pareti del contenitore, incluso quindi il
pistone. All’equilibrio la pressione interna è però bilanciata dalla pressione esterna di equilibrio
dell’aria p0, cioè si ha p = p0, per cui la forza complessiva sul pistone si annulla. Quando il pistone
viene spostato, invece, la pressione esterna rimane immutata mentre quella interna varia con il
volume. Perciò la forza (componente x) da applicare al pistone per spostarlo è pari a F = (p0−p)S,
dove S è l’area della sezione del tubo. Ma come varia la pressione interna con il volume?
Se tutti gli attriti possono essere trascurati, possiamo usare le relazioni termodinamiche di
equilibrio. L’aria in condizioni normali di pressione e temperatura può essere considerata un gas
perfetto con ottima approssimazione. Perciò possiamo utilizzare l’equazione di stato:
equazione di stato dei gas perfetti:
pV = nRT
(4.1)
dove n è il numero di moli di aria contenute nel tubo, V il volume del tubo, T la temperatura
assoluta e R = 8.31 J/K la costante dei gas. Se la temperatura T è costante, la (4.1) ci fornisce la
relazione tra variazioni di volume e di pressione. Tuttavia le variazioni di volume associate a
un’onda, a meno di non considerare casi limite di frequenze bassissime, sono troppo rapide perché
ci sia uno scambio di calore significativo tra l’aria contenuta nel tubo e l’esterno, per cui la
temperatura non può restare costante. In prima approssimazione è invece valido il limite opposto in
cui il calore scambiato può essere completamente trascurato e la trasformazione subita dal gas può
essere considerata perfettamente adiabatica. In questo caso, trascurando gli attriti, possiamo usare
l’equazione delle trasformazioni adiabatiche reversibili di un gas perfetto, che è la seguente:
12
pV γ = costante = p0V0γ (4.2)
legge di una trasformazione adiabatica (reversibile):
dove le costanti p0 e V0 corrispondono alla pressione e volume iniziali, coincidenti con i valori di
equilibrio, e γ è una costante caratteristica del gas. In particolare, per un gas biatomico come l’aria
(dato che è composta prevalentemente da ossigeno e azoto) si ha γ = 7/5. La dipendenza della
pressione dal volume espressa dalla (4.2) è una legge non lineare di potenza. Per piccole variazioni
di volume δV corrispondenti ad uno spostamento del pistone di δL = δV/S, possiamo linearizzare
questa dipendenza mediante uno sviluppo in serie di Taylor attorno al punto di equilibrio troncando
lo sviluppo al primo ordine, ottenendo
p = p0 − γ(p0/V0) δV
(4.3)
da cui la forza applicata al pistone è
F = (γ p0S/L0) δL
(4.4)
dove abbiamo introdotto la costante L0 = V0/S che corrisponde alla lunghezza del tubo in condizioni
di equilibrio. Questa relazione è identica alla (1.1), salvo per la sostituzione del modulo di Young Y
con la costante γp0.
Perciò, tutti i ragionamenti esposti nel primo paragrafo riguardo alla sbarra solida restano validi
senza modifiche per l’aria nel tubo salvo per la sostituzione di Y con γp0. In particolare, il sistema
ammette onde di spostamento longitudinale dell’aria che sono ciò che viene comunemente
chiamato suono (sono utilizzate anche le espressioni onde sonore e onde acustiche; va anche detto
che in una accezione più ampia sono denominate suono anche le onde di spostamento longitudinale
nei liquidi e nei solidi, dove queste ultime coincidono con le onde elastiche studiate nel primo
paragrafo per il caso della sbarra). Queste onde obbediscono alla solita equazione di D’Alembert,
con una velocità caratteristica data dalla (1.2) con Y sostituita da γp0, ossia da
γp0
ρ0
velocità del suono in aria (prima espressione): v 0 =
(4.5)
dove ρ0 è la densità di massa dell’aria all’equilibrio. La densità ρ0 può essere a sua volta calcolata
in termini del numero di moli n, del volume V e della massa molare media dell’aria Mm ≈ 29 g/mol,
sfruttando l’equazione di stato (4.1), come segue:
densità in termini di pressione e temperatura:
ρ0 =
M m p0
RT0
(4.6)
dove T0 è la temperatura di equilibrio del sistema. Inserendo la (4.6) nella (4.5), otteniamo la
seguente espressione alternativa della velocità del suono:
velocità del suono in aria (seconda espressione): v 0 =
γRT0
Mm
(4.7)
Questa espressione è interessante, perché si avvicina molto alla velocità quadratica media delle
molecole dell’aria dovuta all’agitazione termica. Perciò il suono in aria si propaga
approssimativamente alla stessa velocità con cui viaggiano in media le molecole per agitazione
13
termica. Per aria a temperatura ambiente (T0 = 300K), la (4.7) fornisce v0 ≈ 345 m/s, in ottimo
accordo con i dati sperimentali.
L’energia per unità di lunghezza delle onde sonore viaggianti nel tubo può essere dedotta per
analogia con le onde elastiche dall’espressione (6.6) del capitolo precedente, con la semplice
sostituzione della densità lineare ρl con il prodotto ρ0S e del modulo elastico K con il prodotto γp0S.
Va notato che entrambi i termini energetici risultano così proporzionali alla sezione S del tubo.
Questo ci permette di definire un’energia per unità di volume (invece che per unità di lunghezza)
indipendente dalla geometria del tubo come segue:
2
dE 1  ∂ξ  1
 ∂ξ 
= ρ 0   + γp0  
densità di energia del suono (per unità di volume):
dV 2  ∂t  2
 ∂x 
2
(4.8)
Il primo termine di questa espressione corrisponde al contributo di energia cinetica mentre il
secondo termine è associato alle variazioni di energia interna dell’aria, che in questo caso gioca il
ruolo di energia potenziale (al posto di quella elastica). Per un’onda armonica, la (4.8) si semplifica
e diventa identica alla (6.9) con ω2ρ0 oppure γp0k2 al posto di Kk2. Il valore medio della densità di
energia in un’onda armonica è quindi
densità media di energia del suono (onda armonica):
dE
1
1
= ρ 0 ω2 A 2 = γp0 k 2 A 2
dV
2
2
(4.9)
dove A è l’ampiezza (in termini dello spostamento ξ) dell’onda armonica. A partire dall’energia per
unità di volume si definisce anche la cosiddetta intensità dell’onda sonora, che corrisponde alla
potenza dell’onda divisa per la superficie della sezione del tubo su cui è distribuita. In altre parole,
l’intensità fornisce l’energia che fluisce attraverso una sezione del tubo per unità di superficie e per
unità di tempo. L’intensità si ottiene a partire dalla densità (di volume) dell’energia moltiplicandola
semplicemente per la velocità di propagazione v0. Nel caso di onda armonica, l’intensità media è
quindi data da
intensità media del suono (onda armonica):
I=
1
dE
dE
= v0
= v 0 ρ 0 ω2 A 2
2
dSdt
dV
(4.10)
L’intensità data dalla formula precedente possiede le dimensioni di un’energia per unità di tempo e
superficie, ovvero una potenza per unità di superficie. Nel sistema internazionale, le sue unità di
misura naturali sono i watt a metro quadro, ossia W/m2.
In acustica, laddove si ha a che fare con le sensazioni e gli effetti che il suono produce sull’uomo, si
usa però comunemente un’altra “unità di misura” dell’intensità sonora, basata sul confronto, in
scala logaritmica, con una particolare intensità di riferimento I0: i decibel (simbolo dB). La
definizione dell’intensità sonora espressa in decibel a partire da quella espressa in termini di
potenza per unità di area è la seguente:
intensità sonora in decibel:
I dB = 10 log10
I
I0
con I0 = 10−12 W/m2 (4.11)
I decibel vengono a volte anche usati per indicare l’ampiezza A dell’onda sonora. In questo caso,
però, il logaritmo del rapporto tra l’ampiezza A e quella di riferimento A0 viene convenzionalmente
moltiplicato per il fattore 20, anziché 10, a causa del fatto che le ampiezze sono legate alle intensità
14
con la radice quadrata, che corrisponde ad un fattore ½ davanti al logaritmo. Con tale definizione i
valori in decibel dell’intensità e dell’ampiezza di una medesima onda sono uguali, se si scelgono i
valori di riferimento in modo corrispondente.
Va notato che le onde sonore, oltre ad uno spostamento longitudinale oscillatorio dell’aria, si
accompagnano a variazioni locali di densità, pressione e temperatura dell’aria. Per questo motivo
si dice comunemente che il suono è un’“onda di pressione” oppure di densità dell’aria. Per calcolare
queste variazioni, consideriamo in maggiore dettaglio lo spostamento di un elemento infinitesimo di
aria, aiutandoci con la figura seguente.
ξ(x,t)
ξ(x+∆x,t)
situazione al tempo t
situazione all’equilibrio
x
xd
∆x
∆xd
x
Adottiamo una notazione simile a quella usata per la corda tesa. Indichiamo, cioè, con xd(x,t) la
coordinata dinamica, al tempo t, di un “punto materiale” di aria che si trova all’equilibrio iniziale
nel punto x. La coordinata xd è legata allo spostamento ξ dalla relazione ξ(x,t) = xd(x,t) − x.
Consideriamo ora un piccolo elemento di aria che all’equilibrio è compreso in un intervallo di
coordinate ∆x (si veda la figura precedente). Oltre a spostarsi, durante il passaggio dell’onda,
l’elemento considerato cambierà anche la sua estensione lungo x, che passerà da ∆x a
 ∂ξ 
∆xd = xd ( x + ∆x, t ) − xd ( x, t ) = [ x + ∆x + ξ ( x + ∆x, t ) ] − [ x + ξ ( x, t ) ] ≈ ∆x 1 +
 (4.12)
 ∂x 
dove, nell’ultimo passaggio, abbiamo utilizzato lo sviluppo in serie di Taylor di ξ(x+∆x) centrato in
x e troncato al primo ordine. Moltiplicando ambo i membri della (4.12) per la sezione S del tubo si
ottiene il volume “dinamico” ∆Vd dell’elemento di aria seguito nel suo moto in termini del volume
di equilibrio ∆V. Considerando poi il fatto che la massa dell’elemento di aria seguito nel suo moto
resta costante e uguale a quella di equilibrio, ossia che ∆m = ρ0∆V = ρd∆Vd, si ottiene con pochi
passaggi la variazione locale di densità dell’aria
variazioni di densità nel suono: δρ ( x, t ) = ρ d ( x, t ) − ρ 0 = ρ 0
− ( ∂ξ ∂x )
∂ξ
≈ − ρ0
1 + ( ∂ξ ∂x )
∂x
(4.13)
dove l’ultima espressione, approssimata, è valida solo per valori piccoli dello spostamento ξ.
Usando la (4.3) si ottiene anche la corrispondente variazione locale di pressione dell’aria (valida per
piccoli spostamenti ξ):
15
variazioni di pressione in un’onda sonora: δ p( x, t ) = −γ p0
∂ξ
∂x
(4.14)
Una formula analoga, ma che non deriviamo, descrive infine le variazioni locali di temperatura. E’
importante notare che pressione, densità e temperatura variano come la derivata spaziale dello
spostamento ξ. Perciò, laddove lo spostamento di aria causato dall’onda è massimo (in positivo o
negativo) queste variazioni si annullano. Per converso, nelle onde armoniche, le massime variazioni
di pressione, densità e temperatura si raggiungono nei punti dove lo spostamento ξ si annulla.
3.5 Onde elettromagnetiche
Tutte le onde viste finora sono legate al movimento di materia. In questo paragrafo vediamo invece
il primo esempio di onde che non hanno nulla a che fare con il movimento di particelle materiali: le
onde elettromagnetiche. Consideriamo per il momento solo il caso in cui queste onde si propagano
nel vuoto, ossia in assenza di materia.
I campi coinvolti in questo caso sono il campo elettrico E e quello magnetico B, che sostituiscono il
campo di spostamento ξ. In generale dobbiamo considerare la dipendenza di questi due campi dal
punto r nello spazio tridimensionale e dal tempo. Quindi per descrivere un particolare campo
elettromagnetico, al posto della singola funzione ξ(x,t), sono ora necessarie le due funzioni E(r,t) e
B(r,t). Dato inoltre che E, B e r sono tutti vettori, corrispondenti ciascuno a tre coordinate
cartesiane, queste due funzioni vettoriali si traducono in ben sei funzioni scalari, Ex, Ey, Ez, Bx, By e
Bz, ciascuna dipendente dalle quattro variabili (x, y, z e t).
I campi elettromagnetici E e B sono governati in generale dalle equazioni di Maxwell, che
riportiamo qui di seguito in forma differenziale (nelle unità del sistema internazionale), per il caso
di cariche e correnti nulle (ossia nel vuoto):
∇×E = −
equazioni di Maxwell:
∂B
∂t
∇ × B = ε 0 µ0
∂E
(5.1)
∂t
∇⋅E = 0
∇⋅B = 0
In queste equazioni abbiamo introdotto il simbolo ∇ del cosiddetto “operatore gradiente”, che è
definito come un “vettore” le cui tre componenti cartesiane sono le derivate parziali rispetto alle tre
coordinate cartesiane corrispondenti, ossia
operatore gradiente: ∇ = [ ∂ ∂x , ∂ ∂y , ∂ ∂z ] (5.2)
Come qualsiasi “operatore differenziale”, il gradiente non ha in realtà alcun significato se “lasciato
da solo”, ma assume significato solo una volta “applicato” ad una funzione f su cui far operare le
derivate. In particolare, l’operatore gradiente ∇ applicato ad un qualsiasi campo scalare f produce il
cosiddetto gradiente del campo, cioè il campo vettoriale ∇f = [ ∂f ∂x , ∂f ∂y , ∂f ∂z ] . Il “prodotto
scalare” di ∇ con un qualsiasi campo vettoriale A(r) fornisce invece la cosiddetta divergenza del
campo ∇ ⋅ A = ∂Ax ∂x + ∂Ay ∂y + ∂Az ∂z , che è un campo scalare (anche indicato con il simbolo div
16
A). Infine, il prodotto vettoriale di ∇ con un qualsiasi campo vettoriale A(r) fornisce il cosiddetto
rotore del campo ∇ × A = ∂Az ∂y − ∂Ay ∂z , ∂Ax ∂z − ∂Az ∂x , ∂Ay ∂x − ∂Ax ∂y  , che è anch’esso
un campo vettoriale (anche indicato con il simbolo rot A, oppure, in inglese, curl A). Divergenza e
rotore dei campi elettrico e magnetico sono alla base delle equazioni di Maxwell (5.1).
Le equazioni (5.1) valgono in generale (purché nel vuoto). Ora però restringiamo la nostra
attenzione al caso particolare in cui entrambi i campi E e B non dipendono affatto dalle due
variabili y e z, ossia che non vi siano variazioni nel valore assunto dai campi spostandosi
parallelamente agli assi y e z. Questa situazione particolare è detta di simmetria piana, o più
precisamente simmetria per traslazioni parallele al piano yz del sistema. E’ chiaro che una
simmetria piana esatta è irrealizzabile, eccetto nel caso banale in cui i campi siano dappertutto nulli,
perché implica che i due campi si estendano senza annullarsi per y→±∞ e z→±∞, ossia per distanze
infinite. Perciò la situazione di simmetria piana è realizzabile solo in forma approssimata. In pratica
essa richiede che le sorgenti (distribuzioni di cariche e correnti elettriche) che generano i campi
posseggano a loro volta la medesima simmetria.
In queste ipotesi di simmetria piana, tutte le derivate parziali dei campi E e B rispetto alle variabili y
e z si annullano. E’ facile verificare che le (5.1) si riducono allora nelle seguenti 8 equazioni, che
raggruppiamo a due a due in quattro sistemi secondo le componenti dei campi coinvolte:
∂B x
=0
∂t
equazioni per Bx:
∂B x
=0
∂x
(5.3)
∂E x
=0
∂t
equazioni per Ex:
∂E x
=0
∂x
(5.4)
∂E z ∂B y
=
∂x
∂t
equazioni per Ez e By:
∂B y
∂E z
= ε 0µ 0
∂x
∂t
∂E y
equazioni per Ey e Bz:
=−
∂B z
∂t
∂x
∂E y
∂B z
= −ε 0 µ 0
∂x
∂t
(5.5)
(5.6)
Ciascuno dei 6 campi incogniti è ora funzione solo delle due variabili x e t. Grazie alla simmetria
piana, siamo tornati quindi ad una situazione che è a tutti gli effetti unidimensionale (1D).
I due sistemi (5.3) e (5.4) implicano immediatamente che le componenti Ex e Bx del campo
elettromagnetico debbano in effetti essere costanti sia rispetto alla variabile spaziale x che a quella
temporale t, ossia che il campo elettromagnetico corrispondente deve essere perfettamente uniforme
17
e stazionario. Le componenti x del campo elettromagnetico, ossia quelle ortogonali ai piani di
simmetria yz, non presentano alcuna dinamica, ondulatoria o meno.
Le componenti y e z dei campi obbediscono invece alle coppie di equazioni (5.5) e (5.6). In
particolare la prima coppia di equazioni mette in relazione (nel gergo dei fisici si dice anche
“accoppia”) le sole componenti Ez e By; la seconda lega Ey e Bz. Non vi è invece nessuna relazione
tra le componenti y e z dello stesso campo. Tali componenti sono quindi indipendenti.
Possiamo assumere per il momento che i campi di una di queste due coppie, ad esempio Ez e By, si
annullino identicamente (il che ovviamente verifica banalmente l’equazione corrispondente (5.5)) e
concentrarci sul comportamento dei campi dell’altra coppia, cioè Ey e Bz, controllati dalla (5.6).
La (5.6) è un sistema di due equazioni differenziali alle derivate parziali in due funzioni incognite.
Si tratta di un problema matematico nuovo, e non sappiamo ancora come affrontarlo. Un metodo
generale di soluzione è basato sul “solito” metodo della sovrapposizione di (infiniti) modi normali.
Qui invece utilizziamo un semplice “trucco” per trasformare le due equazioni accoppiate in due
equazioni indipendenti, ciascuna contenente una sola funzione incognita. Il procedimento è del tutto
analogo al metodo di sostituzione che si usa per i sistemi di equazioni algebriche (anziché
differenziali), cioè si ricava un’incognita (un campo) in termini dell’altra, ad esempio Bz in termini
di Ey, utilizzando una delle due equazioni, e poi la si sostituisce nell’altra equazione, che diventa
così un’equazione per il solo Ey. Non essendo però possibile invertire una derivata parziale in modo
da ricavare il campo Bz, si opera come segue: (i) si derivano ambo i membri della prima equazione
del sistema (5.6) per x e ambo i membri della seconda equazione del sistema (5.6) per t; (ii) si
ricava la derivata mista ∂2Bz/∂x∂t da una delle due equazioni così ottenute e la si sostitusce nella
seconda (si utilizza qui il fatto che l’ordine di derivazione nella derivata mista non conta). In questo
modo si ottiene la seguente equazione differenziale per il solo campo Ey:
eq. onde del campo e.m. (simmetria piana, polarizzazione y):
∂2Ey
∂x 2
− ε 0µ 0
∂2Ey
∂t 2
= 0 (5.7)
Ma questa equazione è proprio della forma dell’equazione delle onde di D’Alembert, con una
velocità di propagazione
velocità onde e.m.: v 0 = c =
1
ε 0µ 0
(5.8)
Il simbolo c qui introdotto è quello universalmente usato dai fisici per indicare la velocità delle onde
elettromagnetiche nel vuoto. Dato che la luce, come è noto, è “fatta” di onde elettromagnetiche, c è
anche la velocità della luce nel vuoto. Inserendo nella (5.8) i valori delle costanti ε0 e µ0, otteniamo
il suo valore
velocità della luce:
c = 299΄792΄458 m/s ≈ 300΄000 km/s
Oggi, nel sistema internazionale di unità, questo valore di c è assegnato per convenzione ed è quindi
privo di errore sperimentale.5
5
Assegnando un valore convenzionale prestabilito alla velocità della luce c si legano tra loro le unità di lunghezza
(metri) e di tempo (secondi). Infatti oggi il metro è definito a partire dal secondo come lo spazio percorso dalla luce in
un tempo pari a 1/(299792458) secondi. Il valore di c è ovviamente stato scelto in modo da preservare il più possibile
l’estensione del metro che si aveva in base alla precedente definizione.
18
Abbiamo così scoperto che la componente y del campo elettrico E si comporta come un’onda, che
si propaga nella direzione x (verso positivo o negativo) alla velocità c, mantenendo costante la
forma.
E il campo Bz? Così come abbiamo ricavato l’equazione per Ey, possiamo ricavare anche
un’equazione per Bz, che scopriremo essere identica alla (5.7). Quindi anche il campo magnetico Bz
si comporta come un’onda che si propaga nella direzione x alla velocità c. Tuttavia, queste due onde
non sono indipendenti tra loro, come questa nostra derivazione potrebbe far pensare. Infatti, il
metodo che abbiamo utilizzato per ricavare l’equazione (5.7) per Ey e l’equivalente equazione per
Bz non garantisce che il sistema di due equazioni disaccoppiate ottenuto alla fine sia equivalente a
quello iniziale (5.7). Infatti, la derivazione per una variabile (x o t) di ambo i membri di
un’equazione differenziale introduce anche soluzioni aggiuntive, non essendo un’operazione
invertibile.6 Quindi una volta trovate tutte le soluzioni Ey della (5.7) e dell’equazione corrispondente
per Bz, dobbiamo verificare quali di queste sono effettivamente soluzioni anche del sistema iniziale
(5.6) e quali sono invece soluzioni spurie.
Consideriamo ad esempio un’onda Ex e una Bz, entrambe di forma qualsiasi, che viaggiano nella
direzione positiva dell’asse x:
E y ( x, t ) = f E ( x − ct )
Bz ( x, t ) = f B ( x − ct )
(5.9)
Per verificare se questa soluzione obbedisce anche al sistema iniziale (5.6) proviamo a sostituirvela
dentro. Otteniamo così le seguenti equazioni per le funzioni fE e fB:
f E′ = cf B′
(5.10)
f B′ = ε 0 µ0 cf E′ = 1c f E′
dove il segno ( )′ rappresenta qui la derivata della funzione rispetto al suo unico argomento. Queste
due equazioni sono equivalenti. Integrandone una da ambo i membri, otteniamo la seguente
condizione, che deve essere soddisfatta affinché la soluzione (5.9) sia valida anche per il sistema
iniziale (5.6):
f E ( x) = cf B ( x) + costante
(5.11)
Questa condizione vincola cioè le due forme d’onda fE e fB ad essere esattamente uguali, salvo per
una costante additiva arbitraria e per il fattore di proporzionalità c. Quindi il campo magnetico Bz e
quello elettrico Ey delle “due onde” sono strettamente legati tra loro. Se escludiamo le eventuali
componenti costanti dei campi, ossia uniformi e stazionarie (e quindi non ondulatorie), possiamo
riscrivere la (5.11) nella forma seguente:
relazione tra Ey e Bz in onda e.m. che si propaga verso x positivi: E y = cBz (5.12)
6
La situazione è analoga a quando si prende il quadrato di ambo i membri di un’equazione algebrica x = y: l’equazione
risultante x2 = y2 possiede tutte le soluzioni dell’equazione iniziale x = y ma anche tutte quelle dell’equazione x = −y.
Sono introdotte cioè delle soluzioni aggiuntive e l’equazione finale non è equivalente a quella iniziale.
19
Un calcolo analogo per onde che viaggiano verso gli x negativi fornisce invece Ey = −cBz.7 Inoltre,
se si considera la soluzione generale contenente onde che viaggiano in ambedue le direzioni, è
facile dimostrare che le relazioni trovate restano entrambe valide, separatamente per l’onda che
viaggia in un verso e per quella che viaggia nell’altro. In conclusione, è chiaro che non ci può essere
un’onda solo elettrica o solo magnetica. In un’onda i due campi sono sempre inestricabilmente
legati. Per questo motivo l’onda è detta elettromagnetica.
Il legame tra campo elettrico e magnetico di un’onda di forma qualsiasi è illustrato
schematicamente nella figura seguente, dove una “istantanea” dell’onda mostra il vettore campo
elettrico (in rosso) e quello magnetico (in blu) in una regione di spazio (coordinata x). Nella figura
gli assi Bz ed Ey hanno due scale tali da rendere approssimativamente uguali le lunghezze dei vettori
campo elettrico e campo magnetico relativi allo stesso punto.
Bz
Ey
x
Se adesso analizziamo l’equazione (5.5) con lo stesso approccio, otteniamo esattamente gli stessi
risultati, salvo per un cambio di segno nella relazione tra campo Ez e By (cioè Ez = −cBy per onda
che viaggia verso gli x positivi).8 In tutti i casi, quindi, il campo elettrico, quello magnetico e la
direzione di propagazione formano una terna levogira di vettori ortogonali, come gli assi xyz
(nell’ordine) di un normale sistema cartesiano.
In generale, l’onda elettromagnetica potrà avere anche entrambe le componenti y e z di ciascun
campo, elettrico e magnetico. Le componenti possibili dei campi sono quelle trasversali alla
direzione di propagazione, ossia all’asse x, per cui le onde elettromagnetiche sono un altro esempio
di onde trasversali. Fissando l’attenzione su uno solo dei campi, ad esempio il campo elettrico, la
situazione si presenta del tutto analoga a quella discussa nel paragrafo 3.3 a proposito della
polarizzazione delle onde sulla corda tesa. Con la sostituzione r(x,t)→E(x,t) tutte le equazioni del
paragrafo 3.3 per le varie polarizzazioni risultano applicabili alle onde elettromagnetiche piane.
Quindi è possibile definire i vari possibili stati di polarizzazione di un’onda elettromagnetica, quali
polarizzazioni lineari, circolari, ellittiche. Le uniche differenze con il caso della corda tesa si hanno
per le equazioni relative a energia e momento angolare, come discuteremo più avanti.
Prima di concludere, notiamo che la scelta del sistema di riferimento usato in questo paragrafo è
stata del tutto arbitraria. Perciò tutti i risultati che abbiamo ottenuto per una simmetria piana rispetto
al piano yz valgono anche per un qualsiasi altro piano di simmetria. Un’onda piana, ossia per la
7
Questo risultato, d’altronde, è anche quanto si trova a partire dalla (5.12) ruotando il sistema di riferimento di 180°
attorno all’asse y o z, in modo da rovesciare il verso dell’asse x.
8
Anche questo risultato è in realtà scontato, in quanto la coppia (Ey, Bz) si trasforma nella coppia (Ez, −By) per una
rotazione di 90° degli assi y e z attorno all’asse x.
20
quale i campi sono costanti per traslazioni parallele ad un piano qualsiasi, risulterà in ogni caso
propagarsi lungo la direzione perpendicolare al piano di simmetria. Il modulo del campo elettrico
(espresso in volt a metro, V/m, o newton a coulomb, N/C) sarà sempre uguale al modulo del campo
magnetico (espresso in tesla, T) moltiplicato per la velocità della luce c (espressa in m/s).9 Inoltre i
due campi sono sempre ortogonali tra loro e, insieme con la direzione di propagazione dell’onda,
formano una terna levogira (come il sistema normale di assi cartesiani xyz) come quella mostrata
nella figura seguente.
B
E
direzione di
propagazione
dell’onda
Per concludere questo paragrafo, facciamo una piccola parentesi storica per descrivere la scoperta
delle onde elettromagnetiche. Quando Maxwell completò le sue famose equazioni del campo
elettromagnetico, data la sua notevole abilità matematica, gli ci volle ben poco per svolgere i calcoli
mostrati in questo paragrafo. Si accorse così immediatamente del fatto, allora ancora sconosciuto,
che il campo elettromagnetico poteva propagarsi in forma di onde: una previsione di per sé già
interessantissima. Maxwell calcolò poi la velocità di queste onde usando la formula (5.8) e i valori
allora conosciuti sperimentalmente di ε0 e µ0, e trovò che la velocità prevista per le onde
elettromagnetiche era esattamente uguale a quella già nota sperimentalmente della luce (entro gli
errori sperimentali). Questo era un chiaro indizio del fatto che la luce non fosse altro che una forma
particolare di onda elettromagnetica, un’ipotesi che poi si rivelò esatta. In questo modo la teoria
dell’elettromagnetismo si unificava alla teoria dell’ottica, fino ad allora del tutto indipendente,
fornendo così una spiegazione della natura fondamentale della luce: era uno dei momenti più
importanti della storia della scienza! Onde elettromagnetiche generate direttamente da circuiti
elettrici furono dimostrate sperimentalmente da Hertz dopo alcuni anni, confermando così
pienamente la teoria di Maxwell.
3.6 Onde elettromagnetiche armoniche: lo spettro elettromagnetico
Essendo soggette all’equazione di D’Alembert (5.7), le onde elettromagnetiche ammettono come
soluzioni particolari (e modi normali) le onde armoniche10. Come per tutte le onde armoniche,
un’onda armonica elettromagnetica sarà caratterizzata da: una frequenza temporale, angolare ω,
oppure ciclica ν = ω/(2π) e una frequenza spaziale (angolare) k o la corrispondente lunghezza
d’onda λ = 2π/k. Come sempre, frequenza temporale e spaziale (e quindi la lunghezza d’onda) sono
però legate tra loro dalla relazione di dispersione che fissa la velocità delle onde c, e che può essere
scritta in una delle forme equivalenti11
9
Per ricordare questa relazione senza confondersi, è opportuno tenere a mente che in un’onda elettromagnetica il valore
numerico del campo elettrico è sempre molto più grande del valore numerico del campo magnetico, se esprimiamo tutti
i campi in unità del sistema internazionale.
10
In questo paragrafo ci riferiamo in particolare alle onde armoniche viaggianti, ma considerazioni simili valgono anche
per quelle stazionarie.
11
Per non confondervi nel ricordare queste relazioni, utilizzate sempre le dimensioni delle grandezze coinvolte per
controllarle, e non mescolate grandezze angolari e grandezze cicliche nella stessa relazione (a meno di non introdurre
un fattore 2π di conversione).
21
ω = ck
⇔
λν = c (6.1)
Anche se legate tra loro, frequenza e lunghezza d’onda delle onde elettromagnetiche possono
assumere qualsiasi valore positivo, ossia qualsiasi valore nell’intervallo (0,+∞). Questo intervallo
infinito di frequenze possibili è detto spettro elettromagnetico (da non confondere con lo spettro di
Fourier di una particolare onda elettromagnetica). Al variare della frequenza o lunghezza d’onda, la
natura e le caratteristiche dell’onda elettromagnetica nel vuoto non cambiano. In altre parole, tutte
le onde elettromagnetiche sono simili, finché sono nel vuoto. Se però consideriamo le proprietà di
interazione con la materia, troviamo comportamenti molto diversi al variare della frequenza
dell’onda. Questo non ci deve sorprendere, dato che l’interazione di un’onda elettromagnetica con
la materia non è descritta dalle equazioni di Maxwell nel vuoto studiate nel paragrafo precedente.12
La diversità di comportamento ha portato anche all’introduzione di nomi diversi per indicare onde
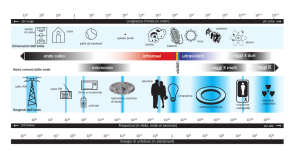
appartenenti a intervalli diversi di frequenze o lunghezze d’onda, o “regioni” diverse dello spettro
elettromagnetico caratterizzate da proprietà di interazione con la materia chiaramente distinte. Nella
tabella seguente riportiamo le regioni principali dello spettro elettromagnetico (queste sono poi
suddivise in sotto-regioni, che qui non consideriamo):
Intervallo λ
Intervallo ν
Nome
Principali proprietà
> 10 cm
< 3 GHz
onde radio
- generate e assorbite da correnti elettriche oscillanti su
corpi conduttori (antenne)
- natura ondulatoria dominante, praticamente impossibile
evidenziarne natura particellare quantistica
- usate per telecomunicazioni a grande distanza
- effetti biologici: nulli o modesti
microonde
- intermedie tra onde radio e raggi infrarossi
- usate nei forni a microonde e per telecomunicazioni a
media distanza (televisione, telefonia cellulare)
0.1 mm – 10 cm 3·109 – 3 ·1012 Hz
0.7 – 100 µm
3·1012 – 4.3 ·1014 Hz
raggi infrarossi
(IR)
- generati e assorbiti da molecole e cristalli (transizioni
rotovibrazionali)
- emessi da tutti i corpi a temperatura ambiente come
radiazione termica
- usati per trasmettere calore e per telecomunicazioni a
breve distanza o in fibra ottica
- effetti biologici: riscaldamento dei tessuti
0.4 – 0.7 µm
4.3·1014 – 7.5 ·1014 Hz
luce visibile
- generata e assorbita da atomi, molecole e cristalli
(transizioni elettroniche)
- è agevole rivelarne natura particellare quantistica
(fotoni) e ondulatoria allo stesso tempo
- usata per visione, fotosintesi, generatori elettrici
fotovoltaici
10 – 400 nm
7.5·1014 – 3 ·1016 Hz
raggi ultravioletti
(UV)
- generati e assorbiti da atomi, molecole e cristalli
(transizioni elettroniche)
- usati per indurre reazioni chimiche e per la fotolitografia
di chip a semiconduttore
- effetti biologici: danni molecolari alle cellule della pelle
10−2 –10 nm
3·1016 – 3 ·1019 Hz
raggi x
- generati e assorbiti da atomi (transizioni elettroniche
profonde)
- prevale natura particellare (fotoni), ma diffrazione nei
cristalli evidenzia natura ondulatoria
- usati per radiografie e per studio struttura cristalli
- effetti biologici: danni molecolari (alterazioni genetiche)
<10 pm
> 3·1019 Hz
raggi γ
- generati e assorbiti da nuclei e in reazioni tra particelle
elementari (subnucleari)
- natura particellare (fotoni) dominante, praticamente
impossibile rivelarne natura ondulatoria
- usati per studiare reazioni nucleari e subnucleari e
fenomeni astrofisici
- effetti biologici: danni molecolari
12
Una comprensione completa dell’interazione tra le onde elettromagnetiche e la materia richiede anche l’uso della
meccanica quantistica e non può essere trattato qui.
22
Ovviamente i confini tra le varie regioni dello spettro non sono così netti come questa tabella può
far pensare, e le classificazioni a volte differiscono nella collocazione esatta dei confini (è una
questione puramente di nome, perché le proprietà delle onde variano comunque con continuità nel
passaggio da una regione all’altra).
La luce visibile ci appare di colore diverso a seconda della frequenza o lunghezza d’onda. I colori
delle varie onde armoniche sono i cosiddetti colori dell’arcobaleno. Ecco una figura che riporta la
parte visibile dello spettro elettromagnetico:
Spettro della luce visibile
luce
ultravioletta
luce
infrarossa
Lunghezza d’onda (nm)
Notate che non tutti i colori sono rappresentati in questa figura. Come mai? Che tipo di onda ad
esempio avrà un colore marrone, oppure bianco? La risposta è che i colori non presenti nello spettro
corrispondono in effetti a onde non armoniche, cioè a onde ottenute sovrapponendo due o più onde
armoniche, come si può verificare sperimentalmente utilizzando un qualsiasi fenomeno fisico che
induca dispersione, ossia separazione delle frequenze, come ad esempio la rifrazione in un prisma
di vetro. Come abbiamo già detto nel capitolo precedente, le onde armoniche sono anche dette
monocromatiche, parola derivata dal greco che significa “ad un solo colore”.
3.7 Energia e intensità delle onde elettromagnetiche
Le onde elettromagnetiche, come le onde meccaniche, trasportano energia. Per calcolare il
contenuto di energia di un’onda, partiamo dall’espressione generale della densità spaziale di energia
elettrica e magnetica associata ai campi dell’onda nel vuoto (si veda un qualsiasi testo elementare di
elettromagnetismo per una derivazione):
densità di energia del campo elettromagnetico:
dU
1
1 2
B
= u = ε0E2 +
dV
2
2µ0
(7.1)
dove abbiamo utilizzato il simbolo U al posto di E per indicare l’energia (per evitare confusione con
il campo elettrico) e abbiamo anche introdotto il simbolo u per indicare la sua densità spaziale, ossia
l’energia per unità di volume.
L’espressione (7.1) ha validità del tutto generale, salvo per il fatto di riferirsi allo spazio vuoto.
Restringendo l’attenzione ad un’onda piana che viaggia in un solo verso, come quelle considerate
nel paragrafo 5, possiamo utilizzare la relazione E = cB tra i moduli dei campi elettrico e magnetico,
e sfruttando c2 = 1/(ε0µ0) scopriamo che i due contributi, elettrico e magnetico, risultano uguali tra
loro. Perciò, in un’onda piana si può utilizzare la seguente espressione semplificata:
densità di energia (per unità di volume) di un’onda elettromagnetica piana:
u = ε 0 E 2 (7.2)
23
Ora restringiamo ulteriormente l’attenzione al caso in cui l’onda elettromagnetica piana sia anche
armonica, per cui possiamo scrivere il campo elettrico nella forma
E = E0 cos(kx−ωt+ϕ)
(7.3)
dove E0 in questo caso indica l’ampiezza dell’onda espressa in termini di campo elettrico, che
rappresenta una delle caratteristiche principali di un’onda elettromagnetica armonica (stiamo
assumendo che l’onda sia polarizzata linearmente, ma tralasciamo di indicare la direzione in cui
l’onda è polarizzata, perché ininfluente). Tenendo conto del fatto che la media di una funzione seno
o coseno quadro è uguale a ½, ossia che ⟨cos2ωt⟩ = ½, possiamo ora scrivere l’espressione della
densità media di energia dell’onda
densità media di energia di onda elettromagnetica armonica:
1
u = ε 0 E 2 = ε 0 E02 (7.4)
2
Come nel caso del suono, a partire dall’energia per unità di volume si definisce anche la cosiddetta
intensità dell’onda elettromagnetica (detta anche irradianza, nel caso di onde luminose, ossia con
frequenza nel dominio del visibile), che corrisponde alla potenza dell’onda per unità di superficie.
In altre parole, l’intensità fornisce l’energia che fluisce attraverso una superficie ortogonale alla
direzione di propagazione dell’onda per unità di superficie e per unità di tempo. L’intensità si
ottiene a partire dalla densità (di volume) dell’energia semplicemente moltiplicandola per la
velocità di propagazione c. Nel caso di onda armonica, l’intensità media è quindi data da
intensità media di onda armonica elettromagnetica:
I=
dU
dU
1
=c
= cε 0 E02
dSdt
dV
2
(7.5)
Nel sistema internazionale, l’intensità di un’onda si misura in W/m2.
L’espressione (7.5) non è molto diversa da quella trovata per le onde meccaniche di vario tipo,
essendo quadratica nell’ampiezza dell’onda. Tuttavia vanno notate alcune interessanti differenze.
Nella (7.5) non compare né la frequenza né la lunghezza d’onda. Un’onda elettromagnetica di una
data ampiezza (in termini di campo elettrico o magnetico) ha la stessa intensità e trasporta la stessa
energia qualsiasi sia la sua frequenza o lunghezza d’onda. In questo l’onda elettromagnetica
differisce dalle onde meccaniche, che tipicamente hanno un contenuto energetico proporzionale al
quadrato della frequenza. Un’altra differenza, legata alla precedente, è nella localizzazione
dell’energia trasportata. Infatti, come si vede dalle (7.1) e (7.2), l’energia è localizzata dove i campi
elettrici e magnetici sono più intensi, mentre nel caso meccanico l’energia è localizzata dove i
campi di spostamento hanno la derivata (spaziale o temporale) più intensa.13
3.8 Onde nello spazio tridimensionale: equazione delle onde 3D
I sistemi fisici considerati finora per studiare i fenomeni ondulatori erano tutti sistemi ad una
dimensione spaziale, il che corrisponde a dire che una sola coordinata basta a definire in modo
completo la posizione su cui occorre specificare il valore del campo. Quindi il campo ξ (o i campi,
se ve ne sono più di uno) è funzione di una sola coordinata spaziale (ad esempio x) e del tempo. In
particolare, nel caso della catena di pendoli o della corda vibrante, il sistema fisico è
intrinsecamente unidimensionale. Invece nel caso del suono e del campo elettromagnetico, i campi
13
Tuttavia, l’analogia tra onde elettromagnetiche e onde meccaniche ritorna ad essere completa se le onde
elettromagnetiche vengono espresse in termini del potenziale vettore A, anziché dei campi E e B.
24
che descrivono il sistema fisico si estendono in realtà in tutto lo spazio tridimensionale, e la nostra
trattazione ad una dimensione si è basata sull’ipotesi che sia presente la cosiddetta simmetria piana,
ossia che nessun campo fisico del sistema dipenda da due coordinate cartesiane (ad esempio y e z),
che definiscono il piano di simmetria. In altre parole il valore del campo resta costante se ci si
sposta in una qualsiasi direzione parallela al piano di simmetria.
Ora passiamo a considerare invece il caso più generale in cui i campi dipendono da tutte e tre le
coordinate spaziali, ossia x, y, z, oltre che dal tempo, ossia in cui il sistema è pienamente
tridimensionale (3D). Il punto di partenza dovrebbe essere quello di determinare l’equazione
differenziale delle onde in 3D. In realtà, come avviene anche nel caso 1D, esistono diverse
equazioni differenziali (o sistemi di equazioni differenziali) che danno luogo a fenomeni ondulatori.
Ma c’è anche un’equazione che costituisce la naturale generalizzazione dell’equazione di
D’Alembert al caso 3D, e che pertanto viene chiamata anch’essa equazione delle onde.
Questa equazione può essere trovata in vari modi. Un possibile approccio è quello di considerare la
più semplice generalizzazione 3D dell’equazione di D’Alembert (la (1.8) del capitolo 2) sulla base
di considerazioni di simmetria legate al fatto che nello spazio 3D tutte le direzioni sono equivalenti
tra loro (questa particolare simmetria prende il nome di isotropia). Le condizioni da imporre alla
nostra equazione 3D sono due: (i) dato che tutte le direzioni sono equivalenti, le variabili x, y e z
corrispondenti alle tre direzioni degli assi cartesiani devono entrare nell’equazione in modo
simmetrico, ossia intercambiabile; (ii) nel caso particolare di simmetria piana rispetto ad un
qualsiasi piano, l’equazione 3D deve ridursi all’equazione 1D di D’Alembert in cui l’unica variabile
spaziale che compare è quella corrispondente all’asse ortogonale al piano di simmetria considerato.
Non è difficile dimostrare che l’unica equazione differenziale lineare nel campo 3D ξ(r,t) =
ξ(x,y,z,t) che soddisfa entrambe le condizioni è la seguente:
∂ 2ξ ∂ 2ξ ∂ 2ξ 1 ∂ 2ξ
equazione differenziale delle onde 3D:
+
+
−
=0
∂x 2 ∂y 2 ∂z 2 v 02 ∂t 2
(8.1)
dove v0 è una qualsiasi costante caratteristica del sistema, che assume il significato di velocità delle
onde nel caso di simmetria piana. Questa equazione può anche essere scritta nella seguente forma
compatta
equazione differenziale delle onde 3D (versione compatta):
∇ 2ξ −
1 ∂ 2ξ
=0
v 02 ∂t 2
(8.2)
Dove abbiamo introdotto il “modulo-quadro” del gradiente, ossia ∇2 (questo simbolo è a volte
sostituito da ∆) corrispondente alla somma delle derivate seconde del campo rispetto alle tre
variabili spaziali cartesiane. Questo operatore differenziale è anche noto con il nome di
“laplaciano”, dal nome del fisico-matematico Laplace.
In alternativa a questo approccio, possiamo trovare l’equazione delle onde 3D considerando un
particolare sistema fisico per il quale ci aspettiamo un comportamento ondulatorio in 3D.
Consideriamo ad esempio nuovamente il campo elettromagnetico nel vuoto. Partiamo sempre dalle
equazioni di Maxwell nel vuoto (5.1) e, senza assumere più la simmetria piana (cioè la non
dipendenza dei campi dalle coordinate y e z), cerchiamo di determinare un’equazione che valga per
un singolo campo, ad esempio quello elettrico E. Per fare questo usiamo lo stesso trucco usato nel
paragrafo 3.5, e cioè calcoliamo prima di tutto il rotore di ambo i membri della prima delle
equazioni di Maxwell (5.1) (ossia il prodotto vettoriale dell’operatore gradiente ∇ per ciascun
termine). Otteniamo così:
25
∇ × ∇ × E = −∇ ×
∂B
∂
= − ∇×B
∂t
∂t
(8.3)
dove nella seconda uguaglianza abbiamo scambiato l’ordine di derivazione tra la variabile tempo e
quelle spaziali. Adesso possiamo sostituire al secondo membro della (8.3) l’espressione del rotore
di B fornita dalla seconda delle equazioni di Maxwell (5.1), ottenendo così la seguente equazione
per il solo campo E:
∇ × ∇ × E = −ε 0 µ0
∂ 2E
∂t 2
(8.4)
Il “rotore del rotore” presente a primo membro può ora essere convertito in una espressione
equivalente utilizzando la formula del prodotto triplo vettoriale a×(b×c) = b (a⋅c) − (a⋅b) c, per cui
si ha:
∇ × ∇ × E = ∇(∇ ⋅ E) − ∇ 2 E (8.5)
Utilizzando infine la terza delle equazioni di Maxwell (5.1), ossia che la divergenza del campo ∇⋅E
si annulla, il primo termine della (8.3) si annulla, per cui otteniamo infine la seguente equazione:
∂ 2E
∇ E − ε 0 µ0 2 = 0
∂t
2
(8.6)
che in effetti è identica all’equazione (8.2). Il fatto che nella (8.6) compaia il vettore E come
incognita anziché lo scalare ξ significa semplicemente che la stessa equazione si applica a ciascuna
componente del campo E, indipendentemente dalle altre componenti. Un’equazione identica alla
(8.6) si trova anche per il campo magnetico B.
Perciò, i campi elettrici e magnetici nello spazio vuoto obbediscono proprio all’equazione delle
onde 3D (8.1), con la costante v 0 = c = 1 ε 0 µ0 . Però, come già avveniva nel caso 1D, la nostra
derivazione dell’equazione (8.6) ha in realtà introdotto soluzioni aggiuntive spurie. In particolare
anche nel caso 3D i campi E e B non sono indipendenti ma risultano strettamente legati tra loro e,
una volta determinato uno dei due, l’altro risulta completamente fissato (salvo per una costante
additiva) a partire da una delle prime due equazioni di Maxwell. Inoltre, l’equazione (8.6) da sola
permetterebbe l’esistenza di onde indipendenti per ciascuna delle tre componenti del campo E. In
realtà le tre componenti non sono indipendenti, perché sono legate tra loro anche dalla terza
equazione di Maxwell (5.1), ossia dal fatto che la divergenza si deve annullare identicamente.
Un esempio di sistema fisico che obbedisce esclusivamente all’equazione delle onde (8.1) senza
vincoli aggiuntivi è quello del suono in aria. In particolare, si può dimostrare che la pressione p e la
densità ρ dell’aria obbediscono proprio all’equazione (8.1), con v0 dato dalla (4.5) o (4.7) già
determinata.
Ora che abbiamo fissato l’equazione differenziale delle onde 3D, iniziamo a studiarne alcune
possibili soluzioni.
26
3.9 Onde armoniche piane (dette anche “onde piane”) in 3D
Un possibile approccio alla risoluzione dell’equazione (8.1) è basato sul metodo della soluzione di
prova esponenziale complessa. Essendoci adesso quattro variabili indipendenti, ossia x, y, z e t, la
nostra soluzione di prova esponenziale avrà la forma seguente:
soluzione di prova equazione delle onde 3D:
ξ = Ae (
i k x x + k y y + k z z −ωt
)
= Aei( k ⋅r −ωt )
(9.1)
dove abbiamo introdotto i coefficienti kx, ky, kz e ω e, nella seconda espressione, abbiamo raccolto i
tre coefficienti che moltiplicano le variabili spaziali in un unico vettore k = (kx, ky, kz), che risulta
moltiplicato scalarmente per il vettore posizione r = (x, y, z). In generale questi coefficienti kx, ky, kz
e ω potrebbero anche assumere valori complessi, ossia l’esponente dell’esponenziale complesso di
prova (9.1) potrebbero essere complessi anziché immaginari puri. Tuttavia è chiaro che nel caso
nostro ω deve essere necessariamente reale, o altrimenti la soluzione (9.1) presenterebbe
un’attenuazione o amplificazione esponenziale che risulterebbe incompatibile con la legge della
conservazione dell’energia. Inoltre, se lo spazio in cui stiamo considerando la nostra soluzione si
estende fino all’infinito in tutte le direzioni, anche i coefficienti kx, ky, kz devono necessariamente
essere reali, perché altrimenti la (9.1) presenterebbe una divergenza all’infinito. E’ però importante
tenere a mente il fatto che quest’ultima condizione viene a cadere se risolviamo l’equazione (9.1) in
una regione di spazio delimitata, anche solo in parte.
E’ chiaro che ω ha il significato fisico di frequenza (angolare) temporale come nel caso 1D e che il
vettore k generalizza al caso 3D il concetto di frequenza spaziale k già introdotto nel caso 1D.
Sostituendo questa soluzione di prova nell’equazione (8.1) e semplificando il fattore esponenziale
comune a tutti i termini, si ottiene la seguente relazione:
k +k +k −
2
x
2
y
2
z
ω2
v02
=0
(9.2)
In pratica, la (9.2) vincola (a meno del segno) il valore di uno dei quattro coefficienti a partire dagli
altri tre, che restano completamente arbitrari. Ad esempio, possiamo fissare arbitrariamente i tre
coefficienti kx, ky, kz, ossia l’intero vettore k, e la frequenza ω risulterà allora fissata dalla seguente
relazione di dispersione (equazione delle onde 3D): ω = ω (k ) = v0 k = v0 k x2 + k y2 + k z2 (9.3)
dove, come al solito, possiamo limitarci a considerare solo le frequenze positive in quanto le
frequenze negative restituiscono le medesime soluzioni una volta che si torna alla notazione reale.
Quando la relazione (9.2) o (9.3) è soddisfatta, allora la soluzione di prova (9.1) funziona
effettivamente ed abbiamo quindi trovato una soluzione particolare dell’equazione delle onde 3D.
Questo tipo di soluzione particolare, che chiaramente generalizza l’onda armonica del caso 1D, è
detta onda armonica piana, ed assume quindi una delle forme seguenti, equivalenti tra loro:
onda armonica piana (notaz. complessa):
ξ = Ac e (
i k x x + k y y + k z z −ω t
)
= Ac e (
i k ⋅r −ωt )
(9.4)
onda armonica piana (notaz. reale): ξ = A cos ( k x x + k y y + k z z − ωt + ϕ ) = A cos ( k ⋅ r − ωt + ϕ ) (9.5)
27
Il vettore k prende il nome di vettore d’onda.14 Il significato fisico di questo vettore k può essere
riconosciuto immediatamente se passiamo ad un nuovo sistema di riferimento cartesiano x′y′z′ con
l’asse x′ parallelo a k. Infatti, in questo sistema di riferimento la (9.4) si riscrive come segue:
onda armonica piana (sistema di riferimento con asse x′ || k):
ξ = Ac e (
i k x′−ω t )
= Ac ei( kx
′−ωt )
(9.6)
dove k = |k| è il modulo del vettore d’onda k. Notate come la (9.6) risulti identica all’espressione di
un’onda armonica 1D nella sola variabile spaziale x′ e in cui le variabili y′ e z′ non compaiono
esplicitamente. Quindi un’onda armonica piana descrive una dinamica del campo ξ che possiede
simmetria piana rispetto al piano perpendicolare al vettore d’onda k, ossia non varia spostandosi
nelle direzioni perpendicolari al vettore k (cioè giacenti nel piano y′z′). Inoltre, l’onda piana si
propaga nella direzione e nel verso fissati dal vettore k. Il modulo k del medesimo vettore fissa il
numero d’onde, ossia la frequenza spaziale dell’onda e quindi la sua lunghezza d’onda λ = 2π/k.
Infine, il modulo k del vettore d’onda fissa anche la frequenza temporale ω tramite la relazione di
dispersione (9.3).
In effetti un altro modo per trovare tutte le soluzioni (9.4), ossia le onde piane, è proprio quello di
prendere la soluzione già trovata nel paragrafo 3.5 per il caso di simmetria piana rispetto al piano yz
e poi applicarvi una rotazione generica, in modo da orientare la direzione di propagazione dell’onda
come si vuole.
Ovviamente le onde armoniche piane sono solo soluzioni particolari dell’equazione delle onde 3D
(8.1). Resta tuttavia aperto il problema di scrivere l’espressione della soluzione generale
dell’equazione delle onde 3D (8.1). Purtroppo, contrariamente al caso 1D, nel caso 3D non esiste
una semplice formula non integrale per la soluzione generale. Si può dimostrare, tuttavia, che anche
in questo caso la soluzione generale può essere scritta come la combinazione lineare di tutte le
possibili onde armoniche piane che si ottengono al variare del vettore d’onda k, ossia nella seguente
forma integrale:
soluzione generale eq. onde 3D (not. compl.): ξ (r, t ) =
∞ ∞ ∞
∫ ∫ ∫ a (k )e
c
i[k ⋅r −ω ( k ) t ]
dk x dk y dk z (9.7)
−∞ −∞ −∞
dove la funzione ω(k) è fissata dalla relazione di dispersione (9.3), ossia ω(k) = v0|k|. La funzione
(complessa) ac(k) rappresenta l’insieme dei coefficienti della combinazione lineare. Per avere la
soluzione generale in notazione reale dobbiamo prendere la parte reale dell’integrale (9.7).
3.10 Onde armoniche sferiche
L’equazione delle onde 3D, nella forma (8.1), è scritta in coordinate cartesiane. In queste coordinate
il problema è particolarmente semplice perché l’equazione differenziale è a coefficienti costanti, per
cui ammette le solite soluzioni esponenziali complesse. Questo ci ha consentito di trovare un
insieme completo di soluzioni particolari, la cui combinazione lineare (sotto forma di integrale
triplo), fornisce una soluzione generale del problema.
14
In generale, e soprattutto nel caso delle onde trasversali, fate attenzione a non confondere il vettore d’onda k con il
vettore ξ(r) che rappresenta, punto per punto, il campo vettoriale dell’onda.
28
Tuttavia, per affrontare problemi fisici che presentano simmetria sferica attorno ad un qualche
punto O dello spazio, le onde piane non sono molto comode perché non posseggono tale simmetria.
E’ vero che l’integrale (9.7) di tutte le onde piane è in grado di descrivere qualsiasi soluzione, ma il
suo utilizzo in pratica è spesso difficile e quanto meno molto laborioso. In molti casi conviene
riformulare il problema dall’inizio in coordinate polari sferiche con origine nel punto O.
Per un qualsiasi punto r = (x, y, z), le coordinate polari sferiche sono le seguenti: la distanza r = |r|
dal centro O del sistema di coordinate (con valori compresi tra 0 e ∞); l’angolo polare θ che
descrive la “latitudine”, ossia l’angolo tra il vettore r e l’asse z (con valori compresi tra 0,
corrispondente al “polo nord” e π, corrispondente al “polo sud”); e l’angolo azimutale ϕ, che
descrive la “longitudine” del punto, ossia l’angolo tra la proiezione sul piano xy del vettore r e
l’asse x, che fa da “meridiano di Greenwich” (con valori compresi tra 0 e 2π). Il campo ξ può essere
allora espresso come funzione delle coordinate sferiche r, θ e ϕ anziché x, y e z, oltre che dal tempo
t, ossia come funzione ξ(r,θ,ϕ,t).
Ora dobbiamo riscrivere anche l’equazione delle onde in coordinate polari sferiche. Questo può
essere ottenuto a partire dalla (8.1) mediante le tre funzioni che esprimono le coordinate x, y e z in
termini di r, θ e ϕ.15 Oppure, più semplicemente, utilizziamo la forma vettoriale (8.2) (che è
indipendente dalle coordinate utilizzate) sostituendovi la seguente espressione (tratta da un qualsiasi
testo di fisica 2 o di metodi matematici) in termini di coordinate polari-sferiche dell’operatore
laplaciano ∇2:
laplaciano in coordinate polari sferiche: ∇ 2 =
1 ∂2
1
∂
∂
1
∂2
θ
(10.1)
r
+
sin
+
∂θ r 2 sin 2 θ ∂ϕ 2
r ∂r 2
r 2 sin θ ∂θ
Sostituendo questa espressione nella (8.2) otteniamo l’equazione delle onde 3D scritta in coordinate
sferiche (notate in particolare come viene eseguita l’applicazione dell’operatore ∇2 alla funzione ξ):
1 ∂2
1
∂ 
∂ξ 
1
∂ 2ξ 1 ∂ 2ξ
−
= 0 (10.2)
( rξ ) + 2
 sin θ
+
r ∂r 2
r sin θ ∂θ 
∂θ  r 2 sin 2 θ ∂ϕ 2 v02 ∂t 2
Questa equazione appare abbastanza complicata. In particolare, essa è ancora un’equazione
differenziale alle derivate parziali lineare e omogenea, ma non è più a coefficienti costanti. Perciò,
non possiamo più usare gli esponenziali complessi come soluzioni di prova nel modo consueto
(almeno non per tutte e quattro le variabili). Impareremo più avanti ad affrontare questo tipo di
equazioni in modo abbastanza generale. Per il momento, ci contentiamo invece di cercare delle
soluzioni particolari che siano particolarmente semplici (scusate il bisticcio di parole).
Cerchiamo, quindi, soluzioni particolari dotate di simmetria sferica, ossia che restino invariate per
rotazioni arbitrarie attorno al punto O. Tali soluzioni, in altre parole, non devono dipendere affatto
dagli angoli θ e ϕ, per cui assumono la seguente forma semplificata
campi aventi simmetria sferica: ξ = ξ(r,t)
(10.3)
15
Per chi si vuole cimentare, le funzioni sono le seguenti: x = r sinθ cosϕ; y = r sinθ sinϕ; z = r cosθ. Per riscrivere una
derivata parziale rispetto ad una coordinata cartesiana in termini di derivate parziali rispetto alle coordinate polari, si
utilizza la regola di derivata di funzione di funzione. Ad esempio ∂/∂x = (∂x/∂r)∂/∂r + (∂x/∂θ)∂/∂θ + (∂x/∂ϕ)∂/∂ϕ = sinθ
cosϕ ∂/∂r + r cosθ cosϕ ∂/∂θ − r sinθ sinϕ ∂/∂ϕ. Analogamente si procede per le altre derivate e con le derivate
seconde.
29
Sostituendo questa espressione nella (10.2), tutte le derivate rispetto a θ e ϕ si annullano
identicamente, e resta la seguente equazione:
2
1 ∂ ( rξ ) 1 ∂ 2ξ
− 2 2 =0
r ∂r 2
v 0 ∂t
(10.4)
Se ora moltiplichiamo per r tutti i termini di questa equazione e introduciamo un nuovo campo η
definito come η(r,t) = r ξ(r,t), troviamo la seguente equazione:
∂ 2η 1 ∂ 2η
−
=0
∂r 2 v 02 ∂t 2
(10.5)
Questa equazione non è altro che l’equazione delle onde 1D o equazione di D’Alembert con la
variabile spaziale r al posto di x. Pertanto ne conosciamo la soluzione generale
η = f(r−v0t) + g(r+v0t)
(10.6)
che riespressa nuovamente in termini del campo ξ ci fornisce la seguente ampia classe di soluzioni
a simmetria sferica dell’equazione delle onde 3D:
onde sferiche di forma qualsiasi:
ξ=
f ( r − v 0t ) g ( r + v 0 t )
+
r
r
(10.7)
I due termini che compaiono in questa soluzione corrispondono rispettivamente ad un’onda sferica
uscente dal centro O, ossia che si allarga progressivamente con velocità v0, ed un’onda sferica
entrante, ossia che converge progressivamente sul centro O. Entrambe le onde hanno forma
qualsiasi ma, nel propagarsi, la loro forma cambia a causa del fattore 1/r. In particolare le onde
uscenti si attenuano lentamente, con l’inverso della distanza dal centro, mentre le onde entranti si
amplificano progressivamente. La densità di energia per unità di volume, e quindi l’intensità
dell’onda, essendo quadratica nel campo, varia invece come 1/r2. Dato che una superficie sferica ha
un’area di 4πr2, il flusso totale di energia uscente su tutta una superficie sferica, dato dall’intensità
dell’onda moltiplicata per la superficie, risulterà costante al variare di r, come ci si aspetta per la
conservazione dell’energia trasportata dall’onda.
In molti problemi fisici l’onda sferica entrante non può esistere, cioè si deve avere g = 0, perché
altrimenti il termine g/r diverge quando l’onda raggiunge il centro O. L’onda sferica uscente,
invece, è spesso una buona approssimazione delle onde generate da una sorgente puntiforme posta
nell’origine delle coordinate O.16
Il caso particolare di onde sferiche armoniche uscenti si ottiene (in notazione complessa) ponendo
nella (10.7) f(x) = Ac exp(ikx) e g = 0, con k numero reale positivo. Si ottiene così:
onda armonica sferica uscente (notazione complessa):
ξ=
Ac i( kr −ωt )
e
(10.8)
r
16
Va detto che in tutti i problemi fisicamente realistici dovrà comunque sempre esistere una regione localizzata attorno
all’origine O in cui l’equazione delle onde 3D (10.2) non sarà più valida, o altrimenti l’onda sferica (anche quella
uscente) divergerà. Spesso è proprio la presenza della sorgente, che necessariamente avrà una estensione finita, a
modificare le equazioni in un intorno dell’origine O.
30
o, prendendone la parte reale, l’equivalente
onda armonica sferica uscente (notazione reale):
ξ=
A
cos ( kr − ωt +ψ ) (10.9)
r
(dove abbiamo usato ψ anziché ϕ per evitare confusione con la coordinata polare ϕ). In queste due
equazioni si è posto ω = kv0, da cui si vede che la grandezza k che definisce un’onda armonica
sferica ha valore pari al modulo |k|del vettore d’onda k di un’onda piana armonica di uguale
frequenza. E’ importante notare e tenere bene a mente che nelle onde sferiche (10.8) e (10.9),
compare il prodotto k r = |k| |r|, ossia il prodotto dei moduli dei vettori k e r e non il prodotto
scalare dei vettori k e r che invece compare nelle onde piane.
Per concludere questo paragrafo, notiamo che le onde armoniche sferiche sono modi normali, dato
che tutto i campo oscilla alla medesima frequenza ω. Tuttavia, esse non costituiscono un insieme di
modi normali abbastanza completo da poter scrivere la soluzione generale dell’equazione delle onde
3D come combinazione lineare di esse. Infatti, solo le soluzioni a simmetria sferica, ossia della
forma (10.7), potranno essere ottenute combinando questi modi normali aventi simmetria sferica,
mentre le soluzioni non sfericamente simmetriche richiederebbero di introdurre altri modi normali
non simmetrici. Questi modi normali non sfericamente simmetrici, ma ottenuti dall’equazione delle
onde scritta in coordinate sferiche, in realtà esistono, ma li introdurremo solo più avanti, nell’ambito
della meccanica quantistica.
3.11 Interferenza
Consideriamo due onde ξ1 e ξ2 che si propagano nello spazio provenendo da due regioni diverse.
Può accadere che, nel corso della loro propagazione, le due onde vengano ad occupare una stessa
regione di spazio. In tal caso, il campo totale ξ in tale regione sarà dato dalla somma dei campi ξ1 e
ξ2 associati alle due onde. Infatti, essendo l’equazione delle onde 3D lineare ed omogenea, la
somma di soluzioni sarà anch’essa soluzione, ossia vale il principio di sovrapposizione.
Nel caso le due onde che si sovrappongono siano armoniche ed abbiano uguale frequenza ω, il
campo totale che si ottiene nella loro sovrapposizione presenta delle modulazioni spaziali della
densità di energia, modulazioni non presenti nelle due onde fin quando queste sono separate.
Questo fenomeno, che ora andiamo ad analizzare teoricamente, prende il nome di interferenza.
I dettagli del fenomeno di interferenza dipendono dalla particolare geometria di sovrapposizione
considerata. Consideriamo un caso particolarmente semplice, in cui le due onde armoniche che si
sovrappongono possono essere considerate come onde piane aventi la medesima direzione di
propagazione x. In questo caso il problema diventa essenzialmente unidimensionale ed è di più
facile trattazione.
Tuttavia, in un problema strettamente 1D (ad esempio sulla catena di pendoli) sarebbe impossibile
avere due onde finite, inizialmente separate, che si sovrappongono in un secondo tempo. Infatti la
velocità delle due onde è la stessa, per cui se sono inizialmente separate e si propagano nella stessa
direzione, le due onde non si “raggiungono” mai. Infatti l’interferenza sulla catena di pendoli o in
altri problemi strettamente 1D si può realizzare solo con onde contropropaganti (e vedremo più
avanti cosa si ottiene in questo caso) oppure generando direttamente una seconda onda all’interno
della prima, introducendo ad esempio nel problema una sorgente localizzata (un pendolo soggetto
ad una forza esterna). Ma questi esempi sarebbero già più complicati di quello che vogliamo
31
considerare. Perciò ricorriamo invece alla geometria tridimensionale di sovrapposizione
rappresentata nella figura seguente:
Onda 2
specchio
semiriflettente
onda risultante 2
Onda 1
onda risultante 1
x
In questa geometria, due onde armoniche ed approssimativamente piane (non sono esattamente
piane perché si suppone abbiano una estensione spaziale finita) inizialmente separate, incidono su
uno specchio semiriflettente (che cioè trasmette e riflette l’onda, per esempio suddividendo
l’energia al 50%). In questo modo le due onde si ritrovano alla fine sovrapposte e viaggianti nella
medesima direzione, in ciascuna delle due direzioni di uscita dello specchio, dando luogo a due
“onde risultanti”.
Consideriamo per il momento una sola di queste due onde risultanti, ad esempio l’onda risultante 2,
che si propaga nella direzione x.
Le due onde ξ1 e ξ2, essendo armoniche piane, sono date dalle seguenti espressioni (in notazione
complessa):
ξ1 = Ac1 ei(kx−ωt)
,
ξ2 = Ac2 ei(kx−ωt)
(11.1)
che assumiamo essere valide già per la regione di sovrapposizione, cioè l’effetto sull’ampiezza
complessa della riflessione o trasmissione parziale è già incluso nelle ampiezze Ac1 e Ac2.
Il campo totale sarà perciò dato dalla somma
ξ = ξ1 + ξ2 = Ac1 ei(kx−ωt) + Ac2 ei(kx−ωt) = (Ac1 + Ac2) ei(kx−ωt) = Ac ei(kx−ωt)
(11.2)
dove
ampiezza complessa risultante dalla sovrapposizione:
Ac = Ac1 + Ac2
(11.3)
è l’ampiezza complessa del campo totale, pari quindi alla somma delle due ampiezze complesse
delle due onde. Notiamo che l’onda risultante è ancora un’onda armonica di uguale frequenza e
32
numero d’onde. Calcoliamo ora esplicitamente l’ampiezza e la fase dell’onda risultante dalla
sovrapposizione:17
ampiezza onda risultante dalla sovrapposizione:
A = Ac = Ac Ac* =
( Ac1 + Ac 2 ) ( Ac*1 + Ac*2 ) =
= A + A + A1 A2 e
2
1
2
2
i (ϕ1 −ϕ2 )
+ A1 A2 e
− i (ϕ1 −ϕ2 )
2
2
Ac1 + Ac 2 + Ac1 Ac*2 + Ac*1 Ac 2 =
(11.4)
= A + A + 2 A1 A2 cos (ϕ1 − ϕ 2 )
2
1
2
2
e
 A sin ϕ1 + A2 sin ϕ 2
fase onda risultante dalla sovrapposizione: ϕ = − arctan 1
 A1 cos ϕ1 + A2 cos ϕ 2



(11.5)
dove si è usato Ac1 = A1 exp(iϕ1) e Ac2 = A2 exp(iϕ2), dove A1 e A2 sono le ampiezze reali delle due
onde che si sovrappongono e ϕ1 e ϕ2 le corrispondenti fasi iniziali. L’espressione della fase
dell’onda risultante non è particolarmente significativa e non ci interessa più di tanto. Invece è
molto importante l’espressione dell’ampiezza dell’onda risultante e la sua dipendenza dalle
caratteristiche delle onde che si sovrappongono. Tuttavia, anziché discutere tale relazione in termini
di ampiezze, trasformiamola prima in una equivalente relazione tra le intensità. Quest’ultima
relazione si ottiene semplicemente uguagliando il quadrato del primo e l’ultimo membro della
(11.4) (o equivalentemente il modulo quadro dei due membri della (11.3)) e poi moltiplicando ambo
i membri per la costante di proporzionalità che sussiste tra l’intensità (media) e il quadrato
dell’ampiezza delle onde armoniche. In questo modo otteniamo facilmente la seguente relazione tra
le intensità delle due onde che si sovrappongono I1 e I2 e quella dell’onda risultante dalla
sovrapposizione, I:
intensità dell’onda risultante dalla sovrapposizione: I = I1 + I 2 + 2 I1 I 2 cos (ϕ1 − ϕ2 ) (11.6)
Una relazione analoga si ottiene per le densità spaziali di energia. La prima cosa da notare è che
l’intensità (ovvero l’energia trasportata) dell’onda risultante non è in generale pari alla somma
delle intensità delle due onde che si sovrappongono. Questo comportamento è appunto denominato
interferenza. C’è invece un termine aggiuntivo, l’ultimo della (11.6), detto termine d’interferenza,
che dipende dalla differenza di fase iniziale delle due onde. Il termine d’interferenza può essere sia
positivo che negativo. Quando esso è positivo, l’onda risultante ha un’intensità maggiore della
somma delle intensità delle due onde componenti, e si dice che c’è “interferenza costruttiva”.
Quando invece il termine d’interferenza è negativo, l’onda risultante ha un’intensità minore della
somma delle intensità, e si dice che c’è “interferenza distruttiva”.
Consideriamo come esempio la sovrapposizione di due onde con la stessa intensità I1 = I2. Se le
onde hanno anche esattamente la stessa fase, ossia ϕ1 = ϕ2, l’onda risultante avrà un’intensità I = 4
I1, cioè doppia rispetto alla semplice somma delle intensità. Questo caso corrisponde alla massima
possibile interferenza costruttiva. Se invece le due onde hanno fase “opposta”, ossia ϕ1 − ϕ2 = ±π,
l’intensità risultante sarà I = 0, cioè le due onde si “annullano a vicenda” e l’onda risultante
scompare completamente! Questo caso corrisponde alla massima possibile interferenza distruttiva.
Per rendersi conto di quanto possa essere sorprendente e contro-intuitivo questo fenomeno,
17
Notate che i medesimi calcoli si possono fare anche lavorando solo in notazione reale, ma sarebbero molto più
laboriosi. Questo è un esempio in cui la notazione complessa è molto vantaggiosa.
33
considerate il caso di due onde luminose: la loro sovrapposizione, in opportune condizioni di
interferenza distruttiva, può dare luogo ad una regione spaziale completamente buia!
Qualcuno potrebbe notare che questa illustrazione del fenomeno di interferenza sembra violare il
principio di conservazione dell’energia. Se c’è dell’energia iniziale contenuta nelle due onde che si
vanno a sovrapporre, come è possibile che quest’energia raddoppi o scompaia del tutto, senza
violare il principio di conservazione? La risposta a questa domanda è legata al modo in cui le onde
vengono a sovrapporsi. Nel nostro esempio, ricordiamo che le due onde si sovrappongono dopo
essere state parzialmente riflesse e parzialmente trasmesse da uno specchio semiriflettente. Questo
dà luogo a due onde risultanti, nelle due direzioni di uscita dello specchio. In entrambe vi sarà
interferenza, e in entrambe l’energia non sarà la somma delle energie delle onde componenti. Ma
un’analisi completa delle variazioni nelle fasi iniziali delle onde prodotte dalla trasmissione e
riflessione nello specchio semiriflettente mostrerebbe che se da un lato c’è interferenza distruttiva,
dall’altro c’è sempre interferenza costruttiva, e che le due interferenze si compensano perfettamente
in modo tale che l’energia totale si conserva.
In pratica, si può dimostrare che in generale quando due onde si sovrappongono ed interferiscono,
l’energia non compare né scompare, ma si redistribuisce dalle zone in cui vi è interferenza
distruttiva alle zone in cui vi è interferenza costruttiva, per cui nel totale l’energia si conserva
sempre.
La formula (11.6) per l’interferenza tra due onde armoniche piane che si propagano nella medesima
direzione) può essere generalizzata facilmente al caso di due onde armoniche qualsiasi (ad esempio
due onde piane che si propagano in direzioni diverse, oppure due onde armoniche sferiche
provenienti da sorgenti diverse, ecc.). Per farlo, iniziamo sostituendo alle espressioni (11.1) per le
due onde armoniche piane, le seguenti
onde armoniche generiche: ξ1 (r, t ) = A1 (r )eiΦ1 (r ,t ) e ξ 2 (r, t ) = A2 (r )eiΦ2 (r ,t )
(11.7)
dove A1(r) e A2(r) sono le ampiezze reali delle due onde e Φ1(r,t) e Φ2(r,t) sono le fasi totali,
definite come tutto quello che compare all’esponente degli esponenziali complessi che descrivono
le onde armoniche (esclusa l’unità immaginaria i). Sia le ampiezze che le fasi totali sono dipendenti
dal punto, specificato con il vettore posizione r. Le fasi totali sono invece funzioni anche del tempo.
Avendo però specificato che stiamo considerando due onde armoniche e di uguale frequenza, le fasi
totali dipendono dal tempo come Φ(r,t) = Φ′(r)−ωt, ossia tramite un termine del tipo −ωt, con lo
stesso ω per entrambe le onde.
Ad esempio, per il caso di due onde piane generiche, date dall’espressione (9.4), le due ampiezze
reali saranno due costanti A1 e A2, e le fasi totali saranno date da
Φ1 = k1⋅r−ωt+ϕ1
e Φ1 = k2⋅r−ωt+ϕ2
(11.8)
Notate che nelle due espressioni per le fasi totali compare lo stesso vettore posizione r, ma due
diversi vettori d’onda k.
Nell’altro esempio, più complesso, di due onde armoniche sferiche, entrambe date da espressioni
analoghe alla (10.8) ma provenienti da due punti diversi A e B (cioè non dall’origine delle
coordinate), le ampiezze e le fasi totali saranno invece date dalle espressioni seguenti:
A1(r) = A1/r1 ,
A2(r) = A2/r2
,
(11.9)
34
Φ1(r,t) = kr1−ωt+ϕ1
,
Φ2(r,t) = kr2−ωt+ϕ2
dove abbiamo introdotto le distanze dalle rispettive sorgenti r1 = |r−rA| e r2 = |r−rB|. Notate che in
questo caso nelle espressioni per le fasi totali compare lo stesso numero d’onde k (e non il vettore
d’onda), che è fissato dalla frequenza ω, ma una diversa distanza r dalla rispettiva sorgente.
A questo punto, ripercorrendo i medesimi ragionamenti fatti per il caso delle due onde piane,
otteniamo nel caso generale il seguente importante risultato:
interferenza (formula generale): I (r ) = I1 (r ) + I 2 (r ) + 2 I1 (r ) I 2 (r ) cos [ Φ1 (r, t ) − Φ 2 (r, t ) ] (11.10)
dove I1(r) e I2(r) sono le intensità (o le densità di energia) di ciascuna onda, ottenute come il
quadrato delle rispettive ampiezze A1(r) e A2(r) moltiplicate per la costante di proporzionalità che le
converte in intensità (o densità di energia). Notate che l’intensità I(r) risultante dall’interferenza non
dipende dal tempo perché la differenza delle due fasi totali Φ1 e Φ2 perde la dipendenza dal tempo,
in quanto i due termini ωt si elidono. Quello che resta fornisce la dipendenza dalla posizione del
termine di interferenza, il che permette di trovare le posizioni in cui si verifica interferenza
costruttiva e quelle in cui si verifica interferenza distruttiva. In particolare, per trovare le regioni di
massima interferenza costruttiva basterà cercare i punti in cui la differenza di fase ∆Φ = Φ1 − Φ2 =
2πn, con n intero qualsiasi. Le regioni di massima interferenza distruttiva saranno invece date dalla
relazione ∆Φ = Φ1 − Φ2 = (2n+1)π.
In entrambi gli esempi considerati (onde piane o onde sferiche), un calcolo esplicito (fatelo!)
mostrerà che le regioni di interferenza costruttiva e distruttiva si alternano nello spazio, dando luogo
alle cosiddette frange d’interferenza.
Prima di concludere questo paragrafo, dobbiamo introdurre un ultimo concetto strettamente
associato al fenomeno dell’interferenza: la coerenza. Avrete probabilmente sentito dire o letto da
qualche parte che, affinché si verifichi il fenomeno dell’interferenza, le due onde che si
sovrappongono (o, equivalentemente, le due sorgenti delle onde) devono essere “coerenti” tra loro.
Che cosa vuol dire? Nel caso di due onde armoniche ideali di uguale frequenza, date cioè dalla
(11.7) con Φ(r,t) = Φ′(r)−ωt, questa richiesta non sarebbe necessaria: le onde armoniche sono
sempre coerenti, per definizione. Tuttavia, come abbiamo già detto, le onde in natura non sono mai
veramente armoniche, ma sono solo approssimativamente tali. Una delle conseguenze di questa non
perfetta armonicità è che la fase iniziale ϕ di un’onda “quasi”-armonica in generale non è
veramente costante nel tempo, ma subisce invece delle fluttuazioni (di solito casuali) nel tempo,
ϕ(t), che sono molto lente rispetto al termine ωt, ossia rispetto al periodo T dell’onda (altrimenti
l’approssimazione armonica non sarebbe valida). In altre parole si ha Φ(r,t) = Φ′(r)−ωt+ϕ(t). Se
consideriamo allora due onde quasi-armoniche con fasi ϕ1(t) e ϕ2(t) entrambe soggette a queste
variazioni casuali nel tempo, il termine d’interferenza della (11.10) sarà anch’esso non più costante
nel tempo, ma mostrerà invece continue fluttuazioni. Se queste fluttuazioni sono del tutto casuali, la
media nel tempo del cos(ϕ1−ϕ2) sarà nulla e l’effetto dell’interferenza in media scompare. Se le
fluttuazioni sono abbastanza rapide che i rivelatori non riescono a seguirle, quello che viene
misurato è solo l’intensità media, e il fenomeno dell’interferenza diventa inosservabile e scompare.
In questo caso, l’intensità (media) di un’onda risultante dalla sovrapposizione di due onde è
semplicemente la somma delle intensità delle onde componenti.
In natura non esistono onde armoniche ideali, il problema descritto quindi in realtà c’è sempre.
Tuttavia, per osservare il fenomeno di interferenza non è necessario proprio che le due fasi iniziali
ϕ1 e ϕ2 siano entrambe perfettamente costanti nel tempo. Basta infatti che la differenza di fase
35
ϕ1−ϕ2 che compare dentro il coseno nella (11.10) rimanga costante nel tempo. Questa proprietà
delle due onde di avere una fase relativa ϕ1−ϕ2 costante nel tempo, anche se ciascuna onda ha una
fase fluttuante, si chiama coerenza di un’onda rispetto all’altra. Coppie di onde reciprocamente
coerenti sono di solito ottenute semplicemente prendendo una sola onda iniziale e scindendola in
due in qualche modo (come con lo specchio semiriflettente). Un apparato che prima suddivida
un’onda in due e poi, dopo aver fatto viaggiare le due onde per cammini diversi, le ricombini
nuovamente per produrre il fenomeno dell’interferenza si chiama interferometro. Interferometri di
vario genere sono utilizzati in molti campi della fisica e della tecnologia, e servono a rivelare
fenomeni che cambiano la fase di una delle due onde rispetto all’altra.
36