Esercitazioni con MicroCap

Esercitazioni con MicroCap
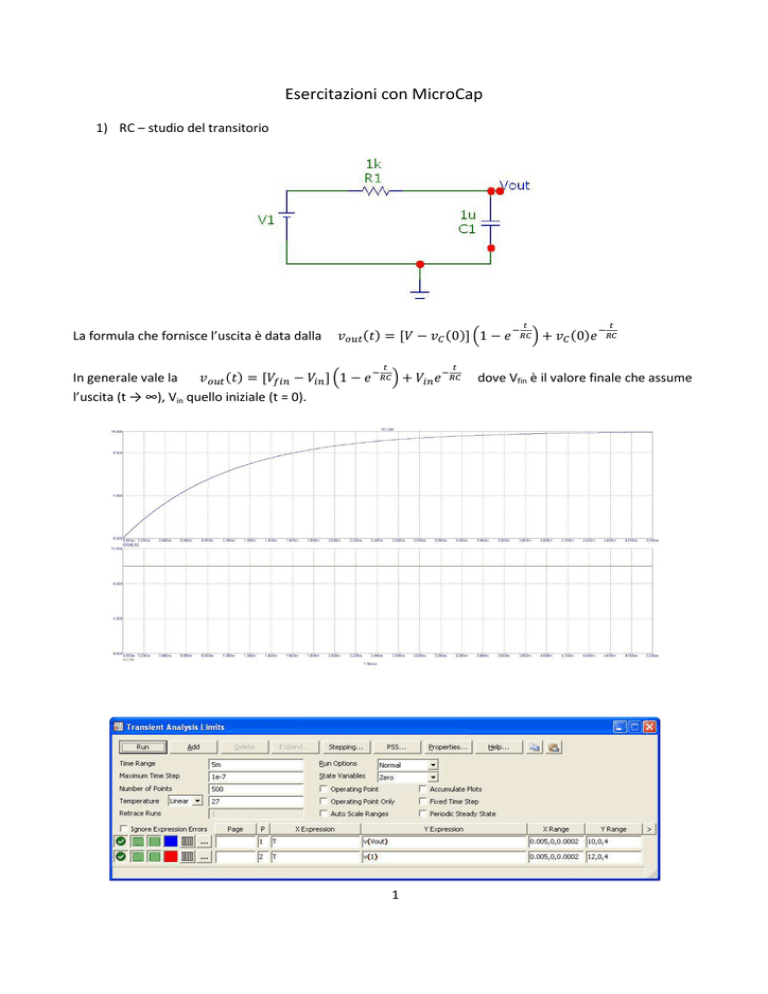
1) RC – studio del transitorio
La formula che fornisce l’uscita è data dalla
0 1 0 In generale vale la
1 l’uscita (t → ∞), Vin quello iniziale (t = 0).
1
dove Vfin è il valore finale che assume
2) RC_AC – studio della risposta in frequenza
La formula del guadagno di tensione sfrutta la formula del partitore:
1
1 !
"
1
" 20&'(
#$
)1 !*
+,
- arctan !
7
7
Per
! 4 1
cioè
per
4 5 6 789 6
Per
! > 1
cioè
per
> 5 6 789 6
:;
:;
#$
#$
< 20&'(
< 20&'(
7
√
7
0+ 789 < 0
)5?
:;
20log !
+ 789 < arctan∞ 90°
:;
La banda passante è data da
F
1
2G!
Nel nostro caso vale
F *HIJ IKL < 159Hz
Per predisporre la simulazione occorre considerare un range di frequenza centrato su tale valore e che si
estenda per un paio di decadi verso i valori più bassi ed altrettanti verso quelli più alti. Il guadagno in dB
sarà certamente un valore non positivo (in quanto il valore numerico è < 1). Per quanto riguarda la fase,
sappiamo che si estende da 0° a -90°.
2
La banda B viene calcolata imponendo la seguente:
"
1
1
20&'(
< 3RF
" 20&'(
$
√1 1
)1 P !*
P !
1
cioè
SP P
2G
1
F
2G!
Quindi: si definisce banda passante il range di frequenza che va da 0 fino al valore rispetto al quale il
guadagno di tensione si abbassa di 3 dB (o, il che è lo stesso, si abbassa fino al valore pari al 70% del valore
massimo, essendo * < 0,7
√
Si lascia al lettore di simulare un passa alto, la cui formula del guadagno è la seguente:
3
!
1 !
3) Verifica – studio della risposta in frequenza
Sia dato un circuito unione di un passa basso e di un passa alto. Le loro costanti di tempo sono una cento
volte l’altra. Valutare la banda passante del circuito.
4
S 1
1
< 0,159kHz
2G* !* 2G10 · 10W · 100 · 10X
S* 1
1
< 15,9kHz
W
2G ! 2G10 · 10 · 10X
F S* S 15,9 0,159 < 15,7kHz
4) Amplificatore operazionale invertente
La formula del guadagno di tensione è data dalla:
*
Con i valori forniti il guadagno è pari a -10, si osserva che fra le due tensioni c’è uno sfasamento di 180°.
Si fa notare nei limiti il massimo timestep, se viene fornito un valore più grande i grafici vengono mal
riprodotti.
5
5) Integratore
Saranno eseguite due analisi, la prima in Transient e la seconda in AC.
1
!
Si prevede un diagramma di Bode del modulo pari ad una retta discendente con pendenza -20dB/decade,
quello della fase pari a 90°.
Simulazione Transient
6
Simulazione AC
In realtà la simulazione tien conto di fattori interni all’operazionale per cui i risultati preventivati sono
rispettati solo in un ristretto range di valori.
7
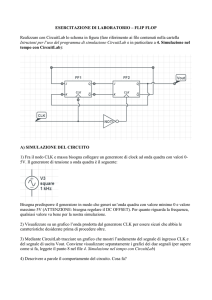
6) Modulatore AM
8
7) Fourier
Il circuito serve a dimostrare come la somma di tante armoniche, fornite dai singoli geenratori sinusoidali,
fornisce una forma d’onda periodica. Nel nostro caso stiamo sommando 6 armoniche di ampiezza
decrescente e di frequenza sempre crescente.
Applicando la formula di Millman otteniamo:
∑[\
∑[\
5:
7:
5:
5
]
9
∑[\
7:
∑[\ ^
I
<
∑[\ 6
8) Fourier2
10
In questo caso abbiamo scelto opportunamente le ampiezze e le frequenze dei singoli generatori, tali da
ottenere un’onda quadra secondo la formula di scomposizione:
S `
4
a1 ,cd
2
G
con ω0 la pulsazione fondamentale data da
I
I
cd 3
3
2GSI I
*H
P
cd 5
e -f
5
con T periodo dell’onda quadra.
Si fa notare che per ottenere un’onda meglio approssimata è necessario sommare altre armoniche.
9) Spettro
Data un’onda quadra, si vuole visualizzare il contenuto frequenziale rappresentando sul piano
cartesiano l’ampiezza delle armoniche che la compongono. Facendo riferimento alla precedente
formula (sviluppo in serie di Fourier), otteniamo:
11
10) Spettro2
In questo esercizio vogliamo mostrare la correlazione fra l’andamento temporale e quello frequenziale.
12
Valutiamo le armoniche di un’onda rettangolare di ampiezza A = 5 volt e frequenza f = 1 MHz.
La prima armonica ha un’ampiezza pari a 5·4/2π ≅ 3,2 e centrata su 1MHz, le altre sono di ampiezza
decrescente e frequenze multiple della prima.
Attenzione che nella simulazione manca la componente continua pari a 2,5.
13