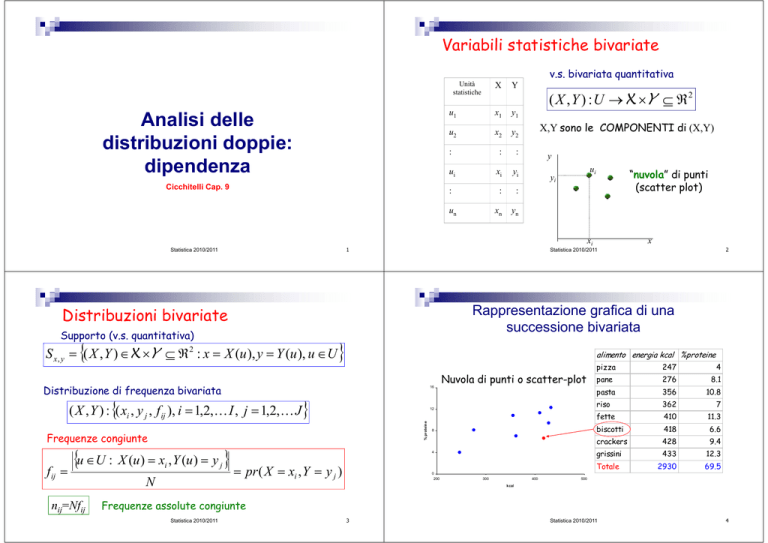
Variabili statistiche bivariate
v.s. bivariata quantitativa
Unità
statistiche
Analisi delle
distribuzioni doppie:
dipendenza
Cicchitelli Cap. 9
{
S x , y = ( X , Y ) ∈ X ×Y ⊆ ℜ 2 : x = X (u ), y = Y (u ), u ∈ U
y1
u2
x2
y2
:
:
:
ui
xi
yi
:
:
:
un
xn
yn
X,Y sono le COMPONENTI di (X,Y)
y
}
16
Nuvola di punti o scatter-plot
% proteine
12
Frequenze congiunte
j
“nuvola” di punti
(scatter plot)
x
2
alimento energia kcal %proteine
( X , Y ) : {( xi , y j , f ij ), i = 1,2, K I , j = 1,2, K J }
{u ∈U : X (u) = x , Y (u) = y }
ui
yi
xi
Distribuzione di frequenza bivariata
nij=Nfij
x1
Rappresentazione grafica di una
successione bivariata
Supporto (v.s. quantitativa)
N
u1
( X , Y ) : U → X ×Y ⊆ ℜ 2
Statistica 2010/2011
Distribuzioni bivariate
f ij =
Y
1
Statistica 2010/2011
i
X
8
4
= pr ( X = xi , Y = y j )
0
200
300
400
pizza
247
4
pane
276
8.1
pasta
356
10.8
riso
362
7
fette
410
11.3
biscotti
418
6.6
crackers
428
9.4
grissini
433
12.3
Totale
2930
69.5
500
kcal
Frequenze assolute congiunte
Statistica 2010/2011
3
Statistica 2010/2011
4
Funzione di ripartizione congiunta
Rappresentazione grafica di una serie bivariata
Fxy ( x, y ) = pr ( X ≤ x, Y ≤ y )
Altezza proporzionale alle
frequenze congiunte
0.09
Distribuzione marginale
0.08
x
0.07
0.06
0.05
f _ ij
0.04
0.03
0.02
S5
S4
0.01
S3
0.00
S2
1
2
y
y
1
2
3
4
5
6
1
4.82 4.49 4.01 3.37 2.57 1.61
2
4.49 3.21 2.73 2.09 1.28 0.32
3
4.01 2.73 4.82 4.17 3.37 2.41
4
3.37 2.09 1.44 6.42 3.85 2.25
5
2.57 1.28 0.64 3.85 8.03 7.70
TOTALE 19.26 13.80 13.64 19.90 19.10 14.29
S x = {X ∈ ℜ : ( x, y ) ∈ S xy , per qualche y ∈ ℜ}
TOT
20.87
14.13
21.51
19.42
24.08
100.00
+∞
⎧
∫−∞ f xy ( x, y)dy
⎪
J
f x ( x) = ⎨
⎪∑ y∈S y f xy ( x, y ) = ∑ f ij
j =1
⎩
S1
3
Per (X,Y) quantitative: stereogramma con volume
proporzionale alle frequenze congiunte
Statistica 2010/2011
5
Distribuzioni condizionate
v.s. discreta
Statistica 2010/2011
6
Indipendenza in distribuzione
∀xi ∈ S x : Y | X = xi ~ Y | X = xi '
Y|X=xi : {(yj,fj|i),j=1,2,…,J}
freq. assolute condizionate
nj|i= nij
fj|i= nij /ni .freq. relative condizionate
TEOREMA
Condizione necessaria e sufficiente perché
Y sia indipendente da X
Σj fj|i = 1
f ij = f i. × f. j
Analogamente possono essere costruite
le J distribuzioni condizionate di X.
Oppure:
Statistica 2010/2011
v.s. continua
7
nij = (ni. × n. j ) / n
Statistica 2010/2011
8
Dipendenza funzionale biunivoca
Dipendenza funzionale univoca
I caratteri X e Y dipendono
funzionalmente uno dall’altro, con I=J
Y dipende funzionalmente da X quando
tutte le distribuzioni condizionate di Y sono
degeneri, con J≤I
Y
Y
y1
X
J n. modalità di Y
I n. modalità di X
x1
x2
x3
TOT
y2
4
0
4
0
2
2
3
0
3
7
2
9
Viceversa, X dipende funzionalmente da Y
quando tutte le distribuzioni condizionate di
X sono degeneri, con I ≤ J
ψ 2 = ∑∑
i =1 j =1
nij2
ni. × n. j
TOT
0
5
0
5
3
0
0
3
0
0
1
1
TOT
3
5
1
9
10
Statistica 2010/2011
(1)
X|Y=yj ~D(x0), j=1,2,…,J
X
Y
y1 y2 y3 Tot
x1 n11 0 n13 n1.
x2 0 n22 0 n2.
Tot n.1 n.2 n.3 N
−1
•In tabelle 2*2
(2)
−1≤ψ ≤ +1 segno di (n11n22-n12n21)
Y|X=xi ~D(y0), i=1,2,…,I
ψ2=J-1
•In tabelle I*J
0 ≤ ψ2 ≤ min[(I-1),(J-1)]
Statistica 2010/2011
y3
Dipendenza funzionale esatta
Indice di contingenza quadratica media
(Pearson)
J
y2
x1
x2
x3
9
Statistica 2010/2011
I
y1
X
TOT
11
Statistica 2010/2011
ψ2=I-1
X
Y
y1 y2 Tot
x1 n11 0 n1.
x2
0 n22 n2.
X3 n31
n3.
Tot n.1 n.2 N
12
Indice χ2 di Pearson
Indice C di Cramèr
ψ
C=
I
J
χ 2 = ∑∑
min[(I − 1), ( J − 1)]
(n
ij
nij* = (ni. × n. j ) / n
2
χ 2 = Nψ 2
χ2 =0 se X e Y sono indipendenti
χ2 ⇒∞ per NÆ∞
C =0indipendenza in distribuzione
C =1dipendenza funzionale esatta
Statistica 2010/2011
)
nij*
i =1 j =1
0 ≤ C≤1
− nij*
13
14
Statistica 2010/2011
Formula per il calcolo
Relazione tra caratteri
Al variare di X in Sx, si osserva una variazione
sistematica della distribuzione di Y?
2
I
J
⎡
⎤
n
ij
2
χ = N ⎢∑∑
− 1⎥
⎢⎣ i =1 j =1 ni. × n. j ⎥⎦
10
6
9
5
ρ=0
8
M(Y)
4
7
6
5
3
4
No variazioni lineari
2
3
2
1
1
I
J
N = ∑∑ nij
0
0
0
1
2
3
fy|X=x costante
i =1 j =1
0
4
1
2
3
4
5
6
7
8
9
10
4
3.5
3
χ2
=0 se X e Y sono indipendenti
χ2 ⇒∞ per NÆ∞
M(Y|X=x) costante
2.5
2
1.5
1
0.5
0
Statistica 2010/2011
15
0
1
2
3
4
16
alimento gruppo %proteine
Dipendenza in media
Studio della relazione tra caratteri
X gruppo
Y proteine
medie per gruppo
Studio della dipendenza di Y da X:
come varia Y|X=x al variare di x in Sx?
U
di posizione
Variabilità
Quantili
frutta
verdura
cereali
TOTALE
0,67
1,78
8,69
4,21
Indici
U1 sottoinsieme
Y|X=1
v.s. condizionata
frutta
Piccolo D. (1999) §7.4 (pagg. 189-194)
17
Statistica 2010/2011
Statistica 2010/2011
1
N
I
I
i =1
i =1
∑ M (Y X = xi )ni. = ∑ M (Y X = xi ) fi.
Frequenze relative
n. figli
NORD CENTRO
0
0.30
0.20
1
0.30
0.40
2
0.20
0.20
3
0.10
0.10
4
0.05
0.10
5
0.05
0.00
TOTALE
1.00
1.00
ni.
150
200
ni. = ∑ j =1 nij , fi. = ni. / N
J
0.9
0.8
0.7
M(Y)
0.6
1
0.2
uva
1
0.5
limoni
1
0.6
arance
1
0.7
pesche
1
0.8
banane
1
1.2
pomodori
2
1
carote
2
1.1
zucchine
2
1.3
lattuga
2
1.8
patate
2
2.1
spinaci
2
3.4
pizza
3
4
biscotti
3
6.6
riso
3
7
pane
3
8.1
crackers
3
9.4
pasta
3
10.8
fette bisc
3
11.3
grissini
3
12.3
Calcolo della media marginale attraverso le
medie condizionate
Media marginale e medie condizionate
M (Y ) =
mele
0.5
fi.
0.33
0.44
fj*yj
SUD
TOTALE n. figli
0.10
0.21
0
0.20
0.32
1
0.25
0.21
2
0.30
0.14
3
0.10
0.08
4
0.05
0.03
5
1.00
1.00 TOTALE
100
450 ni.
0.22
1.00 fi.
NORD CENTRO
0.00
0.00
0.30
0.40
0.40
0.40
0.30
0.30
0.20
0.40
0.25
0.00
1.45
1.50
150
200
0.33
0.44
SUD
TOTALE
0.00
0.00
0.20
0.32
0.50
0.42
0.90
0.43
0.40
0.33
0.25
0.14
2.25
1.65
100
450
0.22
1.00
0.4
0.3
0.2
0.1
M(Y)=1.45×0.33+ 1.50×0.44+ 2.25×0.22=1.65
0
-4
-3
-2
-1
0
1
2
3
4
5
M(Y|X=xi)
Statistica 2010/2011
19
Statistica 2010/2011
20
Indipendenza in media
Misura dell’indipendenza in media
Y
Misura della diversità tra le medie condizionate
dato
X
xi
i =1
DY
j =1
− y ) n ij
2
j
=
∑ ∑ (y
I
J
21
i =1
=
j =1
− y i ) n ij
2
j
DR
+
i =1
+
y = M (Y ), y i = M (Y X = x i ) n i .
DI =
la devianza
i =1
− y ) ni.
2
i
22
Statistica 2010/2011
V(Y ) = M[σ y2 ( x)] + V[μ y ( x)]
− y ) ni.
2
i
DS
Varianza residua
V(Y)=M(σ2y(x))
23
Varianza spiegata
Y
Y
M(Y|X)
Statistica 2010/2011
I
∑ (y
Scomposizione della varianza
I
∑ (y
yi ni.
normalizzare la devianza per ottenere un
indice che varia tra 0 e 1
Dev tot=media dev condizionate+dev medie
∑ ∑ (y
i =1
Conviene
Scomposizione della devianza
J
I
∑
DI=0 sse tutte le medie condizionate sono uguali tra loro
Statistica 2010/2011
I
1
N
Consideriamo
Y indipendente in media da X
se M(Y|X=x)=c, ∀ x∈Sx
y =
xi
X
Indipendenza in media: μy(x)~D(μy)
M(Y|X)
V(Y)=V(μy(x))
xi
X
dipend. funz. esatta:
Y|X~D(μy(x))
24
Indagini ISTAT nel 1982 secondo l'area di studio e il
numero di questionari per indagine
Rapporto di correlazione
Area di studio
V(M(Y | x))
η =
, 0 ≤ ηy2|x ≤ 1
V(Y )
Demografica
2
y| x
Indipendenza in media
se M(Y|X=x)=M(Y) ∀ x∈Sx ⇒η2y|x=0
Statistica 2010/2011
1-|5
5-|10 10-|50
TOT M(Y|X=x) V(Y|X=x)
1
1
0
6
8
76.31
1684.56
Sociale
12
12
10
11
14
59
31.37
1568.34
Economica
39
24
8
14
12
97
18.38
1036.18
Altre
5
0
0
1
0
6
5.67
118.42
Totale
56
37
19
26
32
170
25.17
1395.11
V (M (Y | X ) ) 176.1
=
= 0.126
1395.11
V (Y )
Rapporto di
correlazione
η = η 2 = 0.355
25
>50
0
η y2| x =
Dipendenza funzionale esatta
se V(Y|X=x)=0 ∀ x∈Sx ⇒ η2y|x=1
<=1
Statistica 2010/2011
26












