Problema numerico

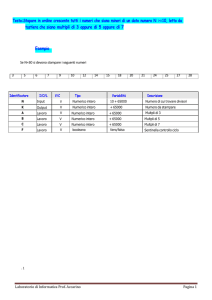
Problema numerico
• Relazione funzionale chiara e non ambigua
tra dati iniziali e la soluzione.
• Dati iniziali e soluzione sono due vettori
finiti
X
F(X)
F
Y
Metodo numerico
• Descrizione matematica dei calcoli che si
devono sviluppare per arrivare alla
soluzione
• Attenzione: in un metodo numerico non e’
detto ci sia la finitezza nel tempo!
• Quando abbiamo un metodo numerico
possiamo costruire un algoritmo
Algoritmo
• Sequenza finita e non ambigua di ordini
(istruzioni) che ai dati iniziali (input)
associano un unico risultato (output) in un
tempo finito
• Per uno stesso metodo numerico si possono
cosruire piu’ algoritmi
Aritmetica floating point
• Insieme dei numeri macchina F(B,s,L,U)
tutti i numeri della forma
x=±0. d1 d2 d3..... dsBm
dove
d1 0 e
L<m<U
(rappresentazione floating point)
• I calcolatori utilizzano 32 o 64 bit per
rappresentare i numeri macchina:
• Singola precisione
1
23
8
segno mantissa esponente
• Doppia precisione
1
segno
52
mantissa
11
esponente
Aritmetica di Matlab
• Matlab lavora in base 2 ma visualizza i risultati
usando la base 10
• Lavora in doppia precisione:16 cifre in base 10
• L=-308, U=+308 (base 2: L=-1022, U=1024)
• Realmax=2.2251E+308 (massimo numero
rappresentabile in valore assoluto)
• Realmin=2.2251E-308 (minimo numero
rappresentabile in valore assoluto)
• Numeri in modulo maggiori di realmax e inferiori
a realmin non possono essere rappresentati
• A un numero piu’grande di realmax (overflow)
matlab associa il “valore speciale” Inf
>>2*realmax
ans=Inf
>>realmin/2
(underflow)
ans=1.1125 E-308
In questo caso una parte di bit destinati alla mantissa
viene usata per l’esponente (perdita di cifre
significative)
>> realmin/10E+16
ans=0
ATTENZIONE: per l’underflow non viene
dato un segnale di errore
• Eps=2-52=2.2E-16 precisione di macchina.
• Per matlab e` il piu’grande numero
macchina tale che eps+1=1
• (la definizione e` il piu’ piccolo numero
macchina tale che 1+eps>1)
Errore propagato
• Nel problema numerico i dati iniziali sono
generalmente affetti da un errore:
• X
X+δx, δx errore inerente i dati
X+δx
F(X+ δx)
δY= -F(X), δY e’ l’errore dovuto alla
propagazione dell’errore inerente δx
(errore propagato)
• La propagazione dell’errore dipende solo
dal problema numerico considerato.
• NON dipende dall’algoritmo usato per fare
i calcoli
• Esempio: calcolare y=exp(ax)
dato iniziale affetto da un errore inerente δx,
calcolo =exp(a(x+ δx))=exp(ax)exp(a δx)
errore (relativo) propagato
| (y- )|/|y|=|1-exp(aδx)|
• a=100, x=10, δx=0.1
errore inerente (relativo): δx/x= 1/100
• errore (relativo) propagato | (y- )|/|y|=exp(10)-1=
2.2025e+004
(Esercizio 3)
• L’errore sul risultato e’ molto piu’ grande
dell’errore iniziale.....
il problema considerato e’ malcondizionato
Altro esempio: calcolare y=sqrt(x) (x>0)
Calcolo =sqrt(x+ δx)
= sqrt(x)sqrt(1+ δx/x) sqrt(x)(1+1/2 δx/x)
l’errore propagato e` |(y- )|/|y| 1/2 δx/x.....
Problema bencondizionato
Condizionamento di un problema
•
•
•
•
x+ δx
|f(x+ δx)-f(x)|/|f(x)| K | δx /x|
K (costante) indice di condizionamento
K grande
problema malcondizionato
(errore propagato molto piu`grande dell’errore sui
dati)
K e` piccolo
problema bencondizionato
(errore propagato dello stesso ordine dell’errore
sui dati)
Nella soluzione di sistemi lineari K=||A|| ||A-1||
Errori nella risoluzione di un
problema (numerico)
•Problema y=f(x),
x1=x+ δx
e1=f(x)-f(x1) errore dovuto
al condizionamento
f
f1
e2=f(x1)- f1(x1) errore di
discretizzazione
Applichiamo l’algorimo e otteniamo un valore
e3= f1(x1)- f2(x1) errore di
f2(x1)
calcolo
Stabilita`numerica
• Riguarda gli algoritmi e precisamente gli
errori di calcolo commessi nella sequenza di
istruzioni dell’algorimo stesso: quando
lavoriamo su un calcolatore usiamo un
insieme di numeri macchina e le operazioni
macchina
si introducono degli errori
di calcolo dovuti agli errori di
arrotondamento
• Per giudicare la bonta` di un algoritmo per il
calcolo di f(x), dobbiamo confrontare
l’output dell’algoritmo f2(x1) con f(x1)
dove x1=fl(x)
• un algoritmo si dice numericamente
stabile se
|f(x1)- f2(x1) |/|f(x1)|
e` dell’ordine della precisione di macchina
Amplificazione errori di calcolo
(instabilita` numerica)
• Cancellazione numerica: perdita di cifre
significative nella sottrazione quando i due
operandi sono vicini tra loro
• Infatti, sappiamo che se nella somma i dati
sono affetti da errore
(a+ a) ±(b+ b)
l’errore relativo sul risultato e’
( a± b)/(a±b)
• La differenza macchina non introduce
alcuna perdita di precisione ma puo`
amplificare gli errori di arrotondamento
presente negli operandi
• a
fl(a), b
fl(b)
• a-b
fl(fl(a)-fl(b))
• Esempio: a=0.147554326 b=0.147251742
Calcolare a-b nell’aritmetica a s=6 cifre
>> a=0.147554326; b=0.147251742
>> digits(6)
>> a1=sym(a,'
d'
)
a1 =.147554
>> a2=sym(b,'
d'
)
a2 =.147252
>> a1-a2
ans =.302e-3
• La vera differenza e` a-b=.3202584 E-3
• Le ultime cifre della mantissa sono alterate in
quanto abbiamo fatto fl(a)-fl(b)
• Adesso prendiamo due numeri piu’ vicini:
• a=0.147554326 b=0.147551742
• calcoliamo a-b nella stessa aritmetica di prima…..
• a1-b1=fl(a)-fl(b)=.2000E-5 mentre a-b=.2584E-5
• (cancellazione numerica esercizi n. 4, 5 )
Sommare tanti addendi
a1+ a2+ a3 +…… an
• Algoritmo piu’ stabile:
ordinare gli addendi in modo che:
|a1 | |a2| | a3 | …… |an |
e poi sommare
(Esercizio n. 8)
Valutazione di un polinomio
p(x)= a1xn+ a2 xn-1 +…… an+1
• P=vettore dei coefficienti, x vettore di punti
in cui effettuare la valutazione
• >>y=polyval(P,x)
• Polyval usa l’algoritmo di Horner (n
moltiplicazioni n somme)
• Scrivere un file di comandi che valuti e
disegni il polnomio
p(x)= x6- 6 x5 + 15x4 - 20x3 +15 x2 - 6x+1
nell’intervallo [0.998, 1.002] con diversi
algoritmi:
1. “valutazione brutale”
2. schema di Horner (polyval)
3. p(x)=(x-1)6
• Altri esempi di instabilita` numerica:
esercizi 6, 7