Crittografia - unimi, Crema

23/10/12
Elementi di Sicurezza e Privatezza
Lezione 5 - Crittografia
Chiara Braghin
[email protected]!
Comunicazione sicura?
canale insicuro
messaggi
Alice
Bob
•  E’ possibile che Alice e Bob comunichino
in modo sicuro attraverso un canale
insicuro?
•  E’ possibile implementare un canale
sicuro virtuale su di un mezzo insicuro?
1
1
23/10/12
CIA over Internet communication
canale insicuro
messaggi
Alice
Bob
Confidenzialità: solo Alice e Bob devono “capire” il
contenuto dei messaggi
Integrità: i messaggi non devono venire modificati
Autenticazione: Alice e Bob vogliono essere sicuri
che il loro interlocutore sia effettivamente chi loro
si aspettano
Non-repudiation: Alice non può negare di aver
spedito un messaggio a Bob (e viceversa)
2
Perché tanto interesse?
•  Chi possono essere Alice e Bob?
w browser/server Web per transazioni elettroniche
(e.g., acquisti on-line)
w on-line banking client e server
w router che si scambiano gli aggiornamenti delle
tabelle di routing w … beh, Bob e Alice in carne e ossa, che si
scambiano messaggi privati!
w altri esempi?
•  In tutti i casi:
w L’informazione deve venire protetta dalla divulgazione e
modifica lungo la rete w L’autenticazione dell’utente è necessaria: quando uno fa
login ci deve essere un modo per verificarne l’identità.
3
2
23/10/12
Come risolvere il problema?
•  Utilizzando primitive crittografiche
w crittare un messaggio (va bene per la
segretezza, ma è sufficiente per garantire
autenticazione e integrità?)
•  Utilizzando protocolli crittografici
w WEP, SSL/TLS, SSH, S-HTTP, PGP
4
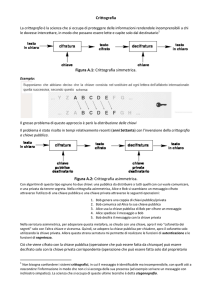
Crittografia
3
23/10/12
Crittografia (1)
•  Dal greco kryptós (=nascosto), e gráphein
(=scrivere), tratta dei metodi per rendere
un messaggio "offuscato” (crittogramma)
in modo da non essere comprensibile a
persone non autorizzate a leggerlo. w  non mira a nascondere il messaggio, ma il suo
significato
w  codificare (testo in chiaro → testo codificato) e
decodificare (testo codificato → testo in chiaro)
informazione
6
Crittografia (2) - Storia
•  Più di 2000 anni fa: comunicazione segreta basata
su steganografia (occultamento del messaggio)
w  23/9/480 a.C. battaglia di Salamina - Serse vs Atene:
tavoletta da scrittura con doppio strato di cera
w  Stessi anni: Istieo manda un messaggio a Aristagora di
Mileto scritto sulla cute
•  ~2000 anni fa: Cifrari per sostituzione
w  Sostituire una lettera con un’altra
w  Cifratura di Cesare (a->D, b->E, c->F, …)
7
4
23/10/12
Crittografia (3) - Storia
•  Alcuni secoli dopo: Cifrari per permutazione
•  Cifrari del rinascimento: utilizzano il
messaggio e le lettere di una chiave per
cifrare il messaggio
w  la base della crittografia moderna
•  1976: Crittografia a chiave pubblica
8
Crittografia (4) - Storia
•  Maria Stuarda, 8/12/1542 – 24/7/1567
regina di Scozia, cugina di Elisabetta I
d’Inghilterra
•  Ernesto “Che” Guevara,
14/6/1928 – 9/10/1967
9
5
23/10/12
Crittografia - Schema generale
chiave di codifica
2.
plaintext
testo in chiaro
Alice
chiave di decodifica
3.
Codifica
ciphertext
testo cifrato
1.
(mittente)
4.
Decodifica
5.
plaintext
Bob
(destinatario)
10
Proprietà di un buon algoritmo di cifratura (1)
•  Sia E la funzione codifica, D la funzione di
decodifica, m un messaggio, k una
chiave:
w  Dk(Ek(m)) = m
•  Ek(m) è semplice da calcolare, dati m e k
•  Dk(x) è semplice da calcolare, dati x e k
w  polinomiale sul massimo tra la lunghezza della
chiave l e quella del messaggio n - spesso lineare
•  Se x = Ek(m), è difficile trovare m senza k
w  esponenziale in min{n,l}
11
6
23/10/12
Proprietà di un buon algoritmo di cifratura (2)
Open design:
Kerchoff’s Principle (1883)
The security of a cryptosystem must not
depend on keeping the algorithm secret.
No security by obscurity:
w  la segretezza è data dalla segretezza della
chiave e dalla robustezza dell’algoritmo
12
Crittografia simmetrica (1)
•  Detta anche Crittografia a chiave privata (o
segreta)
w  Stessa chiave per codifica e decodifica
w  La chiave deve rimanere segreta
chiave K
chiave K
2.
plaintext
1.
3.
Codifica
ciphertext
4.
Decodifica
5.
plaintext
•  La segretezza, autenticazione, integrità del
messaggio sono garantite dalla segretezza della
chiave
13
7
23/10/12
Crittografia simmetrica (2)
•  Vantaggi:
w Di solito usano chiavi di 64-128 bit
(17-34 cifre decimali) e sono molto veloci
•  Svantaggi: w E’ necessario distribuire la chiave segreta
a tutte le coppie di utenti che vogliono
comunicare
14
Crittografia simmetrica (3)
•  Algoritmi basati su cifratura simmetrica:
w  DES - Data Encryption Standard (standard federale nel
1976)
w  Triple DES o 3DES
§  3DESk1,k2(m) = Ek1(Dk2(Ek1(m)))
w  DES-X §  aumenta la lunghezza della chiave effettuando un'operazione di
XOR con dei bit extra prima e dopo l'applicazione del DES
w  AES - Advanced Encryption Standard
§  conosciuto anche come Rijndael
§  vincitore di una competizione internazionale, ideato da due belgi
nel 1998
15
8
23/10/12
Gestione delle chiavi (1) - Naïve
Utenti A1, …, An che vogliono parlare tra loro
•  Ciascuna coppia ha bisogno di una chiave
w  n(n-1)/2 chiavi
•  Le chiavi devono venire concordate
w  Scambio fisico
w  Canale sicuro
w  …
A1
A5
A2
A4
A3
16
Gestione delle chiavi (2) -KDC
A1
Centro di distribuzione
centralizzato (KDC):
• n coppie di chiavi
• Problemi:
w KDC deve essere fidato
w KDC collo di bottiglia e
unico punto di fallimento
w come distribuire le chiavi
condivise con il KDC?
A5
K5
K1
KDC
K4
A4
K2
K3
A2
A3
Se Ai vuole parlare a Aj :
•  Ai → KDC: “collegami a Aj”
•  KDC genera una nuova chiave
Kij
•  KDC → Ai: Eki(Kij)
•  KDC → Aj: Ekj(Kij, “Ai vuole
parlare”)
Ancora naïve
Ø  Nessuna forma di
autenticazione
17
9
23/10/12
Crittografia asimmetrica (1)
• Detta anche Crittografia a chiave
pubblica
w Una chiave per codifica, un’altra per decodifica
w Ogni utente ha una coppia di chiavi:
§ chiave privata: segreto da custodire
§ chiave pubblica: informazione da diffondere
chiave pubblica di Bob KB
2.
Alice
plaintext
1.
chiave privata di Bob K’B
4.
3.
Codifica
ciphertext
Decodifica
5.
plaintext
Bob
•  La segretezza del messaggio è garantita
18
Crittografia asimmetrica (2)
•  Vantaggi:
w  Possibile imporre anche integrità e autenticazione
§  Alice usa la sua chiave privata per crittare
§  Problemi?
•  Svantaggi:
w  Di solito usano chiavi di 1024-2048 bit (circa 160-320
cifre decimali) e sono lenti
w  In genere usati per stabilire una chiave di sessione
•  Algoritmi basati su cifratura asimmetrica
w  RSA (1976)
w  ElGamal (1985)
w  Crittosistema di Rabin (1979)
19
10
23/10/12
Crittografia a chiave segreta vs pubblica
Crittografia a chiave privata
•  Richiede che il mittente e
il destinatario conoscano
la chiave condivisa. •  Q: come concordare la
chiave (specialmente se
mai “incontrati”)?
•  Problema: n persone, per
avere una chiave
condivisa tra tutti sono
necessarie n(n-1)/2
chiavi.
Crittografia a chiave pubblica
• 
• 
• 
• 
• 
Ogni persona ha 2 chiavi:
una chiave pubblica e una
privata.
Mittente e destinatario non
condividono chiavi
La chiave pubblica di
codifica conosciuta da tutti
La chiave privata di
decodifica conosciuta solo
dal destinatario Q: chi garantisce la chiave
pubblica?
20
Algoritmi di cifratura/decifratura
•  Come gestire messaggi molto lunghi?
w Spesso gli algoritmi operano su dimensioni
prefissate
§  E.g. 64 bits per DES
•  Block ciphers
w  Divide il messaggio m in m1, …, mn
§  Aggiunge dei bit finali all’ultimo blocco
w  Usa Ek per produrre x1, …, xn
w  Usa Dk per produrre m1, …, mn
•  Stream ciphers
w  Si basa su di una sequenza pseudo-casuale
21
11
23/10/12
Crittografia perfetta
Def. Nessun testo codificato rilascia informazione alcuna
né sulla chiave usata per la codifica, né sul testo in
chiaro, il quale può essere recuperato se e solo se
la chiave è disponibile
•  Ideale, in teoria: w  nessun tipo di crittoanalisi possibile
w  probabilità nulla di ricavare informazioni
supplementari da un testo codificato
•  Crittografia in pratica quasi mai perfetta 22
Allora abbiamo finito?
•  Crittografia = sicurezza?
•  E’ possibile che Alice e Bob comunichino in
modo sicuro attraverso un canale insicuro
usando la crittografia?
23
12
23/10/12
Alice
?
Bob
24
Allora abbiamo finito?
•  Crittografia = sicurezza?
•  E’ possibile che Alice e Bob comunichino
in modo sicuro attraverso un canale
insicuro usando la crittografia?
•  Purtroppo NO!
w Se Alice manda a Bob un messaggio che
Trudy intercetta e riutilizza? [integrità]
w Quando Bob riceve un messaggio può essere
25
sicuro che sia di Alice? [autenticazione]
13
23/10/12
Crittografia e Integrità
•  La crittografia garantisce anche l’integrità? •  Non sempre…
w  Un attaccante potrebbe intercettare un
messaggio contenente §  “… ti autorizzo a prelevare 1$ dal mio conto” w  e cambiarlo con §  “… ti autorizzo a prelevare 1000$ dal mio conto” w  senza violare la crittografia!
•  Problema: §  i contenuti di un file sono poco “legati” tra loro
§  uso di block ciphers
26
One-way function (1)
•  Detta anche hash function, checksum o
message digest •  h: {0,1}* → {0,1}n:
w  Trasforma i dati in input di lunghezza arbitraria
in un output di lunghezza costante
Possibili
input m
h
Possibili
output h(m)
27
14
23/10/12
One-way function (2) - Proprietà
•  One way (= irreversibile)
w  Dato x, è facile calcolare h(x)
w  Dato y, è difficile trovare x t.c. y=h(x)
[preimage resistance]
w  Dato m, è difficile trovare m’ t.c. h(m) = h(m’)
[second preimage resistance]
•  Collision-resistant w  Difficile trovare m, m’ distinti t.c. h(m)=h(m’)
•  Effetto valanga
w  Una piccola modifica di m deve alterare tutto
h(m)
28
Paradosso del compleanno (1)
•  In crittografia usato per:
w dimensionamento del blocco da cifrare
w provare la proprietà di "resistenza alle
collisioni"
•  Per codici hash di 64 bit w Collisione tra m e m’ con circa 232 tentativi
•  Di solito la dimensione dei codici hash è
di 160 bit (SHA-1)
w Tempo di collisione: 280 tentativi
29
15
23/10/12
Paradosso del compleanno (2)
•  Che probabilità c’è che due persone
in una stessa stanza compiano gli
anni lo stesso giorno?
w in un gruppo di 23 persone 51%; w con 30 persone supera il 70%, w con 50 persone il 97%.
•  Il termine paradosso non è da intendersi nel senso di
una contraddizione logica, ma viene chiamato in
questo modo poiché la verità matematica contraddice
l'intuizione naturale
30
Paradosso del compleanno (3)
31
16
23/10/12
Crittografia e Autenticazione
•  Problemi:
w Le funzioni hash non garantiscono
autenticazione w Come costruire l’equivalente della firma
“su carta” (= auth + non repudiation) ?
w Chi mi garantisce che la chiave pubblica
di Alice sia veramente sua e non di
Trudy?
32
One-way function (3)
2 famiglie:
•  Non-keyed (senza chiave)
w  h : {0,1}* → {0,1}n (e.g. n = 160)
w  h(m) è il message digest di m
w  Usato per integrity, firme digitali, …
w  Esempi:
§  MD4, MD5 (Message Digest) - 128-bit digest
§  SHA/SHS (Secure Hash Algorithm or Standard) 160-bit digest
•  Keyed (con chiave)
w  hk : {0,1}* → {0,1}n (e.g. n = 96)
w  Usato per message integrity e authentication
33
17
23/10/12
MAC (Message Authentication Code) •  Si tratta di una one-way keyed function
w Richiede una chiave segreta condivisa
•  Utilizzo:
w Il mittente spedisce il messaggio m e M1=MAC(m) w Il destinatario riceve entrambe le parti w Il destinatario calcola M2=MAC(m)
§  Se M2 == M1, il messaggio è valido
§  Se M2 != M1, il messaggio è corrotto 34
MAC - Esempio di uso (1)
Trudy
Alice
k
• Send m, hk(m)
m, hk(m)
MAC
Bob
k
• Receive m, hk(m)
•  Nella Rete:
w Trudy non riesce a calcolare il MAC per m’ ≠ m
w Nota: il MAC viene utilizzato per l’integrità,
non per la segretezza
35
18
23/10/12
MAC - Esempio di uso (2)
•  Nel File system:
MAC
file
hpwd(file)
w  il MAC viene verificato quando si vuole
accedere al file
w  la password pwd è necessaria per modificare il
file
36
Firma digitale •  La firma “su carta” garantisce non-repudiation per:
w  Identità
w  Firma di un contratto
•  Schema di firma digitale (basata su crittografia
asimmetrica):
w  Alice pubblica una chiave per la verifica della sua firma
(chiave pubblica)
w  Chiunque può verificare un messaggio firmato da Alice
w  Solo Alice può spedire messaggi firmati
•  Ottiene solo autenticazione e integrità
37
19
23/10/12
Proprietà della firma
•  Funzioni per firmare e verificare
w  Sign(Key-1, m)
w  Verify(Key, x, m) =
OK se x = Sign(Key-1, m)
NO altrimenti
•  Resistente alla contraffazione
w  Non si riesce a calcolare Sign(Key-1, m) da m e Key
w  Resiste all’attacco di forza bruta:
data Key, non si riesce a produrre Sign(Key-1, m)
per nessun m
38
Creazione della firma
1.  Calcolare il message
digest del testo
2.  Codificare il digest
con la chiave privata
del mittente (= firma
digitale)
3.  Creare coppia testo
+firma e spedirla
Testo
in chiaro
digest
hash
Firma
digitale
digest
chiave privata
mittente
Testo
in chiaro
+
Firma
digitale
messaggio inviato
39
20
23/10/12
Verifica della firma
1.  Separare il testo dalla
firma
2.  Decodificare la firma
con la chiave pubblica
del mittente
3.  Calcolare il digest del
testo
4.  Verificare che i due
digest coincidano
1.  sì: accetto (testo OK) 2.  no: rifiuto (testo
alterato)
Firma
digitale
testo
Firma
digitale
testo
chiave pubblica
mittente
Digest 2
hash
Digest 1
?
=
Digest 1
Digest 2
40
Firma digitale - Esempio
Alice vuole firmare
m e spedirlo a Bob
Alice
K-1A
• s = Signk-1A(h(m))
• Send m,s
VerkA(s,m) =
Dati pubblici
Alice 9 kA
…
Bob 9 kB
…
m,s
Ok if s = Sigk(m)
Bob
K-1B
• Receive m,s
• Execute
VerifykA(s, h(m))
No otherwise
•  h rende la firma corta
41
21
23/10/12
Hashing vs. MAC vs. Firme digitali
•  Hashing: checksum “privata”
w  Produce il footprint di un messaggio
w  Deve venire memorizzata separatamente dal messaggio
•  MAC: checksum “cifrata”
w  Il footprint viene protetto da una chiave condivisa e segreta
w  Può venire trasmesso lungo un canale pubblico
•  Firma digitale: non-repudiaton
w  Il footprint viene protetto da una chiave privata
w  Non ci sono dati segreti condivisi con chi verifica la firma
42
22