Capitolo 6 Problemi di flusso su grafo

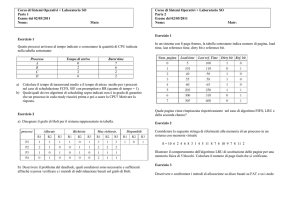
Capitolo 6
Problemi di flusso su grafo
In questo capitolo introdurremo ed analizzeremo il seguente problema: si vuole trasferire,
a minimo costo, un flusso di beni attraverso una rete in modo da soddisfare la domanda
di certi nodi sulla base di quanto procurato da parte di altri nodi.
Sia G = (V, E) un grafo orientato al quale considereremo associato ad ogni arco e ad
ogni nodo un insieme di grandezze che li caratterizzano. In particolare, assoceremo ad ogni
arco (i, j) ∈ E un costo cij che definisce il costo per unità di flusso nell’arco stesso e che
varia linearmente con il flusso; una capacità uij che indichi la massima quantità di flusso
che può scorrere lungo l’arco; infine, un limite inferiore lij che indica la minima quantità
di flusso che deve scorrere nell’arco medesimo. Ad ogni nodo i ∈ V , invece, assoceremo una
grandezza b(i) che indicherà se il nodo è un punto di rifornimento del flusso oppure è un
punto di domanda del flusso; se b(i) > 0 allora il nodo i sarà un nodo di rifornimento del
flusso, se b(i) < 0 allora il nodo i sarà un nodo di domanda del flusso e se b(i) = 0 allora il
P
nodo i sarà un nodo di trasferimento del flusso. In generale, considereremo ∀i∈V b(i) = 0
e che non ci sia dispersione del flusso lungo gli archi.
Per formulare il nostro problema in termini di modello di ottimizzazione, introduciamo
la variabile decisionale xij che rappresenta la quantità di flusso che scorre nell’arco (i, j).
Il Problema di flusso a costo minimo si può formulare nel seguente modo:
81
82
CAPITOLO 6. PROBLEMI DI FLUSSO SU GRAFO
min
X
cij xij
(i,j)∈E
soggetto ai vincoli:
X
j:(i,j)∈E
xij −
X
xji = b(i)
∀i ∈ V
(6.1)
∀(i, j) ∈ E
(6.2)
j:(j,i)∈E
lij ≤ xij ≤ uij
I vincoli 6.1 impongono sia soddisfatto il bilancio di massa ad ogni nodo. Infatti, essi
indicano che in un nodo la quantità di flusso entrante meno la quantità di flusso uscente
deve eguagliare la quantità di flusso rifornita o richiesta. I vincoli 6.2 impongono invece
che siano rispettati i limiti inferiori e superiori della capacità di ogni arco, cioè che il flusso
che scorre rispetti lo spettro di valori di capacità ammessi. In molte applicazioni si ha
per ogni arco che lij = 0, quindi nel seguito considereremo tale valore, se non altrimenti
specificato.
Ogni vettore X di componenti xij , (i, j) ∈ E è chiamato flusso, ogni vettore che soddisfa
gli insiemi di vincoli 6.1 e 6.2 è detto flusso ammissibile.
6.1
Algoritmi di ricerca del cammino minimo su di un
grafo
Gli algoritmi di ricerca del cammino minimo su un grafo costituiscono uno degli argomenti
principali dello studio delle reti di flusso. Le ragioni risiedono nel gran numero di applicazioni reali che possono essere risolte mediante questo modello, nella grande semplicità
nell’ottenere soluzioni in modo molto efficiente, nel fatto che, nonostante la loro semplicità,
catturano alcuni aspetti teorici che sono alla base delle reti di flusso e della teoria dei grafi
e nel fatto che compaiono come sottoproblemi in molte applicazioni.
6.1. ALGORITMI DI RICERCA DEL CAMMINO MINIMO SU DI UN GRAFO
83
Consideriamo un grafo orientato G = (V, E) al quale associamo ad ogni arco (i, j) ∈ E
una lunghezza cij . Il grafo ha un nodo particolare che chiameremo sorgente s. Definiamo
la lunghezza di un cammino orientato nel grafo come la somma delle lunghezze degli archi
nel cammino. Il problema del cammino minimo in un grafo G = (V, E) (in inglese,
shortest path problem, SPP) consiste nel determinare i cammini di lunghezza minima dalla
sorgente s verso ogni altro nodo in V . In termini di flusso, possiamo modellare il problema
supponendo di inviare, a costo minimo, una unità di flusso verso ogni nodo i ∈ V − {s} in
un grafo senza vincoli di capacità. In termini di formulazione matematica, il modello è il
seguente:
X
min
cij xij
(i,j)∈E
soggetto ai vincoli:
X
xij −
j:(i,j)∈E
xji = n − 1
i=s
(6.3)
xji = −1
∀i ∈ V − {s}
(6.4)
xij ≥ 0
∀(i, j) ∈ E
(6.5)
j:(j,i)∈E
j:(i,j)∈E
X
X
xij −
X
j:(j,i)∈E
Nello studio del cammino minimo dobbiamo fare alcune assunzioni:
• Gli archi devono avere lunghezza intera. Questa assunzione non è restrittiva perché
nella rappresentazione nei computer i numeri irrazionali sono convertiti in numeri
razionali e qualunque numero razionale può essere trasformato in un numero intero
moltiplicandolo per un numero sufficientemente grande.
• Il grafo contiene un cammino orientato dalla sorgente s verso qualunque altro nodo
nel grafo.
• Il grafo non contiene cicli di lunghezza negativa. Per la formulazione vista, l’esistenza
di un ciclo W a costo negativo implicherebbe una soluzione non limitata inferiormente
perché potremmo inviare una quantità infinita di flusso lungo W .
84
CAPITOLO 6. PROBLEMI DI FLUSSO SU GRAFO
P1
p
s
P3
k
P2
Figura 6.1: Cammini da s a k.
Dato che esiste un cammino orientato dalla sorgente ad ogni altro nodo del grafo, allora
possiamo dire che esiste un albero dei cammini minimi che dalla sorgente si emana verso
tutti gli altri nodi i cui archi sono gli archi dei diversi cammini. L’esistenza di tale albero
è sostenuta dalla seguente proprietà:
Proprietà 6.1.1 Se il cammino s = n1 , n2 , . . . , nk = k è un cammino minimo dalla sorgente s al nodo k, allora per ogni p = 2, 3, . . . , k − 1, il sottocammino s = n1 , n2 , . . . , np è
il cammino minimo dalla sorgente s al nodo p.
Dimostrazione: Questa proprietà è facile da dimostrare. Infatti, se prendiamo in Figura 6.1 il cammino minimo P1 -P3 da s a k che passa attraverso un certo nodo p, allora il
cammino P2 non è il cammino minimo da s a p. Se P2 fosse il cammino minimo, allora
sarebbe sufficiente prendere il cammino P2 -P3 da s a k per avere un cammino più corto di
P1 -P3 , contraddicendo la sua ottimalità.
Indichiamo ora con d(i) la distanza del nodo i ∈ V da s. La Proprietà 6.1.1 implica
che se P è un cammino minimo da s a k, allora d(j) = d(i) + cij , ∀(i, j) ∈ P ; anche il
viceversa è vero, infatti:
Proprietà 6.1.2 Se d(j) = d(i)+cij , ∀(i, j) ∈ P , allora P deve essere il cammino minimo
tra s e k.
Dimostrazione:
Per dimostrare questa affermazione,
supponiamo che s
=
n1 , n2 , . . . , nk = k sia la successione di nodi nel cammino P . Allora, prendendo la distanza
d(k) ed aggiungendo e togliendo la distanza di ogni nodo in P otteniamo, manipolando
algebricamente l’espressione, che:
d(k) = d(nk ) = (d(nk ) − d(nk−1 )) + (d(nk−1 ) − d(nk−2 )) + . . . + (d(n2 ) − d(n1 ))
6.1. ALGORITMI DI RICERCA DEL CAMMINO MINIMO SU DI UN GRAFO
85
Considerando che d(n1 ) = d(s) = 0 e che per assunzione d(j) − d(i) = cij , abbiamo che:
d(k) = cnk−1 nk + cnk−1 nk−2 + . . . + cn1 n2 =
X
cij
∀(i,j)∈P
Di conseguenza, P è un cammino diretto dalla sorgente s a k di lunghezza d(k) e dato
che per assunzione d(k) è la distanza del cammino minimo del nodo k, allora P deve essere
il cammino minimo del nodo k.
Quanto detto si può riassumere nel seguente risultato:
Proprietà 6.1.3 Un cammino diretto P dalla sorgente s al nodo k è un cammino di
lunghezza minima se e solo se d(j) = d(i) + cij , ∀(i, j) ∈ P .
6.1.1
L’algoritmo di Dijkstra
L’algoritmo di Dijkstra è un algoritmo in grado di risolvere il problema della ricerca del
cammino minimo dalla sorgente s a tutti i nodi. L’algoritmo mantiene una etichetta d(i)
ai nodi che rappresentano un upper bound sulla lunghezza del cammino minimo del nodo i.
Ad ogni passo l’algoritmo partiziona i nodi in V in due insiemi: l’insieme dei nodi etichettati permanentemente e l’insieme dei nodi che sono ancora etichettati temporaneamente.
La distanza dei nodi etichettati permanentemente rappresenta la distanza del cammino
minimo dalla sorgente a tali nodi, mentre le etichette temporanee contengono un valore
che può essere maggiore o uguale alla lunghezza del cammino minimo.
L’idea di base dell’algoritmo è quella di partire dalla sorgente e cercare di etichettare
permanentemente i nodi successori. All’inizio, l’algoritmo pone il valore della distanza
della sorgente a zero ed inizializza le altre distanze ad un valore arbitrariamente alto (per
convenzione, porremo come valore iniziale delle distanze d(i) = +∞, ∀i ∈ V ). Ad ogni
iterazione, l’etichetta del nodo i è il valore della distanza minima lungo un cammino dalla sorgente che contiene, a parte i, solo nodi etichettati permanentemente. L’algoritmo
seleziona il nodo la cui etichetta ha il valore più basso tra quelli etichettati temporaneamente, lo etichetta permanentemente ed aggiorna tutte le etichette dei nodi a lui adiacenti.
L’algoritmo termina quando tutti i nodi sono stati etichettati permanentemente.
86
CAPITOLO 6. PROBLEMI DI FLUSSO SU GRAFO
In Figura 6.2 è riportata la descrizione dell’Algoritmo di Dijkstra. Le operazioni com-
piute dall’algoritmo sono fondamentalmente due: una operazione di selezione del nodo ed
una operazione di aggiornamento delle distanze. La prima seleziona ad ogni passo il nodo
con il valore dell’etichetta più basso, l’altra verifica la condizione d(j) > d(i) + cij e, in
caso positivo, aggiorna il valore dell’etichetta ponendo d(j) = d(i) + cij .
algorithm DIJKSTRA;
begin
S = ∅;
S =V;
∀i ∈ V , d(i) = ∞;
d(s) = 0;
pred(s) = 0;
while |S| < n do
begin
sia i ∈ S un nodo per cui d(i) = min{d(j) : j ∈ S};
S = S ∪ {i};
S = S − {i};
for ∀(i, j) ∈ A(i) do
if d(j) > d(i) + cij then
begin
d(j) = d(i) + cij ;
pred(j) = i;
end;
end;
end;
Figura 6.2: L’algoritmo di Dijkstra
Vediamo un esempio per analizzare i passi effettuati dall’algoritmo.
Esempio 6.1.1 Dato il grafo G in Figura 6.3, calcolare i cammini minimi del nodo sorgente {1} verso gli altri nodi utilizzando l’algoritmo di Dijkstra. Usare le tabelle di Etichetta
nodo, Archi e Predecessore per indicare rispettivamente l’aggiornamento delle etichette dei
nodi, gli archi candidati per ogni nodo ed i predecessori lungo il cammino minimo.
All’inizio, l’algoritmo partiziona i nodi in due insiemi S (nodi etichettati permanentemente) e S (nodi etichettati temporaneamente), pone l’etichetta della sorgente uguale a zero e
6.1. ALGORITMI DI RICERCA DEL CAMMINO MINIMO SU DI UN GRAFO
2
2
2
4
1
2
4
3
1
3
1
4
5
2
6
1
4
2
5
87
8
3
7
Figura 6.3: Grafo per l’Esempio 6.1.1 e corrispondente tabella degli archi.
le etichette degli altri nodi uguali a ∞. Successivamente entra nel ciclo while ed esegue i
seguenti passi:
• seleziona il primo nodo ad etichetta minima, cioè la sorgente s; quindi, per ogni suo
nodo adiacente ad esso, verifica se d(2) > d(1) + c12 , d(3) > d(1) + c13 e d(4) >
d(1) + c14 ; dato che ∞ > 0 + 2 = 2, ∞ > 0 + 4 = 4 e ∞ > 0 + 2 = 2, tutte e tre le
condizioni sono verificate e quindi aggiorno le etichette ed i predecessori nel seguente
modo: d(2) = d(1) + c12 = 0 + 2 = 2 e pred(2) = 1, d(3) = d(1) + c13 = 0 + 4 = 4 e
pred(3) = 1 ed infine d(4) = d(1) + c14 = 0 + 2 = 2 e pred(4) = 1.
• al secondo passo, l’etichetta con il valore più basso è d(2) e quindi seleziono il nodo 2
che diventa etichettato permanentemente. Per i suoi nodi adiacenti si deve verificare
se d(3) > d(2) + c23 e d(5) > d(2) + c25 ; dato che solo la seconda viene verificata
(perché d(3) = 4 > d(2) + c23 = 2 + 2 = 4 non è verificata, mentre è vero che
d(5) = ∞ > d(2) + c25 = 2 + 4 = 6), aggiorno la sua etichetta ponendo d(5) =
d(2) + c25 = 2 + 4 = 6 e pred(5) = 2.
• al terzo passo, l’etichetta di valore più basso è d(4) e quindi seleziono il nodo 4 che
diventa etichettato permanentemente. Per i suoi nodi adiacenti si deve verificare se
d(3) > d(4) + c43 e d(7) > d(4) + c47 ; dato che entrambe sono verificate (perché
d(3) = 4 > d(4) + c43 = 2 + 1 = 3 e d(7) = ∞ > d(4) + c47 = 2 + 5 = 7), aggiorno le
etichette ed ottengo d(3) = 3 e pred(3) = 4, e d(7) = 7 e pred(7) = 4.
88
CAPITOLO 6. PROBLEMI DI FLUSSO SU GRAFO
• al quarto passo, l’etichetta di valore più basso è d(3) e quindi seleziono il nodo 3 che
diventa etichettato permanentemente. Per i suoi nodi adiacenti si deve verificare se
d(5) > d(3) + c35 e d(6) > d(3) + c36 ; dato che è verificata solo la seconda, aggiorno
l’etichetta corrispondente ed ottengo d(6) = 4 e pred(6) = 3.
• al quinto passo, l’etichetta di valore più basso è d(6) e quindi seleziono il nodo 6 che
diventa etichettato permanentemente. Per i suoi nodi adiacenti si deve verificare se
d(7) > d(6) + c68 e d(8) > d(6) + c68 ; dato che entrambe sono verificate, aggiorno le
due etichette ed ottengo d(7) = 6 e pred(7) = 6, e d(8) = 8 e pred(8) = 6.
• al sesto passo, l’etichetta di valore più basso è d(5) e quindi seleziono il nodo 5 che
diventa etichettato permanentemente. Per i suoi nodi adiacenti si deve verificare se
d(6) > d(5) + c56 e d(8) > d(5) + c58 ; dato che solo la seconda è verificata, aggiorno
l’etichetta corrispondente ed ottengo d(8) = 7 e pred(8) = 5.
• al settimo passo, l’etichetta di valore più basso è d(7) e quindi seleziono il nodo 7
che diventa etichettato permanentemente. Per i suoi nodi adiacenti si deve verificare se d(8) > d(7) + c78 ; dato che la relazione non è verificata non effettuo alcun
aggiornamento.
• all’ottavo ed ultimo passo, l’etichetta di valore più basso è d(8) e quindi seleziono il
nodo 8 che diventa etichettato permanentemente. Il nodo non ha nessun adiacente,
quindi l’algoritmo termina.
Nelle due tabelle in Figura 6.4 sono riassunti rispettivamente l’andamento delle etichette
lungo i singoli passi dell’algoritmo e i predecessori dei singoli nodi per ricostruire i cammini
minimi.
Correttezza dell’algoritmo di Dijkstra
Per dimostrare la correttezza dell’algoritmo di Dijkstra facciamo due ipotesi induttive. La
prima è che le etichette di distanza dei nodi in S sono ottime, la seconda che le etichette di
distanza dei nodi sono la lunghezza del cammino minimo dalla sorgente s che contengono
6.1. ALGORITMI DI RICERCA DEL CAMMINO MINIMO SU DI UN GRAFO
89
Figura 6.4: Evoluzione delle etichette dei nodi e lista di adiacenza per il grafo di Figura 6.3.
solo nodi in S. Per dimostrare la prima ipotesi, ricordiamoci che ad ogni passo l’algoritmo
trasferisce un nodo i con l’etichetta più piccola da S a S; quindi, occorre dimostrare che
d(i) è ottima. Ma per le ipotesi induttive poste, d(i) è la lunghezza del cammino minimo
del nodo i tra tutti i cammini che non contengono un nodo di S. Supponiamo allora, per
assurdo, di considerare un cammino P che contiene almeno un nodo k ∈ S, come mostrato
in Figura 6.5 e di decomporre il cammino P nei due sottocammini P1 -P2 : il sottocammino
P1 non contiene un nodo di S, ma termina in un nodo in S; quindi, per ipotesi induttiva
la lunghezza è d(k) e dato che i ha la distanza minima in S, deve risultare che d(k) ≥ d(i)
e quindi il sottocammino P1 deve avere lunghezza almeno d(i). Dato che ogni arco ha
lunghezza non negativa, la lunghezza del sottocammino P2 è non negativa e quindi la
lunghezza del cammino P è almeno d(i).
Per dimostrare che l’algoritmo verifica la seconda ipotesi induttiva, osserviamo che dopo
che è stata effettuata l’etichettatura permanente del nodo i, le etichette di alcuni nodi in
S − {i} decrescono, perché questo è interno al cammino minimo che si sta cercando per
tali nodi. Ma dopo aver permanentemente etichettato un nodo i, l’algoritmo esamina ogni
arco (i, j) ∈ A(i) e se d(j) > d(i) + cij , allora avviene l’aggiornamento d(j) = d(i) + cij ,
pred(j) = i. Quindi, dopo l’aggiornamento, per le ipotesi induttive, il cammino dalla
sorgente al nodo j definito dal vettore dei predecessori soddisfa la Proprietà 6.1.3 e quindi
le etichette di distanza di ogni nodo in S − {i} sono la lunghezza del cammino minimo
90
CAPITOLO 6. PROBLEMI DI FLUSSO SU GRAFO
S
S
i
pred(i)
P2
s
k
P1
Figura 6.5: Disegno per la correttezza di Dijkstra
soggette alla restrizione che ogni nodo del cammino deve appartenere ad S ∪ {i}.
Per quanto riguarda la complessità computazionale dell’algoritmo di Dijkstra partiamo
dalle due operazioni di base che l’algoritmo esegue. In particolare, l’operazione di selezione
dei nodi viene eseguita n volte ed ad ogni passo scandisce ogni nodo etichettato temporaneamente, quindi esegue n + (n − 1) + (n − 2) + . . . + 1 = O(n2 ) iterazioni. L’operazione
di aggiornamento delle etichette viene eseguita |A(i)| volte per ogni nodo i, quindi lungo
P
tutta l’esecuzione dell’algoritmo viene eseguita ∀i∈V |A(i)| = m; dato che ogni operazione di aggiornamento richiede O(1), ne segue che l’algoritmo impiega O(m) per aggiornare le etichette. Riassumendo, dato che O(m) < O(n2 ), la complessità computazionale
dell’algoritmo di Dijkstra è O(n2 ).
Il valore di complessità trovato è il migliore che si può ottenere per grafi molto densi,
mentre può essere migliorato nel caso di grafi sparsi. Infatti, la complessità della operazione di selezione dei nodi pesa considerevolmente di più rispetto alla complessità dell’aggiornamento delle etichette. Di conseguenza sono stati effettuati molti sforzi diretti al
miglioramento dell’efficienza di tale operazione e, in particolare, implementando strutture
dati più elaborate, si è riuscito a diminuire la complessità sino a O(m + n log n) nel caso
di liste di nodi memorizzate come liste di Fibonacci. Rimandiamo il lettore a [10] per una
trattazione completa sulle diverse implementazioni.
6.2. PROBLEMI DI MASSIMO FLUSSO SU GRAFO
6.2
91
Problemi di massimo flusso su grafo
Il problema della ricerca del massimo flusso su di un grafo è un problema complementare a
quello della ricerca del cammino minimo. Infatti, alcuni aspetti del problema del flusso a
costo minimo sono catturati dal problema del cammino minimo nel quale sono considerati
i costi ma non le capacità; il problema del massimo flusso, invece, considera le capacità, ma
non i costi. L’unione dei problemi del cammino minimo e del flusso massimo rappresenta
la combinazione di tutti gli ingredienti di base dell’ottimizzazione delle reti di flusso.
Consideriamo un grafo orientato G = (V, E) nel quale ad ogni arco (i, j) ∈ E sia
assegnata una capacità uij ≥ 0 e sia U = max{uij : uij < ∞, ∀(i, j) ∈ E}. Il Problema
del massimo flusso su di un grafo si può enunciare nel seguente modo: in un grafo
orientato con capacità, determinare il massimo flusso che può essere inviato da un nodo
s chiamato sorgente ad un nodo t chiamato pozzo, senza eccedere le capacità dei singoli
archi. Il problema può essere formulato matematicamente nel seguente modo:
max v
soggetto ai vincoli:
X
xij −
xij −
j:(i,j)∈E
i=s
(6.6)
X
xji = 0
∀i ∈ V − {s} − {t}
(6.7)
xji = −v
i=t
(6.8)
∀(i, j) ∈ E
(6.9)
j:(j,i)∈E
j:(i,j)∈E
X
xji = v
j:(j,i)∈E
j:(i,j)∈E
X
X
xij −
X
j:(j,i)∈E
0 ≤ xij ≤ uij
Il vettore x = {xij } che soddisfa le equazioni scritte conterrà il valore del flusso per
ogni arco (i, j) e la variabile v conterrà il valore totale del flusso. Nell’analisi del problema
del massimo flusso poniamo le seguenti assunzioni:
• Tutte le capacità sono interi non negativi.
92
CAPITOLO 6. PROBLEMI DI FLUSSO SU GRAFO
• Il grafo non contiene un cammino diretto dal nodo s al nodo t composto solo da archi
di capacità infinita. Questa assunzione impedisce che una quantità di flusso infinita
possa scorrere lungo un cammino, rendendo il problema illimitato.
• Se il grafo contiene l’arco (i, j) allora contiene anche l’arco (j, i). Questa assunzione
non è restrittiva perché possiamo sempre aggiungere archi a capacità nulla.
• Il grafo non contiene archi multipli.
Per poter sviluppare l’algoritmo necessario per risolvere il nostro problema, abbiamo
bisogno di definire il concetto di grafo residuo G(x) corrispondente ad un flusso assegnato
x. Supponiamo che un arco (i, j) trasporti xij quantità di flusso. Quindi possiamo ancora
inviare sull’arco uij − xij unità di flusso dal nodo i al nodo j; analogamente, potremmo
inviare xij unità di flusso da j ad i per annullare il flusso che scorre in (i, j). Sulla base
di questa osservazione possiamo definire un grafo residuo, rispetto ad un dato flusso x,
sostituendo ogni arco (i, j) con una coppia di archi: un arco (i, j) con capacità residua
rij = uij − xij e un arco (j, i) con capacità residua rji = xji , come si può notare in
Figura 6.6. Il grafo residuo consiste solo negli archi con capacità residua positiva. Dalla
(xij , uij )
i
rij
j
i
uij − xij
j
⇒
j
i
xji
Figura 6.6: Costruzione del grafo residuo.
definizione di grafo residuo che abbiamo dato, ne segue che la capacità residua è composta
da due componenti: una componente che indica la capacità non utilizzata uij − xij ed
una componente xji che indica il flusso corrente. Quindi, possiamo scrivere che rij =
uij − xij + xji .
Nella Sezione 5.3 abbiamo dato la definizione di taglio in un grafo come la partizione
dei suoi nodi in due insiemi, S e S = V − S, usando la notazione [S, S]. Nel seguito di
questo capitolo faremo riferimento ai tagli di tipo s-t, ovvero quei tagli nei quali s ∈ S
6.2. PROBLEMI DI MASSIMO FLUSSO SU GRAFO
G
2
4
6
(1,2)
4
1
1
1
6
1
1
2
2
5
(1,3)
1
2
1
(1,2)
(2,2)
2
1
(2,2)
3
1
G(x)
(1,2)
(1,2)
1
93
5
3
1
Figura 6.7: Un grafo G con un flusso assegnato x ed il corrispondente grafo residuo G(x).
e t ∈ S. Inoltre, definiremo come archi diretti del taglio [S, S] gli archi (i, j) tali per cui
i ∈ S e j ∈ S e con archi inversi del taglio [S, S] gli archi (i, j) tali per cui i ∈ S e j ∈ S;
indicheremo con (S, S) l’insieme degli archi diretti del taglio [S, S] e con (S, S) l’insieme
degli archi inversi del taglio [S, S]. Per esempio, in Figura 6.8 è riportato un taglio s-t
per il grafo G di Figura 6.7, dove [S, S] = {(1, 3), (3, 4), (4, 6)}, (S, S) = {(1, 3), (4, 6)} e
(S, S) = {(3, 4)}.
2
4
6
1
5
3
Figura 6.8: Un taglio s-t per il grafo di Figura 6.7.
Definizione 6.2.1 Si definisce capacità u[S, S] di un taglio s-t la somma delle capacità
degli archi diretti del taglio, ovvero:
u[S, S] =
X
(i,j)∈(S,S)
uij
(6.10)
94
CAPITOLO 6. PROBLEMI DI FLUSSO SU GRAFO
Si definisce taglio minimo il taglio s-t che tra tutti i possibili tagli s-t ha capacità
minima.
Chiaramente, la capacità di un taglio è un limite superiore della quantità massima di
flusso che possiamo inviare dai nodi in S ai nodi in S rispettando i vincoli di capacità
imposti.
Definizione 6.2.2 Si definisce capacità residua r[S, S] di un taglio s-t la somma delle
capacità residue degli archi diretti del taglio, ovvero:
X
r[S, S] =
rij
(6.11)
(i,j)∈(S,S)
Dato un flusso x su di un grafo, per calcolare il flusso attraverso un taglio s-t possiamo
utilizzare il vincolo di bilancio di massa della formulazione, per cui:
v=
X· X
xij −
∀i∈S j:(i,j)∈E
X
¸
xji
j:(j,i)∈E
Questa espressione si può semplificare notando che se (p, q) ∈ E e p ∈ S e q ∈ S,
allora comparirà un xpq nella prima sommatoria all’interno delle parentesi quadre (quando
i = p), ed un −xpq nella seconda (quando j = q). Considerando che nella sommatoria non
compaiono neanche le componenti di x che fanno riferimento ad archi che hanno solo nodi
in S, possiamo scrivere che:
v=
X
X
xij −
(i,j)∈(S,S)
xij
(6.12)
(i,j)∈(S,S)
Questa relazione indica che il flusso dai nodi in S ai nodi in S è uguale al flusso che
da S va in S, meno il flusso che da S va a S e, dato che il primo membro dell’equazione è
esattamente il valore del flusso, abbiamo che esso eguaglia esattamente il valore del flusso
nel taglio. Considerando che xij ≤ uij e che xij ≥ 0, possiamo scrivere che:
v≤
X
(i,j)∈(S,S)
uij
(6.13)
6.2. PROBLEMI DI MASSIMO FLUSSO SU GRAFO
95
Questo risultato ci indica che il valore di un qualunque flusso sul grafo è minore o al più
uguale alla capacità di un su qualunque taglio s-t. Tale risultato è abbastanza intuitivo
perché ogni flusso che scorre da s a t deve attraversare ogni taglio s-t e, quindi, non ne può
eccedere la capacità.
6.2.1
L’algoritmo di Ford e Fulkerson
Per risolvere il problema del massimo flusso in un grafo attraverso l’algoritmo che stiamo
per introdurre abbiamo bisogno di alcune definizioni sul grafo residuo:
Definizione 6.2.3 Si definisce cammino aumentante nel grafo residuo un cammino
diretto dalla sorgente al pozzo e capacità residua δ la minima capacità residua di ogni
arco nel cammino aumentante.
Nel grafo in Figura 6.7, un cammino aumentante nel grafo G(x) è costituito dagli
archi {(1, 2), (2, 4), (4, 3), (3, 5), (5, 6)} e la capacità residua δ = min{r12 , r24 , r43 , r35 , r56 } =
min{1, 1, 1, 2, 1} = 1. Come si può notare, la capacità residua è sempre maggiore di zero;
quindi, non appena un grafo contiene un cammino aumentante, possiamo inviare ulteriore
flusso dalla sorgente al pozzo.
Quest’ultima osservazione ci suggerisce l’algoritmo per risolvere il problema della ricerca
del massimo flusso. Infatti, potremmo iniziare utilizzando le tecniche di ricerca viste nella
Sezione 5.1 per identificare un cammino da s a t nel grafo G(x) partizionando i nodi del
grafo in due insiemi: nodi etichettati (quelli raggiungibili da s) e nodi non etichettati
(quelli non raggiungibili da s). Se alla fine del processo t è etichettato, allora invio la
massima quantità di flusso, pari alla capacità residua sul cammino aumentante trovato;
quindi, cancello tutte le etichette e ripeto la procedura iterativamente. L’algoritmo termina
quando non riesco ad etichettare t, cioè quando non esiste un cammino aumentante dalla
sorgente al pozzo.
Prima di esporre l’algoritmo, si vuole sottolineare che la ricerca di un cammino aumentante nel grafo residuo G(x) corrisponde alla ricerca in G di un cammino dalla sorgente al
pozzo, non necessariamente orientato, con xij < uij per ogni arco diretto nel verso del cammino e con xij > 0 per ogni arco inverso rispetto al verso del cammino ed esiste un cammino
96
CAPITOLO 6. PROBLEMI DI FLUSSO SU GRAFO
aumentante rispetto ad un certo flusso x se e soltanto se esiste un cammino diretto da s a t
in G(x). Se ad un certo passo dell’algoritmo si aggiorna il flusso con un flusso addizionale
δ, allora xij varierà rispettando la definizione di capacità residua (rij = uij − xij + xji ) o
aumentando xij di δ unità o diminuendo xji di δ unità, oppure si avrà una combinazione
convessa delle due possibilità precedenti.
algorithm FORD&FULKERSON;
begin
etichetta il nodo t;
while t è etichettato do
begin
cancella le etichette di tutte i nodi i ∈ V ;
pred(j) = 0, ∀i ∈ V ;
etichetta s e poni LISTA= {s};
while LISTA6= ∅ e t è non etichettato do
begin
rimuovi un nodo i da LISTA;
for (i, j) ∈ G(x) do
if nodo j è non etichettato then;
begin
pred(j) = i;
etichetta j;
aggiungi j a LISTA;
end;
end;
if t è etichettato then
begin
usa le etichette dei predecessori per trovare all’indietro
il cammino aumentante P da s a t;
δ = min{rij , (i, j) ∈ P };
aumenta di δ unità di flusso lungo P e aggiorna G(x);
end;
end;
end;
Figura 6.9: L’algoritmo di Ford e Fulkerson
Le osservazioni fatte fin qui possono essere formalizzate nell’algoritmo di Ford e Fulkerson descritto in Figura 6.9. La correttezza dell’algoritmo segue dal fatto che sono possibili
due casi: o l’algoritmo trova un cammino aumentante dalla sorgente al pozzo, oppure non
6.2. PROBLEMI DI MASSIMO FLUSSO SU GRAFO
97
riesce a trovare alcun cammino. Se si verifica il secondo caso dobbiamo dimostrare che
allora il flusso è ottimo. Supponiamo quindi che ad un certo passo, S sia l’insieme dei nodi
etichettati e S = V − S l’insieme dei nodi non etichettati, con s ∈ S e t ∈ S. Se l’algoritmo
non può etichettare i nodi in S a partire dai nodi in S, allora rij = 0, ∀(i, j) ∈ (S, S);
inoltre, dato che rij = uij − xij + xji , xij ≤ uij e xji ≥ 0, allora la condizione rij = 0
implica che xij = uij per ogni arco (i, j) ∈ (S, S) e xij = 0 per ogni arco (i, j) ∈ (S, S).
Sostituendo questi valori nell’Equazione 6.12 otteniamo:
v=
X
(i,j)∈(S,S)
xij −
X
X
xij =
(i,j)∈(S,S)
uij = u[S, S]
(6.14)
(i,j)∈(S,S)
Questa relazione mostra che il valore del flusso corrente x eguaglia la capacità del taglio
[S, S] e dato che l’Equazione 6.13 implica che x è il flusso massimo e [S, S] è il taglio minimo,
allora abbiamo dimostrato il seguente risultato:
Teorema 6.2.1 Il valore massimo del flusso dalla sorgente s al pozzo t in un grafo con
capacità eguaglia la capacità del minimo taglio s-t.
Il teorema precedente, che chiameremo Teorema del massimo flusso e del minimo taglio ci dice anche che quando l’algoritmo di Ford e Fulkerson termina con il massimo
flusso, contemporaneamente ci fornisce anche il taglio minimo.
Esempio 6.2.1 Dato il grafo in Figura 6.10, calcolare il flusso massimo dalla sorgente
{1} al pozzo {8} utilizzando l’algoritmo di Ford e Fulkerson, disegnando la successione dei
grafi residui. Indicare il taglio minimo corrispondente al flusso trovato.
Nel grafo in Figura 6.10 il flusso è posto inizialmente a xij = 0 per ogni arco; quindi, il
primo grafo residuo coincide con il grafo di partenza.
• Nella prima iterazione l’algoritmo trova il cammino aumentante {(1, 2), (2, 5), (5, 8)},
con δ = min{r12 , r25 , r58 } = min{4, 2, 4} = 2. L’algoritmo esegue l’aumento del flusso
pari a δ = 2 unità ed aggiorna il grafo residuo, disegnato in Figura 6.11.
98
CAPITOLO 6. PROBLEMI DI FLUSSO SU GRAFO
2
2
4
4
2
6
1
5
3
3
3
2
3
3
2
4
5
6
8
4
7
Figura 6.10: Grafo per l’Esempio 6.2.1.
2
2
2
2
2
6
1
3
5
3
2
4
2
3
3
6
3
2
2
5
8
4
7
Figura 6.11: Il grafo residuo dopo la prima iterazione.
6.2. PROBLEMI DI MASSIMO FLUSSO SU GRAFO
• Nella
seconda
iterazione
l’algoritmo
99
trova
il
cammino
{(1, 2), (2, 4), (4, 7), (7, 8)} con δ = min{r12 , r24 , r47 , r78 } = 2.
aumentante
L’algoritmo ese-
gue l’aumento del flusso pari a δ = 2 unità ed aggiorna il grafo residuo, disegnato in
Figura 6.12.
2
2
4
2
2
6
1
2
4
6
3
1
2
2
3
3
2
3
5
5
8
2
2
7
Figura 6.12: Il grafo residuo dopo la seconda iterazione.
• Nella terza iterazione l’algoritmo trova il cammino aumentante {(1, 3), (3, 5), (5, 8)}
con δ = min{r13 , r35 , r58 } = 2. L’algoritmo esegue l’aumento del flusso pari a δ = 2
unità ed aggiorna il grafo residuo, disegnato in Figura 6.13.
2
2
4
4
3
2
3
4
2
2
3
1
5
2
3
1
4
6
2
5
8
2
2
7
Figura 6.13: Il grafo residuo dopo la terza iterazione.
• Nella quarta iterazione l’algoritmo trova il cammino aumentante {(1, 3), (3, 6), (6, 8)}
con δ = min{r13 , r36 , r68 } = 3. L’algoritmo esegue l’aumento del flusso pari a δ = 3
unità ed aggiorna il grafo residuo, disegnato in Figura 6.14.
• Nella quinta iterazione, l’algoritmo non riesce ad etichettare il pozzo e quindi termina.
100
CAPITOLO 6. PROBLEMI DI FLUSSO SU GRAFO
2
2
4
1
4
2
2
2
3
3
1
5
6
5
1
2
3
2
2
4
8
3
3
2
7
Figura 6.14: Il grafo residuo dopo la quarta iterazione.
Il flusso massimo è pari alla somma degli incrementi eseguiti nei singoli passi, cioè
v ? = 2 + 2 + 2 + 3 = 9. Il taglio minimo è riportato in Figura 6.15.
2
2
4
3
4
2
6
1
5
3
3
3
2
4
6
3
2
5
8
4
7
Figura 6.15: Il taglio minimo del grafo di Figura 6.10.
Complessità computazionale dell’algoritmo di Ford e Fulkerson
Per calcolare la complessità computazionale osserviamo che l’algoritmo esegue una ricerca
per trovare un cammino dalla sorgente al pozzo (che sappiamo essere eseguibile, dalla
Sezione 5.1, in O(m) passi) tante volte quanto è possibile eseguire degli aumenti di flusso.
Per tali aumenti, se le capacità sono intere e limitate da U , allora la capacità di un taglio
(s, N − {s}) è al più nU . Di conseguenza, siccome l’algoritmo aumenta il flusso di almeno
una unità ogni iterazione, ne segue che globalmente l’algoritmo esegue O(nmU ) iterazioni.
6.2. PROBLEMI DI MASSIMO FLUSSO SU GRAFO
101
L’algoritmo visto è sicuramente uno dei più semplici per risolvere il problema del massimo flusso, ma il valore di complessità computazionale è legato al valore di U e questo
potrebbe portare a casi nei quali l’algoritmo non risulta essere efficiente (per esempio, se
U = 2n ). Inoltre, in alcuni casi può eseguire tante iterazioni quante indicate dal caso
peggiore. Per esempio, se si considera l’istanza della Figura 6.16, l’algoritmo potrebbe
selezionare i cammini aumentanti 1 − 3 − 2 − 4 e 1 − 2 − 3 − 4, alternativamente, 106 volte,
ogni volta aumentando il flusso di una unità.
2
2
6
6
10
10
1
4
1
106
106
3
10
106 -1
6
1
106 -1
1
1
1
4
106
3
2
106 -1
106 -1
1
1
106 -1
1
1
1
4
1
106 -1
3
Figura 6.16: Istanza patologica per l’algoritmo di Ford e Fulkerson.
Un altro difetto dell’algoritmo risiede nel fatto che ad ogni passo deve essere rieseguito il
processo di etichettatura e, quindi, le informazioni che si generano sui cammini aumentanti
vengono perse ad ogni passo e si devono ricalcolare di nuovo.
In [10] sono riportati diversi algoritmi efficienti per la risoluzione del problema del
massimo flusso che non risentono dei limiti dell’algoritmo di Ford e Fulkerson.
Indice analitico
Albero, 45
Ricoprente, 46
Minimo, 70
Algoritmo, 18
Densità, 6
Distanza, 42
Embedding planare, 53
di Kruskal, 74
Faccia, 54
di ordinamento topologico, 68
Flusso, 81
di Prim, 76
Foresta, 45
di Dijkstra, 85
Formula di Eulero, 58
di Ford e Fulkerson, 95
di ricerca su grafo, 61
Grafo, 3
Aciclico, 43
in ampiezza, 64
Bipartito, 11, 44
in profondità, 66
Complemento, 9
di ricerca su stringa, 20
Completo, 6
Archi, 3
Denso, 6
Multipli, 3
Dimensione di un, 5
Disegno di un, 53
Bridge, 41
Duale, 55
Ciclo, 14
Euleriano, 46
Clique, 6
k-regolare, 8
Componenti connesse, 40
Ordine di un, 5
Connessione, 16
Orientato, 33
Crescita di funzioni, 22
Piano, 53
Combinazione di, 24
Planare, 53
Cut-vertex, 41
Semplice, 3
102
INDICE ANALITICO
Sparso, 6
Insieme indipendente, 9
Isomorfismo, 37
Classi di equivalenza, 40
K-Fattorizzazione, 8
Lemma Handshaking, 7
Lista di adiacenza, 37
103
Taglio, 71
Teorema
del massimo flusso e minimo taglio, 97
di Eulero, 46
di Kuratowski, 59
Trail, 15
Euleriano, 46
Hamiltoniano, 48
Loop, 3
Vertex covering, 10
Matching, 11
Vicinato, 7
Matrice di adiacenza, 35
Walk, 15
Matrice di incidenza, 34
Nodi, 3
Notazione Big-O, 23
Numero cromatico, 13
Ordinamento topologico, 67
Path, 14, 15
Problema
decisionale, 17
del cammino minimo, 83
del flusso massimo, 91
dell’albero ricoprente minimo, 70
di flusso a costo minimo, 81
Regione, 54
Sottografo, 4
Indotto, 4
Ricoprente, 4
104
INDICE ANALITICO
Bibliografia
[1] AA.VV. Kaliningrad Business Guide. http://guide.kaliningrad.net.
[2] B. Bollobas. Modern graph theory. Springer-Verlag, 1998.
[3] K. Steiglitz C. H. Papadimitriou.
Combinatorial optimization: algorithms and
complexity. Prentice Hall, 1982.
[4] N. Christofides. Graph theory, an algorithmic approach. Academic Press, 1975.
[5] R. Diestel. Graph Theory. Springer-Verlag, 2005.
[6] S. Fortin. The graph isomorphism problem. Technical Report TR96-20, Department
of Computer Science, The University of Alberta, Canada, July 1996.
[7] D. Jungnickel. Graphs, network and algorithms. Springer-Verlag, 1999.
[8] F. Maffioli. Elementi di programmazione matematica. Casa Editrice Ambrosiana,
2000.
[9] R. J. Wilson N. L. Biggs, E. K. Lloyd. Graph Theory 1736-1936. Oxford University
Press, 1999.
[10] J. B. Orlin R. K. Ahuja, T. L. Magnanti. Network Flows. Pearson Education, 1993.
[11] K. H. Rosen. Discrete mathematics and its applications. McGraw Hill Text, 1998.
[12] P. Serafini. Ottimizzazione. Zanichelli, 2000.
[13] A. Ventre. Introduzione ai grafi planari. Zanichelli Editore, 1983.
105
106
[14] D. B. West. Introduction to graph theory. Prentice Hall, 2000.
BIBLIOGRAFIA