Funzioni Complesse di variabile complessa

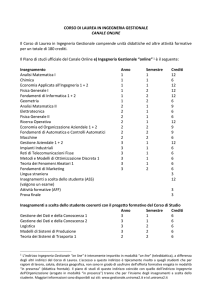
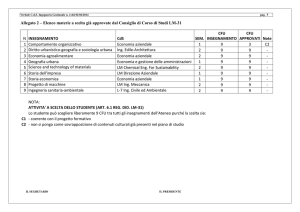
Funzioni Complesse di variabile complessa
Docente:Alessandra Cutrı̀
A. Cutrı̀
17-11-2014
Metodi Matematici per l’ingegneria–Ing. Gestionale
Richiami sui numeri complessi
Indichiamo con C il campo dei Numeri complessi
√
z = x + iy ∈ C, ses x, y ∈ R i := −1 (Rappresentazione
cartesiana dei numeri complessi)
C ∼ R2 : z = x + iy ∈ C ↔ (x, y ) ∈ R2
x = Re(z), y = Im(z)
C NON è ORDINATO
Il complesso coniugato di z = x + iy è z = x − iy
p
p
√
Il modulo |z| = (Rez)2 + (Imz)2 = x 2 + y 2 = zz
Rappresentazione polare del numero complesso
z = ρ(cos θ + i sin θ) con ρ = |z| e per z 6= 0 θ = Argz + 2kπ
con k ∈ Z. Argz ∈ (−π, π) denota l’Argomento principale di z
A. Cutrı̀
17-11-2014
Metodi Matematici per l’ingegneria–Ing. Gestionale
Dati due numeri complessi z0 = x0 + iy0 e z1 = x1 + iy1
Somma: z0 + z1 = (x0 + x1 ) + i(y0 + y1 )
prodotto w = z0 · z1 = (x0 x1 − y0 y1 ) + i(x0 y1 + y0 x1 )
w = ρ0 ρ1 (cos(θ0 + θ1 ) + i sin(θ0 + θ1 ))
quindi |w | = ρ0 ρ1 = |z0 | · |z1 | ed un argomento di w ,
arg (w ) = Argz0 + Argz1 (non è detto che
Argz0 + Argz1 ∈ (−π, π) e dunque che sia l’argomento
principale di w )
se z 6= 0, il reciproco di z si definisce come
1
z
:=
z
|z|2
=
x−iy
x 2 +y 2
se z1 6= 0, quoziente
z0
xo x1 + y0 y1
xo y1 + y0 x1
z0 z1
−i
=
=
2
2
2
z1
|z1 |
x1 + y1
x12 + y12
A. Cutrı̀
17-11-2014
Metodi Matematici per l’ingegneria–Ing. Gestionale
Potenze intere di un numero complesso: Dato
z = x + iy = ρ(cos θ + i sin θ) e n ∈ N si definisce
w = z n = (x + iy )n = ρn (cos(nθ) + i sin(nθ))
Quindi |z n | = |z|n e arg (z n ) = n · arg (z)
Radice n−ma di un numero complesso:
dato z 6= 0, trovare w ∈ C tale che w n = z (n ∈ N). Tale w si
definisce radice n−ma di z
Ogni numero complesso z 6= 0 z = x + iy = ρ(cos θ + i sin θ)
ammette n radici n−me distinte in C date da:
wk = r (cos(φk ) + i sin(φk ))
dove r = (ρ) , φk = ( nθ + k 2π
n ) k = 0, 1, . . . , n − 1
1
n
Se θ = Argz la radice corrispondente a k = 0 si chiama radice
principale di z
A. Cutrı̀
17-11-2014
Metodi Matematici per l’ingegneria–Ing. Gestionale
Funzioni complesse di una variabile complessa
Sia A ⊆ C un aperto connesso di C ∼ R2 .
f :A⊆C→C
Essendo f (z) ∈ C per ogni z ∈ A ⇒ f (z) = u + iv con
u, v ∈ R quindi
f (z) = f (x + iy ) = u(x, y ) + iv (x, y )
u, v : A ⊆ R2 → R
u(x, y ) = Re(f (z)) e v (x, y ) = Im(f (z))
(z, f (z)) ∈ C × C ∼ R4
A. Cutrı̀
17-11-2014
Metodi Matematici per l’ingegneria–Ing. Gestionale
Esempi di Funzioni complesse di una variabile complessa
Funzioni lineari: f (z) = az + b per ogni z ∈ C con a, b ∈ C
1
b = 0. f (z) = az con |a| = 1. Si ha a = e iβ con β ∈ (−π, π)
|f (z)| = |z| ; arg (f (z)) = arg (a) + arg (z) = β + arg (z)
2
dunque l’effetto di f corrisponde ad una rotazione di ogni
punto z del piano complesso di un angolo β
b = 0. f (z) = az con |a| =
6 1. Si ha a = |a|e iβ con
β ∈ (−π, π)
|f (z)| = |a||z| ; arg (f (z)) = arg (a) + arg (z) = β + arg (z)
3
l’effetto di f corrisponde ad una omotetia: contrazione (se
|a| < 1) o dilatazione (se |a| > 1) di ogni punto z del piano più
una rotazione di ogni punto z di un angolo β (l’ordine delle
due operazioni non cambia il risultato)
b 6= 0 si aggiunge una traslazione di b (vettore di componenti
(Reb, Imb)). Conta l’ordine con cui vengono effettuate le
operazioni (rotazione+omotetia) e (traslazione):
z → az → az + b
z → z + b → a(z + b) = az + ab 6= az + b
A. Cutrı̀
17-11-2014
Metodi Matematici per l’ingegneria–Ing. Gestionale
Input :=
Funzioni quadratiche
ComplexMapPlot[z^2, z, VerticalLines[{{0,1},{-1,1}},
PlotPoints->7], PlotRange->All];
f (z) = z 2 per ogni z = x + iy ∈ C
f (z) = (x + iy )2 = x 2 − y 2 + i2xy
Quindi u(x, y ) = x 2 − y 2 e v (x, y ) = 2xy
Vediamo una rappresentazione dell’immagine di un reticolato del
piano tramite
lafamiglie
funzione
f (z) = z 2 :
L'unione delle tre
di segmenti precedenti:
Input :=
ComplexMapPlot[z^2, z, RectangularGrid[{{0,1},{-1,1}},
PlotPoints->7], PlotRange->All];
http://people.ciram.unibo.it/ barozzi/MatheCompl/MatheCompl.html
2 of 16
A. Cutrı̀
17-11-2014
Metodi Matematici per l’ingegneria–Ing.
Gestionale
15-11-2013 15:21
Radice quadrata
Osserviamo che la funzione f (z) = z 2 non è iniettiva: i punti
(x0 , y0 ) e (x0 , −y0 ) hanno la stessa immagine tramite f in quanto
u = x 2 − y02 , v = 2xy0 → x =
v2
v
⇒ u = 2 − y02
2y0
4y0
(nel piano (u, v ) si ha la stessa immagine).
Restringendo f|A dove A = {x + iy : x > 0} = {z : Rez > 0}
diventa iniettiva e la sua immagine (che coinciderà con il
dominio della funzione inversa è
dom(f −1 ) = C \ {x ∈ R : x ≤ 0}
Dato w = ρe iθ 6= 0 troviamo in generale due valori di z tali
che z 2 = w che sono
√ θ
z1 = ρe i 2 Radice principale di w (inversa di f|A )
z2 =
A. Cutrı̀
17-11-2014
√
θ
ρe i( 2 +π)
Metodi Matematici per l’ingegneria–Ing. Gestionale
file:///Users/ikbook/Documents/alessandraimac/didattica/mmigest...
La funzione radice quadrata principale
Tutti i punti del piano complesso hanno immagini con parte reale non negativa.
Input :=
ComplexMapPlot[Sqrt[z], z,
RectangularGrid[{{-2,2},{-2,2}}],
Ticks -> {{-2., -1., 1., 2.}, Automatic}];
Input :=
ComplexMapPlot[Sqrt[z], z,
{Thickness[0.001], PolarGrid[{0,0},{0,2}]},
Ticks -> {{0.5, 1., 1.5}, Automatic}];
http://people.ciram.unibo.it/
barozzi/MatheCompl/MatheCompl.html
La funzione z -> 1/z
Le circonferenze hanno come immagini circonferenze (le rette sono casi limite di circonferenze).
Input :=
ComplexMapPlot[1/z, z, HorizontalLines[{{-2,2},{-2,2}}],
PlotRange->{{-2.5,2.5},{-2.5,2.5}}];
A. Cutrı̀
17-11-2014
Metodi Matematici per l’ingegneria–Ing. Gestionale
Esponenziale complesso
Vogliamo definire una funzione che estende al campo complesso la
definizione x ∈ R → e x . Ricordiamo che
x
x ∈R
lim (1 + )n = e x
n→∞
n
Se consideriamo ora z = x + iy e facciamo
x + iy n
) = e x (cos y + i sin y )
lim (1 +
n→∞
n
n
(con calcolo laborioso si vede che il modulo |(1 + x+iy
n )| tende a
e x e l’argomento tende a y ) Questo ci suggerisce di definire e z :
e z = e x+iy := e x (cos y + i sin y )
Si ha ovviamente u(x, y ) = e x cos y , v (x, y ) = e x sin y
|e z | = e x = e Rez > 0
∀z ∈ C ⇒ |e iy | = 1 ∀y ∈ R
e z1 +z2 = e z1 e z2
e z = e z+2kπi
∀k ∈ Z
Quindi e z è 2πi−periodica
A. Cutrı̀
17-11-2014
Metodi Matematici per l’ingegneria–Ing. Gestionale
Logaritmo complesso
e z 2πi−periodica ⇒ e z non è iniettiva
dato w ∈ C \ {0} (immagine di e z ), l’equazione e z = w ha in
realtà infinite soluzioni z = x + iy . Come si trovano?
w ∈ C \ {0} ⇒ w = ρ(cosθ + i sin θ) = ρe iθ
si devono determinare x, y in modo che e z = w ⇔ e x+iy = ρe iθ
Quindi:
ex = ρ
e iθ = e iy ⇒ x = log ρ , y = θ + 2kπ , k ∈ Z
Otteniamo
z = logC w = log ρ + i(θ + 2kπ)
k ∈Z
Esistono pertanto infiniti logaritmi complessi di w e
Re(logC w ) = log |w |
A. Cutrı̀
Im(logC w ) = arg (w ) + 2kπ
17-11-2014
k∈Z
Metodi Matematici per l’ingegneria–Ing. Gestionale
Logaritmo principale complesso
Se però restringiamo il dominio di e z all’insieme
A = {x + iy : x ∈ R, y ∈ (−π, π)}
e z z ∈ A è iniettiva e la sua immagine è C \ {x ≤ 0} allora se
consideriamo l’inversa della restrizione di e z all’insieme A
otteniamo una funzione ad un solo valore definita su C \ {x ≤ 0}
che prende il nome di Logaritmo principale
Log (z) = log(|z|) + iArg (z)
z ∈ C \ {x ≤ 0}
(Arg (z) è l’Argomento principale di z)
A. Cutrı̀
17-11-2014
Metodi Matematici per l’ingegneria–Ing. Gestionale
Limiti di Funzioni complesse di una variabile complessa
Sia z0 = x0 + iy0 ∈ A ⊆ C (A è un insieme aperto)
lim(x,y )→(x0 .y0 ) u(x, y ) = Re(l)
lim f (z) = l ∈ C ⇔
z→z0
lim(x,y )→(x0 .y0 ) v (x, y ) = Im(l)
f è continua in z0 se e solo se l = f (z0 )
Quindi per lo studio ci si riporta al caso di limiti di funzioni da R2
a R (le funzioni u e v )
A. Cutrı̀
17-11-2014
Metodi Matematici per l’ingegneria–Ing. Gestionale
Derivabilità in senso complesso
Sia A ⊆ C un aperto di C. f : A ⊆ C → C, z0 ∈ A. f è derivabile
in z0 se esiste finito il
lim
z→z0
f (z) − f (z0 )
=: f 0 (z0 )
z − z0
Poiché A è aperto, se z0 ∈ A, esiste un intorno Br (z0 )
(cerchio di centro z0 e raggio r ) contenuto in A e dunque per
z ∈ Br (z0 ) si può considerare il rapporto incrementale
f (z) − f (z0 ) ∈ C e z − z0 ∈ C dunque il rapporto
incrementale si definisce come il quoziente di due numeri
complessi (non avrebbe senso dividere due vettori!!!)
le regole di derivazione di somma, prodotto,quoziente,funzioni
composte,inverse sono analoghe a quelle di funzioni reali di
variabile reale
A. Cutrı̀
17-11-2014
Metodi Matematici per l’ingegneria–Ing. Gestionale
Condizioni CR
Anche se formalmente la definizione di derivabilità in z0 è molto
simile al concetto di derivabilità per funzioni reali di variabile reale,
vedremo che i due concetti sono profondamente diversi e la
condizione di derivabilità complessa è estremamente forte.
Che relazione c’è tra la derivabilità di f in z0 = x0 + iy0 e la
differenziabilità di u(x, y ) = Re(f ) e v (x, y ) = Im(f ) in
(x0 , y0 )? Non sono nozioni equivalenti ma vale il seguente
teorema:
Theorem
Condizioni di Cauchy-Riemann (CR): Sia f : A ⊆ C → C, A
aperto, z0 = x0 + iy0 ∈ A. Allora f è derivabile in z0 se e solo se
u(x, y ) = Ref (x + iy ) e v (x, y ) = Im(f (x + iy )) sono differenziabili
in (x0 , y0 ) e valgono le condizioni di Cauchy-Riemann seguenti:
ux (x0 , y0 ) = vy (x0 , y0 )
uy (x0 , y0 ) = −vx (x0 , y0 )
A. Cutrı̀
17-11-2014
Metodi Matematici per l’ingegneria–Ing. Gestionale
Dimostrazione del teorema CR
Dobbiamo provare che f è derivabile in z0 se e solo se u(x, y ) e
v (x, y ) sono differenziabili in (x0 , y0 ) e valgono le condizioni di
Cauchy-Riemann:
ux (x0 , y0 ) = vy (x0 , y0 )
uy (x0 , y0 ) = −vx (x0 , y0 )
DIM 00 ⇒00 : f derivabile in z0 equivale a
f (z) = f (z0 ) + f 0 (z0 )(z − z0 ) + o(|z − z0 |) z → z0
p
cioè, essendo |z − z0 | = (x − x0 )2 + (y − y0 )2 , indicando
f 0 (z0 ) = A + iB
u(x, y )+iv (x, y ) = u(x0 , y0 )+iv (x0 , y0 )+(A+iB)(x−x0 +i(y −y0 ))+o(|z−
da cui (isolando parte reale e parte immaginaria):
q
u(x, y ) = u(x0 , y0 )+A(x−x0 )−B(y −y0 )+o( (x − x0 )2 + (y − y0 )2 )
q
v (x, y ) = v (x0 , y0 )+B(x−x0 )+A(y −y0 )+o( (x − x0 )2 + (y − y0 )2 )
A. Cutrı̀
17-11-2014
Metodi Matematici per l’ingegneria–Ing. Gestionale
Quindi u e v sono differenziabili in (x0 , y0 ) e
∇u(x0 , y0 ) = (A, −B)
∇v (x0 , y0 ) = (B, A)
da cui segue
ux (x0 , y0 ) = vy (x0 , y0 )
uy (x0 , y0 ) = −vx (x0 , y0 )
ed inoltre
f 0 (z0 ) = ux + ivx = vy − iuy = . . .
DIM 00 ⇐00 :
u(x, y ) = u(x0 , y0 )+ux (x0 , y0 )(x−x0 )+uy (x0 , y0 )(y −y0 )+o(|z−z0 |)
iv (x, y ) = i[v (x0 , y0 )+vx (x0 , y0 )(x−x0 )+vy (x0 , y0 )(y −y0 )+o(|z−z0 |)]
sommando:
f (z) = f (z0 ) + [ux + ivx ](x − x0 ) + [uy + ivy ](y − y0 ) + o(|z − z0 |)
ma, per le condizioni CR, ux + ivx = −iuy + vy dunque, ponendo
f 0 (z0 ) := ux (x0 , y0 ) + ivx (x0 , y0 ) si ha
f (z) = f (z0 ) + f 0 (z0 )(z − z0 ) + o(|z − z0 |)
A. Cutrı̀
17-11-2014
Metodi Matematici per l’ingegneria–Ing. Gestionale
esempi
f (z) = e z è derivabile in ogni punto z ∈ C e f 0 (z) = e z
Infatti,
u(x, y ) = e x cos y , v (x, y ) = e x sin y
sono differenziabili in ogni (x, y )
ed inoltre valgono le condizioni CR:
ux = e x cos y = vy
uy = −e x sin y = −vx
inoltre f 0 (z) = ux + ivx = e x (cos y + i sin y ) = e z
f (z) = z NON è derivabile in alcun punto z ∈ C (è continua
in ogni punto)
Infatti:
u(x, y ) = x , v (x, y ) = −y
A. Cutrı̀
17-11-2014
dunque ux = 1 e vy = −1
Metodi Matematici per l’ingegneria–Ing. Gestionale
f (z) = |z|2 è derivabile SOLTANTO nel punto z = 0 (è
continua in ogni punto)
Infatti: u(x, y ) = x 2 + y 2 e v (x, y ) = 0 dunque vx = vy = 0
mentre ux = 2x e uy = 2y pertanto l’unico punto dove sono
soddisfatte le CR è (0, 0) e f 0 (0) = 0
f (z) = |z| NON è derivabile in alcun punto (è continua in
ogni punto)
Infatti:
v (x, y ) = 0 dunque vx = vy = 0
p
mentre u(x, y ) = x 2 + y 2 NON è differenziabile in (0, 0) ed al di
fuori dell’origine è differenziabile e ux = √ 2x 2 e uy = √ 2y 2
x +y
x +y
pertanto al di fuori di (0, 0) le condizioni CR non sono soddisfatte.
A. Cutrı̀
17-11-2014
Metodi Matematici per l’ingegneria–Ing. Gestionale
Se f (x + iy ) = u(x, y ) + iv (x, y ) è a valori reali (i.e.
v (x, y ) ≡ 0 in A) oppure a valori immaginari puri (i.e.
u(x, y ) ≡ 0 in A). Allora f è derivabile in A (connesso) se e
solo se è Costante in A (perché ∇u ≡ 0 implica per le
condizioni CR che ∇v ≡ 0 e viceversa in A)
Se f è derivabile in un punto z0 = (x0 .y0 ):
CR ⇒ < ∇u(x0 .y0 ), ∇v (x0 .y0 ) >= 0 , k∇u(x0 .y0 )k = k∇v (x0 .y0 )k
ed essendo
∇u(x0 .y0 ) ⊥ {u(x, y ) = u(x0 .y0 )} , ∇v (x0 .y0 ) ⊥ {v (x, y ) = v (x0 .y0 )
le linee di livello u(x, y ) = u(x0 .y0 ) e v (x, y ) = v (x0 .y0 ) sono
tra loro ortogonali
A. Cutrı̀
17-11-2014
Metodi Matematici per l’ingegneria–Ing. Gestionale
Funzioni Olomorfe
Def: f : A ⊆ C → C A aperto, si dice Olomorfa in A se è derivabile
in ogni punto di A con derivata continua. Se A = C allora f
olomorfa si dice Intera. Si dice che f è Olomorfa in z0 ∈ A se f è
olomorfa in un intorno Br (z0 ) ⊆ A.
Le funzioni Olomorfe in A si indicano con H(A)
Se f ∈ H(A) con A ⊆ C Aperto, allora le condizioni CR
implicano che le due forme differenziali:
ω1 := u(x, y )dx − v (x, y )dy
ω2 := v (x, y )dx + u(x, y )dy
sono Chiuse in A e se A ⊆ R2 è Semplicemente connesso
sono Esatte in A
A. Cutrı̀
17-11-2014
Metodi Matematici per l’ingegneria–Ing. Gestionale