Sheet1
Dipartimento di Matematica Corsi di Laurea Magistrale in Matematica
Piano di Studi internazionale – Mobilità Erasmus (da compilare e consegnare insieme al Learning Agreement)
Piano di Studi per la Laurea Magistrale in Matematica per mobilità Erasmus:
la prima colonna indica il Piano di Studi Padovano da inserire via Uniweb nei periodi di compilazione (novembre e aprile),
i corsi segnati con un asterisco * sono quelli sostituiti con gli esami Erasmus dichiarati a fianco;
gli esami sostituiti e quelli sostitutivi sono da riportare nel Learning Agreement.
Studente: Cognome Nome
Matricola: numero
E-mail: email@dove
Telefono: pppnnnnnn
Sede ERASMUS: Università (Stato)
periodo ERASMUS: mm/aaaa-mm/aaaa
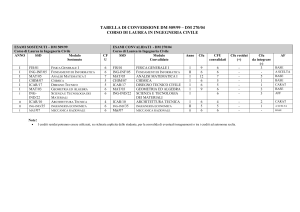
Corsi di Padova:
CFU:
regola A: un esame SSD MAT/02 – Algebra:
* Introduzione alla Teoria degli Anelli
8
regola B: un esame SSD MAT/03 – Geometria:
Geometria Differenziale
8
regola C: due esami SSD MAT/05 – Analisi Matematica:
* Introduzione alle Equazioni alle Derivate Parziali8
Calcolo delle Variazioni
8
regola D: un esame SSD MAT/06 – Probabilità:
* Introduzione ai Processi Stocastici
8
regola E: un esame SSD MAT/07 – Fisica Matematica:
Sistemi Dinamici
6
regola F: uno/due esami caratt. (qualsiasi SSD MAT/):
* Algebra Commutativa
8
CFU sostituiti:
regola G: due esami affini (qualsiasi SSD MAT/, FIS/):
* Fisica Moderna
8
Crittografia
6
regola H: uno o due esami liberi (qualsiasi SSD, 8-14 CFU):
esame Erasmus
6
Topologia
6
regola I: attività obbligatorie:
Attività Seminariale
4
Prova Finale
36
Totale CFU
120
Corsi Erasmus:
CFU sostitutivi:
8
un corso di 'algebra'
7
8
un corso di 'analisi'
10
8
un corso di 'probabilità'
9
8
un corso 'simile'
7
8
un corso 'simile'
6
6
un 'libero'
6
46
Padova, gg/mm/aaaa
45
Firma:
Page 1
Sheet1
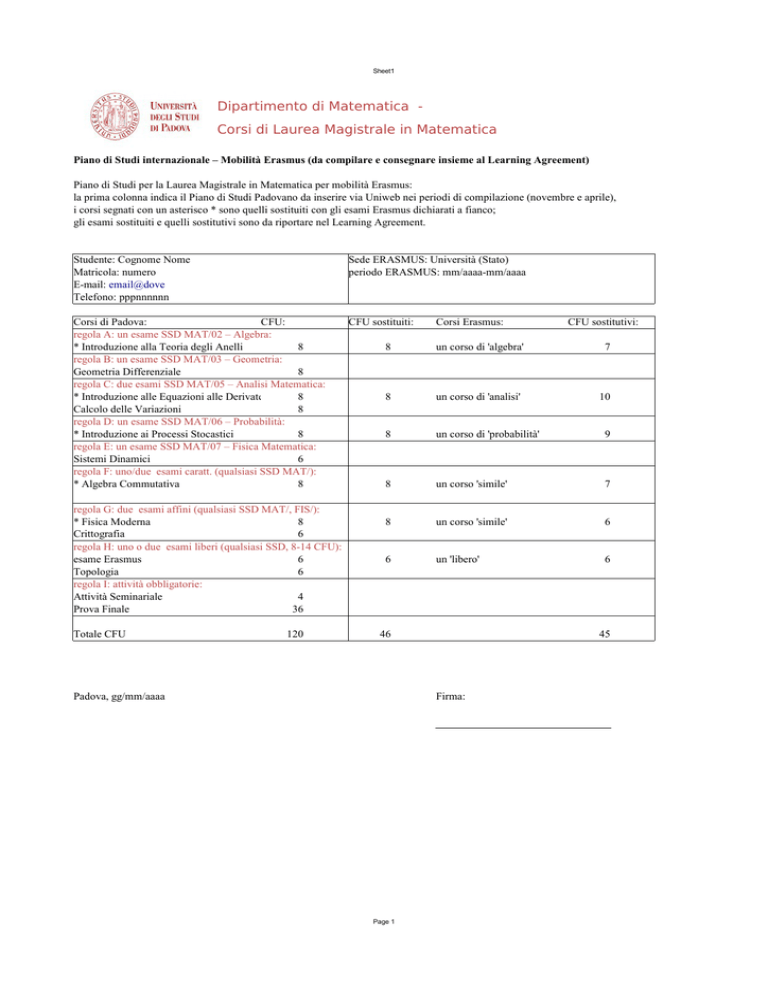
Lista dei corsi per SSD:
sigla:
nome completo
CFU
MAT/01 – Logica:
LM2
FLLF
Logica Matematica 2
6
Fond.Logici dei Ling.Funzionali
6
MAT/02 – Algebra:
ITA
ITG
AM
TRG
TdG
ALA
Introduzione alla Teoria degli
8 Anelli
Introduzione alla Teoria dei 8Gruppi
Anelli e Moduli
6
Teoria della Rappresentazione
6 dei Gruppi
Teoria di Galois
7
Algebra Lineare Applicata 7
MAT/03 – Geometria:
AlC
GA1
GA2
TN1
TN2
GD
CAP
Top
SdR
Algebra Commutativa
Geometria Algebrica 1
Geometria Algebrica 2
Teoria dei Numeri 1
Teoria dei Numeri 2
Geometria Differenziale
Curve Algebriche Piane
Topologia
Superficie di Riemann
8
8
6
8
6
8
7
6
6
MAT/04 – Matematiche Complementari:
MC
Matematiche Complementari6
MEPVS Matematiche Elementari PVS
6
MAT/05 – Analisi Matematica: IEDP
ED
CV
TF
AF2
AnC
F+VC
AR
AF1
Introduzione allae Equazioni8alle Derivate Parziali
Equazioni Differenziali
6
Calcolo delle Variazioni
8
Teoria delle Funzioni
8
Analisi Funzionale 2
8
Analisi Complessa
6
Funzioni di più variabili complesse
6
Analisi Reale
7
Analisi Funzionale 1
6
MAT/06 – Probabilità e Statistica:
IPS
AS
MSF
CP
StM
Introduzione ai Processi Stocastici
8
Analisi Stocastica
7
Metodi Stocastici per la Finanza
7
Calcolo delle Probabilità 7
Statistica Matematica
6
MAT/07 – Fisica Matematica: MS
SD
MH
MFM
MA
Meccanica Superiore
Sistemi Dinamici
Meccanica Hamiltoniana
Modelli Fisico Matematici
Meccanica Analitica
6
7
6
6
6
MAT/08 – Analisi Numerica:
MNAD Metodi Numerici per l'Analisi
7 Dati
MNED Metodi Numerici per le Equazioni
7
Differenziali
TAA
Teoria della Approssimazione
7 e Applicazioni
MAT/09 – Ricerca Operativa:
RO
Ott
Ricerca Operativa
Ottimizzazione
Affini (i precedenti e):
Critto
FiMo
SFD
Crittografia
6
Fisica Moderna
8
Sperimentazioni di Fisica per6 Didattica
8
6
Page 2