Modulo 5 – La programmazione
Unità 1 – Elementi di base
Prof. Antonio Scanu
1 Informatica
Che cos'è l'informatica? Che cosa studia? Per capire che cos'è l'informatica, diciamo che
cosa essa non è; in questo modo possiamo comprendere non soltanto di che cosa si oc cupa questa scienza, ma anche di che cosa si occupa l'informatico, cioè chi studia l'informatica e le sue applicazioni.
Le due domande appena poste sembrerebbero elementari, forse banali, ma le risposte
sono, invece, complesse. Perché, nel linguaggio quotidiano, informatica è un termine di
uso comune, ma dai contorni poco definiti. Ciò a causa dell'accezione comune del termine
"informatica" che fa riferimento all'uso del computer: scrivere una lettera, fare dei calcoli,
installare un software, realizzare delle presentazioni, navigare su Internet, divertirsi con i
videogiochi. Chiesto, secondo il pensiero comune, è ciò di cui si occupa l'informatica e che
dovrebbe saper fare un informatico. Tutto quanto appena detto è, invece, ciò che l'informatica non è!
2 Informatica e matematica
L'informatica affonda le proprie radici nella matematica, ma ormai è una scienza ben distinta. Per comprendere quali sono i rapporti tra matematica e informatica, e quali sono
invece le peculiarità dell'informatica come scienza, ricorriamo a un semplice esempio.
Consideriamo un'operazione matematica semplicissima, che tutti noi sappiamo eseguire:
la divisione tra due numeri. La matematica e l'informatica hanno due punti di vista diversi
su questo problema:
la matematica si occupa di scoprire un procedimento per risolvere il problema;
l'informatica si occupa di codificare questo procedimento in un linguaggio comprensibile ed eseguibile da una macchina.
L'informatica si occupa proprio di codificare la procedura matematica in maniera da renderla comprensibile al computer. Perché proprio a una macchina? I motivi sono tanti e li
riassumiamo in pochi punti:
perché la macchina riesce a eseguire la procedura in modo molto più rapido di
quanto non possa fare l'uomo;
perché l'uomo può commettere errori durante l'esecuzione della procedura, mentre la macchina applicherà sempre in maniera corretta la procedura che è stata
predisposta dall'uomo;
perché, lasciando alla macchina l'esecuzione dei compiti più lunghi, noiosi e ripetitivi, l'uomo può concentrarsi su attività "intellettuali" che non sono di competenza
delle macchine.
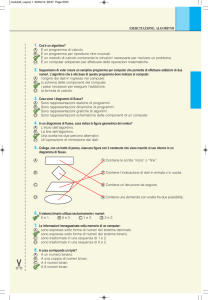
3 Informatica, algoritmi e computer
L'informatica si occupa, quindi, di trovare soluzioni elementari ai problemi. Parliamo di
"soluzioni elementari" perché la macchina non è in grado di svolgere compiti complessi,
anzi è capace di eseguire solo istruzioni semplici ed elementari. Impareremo a conoscere
queste soluzioni elementari con il termine algoritmo.
2
Alla base dell'informatica c'è, quindi, lo studio delle tecniche per la risoluzione dei problemi tramite gli algoritmi. Alla base dell'informatica non c'è il computer, come comunemente
si pensa, ma concetti diversi, quali, per esempio:
le tecniche di progettazione degli algoritmi;
le metodologie per la produzione del software;
i linguaggi di programmazione;
i programmi traduttori (compilatori e interpreti).
La maggior parte degli oggetti elettronici, come i telefoni cellulari, per esempio, è programmata grazie alla preventiva realizzazione di specifici algoritmi. La principale differenza tra
il computer e questi strumenti elettronici è data dal fatto che il computer è capace di ap prendere nuovi algoritmi ed eseguirli autonomamente.
A nessun altro tipo di strumento possiamo far svolgere un nuovo compito, poiché tali stru menti possono svolgere solo le operazioni previste dall'algoritmo che sono già in grado di
interpretare (essi sono, quindi, degli automi), mentre i compiti di un computer sono tutti
da definire e progettare (programmare), grazie agli algoritmi.
Ora possiamo dera una definizione di informatica:
derivato dal francese informatique e coniato dall'ingegnere francese Philippe Dreyfus nel
1962, il termine informatica (contrazione di informazione automatica) si riferisce alla disciplina scientifica che aiuta a risolvere problemi di una parte semplificata della realtà,
tramite tecniche e metodi di analisi, la rappresentazione, elaborazione , la memorizzazione e trasmissioni delle informazioni)
Dalla definizione si evince che l'informatica è una scienza interdisciplinare che riguarda
tutti gli aspetti dcl trattamento dell'informazione mediante procedure automatizzabili e
che il supremo compito di questa scienza e dei suoi studiosi è quello di progettare e sviluppare algoritmi che descrivano e trasformino l'informazione pervenendo, così, alla soluzione automatica dei problemi.
L'informatica è diventata ormai strategica in ogni settore dell'attività umana, nello sviluppo economico e sociale delle popolazioni. Il fatto che esistano persone prive della possibi lità di utilizzarla è divenuto un problema di interesse internazionale. Qiesto divario tra chi
ha la possibilità di utilizzare la tecnologia e chi no viene indicato con il termine digitai divi de e le sue principali cause sono legate alle condizioni economiche, al grado di istruzione
e alle dotazioni infrastrutturali.
Che cos'è e che cosa non è l'informatica:
L'informatica è
L'informatica non è
La scienza che studia i metodi e i processi per risolvere i problemi
La scienza del ragionamento automatico
La scienza che ha come principale applicazione il mondo dei computer e del
software (linguaggi. Algoritmi. Architetture applicazioni. interfacce. Web).
Lo studio dei calcolatori .
L'uso dei computer
L'abilità di navigare su Internet
La tecnica per assemblare i computer
La conoscenza di particolari software
La tecnica per installare software .
La conoscenza di svariati linguaggi di
programmazione .
Soltanto programmare .
3
In conclusione possiamo dire che l'informatica comprende anche le parti appena citate
ma esse, non sono l'informatica.
4 Definizione di algoritmo
Si dice algoritmo una sequenza di azioni, valida per un insieme di dati iniziali ben definito,
che, compiuta da un opportuno esecutore (o processore), trasformi i dati nel risultato finale, attraverso un numero finito di passi elementari e non ambigui.
In questa definizione possiamo individuare tre elementi fondamentali:
dati iniziali e dati finali;
sequenza di azioni (istruzioni oppure passi elementari);
esecutore (oppure processore).
Di seguito si illustrano nel dettaglio i tre suddetti elementi.
Dati iniziali sono gli "elementi" (iniziali o in ingresso) che vengono elaborati dall'algoritmo. I dati finali sono i risultati prodotti dall'algoritmo (finali o in uscita). Per
esempio, in un'addizione (algoritmo), gli addendi sono i dati in ingresso e la somma risultante i dati in uscita.
Sequenza di azioni: un'azione è un'operazione elementare (istruzione), generalmente molto semplice, che compone un passo della serie di operazioni (sequenza) che deve essere eseguita sui dati di ingresso per ottenere il risultato, cioè i
dati in uscita. Questo procedimento prende anche il nome di elaborazione. Per
esempio, un'azione elementare per un algoritmo che esegue la somma di due numeri a più cifre è la somma delle cifre di posizione corrispondente (unità, decine
oppure centinaia).
Esecutore: è il soggetto che "compie" le azioni, cioè legge le istruzioni che devono
essere eseguite sui dati in ingresso, le interpreta e le esegue in modo da elaborare tali dati per trasformarli in risultati, cioè dati in uscita. L'esecutore è una persona oppure una macchina automatica e, naturalmente, le istruzioni devono essere
scritte in modo tale che l'esecutore possa comprenderle ed eseguirle correttamente.
4.1 Risolutore e esecutore
Nell'intero processo di risoluzione di un problema esistono sempre due momenti distinti:
quello della risoluzione, consistente nell'individuazione di una strategia per raggiungere
l'obiettivo, e quello dell'esecuzione di tutte le azioni necessarie descritte nel procedimento
di risoluzione. Quando si risolve un problema è quindi possibile fare riferimento a due tipi
di attori.
Il risolutore: la persona che definisce e costruisce la strategia risolutiva per un dato problema poiché svolge attività di studio e di ricerca legate all'analisi e alla progettazione.
L'esecutore (o processore): colui che esegue le azioni descritte dal risolutore per giungere
concretamente alla soluzione del problema. L'esecutore è un'entità generica che sa soltanto eseguire le azioni elementari suggerite dal risolutore. Non è necessario che l'esecutore conosca gli scopi o il senso complessivo della strategia risolutiva. Il suo compito è
quello di comprendere, interpretare ed eseguire correttamente le istruzioni fornite dal risolutore sul dati iniziali per giungere al dati finali.
4
4.2 Azioni ed istruzioni
Sappiamo che una stra tegia risolutiva è caratterizzata da una serie di passi. Per essere
più precisi, al termine passo dobbiamo sostituire quello di azione.
Si definisce azione un evento di cui sono noti il soggetto, detto esecutore, l'oggetto, o gli
oggetti, su cui l'esecutore deve agire e la trasformazione prodotta su di essi in un'unità finita di tempo.
La frase Daniela mangia una mela puntualizza un'azione, in quanto, in un'unità finita di
tempo, Daniela (esecutore) opera una trasformazione sulla mela (oggetto). Se poniamo
l'accento sull'azione svolta e su come Daniela mangia una mela, risulta evidente che tale
azione è composta da azioni più semplici. Nel dettaglio, infatti, l'azione in questione si può
scomporre nel seguente modo:
Daniela prende una mela;
Daniela sbuccia la mela;
Daniela taglia a fette la mela;
Daniela mastica la mela.
Le azioni devono avvenire in sequenza, una dopo l'altra (non si ritiene quindi possibile che
Daniela tagli a fette la mela e, contemporaneamente, la mastichi).
Un'azione si dice elementare quando non può essere scomposta in altre azioni più semplici. L'azione elementare, detta anche istruzione, è interpretabile in modo univoco dall'esecutore e direttamente eseguibile. Ciò significa che l'esecutore comprende in modo univoco che cosa deve fare e sa come farlo.
Esempio: "Prelevare una somma dal bancomat"
Dati iniziali:
C: codice segreto
I: importo da prelevare
Per descrivere il processo risolutivo possiamo utilizzare la seguente sequenza ordinata di
azioni elementari:
1. introdurre la carta nel lettore
2. digitare il codice segreto C
3. digitare l'importo. da prelevare I
4. ritrarre la carta dal bancomat
5. prelevare le banconote
4.3 Caratteristiche di un algoritmo
L’algoritmo è quindi un metodo per risolvere un problema. È possibile elencare alcune
proprietà o caratteristiche fondamentali che un algoritmo deve possedere:
finitezza: l'algoritmo deve essere composto da un numero finito di passi elementari, che vengono eseguiti un numero finito di volte;
determinatezza: le istruzioni vengono definite senza ambiguità in modo tale da garantire sempre gli stessi risultati a parità di condizioni e indipendentemente dell'esecutore;
5
realizzabilità: le istruzioni devono essere effettivamente realizzabili e conosciute
dall'esecutore che sa come attuarle; inoltre l'algoritmo deve essere fattibile con le
risorse a disposizione.
generalità: l'algoritmo non deve risolvere un problema ma una famiglia di problemi
(per esempio l’algoritmo della moltiplicazione non deve eseguire soltanto 6 * 5,
ma deve essere eseguire tutte le moltiplicazioni possibili;
completo: deve considerare tutti i casi possibili che si possono verificare durante
l'esecuzione, per ogni caso, indicare la soluzione da seguire;
tempo di elaborazione: oltre a essere costituito da un numero finito di istruzioni,
l'algoritmo deve terminare in un tempo finito;
Osservabile nei risultati: possibile verificare i risultati ottenuti.
Come abbiamo già visto, per la risoluzione di un problema è possibile trovare diverse strategie risolutive alle quali corrispondono altrettanti algoritmi. Il parametro che consente di
preferire una strategia, e quindi un algoritmo, rispetto a un'altra è l'efficienza
Un algoritmo si dice efficiente quando:
è corretto, cioè produce il risultato atteso;
è veloce in termini di tempo impiegato per produrre il risultato;
è parsimonioso in termini di risorse allocate per produrre il risultato.
5 I Problemi
Il lavoro dei programmatori,spesso si riassume semplicemente nelle due parole "produrre
programmi": dietro queste parole, però, esiste un insieme di attività complesse ben lontane dalla semplice codifica di un algoritmo in un linguaggio di programmazione (operazione
effettuata dai cosiddetti codificatori o manovali del software).
La programmazione è l'insieme di quelle attività che, a partire da un problema, conducono
alla stesura di un programma la cui esecuzione da parte di un calcolatore ha come risultato la soluzione del problema.
Si parte dal problema per arrivare al programma, individuando la soluzione; la ricerca della soluzione è infatti il compito principale del programmatore e anche il principale problema: come si arriva alla risoluzione di un dato problema.
Alcuni problemi possono apparire più semplici, altri più complessi, altri ancora assurdi. Ma
come facciamo a definire un problema facile, difficile o assurdo? E principalmente: che
cos'è un problema? Sfogliando il dizionario leggiamo che:
un problema è una questione in base alla quale si devono trovare uno, o più elementi
ignoti (la soluzione) partendo dagli elementi noti contenuti nell'enunciato della questione
stessa.
Il concetto di "problema" può avere svariate accezioni in quanto può applicarsi sia a strumenti di valutazione nell'ambito di discipline specifiche, come per i problemi di matematica o fisica, sia a metodologie di sviluppo per l'apprendimento integrato del sapere scientifico, sia alla risoluzione di situazioni "quotidiane
5.1 Risolvere un problema
Non è semplice trovare una soluzione a un problema. Spesso pensiamo di averla trovata
ma, dopo un'attenta verifica, ci rendiamo conto che essa non fornisce i risultati che atten6
devamo. Siamo quindi costretti a trovare una nuova soluzione, e la cerchiamo per tentativi: se un tentativo non ha successo si riprova con un altro, magari sfruttando i punti validi
della soluzione fallita e facendo tesoro dell'insuccesso precedente. Il lavoro mentale volto
alla ricerca della soluzione prende il nome di strategia risolutiva.
Una strategia risolutiva è un insieme di passi da compiere per giungere alla soluzione di
un problema.
La soluzione o risultato o risultato finale è l'obiettivo che vogliamo raggiungere.
Per poter risolvere un problema sono necessarie alcune informazioni iniziali e indispensabili che chiameremo dati iniziali. Consideriamo, per esempio, l'emissione di un biglietto
ferroviario da parte di un addetto in un'agenzia viaggi, il signor Gino. La situazione può essere schematizzata nel seguente modo:
Il cliente, entrando in agenzia, effettua la seguente richiesta:
"vorrei un biglietto per due persone da Roma a Milano per il 20 marzo"
Ottenuto il biglietto, il cliente lo osserverà attentamente per verificare la correttezza delle
informazioni contenute. Il suo criterio di verifica consisterà nel controllare che:
la stazione di partenza coincida con Roma;
la stazione di arrivo sia Milano;
la data corrisponda al 20 marzo;
il numero di persone sia due.
7
La strategia risolutiva di un problema segue, pertanto, la seguente successione di fasi:
l'analisi del problema, che rappresenta lo studio attraverso il quale si riesce a identificare
l'obiettivo da raggiungere e lo stato iniziale del problema, ossia l'insieme dei dati
iniziali oggettivi e significativi che si han no a disposizione;
la progettazione, che specifica le azioni da intraprendere per risolvere il problema,
ossia per trasformare i dati iniziali in dati finali;
la verifica della soluzione, che consente di raggiungere lo stato finale del problema, ossia permette di verificare che i risultati finali ottenuti siano rispondenti agli
obiettivi iniziali. In caso contrario, si dovranno rivedere le specifiche rilevate in fase
di analisi, apportare le modifiche al progetto e verificare nuovamente la soluzione.
5.2 Analisi del problema
Il pensiero occidentale si basa sull'analisi del ragionamento deduttivo e attribuisce all'analisi la stessa importanza connessa alla ricerca della verità. Noi siamo naturalmente portati
all'analisi, in quanto essa rientra nella nostra tradizione culturale: sin da bambini ci hanno
insegnato a esaminare le informazioni di cui abbiamo percezione prima di dedurne un significato.
Quindi l'analisi consiste nell’ affrontare il problema in modo sistematico, considerando i
vari aspetti della formulazione e scomponendo situazioni complesse e piene di incognite
in elementi riconoscibili e accessibili.
La comprensione del problema è necessaria per poter estrarre dalla realtà tutte quelle informazioni che risultano essenziali al fine di risolvere il problema analizzato.
Prima di tutto, occorre delimitare con precisione l'area di interesse da quella di non interesse, ricordo che più ampia è la portata del problema da risolvere e maggiori diventano
le complessità da affrontare sul piano concettuale, progettistico e operativo.
Quindi occorre individuare con precisione l'insieme dei dati ai quali si intende estendere i
risultati e specificarne esattamente le condizioni di eleggibilità, ovvero le caratteristiche
che ne determinano inclusione o l'esclusione (casi particolari e casi limite di funzionamen to).
I passi per fare l'analisi sono.
Comprensione del problema : La formulazione di un qualunque problema non è
mai in "formato informatico"' ma in generale è in forma di un testo descrittivo ottenuto raccogliendo le specifiche richieste del committente, a volte scritto dallo stesso committente e a volte frutto di una serie di colloqui con le persone direttamente
interessate al problema.
Focalizzare gli obiettivi : Spesso un problema è espresso in modo confuso o fuorviante, e una prima esigenza naturale consiste nell'eliminare ogni tipo di ambiguità
dalla sua formulazione. Per ottenere tale risultato è indispensabile eseguire una
operazione di pulizia del testo, intervenendo con il duplice scopo di:
✔ evidenziare i reali obiettivi del problema, le regole e i dati espliciti e impliciti;
✔ eliminare i dettagli inutili e ambigui.
Procedere quindi a una riformulazione dell'enunciato in modo da:
✔ eliminare qualunque possibile forma di ambiguità del testo che porterebbe
a identificare obiettivi errati;
8
✔
✔
evidenziare le informazioni effettivamente necessarie eliminando i dati inutili, superflui o ridondanti;
individuare ed evidenziare le informazioni che sono presenti nel testo non
esplicitamente, ma in forma implicita o sottintesa.
Descrizione: L'analisi del problema deve fornire una breve descrizione di che
cosa si vuole fare evidenziando i possibili vincoli inerenti il problema e i requisiti, ossia specifiche richieste che devono essere soddisfatte Prendiamo in esame il seguente problema: calcolare il prodotto di due numeri interi X e Y.
Nella descrizione del problema si potrebbe dettagliare il fatto che calcoleremo
il prodotto X * Y utilizzando l'addizione. Dobbiamo anche dettagliare i casi che
potrebbero verificarsi e cioè:
✔
✔
se Y = O, il prodotto è O
se Y > O, il prodotto si ottiene sommando Y volte il valore di X.
Definire e descrivere l'area di interesse: Per condurre un'analisi efficace, è importante definire con precisione l'area di interesse separandola da quella di non
interesse. l'area di interesse è composta da:
✔ i dati iniziali, cioè quelli da elaborare, detti anche dati in ingresso al
problema, che devono essere individuati con attenzione nell'insieme dei
dati a disposizione specificando con esattezza le caratteristiche che ne
determinano l'inclusione o l'esclusione (casi particolari e casi limite di
funzionamento). Specificando quali sono i dati di ingresso si definisce
una istanza di problema. Per esempio, considerato il problema P: dato
un naturale n calcolare la somma dei primi n numeri naturali, un'istanza
di P è: risolvere P per n = 12 (ovvero calcolare la somma dei primi 12
numeri naturali). In generale, quindi, un problema può essere visto
come l'insieme di tutte le sue possibili istanze.
✔
dati finali che si vogliono ottenere in funzione degli ingressi, detti anche
dati in uscita del problema.
In gergo informatico ci sì riferisce all'area di interesse del problema con l'espressione specifiche funzionali.
Criterio di verifica : Infine definire un criterio di verifica dei risultati. Per criterio di
verifica intendiamo un controllo sui risultati finali per verificare che questi siano ri spondenti agli obiettivi iniziali.
Naturalmente vi sono anche problemi mal formulati. Ad esempio "calcolare il Massimo
Comun Divisore". non potrà mai essere risolto in quanto mancano le informazioni iniziali e
cioè i valori numerici sui quali calcolare il. Massimo Comun Divisore. Occorre pertanto riformularlo
Il problema di emettere un biglietto ferroviario sarebbe stato mal formulato se si chiede :
vorrei un biglietto per il 20 marzo (senza indicare dove si deve andare )
vorrei un biglietto per Milano (senza indicare la data)
Consideriamo un problema ben formulato. Può accadere che, nonostante vari tentativi di
ricerca della soluzione, non si riesca a trovarne neanche una. In questo caso ci si trova di
fronte a un problema non risolvibile. Possiamo allora affermare che: un problema non è risolvibile se, pur. essendo correttamente formulato, non ammette soluzioni.
Ad esempio: “vorrei un biglietto per due persone da Roma che parte alle 12 per la Luna”
9
5.3 Alcuni Esempi
PROBLEMA: fare una telefonata
Analisi del problema
Desideriamo chiamare un abbonato con il telefono. Dopo aver composto il numero sull'apparecchio telefonico si possono verificare i seguenti casi: l'abbonato risponde. per cui la telefonata viene eseguita con successo,
oppure la telefonata non può essere effettuata perché il telefono è occupato o l'abbonato non risponde.
Specifiche funzionali
Dati iniziali
• numero da comporre
Dati finali
• messaggio "telefonata riuscita"
• messaggio "telefonata non riuscita"
Criterio di verifica:
Telefono a Mario Rossi e mi risponde o non mi risponde ma perche il telefono e occupato o non alza la cor rente. Sarebbe un algoritmo errato se mi rispondesse Luca Sanna.
PROBLEMA: calcolare il prodotto di due numeri interi
Analisi del problema
Dobbiamo considerare due numeri interi, che indichiamo con X e Y, e trovare il loro prodotto. li semplice
procedimento dettato dalla matematica prevede che si possa utilizzare l'addizione. Infatti:
• se Y = 0. il prodotto è 0
• se Y > 0. il prodotto è X + X + ... + X (per Y volte)
Specifiche funzionali
Dati iniziali
• due numeri interi X e Y
Dati finali
• 0, se Y = 0
• X* Y, se Y > 0
Criterio di verifica:
Se digito X=4 e Y=0 ottengo 0
Se digito X=4 e Y=3 ottengo 12
PROBLEMA: trovare il massimo fra tre numeri
Analisi del problema
Per cercare il massimo fra tre numeri. che chiamiamo a, be e, è sufficiente confrontare a con b e trovare il
massimo tra questi due; quindi, una volta ottenuto questo valore. basta confrontarlo con il numero e per ottenere il massimo valore fra I tre forniti.
Specifiche funzionali
Dati iniziali
• tre numeri interi a, b, e
Dati finali
• il valore massimo
Criterio di Verifica:
Se digito 3,5,4 il risultato deve essere 5
10
PROBLEMA: cercare il numero di un utente in un elenco telefonico
Analisi del problema
Un modo piuttosto semplice per Iniziare potrebbe essere quello di osservare la prima coppia (nome, numero
telefonico). Se il nome è uguale a quello cercato, allora il numero telefonico corrispondente è quello cercato e
il problema è risolto. Se questa prima coppia non soddisfa la nostra condizione, dobbiamo passare alla coppia
successiva, ma occorre tenere presente che non dobbiamo oltre passare l'ultima coppia presente in elenco. se
ciò dovesse accadere, significa che il valore cercato non è presente nell'elenco.
Specifiche funzionali
Dati iniziali
• un Insieme ordinato di coppie (nome, numero telefonico) e un nome da ricercare
che indichiamo con X
Dati finali
• il numero telefonico corrispondente all'utente caratterizzato dal nome X (se
presente nell'insieme)
• visualizzazione di un messaggio con il quale si Informa che l'utente non è incluso
nell'elenco (se ['utente non è presente)
Criterio di verifica.
Cerco Mario rossi e mi visualizza 12344 se esiste il numero
5.4 Ricerca della soluzione
A questo punto descriviamo alcuni metodi e strategie di supporto al processo creativo relativo alla ricerca della soluzione di un problema: si tratta di metodi e strumenti di supporto che, da soli, non permettono di raggiungere la soluzione, in quanto risolvere un problema è un processo creativo non automatizzabile in cui il progettista gioca un ruolo fondamentale. Questo significa che la risoluzione richiede non solo un insieme di conoscenze,
ma anche la capacità di utilizzarle per elaborare una strategia risolutiva, quindi non è pos sibile indicare un insieme di regole generali che consentano di trovare automaticamente
la soluzione: in questo processo la creatività è sempre fondamentale e si fonde con le tec niche per risolvere problemi; inoltre, può essere utilizzata anche per ricercare nuove soluzioni più efficienti a problemi già risolti.
L'approccio vincente è sempre quello "molteplice": le diverse metodologie devono essere
sempre utilizzare in combinazione tra loro e unite alle attività creative e artistiche prima
discusse. Possiamo affermare che la ricerca della soluzione è una fase di progetto in cui
conoscenze, tentativi e lavoro metodico si fondono per la definizione della soluzione del
problema.
In definitiva, risolvere un problema è un processo creativo che si può avvalere di alcuni
metodi e strategie che permettono di ricercare una possibile sequenza di operazioni per
raggiungere l'obiettivo proposto (anche se non è certo che tale sequenza di operazioni esista, cioè non è detto che il problema in esame possa effettivamente trovare soluzione).
Risolvere un problema è come individuare il cammino che dallo stato iniziale permette di
raggiungere lo stato finale (soluzione del problema) attraverso un insieme finito di stati intermedi.
Procedimento per tentativi
La soluzione del problema non sempre viene individuata "al primo colpo": alla base del
problem solving c'è infatti la ricerca per tentativi, la maggior parte dei quali generalmente
non ha successo.
11
Non bisogna demordere o demoralizzarsi se di fronte a un problema non si ha subito l'idea per la soluzione o se si inizia un procedimento che ben presto porta in un vicolo cieco:
in tale situazione non resta che escludere la "strada" scelta e cercarne una nuova.
A volte capita anche di arrivare faticosamente a una soluzione che però risulta estremamente complessa e di difficile codifica e/o implementazione; si deve invece tenere presente che la soluzione migliore è sempre la più semplice.
Se quindi ci si rende conto di aver progettato una soluzione complessa è meglio ricominciare tutto da capo e ricercare quella più semplice; il tempo apparentemente perso per risolvere nuovamente il problema verrà sicuramente recuperato nelle successive fasi di sviluppo e soprattutto nella fase di manutenzione.
Sfruttamento dell'esperienza
Fortunatamente, spesso i problemi da risolvere non sono "nuovi" e unici: molti infatti si somigliano e sono correlati fra loro.
La prima regola da rispettare per risolvere i problemi è quella di individuare eventuali similarità con altri problemi. Anzi, per essere sinceri, la prima regola è quella di scoprire se lo
stesso problema non sia già stato risolto da altri, quindi di ricercare l'analogia con problemi risolti in passato, anche più semplici, da noi stessi o da altri programmatori (o matematici) più famosi.
Nel mondo degli algoritmi problemi simili hanno spesso soluzioni simili: il procedimento risolutivo di problemi noti può essere utilizzato, completamente o parzialmente, per la soluzione del nuovo problema.
Ripercorrere il cammino all'indietro (backtracking).
Spesso accade che, nel cammino percorso durante la ricerca della soluzione, ci accorgiamo che la strada seguita non porta a nessuna soluzione. In questo caso è opportuno ripercorrere i propri passi, tornare indietro a un punto del cammino dal quale si possa ripar tire per un'altra strada.
Scomposizione dei problemi
La principale tecnica utilizzata in informatica per la soluzione dei problemi è quella della
scomposizione in sottoproblemi; questo approccio non è proprio della programmazione
ma ha origini antiche ispirate al "divide et impera" degli antichi romani. Infatti non è realistico pensare di risolvere un problema in un'unica azione, sia perché spesso i problemi si
presentano dimensioni consistenti, sia perché spesso, nella ricerca di soluzioni, un problema può essere articolato in sottoproblemi più semplici da risolvere (o addirittura già risol ti) in modo tale che, risolvendo questi ultimi indipendentemente, si possa giungere alla soluzione del problema originale. Si vedrà questo metodo applicato in seguito.
Scomporre il problema in sottoproblemi significa individuare problemi più semplici che
compongono il primo e che sono autonomamente risolvibili; dalla soluzione di tali sottoproblemi è poi possibile ottenere facilmente la soluzione del problema di partenza. La
scomposizione in sottoproblemi avviene:
fissando una serie di sotto-obiettivi da raggiungere durante il processo risolutivo in
modo che ciascuno di essi individui sottoproblemi degni di particolare attenzione;
procedendo in una scomposizione attraverso raffinamenti successivi che deve essere orientata alla definizione di uno o più sottoproblemi facilmente risolvibili (problemi primitivi).
La regola principale è che non esistono regole fisse per la ricerca di sottoproblemi appropriati: esperienza, creatività, intuizione e conoscenza delle tecniche fondamentali sono la
risorsa principale del progettista.
12
6 Il linguaggio
Il linguaggio verbale è la capacità degli uomini di comunicare utilizzando un sistema di se gni vocali.
L'alfabeto è un sistema di segni grafici che l’uomo utilizza per rappresentare i vocaboli di
una lingua.
La lingua è un sistema di vocaboli e di regole con il quale gli individui di una comunità co municano tra loro. Va però sottolineato che il linguaggio verbale (lingua italiana, inglese
ecc.), quello, cioè, il cui alfabeto è caratterizzato da segni rappresentabili con la voce, non
è l'unico tipo di linguaggio che utilizziamo. Se riflettiamo un po', notiamo chiaramente che
comunichiamo anche in altri modi. Quali? Situazioni ce ne sono tante.
Con un sordomuto, ad esempio, utilizziamo un linguaggio gestuale (vedi figura), basato,
cioè, su gesti che rappresentano un'idea o un concetto; in matematica, in stenografia e in
musica adoperiamo un linguaggio ideografico, costituito da particolari simboli che rappresentano un significato: la musica, ad esempio, viene scritta sugli spartiti musicali mediante particolari simboli, che rappresentano le note, le chiavi musicali, le alterazioni e tutto
ciò che il musicista trasformerà in melodia.
Il linguaggio, quindi, è un codice, cioè un insieme di segni e di regole che rendono possibile la comunicazione tra tutti coloro che lo usano.
Si hanno, così, codici verbali, gestuali, musicali, iconici e tanti altri quanti la natura umana
può concepire.
7 Linguaggi naturali e linguaggi formali
I linguaggi possono essere classificati in naturali e formali.
Il linguaggi verbali, scritti e orali, vengono anche indicati come linguaggi naturali. Rientrano in questa categoria, quindi, l'italiano, l'inglese, il tedesco eccetera.
Tutti i linguaggi naturali hanno un proprio alfabeto, cioè l'insieme dei simboli che ognuno
di essi utilizza. Accostando opportunamente i simboli otteniamo le parole: l’insieme di tutte le parole di un linguaggio costituisce. Il suo lessico o vocabolario. Le parole, da sole,
non bastano a comunicare: occorre accostarle opportunamente per formare delle frasi.
Tutti questi accostamenti non sono semplici da realizzare. Consideriamo, ad esempio, le
seguenti parole:
1. igiktew;
2. azzurro; 3. mamma; 4. ihhyjjyuu; 5. papà;
e le seguenti frasi:
1. la mamma fa la spesa; 2. il topo picchia l'elefante;3. la matita studiava all'informatica.
Se adoperiamo le regole della grammatica, è facile affermare che: le parole degli esempi
1 e 4 non fanno parte della lingua italiana e che la frase dell'esempio 3 non è corretta.
La grammatica di un linguaggio comprende l'alfabeto e l'insieme di regole indispensabili
per formare le parole e raggrupparle in frasi corrette.
Seguendo queste regole possiamo affermare che:
le parole degli esempi 1 e 4 sono lessicalmente errate, in quanto l'accostamento
dei simboli dell'alfabeto non produce alcun significato;
la frase 3 è sintatticamente errata.
13
La sintassi è un insieme di regole che definisce la struttura di frasi formalmente correte.
La sintassi ci aiuta a stabilire se una frase appartiene o meno al linguaggio. In questi termini, la frase 3 non è corretta in quanto il complemento è errato. Dovremmo scrivere: la
matita studiava l'informatica. A questo punto possiamo affermare che la frase, pur essen do sintatticamente corretta, è, però, semanticamente errata, ossia priva di significato.
La semantica, quindi, definisce il significato delle parole e delle frasi.
Una delle principali caratteristiche dei linguaggi naturali è la presenza di sinonimi, ambiguità e, talvolta, anche di eccezioni, metafore e allegorie. Facciamo qualche esempio. Se
dobbiamo affermare che uno studente è molto volenteroso, possiamo anche utilizzare gli
aggettivi: zelante, operoso, attivo, alacre, sollecito, dinamico, solerte.
Se proviamo a leggere la frase: “ ieri sera ho visto Giuseppe con un conoscente" è eviden te che può essere interpretata in due modi diversi: "ieri sera ho visto Giuseppe che era in
compagnia di un conoscente" oppure "ieri sera ho visto Giuseppe mentre ero in compagnia di un conoscente".
Se analizziamo le seguenti frasi:
“Questo film è troppo pesante" ; "Questa pietra è troppo pesante"
notiamo che l'aggettivo “pesante” assume significati differenti in funzione del contesto in
cui è inserito. È solo grazie al soggetto che riusciamo ad attribuire un significato all'agget tivo in tale contesto.
Nella prima frase, infatti, assegniamo all'aggettivo "pesante" i significati di noioso, monotono; nella seconda gli attribuiamo il significato di ponderoso, Nei linguaggi naturali, quindi:
a ogni simbolo non corrisponde un solo significato;
un simbolo trasmette molteplici significati in un singolo contesto.
Il linguaggi formali sono invece quelli che l'uomo utilizza per la comunicazione simbolica
quella particolare comunicazione che utilizza simboli astratti applicati a situazioni reali.
In questi linguaggi:
a ogni simbolo corrisponde uno e un solo significato;
un simbolo racchiude lo stesso significato in qualsiasi contesto;
una volta definito, il codice non può esser modificato dagli elementi che lo utilizza no.
Questi linguaggi, quindi, non presentano né sinonimi, né eccezioni, ne ambiguità e sono
controllati da regole prefissate. Per questa singolare caratteristica, si sono dimostrati par ticolarmente utili nel campo della comunicazione uomo-macchina.
Per suonare il pianoforte, l'uomo utilizza il linguaggio della musica. Per studiare la matematica, utilizza il linguaggio matematico. Per programmare, utilizza il linguaggio di programmazione. Precisiamo ancora che l'aggettivo "formale" deve essere inteso come sinonimo di "rigorosamente definito".
Il rigore dei linguaggi formali è molto importante in informatica. Per i linguaggi di programmazione, infatti, le regole linguistiche devono essere assolutamente rigide, in quanto un
computer non ha alcuna capacità di adattarsi a frasi che comunicano seguendo modalità
non previste. Dopo questi chiarimenti generali, siamo in grado di esporre in modo più rigoroso il concetto di programma:
Un programma è la trasformazione dell'algoritmo che risolve un problema in un insieme di
di frasi sintatticamente e semanticamente corrette. Tali frasi utilizzano l'alfabeto, il lessico
14
e le regole del linguaggio di programmazione scelto. Le singole frasi del programma prendono il nome di istruzioni.
8 Linguaggi di programmazione e macchine
I linguaggi di programmazione si sono evoluti di pari passo con i computer e, per questo
motivo, possiamo parlare di generazioni di linguaggi. Tecnicamente, utilizzare un linguaggio corrisponde, dal punto di vista del programmatore, a disporre delle istruzioni per una
macchina piuttosto di un'altra. Pertanto, le nozioni di macchina e di linguaggio sono inti mamente collegate.
La programmazione elettronica nasce intorno agli anni Cinquanta, quando si programmava esclusivamente in linguaggio nativo, ossia il linguaggio macchina del processore fisico.
Questa espressione deriva dal fatto che tale linguaggio era influenzato dall'hardware del
computer, che costringeva il programmatore a utilizzare soltanto i due simboli del sistema
binario (0 e 1) per realizzare i propri programmi, essendo questi gli unici riconosciuti dalle
componenti interne del computer.
Con il passar del tempo ci si è resi conto che programmare in questo modo era complesso
e spesso si commettevano errori. Nasceva, così, l'esigenza di realizzare linguaggi meno
elaborati. Il primo linguaggio simbolico fu l' assembly che introduce la seconda generazione (anni Sessanta). I linguaggi di questa generazione (la seconda), molto vicini al linguaggio macchina e anch'essi dipendenti strettamente dal tipo di computer, venivano detti
“machine oriented”, ossia linguaggi orientati alla macchina.
Con questi linguaggi le sequenze di bit (proprie del linguaggio macchina) venivano sostituite da sigle mnemoniche come, ad esempio, ADD (che significava "somma"), STA, SUB,
LDA, MOVE, scelte in modo da poter essere ricordate facilmente.
Il programma così realizzato veniva caricato in memoria. Qui doveva essere tradotto in linguaggio macchina da un particolare programma traduttore, detto assembler, presente anch'esso in memoria.
Il linguaggio assembly, pur essendo ancora "machine oriented" (orientato alla macchina,
quindi influenzati dall'hardware), cominciava ad avvicinarsi alla logica del programmatore.
Programmare in linguaggio assembly richiedeva una notevole pazienza e una grande competenza tecnica. Purtroppo, molte problematiche create dal linguaggio macchina non furono risolte. L' assembly presentava gli stessi svantaggi del linguaggio macchina. li programmatore non aveva ancora la possibilità di fare operazioni diverse da quelle previste dalla
macchina: infatti, le istruzioni scritte in questo linguaggio corrispondevano solo alle operazioni che la CPU poteva svolgere direttamente. Per queste ragioni, i linguaggi assembly
sono detti linguaggi a basso livello (o di una macchina concreta). Nonostante tutto, è proprio grazie a questo linguaggio che si attua la svolta definitiva nella storia dei linguaggi di
programmazione, grazie all'intuizione di creare un programma in grado di tradurre in codice binario le istruzioni di un altro programma.
15
Da quel momento non fu difficile progettare linguaggi non legati ad alcuna macchina
quanto, piuttosto, a una macchina astratta e, quindi, più vicini alla logica del programmatore e alle espressioni della comunicazione umana: nacquero così i l'inguaggi ad alto livello (orientati all'uomo) o linguaggi della terza generazione.
Secondo questi linguaggi, un programma è costituito da un insieme di istruzioni capaci di
modificare il contenuto della memoria del computer. In questo contesto, quindi, l'istruzione di assegnazione assume un ruolo fondamentale. Questi linguaggi vengono anche detti
linguaggi orientati al problema e sono, attualmente, tra i più diffusi per le applicazioni di
tipo gestionale e scientifico.
Naturalmente, anche i programmi scritti in linguaggio ad alto livello risultano incomprensi bili al computer. Dovranno quindi essere tradotti in codice binario. A ciò provvederanno
appositi programmi del sistema operativo, che si distinguono in compilatori e interpreti, e
che vedremo più avanti.
Successivamente, sono stati sviluppati altri linguaggi di programmazione, tendenti a offrire la possibilità di programmare anche a coloro che non hanno una cultura informatica
molto specialistica: sono i linguaggi di altissimo livello, detti anche UHLL (Ultra High Level
Language) o linguaggi della quarta generazione. La loro caratteristica principale è quella
di consentire all'utente di risolvere problemi di ogni tipo, utilizzando un linguaggio molto vicino a quello che normalmente utilizza nella propria attività.
Esempi classici di UHLL sono i fogli elettronici i linguaggi per la manipolazione delle basi
di dati (ad esempio SQL).
Un settore dell'informatica che ha affascinato per molto tempo gli studiosi è quello dell'intelligenza artificiale, che si propone di costruire sistemi per la soluzione di problemi ritenuti di competenza dell'intelletto, cercando di avvicinarsi a prestazioni di livello umano.
I linguaggi destinati a tali attività fanno parte della quinta generazione e hanno il compito
di risolvere problemi ancora esistenti nella comunicazione uomo-macchina. Tali linguaggi,
infatti, sono rivolti anche alla possibilità, da parte del computer, di utilizzare i linguaggi na turali.
A questo punto potrebbe sorgere spontanea una domanda: quale linguaggio scegliere per
risolvere un problema su un computer?
I linguaggi a basso livello trovano un impiego particolarmente conveniente nella risoluzione di quei problemi in cui la loro caratteristica di essere orientati alla macchina può essere efficacemente sfruttata. Di conseguenza, i linguaggi a basso livello possono essere utilizzati per realizzare programmi traduttori, sistemi operativi, driver di periferiche e, in genere, programmi che richiedono un elevato livello di efficienza.
Al contrario, i linguaggi ad alto livello vengono impiegati per la risoluzione di problemi ap plicativi. Questi linguaggi offrono numerosi vantaggi rispetto a quelli a basso livello.
Tra le loro caratteristiche ricordiamo:
facilità di apprendimento e d'uso (usabilità). I linguaggi ad alto livello sono relativamente vicini al linguaggio naturale e usano simboli e termini propri delle applicazioni scientifiche e commerciali;
indipendenza dalla macchina (portabilità). I programmi scritti in linguaggio ad alto
livello possono essere eseguiti su computer e sistemi operativi differenti (piattaforma);
elevata comprensibilità e modificabilità dei programmi (versatilità). I linguaggi ad
alto livello non sono orientati alla macchina e, quindi, non richiedono una suddivisione particolarmente analitica dei programmi in passi elementari.
16
Linguaggi a basso livello
Linguaggi ad alto livello
Apprendimento
non facile
Facile
Uso
non facile
Facile
Portabilità dei programmi
nulla
Buona
Comprensibilità,modificabilità e riusabilità
scarsa
Buona
9 Compilatori e Interpreti
La possibilità di programmare con linguaggi orientati all'uomo è consentita dall'esistenza
di appositi programmi traduttori.
I compilatori e gli interpreti sono programmi in grado di tradurre le istruzioni formulate in
linguaggio ad alto livello in istruzioni comprensibili al computer, quindi in linguaggio macchina.
Operano però in modo radicalmente diverso tra loro. In particolare:
i compilatori sono programmi che accettano in ingresso un programma scritto in
linguaggio ad alto livello (detto programma sorgente) e lo traducono interamente in
un programma in linguaggio macchina (detto codice eseguibile). A traduzione ultimata, il programma potrà essere eseguito;
gli interpreti sono programmi che accettano in ingresso le singole istruzioni di un
programma sorgente e le traducono una alla volta. L'interprete, quindi, opera schematicamente nel seguente modo:
◦ legge la prima istruzione;
◦ controlla la prima istruzione segnalando la presenza di eventuali errori che il pro grammatore dovrà correggere;
◦ traduce la prima istruzione e là esegue;
◦ continua così, istruzione dopo istruzione, sino al termine del programma.
Abbiamo osservato in precedenza che i due tipi di programma traduttore lavorano in
modo completamente diverso. Per avere le idee ancor più chiare, consideriamo l'analogia
con un interprete impegnato, in un congresso, a tradurre dal cinese all'italiano. Come avviene la traduzione? Essenzialmente in due modi:
se il relatore parla lentamente, fermandosi molto spesso a ogni pausa o fine di periodo, l'interprete traduce verbalmente;
se ciò non accade, l'interprete potrà registrare il discorso del relatore e, successivamente, tradurlo in forma scritta. Tale documento sarà, poi, consegnato al pubblico italiano.
Da questo semplice esempio, si evince facilmente che il secondo modo corrisponde al lavoro del compilatore. Emerge così una sostanziale caratteristica: l'output fornito dai due
programmi è diverso in quanto il compilatore, a differenza dell'interprete, fornisce un nuovo programma scritto in linguaggio macchina. Si pensi ai videogiochi (che sono, naturalmente, programmi): non si può leggere il programma in quanto sono prodotti compilati (e
non interpretati) in linguaggio macchina. Nel mondo del software, nella maggior parte dei
17
casi il codice sorgente è considerato segreto industriale e, pertanto, il produttore cede soltanto il diritto all'uso (la copia di questi programmi è infatti considerata dalla legge un rea to punibile con •sanzioni penali). La differenza di. prestazione tra interprete e compilatore
è in buona parte imputabile alle fasi di lettura e di riconoscimento di ogni istruzione.
Vantaggi
Svantaggi
Compilatore
Interprete
Traduce una sola volta e Produce un nuovo programma
avvenuta la compilazione, non
è più necessario avere il compilatore in memoria, risparmiando, così, notevole quantità di memoria
Può rilevare errori diversi rispetto all’interprete
Consente la segretezza del
programma sorgente
Il programma può essere modificato continuamente, in
modo interattivo, riducendo,
così, i tempi di debugging (ossia di correzione degli errori).
In caso di modifica del programma occorre effettuare
una nuova compilazione traduce il programma ogni volta che
deve essere eseguito
L’esecuzione del programma è
più lenta perché avviene assieme alla traduzione
Durante l’esecuzione del programma, ovviamente, l’interprete è presente in memoria
centrale
Non consente la segretezza
del programma sorgente
È chiaro che il compilatore ha qualche vantaggio in più rispetto all'interprete. Uno dei principali è rappresentato dalla velocità; pensiamo a un programma contenente un ciclo: il
compilatore traduce le istruzioni che lo compongono una sola volta, all'atto della traduzione, mentre l'interprete continuerà a tradurle tutte le volte che il ciclo dovrà essere ripetuto.
Di contro, il vantaggio dell'interprete, rispetto al compilatore, è dato dalla possibilità di modificare continuamente il programma, apportando così veloci correzioni.
I passi da eseguire per creare un file eseguibile sono i seguenti.
Scrittura del programma sorgente e memorizzazione dello stesso all'interno di un file
con estensione adeguata al linguaggio compilato
Compilazione del programma sorgente e ottenimento del programma oggetto memorizzato in un file caratterizzato dall'estensione .obj. Il compilatore, durante la fase di
traduzione del codice sorgente in codice oggetto, verifica la correttezza formale del codice sorgente e segnala la presenza di errori che impediscono la creazione del file oggetto (con un messaggio errore), oppure invia un warning quando rileva errori che consentono comunque di creare il file oggetto; i warning sono avvertimenti di situazioni
anomale che potrebbero creare problemi in fase di esecuzione. Sul programma sorgente il compilatore svolge tre tipi di analisi:
18
analisi lessicale: i caratteri del programma sorgente vengono raggruppati in identificatori, costanti, parole chiave, operatori ecc. Vengono, inoltre, riconosciuti ed eliminati i commenti;
◦ analisi sintattica: viene verificato il rispetto delle regole grammaticali del linguaggio
segnalando eventuali violazioni (errori di sintassi);
◦ analisi semantica: vengono segnalati solo alcuni evidenti errori del programmatore. Di solito alcuni linguaggi rilevano solo errori standard e banali come l'inizializzazione delle variabili.
Linking del programma oggetto con le librerie standard del linguaggio dichiarate nel
codice sorgente a opera di un particolare programma chiamato linker. Il risultato sarà
il programma eseguibile memorizzato in un file caratterizzato dall'estensione .exe.
Schematicamente, le varie fasi possono essere riassunte come in figura.
◦
19