CORSO DI FISICA TECNICA – Tecniche del COSTRUIRE
AA 20010/11
ILLUMINOTECNICA
Lezione n° 1: Natura della luce – Grandezze fotometriche
fondamentali
Corso di Fisica Tecnica – Tecniche del COSTRUIRE - Prof. Paolo ZAZZINI
AA 2010/11
Doppia natura della luce:
ONDULATORIA e CORPUSCOLARE
Teoria corpuscolare (Newton 1643-1727):
La luce è costituita da particelle piccolissime che, penetrando nell’occhio ad alta velocità, provocano la
sensazione della visione
La luce si propaga in linea retta
Spiega la riflessione con la teoria degli urti
elastici (conservazione della q.d.m.)
vx
vx
vy
vy
Non è in grado di spiegare la rifrazione
Teoria ondulatoria
Luce costituita da ONDE ELETTROMAGNETICHE:
perturbazioni periodiche nel tempo e nello spazio del campo elettromagnetico
Maxwell – 1860 Teoria dell’ELETTROMAGNETISMO
Le onde elettromagnetiche si propagano nel vuoto con la stessa velocità della luce (3x108 m/s)
Suggerendo che questo accordo non fosse casuale,
Maxwell sostenne la natura ondulatoria della luce
Corso di Fisica Tecnica – Tecniche del COSTRUIRE - Prof. Paolo ZAZZINI
AA 2010/11
Il modello ondulatorio non spiega tutti i fenomeni
Hertz 1887 - Effetto fotoelettrico – emissione di elettroni da elettrodi bombardati da fotoni, particelle di luce
L’effetto fotoelettrico è spiegabile solo con la natura corpuscolare della luce!!! (Einstein 1905)
Si fa strada di nuovo il modello corpuscolare
Luce costituita da FOTONI, particelle di massa molto piccola presenti in gran numero in un fascio
luminoso, ciascuna con un piccolo contenuto di energia
La teoria quantistica mette d’accordo i due modelli spiegando alcuni fenomeni con il modello
ondulatorio (interferenza e diffrazione) ed altri con quello corpuscolare (scambi energetici)
Teoria quantistica:
Considerando validi sia il modello corpuscolare che quello ondulatorio e mettendoli
d’accordo, permette di valutare il contenuto energetico della luce:
L’energia luminosa che si propaga non è distribuita in maniera uniforme in tutto il fronte d’onda
dell’onda e. m. ma in modo discreto, concentrata in alcuni punti secondo quantità discrete di
energia, dette quanti:
ε=hν
h : costante di Plank = 6.55 10
–27
erg sec
Corso di Fisica Tecnica – Tecniche del COSTRUIRE - Prof. Paolo ZAZZINI
AA 2010/11
Teoria ondulatoria
La luce è una radiazione elettromagnetica caratterizzata da una lunghezza d’onda λ ed una
frequenza ν.
Un’onda elettromagnetica è una perturbazione del campo elettromagnetico che si propaga in
modo periodico nel tempo e nello spazio
λ: lunghezza d’onda = distanza in metri tra due punti allo stesso valore del campo
T: periodo = tempo in secondi che intercorre tra due istanti in cui il campo assume lo stesso valore
ν: frequenza = T
–1
: inverso del periodo: numero di cicli nell’unità di tempo (s-1 = Hz)
c=λ/T=λν
Nel vuoto:
c = 3 108 m/s.
Corso di Fisica Tecnica – Tecniche del COSTRUIRE - Prof. Paolo ZAZZINI
AA 2010/11
Per descrivere i fenomeni luminosi adottiamo il modello ondulatorio con alcune semplificazioni:
Lunghezza d’onda delle radiazioni luminose molto piccola (380-780 nm) rispetto alle dimensioni medie
dei corpi con cui interagisce
Accettata l’ipotesi di propagazione in linea retta con l’approssimazione grafica dei raggi luminosi
Interazione di una radiazione luminosa con una parete
Ei = Er + Ea + Et
Ei
Et
Ei / Ei = (Er + Ea + Et) / Ei
Er
a : coefficiente di assorbimento = Ea / Ei
Ea
La riflessione può essere:
Speculare
r : coefficiente di riflessione = Er / Ei
a+r+t=1
t : coefficiente di trasmissione = Et / Ei
Diffusa
Corso di Fisica Tecnica – Tecniche del COSTRUIRE - Prof. Paolo ZAZZINI
Mista
AA 2010/11
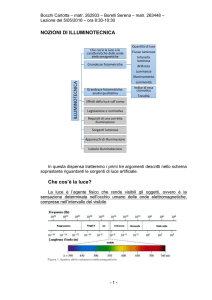
SPETTRO ELETTROMAGNETICO
10-6 nm
Raggi
cosmici
1 nm
Raggi
γ
Raggi
x
1 cm
UV
IR
Microonde
1 km
UHF VHF Onde
corte
Onde
lunghe
FINESTRA OTTICA
Radiazioni visibili
380 Violetto
Blue
Verde
Giallo
Arancio
Rosso
780 nm
Al variare della lunghezza d’onda si considerano le varie tipologie di onde elettromagnetiche che,
conservando le medesime caratteristiche, si differenziano per gli effetti che producono
Le onde visibili occupano un piccolissimo intervallo di lunghezze d’onda (FINESTRA OTTICA) compreso tra
380 e 780 nm all’interno del quale si distinguono le varie componenti cromatiche della luce.
Il prevalere di una o più componenti cromatiche sulle altre attribuisce alla luce una particolare TONALITA’
CROMATICA
Una miscela omogenea di tutte le componenti cromatiche (spettro uniforme) produce una LUCE BIANCA
La luce bianca èd detta ACROMATICA
Corso di Fisica Tecnica – Tecniche del COSTRUIRE - Prof. Paolo ZAZZINI
AA 2010/11
FENOMENO DELLA VISIONE
Determinato da fattori oggettivi:
Intensità della radiazione incidente nell’occhio
e soggettivi:
Sensibilità dell’occhio alle radiazioni visibili
CAPACITA’ VISIVE
La radiazione visiva incide sulla CORNEA (membrana
trasparente)
La lente elastica retrostante (CRISTALLINO) modifica
il raggio di curvatura mettendo a fuoco l’immagine
Le radiazioni incidenti sulla cornea vengono rifratte
verso la RETINA dove si trovano i fotoricettori
concentrati nella FOVEA
Sulla retina si produce una immagine rovesciata che
viene inviata al cervello dove viene raddrizzata
Corso di Fisica Tecnica – Tecniche del COSTRUIRE - Prof. Paolo ZAZZINI
AA 2010/11
I fotoricettori sono CONI e BASTONCELLI, 126 x 106
cellule nervose sensibili alla luce
I BASTONCELLI (120 x 106) più numerosi e più sensibili
Responsabili della visione notturna (SCOTOPICA)
caratterizzata da valori molto bassi dell’energia luminosa
I CONI (6 x 106) molto meno numerosi e meno sensibili
Responsabili della visione diurna (FOTOPICA)
caratterizzata da valori molto più elevati dell’energia
luminosa
I CONI sono di tre tipi: ROSSI, VERDI, BLUE detti colori primari
fondamentali
Ciascuna tipologia contiene fotopigmenti sensibili a diverse lunghezze
d’onda
La percezione dei colori è possibile solo con la visione FOTOPICA
La ricezione dell’immagine da parte di coni e bastoncelli avviene per
scomposizione chimica in conseguenza della quale impulsi
nervosi vengono inviati al cervello
I centri encefalici preposti decodificano il messaggio ricevuto
interpretandolo e raddrizzando l’immagine
Corso di Fisica Tecnica – Tecniche del COSTRUIRE - Prof. Paolo ZAZZINI
AA 2010/11
L’occhio umano è sensibile alla potenza radiante entrante e non all’energia come una pellicola fotografica
Un fascio luminoso entrante su una pellicola la impressiona in funzione dell’apertura dell’obiettivo e del
tempo di esposizione (energia)
Al contrario l’occhio rimane costantemente allo stesso grado di sensibilità che ha all’istante iniziale della
percezione visiva
Sensibilità dell’occhio funzione della lunghezza d’onda
QUALITATIVA: consente di distinguere le tonalità cromatiche delle varie radiazioni
QUANTITATIVA: comporta una reazione più o meno intensa alle varie lunghezze d’onda
Per avere la stessa sensazione visiva sono necessarie potenze radianti diverse alle diverse lunghezze d’onda
La sensibilità è MASSIMA al centro dello v(λ)
spettro (555 nm in visione fotopica e 510 nm in
visione scotopica ) e minima ai lati
1.0
0.9
Fotopica
Scotopica
0.8
VISIBILITA’ V(λ)
0.7
Massima al centro e minima ai lati serve a
misurare la capacità visiva dell’occhio
0.6
0.5
0.4
Coefficiente di VISIBILITA’
0.3
v(λ) = V(λ) /Vmax
0.2
Varia da 0 (a 380 e 780 nm) a 1 (al centro
dello spettro)
0.1
0.4
Corso di Fisica Tecnica – Tecniche del COSTRUIRE - Prof. Paolo ZAZZINI
0.51 0.55
0.7
AA 2010/11
λ(µm)
FLUSSO LUMINOSO
Potenza radiante emessa da una sorgente pesata con la curva di visibilità per tenere conto
della risposta dell’occhio umano e della composizione spettrale della radiazione. Si misura in
lumen (lm).
Flusso monocromatico emesso alla generica lunghezza d’onda λ:
Φ = K ⋅ v (λ ) ⋅ W (λ )
con
Flusso monocromatico emesso per λ = 555 nm
K = 683lm / W
v(λ = 555 nm) = 1
Φ = K ⋅ W (λ )
Flusso con distribuzione continua della potenza radiante tra λ1 e λ2:
λ2
λ2
λ1
λ1
Φ = ∫ K ⋅ v (λ ) ⋅ W (λ ) ⋅ dλ = K ⋅ ∫ v (λ ) ⋅ W (λ ) ⋅ dλ
Campo di emissione esteso all’intero campo di visibilità (380 ÷ 780 nm):
780
Φ = K ⋅ ∫ v (λ ) ⋅ W (λ ) ⋅ dλ
380
Corso di Fisica Tecnica – Tecniche del COSTRUIRE - Prof. Paolo ZAZZINI
AA 2010/11
INTENSITA’ LUMINOSA
Determina la distribuzione spaziale del flusso luminoso nelle varie direzioni
Hp: sorgente puntiforme
“Intensità luminosa”: rapporto tra il flusso luminoso infinitesimo e l’angolo
solido all’interno del quale tale flusso è contenuto nella generica direzione
intorno alla sorgente stessa.
Detta anche densità spaziale angolare del flusso
luminoso.
I=
dΦ
dω
S
dω =
Si misura in lm/sr = candele (cd)
dS
r2
r
E’ utile per determinare le direzioni in cui la sorgente
emette in modo prevalente ed individuare le superfici o
porzioni di superfici illuminate in modo più accentuato
dS
Radiante (rad): angolo piano al centro di una circonferenza sotteso da un arco di lunghezza pari al raggio
Steradiante (sr): angolo solido al centro di una sfera sotteso da una superficie di area paria r2
Corso di Fisica Tecnica – Tecniche del COSTRUIRE - Prof. Paolo ZAZZINI
AA 2010/11
SOLIDO FOTOMETRICO
rappresentazione vettoriale delle intensità luminose nelle varie direzioni intorno alla sorgente ripartizione spaziale del flusso luminoso.
Solido fotometrico di una lampada ad incandescenza in
coordinate polari
Angolo: direzione di emissione;
Lunghezza del raggio: valore dell’intensità in candele.
CURVA FOTOMETRICA
sezione piana del solido fotometrico
Unica curva per sorgenti ad emissione assialsimmetrica
Due o più curve in direzioni notevoli (es. longitudinale e
trasversale) per sorgenti ad emissione asimmetrica
Di solito la curva fotometrica fornisce valori in cd/klm poiché la stessa sorgente può
ospitare lampade di diversa potenza che emettono un flusso diverso
Corso di Fisica Tecnica – Tecniche del COSTRUIRE - Prof. Paolo ZAZZINI
AA 2010/11
Calcolo del flusso emesso dalla sorgente in funzione dell’intensità luminosa:
I=
dΦ
dω
⇒
dΦ = I ⋅ dω
⇒
Φ = ∫ I ⋅ dω
Ω
4π
Φ = ∫ I ⋅ dω
Emissione nell’intero spazio che circonda la sorgente:
0
Intensità luminosa costante in tutte le direzioni
nell’intero spazio intorno alla sorgente:
4π
4π
0
0
Φ = ∫ I ⋅ dω = I ⋅ ∫ dω = 4π ⋅ I
Intensità luminosa costante in tutte le direzioni
all’interno dell’angolo solido Ω:
Φ = I ⋅Ω
Da cui:
il lumen può essere definito come il flusso luminoso emesso da una sorgente
di intensità luminosa uniforme e unitaria in un angolo solido di 1 sr.
Corso di Fisica Tecnica – Tecniche del COSTRUIRE - Prof. Paolo ZAZZINI
AA 2010/11
ILLUMINAMENTO
Effetto prodotto dal flusso luminoso sulla superficie illuminata
Grandezza puntuale: varia punto per punto
S
Si definisce una dS nell’intorno del punto P sulla quale
l’illuminamento si può considerare uniforme
E=
Si misura in lux
dΦ
dS
dφ
P
dS
lm
1lux = 1 2
m
dΦ = E ⋅ dS
⇒
Φ = ∫ E ⋅ dS
S
Nel caso particolare in cui si possa considerare E uniforme sull’intera superficie S, allora si può scrivere:
Φ = E ⋅ ∫ dS = E ⋅ S ⇒ E =
S
Corso di Fisica Tecnica – Tecniche del COSTRUIRE - Prof. Paolo ZAZZINI
Φ
S
AA 2010/11
LEGGE dell’INVERSO DEL QUADRATO DELLA DISTANZA
Incidenza perpendicolare
S
dω
d
I
S: sorgente puntiforme;
I: intensità luminosa nella generica direzione (cd);
dω: angolo solido (sr) nell’intorno della direzione di emissione;
d: distanza tra sorgente e piano illuminato;
dφ: flusso luminoso contenuto in dω;
dS: superficie infinitesima sottesa da dω perpendicolarmente
alla direzione di emissione
dS = d 2 ⋅ dω ⇒ dω =
dS
d2
dS
dΦ
E=
dS
I=
dΦ dΦ 2
=
⋅ d = E ⋅ d2
dω dS
⇒
E=
I
d2
L’illuminamento prodotto da una sorgente puntiforme che emette con una intensità luminosa I in una certa
direzione su una superficie piana perpendicolare alla direzione medesima è direttamente proporzionale al
valore della intensità ed inversamente proporzionale al quadrato della distanza tra la sorgente e la superficie
considerata.
Corso di Fisica Tecnica – Tecniche del COSTRUIRE - Prof. Paolo ZAZZINI
AA 2010/11
Incidenza obliqua su piano orizzontale
E=
dΦ Iα ⋅ dω
=
=
dS
dS
Iα ⋅
S
dS ⋅ cos α
I
d2
= α2 ⋅ cos α
dS
d
d
α
Iα
dScosα
L’illuminamento prodotto da una intensità luminosa Iα su un punto di una
superficie orizzontale con incidenza obliqua è direttamente proporzionale
all’intensità luminosa per il coseno dell’angolo α che definisce la direzione
di vista ed inversamente proporzionale al quadrato della distanza tra la
sorgente ed il punto.
Incidenza obliqua su piano verticale
E=
dΦ Iα ⋅ dω
=
=
dS
dS
Iα ⋅
dS ⋅ senα
I
d2
= α2 ⋅ senα
dS
d
L’illuminamento prodotto da una intensità luminosa Iα su un punto di
una superficie verticale con incidenza obliqua è direttamente
proporzionale all’intensità luminosa per il seno dell’angolo α che
definisce la direzione di vista ed inversamente proporzionale al
quadrato della distanza tra la sorgente ed il punto.
Corso di Fisica Tecnica – Tecniche del COSTRUIRE - Prof. Paolo ZAZZINI
dS
S
α
d
Iα
dSsenα
dS
AA 2010/11
LUMINANZA
Brillanza di una superficie illuminata o di una sorgente luminosa estesa
Dipende dalla quantità di flusso luminoso uscente e dalle dimensioni della superficie
A parità di flusso riflesso o emesso una superficie piccola appare più brillante di una di maggiori dimensioni.
Tutte le sorgenti, se osservate da piccole distanze, sono da considerarsi estese, in particolare gli apparecchi
illuminanti che ospitano lampade di grosse dimensioni.
S
α
Per descrivere meglio tale sensazione si definisce:
α
“Luminanza” L il rapporto tra l’intensità luminosa nella
direzione di osservazione e la proiezione della superficie in
oggetto perpendicolarmente alla direzione di vista.
L=
Scosα
I0
Iα
Iα
S ⋅ cos α
Si misura in cd/m2 = nit
P
P’
Se la superficie S viene vista in direzione perpendicolare, si ha:
α=0 ⇒
I0
L0 =
S
Corso di Fisica Tecnica – Tecniche del COSTRUIRE - Prof. Paolo ZAZZINI
AA 2010/11
LEGGE di LAMBERT o del COSENO
Superficie riflettente o emittente (sorgente riflessa o diretta) a luminanza uniforme, indipendente
dalla direzione di vista: superficie lambertiana , da considerarsi perfettamente diffondente.
Considerata una superficie lambertiana ed indicate, rispettivamente, con L0 e con Lα le luminanze in
direzione perpendicolare e nella generica direzione di osservazione α, per quanto detto, si ha:
L0 = Lα
⇒
I0
Iα
=
⇒
S S ⋅ cos α
I 0 ⋅ S ⋅ cos α = I α ⋅ S
⇒
I α = I 0 ⋅ cos α
L’intensità luminosa emessa da una superficie lambertiana (a luminanza indipendente dalla
direzione di vista) nella generica direzione α è proporzionale alla intensità in direzione
perpendicolare I0 secondo il coseno dell’angolo α formato dalle due direzioni.
S
Curva fotometrica semicircolare:
la relazione scritta è quella esistente tra l’ipotenusa
ed il cateto di un triangolo rettangolo ed ogni
triangolo inscritto in una semicirconferenza è
rettangolo
Corso di Fisica Tecnica – Tecniche del COSTRUIRE - Prof. Paolo ZAZZINI
α
Iα
I0
AA 2010/11
Le formule scritte possono essere utilizzate per calcolare la luminanza di un corpo illuminante
nelle varie direzioni di vista quando questa non viene esplicitamente fornita dal costruttore.
Se indichiamo con Slum la luminanza di un corpo illuminante in direzione verticale verso il basso ed I0
l’intensità emessa in quella stessa direzione, si ha:
L0 =
I0
Slum
Allo stesso modo la luminanza del corpo illuminante nella direzione α va calcolata considerando la
superficie apparente dello stesso, cioè la proiezione di quella reale in direzione perpendicolare
alla direzione di vista
Lα =
Iα
S lum ⋅ cos α
Conoscendo il valore della luminanza di una sorgente per vari angoli di vista è possibile costruire una
spezzata, detta curva di luminanza della sorgente stessa, utile per verificare alcuni aspetti qualitativi
dell’impianto di illuminazione considerato.
Corso di Fisica Tecnica – Tecniche del COSTRUIRE - Prof. Paolo ZAZZINI
AA 2010/11