SPERIMENTAZIONI CON
STIRLING
IL MOTORE AD ARIA CALDA DI
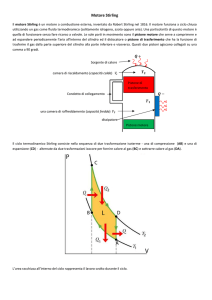
Vista complessiva del motore ad aria calda
Il motore ad aria calda (inventato da R. Stirling, 1816), assieme al motore a vapore, e’ la macchina
termica più antica. E’ una macchina termica in grado di sfruttare un ciclo termodinamico reale per
trasformare energia termica in energia meccanica.
Essa è inoltre una macchina reversibile perché, se gli viene fornita energia meccanica, può
funzionare come macchina frigorifera, assorbendo calore da un corpo freddo e trasferendolo ad un
altro corpo a temperatura maggiore del primo.
Con esso è possibile studiare la trasformazione di calore in lavoro e il trasferimento di calore da un
corpo freddo ad uno caldo a spese di energia esterna.
In particolare e’ possibile studiare e misurare il rendimento di una macchina termica.
Ciclo ideale di Stirling
Il ciclo termodinamico del motore ad aria calda deriva dal ciclo ideale di Stirling, rappresentato in
figura:1a
Esso consiste di una compressione isoterma a temperatura T 1, di un riscaldamento isocoro sino a
temperatura T 2, di una espansione isoterma alla temperatura T 2 con ritorno al volume iniziale, ed
infine di un raffreddamento isocoro che chiude il ciclo riportando la temperatura al valore più basso
T 1 ed alla pressione iniziale.
Laboratorio 2 (meccanica e termodinamica) –F.Balestra
1
1a
1b
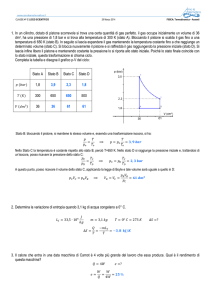
In figura e’ mostrato il ciclo di Stirling ( zona a punti) ed il ciclo di Carnot (zona tratteggiata), tra le
stesse temperature T 1 e T 2. Il teorema di Carnot afferma che il rendimento dei due cicli ideali è lo
stesso, dato che essi operano tra le stesse temperature.
Descrizione del motore di Stirling usato nelle sperimentazioni.(fig. 2)
Figura 2. Schema motore. Particolari del cilindro di vetro calibrato: nella parte inferiore intercapedine ove scorre
l’acqua di raffreddamento con i tubicini di raccordo. Pistone di spostamento: particolare dei fori assiali e delle
intercapedini radiali nella parte inferiore, attraverso i quali fluisce l’aria.
Il cilindro e’ costituito da un tubo in vetro resistente al calore e calibrato internamente con lavoro di
precisione (3). La parte inferiore del cilindro è circondata da un’ intercapedine di raffreddamento in
cui si fa scorrere acqua (4) mediante tubicini connessi agli attacchi (5) e (6).
Laboratorio 2 (meccanica e termodinamica) –F.Balestra
2
La parte superiore del cilindro(3) non è raffreddata . Nel cilindro scorrono due pistoni(1) e (2) che
sono collegati ad un eccentrico (10), imperniato sul volano (9) con dei tiranti in modo tale che il
loro movimento sia sfasato di 90 gradi. Il pistone (1)di lavoro comprime ed espande l’aria nel
cilindro. Il pistone (2)di spostamento, che ha un foro assiale, serve invece per trasferire l’aria
dalla parte superiore del cilindro alla parte inferiore dotata di raffreddamento e viceversa. Il foro
assiale del pistone è dotato di riempimento di lana di rame(7) che ha funzione di rigeneratore. Il
pistone di spostamento a differenza del pistone del lavoro nel suo spostamento non fa variare il
volume.
Una resistenza elettrica (8) fornisce l’energia termica necessaria al funzionamento della macchina
come motore. Il filamento è alimentato da un trasformatore per esperienze, il valore della potenza
elettrica di alimentazione è ottenuta dalle misure di corrente e tensione lette su di un voltmetro ed
un amperometro incorporati nell’alimentatore.
Funzionamento come motore.
Per studiare la conversione di calore in lavoro dobbiamo procurarci una trasformazione, o una serie
di trasformazioni, per mezzo delle quali si possa realizzare indefinitivamente una tale conversione
senza che questo implichi nessuna variazione nello stato del sistema.
A prima vista l’espansione isoterma di un gas ideale sembrerebbe particolarmente adatta per
discutere la trasformazione di calore in lavoro. In tale caso non c’è variazione di energia interna, dal
momento che la temperatura rimane costante si ha che W = Q , cioè del calore è stato
completamente trasformato in lavoro. Questa trasformazione tuttavia implica un cambiamento di
stato del gas. Il volume aumenta e la pressione diminuisce, fino a che raggiunge il valore
atmosferico, a questo punto la trasformazione cessa, pertanto essa non può proseguire all’infinito.
Quello che serve è una serie di trasformazioni che riportino il sistema allo stato iniziale, cioè un
ciclo.
La trasformazione di calore in lavoro si ottiene per mezzo di motori .
Un gas o una miscela di gas contenuti in un cilindro eseguono un ciclo, costringendo così il pistone
a impartire un moto di rotazione a un albero motore contro una forza esterna. E’ necessario che a
un certo punto del ciclo temperatura e pressione del gas aumentino. Nella macchina di Stirling
questo si ottiene per mezzo di una caldaia esterna.
Nel nostro caso un filamento elettrico, riscaldato per effetto Joule, serve a fornire l’energia termica
necessaria a far funzionare la macchina come motore.
Una macchina termica è quindi un dispositivo che fa percorrere ad una certa sostanza un ciclo in
direzione tale che del calore viene assorbito quando la temperatura è alta, una parte viene ceduta a
temperatura più bassa e un certo lavoro netto viene compiuto verso l’esterno
E’ impossibile realizzare una trasformazione il cui unico risultato sia quello di assorbire calore da
un serbatoio caldo e di convertirlo completamente in lavoro.(Enunciato di Kelvin-Plank)
Descriviamo le varie fasi del ciclo quando la macchina funziona come motore. Figura 3
Laboratorio 2 (meccanica e termodinamica) –F.Balestra
3
Riscaldamento Isocoro; Espansione isoterma; Raffreddamento isocoro; Compressione isoterma
V = cost.
T2 = cost
V = cost
T1 = cost
T1 T2
V aumenta
T2 T1
V aumenta
P aumenta
P diminuisce
P diminuisce
P aumenta
Rigeneratore cede calore
|Q2| assorbita
Rigeneratore assorbe calore
|Q1| ceduta
Q BC = n cv (T2 –T1)
LCD =n R T2ln(V D /V C )
QDA=n cv (T1 – T2)
LAB= n R T1ln(V A/V B)
A
B
C
D
Laboratorio 2 (meccanica e termodinamica) –F.Balestra
4
Figure 3. Descrizione delle varie fasi del ciclo del motore.
Analizziamo singolarmente le quattro fasi del ciclo.(figure 3)
Compressione isoterma (tratto AB) (d)
Il pistone superiore rimane a fine corsa trovandosi al punto morto superiore; il pistone inferiore,
muovendosi verso l’alto, comprime il gas (l’aria) e fa lavoro sul gas. Poichè esso è a contatto con le
pareti raffreddate, che funzionano da termostato, il lavoro convertito in calore |Q1| viene ceduto
all’acqua ed il processo e’ isotermico (T1 = cost).
Riscaldamento isocoro ( tratto BC) (a)
Il pistone superiore si muove verso il basso e in questo modo fa passare l’aria dalla parte inferiore
del cilindro alla parte superiore che e’ riscaldata. Fluendo attraverso il rigeneratore assorbe il calore
Q BC.
In questa fase il volume non subisce variazioni (V B = cost) mentre la pressione raggiunge il suo
valore massimo Pc, e la temperatura varia da T1 a T2.
Espansione isoterma (tratto CD) (b)
Il pistone inferiore scende ora verso il basso facendo in modo che l’aria possa assorbire calore, |Q2|,
dal filamento elettrico espandendosi isotermicamente a temperatura T2.
In questa fase l’aria riscaldata è a temperatura T2 e al valore di pressione più elevato. Essa,
espandendosi, spinge il cilindro di lavoro verso il basso che impartisce così un moto di rotazione a
un albero motore contro una forza esterna. In questo modo si genera energia meccanica che si
trasferisce al volano(fase attiva). Il naturale raffreddamento dell’aria durante l’espansione è
compensato dal calore assorbito dal filamento.
Raffreddamento isocoro ( tratto DA) ©
Il pistone superiore torna verso l’alto e l’aria passa dalla zona calda a quella fredda e, fluendo
attraverso il rigeneratore, cede il calore |Q DA | allo stesso; in questo passaggio il gas cede
praticamente lo stesso calore |Q BC | che aveva assorbito al rigeneratore durante la trasformazione
BC.
L’aria va a contatto con le pareti raffreddate del cilindro alla temperatura iniziale T1, mentre il
volume rimane costante al valore V A e la pressione diminuisce al valore iniziale P A
In definitiva:
Durante l’espansione isoterma , il pistone di lavoro riceve “una spinta” che fornisce potenza e una
coppia al volano. Durante la compressione isoterma la coppia della macchina spinge il pistone di
lavoro nell’altro verso in modo da comprimere il gas. Quando il gas è raffreddato la pressione
diminuisce, questo significa che il pistone di lavoro deve eseguire lavoro minore per ricomprimere
il gas nella “spinta di ritorno”, fornendo un guadagno netto di potenza disponibile sull’asse del
volano.
Da un punto di vista più rigoroso:
Vi e’ stato assorbimento di calore Q2 a temperatura costane T2 in una espansione isoterma; l’aria
espandendosi fa lavoro LCD = |Q2|: fase attiva.
Durante la compressione isoterma a temperatura costante più bassa T1 si fa lavoro sul gas,
LAB = |Q1|, che viene ceduta sotto forma di calore all’acqua a temperatura T1.
Non tutto il calore |Q2| assorbito dal termostato (filamento) a temperatura più alta T2 può essere
trasformato in lavoro(postulato Kelvin), una parte |Q1| durante il durante il ciclo viene restituita
all’acqua e pertanto:
L = |Q2| – |Q1 |
Il riempimento di lana di rame ( dotato di buona capacità termica) , ha funzione di assorbire calore
|QDA | dall’aria che lo attraversa provenendo dall’alto e di restituirlo all’aria che fluisce dal basso
Laboratorio 2 (meccanica e termodinamica) –F.Balestra
5
|Q BC |. In questo modo si riduce la dispersione di calore e si migliora il bilancio energetico della
macchina, aumentandone il rendimento.
Il rendimento del ciclo definito come = L / Q2 e’ pertanto <1.
Il risultato netto del ciclo e’ quello di assorbire il calore |Q2| alla temperatura T2, cedere il calore
|Q1| alla temperatura T1 (inferiore) e compiere lavoro L = |Q2| - |Q1| verso l’esterno, mentre le due
trasformazioni isocore a volume costante non implicano globalmente alcuna trasmissione di calore.
Il lavoro L e’ rappresentato nel diagramma PV dall’area compresa all’interno del ciclo, mentre il
calore Q2 assorbito e’ rappresentato dall’area sottesa alla curva che rappresenta l’espansione
isoterma a temperatura T2. Il rapporto tra queste due aree potrebbe fornire una misura del
rendimento
Q Q1
Q
L
T
2
1 1 1 1
Q2
Q2
Q2
T2
Il funzionamento del motore e’ stato descritto in modo semplificato. In realtà i due pistoni si
muovono contemporaneamente e le varie fasi di funzionamento non sono nettamente separate . Il
ciclo ideale e’ inoltre fondato sulle seguenti ipotesi: il gas e’ ideale; non si hanno perdite di gas; non
c’è trasmissione di calore attraverso le pareti del cilindro; non c’è conduzione di calore attraverso il
rigeneratore; non c’è attrito.
Il diagramma reale avrebbe l’aspetto di quello in figura 4:
Figure 4.
Il calcolo dettagliato del rendimento e’ riportato in appendice (A).
Ciclo frigorifero
Una macchina termica è un dispositivo che fa percorrere ad una certa sostanza un ciclo in direzione
tale che del calore viene assorbito quando la temperatura è alta, una parte viene ceduta a
temperatura più bassa e un certo lavoro netto viene compiuto verso l’esterno. Se supponiamo che un
tale ciclo venga percorso nel verso opposto, come risultato netto si avrà l’assorbimento di una certa
quantità di calore a bassa temperatura, la cessione di una quantità maggiore ad alta temperatura e un
certo lavoro netto compiuto sul sistema . Un dispositivo che compia un ciclo in tale direzione si
chiama un frigorifero , e la sostanza che compie il ciclo si dice refrigerante.
Funzionamento come macchina frigorifera
La testata è dotata di un giunto vetro metallo, in cui si introduce un termometro. Si connette per
mezzo di una cinghia il volano della macchina ad un motore elettrico, che fornisce l’energia
meccanica necessaria. (Figura 5)
Quando la macchina ruota in senso orario, l’aria assorbe calore dalla parte superiore della calotta
del cilindro (dove c’è anche il bulbo del termometro e il corpo da raffreddare) e la cede all’acqua di
raffreddamento che si trova a temperatura più alta.
Laboratorio 2 (meccanica e termodinamica) –F.Balestra
6
Figure 5. Vista complessiva della macchina in configurazione: ciclo frigorifero ; pompa termica
A grandi linee, il suo ciclo termodinamico ideale è formato da due trasformazioni a temperatura
costante (isotermiche) e da due a volume costante.
Nella prima fase il pistone di lavoro si sposta vesso il basso; il gas si espande assorbendo calore
dalla parte superiore della calotta del cilindro (espansione isoterma a temperatura costante) (b).
Questo produce una diminuzione della temperatura del gas misurabile per mezzo del termometro.
Nella fase successiva l’aria viene spostata verso il basso dal pistone di spostamento (c). A questo
punto l’aria, nella parte inferiore, viene compressa dal pistone di lavoro (compressione isoterma) (d)
e quindi cede calore all’acqua di raffreddamento.
Nell’ultima fase il pistone di spostamento sposta l’aria verso l’alto mentre quello di lavoro è fermo
al punto morto superiore (a).
Figura 6. Descrizione elle varie fasi del ciclo frigorifero
In definitiva l’aria assorbe calore dalla parte superiore del cilindro e la cede all’acqua di
raffreddamento che si trova a temperatura più alta.
Laboratorio 2 (meccanica e termodinamica) –F.Balestra
7
Il termometro indica la diminuzione di temperatura (introducendo una provetta con dell’acqua si
può produrre ghiacci
Il funzionamento di un frigorifero di Stirling ideale si può schematizzare in queste quattro fasi.
Figura 7. Ciclo frigorifero
12 Mentre il pistone di spostamento resta fermo quello di lavoro si alza, comprimendo il gas
isotermicamente alla temperatura H e cedendo il calore QH al serbatoio caldo. (d)
23 Il pistone spostamento si muove verso la parte calda , costringendo il gas ad attraversare il
rigeneratore e a cedergli il calore QR; il gas entra raffreddato nella parte fredda , tutta la
trasformazione ha luogo a volume costante. La pressione del gas è ridotta. (a)
34 Mentre il pistone di spostamento resta fermo, quello di lavoro si abbassa provocando una
espansione isoterma a temperatura C, durante la quale il gas assorbe il calore QC dal serbatoio
freddo. (b)
41 Il pistone di spostamento si muove verso la parte fredda, costringendo il gas a passare
attraverso il rigeneratore, il tutto a volume costante. In questo passaggio il gas assorbe praticamente
lo stesso calore QR che aveva ceduto al rigeneratore durante la trasformazione 2-3. (c)
Alla fine di questa fase il sistema è ritornato nelle condizioni iniziali e il ciclo si ripete.
QC < QH
Il lavoro fatto sul sistema è W = QH – QC
Nella fase 12 viene ceduto al serbatoio caldo la quantità di calore
QH = W + QC ( quantità di calore assorbita dal corpo freddo + lavoro fatto sul gas nella
compressione)
Non è possibile realizzare una trasformazione il cui unico risultato sia quello di fare passare del
calore da un corpo più freddo a uno più caldo.(enunciato di Clausius)
E’ sempre necessario del lavoro per fare passare del calore da un serbatoio freddo a uno caldo . Nei
frigoriferi domestici , e nel caso appena visto, questo lavoro è compiuto in generale da un motore
elettrico il cui costo di esercizio appare regolarmente sulla bolletta mensile. Sarebbe davvero
splendido dono per l’umanità se non occorresse alcuna energia esterna, ma bisogna ammettere che
l’esperienza indica il contrario.
Laboratorio 2 (meccanica e termodinamica) –F.Balestra
8
Scopo di un frigorifero e’ quello di estrarre quanto più calore e’ possibile da un serbatoio freddo
spendendo il minore lavoro possibile. La quantità che misura quanto bene il frigorifero esegue il suo
compito e’ il coefficiente di prestazione = QC / W = QC/ (QH – QC). Esso può essere molto
maggiore di 1 . Per esempio se esso vale = 5 risulta:
(QH – W) /W =5 cioè QH / W = 6. Il calore liberato alla temperatura superiore e’ sei volte il lavoro
speso W. Se il lavoro e’ fornito da un motore elettrico per ogni joule di energia elettrica fornita si
liberano 6 joule di calore, mentre se si dissipasse 1 joule di energia elettrica in un resistore si
potrebbe avere al massimo 1 joule di calore. E’ assai conveniente scaldare una casa raffreddando
l’esterno; fatto già messo in evidenza per la prima volta da Lord Kelvin nel 1852. Ma solo dal 1938
circa sono apparsi sul mercato molti dispositivi, noti come “pompe di calore”, per scaldare le case
in inverno raffreddando l’esterno.
Invertendo il senso di rotazione per mezzo del regolatore, l’aria del cilindro assorbe calore
dall’acqua (che in questo caso ha la funzione di sorgente di calore) e lo trasferisce alla parte
superiore del cilindro che tende a riscaldarsi di più. Questo modo viene anche detto funzionamento
a pompa termica.
In entrambi i casi la macchina funziona come macchina frigorifera, assorbe calore da un corpo
freddo cedendolo ad uno caldo.
Figura 8 . Descrizione delle fasi di funzionamento come pompa termica
Laboratorio 2 (meccanica e termodinamica) –F.Balestra
9
Appendice (A)
Calcolo del rendimento del motore
Durante le isoterme viene assorbita una quantità di calore |Q2| a temperatura T2 (CD) e viene
ceduta una quantità di calore |Q1| a temperatura T1(AB), compiendo lavoro esterno L = |Q2| - |Q1|
Il calore scambiato e’ Q = dU + L ( Io principio termodinamica)
Se T =cost. dU = 0 e Q = L. dL = PdV
per un gas perfetto PV = nRT e P = nRT/V
Il lavoro fatto dal gas lungo la CD a temperatura T2 costante vale:
LCD = PdV = nRT 2 dV/V = nR T 2 ln (V D /V C ) = |Q2| calore assorbito
Il lavoro fatto sul gas, lungo AB a T1 costante vale:
LAB = PdV = nRT 1 dV/V = nR T 1 ln (V B /V A ) = |Q1| calore ceduto
Il lavoro complessivo eseguito nel ciclo e’ la somma di quelli relativi alle singole trasformazioni
L = nR T 1 ln (V B/V A )+ nR T 2 ln (V D /V C ).
Tenendo conto che V A = V D e V B = V C si ha:
L = n R (T2 –T1)ln (V D /V C )
Durante le trasformazioni isocore(V = cost.) il lavoro compiuto è nullo:
dL = PdV = 0 .
La quantità di calore scambiata è eguale alla variazione di energia interna Q = dU = n c v dT ;
cv = calore specifico de gas a volume costante.
Q BC = n cv dT = n c v (T 2 –T 1) = calore ceduto al gas dal rigeneratore
Q DA = n cv dT = n c v (T 1 – T 2) = calore assorbito dal gas dal rigeneratore
Gli scambi di calore lungo le isocore sono equali ma di segno opposto. La loro somma è nulla: non
influenzano quindi il rendimento.
Il sistema riceve calore dall’esterno durante le trasformazioni BA e DC :
Q = n cv ( T1 – T2) + n R T 2 ln (V D /V C ).
Il rendimento del motore è definito come:
= L/Q = (|Q2| -|Q1| )/(|Q2| + QBC ) = lavoro fatto dalla macchina durante il ciclo/ calore assorbito
dall’esterno.
Laboratorio 2 (meccanica e termodinamica) –F.Balestra
10
= L/Q = n R (T2 –T1)ln (V D /V C ) / [n c v ( T1 – T2) + n R T 2 ln (VD /V C )].
Rendimento che sarebbe minore di quello della macchina di Carnot. Il dispositivo del rigeneratore
ha lo scopo di incamerare il calore nella trasformazione DA per poi restituirlo , nella stessa quantità,
nella fase della trasformazione BC. Questo fatto può fare trascurare il termine
Q BC = n cv ( T 1 – T 2) nell’espressione del rendimento , che diventa:
= L/ |Q2 | = n R (T 2 –T 1)ln (V D /V C ) / nR T 2 ln (VD /V C ) = 1 – (T2 / T1 ).
Questa e’ l’espressione nota del rendimento della macchina di Carnot funzionante tra le stesse
temperature. Il ciclo ideale di Stirling approssima quello di Carnet, infatti in Stirling si hanno due
isocore lungo le quali la stessa quantità di calore prima viene assorbita dal gas, poi viene ceduta al
gas senza reale scambio di calore con l’esterno: si comportano quindi come due adiabatiche.
Misura del rendimento mediante il metodo del freno dinamometrico. (vedere i
dettagli nelle monografie)
Il rendimento della macchina si può ottenere dalla conoscenza di T 1 e T 2, oppure dal rapporto delle
due aree ottenute nel diagramma PV, l’una compresa nel ciclo (rappresentante L) e l’altra quella
sottesa dalla isoterma a temperatura T 2 (rappresentante Q2).
Nella pratica il rendimento si determina nel modo seguente.
Viene definito: = potenza meccanica / potenza elettrica assorbita
La potenza meccanica si può determinare col metodo della coppia massima facendo uso di un freno
dinamometrico.
Si pone in funzione il motore dando tensione alla resistenza ed imprimendo al volano una spinta
iniziale.
La frequenza di rotazione libera del motore si ottiene per mezzo del contagiri (Figura 10 c) che
misura il numero di giri effettuati dal motore.
Sia N = numero di giri liberi/minuto
Come primo passo si misura N ad intervalli regolari ( es: 1 minuto) sino a che N rimane circa
costante e il motore arriva a regime. Si riporta su grafico ( Fig. 10 a)l’andamento di N in funzione
del tempo. Si calcola la frequenza di rotazione a regime ( N ± N giri al minuto).
Laboratorio 2 (meccanica e termodinamica) –F.Balestra
11
Figure 10a, 10 b, 10 c
Si avvolge sull’asse del volano, nel senso di rotazione del motore, una treccia di rame o di nylon ,
ad una estremità della quale e’ collegato un dinamometro . L’altra estremità e’ tenuta ferma con la
mano, e non tirata, in modo che si possa assumere che la forza applicata a questo estremo sia nulla:
F’ = 0 ( Figura 10 b)
Tirando il dinamometro si applica alla treccia una forza F di intensità sufficiente a produrre una
piccola diminuzione della frequenza di rotazione N (es: 5-10 giri al minuto). Tale forza è la
risultante delle forze di attrito che agiscono tra la parte avvolta della treccia sul mozzo del volano ed
il mozzo stesso. Si misura F mediante il dinamometro. L’errore di sensibilità del dinamometro
fornisce l’errore di misura di F :F.
Si misura N’ il numero di giri a carico (giri al minuto) ottenendo quindi
N = N – N’
In pratica e’ conveniente misurare N a vuoto, attendere 1 minuto, applicare la forza frenante F ,
misurare N’ (giri al minuto) del motore frenato ed ottenere N .
La potenza meccanica del motore ha espressione :
P=M
M rappresenta la coppia massima del motore [N m]
= 2 n rappresenta la velocità angolare [ rad /s]
n rappresenta il numero di giri al secondo = N/60 [giri/s]
Applicando la forza frenante F si misura N’ < N
’ = 2 n’ rappresenta la velocità angolare del motore frenato [rad / s]
n’ = N’/60 giri al secondo del motore frenato.
Il momento della forza frenante rispetto all’asse di rotazione O vale:
Mf = F d/2.
d rappresenta il diametro del mozzo su cui si avvolge la treccia e d/2 il braccio della forza rispetto
ad O. Il diametro d viene misurato con un calibro.
Applicando il teorema di conservazione dell’energia la potenza massima:
P = M = M ' + (F d/2) '
è eguale alla somma della potenza ora disponibile sull’asse più la potenza dissipata dalle forze di
attrito F.
Dalla relazione precedente si ottiene:
M = M' + F d/2 ; M ( ' ) = F ' d/2; e infine la coppia massima
M = F (d/2) ’/( ') = F (d/2)N’/(N – N’)[N m]
La potenza meccanica si esprime ora come:
P = M = F (d/2)' ' ) = F (d/2) 2 N N’/(N – N’)[ watt]
Il rendimento si ottiene dalla relazione: = P/ P elettrica
La potenza elettrica PE e’ misurata con un wattmetro.
Per una data forza di frenamento F si può ripetere più volte il procedimento ottenendo diverse
coppie di valori (Ni, Ni’) .
Come valori di N ed N' si possono assumere i valori medi dei valori Ni ed N'i
Laboratorio 2 (meccanica e termodinamica) –F.Balestra
12
Si può ripetere tutto il procedimento per diversi valori di forza frenante Fj.
Per un dato valore della forza frenante F occorre calcolare:
La coppia massima : M = F (d/2) N’/(N – N’) [ N m] e l’errore M
La potenza meccanica: P = F (d/2) 2 N N’/(N – N’) [ watt] e l’errore P
Il rendimento : = P/P E e l’errore
Valutazione degli errori.
L'errore su M , P, , si ricavano mediante la propagazione degli errori. Essi vengono supposti
indipendenti.
2M = (M/N)2 2N + (M/N’)2 2N’ +(M/d)2 2d +(M/F)2 2 F
2P = (P/N)2 2N + (P/N’)2 2N’ +(P/d)2 2d +(P/F)2 2 F
2= (/P)2 2P + (/P E)2P
I dinamometri in uso di solito esprimono le forze e l’errore di sensibilità in g forza o kg forza , le
espressioni sopra riportate ( in SI) richiedono che le forze siano espresse in newton. {1 kg forza =
9.81 N}
Se si disponesse di una sola misura di N e N' come errore su N e N’ si potrebbe assumere l’errore di
sensibilità del contagiri.
Disponendo di più misure ( N i, N’i) come valori di N e N’ si possono assumere i valori medi delle
Ni , N’i e come errori 2N ,2N’ gli errori sui valori medi delle Ni ed N’i.
I valori e gli errori su M P e si possono ottenere anche valutando per ogni coppia di valore Ni, N’i
, e per un dato valore di d e F i valori Mi, Pi, ed i . Da essi si ottengono i valori medi di M , P ed
che rappresentano le migliori stime delle grandezze, e come errori gli errori sui valori medi .
Se la misura e’ ripetuta per diversi valori della forza frenante Fj per ognuna di esse si ottengono i
valori di Mj , P j , j.
Applicando, per esempio il test di Student, il confronto tra i diversi valori Mj , P j , j puo’ indicare
se essi dipendono dal carico ( forza frenante Fj). Se i valori sono consistenti , e non dipendono da
Fj, la media pesata dei diversi valori Mj , Pj , j fornisce la migliore stima delle grandezze ottenute
da tutte le misurazioni.
Laboratorio 2 (meccanica e termodinamica) –F.Balestra
13
Misura del potere refrigerante e calorifico( vedere maggiori dettagli nelle
monografie)
Figure 11
Figure 12
Per fare funzionare la macchina come macchina frigorifera si sostituisce la testata dotata di
filamento di riscaldamento con un’altra fornita di giunto vetro-metallo , in cui si può introdurre un
termometro. Si connette per mezzo di una cinghia il volano della macchina al motore che fornisce
l’energia meccanica necessaria. Un regolatore del motore può comandare la rotazione della
macchina in senso orario o antiorario. Figura(11)
Quando la macchina ruota in senso orario ( lo stesso di quando funziona come motore) l’aria
assorbe calore dalla parte superiore fredda del cilindro e lo cede all’acqua di raffreddamento che si
trova a temperatura più alta . Il termometro indica diminuzione di temperatura (ciclo frigorifero).
Invertendo il senso di rotazione per mezzo del regolatore, l’aria del cilindro assorbe calore
dall’acqua ( che in questo caso funziona come sorgente di calore) e lo trasferisce alla parte superiore
del cilindro che tende a riscaldarsi sempre di più e la temperatura rilevata dal termometro cresce (
pompa di calore).
In entrambi i casi la macchina funziona come macchina frigorifera, assorbendo calore da un corpo
freddo e cedendolo ad un corpo caldo.
Come potere calorifico e potenza refrigerante si definisce la quantità di calore sottratta o fornita alla
calotta superiore della macchina nell’unità di tempo: Q/t [ J/s o W].
La temperatura in funzione del tempo viene rilevata ad intervalli regolari ( 5 s) e riportata su di un
grafico T(t). (Figure 12, 13)
La temperatura varia in funzione del tempo: diminuisce quando la macchina funziona come ciclo
frigorifero ed aumenta quando si inverte il senso di rotazione ed essa funziona da pompa di calore.
Partendo da temperatura ambiente si fa percorre un ciclo frigorifero fino a quando la temperatura
diminuisce e si stabilizza intorno ad un dato valore minore di 0; si inverte poi il verso di rotazione e
si fa percorrere il ciclo come pompa di calore fino a quando la temperatura cresce e si stabilizza
intorno ad un dato valore maggiore di 0 , si inverte infine il verso di rotazione e si fa percorrere
ancora una volta il ciclo frigorifero.
I dati, prima riportati su un grafico T(t) ,vengono interpolati linearmente nel tratto iniziale, vicino
alla temperatura ambiente, nell’intervallo di tempo in cui non vi sono scambi rilevanti di calore tra
il sistema e l’ambiente esterno.
Laboratorio 2 (meccanica e termodinamica) –F.Balestra
14
Andamento della temperatura T in funzione del tempo
Figura 13
I valori di T/t per gli intervalli di tempo t in cui il grafico è lineare, sono proporzionali alla
quantità di calore sottratta o fornita dalla macchina nell’unita’ di tempo: Q/ t = C T/t [ W] . C
rappresenta la capacità termica .
I valori di T/ t rappresentano la pendenza b della retta che meglio interpola la serie di dati ( Ti, ti)
selezionati. Il valore del coefficiente di correlazione applicato alle coppie di valori (Ti, ti) può
fornire l’indicazione se tale serie di punti sono correlati linearmente. Il metodo dei minimi
quadrati applicato alla serie di valori (Ti ± Ti, ti) fornisce i parametri a ± a , b ± b della
funzione lineare :T = a + b t. Il test 2 permette di controllare se l’andamento lineare e’ corretto.
Come errore sui valori Ti si può assumere l’errore di sensibilità del termometro ( 1 oC)
Per ogni ciclo percorso, in prossimità dello stesso intervallo di temperatura (ambiente) si possono
ottenere i valori: b = T/ t corrispondenti al ciclo frigorifero (bf) e calorifico (bc).
Il confronto tra i valori bc e bf ( test normale) può fornire l’informazione se i poteri calorifici e
refrigeranti della macchina in tali condizioni hanno lo stesso valore.
Tali valori sono funzione del tempo: la calotta superiore della macchina non è coibentata ed è in
collegamento termico con l’ambiente esterno cedendo o assorbendo calore da esso. Quindi la
Capacita’ C termica del sistema varia, e a parità di potenza fornita, varia di conseguenza anche
T/t.
Laboratorio 2 (meccanica e termodinamica) –F.Balestra
15
Misura del rendimento col metodo dell’area del ciclo.
Figure 14
Figure 15
Si collega un tubicino di plastica all’apposita connessione sulla biella del pistone (1) di lavoro, che
lo pone in comunicazione con l’interno del cilindro ( Figura 14 ) ad un sensore di pressione che e’
in grado di fornire la pressione dell’aria all’interno del cilindro in funzione del tempo. Al pistone
(1) di lavoro e’anche collegato con un spttile filo un sensore di spostamento , che misura lo
spostamento del pistone in funzione del tempo, e da questo , nota la sezione del motore, si misura il
volume dell’aria .
Noti P e V si puo’ ottenere il diagramma PV( Figura 15) e il ciclo del motore. Si puo’ quindi
determinare l’area all’interno del ciclo, e l’area sottesa dalla isoterma a temperatura piu’ elevata.
Esse rappresentano rispettivamente il lavoro fornito ed il calore assorbito dal motore. Il loro
rapporto fornisce il rendimento.
Si puo’ misurare il numero di giri al secondo n del volano del motore. Il prodotto di n per l’area del
ciclo, Lc, rappresenta la potenza fornita dal motore :PM = Lc n [ J/s; watt]
Il rapporto tra tale potenza P M e la potenza elettrica fornita dal filamento riscaldato P E puo’ fornire
il rendimento.
Laboratorio 2 (meccanica e termodinamica) –F.Balestra
16
Laboratorio 2 (meccanica e termodinamica) –F.Balestra
17