4033 SCIENZA DELLE FINANZE – CLEFIN
CLASSE 12
ESERCITAZIONE DEL 24 maggio 2002
1. Effetti di un’imposta sulle quantità prodotte a carico dei produttori
In equilibrio parziale ed in riferimento al bene x, si supponga di avere un’imposta
formalmente a carico dei produttori. Nel caso in cui sia la domanda sia l’offerta abbiano
elasticità finita e diversa da zero, si identifichi come si ripartisce il carico fiscale effettivo
tra produttori e consumatori.
Come si modifica l’analisi quando la domanda è perfettamente rigida?
Soluzione
Dal momento che l’imposta grava formalmente sui produttori, per ogni unità prodotta le
imprese devono pagare t lire di imposta all’erario: pertanto, i costi per le imprese
aumentano. In particolare, aumentano sia i costi totali CT = C(x), sia i costi marginali CM =
C’(x) e quindi avremo:
CT = C(x) + tx
CM = C’(x) + t
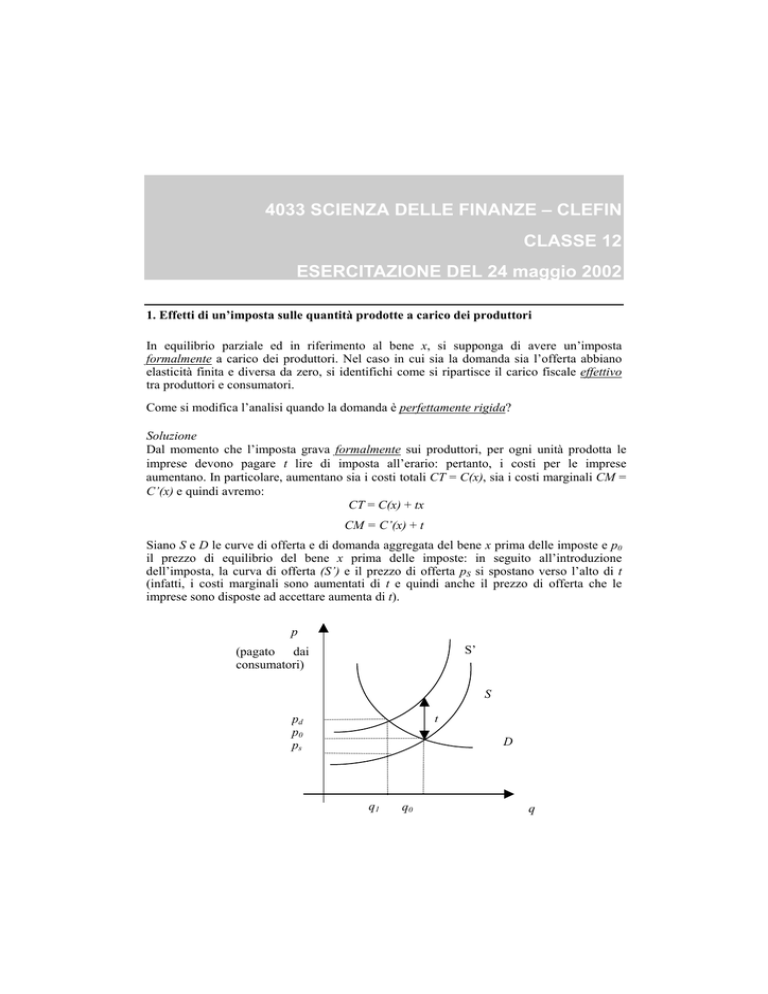
Siano S e D le curve di offerta e di domanda aggregata del bene x prima delle imposte e p0
il prezzo di equilibrio del bene x prima delle imposte: in seguito all’introduzione
dell’imposta, la curva di offerta (S’) e il prezzo di offerta pS si spostano verso l’alto di t
(infatti, i costi marginali sono aumentati di t e quindi anche il prezzo di offerta che le
imprese sono disposte ad accettare aumenta di t).
p
S’
(pagato dai
consumatori)
S
pd
p0
ps
t
D
q1
q0
q
Di conseguenza, la quantità prodotta di bene x diminuisce e il prezzo di acquisto al lordo
dell’imposta, pd, aumenta: i consumatori pagano un prezzo più alto e quindi sopportano una
parte dell’onere fiscale.
Sebbene l’imposta sia formalmente a carico dei produttori, si verifica una traslazione
dell’onere sui consumatori: come si può vedere nel grafico, non necessariamente tale
traslazione è totale. Infatti, se l’aumento del prezzo pagato dai consumatori è inferiore a t, il
prezzo al netto dell’imposta, cioè quello percepito dai produttori, ps , diminuisce: l’imposta
grava, pertanto, almeno in parte sui produttori e la traslazione è soltanto parziale.
Se la domanda è perfettamente rigida, invece, anche se in seguito all’introduzione
dell’imposta la curva di offerta S si sposta verso l’alto di t, la quantità prodotta di bene x
resta inalterata: il prezzo di acquisto lordo, pd, aumenta esattamente di t, mentre il prezzo
netto, ps, resta inalterato. In questo caso, pertanto, l’onere fiscale dal punto di vista effettivo
grava interamente sui consumatori (traslazione totale). Possiamo concludere che, a
prescindere dal contribuente de jure, la ripartizione effettiva dell’onere tra consumatori e
produttori dipende dall’elasticità delle curve di domanda e di offerta.
S’
P
(pagato dai
consumatori)
S
D
PD
t
p0 = pS
q0 = q1
q
2. Effetti di un’imposta sulle quantità prodotte a carico dei consumatori
Sia p=20-3q la curva di domanda e p=10+2q la curva di offerta di mercato relative ad un
certo bene x. Si ipotizzi di introdurre un'imposta ad valorem a carico del consumatore di
aliquota pari al 10%:
Calcolare la ripartizione dell'onere dell'imposta tra consumatore e produttore.
Soluzione
a)
Per poter stabilire la ripartizione dell’onere di imposta tra consumatore e produttore,
dobbiamo inizialmente determinare il prezzo e la quantità di equilibrio pre-imposta,
considerando l’intersezione tra la curva di domanda e quella di offerta per il bene x:
20 – 3q = 10 + 2q
q* = 2, p* = 14.
2
In seguito all’introduzione dell’imposta a carico dei consumatori, a parità di prezzo
ricevuto dai produttori, la quantità domandata dai consumatori sarà minore: la curva di
domanda si abbassa di t (= aliquota di imposta) e quindi il prezzo e la quantità di
equilibrio dopo l’imposta non sono più gli stessi di prima.
p
(ricevuto dai
produttori)
A
S
pc
H
p*
p**
B
C
t
D’
q**
D
q*
q
Infatti, la nuova curva di domanda (D’) è ora:
p(1+0,1) = 20 – 3q
e il nuovo equilibrio si avrà in corrispondenza dell’intersezione tra la curva di offerta
(S) e la nuova curva di domanda (D’):
20 – 3q = (1 + 0,1 ) ( 10 + 2q)
q** = 1,7, p** = 13,5.
p** indica il prezzo ricevuto dai produttori: il prezzo pagato dai consumatori, invece,
comprende anche l’imposta:
pc = p** (1 + 0,1) = 14,85.
Come si può notare, quindi, l’imposta non grava effettivamente soltanto sui
consumatori, ma in parte anche sui produttori: altrimenti, i consumatori avrebbero
dovuto pagare il prezzo originario aumentato di un importo pari all’imposta, cioè:
p(1 + 0,1) = 15,4.
Quindi, l’imposta grava per il 3,7% sui produttori e per il 6,3% sui consumatori.
3. Effetti delle imposte sulle decisioni individuali
Un individuo vive due periodi. Nel primo riceve un reddito pari a Y e consuma un
ammontare C1≤Y. Risparmia il resto (S) e lo investe al tasso di interesse r. Nel secondo
periodo consuma un ammontare C2, corrispondente a quanto risparmiato nel primo periodo
e al relativo interesse.
3
A) determinare algebricamente il vincolo di bilancio intertemporale dell'individuo, in
assenza di imposizione e in presenza di un’imposta proporzionale sul reddito realizzato in
ogni periodo;
B) illustrare graficamente i due vincoli di bilancio nel piano (C1,C2);
C) discutere l’effetto di un’imposta proporzionale sul reddito, mostrando gli effetti di
reddito e di sostituzione.
Soluzione:
A) Consideriamo dapprima il caso senza imposizione fiscale. Nel primo periodo
l’individuo risparmia un ammontare:
S = Y − C1 .
Nel secondo periodo consuma un ammontare pari al risparmio e agli interessi che ne ricava,
dunque:
C2 = (1 + r ) ⋅ S .
Sostituendo il valore di S si ottiene il vincolo di bilancio intertemporale dell’individuo che
mostra le possibilità di consumo nel primo e secondo periodo:
C2 = (1 + r ) ⋅ (Y − C1 ) .
Per ottenere il vincolo di bilancio intertemporale in presenza di imposte bisogna
considerare che l’individuo pagherà un’imposta con aliquota t sul reddito, Y, del primo
periodo e su quello, pari a rS, del secondo:
S = Y (1 − t ) − C1
C2 = [1 + r (1 − t )] ⋅ S
Sostituendo S si ricava il vincolo di bilancio:
C2 = [(1 + r − rt ) ⋅ (1 − t )] ⋅ Y − (1 + r − rt ) ⋅ C1 .
B) I due vincoli di bilancio definiscono due rette nel piano (C1,C2) con coefficienti angolari
pari a -(1+r) e a -(1+r-rt) rispettivamente. Il vincolo di bilancio in presenza di imposta è
dunque meno inclinato dell’altro. Inoltre, laddove il primo incontra l’asse delle ascisse in
corrispondenza di Y, il secondo lo incontra in corrispondenza di Y(1-t): l’imposta riduce
infatti di tY l’ammontare massimo di consumo effettuabile nel primo periodo. I due vincoli
sono rappresentati nel grafico da V (il vincolo senza imposta) e da Vt (quello in presenza di
imposta).
C2
V
P
N
Vc
E
Vt
G
M
O
I
F
I’
A
BC
Y(1-t)
Y
C1
C) Prima dell’introduzione dell’imposta l’individuo sceglierà una combinazione di
consumo nel primo e nel secondo periodo corrispondente al punto E, sulla curva di
indifferenza I. A seguito dell’introduzione dell’imposta il punto scelto diventa F, sulla
4
curva di indifferenza I’, associata ad un livello di utilità inferiore. Il consumo nel primo
periodo si ridurrà da OC a OB e quello nel secondo periodo da OP a OM.
L’effetto dell’imposta può essere scomposto in un effetto di reddito, dovuto al minor
reddito disponibile, e in un effetto di sostituzione, dovuto alla minore convenienza del
risparmio. Per mostrare graficamente tali effetti consideriamo un vincolo di bilancio
parallelo a quello in assenza dell’imposta tangente la curva di indifferenze I’. Tale vincolo
di bilancio, indicato con VC in figura, corrisponde a quello che si avrebbe con un’imposta
che assicurasse lo stesso livello di utilità al consumatore senza alterare la convenienza
relativa del consumo nel primo e nel secondo periodo. In tal caso il punto scelto
dall’individuo sarebbe G, con un corrispondente consumo nel primo periodo pari ad OA e
nel secondo pari a ON. I segmenti AC e PN indicano l’effetto di reddito dell’imposta, che
comporta una riduzione del consumo in tutti e due i periodi (supposto il consumo bene
“normale”). I segmenti AB e MN indicano invece l’effetto di sostituzione, che rendendo
meno attraente il risparmio, spinge ad aumentare il consumo nel primo periodo e ridurlo nel
secondo. L’effetto complessivo sul consumo nel primo periodo è ambiguo, dipendendo
dalla forza relativa di effetto di reddito e di sostituzione. Il consumo nel secondo periodo
viene invece sicuramente ridotto, visto che sia l’effetto di reddito che quello di sostituzione
agiscono nello stesso senso.
4. Imposizione indiretta sui beni
L’eccesso di pressione delle imposte indirette è causato dalla distorsione dei prezzi relativi.
E’ corretto quindi affermare che la struttura ottimale di tali imposte sia data da aliquote ad
valorem uniformi?
Si considerino due beni le cui curve di domanda compensata siano rispettivamente:
p a = 10(q a )−1
pb = 5(qb )−2
In un contesto di equilibrio parziale, ipotizzando che i prezzi alla produzione siano fissi
(elasticità della curva di offerta infinita), se l'aliquota d'imposta applicata al bene B è pari al
7% quale deve essere l'aliquota da applicare al bene A in modo da minimizzare l'eccesso di
pressione?
Soluzione
Un’imposizione indiretta uniforme si traduce in una riduzione proporzionale del potere
d’acquisto del reddito. Se ad esempio il consumatore percepisce unicamente redditi da
lavoro l’imposizione uniforme è equivalente ad un’imposta sul salario:
n
∑ (1 + t ) pi qi = wL
i =1
n
∑ pi qi =
i =1
w
L
(1 + t )
n
⇒
(1 + t )∑ pi qi = wL
⇒
i =1
n
⇒
∑ pi qi = (1 − t ')wL
i =1
con t’=t/(1+t). Quindi un’imposizione indiretta uniforme non modifica i prezzi relativi fra
beni ma distorce il prezzo relativo del tempo libero rispetto al consumo. Questa seconda
distorsione produce ovviamente un eccesso di pressione che potrebbe essere superiore a
quello prodotto da un’imposizione indiretta con aliquote differenziate. Infatti Ramsey ha
dimostrato che la struttura delle aliquote ad valorem sulle merci che minimizzano l’eccesso
di pressione dipende dalle elasticità delle curve di domanda secondo la regola:
5
~ k
ti =
ηi
dove ηi rappresenta appunto l’elasticità della domanda definita come
∂q p
η=
∂p q
L’elasticità del bene a è quindi pari a
P
1
ηa = − 10 P − 2
= − 10 P − 2
=1
10 P −1
10 P − 2
mentre per b si ha
1
ηb = −
5 − 2 −1
P
2
P
1
−
5P 2
1
= −
5 − 2 −1
P
2
1
1
− −1
5P 2
=
1
2
Per la regola di Ramsey deve valere
~
~
ta η a = tb ηb
Quindi l’aliquota ottimale per a è pari a 0,07*0,5 = 0,035. g
5. Efficienza delle imposte sul risparmio
Si consideri un individuo che vive per due periodi. Nel primo periodo offre lavoro
ottenendo un reddito pari a W. Il reddito guadagnato viene in parte consumato subito ed in
parte risparmiato per finanziare il consumo nel secondo periodo.
a)
Scrivere il vincolo di bilancio intertemporale.
b)
Dimostrare che l’introduzione di una imposta sul consumo con aliquota uniforme
tra i due periodi equivale ad un’imposta sul reddito da lavoro.
c)
Dimostrare che un’imposta sul consumo con aliquote differenziate fra i due
periodi equivale a sottoporre ad imposizione sia il reddito da lavoro che gli interessi.
d)
Sulla base della conclusione raggiunta al punto c) discutere, utilizzando la teoria
della imposizione ottimale sui beni, l’opportunità di sottoporre ad imposizione gli
interessi.
Soluzione
a) Il vincolo di bilancio intertemporale stabilisce che il valore attuale del consumo sui due
periodi deve essere pari al reddito guadagnato
C2
C1 +
=W .
(1 + r )
b) Con un’imposta sul consumo con aliquote uniformi il vincolo diviene
(1 + t )C1 + (1 + t ) C 2 = W
(1 + r )
che può essere scritto in maniera equivalente
C2
W
.
C1 +
=
(1 + r ) (1 + t )
Ponendo
(1 − t ') = 1 .
(1 + t )
6
possiamo scrivere
C2
C1 +
= (1 − t ')W .
(1 + r )
Quest’ultima espressione rappresenta il vincolo di bilancio in presenza di un’imposta sul
reddito da lavoro con aliquota t’. L’imposta sul consumo è quindi equivalente ad
un’imposta sul reddito da lavoro.
c) Con imposte sul consumo differenziate il vincolo di bilancio diviene
(1 + t1 )C1 + (1 + t 2 ) C 2 = W
(1 + r )
da cui
(1 + t 2 ) C 2 = W .
C1 +
(1 + t1 ) (1 + r ) (1 + t1 )
Ponendo
(1 + t 2 ) 1 e
1
=
(1 + r (1 − t r )) (1 + t1 ) (1 + r )
(1 − t ') =
1
(1 + t1 )
.
il vincolo di bilancio può essere scritto come
C2
C1 +
= (1 − t ')W .
(1 + r (1 − tr ))
Quest’ultima espressione rappresenta il vincolo di bilancio interperiodale quando gli
interessi sono assoggettati ad un’aliquota pari a tr mentre sul reddito da lavoro grava
un’aliquota pari a t’. Quindi un’imposta sul consumo con aliquote differenziate fra i due
periodi equivale a sottoporre ad imposizione sia il reddito da lavoro che gli interessi.
d) La regola di Ramsey stabilisce che aliquote uniformi minimizzano l’eccesso di pressione
solo se le elasticità delle domande dei beni considerati sono uguali tra di loro. Quindi se
l’elasticità della domanda di consumo oggi e l’elasticità della domanda di consumo domani
sono uguali fra di loro è ottimale tassare il consumo con aliquote uniformi. Come
dimostrato nel punto b) ciò equivale a tassare i soli redditi da lavoro. Se invece l’elasticità
della domanda di consumo oggi e l’elasticità della domanda di consumo domani sono
differenti, è ottimale tassare consumo oggi e consumo domani con aliquote differenziate.
Come dimostrato nel punto c) ciò equivale a tassare non solo i redditi da lavoro ma anche
gli interessi.g
6. Incidenza in un mercato concorrenziale al variare del soggetto passivo dell’imposta
Nel paese X fino all'anno t i datori di lavoro hanno pagato dei contributi sociali pari a
25.000 lire per ora di lavoro. Nell'anno t+1 il governo decide di spostare l'onere di tale
contributo sui lavoratori nella speranza di ridurre il costo del lavoro per le imprese ed
aumentare l'occupazione.
Assumendo che i mercati siano perfettamente concorrenziali, si determini in primo luogo la
variazione del salario lordo orario pagato dai datori di lavoro causata dalla manovra sotto le
due ipotesi alternative
a) l'offerta di lavoro sia infinitamente elastica.
b) l'offerta di lavoro sia rigida.
Successivamente si illustri graficamente, nel caso generale con curve di domanda ed offerta
ad elasticità finita, l'effetto di tale manovra sul livello di occupazione di equilibrio
spiegando se esso aumenta, diminuisce o rimane costante.
7
Soluzione
La teoria dell’incidenza dell’imposta in concorrenza perfetta evidenzia che gli agenti con
domande o offerte completamente rigide sopportano l’intero onere dell’imposta. Al
contrario gli agenti con domande oppure offerte completamente elastiche riescono a
traslare completamente l’imposta.
Nel caso dell’offerta di lavoro infinitamente elastica saranno i datori di lavoro a sopportare
di fatto l’intero onere dell’imposta. I lavoratori sono disposti a lavorare solo se
percepiscono un dato salario netto, diciamo pari a ω , per cui i datori di lavoro dovranno
comunque pagare un salario lordo pari a w = ω + 0,25 sia che i contributi siano
formalmente a loro carico sia che siano a carico dei lavoratori. La manovra non
modificherà quindi il salario lordo.
Nel caso di offerta di lavoro rigida i lavoratori sono disposti a ricevere qualsiasi salario pur
di lavorare un numero dato di ore in totale. I datori di lavoro sono disposti ad utilizzare
l’intera offerta di lavoro solo se pagano un salario lordo non superiore ad un particolare
valore, diciamo w . Quindi l’onere dell’imposta ricade interamente sui lavoratori che
percepiranno un salario netto pari a ω = w - 0,25. Anche in questo caso la manovra non
modificherà il salario lordo.
Nei due casi particolari presi in esame la manovra non ha quindi alcun effetto sui prezzi di
equilibrio e sull’occupazione. Questa conclusione è in realtà sempre valida in mercati
concorrenziali a prescindere dalle elasticità delle curve di domanda ed offerta. Per
dimostrarlo ricorriamo ad una rappresentazione grafica.
S'
S
S
dai
dt
t
w
w
w
w
0
w
0
w
D
(a)
L
1
L
t
D
D'
L
(b)
0
L
1
L
L
0
Le curve S e D indicano rispettivamente le curve di offerta e di domanda di lavoro in
assenza di contributi. Il livello di occupazione di equilibrio è L0 ed il salario lordo, w0,
coincide con il salario netto. La figura (b) rappresenta l’equilibrio di mercato con dei
contributi pari a t a carico dei datori di lavoro. Sulle ordinate viene rappresentato il salario
netto. Rispetto alla situazione di assenza di contributi la curva di domanda di lavoro si
sposta verso il basso in quanto per assicurare un certo salario netto i datori di lavoro
devono pagare un salario lordo superiore. L’onere dell’imposta si distribuisce fra
lavoratori, che pagano w - w0, e lavoratori, che pagano w0 - ω, producendo una riduzione
dell’occupazione da L0 a L1.
Nella figura (a) viene rappresentato invece l’equilibrio con i contributi a carico dei
lavoratori. Sulle ordinate viene ora rappresentato il salario lordo per cui la curva di offerta
si sposta verso l’alto. Infatti la presenza dei contributi induce una riduzione dell’offerta di
8
lavoro per ogni livello di salario lordo. Dal confronto delle due figure si può verificare che
se l’ammontare dei contributi orari è uguale, i salari netti e lordi di equilibrio ed il livello di
occupazione coincidono nei due casi. Possiamo concludere che gli effetti economici di un
tributo in concorrenza perfetta non dipendono dall’identità del contribuente de jure. g
7. Incidenza di un’imposta sui profitti in monopolio
Il meccanismo del credito d’imposta viene spesso giustificato richiamando la necessità di
rimborsare al percettore del dividendo l’Irpeg pagata a monte dalla società. Si discuta tale
argomentazione con riferimento ad una società che opera in regime di monopolio ed
assumendo che l’Irpeg possa essere equiparata ad un’imposta sui profitti.
Soluzione
profitto (π)
Se la proprietà della società controlla direttamente la gestione è ragionevole supporre che le
scelte di produzione verranno prese con l’obiettivo di massimizzare il profitto. In assenza
di imposte il profitto ottenibile per vari livelli di produzione è rappresentato dalla curva π
nella figura seguente.
π
π(1−t)
C A
π1
π2
vincolo
di profitto
B
q*
q1
q
In assenza di imposta la società sceglierà di produrre q*. Se si introduce un’imposta
proporzionale sui profitti con aliquota t, la curva di profitto si sposta verso il basso
divenendo π(1-t). La quantità che massimizza i profitti resta ancora q*. Dato che la quantità
offerta sul mercato non varia non varierà neanche il prezzo di equilibrio. Quindi i
consumatori non saranno incisi dall’imposta che ricade invece interamente sui profitti della
società. In questo caso correttamente il credito d’imposta rimborsa l’Irpeg pagata sugli utili.
Si supponga ora che la proprietà deleghi la gestione ai manager. Richiamando
l’impostazione iniziata da Baumol assumiamo che i manager siano motivati dalla
massimizzazione del fatturato (in quanto prestigio e remunerazione sono legati a tale
variabile) ma che debbano comunque garantire un livello di profitto minimo per gli
azionisti. In assenza di imposte la società produrrà in questo caso q1, ossia la quantità
massima che rispetta il vincolo di profitto. L’introduzione dell’imposta in questo caso
induce i manager a ridurre la quantità prodotta al fine di rispettare il vincolo di profitto
minimo. Dato che il profitto netto resta pari a π1 l’imposta è interamente traslata sui
consumatori (il prezzo del bene deve aumentare in quanto se ne produce di meno) e sui
fattori produttivi (le cui remunerazioni si riducono in quanto si riduce la loro domanda).
9