La circuitazione di B

Lezione VI
La circuitazione di B
1/17
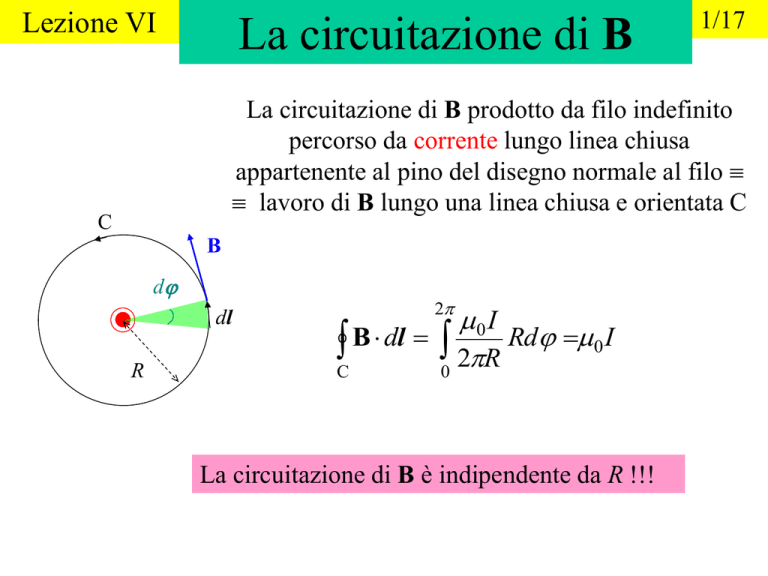
La circuitazione di B prodotto da filo indefinito
percorso da corrente lungo linea chiusa
appartenente al pino del disegno normale al filo 
 lavoro di B lungo una linea chiusa e orientata C
C
B
d
dl
R
2
0 I
 B  dl   2R Rd 0 I
C
0
La circuitazione di B è indipendente da R !!!
Lezione VI
La circuitazione di B
Il risultato vale per qualunque
linea chiusa che concatena la
corrente. Il contributo di un tratto
di C dipende solo dall’angolo d
sotto cui è vista da I
2
 B  dl  
C
0
0 I
 Rd  0 I
2R
Se C non concatena la
corrente la circuitazione di B
è nulla. L'integrale da A a B
(lungo il verso positivo di C)
è proporzionale a 0, quello
da B ad A a 0.
B
dl
R
d
C
2/17
B
B
B
d

dl
dl'
0
A
Lezione VI
3/17
La circuitazione di B
La circuitazione di B lungo una linea chiusa
C è uguale a 0 per la somma delle correnti
concatenate con C (legge di Ampère)
 B  dl  0 c IC
'
I
C
C
I3
I1
I3
I4
C
I2
'C I c  I 1  I 2
Lezione VI
La circuitazione di B
4/17
Nel caso di correnti non filiformi di densità J, la corrente
concatenata è pari al flusso di J su una qualunque superficie
appoggiata su C e orientata secondo la regola della mano destra
(dita lungo verso positivo di C, pollice nella direzione positiva della
normale ad S)
 B  dl  0  J  ndS
C
J
S
n
J
S
C
dl
B
J
n
J
Lezione VI
La circuitazione di B
5/17
La circuitazione di B lungo una linea chiusa qualunque C è sempre uguale al flusso di rotB su S con contorno C ; per il teorema di Ampère tale
circuitazione è pari al flusso per S della densità di corrente (concatenata)
 B  dl     B  n dS  0  J  ndS
C
S
Il teorema di Ampère vale se e solo se gli
integrandi degli integrali su S sono uguali
(forma puntuale del teorema di Ampère)
S
rot B    B   0 J
Ampère vale
NB. Perché l'integrale di J su S dipenda
solo dal contorno C di S è necessario che   J  0 solo se la
corrente è
Il rotore di un qualunque vettore è sempre
divrot B      B  0 solenoidale!!!
solenoidale
Lezione VI
Il campo magnetico B
J
1
Cavo conduttore cilindrico di raggio R, densità di
corrente uniforme pari a I0/R2
B
 B  ds  B  2 d   0 I (d )
 0 I (d )
B
2d
2
B
d2
d  R  I (d )  2 I 0
R
d  R  I (d )  I 0
con
0 I 0
2R
B
0
6/17
R
2R
0 I 0
d  R  B(d ) 
d (caso1)
2
2R
0 I 0
d  R  I (d ) 
(caso2)
2d
d
Lezione VI
Il campo magnetico B
La lastra indefinita di corrente con densità J e spessore s
B
l
C
z
s
y
J
J
x
B
2lB  0 slJ   B 
0 sJ
2
B è costante per distanze dalla lastra piccole rispetto
alla sua dimensione
7/17
Lezione VI
Il campo magnetico H
8/17
Solenoide indefinito con n spire di corrente I in un tratto L. Solo il campo
interno contribuisce alla circuitazione perché molto maggiore di quello
esterno. Il campo del solenoide infinito è omogeneo
Bext ~ 0
Bint l   0 nI 
I
B

Bint 
0  I  n
B
l

B
n
H
I
0
l
l
Il campo magnetico H si misura in
ampèrespira/metro
Lezione VI
9/17
Forze su correnti
B produce una forza f su un tratto di
conduttore l percorso da corrente I
(seconda legge di Laplace)
f  I  Δl  B
l lungo x, B lungo y e f lungo z)
Nord
I
l
B
Sud
f
Lezione VI
Forze su correnti
f
z
x
10/17
I
l
y
Sud
B
Nord
La forza è perpendicolare al piano individuato da l e B
Un osservatore orientato piedi-testa come f deve ruotare l
in senso antiorario di meno di 180° per sovrapporlo a B.
"regola della mano sinistra" = medio su l, indice su B, pollice su f
Lezione VI
Forze su correnti
11/17
Forze tra fili percorsi da correnti
I1
0 I1I 2
f12  I1l1  B2 
l1
2 r
I2
B2
B1
l1
f21
f12
O
P
z
B2
y
r
L’ampere di corrente è stato
definito grazie alle forze su fili
x
correnti equiverse si attirano
correnti opposte si respingono
Lezione VI
Spira di corrente in B
12/17
B
z
y
x
n
F
I
F
I
I
F
I
F
l
Spira quadrata di lato l percorsa da corrente I e normale n orientata
con la regola della mano destra. In un campo B diretto come n
ogni lato è sottoposto a una forza F=lIB diretta verso l’esterno. Le
forze si annullano a coppie e tendono ad allargare la spira e ad
aumentare il flusso di B concatenato con la spira.
Lezione VI
Spira di corrente in B
B
F  Il  B
M  Il 2n  B
z
M
y
F
x
n
I
F
I
I
I
l
Quando B è nel piano della spira (diretto come y) sui lati
paralleli a x si esercita una forza F=IlB perpendicolare al piano.
Le forze sui lati paralleli a x formano una coppia di momento
M=Il2B che tende a portare la normale n alla spira lungo B
13/17
Lezione VI
Forze su correnti
14/17
Forze tra fili percorsi da correnti
I1
f12
I2
0 I1I 2
 I1l1  B 2 
l1
2 r
B2
B1
l1
f21
f12
O
P
z
B2
y
r
L’ampere di corrente è stato
definito grazie alle forze su fili
x
correnti equiverse si attirano
correnti opposte si respingono
Lezione VI
15/17
Spira di corrente in B
La spira di corrente è libera
di ruotare lungo il suo asse
parallelo ad x ( i) in un
campo B uniforme || z
B
fb
n

fa
a
forza su lato lungo a
f a  IaBj
momento delle forze fa e fa
M   IabB sin i
fa
b
z
I
fb
y
x
Il momento delle forze fb è nullo poiché le forze hanno la stessa retta
d'azione (braccio nullo)
Lezione VI
16/17
Spira di corrente in B
Il momento magnetico della spira rettangolare della figura precedente è
mmag  Iabn  Iabcos   k  sin   j
i
j
Definizione generale del
momento delle forze  M  m mag  B  0  Iab sin 
agenti su spira
0
0
espressione precedente 
E p  mmag  B  IabB cos
k
Iab cos  
B
  IabB sin i
Energia potenziale di un dipolo


90 
90 
E p    M x d '  IabB  sin  ' d '  IabB cos
L’energia potenziale del dipolo magnetico è il lavoro del momento
cambiato di segno. Il momento di forze sul dipolo è la derivata
dell’energia potenziale rispetto a  cambiata di segno
Lezione VI
Il campo magnetico B
17/17
La spira percorsa da corrente in B
tende a ruotare/spostarsi in modo da
concatenare il massimo flusso
positivo di B.