cliccando qui

CINEMATICA
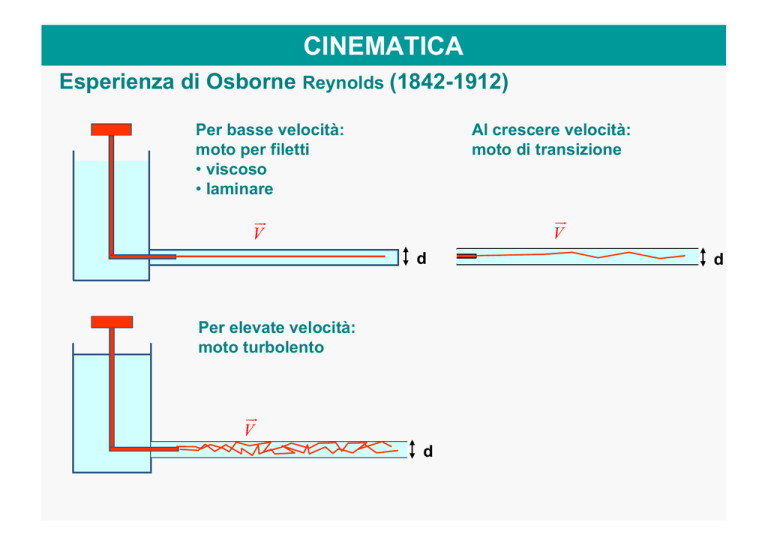
Esperienza di Osborne Reynolds (1842-1912)
Per basse velocità:
moto per filetti
• viscoso
• laminare
Al crescere velocità:
moto di transizione

V

V
d
Per elevate velocità:
moto turbolento

V
d
d
CINEMATICA
Per definire il REGIME di moto si individua il:
Numero indice di Reynolds (adimensionale)
Re 
V d V d V d

=




Re è inteso anche come:
dove:
V = velocità media [ V ] = m.s-1
 = densità
[  ] = kg/m3
d = dimensione caratteristica del moto [ d ] = m
 = viscosità dinamica [  ] = Nm-2.s
Re =
energia cinetica per unità di volume
sforzo viscoso
REGIME di moto
Moto laminare: Re < 2500
Moto di transizione: 2500 < Re < 3000
Moto turbolento: Re > 3000
CINEMATICA
La cinematica studia il campo di moto (velocità, traiettoria), mediante due
possibili approcci:
1. Metodo Lagrangiano:
- si fissa l’attenzione sulla singola particella e si segue il suo percorso nel tempo;
- si determina la velocità della particella riferita al suo baricentro
- sistema di riferimento è solidale con la particella
z0
z
P0
y0
y
P = P (P0 ,t)
x0
x
CINEMATICA
2. Metodo Euleriano:
- si fissa l’attenzione su una posizione nel campo di moto, attraverso la quale
passano le particelle, e si osserva ciò che accade in quella posizione nel tempo
- sistema di riferimento (x,y,z) è fisso
V = V (P ,t) = V (x, y, z,t) = V (x  t  , y  t  , z  t  ,t)
PRINCIPALI GRANDEZZE LINEARI DELLA CINEMATICA
Traiettoria: linea luogo geometrico dei punti che una particella, istante dopo
istante, va ad occupare. Fa riferimento al punto di vista lagrangiano
Linea di corrente o di flusso: luogo geometrico dei punti nei quali, in un
determinato istante temporale, la velocità è tangente
Linea di fumo: luogo geometrico dei punti occupati da particelle che, in un
determinato istante precedente, sono passate per un punto fisso dello spazio
Tubo di flusso: inviluppo di linee di flusso passanti per una linea chiusa
in ogni punto della superficie del tubo di flusso la velocità è tangente

n

V
DEF:
 
dQ  V  ndA
dQ  VndA

n

V
Q 
V
n
dA
A
V m e d ia
m3
Q  
s
Q
1


A
A
V
A
n
dA
Portata
elementare
Portata del tubo
flusso
Velocità media
del tubo flusso
Tipi di moto
Moto vario
 
V  V ( x, y, z, t)
e traiettoria  linea di corrente
Moto permanente
e traiettoria  linea di corrente
 
V  V ( x, y, z)
Moto uniforme

V  c o s ta n te
e traiettoria 
linea di corrente
Accelerazione
 
V  V [ x ( t ), y ( t ), z ( t ), t ]
Sia il vettore velocità:
Regola di derivazione Euleriana



  V
V
V
dV 
dt 
dx 
dy 
t
x
y




 d V
V
 V  dx   V
A




dt
t
 x  dt   y
u

V
dz
z

 dy   V  dz 




dt

z
dt




v






dV
V
V
V
V
A 

 u
 v
 w
dt
t
x
y
z
Derivata
totale
Derivata
locale
Derivata
convettiva
w
EQUAZIONE DI CONTINUITÀ IN FORMA INDEFINITA
Sia la velocità:
V  ui  v j  wk
Nell’unità di tempo:
 u dydz
Massa
entrante

  u  
dx  dydz
 u 
x


Massa
uscente
kg m
2


m
essendo:   u dydz  
m3 s
e quindi moltiplicando per dt si ottiene la massa entrante/uscente nel
tempo dt .
La differenza tra la massa uscente e quella entrante nel tempo dt è pari a:
  u 
x
dx dydzdt
se consideriamo le due facce di normale x
e analogamente si ottiene se valutiamo le coppie di
facce normali a y e z.
La variazione nel tempo dt della
massa all’interno del volumetto è:

dm  
dxdydzdt
t
La variazione della massa all’interno del volumetto nel tempo dt deve
uguagliare la differenza tra massa entrante nel volumetto e massa uscente
nello stesso tempo dt
   u     v     w 





y
z 
t
 x
     u     v     w  



0
t  x
y
z 


 div  V  0
t
 
Equazione di continuità in forma
indefinita (per fluido comprimibile)
Se fluido incomprimibile, cioè  = cost
Allora si ha:
divV  0
Equazione di continuità in forma indefinita
per fluido incomprimibile
EQUAZIONE DI CONTINUITÀ IN FORMA GLOBALE
Massa
entrante

V

n
Massa uscente
W
A

n
Integriamo l’eq. indefinita di continuità
sull’intero volume, cioè:

W
Dopo alcuni passaggi:

 
 
  t  div  V  dW  0
 
A
 
 V  ndA 

W

dW
t
Equazione globale di continuità
(per i fluidi comprimibili)
EQUAZIONE DI CONTINUITÀ IN FORMA GLOBALE

Se fluido incomprimibile, cioè  = cost, si ha:

A
V  n dA 
Alat

n

V
Ae

V

n

Ae
V  n dA 

A
Au

 V  ndA  0
V  n dA  0

n 
V
Au
Qe  Qu
Equazione globale di continuità
per i fluidi incomprimibili
EQUAZIONE DI CONTINUITÀ PER UNA CORRENTE
Se applichiamo stesso procedimento ad una corrente, alla fine si ottiene:
 (  Q )  (  A)

0
s
t
Equazione indefinita di
continuità applicata ad una
corrente
Se fluido incomprimibile,
cioè  = cost,
ed inoltre A = cost nel tempo
Q
0
s
Q  cost
lungo s, ovvero:
Qe=Qu