1
2
Fondamenti e didattica della matematica B
Geometria delle similitudini
5 marzo 2007
Marina Bertolini ([email protected])
Dipartimento di Matematica F.Enriques
Università degli Studi di Milano
Fondamenti e didattica della matematica B – p. 1
3
Fondamenti e didattica della matematica B – p. 2
4
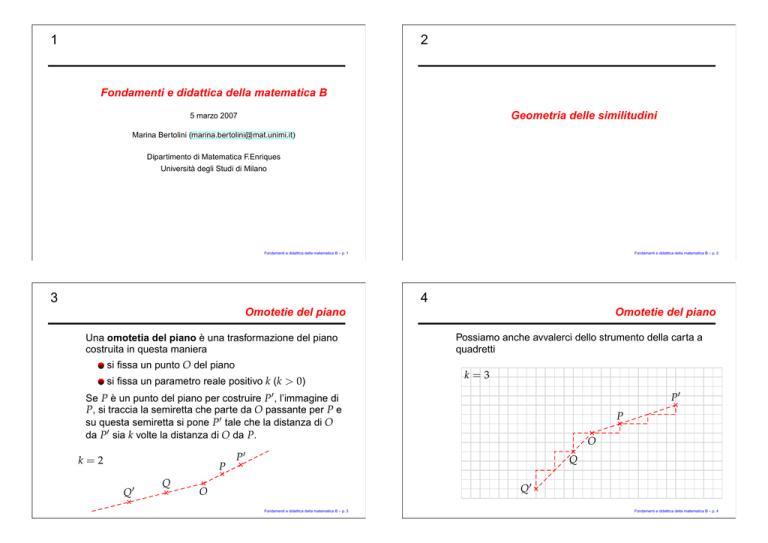
Omotetie del piano
Una omotetia del piano è una trasformazione del piano
costruita in questa maniera
si fissa un punto O del piano
si fissa un parametro reale positivo k (k > 0)
Omotetie del piano
Possiamo anche avvalerci dello strumento della carta a
quadretti
k=3
P′
Se P è un punto del piano per costruire P′ , l’immagine di
P, si traccia la semiretta che parte da O passante per P e
su questa semiretta si pone P′ tale che la distanza di O
da P′ sia k volte la distanza di O da P.
k=2
P
Q′
Q
P
O
P′
Q
Q′
O
Fondamenti e didattica della matematica B – p. 3
Fondamenti e didattica della matematica B – p. 4
5
6
Omotetie e figure geometriche
Omotetie
Se k = 1 ad ogni punto P del piano corrisponde P
stesso.
La trasformazione del piano per cui per ogni
punto P si ha f ( P) = P è detta trasformazione
identica (è anche detta identità).
Se consideriamo una figura geometrica, possiamo
pensare di applicare l’omotetia a tutti i punti della figura
k=2
Nella definizione data si è posto k > 0. Se infatti
avessimo ammesso il valore k = 0 la costruzione
geometrica descritta sarebbe ancora possibile, ma
ad ogni punto P del piano sarebbe associato il
punto O.
In questo caso non si avrebbe una
corrispondenza biunivoca.
O
Fondamenti e didattica della matematica B – p. 5
7
Fondamenti e didattica della matematica B – p. 6
8
Omotetie e figure geometriche
Se consideriamo figure geometriche più semplici non
abbiamo bisogno di applicare l’omotetia a tutti i punti
della figura
Poligoni
Analogamente se consideriamo un poligono
k=3
B′
k=2
D′
C
B
A′
L’immagine di un
segmento è un
segmento
A
O
C′
L’immagine di un
poligono è un poligono
D
O
B′
B
A
A′
I lati del poligono triplicano.
Fondamenti e didattica della matematica B – p. 7
Fondamenti e didattica della matematica B – p. 8
9
10
Omotetie
Omotetie
Considerando una omotetia di centro O e rapporto k:
Considerando una omotetia di centro O e rapporto k:
l’immagine di un segmento AB è ancora un
segmento A′ B′
la lunghezza del segmento A′ B′ è pari a k volte
la lunghezza del segmento AB
l’immagine di una retta è una retta
l’immagine di una circonferenza è una circonferenza
di lunghezza k volte la lunghezza della
circonferenza di partenza mentre l’area del
cerchio compreso è k2 volte l’area della figura di
partenza
l’immagine di un poligono è un poligono con lo
stesso numero di lati
la misura di ogni lato del poligono viene
moltiplicata per k
ne consegue che il perimetro del poligono viene
moltiplicato per k
[è
dati tre punti A, B e C, la misura dell’angolo ABC
′ B′ C′
\
uguale alla misura dell’angolo A
l’area del poligono viene moltiplicata per k2
Fondamenti e didattica della matematica B – p. 9
11
Fondamenti e didattica della matematica B – p. 10
12
Omotetie e similitudini
Le omotetie appartengono ad una classe più ampia di
trasformazioni: le similitudini.
Per le omotetie siamo stati in grado di esplicitare la
costruzione geometrica che permette (dati il punto O e la
costante reale positiva k) di costruire l’immagine di un
qualsiasi punto del piano.
Per le similitudini invece daremo una definizione astratta.
Similitudini
Definizione – Una similitudine è una trasformazione f
del piano che verifica le condizioni seguenti
Le distanze vengono mutate, ma vengono mutate in
rapporto costante. Cioè possiamo trovare un
numero k tale che se la distanza di due punti P e Q
vale TOT, allora la distanza tra i loro corrispondenti
f ( P) e f ( Q) vale k · TOT .
Gli angoli non cambiano. Cioè comunque si fissino
tre punti A, B e C, l’angolo da questi individuato è
uguale all’angolo individuato dai loro corrispondenti
f ( A ), f ( B ) e f ( C ).
Fondamenti e didattica della matematica B – p. 11
Fondamenti e didattica della matematica B – p. 12
13
14
Similitudini
Similitudini
La definizione di similitudine può quindi essere data
mettendo una delle due condizioni oppure l’altra
indistintamente.
La condizione sulle distanze è una condizione di
proporzionalità tra le misure dei segmenti.
Se abbiamo un segmento a e un segmento b, allora,
indicando con a′ e b′ le rispettive immagini, vale la
proporzione (tra le loro misure)
Dalla definizione di similitudine si possono dedurre
alcune proprietà geometriche:
a′ : a = b′ : b
se tre punti A, B e C sono allineati, allora anche
f ( A), f ( B) e f (C ) sono allineati (per la condizione
sugli angoli)
più precisamente
a′ : a = b′ : b = k
l’immagine di una retta è una retta, l’immagine di un
segmento è un segmento, . . .
Fondamenti e didattica della matematica B – p. 13
15
Fondamenti e didattica della matematica B – p. 14
16
Similitudini
Similitudini
Le isometrie sono similitudini di rapporto k = 1
Le omotetie sono similitudini
infatti le omotetie soddisfano sia la condizione sulle
distanze che la condizione sugli angoli
Si dimostra che ogni similitudine si può ottenere come
composizione di una omotetia e di una isometria.
Ci sono però similitudini che non sono omotetie.
Fondamenti e didattica della matematica B – p. 15
Fondamenti e didattica della matematica B – p. 16
17
18
Figure simili
Definizione – Due figure del piano si dicono simili se è
possibile costruire una similitudine del piano che manda
la prima figura nella seconda.
Figure simili
La geometria delle similitudini studia le proprietà in
comune a due figure simili.
Dalla definizione di figure simili, per capire quindi se due
figure sono simili occorre costruire una similitudine (di
tutto il piano) che mandi la prima figura nella seconda.
Fondamenti e didattica della matematica B – p. 17
19
Fondamenti e didattica della matematica B – p. 18
20
Quadrati
Scorciatoie
Questo a volte può sembrare un problema di non facile
soluzione.
Quello di cui abbiamo bisogno sono delle scorciatoie
che ci permettano, date due figure, di stabilire se le figure
sono simili senza costruire esplicitamente una
similitudine.
Queste scorciatoie sono dette criteri di similitudine.
Fondamenti e didattica della matematica B – p. 19
Fondamenti e didattica della matematica B – p. 20
21
22
Poligoni
Poligoni
Inoltre, se supponiamo che i due poligoni siano simili, le
proprietà delle similitudini ci dicono anche
Consideriamo due poligoni del piano. Se i due poligoni
sono simili, significa che esiste una corrispondenza
biunivoca di tutto il piano che manda il primo poligono nel
secondo.
se misuriamo l’angolo del primo poligono in A e
misuriamo l’angolo del secondo poligono in A′ ,
allora questi angoli sono uguali
e questo vale per qualunque vertice del poligono
si vada a scegliere
In particolare questa corrispondenza biunivoca di tutto il
piano farà corrispondere ad ogni vertice del primo
poligono uno e un solo vertice del secondo poligono, e
viceversa. Analogamente per i lati.
alla similitudine è associata una costante di
proporzionalità k, e questo implica che il rapporto tra
le misure dei lati
In altre parole la corrispondenza biunivoca del piano
induce una corrispondenza biunivoca tra i vertici dei due
poligoni, e tra i lati corrispondenti.
A′ B′
=k
AB
e questo vale per qualunque lato del poligono si
vada a scegliere
Fondamenti e didattica della matematica B – p. 21
23
Fondamenti e didattica della matematica B – p. 22
24
Poligoni
Abbiamo cioè concluso che se due poligoni ( ABCD . . . e
A′ B′ C′ D ′ . . . sono simili), allora
Rettangoli
Questi rettangoli sono simili?
1. gli angoli sono uguali (nel senso che l’angolo nel
vertice A è uguale all’angolo nel vertice A′ e così
via per gli altri vertici)
2. i lati sono in rapporto costante (nel senso che il
rapporto tra le misure di AB e A′ B′ è uguale al k
associato alla similitudine, e così via per gli altri lati)
ATTENZIONE: le condizioni 1 e 2 sono quindi
condizioni necessarie perché i due poligoni siano simili.
Quello che ci serve sono invece condizioni sufficienti
per stabilire che due poligoni siano simili.
Fondamenti e didattica della matematica B – p. 23
D
C
A
B
D′
C′
A′
B′
In verde abbiamo costruito una omotetia di centro A′ e
k = 2.
(NOTA: in questo esempio le lettere sono fuorvianti
rispetto al problema)
Fondamenti e didattica della matematica B – p. 24
25
26
Rettangoli
Triangoli
Due rettangoli sono simili se, detta b la base del primo
rettangolo e b′ la base del secondo rettangolo e detta h
l’altezza del primo rettangolo e h′ l’altezza del secondo
rettangolo, vale la proporzione
Anche per i triangoli abbiamo delle scorciatoie
due triangoli sono simili se esiste una
corrispondenza tra gli angoli del primo triangolo e gli
angoli del secondo tale che gli angoli corrispondenti
sono uguali
h
b
=
b′
h′
due triangoli sono simili se esiste una
corrispondenza tra i lati del primo triangolo e i lati
del secondo triangolo tale che i lati corrispondenti
sono in proporzione
CONSEGUENZA: due quadrati sono sempre simili.
due triangoli sono simili se un angolo del primo è
uguale ad un angolo del secondo e i lati adiacenti a
questi due angoli sono in proporzione
Fondamenti e didattica della matematica B – p. 25
27
Fondamenti e didattica della matematica B – p. 26
28
Triangoli rettangoli
Dati due triangoli rettangoli
Per verificare se due triangoli rettangoli sono simili (una
volta poste le “lettere” come nel lucido precedente) è
sufficiente verificare una (una soltanto!) delle condizioni
seguenti
C′
C
γ′
γ
b
A
β
α
c
a′
b′
a
B A′
Triangoli rettangoli
β = β′
γ = γ′
β′
α′
c′
B′
come possiamo stabilire se sono simili?
b′ /b = a′ /a
c′ /c = a′ /a
c′ /c = b′ /b
...
Fondamenti e didattica della matematica B – p. 27
Fondamenti e didattica della matematica B – p. 28
29
30
Triangoli rettangoli
Altre figure
Osserviamo che le condizioni di tipo
Come è possibile stabilire se le seguenti figure sono
simili?
c′ /c = b′ /b
possono essere scritte invece
b/c = b′ /c′
Questo significa che possiamo associare al primo
triangolo il numero b/c e possiamo associare al secondo
triangolo il numero b′ /c′ (questi sono infatti due numeri
che dipendono dal singolo triangolo)
e concludere che due triangoli rettangoli sono simili se e
solo se il numero che associo loro è uguale.
Fondamenti e didattica della matematica B – p. 29
31
Fondamenti e didattica della matematica B – p. 30
32
Esercizio
I seguenti triangoli sono simili.
B′
k=
Esercizio
I seguenti rombi sono simili?
A′ B′
AB
=
√
5
1
A′
C
A
C′
B
Il numero associato ad entrambi i triangoli è
A′ C ′
A′ B′
=
AC
AB
=3
Qual è il rapporto di similitudine?
Che rapporto c’è tra le aree dei due triangoli?
Fondamenti e didattica della matematica B – p. 31
La similitudine dei triangoli evidenziati garantisce la
similitudine dei rombi.
Fondamenti e didattica della matematica B – p. 32
33
34
Un gioco
Similitudini e quadrettatura
Per costruire figure simili può essere utile utilizzare
quadrettature di dimensioni differenti
Prendete un foglio di carta a quadretti, e scegliete un
punto P. Seguite quanto faccio io a video, ma
raddoppiate il numero di
quadretti rispetto a quello che
faccio io
se io vado “a destra”, voi
andate “in alto” sul vostro foglio
se io vado “in alto”, voi andate
“a sinistra”
se io vado “a sinistra”, voi
andate “in basso”
se io vado “in basso”, voi
andate “a destra”
Fondamenti e didattica della matematica B – p. 33
35
Fondamenti e didattica della matematica B – p. 34
36
Un gioco
Il gioco che abbiamo fatto, costruisce una similitudine
convincetevi del fatto che quello che abbiamo fatto è
effettivamente costruire una similitudine
Similitudini e aree
Che cosa significa l’espressione raddoppiare una figura ?
Disegniamo due rettangoli di cui uno con i lati doppi
dell’altro
costruire situazioni analoghe a questa modificando
le “regole del gioco”
3
4
1
2
L’area risulta moltiplicata per 4
Fondamenti e didattica della matematica B – p. 35
Fondamenti e didattica della matematica B – p. 36
37
Similitudini e aree
L’esempio del rettangolo riflette una situazione generale
Se due figure sono simili tramite una
similitudine di rapporto k, allora il rapporto tra le
aree delle due figure è k2
Fondamenti e didattica della matematica B – p. 37












